Algorithms Third Edition in C++ Part 5. Graph Algorithms (2006)
CHAPTER EIGHTEEN
Graph Search
18.7 Breadth-First Search
Suppose that we want to find a shortest path between two specific vertices in a graph—a path connecting the vertices with the property that no other path connecting those vertices has fewer edges. The classical method for accomplishing this task, called breadth-first search (BFS), is also the basis of numerous algorithms for processing graphs, so we consider it in detail in this section. DFS offers us little assistance in solving this problem, because the order in which it takes us through the graph has no relationship to the goal of finding shortest paths. In contrast, BFS is based on this goal. To find a shortest path from v to w, we start at v and check for w among all the vertices that we can reach by following one edge, then we check all the vertices that we can reach by following two edges, and so forth.
When we come to a point during a graph search where we have more than one edge to traverse, we choose one and save the others to be explored later. In DFS, we use a pushdown stack (that is managed by the system to support the recursive search function) for this purpose. Using the LIFO rule that characterizes the pushdown stack corresponds to exploring passages that are close by in a maze: We
Figure 18.21 Breadth-first search
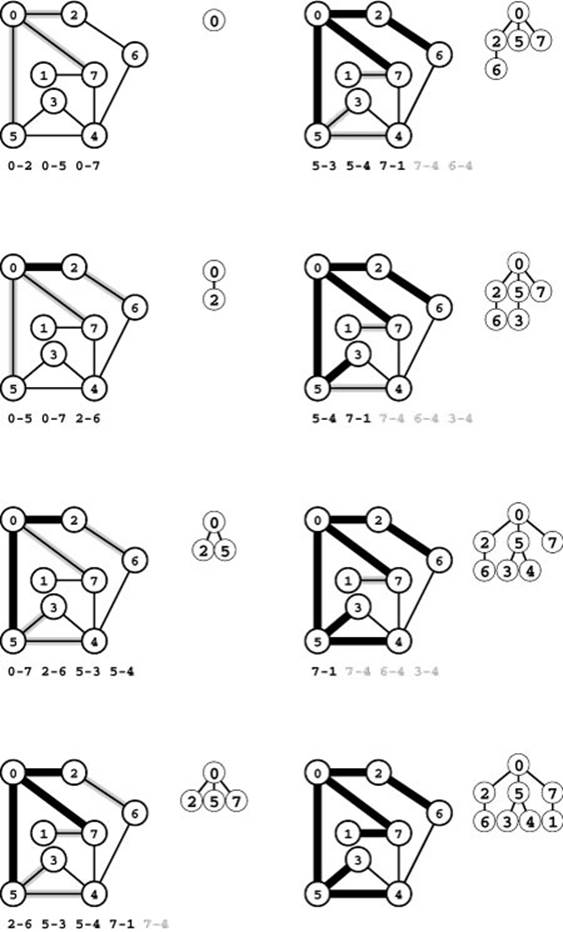
This figure traces the operation of BFS on our sample graph. We begin with all the edges adjacent to the start vertex on the queue (top left). Next, we move edge 0-2 from the queue to the tree and process its incident edges 2-0 and 2-6 (second from top, left). We do not put 2-0 on the queue because 0 is already on the tree. Third, we move edge 0-5 from the queue to the tree; again 5’s incident edge (to 0) leads nowhere new, but we add 5-3 and 5-4 to the queue (third from top, left). Next, we add 0-7 to the tree and put 7-1 on the queue (bottom left).
The edge 7-4 is printed in gray because we could also avoid putting it on the queue, since there is another edge that will take us to 4 that is already on the queue. To complete the search, we take the remaining edges off the queue, completely ignoring the gray edges when they come to the front of the queue (right). Edges enter and leave the queue in order of their distance from 0.
choose, of the passages yet to be explored, the one that was most recently encountered. In BFS, we want to explore the vertices in order of their distance from the start. For a maze, doing the search in this order might require a search team; within a computer program, however, it is easily arranged: We simply use a FIFO queue instead of a stack.
Program 18.8 is an implementation of BFS. It is based on maintaining a queue of all edges that connect a visited vertex with an unvisited vertex. We put a dummy self-loop to the start vertex on the queue, then perform the following steps until the queue is empty:
• Take edges from the queue until finding one that points to an unvisited vertex.
• Visit that vertex; put onto the queue all edges that go from that vertex to unvisited vertices.
Figure 18.21 shows the step-by-step development of BFS on a sample graph.
As we saw in Section 18.4, DFS is analogous to one person exploring a maze. BFS is analogous to a group of people exploring by fanning out in all directions. Although DFS and BFS are different in many respects, there is an essential underlying relationship between the two methods—one that we noted when we briefly considered the methods in Chapter 5. In Section 18.8, we consider a generalized graph-searching method that we can specialize to include these two algorithms and a host of others. Each algorithm has particular dynamic characteristics that we use to solve associated graph-processing problems. For BFS, the distance from each vertex to the start vertex (the length of a shortest path connecting the two) is the key property of interest.
Property 18.9 During BFS, vertices enter and leave the FIFO queue in order of their distance from the start vertex.
Proof: A stronger property holds: The queue always consists of zero or more vertices of distance k from the start, followed by zero or more vertices of distance k + 1 from the start, for some integer k. This stronger property is easy to prove by induction.
For DFS, we understood the dynamic characteristics of the algorithm with the aid of the DFS search forest that describes the recursive-call structure of the algorithm. An essential property of that forest is that the forest represents the paths from each vertex back to the place
Program 18.8 Breadth-first search
This graph-search class visits a vertex by scanning through its incident edges, putting any edges to unvisited vertices onto the queue of vertices to be visited. Vertices are marked in the visit order given by the vector ord. The search function that is called by the constructor builds an explicit parent-link representation of the BFS tree (the edges that first take us to each node) in another vector st, which can be used to solve basic shortest-paths problems (see text).

that the search started for its connected component. As indicated in the implementation and shown in Figure 18.22, such a spanning tree also helps us to understand BFS. As with DFS, we have a forest that characterizes the dynamics of the search, one tree for each connected component, one tree node for each graph vertex, and one tree edge for each graph edge. BFS corresponds to traversing each of the trees in this forest in level order. As with DFS, we use a vertex-indexed vector
Program 18.9 Improved BFS
To guarantee that the queue that we use during BFS has at most V entries, we mark the vertices as we put them on the queue.
void searchC(Edge e)
{ QUEUE<Edge> Q;
Q.put(e); ord[e.w] = cnt++;
while (!Q.empty())
{
e = Q.get(); st[e.w] = e.v;
typename Graph::adjIterator A(G, e.w);
for (int t = A.beg(); !A.end(); t = A.nxt())
if (ord[t] == -1)
{ Q.put(Edge(e.w, t)); ord[t] = cnt++; }
}
}
to represent explicitly the forest with parent links. For BFS, this forest carries essential information about the graph structure:
Property 18.10 For any node w in the BFS tree rooted at v, the tree path from v to w corresponds to a shortest path from v to w in the corresponding graph.
Proof: The tree-path lengths from nodes coming off the queue to the root are nondecreasing, and all nodes closer to the root than w are on the queue; so no shorter path to w was found before it comes off the queue, and no path to w that is discovered after it comes off the queue can be shorter than w’s tree path length. •
As indicated in Figure 18.21 and noted in Chapter 5, there is no need to put an edge on the queue with the same destination vertex as any edge already on the queue, since the FIFO policy ensures that we will process the old queue edge (and visit the vertex) before we get to the new edge. One way to implement this policy is to use a queue ADT implementation where such duplication is disallowed by an ignore-the-new-item policy (see Section 4.7). Another choice is to use the global vertex-marking vector for this purpose: Instead of marking a vertex as having been visited when we take it off the queue,
Figure 18.22 BFS tree
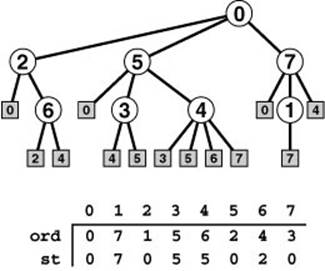
This tree provides a compact description of the dynamic properties of BFS, in a manner similar to the tree depicted in Figure 18.9. Traversing the tree in level order tells us how the search proceeds, step by step: first we visit 0; then we visit 2, 5, and 7; then we check from 2 that 0 was visited and visit 6; and so forth. Each tree node has a child representing each of the nodes adjacent to it, in the order they were considered by the BFS. As in Figure 18.9, links in the BFS tree correspond to edges in the graph: if we replace edges to external nodes by lines to the indicated node, we have a drawing of the graph. Links to external nodes represent edges that were not put onto the queue because they led to marked nodes: they are either parent links or cross links that point to a node either on the same level or one level closer to the root.
The st vector is a parent-link representation of the tree, which we can use to find a shortest path from any node to the root. For example, 3-5-0 is a path in the graph from 3 to 0, since st[3] is 5 and st[5] is 0. No other path from 3 to 0 is shorter.
we do so when we put it on the queue. Testing whether a vertex is marked (whether its entry has changed from its initial sentinel value) then stops us from putting any other edges that point to the same vertex on the queue. This change, shown in Program 18.9, gives a BFS implementation where there are never more than V edges on the queue (one edge pointing to each vertex, at most).
Property 18.11 BFS visits all the vertices and edges in a graph in time proportional to V2for the adjacency-matrix representation and to V + E for the adjacency-lists representation.
Proof: As we did in proving the analogous DFS properties, we note by inspecting the code that we check each entry in the adjacency-matrix row or in the adjacency list precisely once for every vertex that we visit, so it suffices to show that we visit each vertex. Now, for each connected component, the algorithm preserves the following invariant: All vertices that can be reached from the start vertex (i) are on the BFS tree, (ii) are on the queue, or (iii) can be reached from a vertex on the queue. Each vertex moves from (iii) to (ii) to (i), and the number of vertices in (i) increases on each iteration of the loop, so that the BFS tree eventually contains all the vertices that can be reached from the start vertex. Thus, as we did for DFS, we consider BFS to be a linear-time algorithm.
With BFS, we can solve the spanning tree, connected components, vertex search, and several other basic connectivity problems that we described in Section 18.4, since the solutions that we considered depend on only the ability of the search to examine every node and edge connected to the starting point. As we shall see, BFS and DFS are representative of numerouus algorithms that have this property. Our primary interest in BFS, as mentioned at the outset of this section, is that it is the natural graph-search algorithm for applications where we want to know a shortest path between two specified vertices. Next, we consider a specific solution to this problem and its extension to solve two related problems.
Shortest path Find a shortest path in the graph from v to w. We can accomplish this task by starting a BFS that maintains the parent-link representation st of the search tree at v, then stopping when we reach w. The path up the tree from w to v is a shortest path. For example, after construction a BFS<Graph> object bfs a client could use the following code to print the path connecting w to v:
for (t = w; t !=v; t = bfs.ST(t)) cout << t << “-”;
cout << v << endl;
To get the path from v to w, replace the cout operations in this code by stack pushes, then go into a loop that prints the vertex indices after popping them from the stack. Or, start the search at w and stop at v in the first place.
Single-source shortest paths Find shortest paths connecting a given vertex v with each other vertex in the graph. The full BFS tree rooted at v provides a way to accomplish this task: The path from each vertex to the root is a shortest path to the root. Therefore, to solve the problem, we run BFS to completion starting at v. The st vector that results from this computation is a parent-link representation of the BFS tree, and the code in the previous paragraph will give the shortest path to any other vertex w.
All-pairs shortest paths Find shortest paths connecting each pair of vertices in the graph. The way to accomplish this task is to use a BFS class that solves the single-source problem for each vertex in the graph and supports member functions that can handle huge numbers of shortest-path queries efficiently by storing the path lengths and parent-link tree representations for each vertex (see Figure 18.23). This preprocessing requires time proportional to V E and space proportional to V2, a potentially prohibitive cost for huge sparse graphs. However, it allows us to build an ADT with optimal performance: After investing in the preprocessing (and the space to hold the results), we can return shortest-path lengths in constant time and the paths themselves in time proportional to their length (see Exercise 18.55).
These BFS-based solutions are effective, but we do not consider implementations in any further detail here, because they are special cases of algorithms that we consider in detail in Chapter 21. The term shortest paths in graphs is generally taken to describe the corresponding problems for digraphs and networks. Chapter 21 is devoted to this topic. The solutions that we examine there are strict generalizations of the BFS-based solutions described here.
The basic characteristics of BFS search dynamics contrast sharply with those for DFS search, as illustrated in the large graph depicted in Figure 18.24, which you should compare with Figure 18.13. The tree
Figure 18.23 All-pairs shortest paths example
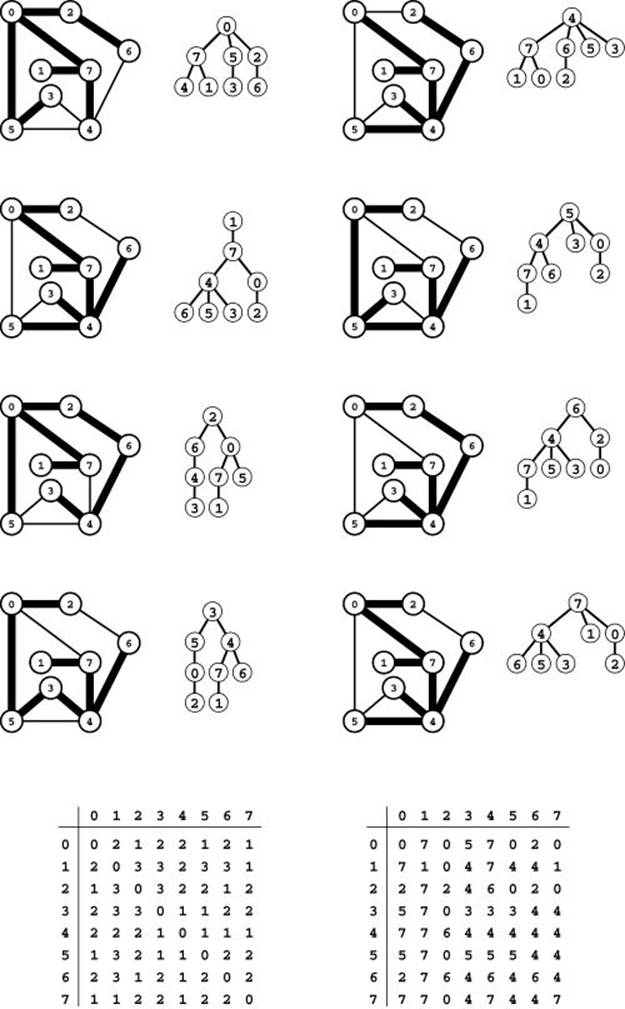
These figures depict the result of doing BFS from each vertex, thus computing the shortest paths connecting all pairs of vertices. Each search gives a BFS tree that defines the shortest paths connecting all graph vertices to the vertex at the root. The results of all the searches are summarized in the two matrices at the bottom. In the left matrix, the entry in row v and column w gives the length of the shortest path from v to w (the depth of v in w’s tree). Each row of the right matrix contains the st array for the corresponding search. For example, the shortest path from 3 to 2 has three edges, as indicated by the entry in row 3 and column 2 of the left matrix. The third BFS tree from the top on the left tells us that the path is 3-4-6-2, and this information is encoded in row 2 in the right matrix. The matrix is not necessarily symmetric when there is more than one shortest path, because the paths found depend on the BFS search order. For example, the BFS tree at the bottom on the left and row 3 of the right matrix tell us that the shortest path from 2 to 3 is 2-0-5-3.
Figure 18.24 Breadth-first search
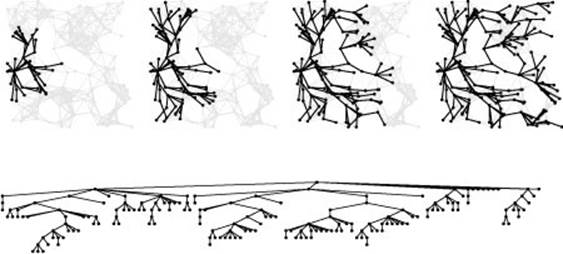
This figure illustrates the progress of BFS in random Euclidean near-neighbor graph (left), in the same style as Figure 18.13. As is evident from this example, the search tree for BFS tends to be quite short and wide for this type of graph (and many other types of graphs commonly encountered in practice). That is, vertices tend to be connected to one another by rather short paths. The contrast between the shapes of the DFS and BFS trees is striking testimony to the differing dynamic properties of the algorithms.
is shallow and broad, and demonstrates a set of facts about the graph being searched different from those shown by DFS. For example,
• There exists a relatively short path connecting each pair of vertices in the graph.
• During the search, most vertices are adjacent to numerous unvisited vertices.
Again, this example is typical of the behavior that we expect from BFS, but verifying facts of this kind for graph models of interest and graphs that arise in practice requires detailed analysis.
DFS wends its way through the graph, storing on the stack the points where other paths branch off; BFS sweeps through the graph, using a queue to remember the frontier of visited places. DFS explores the graph by looking for new vertices far away from the start point, taking closer vertices only when dead ends are encountered; BFS completely covers the area close to the starting point, moving farther away only when everything nearby has been examined. The order in which the vertices are visited depends on the graph structure and representation, but these global properties of the search trees are more informed by the algorithms than by the graphs or their representations.
The key to understanding graph-processing algorithms is to realize not only that various different search strategies are effective ways to learn various different graph properties, but also that we can implement many of them uniformly. For example, the DFS illustrated in Figure 18.13 tells us that the graph has a long path, and the BFS illustrated in Figure 18.24 tells us that it has many short paths. Despite these marked dynamic differences, DFS and BFS are similar, essentially differing in only the data structure that we use to save edges that are not yet explored (and the fortuitous circumstance that we can use a recursive implementation for DFS with the system maintaining an implicit stack for us). Indeed, we turn next to a generalized graph-search algorithm that encompasses DFS, BFS, and a host of other useful strategies and will serve as the basis for solutions to numerous classic graph-processing problems.
Exercises
18.50 Draw the BFS forest that results from a standard adjacency-lists BFS of the graph
3-7 1-4 7-8 0-5 5-2 3-8 2-9 0-6 4-9 2-6 6-4.
18.51 Draw the BFS forest that results from a standard adjacency-matrix BFS of the graph
3-7 1-4 7-8 0-5 5-2 3-8 2-9 0-6 4-9 2-6 6-4.
• 18.52 Modify Programs 18.8 and 18.9 to use an STL queue instead of the ADT from Section 4.8.
• 18.53 Give a BFS implementation (a version of Program 18.9) that uses a queue of vertices (see Program 5.22). Include a test in the BFS search code to ensure that no duplicates go on the queue.
18.54 Give the all-shortest-path matrices (in the style of Figure 18.23) for the graph
3-7 1-4 7-8 0-5 5-2 3-8 2-9 0-6 4-9 2-6 6-4,
assuming that you use the adjacency-matrix representation.
18.55 Develop a shortest-paths class, which supports shortest-path queries after preprocessing to compute all shortest paths. Specifically, define a two-dimensional matrix as a private data member, and write a constructor that assigns values to all its entries as illustrated in Figure 18.23. Then, implement two query functions length(v, w) (that returns the shortest-path length between v and w) and path(v, w) (that returns the vertex adjacent to v that is on a shortest path between v and w).
• 18.56 What does the BFS tree tell us about the distance from v to w when neither is at the root?
18.57 Develop a class whose objects know the path length that suffices to connect any pair of vertices in a graph. (This quantity is known as the graph’s diameter). Note: You need to define a convention for the return value in the case that the graph is not connected.
18.58 Give a simple optimal recursive algorithm for finding the diameter of a tree (see Exercise 18.57).
• 18.59 Instrument the BFS class Program 18.9 by adding member functions (and appropriate private data members) that return the the height of the BFS tree and the percentage of edges that must be processed for every vertex to be seen.
• 18.60 Run experiments to determine empirically the average values of the quantities described in Exercise 18.59 for graphs of various sizes, drawn from various graph models (see Exercises 17.64–76).
All materials on the site are licensed Creative Commons Attribution-Sharealike 3.0 Unported CC BY-SA 3.0 & GNU Free Documentation License (GFDL)
If you are the copyright holder of any material contained on our site and intend to remove it, please contact our site administrator for approval.
© 2016-2025 All site design rights belong to S.Y.A.