Algorithms Third Edition in C++ Part 5. Graph Algorithms (2006)
CHAPTER NINETEEN
Digraphs and DAGs
19.9 Transitive Closure Revisited
By putting together the results of the previous two sections, we can develop an algorithm to solve the abstract–transitive-closure problem for digraphs that—although it offers no improvement over a DFS-based solution in the worst case—will provide an optimal solution in many situations.
The algorithm is based on preprocessing the digraph to build the latter’s kernel DAG (see Property 19.2). The algorithm is efficient if the kernel DAG is small relative to the size of the original digraph. If the digraph is a DAG (and therefore is identical to its kernel DAG) or if it has just a few small cycles, we will not see any significant cost savings; however, if the digraph has large cycles or large strong components (and therefore a small kernel DAG), we can develop optimal or near-optimal algorithms. For clarity, we assume the kernel DAG to be sufficiently small that we can afford an adjacency-matrix representation, although the basic idea is still effective for larger kernel DAGs.
To implement the abstract transitive closure, we preprocess the digraph as follows:
• Find its strong components
• Build its kernel DAG
• Compute the transitive closure of the kernel DAG
We can use Kosaraju’s, Tarjan’s, or Gabow’s algorithm to find the strong components; a single pass through the edges to build the kernel DAG (as described in the next paragraph); and DFS (Program 19.9) to compute its transitive closure. After this preprocessing, we can immediately access the information necessary to determine reachability.
Once we have a vertex-indexed vector with the strong components of a digraph, building an adjacency-matrix representation of its kernel DAG is a simple matter. The vertices of the DAG are the component numbers in the digraph. For each edge s-t in the original digraph, we simply set D->adj[sc[s]][sc[t]] to 1. We would have to cope with duplicate edges in the kernel DAG if we were using an adjacency-lists representation—in an adjacency matrix, duplicate edges simply correspond to setting to 1 a matrix entry that has already been set to 1. This small point is significant because the number of duplicate edges is potentially huge (relative to the size of the kernel DAG) in this application.
Property 19.17 Given two vertices s and t in a digraph D, let sc ( s ) and sc ( t ) , respectively, be their corresponding vertices in D’s kernel DAG K. Then, t is reachable from s in D if and only if sc ( t ) is reachable from sc ( s ) in K.
This simple fact follows from the definitions. In particular, this property assumes the convention that a vertex is reachable from itself (all vertices have self-loops). If the vertices are in the same strong component ( sc ( s ) = sc ( t )), then they are mutually reachable.
Program 19.13 Strong-component–based transitive closure
This class implements the (abstract) transitive closure interface for di-graphs by computing the strong components (using, say Program 19.11), kernel DAG, and the transitive closure of the kernel DAG (using Program 19.9). It assumes that class SC has a public member function ID that returns the strong component index (from the id array) for any given vertex. These numbers are the vertex indices in the kernel DAG. A vertex t is reachable from a vertex s in the digraph if and only if ID(t) is reachable from ID(s) in the kernel DAG.

We determine whether a given vertex t is reachable from a given vertex s inthesamewayaswebuiltthekernelDAG:Weusethevertex-indexed vector computed by the strong-components algorithm to get the component numbers sc ( s ) and sc ( t ) (in constant time), which we interpret as abstract vertex indices for the kernel DAG. Using them as vertex indices for the transitive closure of the kernel DAG tells us the result.
Program 19.13 is an implementation of the abstract–transitive-closure ADT that embodies these ideas. We use an abstract –transitive-closure interface for the kernel DAG as well. The running time of this implementation depends not just on the number of vertices and edges in the digraph but also on properties of its kernel DAG. For purposes of analysis, we suppose that we use an adjacency-matrix representation for the kernel DAG because we expect the kernel DAG to be small, if not also dense.
Property 19.18 We can support constant query time for the abstract transitive closure of a digraph with space proportional to V + V2 and time proportional to E + V2 + vx for preprocessing (computing the transitive closure), where v is the number of vertices in the kernel DAG and x is the number of cross edges in its DFS forest.
Proof: Immediate from Property 19.13.
If the digraph is a DAG, then the strong-components computation provides no new information, and this algorithm is the same as Program 19.9; in general digraphs that have cycles, however, this algorithm is likely to be significantly faster than Warshall’s algorithm or the DFS-based solution. For example, Property 19.18 immediately implies the following result.
Property 19.19 We can support constant query time for the abstract transitive closure of any digraph whose kernel DAG has less than ![]() vertices with space proportional to V and time proportional to E + V for preprocessing.
vertices with space proportional to V and time proportional to E + V for preprocessing.
Proof:Take v < ![]() in Property 19.18 and note that x < v2.
in Property 19.18 and note that x < v2.
We might consider other variations on these bounds. For example, if we are willing to use space proportional to E, we can achieve the same time bounds when the kernel DAG has up to ![]() vertices. Moreover, these time bounds are conservative because they assume that the kernel DAG is dense with cross edges—and certainly it need not be so.
vertices. Moreover, these time bounds are conservative because they assume that the kernel DAG is dense with cross edges—and certainly it need not be so.
The primary limiting factor in the applicability of this method is the size of the kernel DAG. The more similar our digraph is to a DAG (the larger its kernel DAG), the more difficulty we face in computing its transitive closure. Note that (of course) we still have not violated the lower bound implicit in Property 19.9, since the algorithm runs in time proportional to V3 for dense DAGs; we have, however, significantly broadened the class of graphs for which we can avoid this worst-case performance. Indeed, constructing a random-digraph model that produces digraphs for which the algorithm is slow is a challenge (see Exercise 19.142).
Table 19.2 Properties of random digraphs
This table shows the numbers of edges and vertices in the kernel DAGs for random digraphs generated from two different models (the directed versions of the models in Table 18.1). In both cases, the kernel DAG becomes small (and is sparse) as the density increases.
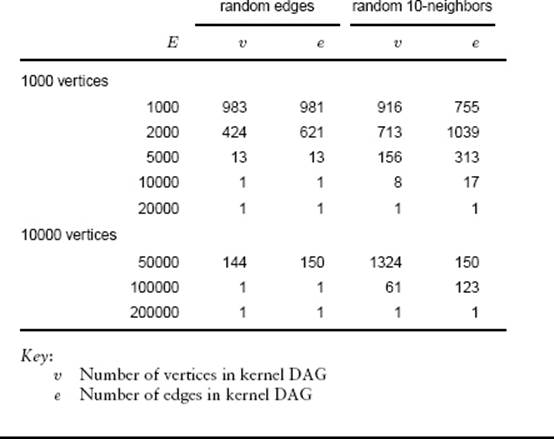
Table 19.2 displays the results of an empirical study; it shows that random digraphs have small kernel DAGs even for moderate densities and even in models with severe restrictions on edge placement. Although there can be no guarantees in the worst case, we can expect to see huge digraphs with small kernel DAGs in practice. When we do have such a digraph, we can provide an efficient implementation of the abstract–transitive-closure ADT.
Exercises
• 19.138 Develop a version of the implementation of the abstract transitive closure for digraphs based on using a sparse-graph representation of the kernel DAG. Your challenge is to eliminate duplicates on the list without using an excessive amount of time or space (see Exercise 19.65).
• 19.139 Show the kernel DAG computed by Program 19.13 and its transitive closure for the digraph
3-7 1-4 7-8 0-5 5-2 3-8 2-9 0-6 4-9 2-6 6-4.
• 19.140 Convert the strong-component–based abstract–transitive-closure implementation (Program 19.13) into an efficient program that computes the adjacency matrix of the transitive closure for a digraph represented with an adjacency matrix, using Gabow’s algorithm to compute the strong components and the improved Warshall’s algorithm to compute the transitive closure of the DAG.
19.141 Do empirical studies to estimate the expected size of the kernel DAG for various types of digraphs (see Exercises 19.11–18).
•• 19.142 Develop a random-digraph model that generates digraphs that have large kernel DAGs. Your generator must generate edges one at a time, but it must not make use of any structural properties of the resulting graph.
19.143 Develop an implementation of the abstract transitive closure in a digraph by finding the strong components and building the kernel DAG, then answering reachability queries in the affirmative if the two vertices are in the same strong component, and doing a DFS in the DAG to determine reachability otherwise.
All materials on the site are licensed Creative Commons Attribution-Sharealike 3.0 Unported CC BY-SA 3.0 & GNU Free Documentation License (GFDL)
If you are the copyright holder of any material contained on our site and intend to remove it, please contact our site administrator for approval.
© 2016-2025 All site design rights belong to S.Y.A.