Algorithms Third Edition in C++ Part 5. Graph Algorithms (2006)
CHAPTER NINETEEN
Digraphs and DAGs
19.10 Perspective
In this chapter, we have considered algorithms for solving the topological-sorting, transitive-closure, and shortest-paths problems for digraphs and for DAGs, including fundamental algorithms for finding cycles and strong components in digraphs. These algorithms have numerous important applications in their own right and also serve as the basis for the more difficult problems involving weighted graphs that we consider in the next two chapters. Worst-case running times of these algorithms are summarized in Table 19.3.
In particular, a common theme through the chapter has been the solution of the abstract–transitive-closure problem, where we wish
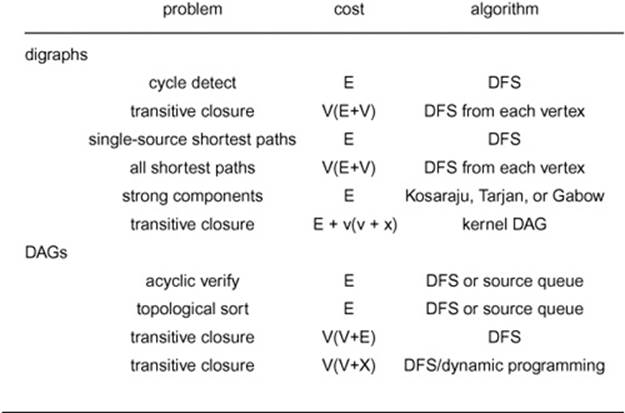
Table 19.3 Worst-case cost of digraph-processing operations
This table summarizes the cost (worst-case running time) of algorithms for various digraph-processing problems considered in this chapter, for random graphs and graphs where edges randomly connect each vertex to one of 10 specified neighbors. All costs assume use of the adjacency-list representation; for the adjacency-matrix representation the E entries become V2 entries, so, for example, the cost of computing all shortest paths is V3. The linear-time algorithms are optimal, so the costs will reliably predict the running time on any input; the others may be overly conservative estimates of cost, so the running time may be lower for certain types of graphs. Performance characteristics of the fastest algorithms for computing the transitive closure of a digraph depend on the digraph’s structure, particularly the size of its kernel DAG.
to support an ADT that can determine quickly, after preprocessing, whether there is a directed path from one given vertex to another. Despite a lower bound that implies that our worst-case preprocessing costs are significantly higher than V2, the method discussed in Section 19.7 melds the basic methods from throughout the chapter into a simple solution that provides optimal performance for many types of digraphs—the significant exception being dense DAGs. The lower bound suggests that better guaranteed performance on all graphs will be difficult to achieve, but we can use these methods to get good performance on practical graphs.
The goal of developing an algorithm with performance characteristics similar to the union-find algorithms of Chapter 1 for dense di-graphs remains elusive. Ideally, we would like to define an ADT where we can add directed edges or test whether one vertex is reachable from another and to develop an implementation where we can support all the operations in constant time (see Exercises 19.153 through 19.155). As discussed in Chapter 1, we can come close to that goal for undirected graphs, but comparable solutions for digraphs or DAGs are still not known. (Note that removing edges presents a challenge even for undirected graphs.) Not only does this dynamic reachability problem have both fundamental appeal and direct application in practice, but also it plays a critical role in the development of algorithms at a higher level of abstraction. For example, reachability lies at the heart of the problem of implementing the network simplex algorithm for the min-cost flow problem, a problem-solving model of wide applicability that we consider in Chapter 22.
Many other algorithms for processing digraphs and DAGs have important practical applications and have been studied in detail, and many digraph-processing problems still call for the development of efficient algorithms. The following list is representative.
Dominators Given a DAG with all vertices reachable from a single source r, a vertex s dominates a vertex t if every path from r to t contains s. (In particular, each vertex dominates itself.) Every vertex v other than the source has an immediate dominator that dominates v but does not dominate any dominator of v but v and itself. The set of immediate dominators is a tree that spans all vertices reachable from the source. This structure is important in compiler implementations. The dominator tree can be computed in linear time with a DFS-based approach that uses several ancillary data structures, although a slightly slower version is typically used in practice.
Transitive reduction Given a digraph, find a digraph that has the same transitive closure and the smallest number of edges among all such digraphs. This problem is tractable (see Exercise 19.150); but if we restrict it to insist that the result be a subgraph of the original graph, it is NP-hard.
Directed Euler path Given a digraph, is there a directed path connecting two given vertices that uses each edge in the digraph exactly once? This problem is easy by essentially the same arguments as for the corresponding problem for undirected graphs, which we considered in Section 17.7(see Exercise 17.92).
Directed mail carrier Given a digraph, find a directed tour with a minimal number of edges that uses every edge in the graph at least once (but is allowed to use edges multiple times). As we shall see in Section 22.7, this problem reduces to the mincost-flow problem and is therefore tractable.
Directed Hamilton path Find the longest simple directed path in a digraph. This problem is NP-hard, but it is easy if the digraph is a DAG (see Exercise 19.114).
Uniconnected subgraph A digraph is said to be uniconnected if there is at most one directed path between any pair of vertices. Given a digraph and an integer k, determine whether there is a uniconnected subgraph with at least k edges. This problem is known to be NP-hard for general k.
Feedback vertex set Decide whether a given digraph has a subset of at most k vertices that contains at least one vertex from every directed cycle in G. This problem is known to be NP-hard.
Even cycle Decide whether a given digraph has a cycle of even length. As mentioned in Section 17.8, this problem, while not intractable, is so difficult to solve that no one has yet devised an algorithm that is useful in practice.
Just as for undirected graphs, myriad digraph-processing problems have been studied, and knowing whether a problem is easy or intractable is often a challenge (see Section 17.8). As indicated throughout this chapter, some of the facts that we have discovered about digraphs are expressions of more general mathematical phenomena, and many of our algorithms have applicability at levels of abstraction different from that at which we have been working. On the one hand, the concept of intractability tells us that we might encounter fundamental roadblocks in our quest for efficient algorithms that can guarantee efficient solutions to some problems. On the other hand, the classic algorithms described in this chapter are of fundamental importance and have broad applicability, as they provide efficient solutions to problems that arise frequently in practice and would otherwise be difficult to solve.
Exercises
19.144 Adapt Programs 17.18 and 17.19 to implement an ADT function for printing an Euler path in a digraph, if one exists. Explain the purpose of any additions or changes that you need to make in the code.
• 19.145 Draw the dominator tree of the digraph
3-7 1-4 7-8 0-5 5-2 3-0 2-9 0-6 4-9 2-6
6-4 1-5 8-2 9-0 8-3 4-5 2-3 1-6 3-5 7-6.
•• 19.146 Write class that uses DFS to create a parent-link representation of the dominator tree of a given digraph ( see reference section ).
• 19.147 Find a transitive reduction of the digraph
3-7 1-4 7-8 0-5 5-2 3-0 2-9 0-6 4-9 2-6
6-4 1-5 8-2 9-0 8-3 4-5 2-3 1-6 3-5 7-6.
• 19.148 Find a subgraph of the digraph
3-7 1-4 7-8 0-5 5-2 3-0 2-9 0-6 4-9 2-6
6-4 1-5 8-2 9-0 8-3 4-5 2-3 1-6 3-5 7-6
that has the same transitive closure and the smallest number of edges among all such subgraphs.
• 19.149 Prove that every DAG has a unique transitive reduction, and give an efficient ADT function implementation for computing the transitive reduction of a DAG.
• 19.150 Write an efficient ADT function for digraphs that computes a transitive reduction.
19.151 Give an algorithm that determines whether or not a given digraph is uniconnected. Your algorithm should have a worst-case running time proportional to V E.
19.152 Find the largest uniconnected subgraph in the digraph
3-7 1-4 7-8 0-5 5-2 3-0 2-9 0-6 4-9 2-6
6-4 1-5 8-2 9-0 8-3 4-5 2-3 1-6 3-5 7-6.
• 19.153 Develop a digraph class implemention that supports inserting an edge, removing an edge, and testing whether two vertices are in the same strong component, such that construction, edge insertion, and edge removal all take linear time and strong-connectivity queries take constant time, in the worst case.
• 19.154 Solve Exercise 19.153, in such a way that edge insertion, edge removal, and strong-connectivity queries all take time proportional to log V in the worst case.
••• 19.155 Solve Exercise 19.153, in such a way that edge insertion, edge removal, and strong-connectivity queries all take near-constant time (as they do for the union-find algorithms for connectivity in undirected graphs).