Algorithms Third Edition in C++ Part 5. Graph Algorithms (2006)
CHAPTER TWENTY-TWO
Network Flow
22.7 Mincost-Flow Reductions
Mincost flow is a general problem-solving model that can encompass a variety of useful practical problems. In this section, we substantiate this claim by proving specific reductions from a variety of problems to mincost flow.
The mincost-flow problem is obviously more general than the maxflow problem, since any mincost maxflow is an acceptable solution to the maxflow problem. Specifically, if we assign to the dummy edge a cost 1 and to all other edges a cost 0 in the construction of Program 22.42, any mincost maxflow minimizes the flow in the dummy edge and therefore maximizes the flow in the original network. Therefore, all the problems discussed in Section 22.4 that reduce to the maxflow problem also reduce to the mincost-flow problem. This set of problems includes bipartite matching, feasible flow, and mincut, among numerous others.
More interesting, we can examine properties of our algorithms for the mincost-flow problem to develop new generic algorithms for the maxflow problem. We have already noted that the generic cycle-canceling algorithm for the mincost-maxflow problem gives a generic augmenting-path algorithm for the maxflow problem. In particular, this approach leads to an implementation that finds augmenting paths without having to search the network (see Exercises 22.133 and 22.134). On the other hand, the algorithm might produce zero-flow augmenting paths, so its performance characteristics are difficult to evaluate (see reference section).
The mincost-flow problem is also more general than the shortest-paths problem, by the following simple reduction.
Property 22.29 The single-source–shortest-paths problem (in networks with no negative cycles) reduces to the mincost–feasible-flow problem.
Proof: Given a single-source–shortest-paths problem (a network and a source vertex s), build a flow network with the same vertices, edges, and edge costs; and give each edge unlimited capacity. Add a new source vertex with an edge to s that has cost zero and capacity V-1 and a new sink vertex with edges from each of the other vertices with costs zero and capacities 1. This construction is illustrated in Program 22.51.
Solve the mincost–feasible-flow problem on this network. If necessary, remove cycles in the solution to produce a spanning-tree solution. This spanning tree corresponds directly to a shortest-paths spanning tree of the original network. Detailed proof of this fact is left as an exercise (seeExercise 22.138).
Thus, all the problems discussed in Section 21.6 that reduce to the single-source–shortest-paths problem also reduce to the mincost-flow problem. This set of problems includes job scheduling with deadlines and difference constraints, among numerous others.
As we found when studying maxflow problems, it is worthwhile to consider the details of the operation of the network simplex algorithm when solving a shortest-paths problem using the reduction of Property 22.29. In this case, the algorithm maintains a spanning tree rooted at the source, much like the search-based algorithms that we considered in Chapter 21, but the node potentials and reduced costs provide increased flexibility in developing methods to choose the next edge to add to the tree.
We do not generally exploit the fact that the mincost-flow problem is a proper generalization of both the maxflow and the shortest-paths problems, because we have specialized algorithms with better performance guarantees for both problems. If such implementations are not available, however, a good implementation of the network simplex algorithm is likely to produce quick solutions to particular instances of both problems. Of course, we must avoid reduction loops when using or building network-processing systems that take advantage of such reductions. For example, the cycle-canceling implementation in Program 22.9 uses both maxflow and shortest paths to solve the mincost-flow problem (see Exercise 21.96).
Next, we consider equivalent network models. First, we show that assuming that costs are nonnegative is not restrictive, as we can transform networks with negative costs into networks without them.
Property 22.30 In mincost-flow problems, we can assume, without loss of generality, that edge costs are nonnegative.
Proof: We prove this fact for feasible mincost flows in distribution networks. The same result is true for mincost maxflows because of the equivalence of the two problems proved in Property 22.22 (see Exercises 22.143 and 22.144).
Given a distribution network, we replace any edge u-v that has cost x < 0 and capacity c by an edge v-u of the same capacity that has cost −x (a positive number). Furthermore, we can decrement the supply-demand value of u by c and increment the supply-demand value of v by c. This operation corresponds to pushing c units of flow from u to v and adjusting the network accordingly.
For negative-cost edges, if a solution to the mincost-flow problem for the transformed network puts flow f in the edge v-u, we put flow c − f in u-v in the original network; for positive-cost edges, the transformed network has the same flow as in the original. This flow assignment preserves the supply or demand constraint at all the vertices.
The flow in v-u in the transformed network contributes fx to the cost and the flow in u-v in the original network contributes −cx + fx to the cost. The first term in this expression does not depend on the flow, so the cost of any flow in the transformed network is equal to the cost of the corresponding flow in the original network plus the sum of the products of the capacities and costs of all the negative-cost edges (which is a negative quantity). Any minimal-cost flow in the transformed network is therefore a minimal-cost flow in the original network.
This reduction shows that we can restrict attention to positive costs, but we generally do not bother to do so in practice because our implementations in Sections 22.5 and 22.6 work exclusively with residual networks and handle negative costs with no difficulty. It is important to have somelower bound on costs in some contexts, but that bound does not need to be zero (see Exercise 22.145).
Next, we show, as we did for the maxflow problem, that we could, if we wanted, restrict attention to acyclic networks. Moreover, we can also assume that edges are uncapacitated (there is no upper bound on the amount of flow in the edges). Combining these two variations leads to the following classic formulation of the mincost-flow problem.
Transportation Solve the mincost-flow problem for a bipartite distribution network where all edges are directed from a supply vertex to a demand vertex and have unlimited capacity. As discussed at the beginning of this chapter (see Figure 22.2), the usual way to think of this problem is as modeling the distribution of goods from warehouses (supply vertices) to retail outlets (demand vertices) along distribution channels (edges) at a certain cost per unit amount of goods.
Property 22.31 The transportation problem is equivalent to the mincost-flow problem.
Proof: Given a transportation problem, we can solve it by assigning a capacity for each edge higher than the supply or demand values of the vertices that it connects and solving the resulting mincost–feasible-flow problem on the resulting distribution network. Therefore, we need only to establish a reduction from the standard problem to the transportation problem.
For variety, we describe a new transformation, which is linear only for sparse networks. A construction similar to the one that we used in the proof of Property 22.16 establishes the result for nonsparse networks (see Exercise 22.148).
Given a standard distribution network with V vertices and E edges, build a transportation network with V supply vertices, E demand vertices and 2E edges, as follows. For each vertex in the original network, include a vertex in the bipartite network with supply or demand value set to the original value plus the sum of the capacities of the outgoing edges; and for each edge u-v in the original network with capacity c, include a vertex in the bipartite network with supply or demand value -c (we use the notation [u-v] to refer to this vertex). For each edge u-v in the original network, include two edges in the bipartite network: one from u to [u-v] with the same cost, and one from v to [u-v] with cost 0.
The following one-to-one correspondence preserves costs between flows in the two networks: An edge u-v has flow value f in the original network if and only if edge u-[u-v] has flow value f, and edge v-[u-v] has flow value c-f in the bipartite network (those two flows must sum to c because of the supply–demand constraint at vertex [u-v]. Thus, any mincost flow in one network corresponds to a mincost flow in the other.
Since we have not considered direct algorithms for solving the transportation problem, this reduction is of academic interest only. To use it, we would have to convert the resulting problem back to a (different) mincost-flow problem, using the simple reduction mentioned at the beginning of the proof of Property 22.31. Perhaps such networks admit more efficient solutions in practice; perhaps they do not. The point of studying the equivalence between the transportation problem and the mincost-flow problem is to understand that removing capacities and restricting attention to bipartite networks would seem to simplify the mincost-flow problem substantially; however, that is not the case.
We need to consider another classical problem in this context. It generalizes the bipartite-matching problem that is discussed in detail in Section 22.4. Like that problem, it is deceptively simple.
Assignment Given a weighted bipartite graph, find a set of edges of minimum total weight such that each vertex is connected to exactly one other vertex.
For example, we might generalize our job-placement problem to include a way for each company to quantify its desire for each applicant (say by assigning an integer to each applicant, with lower integers going to the better applicants) and for each applicant to quantify his or her desire for each company. Then, a solution to the assignment problem would provide a reasonable way to take these relative preferences into account.
Property 22.32 The assignment problem reduces to the mincost-flow problem.
Proof: This result can be established via a simple reduction to the transportation problem. Given an assignment problem, construct a transportation problem with the same vertices and edges, with all vertices in one of the sets designated as supply vertices with value 1 and all vertices in the other set designated as demand vertices with value 1. Assign capacity 1 to each edge, and assign a cost corresponding to that edge’s weight in the assignment problem. Any solution to this instance of the transportation problem is simply a set of edges of minimal total cost that each connect a supply vertex to a demand vertex and therefore corresponds directly to a solution to the original assignment problem.
Reducing this instance of the transportation problem to the mincost-maxflow problem gives a construction that is essentially equivalent to the construction that we used to reduce the bipartite-matching problem to the maxflow problem (see Exercise 22.158).
This relationship is not known to be an equivalence. There is no known way to reduce a general mincost-flow problem to the assignment problem. Indeed, like the single-source–shortest-paths problem and the maxflow problem, the assignment problem seems to be easier than the mincost-flow problem in the sense that algorithms that solve it are known that have better asymptotic performance than the best known algorithms for the mincost-flow problem. Still, the network simplex algorithm is sufficiently well refined that a good implementation of it is a reasonable choice for solving assignment problems. Moreover, as with maxflow and shortest paths, we can tailor the network simplex algorithm to get improved performance for the assignment problem (see reference section).
Our next reduction to the mincost-flow problem brings us back to a basic problem related to paths in graphs like the ones that we first considered in Section 17.7. As in the Euler-path problem, we want a path that includes all the edges in a graph. Recognizing that not all graphs have such a path, we relax the restriction that edges must appear only once.
Mail carrier Given a network (weighted digraph), find a cyclic path of minimal weight that includes each edge at least once (see Figure 22.52). Recall that our basic definitions in Chapter 17 make the distinction between cyclic paths (which may revisit vertices and edges) and cycles (which consist of distinct vertices, except the first and the final, which are the same).
The solution to this problem would describe the best route for a mail carrier (who has to cover all the streets on her route) to follow. A solution to this problem might also describe the route that a snow-plow should take during a snowstorm, and there are many similar applications.
The mail carrier’s problem is an extension of the Euler-tour problem that we discussed in Section 17.7: The solution to Exercise 17.92 is a simple test for whether a digraph has an Euler tour, and Program 17.14 is an effective way to find an Euler tour for such digraphs. That tour solves the mail carrier’s problem because it includes each edge exactly once—no path could have lower weight. The problem becomes more difficult when indegrees and outdegrees are not necessarily
Figure 22.52 Mail carrier’s problem
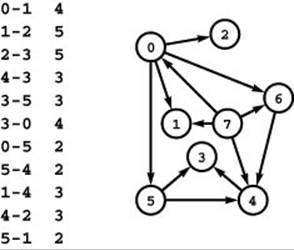
Finding the shortest path that includes each edge at least once is a challenge even for this small network, but the problem can be solved efficiently through reduction to the mincost-flow problem.
equal. In the general case, some edges must be traversed more than once: The problem is to minimize the total weight of all the multiply traversed edges.
Property 22.33 The mail carrier’s problem reduces to the mincost-flow problem.
Proof: Given an instance of the mail carrier’s problem (a weighted digraph), define a distribution network on the same vertices and edges, with all the vertex supply or demand values set to 0, edge costs set to the weights of the corresponding edge, and no upper bounds on edge capacities, but all edge capacities constrained to be greater than 1. We interpret a flow value f in an edge u-v as saying that the mail carrier needs to traverse u-v a total of f times.
Find a mincost flow for this network by using the transformation of Exercise 22.146 to remove the lower bound on edge capacities. The flow-decomposition theorem says that we can express the flow as a set of cycles, so we can build a cyclic path from this flow in the same way that we built an Euler tour in an Eulerian graph: We traverse any cycle, taking a detour to traverse another cycle whenever we encounter a node that is on another cycle.
A careful look at the mail carrier’s problem illustrates yet again the fine line between trivial and intractable in graph algorithms. Suppose that we consider the two-way version of the problem where the network is undirected, and the mail carrier must travel in both directions along each edge. Then, as we noted in Section 18.5, depth-first search (or any graph search) will provide an immediate solution. If, however, it suffices to traverse each undirected edge in either direction, then a solution is significantly more difficult to formulate than is the simple reduction to mincost flow that we just examined, but the problem is still tractable. If some edges are directed and others undirected, the problem becomes NP-hard (see reference section).
These are only a few of the scores of practical problems that have been formulated as mincost-flow problems. The mincost-flow problem is even more versatile than the maxflow problem or shortest-paths problems, and the network simplex algorithm effectively solves all problems encompassed by the model.
As we did when we studied maxflow, we can examine how any mincost-flow problem can be cast as an LP problem, as illustrated in
Figure 22.53 LP formulation of a mincostmaxflow problem

This linear program is equivalent to the mincost-maxflow problem for the sample network of Program 22.40. The edge equalities and vertex inequalities are the same as in Program 22.39, but the objective is different. The variable c represents the total cost, which is a linear combination of the other variables. In this case, c =− 9x50 +3x01 + x 02 + x 13 + x14 +4x23 +2x24 +2x35 + x 45.
Figure 22.53. The formulation is a straightforward extension of the maxflow formulation: We add equations that set a dummy variable to be equal to the cost of the flow, then set the objective so as to minimize that variable. LP models allow addition of arbitrary (linear) constraints. Some constraints may lead to problems that still may be equivalent to mincost-flow problems, but others do not. That is, many problems do not reduce to mincost-flow problems: In particular, LP encompasses a much broader set of problems. The mincost-flow problem is a next step toward that general problem-solving model, which we consider in Part 8.
There are other models that are even more general than the LP model; but LP has the additional virtue that, while LP problems are in general more difficult than mincost-flow problems, effective and efficient algorithms have been invented to solve them. Indeed, perhaps the most important such algorithm is known as the simplex method: The network simplex method is a specialized version of the simplex method that applies to the subset of LP problems that correspond to mincost-flow problems, and understanding the network simplex algorithm is a helpful first step in understanding the simplex algorithm.
Exercises
• 22.133 Show that, when the network simplex algorithm is computing a maxflow, the spanning tree is the union of t-s, a tree containing s and a tree containing t.
22.134 Develop a maxflow implementation based on Exercise 22.133. Choose an eligible edge at random.
22.135 Show, in the style of Program 22.50, the process of computing a maxflow in the flow network shown in Program 22.10 using the reduction described in the text and the network simplex implementation of Program 22.14.
22.136 Show, in the style of Program 22.50, the process of finding shortest paths from 0 in the flow network shown in Program 22.10 using the reduction described in the text and the network simplex implementation of Program 22.14.
• 22.137 Prove that all edges in the spanning tree described in the proof of Property 22.29 are on paths directed from the source to leaves.
• 22.138 Prove that the spanning tree described in the proof of Property 22.29 corresponds to a shortest-paths tree in the original network.
22.139 Suppose that you use the network simplex algorithm to solve a problem created by a reduction from the single-source–shortest-paths problem as described in the proof of Property 22.29. (i) Prove that the algorithm never uses a zero-cost augmenting path. (ii) Show that the edge that leaves the cycle is always the parent of the destination vertex of the edge that is added to the cycle. (iii) As a consequence of Exercise 22.138, the network simplex algorithm does not need to maintain edge flows. Provide a full implementation that takes advantage of this observation. Choose the new tree edge at random.
22.140 Suppose that we assign a positive cost to each edge in a network. Prove that the problem of finding a single-source–shortest-paths tree of minimal cost reduces to the mincost-maxflow problem.
22.141 Suppose that we modify the job-scheduling-with-deadlines problem in Section 21.6 to stipulate that jobs can miss their deadlines, but that they incur a fixed positive cost if they do. Show that this modified problem reduces to the mincost-maxflow problem.
22.142 Implement a class that finds mincost maxflows in distribution networks with negative costs. Use your solution to Exercise 22.105 (which assumes that costs are all nonnegative).
• 22.143 Suppose that the costs of 0-2 and 1-3 in Program 22.40 are -1, instead of 1. Show how to find a mincost maxflow by transforming the network to a network with positive costs and finding a mincost maxflow of the new network.
22.144 Implement a class that finds mincost maxflows in networks with negative costs. Use MINCOST (which assumes that costs are all nonnegative).
• 22.145 Do the implementations in Sections 22.5 and 22.6 depend in a fundamental way on costs being nonnegative? If they do, explain how; if they do not, explain what fixes (if any) are required to make them work properly for networks with negative costs, or explain why no such fixes are possible.
22.146 Extend your feasible-flow ADT from Exercise 22.74 to include lower bounds on the capacities of edges. Implement a class that computes a mincost maxflow that respects these bounds (if one exists).
22.147 Give the result of using the reduction in the text to reduce the flow network described in Exercise 22.112 to the transportation problem.
• 22.148 Show that the mincost-maxflow problem reduces to the transportation problem with just V extra vertices and edges by using a construction similar to the one used in the proof of Property 22.16.
• 22.149 Implement a class for the transportation problem that is based on the simple reduction to the mincost-flow problem given in the proof of Property 22.30.
• 22.150 Develop a class implementation for the mincost-flow problem that is based on the reduction to the transportation problem described in the proof of Property 22.31.
• 22.151 Develop a class implementation for the mincost-flow problem that is based on the reduction to the transportation problem described in Exercise 22.148.
22.152 Write a program to generate random instances of the transportation problem, then use them as the basis for empirical tests on various algorithms and implementations to solve that problem.
22.153 Find a large instance of the transportation problem online.
22.154 Run empirical studies to compare the two different methods of reducing arbitrary mincost-flow problems to the transportation problem that are discussed in the proof of Property 22.31.
22.155 Write a program to generate random instances of the assignment problem, then use them as the basis for empirical tests on various algorithms and implementations to solve that problem.
22.156 Find a large instance of the assignment problem online.
22.157 The job-placement problem described in the text favors the employers (their total weights are maximized). Formulate a version of the problem such that applicants also express their wishes. Explain how to solve your version.
22.158 Do empirical studies to compare the performance of the two network simplex implementations in Section 22.6 for solving random instances of the assignment problem (see Exercise 22.155) with V vertices and E edges, for a reasonable set of values for V and E.
22.159 The mail carrier’s problem clearly has no solution for networks that are not strongly connected (the mail carrier can visit only those vertices that are in the strong component where she starts), but that fact is not mentioned in the reduction of Property 22.33. What happens when we use the reduction on a network that is not strongly connected?
22.160 Run empirical studies for various weighted graphs (see Exercises 21.4– 8) to determine average length of the mail carrier’s path.
22.161 Give a direct proof that the single-source–shortest-paths problem reduces to the assignment problem.
22.162 Describe how to formulate an arbitrary assignment problem as an LP problem.
• 22.163 Do Exercise 22.18 for the case where the cost value associated with each edge is -1 (so you minimize unused space in the trucks).
• 22.164 Devise a cost model for Exercise 22.18 such that the solution is a maxflow that takes a minimal number of days.
All materials on the site are licensed Creative Commons Attribution-Sharealike 3.0 Unported CC BY-SA 3.0 & GNU Free Documentation License (GFDL)
If you are the copyright holder of any material contained on our site and intend to remove it, please contact our site administrator for approval.
© 2016-2026 All site design rights belong to S.Y.A.