Beginning Object-Oriented Programming with C# (2012)

Part II

Understanding C# Syntax

Chapter 3: Understanding Data Types

Chapter 4: Understanding C# Statements

Chapter 5: Understanding Reference Data Types

Chapter 6: Making Decisions in Code

Chapter 7: Statement Repetition Using Loops

Chapter 8: Understanding Arrays and Collections

Chapter 3

Understanding Data Types

What you will learn in this chapter:

· Integer data types

· The range of values for different data types

· Floating-point data types

· Which data type should be used to represent financial data

· The boolean data type

· When to use one data type versus anotherIntelliSense

wrox.com code downloads for this chapter

You can find the wrox.com code downloads for this chapter at www.wrox.com/remtitle.cgi?isbn=9781118336922 on the Download Code tab. The code in the Chapter03 folder is individually named according to the names throughout this chapter.

As you learned in Chapter 2, most computer programs are centered on solving problems by taking data in one form, transforming it in some manner, and then presenting that new data to the user. The data the computer manipulates can be stored in many different shapes and sizes. When you finish this chapter you will have a good understanding of why C# offers you such flexibility to select a data type.

Computer Data

Computer programs usually input data in one form, process it, and then show the new data on the computer screen. This can invite the question: What is data? Simply stated, data is information. Computer data is information stored in a variable for use in a program. In a broad sense, there are two basic kinds of computer data: numeric data and textual data.

Numeric data is any kind of data that can have arithmetic operations performed on it. You can add, subtract, multiply, and divide numeric data. You can perform other operations on numeric data, such as finding a square root, a sine, or a cosine of a numeric quantity, and so on. You will also see numeric data types referred to as value types. The precise meaning of this term is discussed in Chapter 5. For now, however, you can think of them as those data types whose variables can have data stored directly into them.

Textual data are character representations of data. Your name is a piece of data that can be represented in a program in a textual fashion. Some students become confused when you ask them whether a ZIP code is numeric or textual information. Because ZIP codes are usually not manipulated in mathematical expressions (for example, you wouldn't need to multiply or divide a ZIP code), they are usually treated as textual information.

Integer Data Types

An integer data type is any numeric value expressed as a whole number. Integer values cannot have a fractional component associated with them. If you try to assign a fractional value to an integer variable, C# truncates the value. For example, if val is an integer data type, the statement

val = 6.9999;

assigns the value of 6 to val. This means that integer operations on fractional values do not round those values; they truncate them. That is, if an integer data type has a fractional value, C# simply throws away the fractional component.

Table 3.1 lists the various integer data types that you can use in your programs.

Table 3.1 Integer Data Types

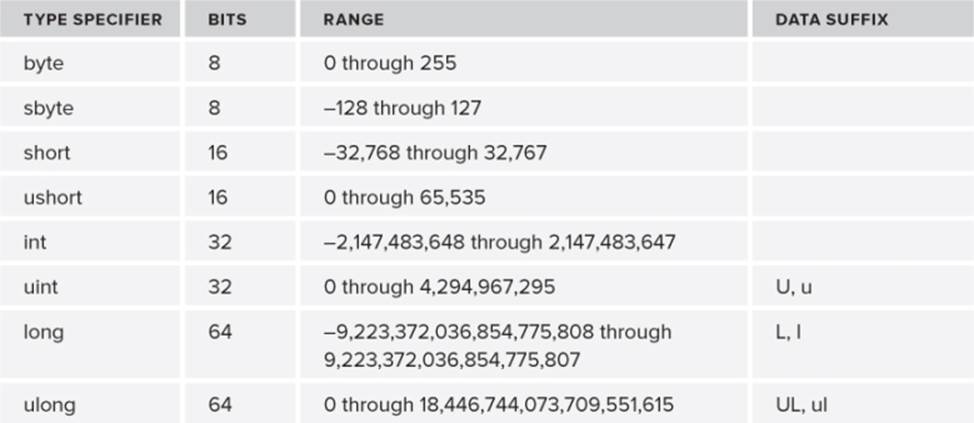
As you can see in Table 3.1, some data types are prefixed with the letter “s” (sbyte) while others are prefixed with the letter “u”. The “s” means the data are signed quantities, while the “u” means they are unsigned quantities. (The next section explains why these are important distinctions.)

Data suffixes are used to tell the compiler the data type being used in an expression. For example,

long bigNum;

// some code…

bigNum = 15L;

tells the compiler unequivocally that the numeric constant is 15 expressed as a long data type. If the suffix is not used, the compiler may complain that an int is being assigned into a long. Also, although lower case suffixes are recognized by the compiler, you should use only upper case suffixes. They are easier to see, plus the lower case “el” looks a lot like the digit “1” and may make debugging harder than it should be.

Range of Integer Data Types

Each of the integer data types has a range of values that it can accommodate. Consider the byte data type, which uses 8 bits. A binary digit, or bit, is the smallest unit of computer storage and may assume the value of on (1) or off (0). This means that the most basic unit of information in a computer—the bit—has only two possible states: on and off. Because there are only two possible states, information is stored in a computer in a binary, or base-2, format. Although you perform mathematical operations using a base-10 numbering system, the computer prefers base-2 numbers.

From an engineering standpoint, it is more convenient to group the bits into a larger unit called a byte. A byte is a collection of 8 bits. Because each bit has two possible values, a byte can have 2⁸, or 256, unique combinations. If you refer to Table 3.1, you can see that a byte data type can represent the values 0 through 255.

Understanding Binary Numbers

Wait a minute! Eight bits can be used to represent 256 values, not 255? So why is the range of a byte limited to 255? The reason is that 8 bits can represent 256 unique values, and one of those values is zero. Therefore, if all bits are turned off, the byte has a value of 0. If all bits are turned on, the byte has the value 255. Table 3.2 further illustrates the relationship between bits and their associated numeric values.

Table 3.2 Bit Positions and Their Binary Equivalents

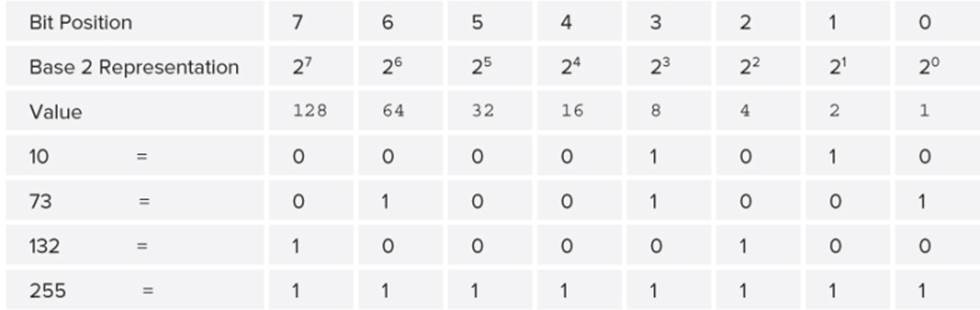
Referring to Table 3.2, you can see the numeric value of a byte depends upon which bits are turned on. For example, for the value 73, you see

01001001

which is interpreted as

0 + 64 + 0 + 0 + 8 + 0 + 0 + 1

If you sum up the values, the total is 73. If all the bits are turned on, the byte appears as this:

11111111

which becomes this:

128 + 64 + 32 +16 + 8 + 4 + 2 + 1

and totals 255.

Signed Integer Values

Given this information, why is the sbyte data type limited to a maximum value of 128? The reason is that the sbyte data type is a signed byte. Because it is signed, sbyte data may assume positive or negative values. The highest bit of the byte (bit position 7) is used to store the sign of the number. For signed numbers, the high bit is called the sign bit. If the sign bit is turned on, it is a negative number. If the sign bit is turned off, it is a positive number. Because of the sign bit, only seven bits (2⁷ combinations) are available instead of eight bits (2⁸combinations). Because 2⁷ is 128, only 128 unique values are possible, and because 0 is one of those values, the maximum positive value is 127. If the sign bit is turned on, you still have 128 unique values available, all of which can be negative. This is true because you have already accounted for the value 0 in the positive range of values. This means the negative range extends from −1 to −128. Referring to Table 3.1, you can see that if the range of permissible values begins with 0, that integer data type does not use a sign bit. If the range includes negative values, it does use a sign bit. You can also see that integer data types that do use a sign bit have a maximum value that is approximately one-half that of their corresponding unsigned data types. The reason, of course, is that the highest bit is reserved for the sign of the number.

Which Integer Should You Use?

One problem beginning programmers face is deciding which integer data type to use. There is no single correct answer. There are, however, several factors to keep in mind:

· Range of values: If you are interested only in counting the number of healthy teeth in a person's mouth, the byte data type works. On the other hand, if you measure the day's high temperature, even an sbyte may not have enough range if your sample site includes both Death Valley and Juneau, Alaska. Always err on the high side so that you have sufficient range to accommodate your needs.

· Memory limitations: For most of the applications you write, you probably have at least half a gigabyte of memory available to you. If you select a long data type instead of an int, chances are the 4 extra bytes used per integer value aren't going to gobble up much additional memory. However, if you write programs for a toaster or an engine sensor, it could be that memory limitations for the device are restrictive. In such cases you would want to select the smallest data type with sufficient range to do the job.

· Processor considerations: Each computer has a central processing unit, which is the heart of a computer. Back in the late 1970s, CPUs had internal storage units, called registers, which could process data in 1-byte (8-bit) chunks. Later, the CPU registers had 16-bit registers, then 32-bit registers, and finally 64-bit registers. Integer data types that can snuggle neatly into a register without adding or losing bits may have a slight speed advantage for some of the operations a CPU performs on the data. What this means is that a 32-bit CPU may actually process a 32-bit integer faster than a 16-bit integer even though the 16-bit integer is smaller. Although the performance hit on a single mismatch is small, this could make a difference when millions of calculations are performed repeatedly.

· Library considerations: You already know that the .NET Framework provides thousands of classes for you. Some of these classes have methods you might use often. For example, the math class includes a square root method. You send a data value to the method, and it sends that value's square root back to you. Most of the math methods (such as Sqrt(), Cos(), and Pow()) ask that you send a double data type (discussed later in the section on floating point data types) to it, and the method returns the answer as a double. If that's the case, it would make sense to have all the data types be double if they interact with the math classes. If you don't supply a data type that matches what a method expects, the compiler must generate code to do the conversion before the data even get to the method. Although the time to process this additional “conversion code” is small, in a large program loop that involves many such conversions, the time penalty can be noticeable.

· Convention: Sometimes convention (a nicer word for “habit”) determines the data type used with certain programming constructs. For example, in Chapter 8 you learn about program loops that use a variable to control the loop. Convention finds that an int data type is most often used to control program loops. Although there may be other reasons to use an int to control the loop (such as processor considerations and native register sizes), most programmers simply define an int to control the loop without a whole lot of thought. Convention doesn't necessarily make a choice of data type right, but it may explain why so many programmers tend to use certain data types with certain programming constructs.

In the final analysis, the range of values is probably the most important factor to consider when selecting an integer data type. With a little experience, you develop a knack to select the proper data types for the task at hand.

Variable Naming Rules and Conventions

Before you create your first program, you need to understand program variables. A variable is simply a name you give to a specific piece of data. Back in the dark ages of programming, you might store an integer value at memory address 900,000. In those days there were no variable names. You simply typed in 900000 anytime you wanted to reference that integer value. It didn't take long before programmers started writing programming tools that let them use symbolic names (such as operand1) for memory addresses, which made the act of writing programs much easier and less error-prone, hence the advent of variable names.

A variable name, also called an identifier, has several syntax rules you must follow to keep the Visual Studio compiler happy. These syntax rules are as follows:

· Variable names may begin only with an alpha character (a through z, A through Z) or an underscore character (_).

· Punctuation characters and operators are not allowed.

· The variable name cannot be a C# keyword.

· Digit characters are allowed after the first character (for example, Apollo5, but not 5Apollo).

Although it is not a rule, you should always try to use variable names that make sense in the context in which they are used. In the preceding code, operand1 is a better name than o1 even though Visual Studio accepts either name. A second convention, called camel notation, is that long variable names start with lowercase letters and that each following word in the name is capitalized, as in myHatSize. Camel notation makes it easier to read the variable names. The code in the btnCalc_Click() event adheres these rules and conventions for naming the flag, operand1, operand2, and resultvariables.

Let's put what you've learned about data types to work in a simple program that uses integer data.

Try It Out: A Program Using Integer Data (Chapter03.zip)

Now write a simple program that accepts two values from the keyboard and performs a mathematical operation on the two values. As always, you need a plan to guide you as you write the program. The basis for the plan is always the Five Program Steps.

1. Formulate a program plan. Because this is a simple program, it doesn't need any special Initialization step code beyond what Visual Studio does for you automatically. The Input step suggests that you want to collect two integer values from the user. The Process step states that you want to perform some math operation on the data values entered by the user. Assume you want to divide the two numbers. Because Windows programs are event-driven, you need to add a Calculate button to begin the processing of the data. The Output step assumes that you want to show the user the end result of the math operation division in your program. There's nothing special for you to do in the Termination step, so you can just provide an Exit button to end the program.

2. Select New → Project from the main menu.

3. Select Empty Project from the Template Window. (Make sure it's for C# if you have the full Visual Studio.)

4. Type in the name and location for the new project. This can be any folder name and location you want. However, you might consider making a new folder on your C drive. Call it something such as BookExamples and then create subfolders for each chapter of this book and place the code in those subfolders.

5. Select Project → Add References, selecting System.dll, System.Drawing.dll, and System .Windows.Forms.dll. (Or click the Recent Tab, and select from there.)

6. Select Project → Add New Item; select Code File, and name the file frmMain.cs.

7. Place the cursor in the Source window, and copy the C# template code you saved in a file from Chapter 2 (Listing 2-1) into frmMain.cs..

8. Select Project → Properties → Application. Set Output Type to Windows Application, and set Startup Object to frmMain.

9. Highlight the frmMain.cs file in the Solution Explorer window, and click the View Designer icon.

10. Add the controls presented in Table 3.3 to frmMain.

Table 3.3 Controls for Integer Program

When you finish, your form should look similar to Figure 3.1.

Figure 3.1 User interface for integer data program

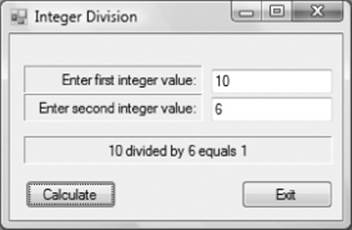
11. In the Design View, double-click on the btnCalc button, which causes Visual Studio to add the stub code for the button click event. The double-click event automatically switches you to the Source Window. Now add the button click code shown in Listing 3-1 to the stub code. The code is part of the Chapter03.ZIP file.

Listing 3-1: Button Click Event Code

private void btnCalc_Click(object sender, EventArgs e)

{

bool flag;

int operand1;

int operand2;

int answer;

// Input Step

// Check first input…

flag = int.TryParse(txtOperand1.Text, out operand1);

if (flag == false)

{

MessageBox.Show("Enter a whole number", "Input Error");

txtOperand1.Focus();

return;

}

// Check second input…

flag = int.TryParse(txtOperand2.Text, out operand2);

if (flag == false)

{

MessageBox.Show("Enter a whole number", "Input Error");

txtOperand2.Focus();

return;

}

// Process Step

answer = operand1 / operand2;

// Display Step

txtResult.Text = operand1.ToString() + " divided by " +

operand2.ToString() +

" equals " +answer.ToString();

txtResult.Visible = true;

}

private void btnExit_Click(object sender, EventArgs e)

{

Close();

}

How It Works

When you run the program, you can find that the action is done in the Process step, which you have tied to the button click event for btnCalc. You begin the code for the btnCalc() click event by defining a boolean variable named flag, followed by the definitions for three integer variables of type int. (boolean variables can only have the values associated with logic true or logic false. These are covered at the end of the chapter.)

Using the TryParse( ) Method

The next statement in the program is this:

flag = int.TryParse(txtOperand1.Text, out operand1);

The statement may seem rather formidable, but it actually isn't.

The purpose of the int.TryParse() method is to examine what the user entered from the keyboard to see if that input can be converted into an integer data type. You know it's attempting an integer conversion from textual data to an integer because of the keyword int before TryParse().

Wait a minute! What's the dot operator doing between the int and TryParse()? C# provides you with a class for every data type. In this example, when you type in the keyword int and then the dot operator, you can see Visual Studio pop up a small window that looks like Figure 3.2.

Figure 3.2 The int class properties and methods

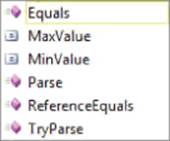
If you look closely at Figure 3.2, you can see four lines begin with a 3-D cube and two lines begin with a square. The cubes represent class methods, whereas the squares are for class properties. As you can see in the figure, the int class has several methods, including TryParse(). Therefore, in the code statement, the dot operator is used because you want to call the TryParse()class method found in the int class. Sometimes, you will see the term wrapper class, which often means that some piece of data is “wrapped” inside a class. The int class shown here is an example of a wrapper class because the basic data type provides you with specific properties and methods to make it a little more flexible.

Keep in mind that anything the user types into a textbox is entered as textual data. However, your program wants to manipulate numeric data in the form of integers. Simply stated, the purpose of TryParse() is to convert apples (textual data) into oranges (numeric data).

Sometimes, users do make typing errors and the conversion doesn't go smoothly. If you look at your keyboard, you can see it's not too hard to accidentally hit the o (oh) key when you meant to hit the 0 (zero) key. They're only about one-half an inch apart. What TryParse() does is examine each character the user typed into the txtOperand1 textbox to make sure it was a digit character. Now simplify what comprises the TryParse() statement:

flag = int.TryParse(txtOperand1.Text, out operand1);

This is actually nothing more than what you've seen before:

flag = Object . MethodName(argument1, argument2);

You have an assignment operator (=) with two operands. The operand on the left is a boolean variable named flag, and the operand on the right is an object named int. You use the dot operator to get inside the object and use the TryParse() method buried inside the int object. TryParse()needs two pieces of information, called arguments, sent to it to perform its job. In this example, the TryParse() method wants the Text property of the txtOperand1 object and an integer variable you defined as operand1 sent to it. Why does TryParse() need this information? Simply stated,argument1 supplies the property with the textual data to be examined, and argument2 gives the method a place to store the numeric result of the conversion if everything goes well. The flag variable simply holds the value that TryParse() returns when it's done doing its thing. If the conversion were completed successfully, TryParse() returns true. If things didn't go so well, TryParse() returns false. You can then test the value of flag to see how the conversion faired with an if statement, as was done here. (You learn about the C# if statement in detail in Chapter 6.)

Now refer to the original code you typed in for the TryParse() statement. If TryParse() finds that the user did type in all digit characters, it converts those digit characters (which are textual data) into numeric data of type int. It takes that new numeric value and places it into operand1. Because the conversion of the textual data in the Text property of the txtOperand1 object was successful, it returns the boolean value true. This value (true) then gets assigned into flag. Therefore, a successful call to the TryParse() method converts the textual data of the Text property of the txtOperand1 object and places that integer number into the second argument of the call to TryParse(). Because you use the TryParse() method found inside the int object, the data is converted to an int data type and copied into the int variable named operand1.

Calling a Method

The term calling a method refers to the process of directing program control to a method to perform some particular task. You might also see the term caller used with calling a method. A caller is a point of execution in a program, not a person or thing. In the btnCalc_Click()code presented earlier, the first line after the data definitions of operand1, operand2, and result is a call to the TryParse() method of an int object. To refer to the process to call the TryParse() method, a programmer might say, “btnCalc calls TryParse().” Another programmer might say, “flag calls TryParse().” Either phrase simply means that program control jumps away from the current sequence to execute the program statements in the btnCalc_Click() method to execute those statements found in the TryParse() method.

When the program finishes executing the statements in TryParse(), program control is sent back to the point at which TryParse() was called. This process to send control back to the point at which the method was called is associated with the phrase return to the caller.

If the method returns some form of data, such as the boolean value true or false, as part of its task, you might hear the phrase, “The method returns true (or false) to the caller.” In the example, TryParse() is designed to return the boolean value of either true or false to the caller. The way to visualize what happens is to look at the state of the information just before the TryParse() method is called:

flag = int.TryParse(txtOperand1.Text, out operand1);

This shows the information that is about to be sent to TryParse(). When TryParse() finishes its job to examine the contents of txtOperand1.Text, it returns true or false to the caller. Assuming the user typed in only digit characters, operand1 contains the numeric value of the user's input, and true is returned to the caller. Therefore, when program control returns to the caller, the statement appears to be the following:

flag = true;

This means that TryParse() has done its job and converted the user's textual input into a numeric value now stored in operand1 and returned true to the caller.

The terms and phrases introduced here are used throughout the text.

If the user typed in something other than digit characters into the textbox, TryParse() cannot successfully convert the textual characters into a numeric value. In that case, TryParse() sets operand1 to 0 and returns the value false. The return value (false) is then assigned into the boolean variable named flag.

You might wonder, “Why mess around with returning true or false to the caller? Why not just set the second argument to zero if the conversion fails and be done with it?” The problem is that zero is a legitimate integer value, and the TryParse()method must cope gracefully if the value is 0. If you return 0 regardless of what the user types in, how would you know if the value is good or bad? If the user wants the value to be zero but accidentally hits the “o” key, it appears that the conversion was successful when it shouldn't be. By returning a boolean value from the call, you can test to see if the conversion failed.

An example might help reinforce what's being done. Suppose the user enters 1234 for the input into the txtOperand1 textbox object. The statement line looks like this:

flag = int.TryParse(txtOperand1.Text, out operand1);

It becomes this:

? = int.TryParse("1234", out ?);

The flag and operand1 values are shown as question marks because, at the moment, they could contain unknown garbage values. After TryParse() examines the string of input data from the txtOperand1 textbox object (1234), it decides that it can successfully convert those digit characters into a numeric value of type int. Because the conversion is successful, TryParse() sets operand1 to the new value (1234) and returns true to the caller. In this case, the caller is the assignment operator that takes the return value (true) and assigns it into the flag variable. The end result is as follows:

true = int.TryParse("1234", out 1234);

The keyword out in the second argument to TryParse() is required and tells Visual Studio it's okay to use operand1 as an argument even though it hasn't yet been initialized to a meaningful value.

The code that follows the TryParse() method call tests the flag variable to see if the conversion were successful . If the conversion failed, the if statement sees that flag is false, and the program executes the code controlled by the if statement. (Chapter 6 discusses if statements in detail.) The statements following the if keyword are executed only if the flag variable is false:

if (flag == false)

{

MessageBox.Show("Enter a whole number", "Input Error");

txtOperand1.Focus();

return;

}

The program then creates a MessageBox object and uses its Show() method to display an error message on the screen. After the user reads and dismisses the error message, the program calls the Focus() method of the txtOperand1 object. A call to the Focus() method causes the program to place the cursor back into its textbox. The return keyword causes the program to leave the btnCalc click event code and redisplay the frmMain form object. The cursor sits in the txtOperand1 textbox waiting for the user to enter a proper integer value.

The same sequence of checks is performed on the contents of the txtOperand2 textbox object. The TryParse() method performs the same checks on the textual data held in the Text property of txtOperand2.

Processing and Displaying the Result

After both operands are assigned values from their associated textboxes, you are ready to perform the division operation. The forward slash (/) is the C# operator for division. The code to perform the calculation and display the results is shown here.

answer = operand1 / operand2;

txtResult.Text = operand1.ToString() + " divided by " +

operand2.ToString() +

" equals " +answer.ToString();

txtResult.Visible = true;

Because you want to use the division operator, the first statement divides the integer operand1 value by the operand2 value. The assignment operator then assigns the result of that division expression into the variable named answer.

All you need to do now is display the answer for the user to see. However, again you have the “apples and oranges” problem. That is, operand1, operand2, and answer are all numeric data, but you need to display them in a textbox that expects the data to be in textual form. As mentioned earlier , each variable of a given value type has a wrapper class associated with it, which provides certain properties and methods. One of those available methods is ToString(). The purpose of the ToString() method is to take the current numeric value of the integer object and convert it into textual data. You can think of ToString()as a reversal of the TryParse()method. In this example, ToString() simply takes the numeric value of the variable operand1 and converts it into the appropriate sequence of digit characters.

After all three values have been converted into text, each text representation of the value is concatenated to the next piece of text by means of the concatenation operator (the + operator). After all the text is concatenated together, the combined text is assigned into the Text property of thetxtResult object. (Concatenation is a fifty-cent word that means to “append to.”)

The last thing the program does is set the Visible property of the txtResult object to true. You do this because when you designed the user interface, you set the Visible property to false. Therefore, when the user first runs the program, he cannot see the textbox that ultimately displays the results. Although this program is simple and doesn't have a lot of “clutter” on the form, this technique to hide the display step objects until they contain something useful may help to declutter the user interface while the user performs the input step. Hiding the textbox also prevents the user from attempting to type something into this textbox.

You might want to experiment with your program a bit. Try changing the math operator from division to addition (+), subtraction (-), multiplication (*), and modulo divide (%) in the program statement line just after the Process step comment. (Modulo divide, %, gives you the remainder of division operation.)

Another interesting thing to do is enter input data that “breaks” the code. For example, what happens if you enter a zero as the second operand in the current program? What happens if you enter huge values that you know exceed the range of the data type (refer to Table 3.1) you selected? Breaking your code is a great way to discover the limitations of the data and the kinds of problems you run into out there in the “real world.” Even more important, you can see how Visual Studio complains to you when that type of error creeps into your programs. This can help you when you try to debug programs in later chapters.

Floating-Point Data Types

A floating-point data type is a numeric data type, but it can represent fractional values. Table 3.4 shows the floating-point data types and their associated ranges.

Table 3.4 Floating-Point Data Types

The range of values for either type of floating-point number is quite large (refer to Table 3.4). Usually you select floating-point values when you need the data to reflect fractional values, or you need to use small or large numbers in your program.

In the following Try It Out sections, you create a program that uses floating point numbers in place of the integer numbers used in the previous program.

Try It Out: A Program Using Floating-Point Numbers (Chapter03.zip)

You can modify your program that used integer numbers to work with floating-point numbers fairly easily. Assuming you still have the code from the previous Try It Out loaded into Visual Studio:

1. Change the statement lines in the btnCalc click event code from

int operand1;

int operand2;

int answer;

to this:

float operand1;

float operand2;

float answer;

2. Now try to run the program.

How It Works

After you make the changes, run the program. You get the following error message:

The best overloaded method match for 'int.TryParse(string, out int)' has some

invalid arguments.

What this error message tells you is that TryParse() is confused because it expects the second argument to be an integer, but you've passed operand1 as a float data type. This isn't a serious problem because each of the data types has its own version of TryParse(). Change the TryParse()method calls in the program to the following:

flag = float.TryParse(txtOperand1.Text, out operand1);

This change uses the float wrapper class for the conversion process.

Now compile and run the program. When you ran the integer version of the program and supplied the two input values as 10 and 6, the answer was 1. The reason for this is that integer math doesn't allow a fractional component. The integer version of the program simply truncated the result to 1. If you use those same inputs in the float version of the program, the result becomes 1.666667, as shown in Figure 3.3. (You didn't change the labels, so those still show the prompt for integer data. You can easily change these if you want.)

Figure 3.3 Program using float data type

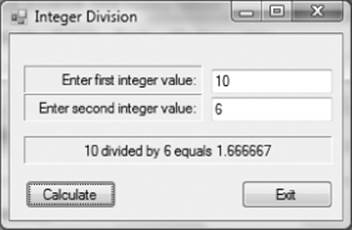
The result of the float division presents a fractional value, which was not possible when the int data type was used.

Try It Out: A Program That Tests Floating-Point Precision (Chapter03.zip)

Using the same program you just wrote in the previous Try It Out, make the following change to that program. Note how we change the data type from the previous version to use the double data type here:

1. Change

float operand1;

float operand2;

float answer;

to

double operand1;

double operand2;

double answer;

Do you need to change the data type for the call to the TryParse() method? (Hint: Only if you want the program to run.)

2. Now recompile, and rerun the program with the same inputs.

Search and Replace in Visual Studio

In the float version of the program under discussion, you were directed to change all instances of the keyword float to double. You could search through the program code looking for each occurrence of the float keyword and change it to double. However, this is exactly the type of no-brainer task perfectly suited for the computer to do for you.

If you want to search the entire program for a specific word or phrase, place the cursor at the top of the program in the Source window and press Ctrl+F. You should quickly see the Find and Replace dialog box. There are two options immediately below the title bar. Select the Quick Replace option. Now type in what you are looking for (such as float) and then enter what you want to replace it with (such as double). The Find and Replace dialog box should look like what is shown in Figure 3.4.

Figure 3.4 Using Find and Replace

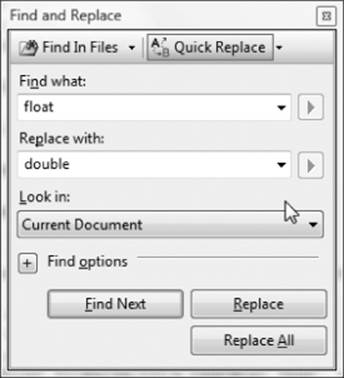
You should now click the Find Next button to find the next occurrence of the word float in the program source code. If you want to change that occurrence of the word float to double, click the Replace button. The word float is then replaced with double, and the program proceeds to the next float keyword it finds in the program.

There is a tremendous temptation to click the Replace All button, which goes through the entire source code file and automatically makes the replacements without asking you to click the Replace button. Don't cave in to this temptation! Search and Replace has the innate intelligence of a box of rocks. Suppose you want to change from an int to a double. You type those inputs into the dialog box and press Replace All. Now, when you look at your source code, you find the old program line,

int interestRate;

has been changed to:

double doubleerestRate;

This is probably not what you wanted to do. The sad thing is that your code will still execute correctly because all instances of interestRate were faithfully changed to doubleerestRate. However, your effort to pick a meaningful variable name has been tossed out the window. Suggestion: Never ever use Replace All. Use the Find Next and Replace buttons only. A safer way to rename a variable is to right click the variable name at its point of definition and select the Refactor Í Rename menu options. You are then given a dialog that allows you to change the variable name.

How It Works

Now the result is 1.66666666666667. Notice there are more digit characters in the answer using the double data type version than when you used the float version. This is because the precision of a float is limited to 7 digits, whereas the precision of a double is 15 digits.

The precision of a number refers to the number of significant digits that a data type can represent. Referring Table 3.4, you can see that a float can represent a number with a value as large as 1.0 e38. That's a number with up to 38 digits. However, because the precision of a float is limited to only 7 digits, only the first 7 digits of that number are significant. The remaining 31 digits are simply the computer's best guess as to the rest of the digits in the number. When you changed the data type to double, you increased the precision to 15 digits. Although the answer could go on for up to 308 digits for a double, the computer gave up after 15 digits and said, “The heck with it; 1.66666666666667 is as good as it gets.”

Which Floating-Point Data Type Should You Use?

It's probably obvious from Table 3.4 that the increased precision for a double is possible because C# uses twice as much memory to store a double as a float. This invites the question…again, “Which floating-point data type should you use?” Once again, the answer is, “It depends.” The same factors that influence your choice of integer data types (memory limitations, processor and library considerations, convention, and so on) play a part to make the right data type choice. The processor and library considerations, however, are especially important when you deal with floating-point data.

First, Intel's Pentium-class CPU has a math coprocessor built into it. The math coprocessor is specifically designed to make floating-point math operations as fast as possible. Using the math coprocessor involves no special coding work on your part. Floating-point data is automatically routed to the math coprocessor when your program performs math operations on floating-point data.

Second, almost all the methods in the Math class (Sqrt(), Pow(), Log(), Cos(), and so on) expect to use the double data type. Again, if you pass a float data type to the Sqrt() method of the Math class, code must be executed to expand the data value from 32 bits to 64 bits. The process to expand a data value from a smaller to a larger number of bits is called data widening. After Sqrt() has done its job, code must be executed to shrink the result back to the 32 bits your float data type demands. The process to shrink a data value from a larger to smaller number of bits is called data narrowing. The code associated with data narrowing and data widening can be avoided if you use a double data type when using the methods found in the Math class.

Finally, the two floating-point data types give you different levels of precision. The double data type has more than twice the number of significant digits of a float data type. Unless there are severe memory limitations and given the other advantages to use a double data type, most of the time you should use the double data type for floating-point operations.

Monetary Values: The Decimal Data Type

It might seem that the double data type would also be a good choice for monetary values. The only problem is that even 15 digits of precision may not be enough to represent important monetary values. To overcome the problems associated with limited precision in financial calculations, C# created the decimal data type. Table 3.5 shows the details of the decimal data type.

Table 3.5 Range for Decimal Data Type

The greatest advantage of the decimal data type is that is has 28 digits of precision—almost twice the precision of a double. This means that even in financial calculations involving large amounts you can keep track of the pennies. The disadvantage of the decimal data type is that each variable takes 16 bytes of memory to store its value. Also, because the math coprocessor is not set up to handle 16 bytes, math operations on the decimal data type are much slower than they are on the double data type.

The program in the next Try It Out is used to see the impact that changing the data type has on the precision of the numbers.

Try It Out: A Program That Tests decimal Precision (Chapter03.zip)

You can modify the program you've been using to test the various data types by simply changing the int keywords in the code listing presented for the btnCalc_Click() method with the decimal keyword.

1. Change

double operand1;

double operand2;

double answer;

to

decimal operand1;

decimal operand2;

decimal answer;

2. Now run the program, using the same input values of 10 and 6 for the two operands. What happened? Did you change the TryParse() call? (The devil is in the details.)

How It Works

Figure 3.5 shows the output for the program. (The input prompts for the two label objects or the text for the frmMain object are not changed, so the word “integer” is a little misleading in the figure. Change them if you want.)

Figure 3.5 Program run using decimal data type

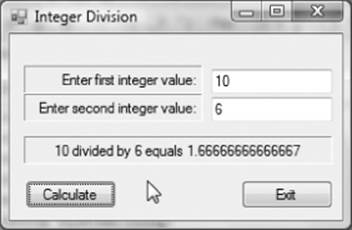
The program runs exactly as the earlier versions of this program with one major exception: The result has significantly more digits in the answers in Figure 3.5; the enhanced precision of the decimal data type is so large the answer doesn't fit in the textbox space allocated for it. Because nobody likes to throw money away, the expanded precision of the decimal data type is a good thing in financial calculations.

Using IntelliSense to Locate Program Errors

After you change the variable's data types to the decimal data type, try inserting the following program statement into the program just after the definition of answer but before the call to the TryParse() method:

operand1 = .5;

When you compile the program, a squiggly blue line appears under .5 in the statement. The blue squiggly line points out that Visual Studio sensed an error in the statement line where the squiggly blue line appears.

Syntax Rules and Error Messages

IntelliSense is the name Microsoft has given to the part of Visual Studio responsible for checking your statements to make sure they obey the syntax rules of C#. A syntax rule simply refers to the language rules C# expects you to follow to form a valid C# program statement. (You can find more details on language rules in Chapter 4.) Just as the English language expects a sentence to have a noun and a verb, C# has rules it expects you to follow when you write program statements.

If you break (or bend) the syntax rules of C#, IntelliSense draws a blue squiggly line under the offending part of the statement. If you move the cursor over the blue line, IntelliSense provides you with some information about the error. This information about the nature of the error is presented in the form of an error message. In the preceding statement, the error message is as follows:

Literal of type double cannot be implicitly converted to type 'decimal';

use an 'M'suffix to create a literal of this type

In other words, Visual Studio is confused about what .5 is. You have defined operand1 as a decimal data type, but you are trying to assign the value .5 into it. Unless told otherwise, whenever IntelliSense sees a fractional value like .5 in the source code, it assumes you want to use a double data type. (A pure number such as .5 in a program's source code is called a numeric literal because a variable is not used to store the value. Instead, the numeric value is “literally” part of the program's source code.) Therefore, IntelliSense sees your program statement attempting to take a double data value (.5) and put it into a decimal data type (operand1). This is like trying to make a person who wears a size-4 shoe walk around in a size 8…. It just doesn't fit right. The error message is saying the same thing, only a little more formally. In its own way, the IntelliSense error message says this:

The literal .5 looks like a double to me and I cannot convert it to type 'decimal'

for you; use an 'M' suffix to create a literal of this type

Okay…that makes sense. Now, follow its recommendation and correct the statement to see what happens. The corrected line should be

operand1 = .5M;

Using the information in Table 3.5, you can make the meaning of the literal .5 crystal-clear to IntelliSense by placing the decimal data type's suffix, M, after the literal. After you make this change, voila!…the squiggly blue line disappears.

As a general rule, whenever you see the dreaded squiggly blue line, move the cursor over the blue line and read the error message IntelliSense gives you. Sometimes the message may appear a bit cryptic, but with a little experience you can begin to interpret the error messages correctly.

The Disappearing Squiggly Blue Line

When IntelliSense finds an error, it does its best to pinpoint what it thinks is the exact line number of the program error and draw the squiggly blue line there. Most of the time IntelliSense does a great job identifying the exact statement in which the error occurred. Other times, however, the nature of the error is such that IntelliSense doesn't realize an error has occurred until it has examined several more lines. In situations in which the line with the squiggly blue line appears to be syntactically correct, look at the lines immediately above it for a statement that is amiss.

Note that the squiggly blue line does not always disappear when you correct the error in the statement line. The best way to determine if a program change does fix an error is to recompile the program to see if the error message and dreaded squiggly blue line disappear.

Finally, the squiggly line may also appear red. The red squiggly line is often associated with a missing statement element. For example, if you type in the following:

int i

a red squiggly line would appear at the end of the line to inform you that you forgot to add a semicolon at the end of the line. Chapter 11 has a lot more detail about program bugs and debugging.

The Boolean Data Type

Of the two fundamental types of data, numeric and textual, thus far you have studied only numeric data types. (You can read more about textual data types in Chapter 6.) The boolean data type is one of those gray areas that doesn't exactly fit into either a numeric or textual data type. Although it is not a precise fit, you learn about the bool data type with the numeric data types because it is used to reflect the state of a piece of data, rather than some textual representation of that data.

One of the elemental features of a computer is that it can make decisions based upon the data it processes. You have seen this decision-making ability in the sample programs. For example, in the integer-division program you wrote earlier, you had the following program statements:

flag = int.TryParse(txtOperand1.Text, out operand1);

if (flag == false)

{

MessageBox.Show("Enter a whole number", "Input Error");

txtOperand1.Focus();

return;

}

The variable named flag that was set by the call to TryParse() was used to decide whether the user had typed in a valid integer number into the Text property of the txtOperand1 textbox object. If the user input could be converted successfully into an integer value, flag was set to true, and the value of operand1 was set to the value entered by the user. If the user entered text that could not be converted to an integer (such as the letter o instead of the zero digit character, 0), flag was set to false and operand1 was set to 0. In that case, an error message displays and the user is given another chance to enter the data.

In the preceding code snippet, flag is a boolean variable. Boolean variables are defined by the bool keyword. (You can see the definition of flag in the btnCalc_Click() method shown earlier in this chapter.) Table 3.6 shows the relevant information for a bool data type.

Table 3.6 The Boolean Data Type

Referring to Table 3.6, there is no “range” for a boolean variable. A bool data type can hold only two possible values: true or false. Therefore, a boolean variable is used to hold the state of the variable, not a specific value.

If you've ever had a logic course, you've been exposed to truth tables where conditions are stated as either true or false. Quite often those conditions are presented with 1 representing true and 0 representing false. You cannot, however, use 1 and 0 to represent true and false in a C# program. First, true and false in C# are keywords, and IntelliSense knows that these are the only two values you can store in a bool variable. If you type in the statement

flag = 0;

IntelliSense issues an error message stating

Constant value '0' cannot be converted to a 'bool'

This message tells you that Visual Studio is unhappy with your attempt to assign a zero (an integer literal) into the boolean variable named flag. If you change the zero to false and recompile the program, the error message goes away because flag now is assigned the proper type of data.

Don't Use a bool Data Type for the Wrong Purpose

Because a bool data type can reflect only the states true or false, it cannot be used to count data. A bool variable should be used only when the information associated with the variable truly can have only two states. For example, a programmer was hired to write a program to track information about the members of a club. One of the variables, named Status, was implemented as a bool with the interpretation that true meant the person was an active member of the club and false meant the person was not an active member. After the program was written, the club noticed that the program didn't properly handle a member who had been granted a temporary leave of absence. This little change by the club caused the program to fail because the boolean Status variable was now asked to record three states: 1) active member, 2) inactive member, and 3) member on leave of absence. The programmer had to go back into the code and change Status from a bool to an int.

The lesson is simple: use a bool only when you are absolutely certain that the only possible states for the variable are true and false.

Summary

The discussion in this chapter concentrated on the various value types of data that you can use in your C# programs. More specifically, you learned about the various numeric data types you can use. Any time you want to manipulate data in a mathematical way, you will likely use one of the numeric data types discussed in this chapter. You also read about the bool data type in this chapter because it is a value type; although, it is not manipulated in a mathematical sense. (The char value type is excluded from this chapter even though it is a value type. Because its use is associated with textual data, its discussion is postponed until Chapter 6.)

In the next chapter you expand on your understanding of the basic value types and how they are used in a program. Make sure you understand what the different value types are and how they may be used in a program before advancing to Chapter 4.

Exercises

You can find the answers to the following exercises in Appendix A.

1. Why does C# support unsigned data types?

2. Identify each of the following variable names as legal or illegal.

3. Explain the following statement:

int len = txtInput.Text.Length;

4. What are the major differences between the float and double data types?

5. Suppose you want to generate a series of values that simulate throwing a pair of dice. Write a method named ThrowDice() that returns a value that is the sum of the two dice.

6. Gold can be used in financial transactions. With gold priced approximately $1,600 per ounce, what data type would you use to process financial transactions that use gold as the medium of exchange and why?

What You Learned in This Chapter