Programming in C (Fourth Edition) (2015)
11. Operations on Bits
As mentioned on previous occasions, the C language was developed with systems programming applications in mind. Pointers are the perfect case in point because they give the programmer an enormous amount of control over and access into the computer’s memory. Along these same lines, systems programmers frequently must get in and “twiddle with the bits” of particular computer words. You will learn how to manipulate bits with C-programming operators, including
![]() The bitwise AND operator
The bitwise AND operator
![]() The bitwise inclusive OR operator
The bitwise inclusive OR operator
![]() The bitwise exclusive OR operator
The bitwise exclusive OR operator
![]() The ones complement operator
The ones complement operator
![]() The left shift operator
The left shift operator
![]() The right shift operator
The right shift operator
![]() Bit fields
Bit fields
The Basics of Bits
Recall from the discussions in the previous chapter the concept of a byte. On most computer systems, a byte consists of eight smaller units called bits. A bit can assume either of two values: 1 or 0. So a byte stored at address 1000 in a computer’s memory, for example, might be conceptualized as a string of eight binary digits as shown:
01100100
The rightmost bit of a byte is known as the least significant or low-order bit, whereas the leftmost bit is known as the most significant or high-order bit. If you treat the string of bits as an integer, the rightmost bit of the preceding byte represents 20 or 1, the bit immediately to its left represents 21 or 2, the next bit 22 or 4, and so on. Therefore, the preceding binary number represents the value 22 + 25 + 26 = 4 + 32 + 64 = 100 decimal.
The representation of negative numbers is handled slightly differently. Most computers represent such numbers using a so-called “twos complement” notation. Using this notation, the leftmost bit represents the sign bit. If this bit is 1, the number is negative; otherwise, the bit is 0 and the number is positive. The remaining bits represent the value of the number. In twos complement notation, the value −1 is represented by all bits being equal to 1:
11111111
A convenient way to convert a negative number from decimal to binary is to first add 1 to the value, express the absolute value of the result in binary, and then “complement” all the bits; that is, change all 1s to 0s and 0s to 1s. So, for example, to convert -5 to binary, 1 is added, which gives -4; 4 expressed in binary is 00000100, and complementing the bits produces 11111011.
To convert a negative number from binary back to decimal, first complement all of the bits, convert the result to decimal, change the sign of the result, and then subtract 1.
Given this discussion about twos complement representation, the largest positive number that can be stored into n bits is 2n−1−1. So in eight bits, you can store a value up to 27 − 1, or 127. Similarly, the smallest negative number that can be stored into n bits is −2n−1, which in an eight-bit byte comes to −128. (Can you figure out why the largest positive and smallest negative values are not of the same magnitude?)
On most of today’s processors, integers occupy four contiguous bytes, or 32 bits, in the computer’s memory. The largest positive value that can, therefore, be stored into such an integer is 231−1 or 2,147,483,647, whereas the smallest negative number that can be stored is −2,147,483,648.
In Chapter 3, “Variables, Data Types, and Arithmetic Expressions,” you were introduced to the unsigned modifier and learned that it could be used to effectively increase the range of a variable. This is because the leftmost bit is no longer needed to store the sign of the number because you are only dealing with positive integers. This “extra” bit is used to increase the magnitude of the value stored in that variable by a factor of 2. More precisely, n bits can now be used to store values up to 2n−1. On a machine that stores integers in 32 bits, this means that unsigned integers can range in value from 0 through 4,294,967,296.
Bit Operators
Now that you have learned some preliminaries, it’s time to discuss the various bit operators that are available. Table 11.1 lists the C operators you can use to manipulate bits.
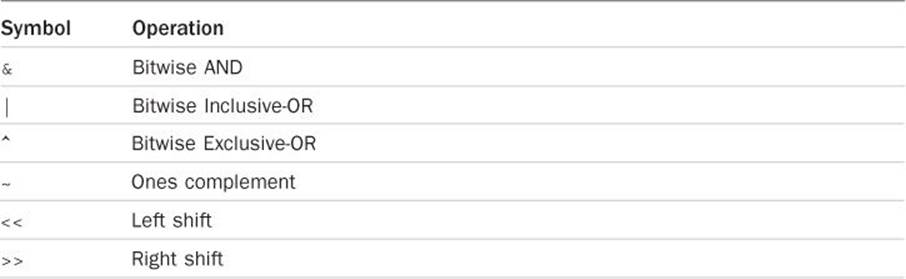
Table 11.1 Bit operators
All the operators listed in Table 11.1, with the exception of the ones complement operator ~, are binary operators and as such take two operands. Bit operations can be performed on any type of integer value in C—be it int, short, long, long long, and signed or unsigned—and on characters, but cannot be performed on floating-point values.
The Bitwise AND Operator
When two values are ANDed in C, the binary representations of the values are compared bit by bit. Each corresponding bit that is a 1 in the first value and a 1 in the second value produces a 1 in the corresponding bit position of the result; anything else produces a 0. If b1 and b2 represent corresponding bits of the two operands, then the following table, called a truth table, shows the result of b1 ANDed with b2 for all possible values of b1 and b2.
b1 b2 b1 & b2
—————————————————————
0 0 0
0 1 0
1 0 0
1 1 1
So, for example, if w1 and w2 are defined as short ints, and w1 is set equal to 25 and w2 is set equal to 77, then the C statement
w3 = w1 & w2;
assigns the value 9 to w3. This can be more easily seen by treating the values of w1, w2, and w3 as binary numbers. Assume that you are dealing with a short int size of 16 bits.
w1 0000000000011001 25
w2 0000000001001101 & 77
-------------------------
w3 0000000000001001 9
If you think about the way the logical AND operator && works (true only if both operands are true), you will be able to more easily remember the way the bitwise AND operator works. Incidentally, make sure that you don’t get these two operators confused! The logical AND operator && is used in logical expressions for producing a true/false result; it does not perform a bitwise AND.
Bitwise ANDing is frequently used for masking operations. That is, this operator can be used to easily set specific bits of a data item to 0. For example, the statement
w3 = w1 & 3;
assigns to w3 the value of w1 bitwise ANDed with the constant 3. This has the effect of setting all of the bits in w3, other than the rightmost two bits, to 0, and of preserving the rightmost two bits from w1.
As with all binary arithmetic operators in C, the binary bit operators can also be used as assignment operators by tacking on an equal sign. So the statement
word &= 15;
performs the same function as
word = word & 15;
and has the effect of setting all but the rightmost four bits of word to 0.
When using constants in performing bitwise operations, it is usually more convenient to express the constants in either octal or hexadecimal notation. The choice as to which to use is usually influenced by the size of the data with which you are dealing. For example, when dealing with 32-bit computers, hexadecimal notation is often used because 32 is an even multiple of 4 (the number of bits in a hexadecimal digit).
Program 11.1 is presented to illustrate the bitwise AND operator. Because you are dealing with only positive values in this program, all integers have been declared as unsigned int variables.
Program 11.1 The Bitwise AND Operator
// Program to demonstrate the bitwise AND operator
#include <stdio.h>
int main (void)
{
unsigned int word1 = 077u, word2 = 0150u, word3 = 0210u;
printf ("%o ", word1 & word2);
printf ("%o ", word1 & word1);
printf ("%o ", word1 & word2 & word3);
printf ("%o\n", word1 & 1);
return 0;
}
Program 11.1 Output
50 77 10 1
Recall that if an integer constant has a leading 0, it represents an octal (base 8) constant in C. Therefore, the three unsigned ints, word1, word2, and word3, are given initial octal values of 077, 0150, and 0210, respectively. Recall also from Chapter 3 that if a u or U follows an integer constant, it is treated as unsigned.
The first printf call displays octal 50 as the result of bitwise ANDing word1 with word2. The following depicts how this value was calculated:
word1 ... 000 111 111 077
word2 ... 001 101 000 & 0150
------------------------------
... 000 101 000 050
Only the rightmost nine bits of the previous values are shown because all bits to the left are 0. The binary numbers have been arranged in groups of three bits to make it easier to translate back and forth between binary and octal.
The second printf() call results in the display of octal 77, which is the result of ANDing word1 with itself. By definition, any quantity x, when ANDed with itself, produces x.
The third printf() call displays the result of ANDing word1, word2, and word3 together. The operation of bitwise ANDing is such that it makes no difference whether an expression such as a & b & c is evaluated as (a & b) & c or as a & (b & c), but for the record, evaluation proceeds from left to right. It is left as an exercise to you to verify that the displayed result of octal 10 is the correct result of ANDing word1 with word2 with word3.
The final printf() call has the effect of extracting the rightmost bit of word1. This is actually another way of testing if an integer is even or odd because that rightmost bit of any odd integer is 1 and of any even integer is 0. Therefore when the if statement
if ( word1 & 1 )
...
is executed, the expression is true if word1 is odd (because the result of the AND operation is 1) and false if it is even (because the result of the AND operation is 0). (Note: On machines that use a ones complement representation for numbers, this does not work for negative integers.)
The Bitwise Inclusive-OR Operator
When two values are bitwise Inclusive-ORed in C, the binary representation of the two values are once again compared bit by bit. This time, each bit that is a 1 in the first value or a 1 in the second value produces a 1 in the corresponding bit of the result. The truth table for the Inclusive-OR operator is shown next.
b1 b2 b1 | b2
————————————————————
0 0 0
0 1 1
1 0 1
1 1 1
So, if w1 is an unsigned int equal to octal 0431 and w2 is an unsigned int equal to octal 0152, then a bitwise Inclusive-OR of w1 and w2 produces a result of octal 0573 as shown:
w1 ... 100 011 001 0431
w2 ... 001 101 010 | 0152
------------------------------
... 101 111 011 0573
As was pointed out with the bitwise AND operator, be sure to not confuse the operation of bitwise ORing (|) with that of logical ORing (||), the latter operation being used to determine if either of two logical values is true.
Bitwise Inclusive-ORing, frequently called just bitwise ORing, is used to set some specified bits of a word to 1. For example, the statement
w1 = w1 | 07;
sets the three rightmost bits of w1 to 1, regardless of the state of these bits before the operation was performed. Of course, you could have used a special assignment operator in the statement, as follows:
w1 |= 07;
Presentation of a program example illustrating the use of the Inclusive-OR operator is deferred until later in this chapter.
The Bitwise Exclusive-OR Operator
The bitwise Exclusive-OR operator, which is often called the XOR operator, works as follows: For corresponding bits of the two operands, if either bit is a 1—but not both—the corresponding bit of the result is a 1; otherwise it is a 0. The truth table for this operator is as shown.
b1 b2 b1 ^ b2
—————————————————————
0 0 0
0 1 1
1 0 1
1 1 0
If w1 and w2 were set equal to octal 0536 and octal 0266, respectively, then the result of w1 Exclusive-ORed with w2 would be octal 0750, as illustrated:
w1 ... 101 011 110 0536
w2 ... 010 110 110 ^ 0266
------------------------------
... 111 101 000 0750
One interesting property of the Exclusive-OR operator is that any value Exclusive-ORed with itself produces 0. Historically, this trick was often used by assembly language programmers as a fast way to set a value to 0 or to compare two values to see if they were equal. This method is not recommended for use in C programs, however, as it doesn’t save time and most likely makes the program more obscure.
Another interesting application of the Exclusive-OR operator is that it can be used to effectively exchange two values without the need for an extra memory location. You know that you would normally interchange two integers called i1 and i2 with a sequence of statements such as
temp = i1;
i1 = i2;
i2 = temp;
Using the Exclusive-OR operator, you can exchange values without the need of the temporary storage location:
i1 ^= i2;
i2 ^= i1;
i1 ^= i2;
It is left as an exercise to you to verify that the previous statements do in fact succeed in interchanging the values of i1 and i2.
The Ones Complement Operator
The ones complement operator is a unary operator, and its effect is to simply “flip” the bits of its operand. Each bit of the operand that is a 1 is changed to a 0, and each bit that is a 0 is changed to a 1. The truth table is shown next simply for the sake of completeness.
b1 ~b1
——————
0 1
1 0
If w1 is a short int that is 16 bits long, and is set equal to octal 0122457, then taking the ones complement of this value produces a result of octal 0055320:
w1 1 010 010 100 101 111 0122457
~w1 0 101 101 011 010 000 0055320
The ones complement operator (~) should not be confused with the arithmetic minus operator (−) or with the logical negation operator (!). So if w1 is defined as an int, and set equal to 0, then −w1 still results in 0. If you apply the ones complement operator to w1, you end up with w1being set to all ones, which is −1 when treated as a signed value in twos complement notation. Finally, applying the logical negation operator to w1 produces the result true (1) because w1 is false (0).
The ones complement operator is useful when you don’t know the precise bit size of the quantity that you are dealing with in an operation. Its use can help make a program more portable—in other words, less dependent on the particular computer on which the program is running and, therefore, easier to get running on a different machine. For example, to set the low-order bit of an int called w1 to 0, you can AND w1 with an int consisting of all 1s except for a single 0 in the rightmost bit. So a statement in C such as
w1 &= 0xFFFFFFFE;
works fine on machines in which an integer is represented by 32 bits.
If you replace the preceding statement with
w1 &= ~1;
w1 gets ANDed with the correct value on any machine because the ones complement of 1 is calculated and consists of as many leftmost one bits as are necessary to fill the size of an int (31 leftmost bits on a 32-bit integer system).
Program 11.2 summarizes the various bitwise operators presented thus far. Before proceeding, however, it is important to mention the precedences of the various operators. The AND, OR, and Exclusive-OR operators each have lower precedence than any of the arithmetic or relational operators, but higher precedence than the logical AND and logical OR operators. The bitwise AND is higher in precedence than the bitwise Exclusive-OR, which in turn is higher in precedence than the bitwise OR. The unary ones complement operator has higher precedence than any binary operator. For a summary of these operator precedences, see Appendix A, “C Language Summary.”
Program 11.2 Illustrate Bitwise Operators
/* Program to illustrate bitwise operators */
#include <stdio.h>
int main (void)
{
unsigned int w1 = 0525u, w2 = 0707u, w3 = 0122u;
printf ("%o %o %o\n", w1 & w2, w1 | w2, w1 ^ w2);
printf ("%o %o %o\n", ~w1, ~w2, ~w3);
printf ("%o %o %o\n", w1 ^ w1, w1 & ~w2, w1 | w2 | w3);
printf ("%o %o\n", w1 | w2 & w3, w1 | w2 & ~w3);
printf ("%o %o\n", ~(~w1 & ~w2), ~(~w1 | ~w2));
w1 ^= w2;
w2 ^= w1;
w1 ^= w2;
printf ("w1 = %o, w2 = %o\n", w1, w2);
return 0;
}
Program 11.2 Output
505 727 222
37777777252 37777777070 37777777655
0 20 727
527 725
727 505
w1 = 707, w2 = 525
You should work out each of the operations from Program 11.2 with a paper and pencil to verify that you understand how the results were obtained. The program was run on a computer that uses 32 bits to represent an int.
In the fourth printf() call, it is important to remember that the bitwise AND operator has higher precedence than the bitwise OR, because this fact influences the resulting value of the expression.
The fifth printf() call illustrates DeMorgan’s rule, namely that ~(~a & ~b) is equal to a | b and that ~(~a | ~b) is equal to a & b. The sequence of statements that follow next in the program verifies that the exchange operation works as discussed in “The Bitwise Exclusive-OR Operator” section.
The Left Shift Operator
When a left shift operation is performed on a value, the bits contained in the value are literally shifted to the left. Associated with this operation is the number of places (bits) that the value is to be shifted. Bits that are shifted out through the high-order bit of the data item are lost, and 0s are always shifted in through the low-order bit of the value. So if w1 is equal to 3, then the expression
w1 = w1 << 1;
which can also be expressed as
w1 <<= 1;
results in 3 being shifted one place to the left, which results in 6 being assigned to w1:
w1 ... 000 011 03
w1 << 1 ... 000 110 06
The operand on the left of the << operator is the value to be shifted, whereas the operand on the right is the number of bit positions by which the value is to be shifted. If you shift w1 one more place to the left, you end up with octal 014 as the value of w1:
w1 ... 000 110 06
w1 << 1 ... 001 100 014
Left shifting actually has the effect of multiplying the value that is shifted by two. In fact, some C compilers automatically perform multiplication by a power of two by left shifting the value the appropriate number of places because shifting is a much faster operation than multiplication on most computers.
A program example illustrating the left shift operator is presented after the right shift operator has been described.
The Right Shift Operator
As implied from its name, the right shift operator >> shifts the bits of a value to the right. Bits shifted out of the low-order bit of the value are lost. Right shifting an unsigned value always results in 0s being shifted in on the left; that is, through the high-order bits. What is shifted in on the left for signed values depends on the sign of the value that is being shifted and also on how this operation is implemented on your computer system. If the sign bit is 0 (meaning the value is positive), 0s are shifted in regardless of which machine you are running. However, if the sign bit is 1, on some machines 1s are shifted in, and on others 0s are shifted in. This former type of operation is known as an arithmetic right shift, whereas the latter is known as a logical right shift.
Never make any assumptions about whether a system implements an arithmetic or a logical right shift. A program that shifts signed values right might work correctly on one system but fail on another due to this type of assumption.
If w1 is an unsigned int, which is represented in 32 bits, and w1 is set equal to hexadecimal F777EE22, then shifting w1 one place to the right with the statement
w1 >>= 1;
sets w1 equal to hexadecimal 7BBBF711.
w1 1111 0111 0111 0111 1110 1110 0010 0010 F777EE22
w1 >> 1 0111 1011 1011 1011 1111 0111 0001 0001 7BBBF711
If w1 were declared to be a (signed) short int, the same result would be produced on some computers; on others, the result would be FBBBF711 if the operation were performed as an arithmetic right shift.
It should be noted that the C language does not produce a defined result if an attempt is made to shift a value to the left or right by an amount that is greater than or equal to the number of bits in the size of the data item. So, on a machine that represents integers in 32 bits, for example, shifting an integer to the left or right by 32 or more bits is not guaranteed to produce a defined result in your program. You should also note that if you shift a value by a negative amount, the result is also undefined.
A Shift Function
Now, it’s time to put the left and right shift operators to work in an actual program example, as shown in Program 11.3. Some computers have a single machine instruction to shift a value to the left if the shift count is positive and to the right if the shift count is negative. Now, write a function in C to mimic this type of operation. You can have the function take two arguments: the value to be shifted and the shift count. If the shift count is positive, the value is shifted left the designated number of places; otherwise, the value is shifted right the number of places as specified by the absolute value of the shift count.
Program 11.3 Implementing a Shift Function
// Function to shift an unsigned int left if
// the count is positive, and right if negative
#include <stdio.h>
unsigned int shift (unsigned int value, int n)
{
if ( n > 0 ) // left shift
value <<= n;
else // right shift
value >>= -n;
return value;
}
int main (void)
{
unsigned int w1 = 0177777u, w2 = 0444u;
unsigned int shift (unsigned int value, int n);
printf ("%o\t%o\n", shift (w1, 5), w1 << 5);
printf ("%o\t%o\n", shift (w1, -6), w1 >> 6);
printf ("%o\t%o\n", shift (w2, 0), w2 >> 0);
printf ("%o\n", shift (shift (w1, -3), 3));
return 0;
}
Program 11.3 Output
7777740 7777740
1777 1777
444 444
177770
The shift() function shown in Program 11.3 declares the type of the argument value to be unsigned int, thus ensuring that a right shift of value will be zero filled; in other words, performed as a logical right shift.
If the value of n, which is the shift count, is greater than zero, the function shifts value left n bits. If n is negative (or zero), the function performs a right shift, where the number of places that value is shifted is obtained by negating the value of n.
The first call to the shift() function from the main() routine specifies that the value of w1 is to be left shifted five bits. The printf() call that displays the result of the call to the shift() function also displays the result of directly shifting w1 left five places so that these values can be compared.
The second call to the shift() function has the effect of shifting w1 six places to the right. The result returned by the function is identical to the result obtained by directly shifting w1 to the right six places, as verified by the program’s output.
In the third call to shift(), a shift count of zero is specified. In this case, the shift function performs a right shift of value by zero bits, which, as you can see from the program’s output, has no effect on the value.
The final printf() call illustrates nested function calls to the shift() function. The innermost call to shift() is executed first. This call specifies that w1 is to be shifted right three places. The result of this function call, which is 0017777, is then passed to the shift() function to be shifted to the left three places. As you can see from the program’s output, this has the net effect of setting the low-order three bits of w1 to 0. (Of course, you know by now that this could also have been done by simply ANDing w1 with ~7.)
Rotating Bits
For the next program example, which ties together some of the bit operations presented in this chapter, you will develop a function to rotate a value to the left or right. The process of rotation is similar to shifting, except that when a value is rotated to the left, the bits that are shifted out of the high-order bits are shifted back into the low-order bits. When a value is rotated to the right, the bits that are shifted out of the low-order bits of the value are shifted back into the high-order bits. So, if you are dealing with 32-bit unsigned integers, the value hexadecimal 80000000 rotated to the left by one bit produces hexadecimal 00000001 because the 1 from the sign bit that is normally lost by a left shift of one bit is brought around and shifted back into the low-order bit.
Your function takes two arguments: the first, the value to be rotated, and the second, the number of bits by which the object is to be rotated. If this second argument is positive, you rotate the value to the left; otherwise, you rotate the value to the right.
You can adopt a fairly straightforward approach to implementing your rotate function. For example, to compute the result of rotating x to the left by n bits, where x is of type int and n ranges from 0 to the number of bits in an int minus 1, you can extract the leftmost n bits of x, shift x to the left by n bits, and then put the extracted bits back into x at the right. A similar algorithm also can be used to implement the right rotate function.
Program 11.4 implements the rotate() function using the algorithm described previously. This function makes the assumption that an int uses 32 bits on the computer. Exercises at the end of the chapter show one way to write this function so that this assumption does not have to be made.
Program 11.4 Implementing a Rotate Function
// Program to illustrate rotation of integers
#include <stdio.h>
int main (void)
{
unsigned int w1 = 0xabcdef00u, w2 = 0xffff1122u;
unsigned int rotate (unsigned int value, int n);
printf ("%x\n", rotate (w1, 8));
printf ("%x\n", rotate (w1, -16));
printf ("%x\n", rotate (w2, 4));
printf ("%x\n", rotate (w2, -2));
printf ("%x\n", rotate (w1, 0));
printf ("%x\n", rotate (w1, 44));
return 0;
}
// Function to rotate an unsigned int left or right
unsigned int rotate (unsigned int value, int n)
{
unsigned int result, bits;
// scale down the shift count to a defined range
if ( n > 0 )
n = n % 32;
else
n = -(-n % 32);
if ( n == 0 )
result = value;
else if ( n > 0 ) { // left rotate
bits = value >> (32 - n);
result = value << n | bits;
}
else { // right rotate
n = -n;
bits = value << (32 - n);
result = value >> n | bits;
}
return result;
}
Program 11.4 Output
cdef00ab
ef00abcd
fff1122f
bfffc448
abcdef00
def00abc
The function first ensures that the shift count, n, is valid. The code
if ( n > 0 )
n = n % 32;
else
n = -(-n % 32);
checks first to see if n is positive. If it is, the value of n modulo the size of an int (assumed to be 32 in this example) is calculated and stored back inside n. This places the shift count in the range of 0 through 31. If n is negative, its value is negated before the modulus operator is applied. This is done because C does not define the sign of the result of applying the modulus operator to a negative value. Your machine can produce either a positive or negative result. By negating the value first, you ensure the result is positive. You then apply the unary minus operator to the result to turn it negative again; that is, within the range of values −31 through 0.
If the adjusted shift count is 0, the function simply assigns value to result. Otherwise, it proceeds with the rotation.
An n-bit rotation to the left is divided into three steps by the function. First, the n leftmost bits of value are extracted and shifted to the right. This is done by shifting value to the right by the size of an int (in our case, 32) minus n. Next, value is shifted n bits to the left, and finally, the extracted bits are ORed back in. A similar procedure is followed to rotate value to the right.
In the main() routine, note the use of hexadecimal notation for a change. The first call to the rotate() function specifies that the value of w1 is to be rotated eight bits to the left. As can be seen from the program’s output, the hexadecimal value cdef00ab is returned by the rotate()function, which is in fact abcdef00 rotated to the left eight bits.
The second call to the rotate() function has the effect of rotating the value of w1 16 bits to the right.
The next two calls to the rotate() function do similar things with the value of w2 and are fairly self-explanatory. The next-to-last call to rotate() specifies a rotate count of 0. The program’s output verifies that in such a case the function simply returns the value unchanged.
The final call to rotate() specifies a left rotate 44 places. This has the net effect of rotating the value left 12 bits (44 % 32 is 12).
Bit Fields
With the bit operators discussed previously, you can proceed to perform all sorts of sophisticated operations on bits. Bit operations are frequently performed on data items that contain packed information. Just as a short int can be used to conserve memory space on some computers, so can you pack information into the bits of a byte or word if you do not need to use the entire byte or word to represent the data. For example, flags that are used for a Boolean true or false condition can be represented in a single bit on a computer. Declaring a char variable that will be used as a flag uses eight bits (one byte) on most computers, and a _Bool variable is likely to use eight bits as well. In addition, if you need to store many flags inside a large table, the amount of memory that is wasted could become significant.
Two methods are available in C that can be used to pack information together to make better use of memory. One way is to simply represent the data inside a normal int, for example, and then access the desired bits of the int using the bit operators described in the previous sections. Another way is to define a structure of packed information using a C construct known as a bit field.
To illustrate how the first method can be used, suppose you want to pack five data values into a word because you have to maintain a very large table of these values in memory. Assume that three of these data values are flags, which you call f1, f2, and f3; the fourth value is an integer called type, which ranges from 1 to 255; and the final value is an integer called index, which ranges from 0 to 100,000.
Storing the values of the flags f1, f2, and f3 only requires three bits of storage, one bit for the true/false value of each flag. Storing the value of the integer type, which ranges from 1 to 255, requires eight bits of storage. Finally, storing the value of the integer index, which can assume a value from 0 to 100,000, requires 18 bits. Therefore, the total amount of storage needed to store the five data values, f1, f2, f3, type, and index, is 29 bits. You could define an integer variable that could be used to contain all five of these values, as in
unsigned int packed_data;
and could then arbitrarily assign specific bits or fields inside packed_data to be used to store the five data values. One such assignment is depicted in Figure 11.1, which assumes that the size of packed_data is 32 bits.
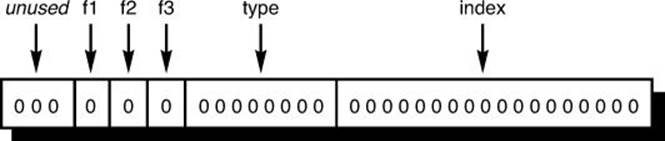
Figure 11.1 Bit field assignments in packed_data.
Note that packed_data has three unused bits. You can now apply the correct sequence of bit operations to packed_data to set and retrieve values to and from the various fields of the integer. For example, you can set the type field of packed_data to 7 by shifting the value 7 the appropriate number of places to the left and then ORing it into packed_data:
packed_data |= 7 << 18;
or you can set the type field to the value n, where n is between 0 and 255, by the statement
packed_data |= n << 18;
To ensure that n is between 0 and 255, you can AND it with 0xff before it is shifted.
Of course, the preceding statements only work if you know that the type field is zero; otherwise, you must zero it first by ANDing it with a value (frequently called a mask) that consists of 0s in the eight bit locations of the type field and 1s everywhere else:
packed_data &= 0xfc03ffff;
To save yourself the bother of having to explicitly calculate the preceding mask, and also to make the operation independent of the size of an integer, you could instead use the following statement to set the type field to zero:
packed_data &= ~(0xff << 18);
Combining the statements described previously, you can set the type field of packed_data to the value contained in the eight low-order bits of n, irrespective of any value previously stored in this field, with the following statement:
packed_data = (packed_data & ~(0xff << 18)) | ((n & 0xff) << 18);
In the preceding code, some of the parentheses are superfluous but were added to aid readability.
You can see how complex the preceding expression is for accomplishing the relatively simple task of setting the bits in the type field to a specified value. Extracting a value from one of these fields is not as bad: The field can be shifted into the low-order bits of the word and then ANDed with a mask of the appropriate bit length. So, to extract the type field of packed_data and assign it to n, the statement
n = (packed_data >> 18) & 0xff;
does the trick.
The C language does provide a more convenient way of dealing with bit fields. This method uses a special syntax in the structure definition that allows you to define a field of bits and assign a name to that field. Whenever the term “bit fields” is applied to C, it is this approach that is referenced.
To define the bit field assignments previously mentioned, you can define a structure called packed_struct, for example, as follows:
struct packed_struct
{
unsigned int :3;
unsigned int f1:1;
unsigned int f2:1;
unsigned int f3:1;
unsigned int type:8;
unsigned int index:18;
};
The structure packed_struct is defined to contain six members. The first member is not named. The :3 specifies three unnamed bits. The second member, called f1, is also an unsigned int. The :1 that immediately follows the member name specifies that this member is to be stored in one bit. The flags f2 and f3 are similarly defined as being a single bit in length. The member type is defined to occupy eight bits, whereas the member index is defined as being 18 bits long.
The C compiler automatically packs the preceding bit field definitions together. The nice thing about this approach is that the fields of a variable defined to be of type packed_struct can now be referenced in the same convenient way normal structure members are referenced. So, if you declare a variable called packed_data as follows:
struct packed_struct packed_data;
you could easily set the type field of packed_data to 7 with the simple statement
packed_data.type = 7;
or you could set this field to the value of n with the similar statement
packed_data.type = n;
In this last case, you need not worry about whether the value of n is too large to fit into the type field; only the low-order eight bits of n will be assigned to packed_data.type.
Extraction of the value from a bit field is also automatically handled, so the statement
n = packed_data.type;
extracts the type field from packed_data (automatically shifting it into the low-order bits as required) and assigns it to n.
Bit fields can be used in normal expressions and are automatically converted to integers. So the statement
i = packed_data.index / 5 + 1;
is perfectly valid, as is
if ( packed_data.f2 )
...
which tests if flag f2 is true or false. One thing worth noting about bit fields is that there is no guarantee whether the fields are internally assigned from left to right or from right to left. This should not present a problem unless you are dealing with data that was created by a different program or by a different machine. In such cases, you must know how the bit fields are assigned and make the declarations appropriately. You could have defined the structure packed_struct as
struct packed_struct
{
unsigned int index:9;
unsigned int type:4;
unsigned int f3:1;
unsigned int f2:1;
unsigned int f1:1;
unsigned int :3;
};
to achieve the same representation on a machine that assigns fields from right to left as depicted in Figure 11.1. Never make any assumptions about how structure members—whether they contain bit field members or not—are stored.
You can also include normal data types within a structure that contains bit fields. So if you want to define a structure that contained an int, a char, and two one-bit flags, the following definition is valid:
struct table_entry
{
int count;
char c;
unsigned int f1:1;
unsigned int f2:1;
};
Certain points are worth mentioning with respect to bit fields. They can only be declared to be of integer or _Bool type. If just int is used in the declaration, it’s implementation dependent whether this is interpreted as a signed or unsigned value. To play it safe, use the explicit declarationssigned int or unsigned int. A bit field cannot be dimensioned; that is, you cannot have an array of fields, such as flag:1[5]. Finally, you cannot take the address of a bit field, and, therefore, there is obviously no such thing as a type “pointer to bit field.”
Bit fields are packed into units as they appear in the structure definition, where the size of a unit is defined by the implementation and is most likely a word.
The C compiler does not rearrange the bit field definitions to try to optimize storage space.
A final point concerning the specification of fields concerns the special case of an unnamed field of length 0. This can be used to force alignment of the next field in the structure at the start of a unit boundary.
This concludes the discussion of bit operations in C. You can see how much power and flexibility the C language provides for the efficient manipulation of bits. Operators are conveniently provided in the language for performing bitwise AND, Inclusive-OR, Exclusive-OR, ones complement, and left and right shift operations. A special bit field format enables you to allocate a specified number of bits for a data item and to easily set and retrieve its value without having to use masking and shifting.
See Chapter 13, ”Extending Data Types with the Enumerated Data Type, Type Definitions, and Data Type Conversions,” for a discussion on what happens when you perform bitwise operations between two values of differing integral types, for example between an unsigned long intand a short int.
Before proceeding to the next chapter, try the following exercises to test your understanding of bit operations in C.
Exercises
1. Type in and run the four programs presented in this chapter. Compare the output produced by each program with the output presented after each program in the text.
2. Write a program that determines whether your particular computer performs an arithmetic or a logical right shift.
3. Given that the expression ~0 produces an integer that contains all 1s, write a function called int_size() that returns the number of bits contained in an int on your particular machine.
4. Using the result obtained in exercise 3, modify the rotate() function from Program 11.4 so that it no longer makes any assumptions about the size of an int.
5. Write a function called bit_test() that takes two arguments: an unsigned int and a bit number n. Have the function return 1 bit number n if it is on inside the word, and 0 if it is off. Assume that bit number 0 references the leftmost bit inside the integer. Also write a corresponding function called bit_set() that takes two arguments: an unsigned int and a bit number n. Have the function return the result of turning bit n on inside the integer.
6. Write a function called bitpat_search() that looks for the occurrence of a specified pattern of bits inside an unsigned int. The function should take three arguments and should be called as shown:
bitpat_search (source, pattern, n)
The function searches the integer source, starting at the leftmost bit, to see if the rightmost n bits of pattern occur in source. If the pattern is found, have the function return the number of the bit at which the pattern begins, where the leftmost bit is bit number 0. If the pattern is not found, then have the function return −1. So, for example, the call
index = bitpat_search (0xe1f4, 0x5, 3);
causes the bitpat_search() function to search the number 0xe1f4 ( = 1110 0001 1111 0100 binary ) for the occurrence of the three-bit pattern 0x5 (= 101 binary). The function returns 11 to indicate that the pattern was found in the source beginning with bit number 11.
Make certain that the function makes no assumptions about the size of an int (see exercise 3 in this chapter).
7. Write a function called bitpat_get() to extract a specified set of bits. Have it take three arguments: the first an unsigned int, the second an integer starting bit number, and the third a bit count. Using the convention that bit numbering starts at 0 with the leftmost bit, extract the specified number of bits from the first argument and return the result. So the call
bitpat_get (x, 0, 3)
extracts the three leftmost bits from x. The call
bitpat_get (x, 3, 5)
extracts five bits starting with the fourth bit in from the left.
8. Write a function called bitpat_set() to set a specified set of bits to a particular value. The function should take four arguments: a pointer to an unsigned int in which the specified bits are to be set; another unsigned int containing the value to which the specified bits are to be set, right adjusted in the unsigned int; a third int that specifies the starting bit number (with the leftmost bit numbered 0); and a fourth int specifying the size of the field. So the call
bitpat_set (&x, 0, 2, 5);
has the effect of setting the five bits contained in x, beginning with the third bit from the left (bit number 2), to 0. Similarly, the call
bitpat_set (&x, 0x55u, 0, 8);
sets the eight leftmost bits of x to hexadecimal 55.
Make no assumptions about the particular size of an int (refer to exercise 3 in this chapter).
All materials on the site are licensed Creative Commons Attribution-Sharealike 3.0 Unported CC BY-SA 3.0 & GNU Free Documentation License (GFDL)
If you are the copyright holder of any material contained on our site and intend to remove it, please contact our site administrator for approval.
© 2016-2025 All site design rights belong to S.Y.A.