Programming in C (Fourth Edition) (2015)
6. Working with Arrays
The C language provides a capability that enables you to define a set of ordered data items known as an array. This chapter describes how arrays can be defined and manipulated. In later chapters, you learn more about arrays to illustrate how well they work together with program functions, structures, character strings, and pointers. But before you get to those topics, you first need to cover the basics of arrays, including
![]() Setting up simple arrays
Setting up simple arrays
![]() Initializing arrays
Initializing arrays
![]() Working with character arrays
Working with character arrays
![]() Using the const keyword
Using the const keyword
![]() Implementing multidimensional arrays
Implementing multidimensional arrays
![]() Creating variable-length arrays
Creating variable-length arrays
Suppose you have a set of grades that you want to read into the computer, and suppose that you want to perform some operations on these grades, such as rank them in ascending order, compute their average, or find their median. In Program 5.2, you were able to calculate the average of a set of grades by simply adding each grade into a cumulative total as each grade was entered. However, if you want to rank the grades into ascending order, for example, you need to do something further. If you think about the process of ranking a set of grades, you quickly realize that you cannot perform such an operation until each and every grade has been entered. Therefore, using the techniques described previously, you would read in each grade and store it into a unique variable, perhaps with a sequence of statements such as the following:
printf ("Enter grade 1\n");
scanf ("%i", &grade1);
printf ("Enter grade 2\n");
scanf ("%i", &grade2);
. . .
After the grades have been entered, you can then proceed to rank them. This can be done by setting up a series of if statements to compare each of the values to determine the smallest grade, the next smallest grade, and so on, until the maximum grade has been determined. If you sit down and try to write a program to perform precisely this task, you soon realize that for any reasonably sized list of grades (where reasonably sized is probably only about 10), the resulting program is quite large and complex. All is not lost, however, as this is one instance in which the array comes to the rescue.
Defining an Array
You can define a variable called grades, which represents not a single value of a grade, but an entire set of grades. Each element of the set can then be referenced by means of a number called an index number or subscript. Whereas in mathematics a subscripted variable, xi, refers to the ith element x in a set, in C the equivalent notation is as follows:
x[i]
So the expression
grades[5]
(read as “grades sub 5”) refers to element number 5 in the array called grades. Array elements begin with the number zero, so
grades[0]
actually refers to the first element of the array. (For this reason, it is easier to think of it as referring to element number zero, rather than as referring to the first element.)
An individual array element can be used anywhere that a normal variable can be used. For example, you can assign an array value to another variable with a statement such as the following:
g = grades[50];
This statement takes the value contained in grades[50] and assigns it to g. More generally, if i is declared to be an integer variable, the statement
g = grades[i];
takes the value contained in element number i of the grades array and assigns it to g. So if i is equal to 7 when the preceding statement is executed, the value of grades[7] is assigned to g.
A value can be stored in an element of an array simply by specifying the array element on the left side of an equal sign. In the statement
grades[100] = 95;
the value 95 is stored in element number 100 of the grades array. The statement
grades[i] = g;
has the effect of storing the value of g in grades[i].
The capability to represent a collection of related data items by a single array enables you to develop concise and efficient programs. For example, you can easily sequence through the elements in the array by varying the value of a variable that is used as a subscript in the array. So the forloop
for ( i = 0; i < 100; ++i )
sum += grades[i];
sequences through the first 100 elements of the array grades (elements 0 through 99) and adds the value of each grade into sum. When the for loop is finished, the variable sum then contains the total of the first 100 values of the grades array (assuming sum was set to zero before the loop was entered).
When working with arrays, remember that the first element of an array is indexed by zero, and the last element is indexed by the number of elements in the array minus one.
In addition to integer constants, integer-valued expressions can also be used inside the brackets to reference a particular element of an array. So if low and high are defined as integer variables, the statement
next_value = sorted_data[(low + high) / 2];
assigns the value indexed to the variable next_value by evaluating the expression (low + high) / 2. If low is equal to 1 and high is equal to 9, the value of sorted_data[5] is assigned to next_value. In addition, if low is equal to 1 and high is equal to 10, the value ofsorted_data[5] is also referenced because you know that an integer division of 11 by 2 gives the result of 5.
Just as with variables, arrays must also be declared before they are used. The declaration of an array involves declaring the type of element that will be contained in the array—such as int, float, or char—as well as the maximum number of elements that will be stored inside the array. (The C compiler needs this latter information to determine how much of its memory space to reserve for the particular array.)
As an example, the declaration
int grades[100];
declares grades to be an array containing 100 integer elements. Valid references to this array can be made by using subscripts from 0 through 99. But be careful to use valid subscripts because C does not do any checking of array bounds for you. So a reference to element number 150 of array grades, as previously declared, does not necessarily cause an error but does most likely cause unwanted, if not unpredictable, program results.
To declare an array called averages that contains 200 floating-point elements, the declaration
float averages[200];
is used. This declaration causes enough space inside the computer’s memory to be reserved to contain 200 floating-point numbers. Similarly, the declaration
int values[10];
reserves enough space for an array called values that could hold up to 10 integer numbers. You can better conceptualize this reserved storage space by referring to Figure 6.1.

Figure 6.1 The array values in memory.
The elements of arrays declared to be of type int, float, or char can be manipulated in the same fashion as ordinary variables. You can assign values to them, display their values, add to them, subtract from them, and so on. So, if the following statements appear in a program, the arrayvalues would contain the numbers as shown in Figure 6.2.

Figure 6.2 values with some initialized elements.
int values[10];
values[0] = 197;
values[2] = -100;
values[5] = 350;
values[3] = values[0] + values[5];
values[9] = values[5] / 10;
--values[2];
The first assignment statement has the effect of storing the value 197 in values[0]. In a similar fashion, the second and third assignment statements store −100 and 350 into values[2] and values[5], respectively. The next statement adds the contents of values[0] (which is197) to the contents of values[5] (which is 350) and stores the result of 547 in values[3]. In the following program statement, 350—the value contained in values[5]—is divided by 10 and the result is stored in values[9]. The last statement decrements the contents ofvalues[2], which has the effect of changing its value from −100 to −101.
The preceding program statements are incorporated into Program 6.1. The for loop sequences through each element of the array, displaying its value at the terminal in turn.
Program 6.1 Working with an Array
#include <stdio.h>
int main (void)
{
int values[10];
int index;
values[0] = 197;
values[2] = -100;
values[5] = 350;
values[3] = values[0] + values[5];
values[9] =
values[5] / 10;
--values[2];
for ( index = 0; index < 10; ++index )
printf ("values[%i] = %i\n", index, values[index]);
return 0;
}
Program 6.1 Output
values[0] = 197
values[1] = -2
values[2] = -101
values[3] = 547
values[4] = 4200224
values[5] = 350
values[6] = 4200326
values[7] = 4200224
values[8] = 8600872
values[9] = 35
The variable index assumes the values 0 through 9 as the last valid subscript of an array is always one less than the number of elements (due to that zeroth element). Because you never assigned values to five of the elements in the array—elements 1, 4, and 6 through 8—the valuesthat are displayed for them are meaningless. You will probably see different values than what are displayed here. For this reason, no assumption should ever be made as to the value of an uninitialized variable or array element.
Using Array Elements as Counters
It’s now time to consider a slightly more practical example. Suppose you took a telephone survey to discover how people felt about a particular television show and you asked each respondent to rate the show on a scale from 1 to 10, inclusive. After interviewing 5,000 people, you accumulated a list of 5,000 numbers. Now, you want to analyze the results. One of the first pieces of data you want to gather is a table showing the distribution of the ratings. In other words, you want to know how many people rated the show a 1, how many rated it a 2, and so on up to 10.
Although not an impossible chore, it would be a bit tedious to go through each response and manually count the number of responses in each rating category. In addition, if you have a response that could be answered in more than 10 ways (consider the task of categorizing the age of the respondent), this approach would be even more unreasonable. So, you want to develop a program to count the number of responses for each rating. The first impulse might be to set up 10 different counters, called perhaps rating_1 through rating_10, and then to increment the appropriate counter each time the corresponding rating was entered. But once again, if you are dealing with more than 10 possible choices, this approach could become a bit tedious. And besides, an approach that uses an array provides the vehicle for implementing a much cleaner solution, even in this case.
You can set up an array of counters called ratingCounters, for example, and then you can increment the corresponding counter as each response is entered. To conserve space in this book, Program 6.2 assumes you are dealing with only 20 responses. In addition, it’s always good practice to first get a program working on a smaller test case before proceeding with the full set of data because problems that are discovered in the program are much easier to isolate and debug if the amount of test data is small.
Program 6.2 Demonstrating an Array of Counters
#include <stdio.h>
int main (void)
{
int ratingCounters[11], i, response;
for ( i = 1; i <= 10; ++i )
ratingCounters[i] = 0;
printf ("Enter your responses\n");
for ( i = 1; i <= 20; ++i ) {
scanf ("%i", &response);
if ( response < 1 || response > 10 )
printf ("Bad response: %i\n", response);
else
++ratingCounters[response];
}
printf ("\n\nRating Number of Responses\n");
printf ("------ -------------------\n");
for ( i = 1; i <= 10; ++i )
printf ("%4i%14i\n", i, ratingCounters[i]);
return 0;
}
Program 6.2 Output
Enter your responses
6583965715
Bad response: 15
551741055689
Rating Number of Responses
------ -------------------
1 1
2 0
3 1
4 1
5 6
6 3
7 2
8 2
9 2
10 1
The array ratingCounters is defined to contain 11 elements. A valid question you might ask is, “If there are only 10 possible responses to the survey, why is the array defined to contain 11 elements rather than 10?” The answer lies in the strategy for counting the responses in each particular rating category. Because each response can be a number from 1 to 10, the program keeps track of the responses for any one particular rating by simply incrementing the corresponding array element (after first checking to make certain that the user entered a valid response between 1 and 10). For example, if a rating of 5 is typed in, the value of ratingCounters[5] is incremented by one. By employing this technique, the total number of respondents who rated the TV show a 5 are contained in ratingCounters[5].
The reason for 11 elements versus 10 should now be clear. Because the highest rating number is a 10, you must set up your array to contain 11 elements to index ratingCounters[10], remembering that because of the zeroth element, the number of elements in an array is always one more than the highest index number. Because no response can have a value of zero, ratingCounters[0] is never used. In fact, in the for loops that initialize and display the contents of the array, note that the variable i starts at 1, and thereby bypasses the initialization and display ofratingCounters[0].
As a point of discussion, you could have developed your program to use an array containing precisely 10 elements. Then, when each response was keyed in by the user, you could have instead incremented ratingCounters[response - 1]. This way, ratingCounters[0] would have contained the number of respondents who rated the show a 1, ratingCounters[1] the number who rated the show a 2, and so on. This is a perfectly fine approach. The only reason it was not used is because storing the number of responses of value n inside ratingCounters[n]is a slightly more straightforward approach.
Generating Fibonacci Numbers
Study Program 6.3, which generates a table of the first 15 Fibonacci numbers, and try to predict its output. What relationship exists between each number in the table?
Program 6.3 Generating Fibonacci Numbers
// Program to generate the first 15 Fibonacci numbers
#include <stdio.h>
int main (void)
{
int Fibonacci[15], i;
Fibonacci[0] = 0; // by definition
Fibonacci[1] = 1; // ditto
for ( i = 2; i < 15; ++i )
Fibonacci[i] = Fibonacci[i-2] + Fibonacci[i-1];
for ( i = 0; i < 15; ++i )
printf ("%i\n", Fibonacci[i]);
return 0;
}
Program 6.3 Output
0
1
1
2
3
5
8
13
21
34
55
89
144
233
377
The first two Fibonacci numbers, called F0 and F1, are defined to be 0 and 1, respectively. Thereafter, each successive Fibonacci number Fi is defined to be the sum of the two preceding Fibonacci numbers Fi−2 and Fi−1. So F2 is calculated by adding together the values of F0 and F1. In the preceding program, this corresponds directly to calculating Fibonacci[2] by adding the values Fibonacci[0] and Fibonacci[1]. This calculation is performed inside the for loop, which calculates the values of F2 through F14 (or, equivalently, Fibonacci[2] throughFibonacci[14]).
Fibonacci numbers actually have many applications in the field of mathematics and in the study of computer algorithms. The sequence of Fibonacci numbers historically originated from the “rabbits problem”: If you start with a pair of rabbits and assume that each pair of rabbits produces a new pair of rabbits each month, that each newly born pair of rabbits can produce offspring by the end of their second month, and that rabbits never die, how many pairs of rabbits will you have after the end of one year? The answer to this problem rests in the fact that at the end of the nth month, there will be a total of Fn+2 rabbits. Therefore, according to the table from Program 6.3, at the end of the twelfth month, you will have a total of 377 pairs of rabbits.
Using an Array to Generate Prime Numbers
Now, it’s time to return to the prime number program that you developed in Chapter 5, “Making Decisions,” and see how the use of an array can help you to develop a more efficient program. In Program 5.10A, the criteria that you used for determining if a number was prime was to divide the prime candidate by all successive integers from 2 up to the number −1. In exercise 7 in Chapter 5, you noted two inefficiencies with this approach that could easily be corrected. But even with these changes, the approach used is still not efficient. Although such questions of efficiency might not be important when dealing with a table of prime numbers up to 50, these questions do become important, for example, when you start thinking about generating a table of prime numbers up to 100,000.
An improved method for generating prime numbers involves the notion that a number is prime if it is not evenly divisible by any other prime number. This stems from the fact that any nonprime integer can be expressed as a multiple of prime factors. (For example, 20 has the prime factors 2, 2, and 5.) You can use this added insight to develop a more efficient prime number program. The program can test if a given integer is prime by determining if it is evenly divisible by any other previously generated prime. By now the term “previously generated” should trigger in your mind the idea that an array must be involved here. You can use an array to store each prime number as it is generated.
As a further optimization of the prime number generator program, it can be readily demonstrated that any nonprime integer n must have as one of its factors an integer that is less than or equal to the square root of n. This means that it is only necessary to determine if a given integer is prime by testing it for even divisibility against all prime factors up to the square root of the integer.
Program 6.4 incorporates the previous discussions into a program to generate all prime numbers up to 50.
Program 6.4 Revising the Program to Generate Prime Numbers, Version 2
#include <stdio.h>
#include <stdbool.h>
// Modified program to generate prime numbers
int main (void)
{
int p, i, primes[50], primeIndex = 2;
bool isPrime;
primes[0] = 2;
primes[1] = 3;
for ( p = 5; p <= 50; p = p + 2 ) {
isPrime = true;
for ( i = 1; isPrime && p / primes[i] >= primes[i]; ++i )
if ( p % primes[i] == 0 )
isPrime = false;
if ( isPrime == true ) {
primes[primeIndex] = p;
++primeIndex;
}
}
for ( i = 0; i < primeIndex; ++i )
printf ("%i ", primes[i]);
printf ("\n");
return 0;
}
Program 6.4 Output
2 3 5 7 11 13 17 19 23 29 31 37 41 43 47
The expression
p / primes[i] >= primes[i]
is used in the innermost for loop as a test to ensure that the value of p does not exceed the square root of primes[i]. This test comes directly from the discussions in the previous paragraph. (You might want to think about the math a bit.)
Program 6.4 starts by storing 2 and 3 as the first two primes in the array primes. This array has been defined to contain 50 elements, even though you obviously don’t need that many locations for storing the prime numbers. The variable primeIndex is initially set to 2, which is the next free slot in the primes array. A for loop is then set up to run through the odd integers from 5 to 50. After the Boolean variable isPrime is set to true, another for loop is entered. This loop successively divides the value of p by all of the previously generated prime numbers that are stored in the array primes. The index variable i starts at 1 because it is not necessary to test any values of p for divisibility by primes[0] (which is 2). This is true because our program does not even consider even numbers as possible primes. Inside the loop, a test is made to see if the value of p is evenly divisible by primes[i], and if it is, then isPrime is set false. The for loop continues execution so long as the value of isPrime is true and the value of primes[i] does not exceed the square root of p.
After exiting the for loop, a test of the isPrime flag determines whether to store the value of p as the next prime number inside the primes array.
After all values of p have been tried, the program displays each prime number that has been stored inside the primes array. The value of the index variable i varies from 0 through primeIndex - 1 because primeIndex was always set pointing to the next free slot in the primesarray.
Initializing Arrays
Just as you can assign initial values to variables when they are declared, so can you assign initial values to the elements of an array. This is done by simply listing the initial values of the array, starting from the first element. Values in the list are separated by commas and the entire list is enclosed in a pair of braces.
The statement
int counters[5] = { 0, 0, 0, 0, 0 };
declares an array called counters to contain five integer values and initializes each of these elements to zero. In a similar fashion, the statement
int integers[5] = { 0, 1, 2, 3, 4 };
sets the value of integers[0] to 0, integers[1] to 1, integers[2] to 2, and so on.
Arrays of characters are initialized in a similar manner; thus the statement
char letters[5] = { 'a', 'b', 'c', 'd', 'e' };
defines the character array letters and initializes the five elements to the characters 'a', 'b', 'c', 'd', and 'e', respectively.
It is not necessary to completely initialize an entire array. If fewer initial values are specified, only an equal number of elements are initialized. The remaining values in the array are set to zero. So the declaration
float sample_data[500] = { 100.0, 300.0, 500.5 };
initializes the first three values of sample_data to 100.0, 300.0, and 500.5, and sets the remaining 497 elements to zero.
By enclosing an element number in a pair of brackets, specific array elements can be initialized in any order. For example,
float sample_data[500] = { [2] = 500.5, [1] = 300.0, [0] = 100.0 };
initializes the sample_data array to the same values as shown in the previous example. And the statements
int x = 1233;
int a[10] = { [9] = x + 1, [2] = 3, [1] = 2, [0] = 1 };
define a 10-element array and initialize the last element to the value of x + 1 (or to 1234), and the first three elements to 1, 2, and 3, respectively.
Unfortunately, C does not provide any shortcut mechanisms for initializing array elements. That is, there is no way to specify a repeat count, so if it were desired to initially set all 500 values of sample_data to 1, all 500 would have to be explicitly spelled out. In such a case, it is better to initialize the array inside the program using an appropriate for loop.
Program 6.5 illustrates two types of array-initialization techniques.
Program 6.5 Initializing Arrays
#include <stdio.h>
int main (void)
{
int array_values[10] = { 0, 1, 4, 9, 16 };
int i;
for ( i = 5; i < 10; ++i )
array_values[i] = i * i;
for ( i = 0; i < 10; ++i )
printf ("array_values[%i] = %i\n", i, array_values[i]);
return 0;
}
Program 6.5 Output
array_values[0] = 0
array_values[1] = 1
array_values[2] = 4
array_values[3] = 9
array_values[4] = 16
array_values[5] = 25
array_values[6] = 36
array_values[7] = 49
array_values[8] = 64
array_values[9] = 81
In the declaration of the array array_values, the first five elements of the array are initialized to the square of their element number (for example, element number 3 is set equal to 32 or 9). The first for loop shows how this same type of initialization can be performed inside a loop. This loop sets each of the elements 5 through 9 to the square of its element number. The second for loop simply runs through all 10 elements to display their values at the terminal.
Character Arrays
The purpose of Program 6.6 is to simply illustrate how a character array can be used. However, one point is worthy of discussion. Can you spot it?
Program 6.6 Introducing Character Arrays
#include <stdio.h>
int main (void)
{
char word[] = { 'H', 'e', 'l', 'l', 'o', '!' };
int i;
for ( i = 0; i < 6; ++i )
printf ("%c", word[i]);
printf ("\n");
return 0;
}
Program 6.6 Output
Hello!
The most notable point in the preceding program is the declaration of the character array word. There is no mention of the number of elements in the array. The C language allows you to define an array without specifying the number of elements. If this is done, the size of the array is determined automatically based on the number of initialization elements. Because Program 6.6 has six initial values listed for the array word, the C language implicitly dimensions the array to six elements.
This approach works fine so long as you initialize every element in the array at the point that the array is defined. If this is not to be the case, you must explicitly dimension the array.
In the case of using index numbers in the initialization list, as in
float sample_data[] = { [0] = 1.0, [49] = 100.0, [99] = 200.0 };
the largest index number specified sets the size of the array. In this case, sample_data is set to contain 100 elements, based on the largest index value of 99 that is specified.
Base Conversion Using Arrays
The next program further illustrates the use of integer and character arrays. The task is to develop a program that converts a positive integer from its base 10 representation into its equivalent representation in another base up to base 16. As inputs to the program, you specify the number to be converted and also the base to which you want the number converted. The program then converts the keyed-in number to the appropriate base and displays the result.
The first step in developing such a program is to devise an algorithm to convert a number from base 10 to another base. An algorithm to generate the digits of the converted number can be informally stated as follows: A digit of the converted number is obtained by taking the modulo of the number by the base. The number is then divided by the base, with any fractional remainder discarded, and the process is repeated until the number reaches zero.
The outlined procedure generates the digits of the converted number starting from the rightmost digit. See how this works in the following example. Suppose you want to convert the number 10 into base 2. Table 6.1 shows the steps that would be followed to arrive at the result.
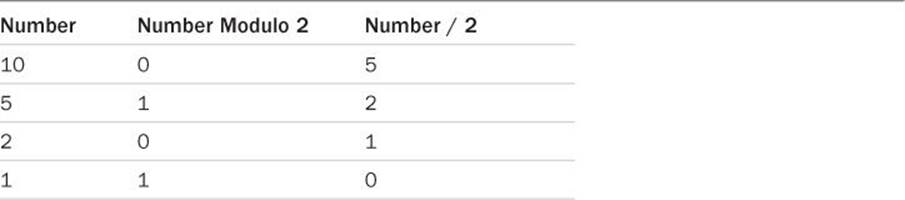
Table 6.1 Converting an Integer from Base 10 to Base 2
The result of converting 10 to base 2 is, therefore, seen to be 1010, reading the digits of the “Number Modulo 2” column from the bottom to the top.
To write a program that performs the preceding conversion process, you must take a couple of things into account. First, the fact that the algorithm generates the digits of the converted number in reverse order is not very nice. You certainly can’t expect the user to read the result from right to left, or from the bottom of the page upward. Therefore, you must correct this problem. Rather than simply displaying each digit as it is generated, you can have the program store each digit inside an array. Then, when you’ve finished converting the number, you can display the contents of the array in the correct order.
Second, you must realize that you specified for the program to handle conversion of numbers into bases up to 16. This means that any digits of the converted number that are between 10 and 15 must be displayed using the corresponding letters, A through F. This is where our character array enters the picture.
Examine Program 6.7 to see how these two issues are handled. This program also introduces the type qualifier const, which is used for variables whose value does not change in a program.
Program 6.7 Converting a Positive Integer to Another Base
// Program to convert a positive integer to another base
#include <stdio.h>
int main (void)
{
const char baseDigits[16] = {
'0', '1', '2', '3', '4', '5', '6', '7',
'8', '9', 'A', 'B', 'C', 'D', 'E', 'F' };
int convertedNumber[64];
long int numberToConvert;
int nextDigit, base, index = 0;
// get the number and the base
printf ("Number to be converted? ");
scanf ("%ld", &numberToConvert);
printf ("Base? ");
scanf ("%i", &base);
// convert to the indicated base
do {
convertedNumber[index] = numberToConvert % base;
++index;
numberToConvert = numberToConvert / base;
}
while ( numberToConvert != 0 );
// display the results in reverse order
printf ("Converted number = ");
for (--index; index >= 0; --index ) {
nextDigit = convertedNumber[index];
printf ("%c", baseDigits[nextDigit]);
}
printf ("\n");
return 0;
}
Program 6.7 Output
Number to be converted? 10
Base? 2
Converted number = 1010
Program 6.7 Output (Rerun)
Number to be converted? 128362
Base? 16
Converted number = 1F56A
The const Qualifier
The compiler allows you to associate the const qualifier with variables whose values will not be changed by the program. That is, you can tell the compiler that the specified variables have a constant value throughout the program’s execution. If you try to assign a value to a const variable after initializing it, or try to increment or decrement it, the compiler might issue an error message, although it is not required to do so. One of the motivations for the const attribute in the language is that it allows the compiler to place your const variables into read-only memory. (Normally, the instructions of your program are also placed into read-only memory.)
As an example of the const attribute, the line
const double pi = 3.141592654;
declares the const variable pi. This tells the compiler that this variable will not be modified by the program. If you subsequently wrote a line like this in your program:
pi = pi / 2;
the gcc compiler would give you an error message similar to this:
foo.c:16: error: assignment of read-only variable 'pi'
Returning to Program 6.7, the character array baseDigits is set up to contain the 16 possible digits that will be displayed for the converted number. It is declared as a const array because its contents will not be changed after it is initialized. Note that this fact also aids in the program’s readability.
The array convertedNumber is defined to contain a maximum of 64 digits, which holds the results of converting the largest possible long integer to the smallest possible base (base 2) on just about all machines. The variable numberToConvert is defined to be of type long int so that relatively large numbers can be converted if desired. Finally, the variables base (to contain the desired conversion base) and index (to index into the convertedNumber array) are both defined to be of type int.
After the user keys in the values of the number to be converted and the base—note that the scanf() call to read in a long integer value takes the format characters %ld—the program then enters a do loop to perform the conversion. The do was chosen so that at least one digit appears in the convertedNumber array even if the user keys in the number zero to be converted.
Inside the loop, the numberToConvert modulo the base is computed to determine the next digit. This digit is stored inside the convertedNumber array, and the index in the array is incremented by 1. After dividing the numberToConvert by the base, the conditions of the doloop are checked. If the value of numberToConvert is 0, the loop terminates; otherwise, the loop is repeated to determine the next digit of the converted number.
When the do loop is complete, the value of the variable index is the number of digits in the converted number. Because this variable is incremented one time too many inside the do loop, its value is initially decremented by 1 in the for loop. The purpose of this for loop is to display the converted number at the terminal. The for loop sequences through the convertedNumber array in reverse sequence to display the digits in the correct order.
Each digit from the convertedNumber array is in turn assigned to the variable nextDigit. For the numbers 10 through 15 to be correctly displayed using the letters A through F, a lookup is then made inside the array baseDigits, using the value of nextDigit as the index. For the digits 0 through 9, the corresponding location in the array baseDigits contains nothing more than the characters '0' through '9' (which as you recall are distinct from the integers 0 through 9). Locations 10 through 15 of the array contain the characters 'A' through 'F'. So, if the value of nextDigit is 10, for example, the character contained in baseDigits[10], or 'A', is displayed. And if the value of nextDigit is 8, the character '8' as contained in baseDigits[8] is displayed.
When the value of index becomes less than zero, the for loop is finished. At this point, the program displays a newline character, and program execution is terminated.
Incidentally, you might be interested in knowing that you could have easily avoided the intermediate step of assigning the value of convertedNumber[index] to nextDigit by directly specifying this expression as the subscript of the baseDigits array in the printf() call. In other words, the expression
baseDigits[ convertedNumber[index] ]
could have been supplied to the printf() routine with the same results achieved. Of course, this expression is a bit more cryptic than the two equivalent expressions used by the program.
It should be pointed out that the preceding program is a bit sloppy. No check was ever made to ensure that the value of base was between 2 and 16. If the user had entered 0 for the value of the base, the division inside the do loop would have been a division by zero. You should never allow this to happen. In addition, if the user had keyed in 1 as the value of the base, the program would enter an infinite loop because the value of numberToConvert would never reach zero. If the user had entered a base value that was greater than 16, you might have exceeded the bounds of thebaseDigits array later in the program. That’s another “gotcha” that you must avoid because the C system does not check this condition for us.
In Chapter 7, “Working with Functions,” you rewrite this program and resolve these issues. But now, it’s time to look at an interesting extension to the notion of an array.
Multidimensional Arrays
The types of arrays that you have been exposed to so far are all linear arrays—that is, they all dealt with a single dimension. The C language allows arrays of any dimension to be defined. In this section, you take a look at two-dimensional arrays.
One of the most natural applications for a two-dimensional array arises in the case of a matrix. Consider the 4 × 5 matrix shown in Table 6.2.

Table 6.2 A 4 × 5 Matrix
In mathematics, it is quite common to refer to an element of a matrix by use of a double subscript. So if you call the preceding matrix M, the notation Mi,j refers to the element in the ith row, jth column, where i ranges from 1 to 4, and j ranges from 1 to 5. The notation M3,2 refers to the value 20, which is found in the 3rd row, 2nd column of the matrix. In a similar fashion, M4,5 refers to the element contained in the 4th row, 5th column: the value 6.
In C, you can use an analogous notation when referring to elements of a two-dimensional array. However, because C likes to start numbering things at zero, the 1st row of the matrix is actually row 0, and the 1st column of the matrix is column 0. The preceding matrix would then have row and column designations, as shown in Table 6.3.
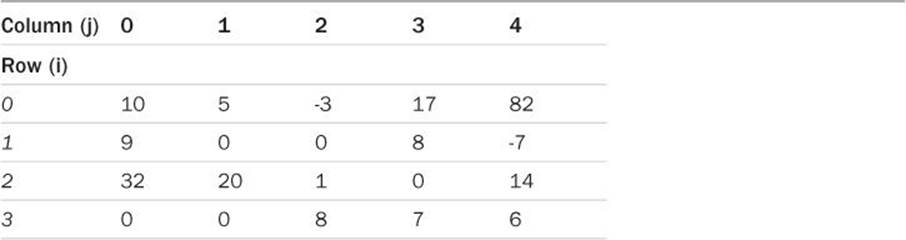
Table 6.3 A 4 × 5 Matrix in C
Whereas in mathematics the notation Mi,j is used, in C the equivalent notation is
M[i][j]
Remember, the first index number refers to the row number, whereas the second index number references the column. So the statement
sum = M[0][2] + M[2][4];
adds the value contained in row 0, column 2—which is −3—to the value contained in row 2, column 4—which is 14—and assigns the result of 11 to the variable sum.
Two-dimensional arrays are declared the same way that one-dimensional arrays are; thus
int M[4][5];
declares the array M to be a two-dimensional array consisting of 4 rows and 5 columns, for a total of 20 elements. Each position in the array is defined to contain an integer value.
Two-dimensional arrays can be initialized in a manner analogous to their one-dimensional counterparts. When listing elements for initialization, the values are listed by row. Brace pairs are used to separate the list of initializers for one row from the next. So to define and initialize the arrayM to the elements listed in Table 6.3, a statement such as the following can be used:
int M[4][5] = {
{ 10, 5, -3, 17, 82 },
{ 9, 0, 0, 8, -7 },
{ 32, 20, 1, 0, 14 },
{ 0, 0, 8, 7, 6 }
};
Pay particular attention to the syntax of the preceding statement. Note that commas are required after each brace that closes off a row, except in the case of the final row. The use of the inner pairs of braces is actually optional. If not supplied, initialization proceeds by row. Thus, the preceding statement could also have been written as follows:
int M[4][5] = { 10, 5, -3, 17, 82, 9, 0, 0, 8, -7, 32,
20, 1, 0, 14, 0, 0, 8, 7, 6 };
As with one-dimensional arrays, it is not required that the entire array be initialized. A statement such as
int M[4][5] = {
{ 10, 5, -3 },
{ 9, 0, 0 },
{ 32, 20, 1 },
{ 0, 0, 8 }
};
only initializes the first three elements of each row of the matrix to the indicated values. The remaining values are set to 0. Note that, in this case, the inner pairs of braces are required to force the correct initialization. Without them, the first two rows and the first two elements of the third row would have been initialized instead. (Verify to yourself that this is the case.)
Subscripts can also be used in the initialization list, in a like manner to single-dimensional arrays. So the declaration
int matrix[4][3] = { [0][0] = 1, [1][1] = 5, [2][2] = 9 };
initializes the three indicated elements of matrix to the specified values. The unspecified elements are set to zero by default.
Variable Length Arrays1
1. The ANSI C11 standard makes support for variable length arrays optional. Check your compiler documentation to see if in fact this feature is supported.
This section discusses a feature in the language that enables you to work with arrays in your programs without having to give them a constant size.
In the examples in this chapter, you have seen how the size of an array is declared to be of a specific size. The C language allows you to declare arrays of a variable size. For example, Program 6.3 only calculates the first 15 Fibonacci numbers. But what if you want to calculate 100 or even 500 Fibonacci numbers? Or, what if you want to have the user specify the number of Fibonacci numbers to generate? Study Program 6.8 to see one method for resolving this problem.
Program 6.8 Generating Fibonacci Numbers Using Variable Length Arrays
// Generate Fibonacci numbers using variable length arrays
#include <stdio.h>
int main (void)
{
int i, numFibs;
printf ("How many Fibonacci numbers do you want (between 1 and 75)? ");
scanf ("%i", &numFibs);
if (numFibs < 1 || numFibs > 75) {
printf ("Bad number, sorry!\n");
return 1;
}
unsigned long long int Fibonacci[numFibs];
Fibonacci[0] = 0; // by definition
Fibonacci[1] = 1; // ditto
for ( i = 2; i < numFibs; ++i )
Fibonacci[i] = Fibonacci[i-2] + Fibonacci[i-1];
for ( i = 0; i < numFibs; ++i )
printf ("%llu ", Fibonacci[i]);
printf ("\n");
return 0;
}
Program 6.8 Output
How many Fibonacci numbers do you want (between 1 and 75)? 50
0 1 1 2 3 5 8 13 21 34 55 89 144 233 377 610 987 1597 2584
4181 6765 10946 17711 28657 46368 75025 121393 196418 317811 514229
832040 1346269 2178309 3524578 5702887 9227465 14930352 24157817
39088169 63245986 102334155 165580141 267914296 433494437 701408733
1134903170 1836311903 2971215073 4807526976 7778742049
Program 6.8 has several points worth discussing. First, the variables i and numFibs are declared. The latter variable is used to store the requested number of Fibonacci numbers that the user wants to generate. Notice the range of the entered value is checked by the program, which is good programming practice. If the value is out of range (that is, less than 1 or greater than 75), the program displays a message and returns a value of 1. Executing the return statement at that point in the program causes the program to terminate immediately, and no further statements are executed. As noted in Chapter 2, “Compiling and Running Your First Program,” the nonzero value that is returned indicates by convention that the program terminated with an error condition, and that fact could be tested by another program if desired.
After the number has been entered by the user, you see the statement
unsigned long long int Fibonacci[numFibs];
The Fibonacci array is declared to contain numFibs elements. This is called a variable length array because the size of the array is specified by a variable and not by a constant expression. Also, as previously noted, a variable can be declared anywhere in a program, as long as the declaration occurs before the variable is first used. So although this declaration appears out of place, it’s perfectly legitimate. It’s not usually considered good programming style to do this, however, mainly because, by convention, the variable declarations are often grouped together so someone reading the program can see the variables and their types in one place.
Because Fibonacci numbers get large very quickly, the array is declared to contain the largest positive integer value you can specify, namely an unsigned long long int. As an exercise, you might want to determine the largest Fibonacci number that you can store inside anunsigned long long int variable on your computer.
The rest of the program is self-explanatory: The requested number of Fibonacci numbers are calculated and then displayed to the user. The execution of the program is then complete.
A technique known as dynamic memory allocation is also often used to allocate space for arrays while a program is executing. This involves using functions such as malloc() and calloc() that are in the standard C library. This topic is discussed in detail in Chapter 16, “Miscellaneous and Advanced Features.”
You have seen how arrays are powerful constructs that are available in virtually all programming languages. A program example showing the use of multidimensional arrays is deferred to Chapter 7, which begins a detailed discussion of one of the most important concepts in the C language—the program function. Before proceeding to that chapter, however, try to work the following exercises.
Exercises
1. Type in and run the eight programs presented in this chapter. Compare the output produced by each program with the output presented after each program in the text.
2. Modify Program 6.1 so that the elements of the array values are initially set to 0. Use a for loop to perform the initialization.
3. Program 6.2 permits only 20 responses to be entered. Modify that program so that any number of responses can be entered. So that the user does not have to count the number of responses in the list, set up the program so that the value 999 can be keyed in by the user to indicate that the last response has been entered. (Hint: You can use the break statement here if you want to exit your loop.)
4. Write a program that calculates the average of an array of 10 floating-point values.
5. What output do you expect from the following program?
#include <stdio.h>
int main (void)
{
int numbers[10] = { 1, 0, 0, 0, 0, 0, 0, 0, 0, 0 };
int i, j;
for ( j = 0; j < 10; ++j )
for ( i = 0; i < j; ++i )
numbers[j] += numbers[i];
for ( j = 0; j < 10; ++j )
printf ("%i ", numbers[j]);
printf ("\n");
return 0;
}
6. You don’t need to use an array to generate Fibonacci numbers. You can simply use three variables: two to store the previous two Fibonacci numbers and one to store the current one. Rewrite Program 6.3 so that arrays are not used. Because you’re no longer using an array, you need to display each Fibonacci number as you generate it.
7. Prime numbers can also be generated by an algorithm known as the Sieve of Eratosthenes. The algorithm for this procedure is presented here. Write a program that implements this algorithm. Have the program find all prime numbers up to n = 150. What can you say about this algorithm as compared to the ones used in the text for calculating prime numbers?
Sieve of Eratosthenes Algorithm
To Display All Prime Numbers Between 1 and n
Step 1: Define an array of integers P. Set all elements Pi to 0, 2 <= i <= n.
Step 2: Set i to 2.
Step 3: If i > n, the algorithm terminates.
Step 4: If Pi is 0, then i is prime.
Step 5: For all positive integer values of j, such that i x j ≤ n, set Pixj to 1.
Step 6: Add 1 to i and go to step 3.
8. Find out if your compiler supports variable-length arrays. If it does, write a small program to test the feature out.
All materials on the site are licensed Creative Commons Attribution-Sharealike 3.0 Unported CC BY-SA 3.0 & GNU Free Documentation License (GFDL)
If you are the copyright holder of any material contained on our site and intend to remove it, please contact our site administrator for approval.
© 2016-2025 All site design rights belong to S.Y.A.