Programming in C (Fourth Edition) (2015)
7. Working with Functions
Behind all well-written programs in the C programming language lies the same fundamental element—the function. You’ve used functions in every program that you’ve encountered so far. The printf() and scanf() routines are examples of functions. Indeed, each and every program also uses a function called main(). You may be wondering, “What’s the big deal about functions?” When you start breaking down the your programming task into functions, your code will be easier to write, read, understand, debug, modify, and maintain. Obviously, anything that can accomplish all of these things is worthy of a bit of fanfare. As a result this is a chapter packed with important information, including
![]() Understanding the basics of functions.
Understanding the basics of functions.
![]() Explaining local, global, automatic, and static variables.
Explaining local, global, automatic, and static variables.
![]() Using single-dimensional and multi-dimensional arrays with functions.
Using single-dimensional and multi-dimensional arrays with functions.
![]() Returning data from functions
Returning data from functions
![]() Using functions to execute top-down programming
Using functions to execute top-down programming
![]() Calling functions from within other functions, as well as recursive functions.
Calling functions from within other functions, as well as recursive functions.
Defining a Function
First, you must understand what a function is, and then you can proceed to find out how it can be most effectively used in the development of programs. Go back to the very first program that you wrote (Program 2.1), which displayed the phrase “Programming is fun.”:
#include <stdio.h>
int main (void)
{
printf ("Programming is fun.\n");
return 0;
}
Here is a function called printMessage() that does the same thing:
void printMessage (void)
{
printf ("Programming is fun.\n");
}
The differences between printMessage() and the function main() from Program 2.1 is in the first and last line. The first line of a function definition tells the compiler (in order from left to right) four things about the function:
1. Who can call it (discussed in Chapter 14, “Working with Larger Programs”)
2. The type of value it returns
3. Its name
4. The arguments it takes
The first line of the printMessage() function definition tells the compiler that the function returns no value (the first use of the keyword void), its name is printMessage, and that it takes no arguments (the second use of the keyword void). You learn more details about the voidkeyword shortly.
Obviously, choosing meaningful function names is just as important as choosing meaningful variable names—the choice of names greatly affects the program’s readability.
Recall from discussions of Program 2.1 that main() is a specially recognized name in the C system that always indicates where the program is to begin execution. You must always have a main(). You can add a main() function to the preceding code to end up with a complete program, as shown in Program 7.1.
Program 7.1 Writing a Function in C
#include <stdio.h>
void printMessage (void)
{
printf ("Programming is fun.\n");
}
int main (void)
{
printMessage ();
return 0;
}
Program 7.1 Output
Programming is fun.
Program 7.1 consists of two functions: printMessage() and main(). Program execution always begins with main(). Inside that function, the statement
printMessage ();
appears. This statement indicates that the function printMessage() is to be executed. The open and close parentheses are used to tell the compiler that printMessage() is a function and that no arguments or values are to be passed to this function (which is consistent with the way the function is defined in the program). When a function call is executed, program execution is transferred directly to the indicated function. Inside the printMessage() function, the printf() statement is executed to display the message “Programming is fun.”. After the message has been displayed, the printMessage() routine is finished (as signaled by the closing brace) and the program returns to the main() routine, where program execution continues at the point where the function call was executed. By this time you may have noted that the terms function and routineare used interchangeably—the two terms basically mean the same thing.
Note that it is acceptable to insert a return statement at the end of printMessage() like this:
return;
Because printMessage() does not return a value, no value is specified for the return. This statement is optional because reaching the end of a function without executing a return has the effect of exiting the function anyway without returning a value. In other words, either with or without the return statement, the behavior on exit from printMessage() is identical.
As mentioned previously, the idea of calling a function is not new. The printf() and scanf() routines are both program functions. The main distinction here is that these routines did not have to be written by you because they are a part of the standard C library. When you use theprintf() function to display a message or program results, execution is transferred to the printf() function, which performs the required tasks and then returns back to the program. In each case, execution is returned to the program statement that immediately follows the call to the function.
Now try to predict the output from Program 7.2.
Program 7.2 Calling Functions
#include <stdio.h>
void printMessage (void)
{
printf ("Programming is fun.\n");
}
int main (void)
{
printMessage ();
printMessage ();
return 0;
}
Program 7.2 Output
Programming is fun.
Programming is fun.
Execution of the preceding program starts at main(), which contains two calls to the printMessage() function. When the first call to the function is executed, control is sent directly to the printMessage() function, which displays the message “Programming is fun.” and then returns to the main() routine. Upon return, another call to the printMessage() routine is encountered, which results in the execution of the same function a second time. After the return is made from the printMessage() function, execution is terminated.
As a final example of the printMessage() function, try to predict the output from Program 7.3
Program 7.3 More on Calling Functions
#include <stdio.h>
void printMessage (void)
{
printf ("Programming is fun.\n");
}
int main (void)
{
int i;
for ( i = 1; i <= 5; ++i )
printMessage ();
return 0;
}
Program 7.3 Output
Programming is fun.
Programming is fun.
Programming is fun.
Programming is fun.
Programming is fun.
Arguments and Local Variables
When the printf() function is called, you always supply one or more values to the function, the first value being the format string and the remaining values being the specific program results to be displayed. These values, called arguments, greatly increase the usefulness and flexibility of a function. Unlike your printMessage() routine, which displays the same message each time it is called, the printf() function displays whatever you tell it to display.
You can define a function that accepts arguments. In Chapter 4, “Program Looping,” you developed an assortment of programs for calculating triangular numbers. Here, you define a function to generate a triangular number, called appropriately enough,calculateTriangularNumber(). As an argument to the function, you specify which triangular number to calculate. The function then calculates the desired number and displays the results at the terminal. Program 7.4 shows the function to accomplish this task and a main() routine to try it out.
Program 7.4 Calculating the nth Triangular Number
// Function to calculate the nth triangular number
#include <stdio.h>
void calculateTriangularNumber (int n)
{
int i, triangularNumber = 0;
for ( i = 1; i <= n; ++i )
triangularNumber += i;
printf ("Triangular number %i is %i\n", n, triangularNumber);
}
int main (void)
{
calculateTriangularNumber (10);
calculateTriangularNumber (20);
calculateTriangularNumber (50);
return 0;
}
Program 7.4 Output
Triangular number 10 is 55
Triangular number 20 is 210
Triangular number 50 is 1275
Function Prototype Declaration
The function calculateTriangularNumber() requires a bit of explanation. The first line of the function:
void calculateTriangularNumber (int n)
is called the function prototype declaration. It tells the compiler that calculateTriangularNumber() is a function that returns no value (the keyword void) and that takes a single argument, called n, which is an int. The name that is chosen for an argument, called its formal parameter name, as well as the name of the function itself, can be any valid name formed by observing the naming rules outlined in Chapter 3, “Variables, Data Types, and Arithmetic Expressions,” for forming variable names. For obvious reasons, you should choose meaningful names.
After the formal parameter name has been defined, it can be used to refer to the argument anywhere inside the body of the function.
The beginning of the function’s definition is indicated by the opening curly brace. Because you want to calculate the nth triangular number, you have to set up a variable to store the value of the triangular number as it is being calculated. You also need a variable to act as your loop index. The variables triangularNumber and i are defined for these purposes and are declared to be of type int. These variables are defined and initialized in the same manner that you defined and initialized your variables inside the main routine in previous programs.
Automatic Local Variables
Variables defined inside a function are known as automatic local variables because they are automatically “created” each time the function is called, and because their values are local to the function. The value of a local variable can only be accessed by the function in which the variable is defined. Its value cannot be accessed by any other function. If an initial value is given to a variable inside a function, that initial value is assigned to the variable each time the function is called.
When defining a local variable inside a function, it is more precise in C to use the keyword auto before the definition of the variable. An example of this is as follows:
auto int i, triangularNumber = 0;
Because the C compiler assumes by default that any variable defined inside a function is an automatic local variable, the keyword auto is seldom used, and for this reason it is not used in this book.
Returning to the program example, after the local variables have been defined, the function calculates the triangular number and displays the results. The closing brace then defines the end of the function.
Inside the main() routine, the value 10 is passed as the argument in the first call to calculateTriangularNumber(). Execution is then transferred directly to the function where the value 10 becomes the value of the formal parameter n inside the function. The function then proceeds to calculate the value of the 10th triangular number and display the result.
The next time that calculateTriangularNumber() is called, the argument 20 is passed. In a similar process, as described earlier, this value becomes the value of n inside the function. The function then proceeds to calculate the value of the 20th triangular number and display the answer at the terminal.
For an example of a function that takes more than one argument, rewrite the greatest common divisor program (Program 4.7) in function form. The two arguments to the function are the two numbers whose greatest common divisor (gcd) you want to calculate. See Program 7.5.
Program 7.5 Revising the Program to Find the Greatest Common Divisor
/* Function to find the greatest common divisor
of two nonnegative integer values */
#include <stdio.h>
void gcd (int u, int v)
{
int temp;
printf ("The gcd of %i and %i is ", u, v);
while ( v != 0 ) {
temp = u % v;
u = v;
v = temp;
}
printf ("%i\n", u);
}
int main (void)
{
gcd (150, 35);
gcd (1026, 405);
gcd (83, 240);
return 0;
}
Program 7.5 Output
The gcd of 150 and 35 is 5
The gcd of 1026 and 405 is 27
The gcd of 83 and 240 is 1
The function gcd() is defined to take two integer arguments. The function refers to these arguments through their formal parameter names u and v. After declaring the variable temp to be of type int, the program displays the values of the arguments u and v, together with an appropriate message. The function then calculates and displays the greatest common divisor of the two integers.
You might be wondering why there are two printf() statements inside the function gcd. You must display the values of u and v before you enter the while loop because their values are changed inside the loop. If you wait until after the loop has finished, the values displayed for u and vdo not at all resemble the original values that were passed to the routine. Another solution to this problem is to assign the values of u and v to two variables before entering the while loop. The values of these two variables can then be displayed together with the value of u (the greatest common divisor) using a single printf() statement after the while loop has completed.
Returning Function Results
The functions in Programs 7.4 and 7.5 perform some straightforward calculations and then display the results of the calculations at the terminal. However, you might not always want to have the results of your calculations displayed. The C language provides you with a convenient mechanism whereby the results of a function can be returned to the calling routine. This is not new to you because you’ve used it in all previous programs to return from main. The general syntax of this construct is straightforward enough:
return expression;
This statement indicates that the function is to return the value of expression to the calling routine. Parentheses are placed around expression by some programmers as a matter of programming style, but their use is optional.
An appropriate return statement is not enough. When the function declaration is made, you must also declare the type of value the function returns. This declaration is placed immediately before the function’s name. Each of the previous examples in this book defined the function main()to return an integer value, which is why the keyword int is placed directly before the function name. On the other hand, a function declaration that starts like this:
float kmh_to_mph (float km_speed)
begins the definition of a function kmh_to_mph, which takes one float argument called km_speed and which returns a floating-point value. Similarly,
int gcd (int u, int v)
defines a function gcd with integer arguments u and v that returns an integer value. In fact, you can modify Program 7.5 so that the greatest common divisor is not displayed by the function gcd but is instead returned to the main() routine, as shown in Program 7.6.
Program 7.6 Finding the Greatest Common Divisor and Returning the Results
/* Function to find the greatest common divisor of two
nonnegative integer values and to return the result */
#include <stdio.h>
int gcd (int u, int v)
{
int temp;
while ( v != 0 ) {
temp = u % v;
u = v;
v = temp;
}
return u;
}
int main (void)
{
int result;
result = gcd (150, 35);
printf ("The gcd of 150 and 35 is %i\n", result);
result = gcd (1026, 405);
printf ("The gcd of 1026 and 405 is %i\n", result);
printf ("The gcd of 83 and 240 is %i\n", gcd (83, 240));
return 0;
}
Program 7.6 Output
The gcd of 150 and 35 is 5
The gcd of 1026 and 405 is 27
The gcd of 83 and 240 is 1
After the value of the greatest common divisor has been calculated by the gcd() function, the statement
return u;
is executed. This has the effect of returning the value of u, which is the value of the greatest common divisor, back to the calling routine.
You might be wondering what you can do with the value that is returned to the calling routine. As you can see from the main() routine, in the first two cases, the value that is returned is stored in the variable result. More precisely, the statement
result = gcd (150, 35);
says to call the function gcd() with the arguments 150 and 35 and to store the value that is returned by this function in the variable result.
The result that is returned by a function does not have to be assigned to a variable, as you can see by the last statement in the main() routine. In this case, the result returned by the call
gcd (83, 240)
is passed directly to the printf() function, where its value is displayed.
A C function can only return a single value in the manner just described. Unlike some other languages, C makes no distinction between subroutines (procedures) and functions. In C, there is only the function, which can optionally return a value. If the declaration of the type returned by a function is omitted, the C compiler assumes that the function returns an int—if it returns a value at all. Some C programmers take advantage of the fact that functions are assumed to return an int by default and omit the return type declaration. This is poor programming practice and should be avoided. When a function returns a value, make certain you declare the type of value returned in the function’s header, if only for the sake of improving the program’s readability. In this manner, you can always identify from the function header not only the function’s name and the number and type of its arguments, but also if it returns a value and the returned value’s type.
As noted earlier, a function declaration that is preceded by the keyword void explicitly informs the compiler that the function does not return a value. A subsequent attempt at using the function in an expression, as if a value were returned, results in a compiler error message. For example, because the calculateTriangularNumber() function of Program 7.4 did not return a value, you placed the keyword void before its name when defining the function. Subsequently attempting to use this function as if it returned a value, as in
number = calculateTriangularNumber (20);
results in a compiler error.
In a sense, the void data type is actually defining the absence of a data type. Therefore, a function declared to be of type void has no value and cannot be used as if it does have a value in an expression.
In Chapter 5, “Making Decisions,” you wrote a program to calculate and display the absolute value of a number. Now, write a function that takes the absolute value of its argument and then returns the result. Instead of using integer values as you did in Program 5.1, write this function to take a floating value as an argument and to return the answer as type float, as shown in Program 7.7.
Program 7.7 Calculating the Absolute Value
// Function to calculate the absolute value
#include <stdio.h>
float absoluteValue (float x)
{
if ( x < 0 )
x = -x;
return x;
}
int main (void)
{
float f1 = -15.5, f2 = 20.0, f3 = -5.0;
int i1 = -716;
float result;
result = absoluteValue (f1);
printf ("result = %.2f\n", result);
printf ("f1 = %.2f\n", f1);
result = absoluteValue (f2) + absoluteValue (f3);
printf ("result = %.2f\n", result);
result = absoluteValue ( (float) i1 );
printf ("result = %.2f\n", result);
result = absoluteValue (i1);
printf ("result = %.2f\n", result);
printf ("%.2f\n", absoluteValue (-6.0) / 4 );
return 0;
}
Program 7.7 Output
result = 15.50
f1 = -15.50
result = 25.00
result = 716.00
result = 716.00
1.50
The absoluteValue() function is relatively straightforward. The formal parameter called x is tested against zero. If it is less than zero, the value is negated to take its absolute value. The result is then returned back to the calling routine with an appropriate return statement.
You should note some interesting points with respect to the main() routine that tests out the absoluteValue() function. In the first call to the function, the value of the variable f1, initially set to −15.5, is passed. Inside the function itself, this value is assigned to the variable x. Because the result of the if test is TRUE, the statement that negates the value of x is executed, thereby setting the value of x to 15.5. In the next statement, the value of x is returned to the main() routine where it is assigned to the variable result and is then displayed.
When the value of x is changed inside the absoluteValue() function, this in no way affects the value of the variable f1. When f1 was passed to the absoluteValue() function, its value was automatically copied into the formal parameter x by the system. Therefore, any changes made to the value of x inside the function affect only the value of x and not the value of f1. This is verified by the second printf() call, which displays the unchanged value of f1. Make certain you understand that it’s not possible for a function to directly change the value of any of its arguments—it can only change copies of them.
The next two calls to the absoluteValue() function illustrate how the result returned by a function can be used in an arithmetic expression. The absolute value of f2 is added to the absolute value of f3 and the sum is assigned to the variable result.
The fourth call to the absoluteValue() function introduces the notion that the type of argument that is passed to a function should agree with the type of argument as declared inside the function. Because the function absoluteValue() expects a floating value as its argument, the integer variable i1 is first cast to type float before the call is made. If you omit the cast operation, the compiler does it for you anyway because it knows the absoluteValue() function is expecting a floating argument. (This is verified by the fifth call to the absoluteValue()function.) However, it’s clearer what’s going on if you do the casting yourself rather than relying on the system to do the conversion for you.
The final call to the absoluteValue() function shows that the rules for evaluation of arithmetic expressions also pertain to values returned by functions. Because the value returned by the absoluteValue() function is declared to be of type float, the compiler treats the division operation as the division of a floating-point number by an integer. As you recall, if one operand of a term is of type float, the operation is performed using floating arithmetic. In accordance with this rule, the division of the absolute value of −6.0 by 4 produces a result of 1.5.
Now that you’ve defined a function that computes the absolute value of a number, you can use it in any future programs in which you might need such a calculation performed. In fact, the next program (Program 7.8) is just such an example.
Functions Calling Functions Calling...
With most cell phones having calculator apps on them, it’s usually no big deal to find the square root of a particular number should the need arise. But years ago, students were taught manual techniques that could be used to arrive at an approximation of the square root of a number. One such approximation method that lends itself most readily to solution by a computer is known as the Newton-Raphson Iteration Technique. In Program 7.8, you write a square root function that uses this technique to arrive at an approximation of the square root of a number.
The Newton-Raphson method can be easily described as follows. You begin by selecting a “guess” at the square root of the number. The closer that this guess is to the actual square root, the fewer the number of calculations that have to be performed to arrive at the square root. For the sake of argument, however, assume that you are not very good at guessing and, therefore, always make an initial guess of 1.
The number whose square root you want to obtain is divided by the initial guess and is then added to the value of guess. This intermediate result is then divided by 2. The result of this division becomes the new guess for another go-around with the formula. That is, the number whose square root you are calculating is divided by this new guess, added into this new guess, and then divided by 2. This result then becomes the new guess and another iteration is performed.
Because you don’t want to continue this iterative process forever, you need some way of knowing when to stop. Because the successive guesses that are derived by repeated evaluation of the formula get closer and closer to the true value of the square root, you can set a limit that you can use for deciding when to terminate the process. The difference between the square of the guess and the number itself can then be compared against this limit—usually called epsilon (ε). If the difference is less than ε, the desired accuracy for the square root has been obtained and the iterative process can be terminated.
This procedure can be expressed in terms of an algorithm, as shown next.
Newton-Raphson Method to Compute the Square Root of x
Step 1. Set the value of guess to 1.
Step 2. If |guess2 - x| < ε, proceed to step 4.
Step 3. Set the value of guess to (x / guess + guess) / 2 and return to step 2.
Step 4. The guess is the approximation of the square root.
It is necessary to test the absolute difference of guess2 and x against ε in step 2 because the value of guess can approach the square root of x from either side.
Now that you have an algorithm for finding the square root at your disposal, it once again becomes a relatively straightforward task to develop a function to calculate the square root. For the value of ε in the following function, the value .00001 was arbitrarily chosen. See the example inProgram 7.8.
Program 7.8 Calculating the Square Root of a Number
// Function to calculate the absolute value of a number
#include <stdio.h>
float absoluteValue (float x)
{
if ( x < 0 )
x = -x;
return (x);-
}
// Function to compute the square root of a number
float squareRoot (float x)
{
const float epsilon = .00001;
float guess = 1.0;
while ( absoluteValue (guess * guess - x) >= epsilon )
guess = ( x / guess + guess ) / 2.0;
return guess;
}
int main (void)
{
printf ("squareRoot (2.0) = %f\n", squareRoot (2.0));
printf ("squareRoot (144.0) = %f\n", squareRoot (144.0));
printf ("squareRoot (17.5) = %f\n", squareRoot (17.5));
return 0;
}
Program 7.8 Output
squareRoot (2.0) = 1.414216
squareRoot (144.0) = 12.000000
squareRoot (17.5) = 4.183300
The actual values that are displayed by running this program on your computer system might differ slightly in the less significant digits.
The preceding program requires a detailed analysis. The absoluteValue() function is defined first. This is the same function that was used in Program 7.7.
Next, you find the squareRoot() function. This function takes one argument named x and returns a value of type float. Inside the body of the function, two local variables named epsilon and guess are defined. The value of epsilon, which is used to determine when to end the iteration process, is set to .00001. You can change epsilon to an even smaller value.
The smaller the value of epsilon, the more accurate the result will be, but a smaller value will also take more time to calculate the result. The value of your guess at the square root of the number is initially set to 1.0. These initial values are assigned to these two variables each time that the function is called.
After the local variables have been declared, a while loop is set up to perform the iterative calculations. The statement that immediately follows the while condition is repetitively executed as long as the absolute difference between guess2 and x is greater than or equal to epsilon. The expression
guess * guess - x
is evaluated and the result of the evaluation is passed to the absoluteValue function. The result returned by the absoluteValue function is then compared against the value of epsilon. If the value is greater than or equal to epsilon, the desired accuracy of the square root has not yet been obtained. In that case, another iteration of the loop is performed to calculate the next value of guess.
Eventually, the value of guess is close enough to the true value of the square root, and the while loop terminates. At that point, the value of guess is returned to the calling program. Inside the main() function, this returned value is passed to the printf() function, where it is displayed.
You might have noticed that both the absoluteValue() function and the squareRoot() function have formal parameters named x. The C compiler doesn’t get confused, however, and keeps these two values distinct.
In fact, a function always has its own set of formal parameters. So the formal parameter x used inside the absoluteValue() function is distinct from the formal parameter x used inside the squareRoot() function.
The same is true for local variables. You can declare local variables with the same name inside as many functions as you want. The C compiler does not confuse the usage of these variables because a local variable can only be accessed within the function it is defined. Another way of saying this is that the scope of a local variable is the function in which it is defined. (As you discover in Chapter 10, “Pointers,” C does provide a mechanism for indirectly accessing a local variable from outside of a function.)
Based upon this discussion, you can understand that when the value of guess2 - x is passed to the absoluteValue() function and assigned to the formal parameter x, this assignment has absolutely no effect on the value of x inside the squareRoot() function.
Declaring Return Types and Argument Types
As mentioned previously, the C compiler assumes that a function returns a value of type int as the default case. More specifically, when a call is made to a function, the compiler assumes that the function returns a value of type int unless either of the following has occurred:
1. The function has been defined in the program before the function call is encountered.
2. The value returned by the function has been declared before the function call is encountered.
In Program 7.8, the absoluteValue() function is defined before the compiler encounters a call to this function from within the squareRoot() function. The compiler knows, therefore, that when this call is encountered, the absoluteValue() function will return a value of typefloat. Had the absoluteValue() function been defined after the squareRoot() function, then upon encountering the call to the absoluteValue() function, the compiler would have assumed that this function returned an integer value. Most C compilers catch this error and generate an appropriate diagnostic message.
To be able to define the absoluteValue() function after the squareRoot() function (or even in another file—see Chapter 14), you must declare the type of result returned by the absoluteValue() function before the function is called. The declaration can be made inside thesquareRoot() function itself, or outside of any function. In the latter case, the declaration is usually made at the beginning of the program.
Not only is the function declaration used to declare the function’s return type, but it is also used to tell the compiler how many arguments the function takes and what their types are.
To declare absoluteValue() as a function that returns a value of type float and that takes a single argument, also of type float, the following declaration is used:
float absoluteValue (float);
As you can see, you just have to specify the argument type inside the parentheses, and not its name. You can optionally specify a “dummy” name after the type if you want:
float absoluteValue (float x);
This name doesn’t have to be the same as the one used in the function definition—the compiler ignores it anyway.
A foolproof way to write a function declaration is to simply use your text editor to make a copy of the first line from the actual definition of the function. Remember to place a semicolon at the end.
If the function doesn’t take an argument, use the keyword void between the parentheses. If the function doesn’t return a value, this fact can also be declared to thwart any attempts at using the function as if it does:
void calculateTriangularNumber (int n);
If the function takes a variable number of arguments (such as is the case with printf() and scanf()), the compiler must be informed. The declaration
int printf (char *format, ...);
tells the compiler that printf() takes a character pointer as its first argument (more on that later), and is followed by any number of additional arguments (the use of the ...). The functions printf() and scanf() are declared in the special file stdio.h. This is why you have been placing the following line at the start of each of your programs:
#include <stdio.h>
Without this line, the compiler can assume printf() and scanf() take a fixed number of arguments, which could result in incorrect code being generated.
The compiler automatically converts your arguments to the appropriate types when a function is called, but only if you have placed the function’s definition or have declared the function and its argument types before the call.
Here are some reminders and suggestions about functions:
1. Remember that, by default, the compiler assumes that a function returns an int.
2. When defining a function that returns an int, define it as such.
3. When defining a function that doesn’t return a value, define it as void.
4. The compiler converts your arguments to agree with the ones the function expects only if you have previously defined or declared the function.
5. To play it safe, declare all functions in your program, even if they are defined before they are called. (You might decide later to move them somewhere else in your file or even to another file.)
Checking Function Arguments
The square root of a negative number takes you away from the realm of real numbers and into the area of imaginary numbers. So what happens if you pass a negative number to your squareRoot function? The fact is, the Newton-Raphson process would never converge; that is, the value ofguess would not get closer to the correct value of the square root with each iteration of the loop. Therefore, the criteria set up for termination of the while loop would never be satisfied, and the program would enter an infinite loop. Execution of the program would have to be abnormally terminated by typing in some command or pressing a special key combination (such as Ctrl+C).
Obviously, you should modify the program to correctly account for this situation. You could put the burden on the calling routine and mandate that it never pass a negative argument to the squareRoot() function. Although this approach might seem reasonable, it does have its drawbacks. Eventually, you would develop a program that used the squareRoot() function but which forgot to check the argument before calling the function. If a negative number were then passed to the function, the program would go into an infinite loop as described and would have to be aborted.
A much wiser and safer solution to the problem is to place the onus of checking the value of the argument on the squareRoot() function itself. In that way, the function is “protected” from any program that uses it. A reasonable approach to take is to check the value of the argument xinside the function and then (optionally) display a message if the argument is negative. The function can then immediately return without performing its calculations. As an indication to the calling routine that the squareRoot() function did not work as expected, a value not normally returned by the function could be returned.1
1. The square root routine in the standard C library is called sqrt() and it returns a domain error if a negative argument is supplied. The actual value that is returned is implementation-defined. On some systems, if you try to display such a value, it displays as nan, which means not a number.
The following is a modified squareRoot() function, which tests the value of its argument and which also includes a prototype declaration for the absoluteValue() function as described in the previous section.
/* Function to compute the square root of a number.
If a negative argument is passed, then a message
is displayed and -1.0 is returned. */
float squareRoot (float x)
{
const float epsilon = .00001;
float guess = 1.0;
float absoluteValue (float x);
if ( x < 0 )
{
printf ("Negative argument to squareRoot.\n");
return -1.0;
}
while ( absoluteValue (guess * guess - x) >= epsilon )
guess = ( x / guess + guess ) / 2.0;
return guess;
}
If a negative argument is passed to the preceding function, an appropriate message is displayed, and the value −1.0 is immediately returned to the calling routine. If the argument is not negative, calculation of the square root proceeds as previously described.
As you can see from the modified squareRoot() function (and as you also saw in the last example from Chapter 6, “Working with Arrays”), you can have more than one return statement in a function. Whenever a return is executed, control is immediately sent back to the calling function; any program statements in the function that appear after the return are not executed. This fact also makes the return statement ideal for use by a function that does not return a value. In such a case, as noted earlier in this chapter, the return statement takes the simpler form
return;
because no value is to be returned. Obviously, if the function is supposed to return a value, this form cannot be used to return from the function.
Top-Down Programming
The notion of functions that call functions that in turn call functions, and so on, forms the basis for producing good, structured programs. In the main() routine of Program 7.8, the squareRoot() function is called several times. All the details concerned with the actual calculation of the square root are contained within the squareRoot() function itself, and not within main(). Thus, you can write a call to this function before you even write the instructions of the function itself, as long as you specify the arguments that the function takes and the value that it returns.
Later, when proceeding to write the code for the squareRoot() function, this same type of top-down programming technique can be applied: You can write a call to the absoluteValue() function without concerning yourself at that time with the details of operation of that function. All you need to know is that you can develop a function to take the absolute value of a number.
The same programming technique that makes programs easier to write also makes them easier to read. Thus, the reader of Program 7.8 can easily determine upon examination of the main() routine that the program is simply calculating and displaying the square root of three numbers. She need not sift through all of the details of how the square root is actually calculated to glean this information. If she wants to get more involved in the details, she can study the specific code associated with the squareRoot() function. Inside that function, the same discussion applies to theabsoluteValue() function. She does not need to know how the absolute value of a number is calculated to understand the operation of the squareRoot() function. Such details are relegated to the absoluteValue() function itself, which can be studied if a more detailed knowledge of its operation is desired.
Functions and Arrays
As with ordinary variables and values, it is also possible to pass the value of an array element and even an entire array as an argument to a function. To pass a single array element to a function (which is what you did in Chapter 6 when you used the printf() function to display the elements of an array), the array element is specified as an argument to the function in the normal fashion. So, to take the square root of averages[i] and assign the result to a variable called sq_root_result, a statement such as
sq_root_result = squareRoot (averages[i]);
does the trick.
Inside the squareRoot() function itself, nothing special has to be done to handle single array elements passed as arguments. In the same manner as with a simple variable, the value of the array element is copied into the value of the corresponding formal parameter when the function is called.
Passing an entire array to a function is an entirely new ball game. To pass an array to a function, it is only necessary to list the name of the array, without any subscripts, inside the call to the function. As an example, if you assume that gradeScores has been declared as an array containing 100 elements, the expression
minimum (gradeScores)
in effect passes the entire 100 elements contained in the array gradeScores to the function called minimum(). Naturally, on the other side of the coin, the minimum() function must be expecting an entire array to be passed as an argument and must make the appropriate formal parameter declaration. So the minimum() function might look something like this:
int minimum (int values[100])
{
...
return minValue;
}
The declaration defines the function minimum() as returning a value of type int and as taking as its argument an array containing 100 integer elements. References made to the formal parameter array values reference the appropriate elements inside the array that was passed to the function. Based upon the function call previously shown and the corresponding function declaration, a reference made to values[4], for example, would actually reference the value of gradeScores[4].
For your first program that illustrates a function that takes an array as an argument, you can write a function minimum to find the minimum value in an array of 10 integers. This function, together with a main() routine to set up the initial values in the array, is shown in Program 7.9.
Program 7.9 Finding the Minimum Value in an Array
// Function to find the minimum value in an array
#include <stdio.h>
int minimum (int values[10])
{
int minValue, i;
minValue = values[0];
for ( i = 1; i < 10; ++i )
if ( values[i] < minValue )
minValue = values[i];
return minValue;
}
int main (void)
{
int scores[10], i, minScore;
int minimum (int values[10]);
printf ("Enter 10 scores\n");
for ( i = 0; i < 10; ++i )
scanf ("%i", &scores[i]);
minScore = minimum (scores);
printf ("\nMinimum score is %i\n", minScore);
return 0;
}
Program 7.9 Output
Enter 10 scores
69976587698678679290
Minimum score is 65
The first thing that catches your eye inside main() is the prototype declaration for the minimum() function. This tells the compiler that minimum() returns an int and takes an array of 10 integers. Remember, it’s not necessary to make this declaration here because the minimum()function is defined before it’s called from inside main(). However, play it safe throughout the rest of this text and declare all functions that are used.
After the array scores is defined, the user is prompted to enter 10 values. The scanf() call places each number as it is keyed in into scores[i], where i ranges from 0 through 9. After all the values have been entered, the minimum() function is called with the array scores as an argument.
The formal parameter name values is used to reference the elements of the array inside the function. It is declared to be an array of 10 integer values. The local variable minValue is used to store the minimum value in the array and is initially set to values[0], the first value in the array. The for loop sequences through the remaining elements of the array, comparing each element in turn against the value of minValue. If the value of values[i] is less than minValue, a new minimum in the array has been found. In such a case, the value of minValue is reassigned to this new minimum value and the scan through the array continues.
When the for loop has completed execution, minValue is returned to the calling routine, where it is assigned to the variable minScore and is then displayed.
With your general-purpose minimum() function in hand, you can use it to find the minimum of any array containing 10 integers. If you had five different arrays containing 10 integers each, you could simply call the minimum() function five separate times to find the minimum value of each array. In addition, you can just as easily define other functions to perform tasks, such as finding the maximum value, the median value, the mean (average) value, and so on.
By defining small, independent functions that perform well-defined tasks, you can build upon these functions to accomplish more sophisticated tasks and also make use of them for other related programming applications. For example, you could define a function statistics(), which takes an array as an argument and perhaps, in turn, calls a mean() function, a standardDeviation() function, and so on, to accumulate statistics about an array. This type of program methodology is the key to the development of programs that are easy to write, understand, modify, and maintain.
Of course, your general-purpose minimum() function is not so general purpose in the sense that it only works on an array of precisely 10 elements. But this problem is relatively easy to rectify. You can extend the versatility of this function by having it take the number of elements in the array as an argument. In the function declaration, you can then omit the specification of the number of elements contained in the formal parameter array. The C compiler actually ignores this part of the declaration anyway; all the compiler is concerned with is the fact that an array is expected as an argument to the function and not how many elements are in it.
Program 7.10 is a revised version of Program 7.9 in which the minimum() function finds the minimum value in an integer array of arbitrary length.
Program 7.10 Revising the Function to Find the Minimum Value in an Array
// Function to find the minimum value in an array
#include <stdio.h>
int minimum (int values[], int numberOfElements)
{
int minValue, i;
minValue = values[0];
for ( i = 1; i < numberOfElements; ++i )
if ( values[i] < minValue )
minValue = values[i];
return minValue;
}
int main (void)
{
int array1[5] = { 157, -28, -37, 26, 10 };
int array2[7] = { 12, 45, 1, 10, 5, 3, 22 };
int minimum (int values[], int numberOfElements);
printf ("array1 minimum: %i\n", minimum (array1, 5));
printf ("array2 minimum: %i\n", minimum (array2, 7));
return 0;
}
Program 7.10 Output
array1 minimum: -37
array2 minimum: 1
This time, the function minimum() is defined to take two arguments: first, the array whose minimum you want to find and second, the number of elements in the array. The open and close brackets that immediately follow values in the function header serve to inform the C compiler thatvalues is an array of integers. As stated previously, the compiler really doesn’t need to know how large it is.
The formal parameter numberOfElements replaces the constant 10 as the upper limit inside the for statement. So the for statement sequences through the array from values[1] through the last element of the array, which is values[numberOfElements - 1].
In the main() routine, two arrays called array1 and array2 are defined to contain five and seven elements, respectively.
Inside the first printf() call, a call is made to the minimum() function with the arguments array1 and 5. This second argument specifies the number of elements contained in array1. The minimum() function finds the minimum value in the array and the returned result of −37 is then displayed. The second time the minimum() function is called, array2 is passed, together with the number of elements in that array. The result of 1 as returned by the function is then passed to the printf() function to be displayed.
Assignment Operators
Study Program 7.11 and try to guess the output before looking at the actual program results.
Program 7.11 Changing Array Elements in Functions
#include <stdio.h>
void multiplyBy2 (float array[], int n)
{
int i;
for ( i = 0; i < n; ++i )
array[i] *= 2;
}
int main (void)
{
float floatVals[4] = { 1.2f, -3.7f, 6.2f, 8.55f };
int i;
void multiplyBy2 (float array[], int n);
multiplyBy2 (floatVals, 4);
for ( i = 0; i < 4; ++i )
printf ("%.2f ", floatVals[i]);
printf ("\n");
return 0;
}
Program 7.11 Output
2.40 -7.40 12.40 17.10
When you were examining Program 7.11, your attention surely must have been drawn to the following statement:
array[i] *= 2;
The effect of the “times equals” operator (*=) is to multiply the expression on the left side of the operator by the expression on the right side of the operator and to store the result back into the variable on the left side of the operator. So, the previous expression is equivalent to the following statement:
array[i] = array[i] * 2;
Getting back to the main point to be made about the preceding program, you might have realized by now that the function multiplyBy2() actually changes values inside the floatVals array. Isn’t this a contradiction to what you learned before about a function not being able to change the value of its arguments? Not really.
This program example points out one major distinction that must always be kept in mind when dealing with array arguments: if a function changes the value of an array element, that change is made to the original array that was passed to the function. This change remains in effect even after the function has completed execution and has returned to the calling routine.
The reason an array behaves differently from a simple variable or an array element—whose value cannot be changed by a function—is worthy of explanation. As mentioned previously, when a function is called, the values that are passed as arguments to the function are copied into the corresponding formal parameters. This statement is still valid. However, when dealing with arrays, the entire contents of the array are not copied into the formal parameter array. Instead, the function gets passed information describing where in the computer’s memory the array is located. Any changes made to the formal parameter array by the function are actually made to the original array passed to the function, and not to a copy of the array. Therefore, when the function returns, these changes still remain in effect.
Remember, the discussion about changing array values in a function applies only to entire arrays that are passed as arguments, and not to individual elements, whose values are copied into the corresponding formal parameters and, therefore, cannot be permanently changed by the function.Chapter 10 discusses this concept in greater detail.
Sorting Arrays
To further illustrate the idea that a function can change values in an array passed as an argument, you will develop a function to sort (rank) an array of integers. The process of sorting has always received much attention by computer scientists, probably because sorting is an operation that is so commonly performed. Many sophisticated algorithms have been developed to sort a set of information in the least amount of time, using as little of the computer’s memory as possible. Because the purpose of this book is not to teach such sophisticated algorithms, you develop a sort()function that uses a fairly straightforward algorithm to sort an array into ascending order. Sorting an array into ascending order means rearranging the values in the array so that the elements progressively increase in value from the smallest to the largest. By the end of such a sort, the minimum value is contained in the first location of the array, whereas the maximum value is found in the last location of the array, with values that progressively increase in between.
If you want to sort an array of n elements into ascending order, you can do so by performing a successive comparison of each of the elements of the array. You can begin by comparing the first element in the array against the second. If the first element is greater in value than the second, you simply “swap” the two values in the array; that is, exchange the values contained in these two locations.
Next, compare the first element in the array (which you now know is less than the second) against the third element in the array. Once again, if the first value is greater than the third, you exchange these two values. Otherwise, you leave them alone. Now, you have the smallest of the first three elements contained in the first location of the array.
If you repeat the previous process for the remaining elements in the array—comparing the first element against each successive element and exchanging their values if the former is larger than the latter—the smallest value of the entire array is contained in the first location of the array by the end of the process.
If you now did the same thing with the second element of the array, that is, compare it against the third element, then against the fourth, and so on; and if you exchange any values that are out of order, you end up with the next smallest value contained in the second location of the array when the process is complete.
It should now be clear how you can go about sorting the array by performing these successive comparisons and exchanges as needed. The process stops after you have compared the next-to-last element of the array against the last and have interchanged their values if required. At that point, the entire array has been sorted into ascending order.
The following algorithm gives a more concise description of the preceding sorting process. This algorithm assumes that you are sorting an array a of n elements.
Simple Exchange Sort Algorithm
Step 1. Set i to 0.
Step 2. Set j to i + 1.
Step 3. If a[i] > a[j], exchange their values.
Step 4. Set j to j + 1. If j < n, go to step 3.
Step 5. Set i to i + 1. If i < n - 1, go to step 2.
Step 6. a is now sorted in ascending order.
Program 7.12 implements the preceding algorithm in a function called sort, which takes two arguments: the array to be sorted and the number of elements in the array.
Program 7.12 Sorting an Array of Integers into Ascending Order
// Program to sort an array of integers into ascending order
#include <stdio.h>
void sort (int a[], int n)
{
int i, j, temp;
for ( i = 0; i < n - 1; ++i )
for ( j = i + 1; j < n; ++j )
if ( a[i] > a[j] ) {
temp = a[i];
a[i] = a[j];
a[j] = temp;
}
}
int main (void)
{
int i;
int array[16] = { 34, -5, 6, 0, 12, 100, 56, 22,
44, -3, -9, 12, 17, 22, 6, 11 };
void sort (int a[], int n);
printf ("The array before the sort:\n");
for ( i = 0; i < 16; ++i )
printf ("%i ", array[i]);
sort (array, 16);
printf ("\n\nThe array after the sort:\n");
for ( i = 0; i < 16; ++i )
printf ("%i ", array[i]);
printf ("\n");
return 0;
}
Program 7.12 Output
The array before the sort:
34 -5 6 0 12 100 56 22 44 -3 -9 12 17 22 6 11
The array after the sort:
-9 -5 -3 0 6 6 11 12 12 17 22 22 34 44 56 100
The sort() function implements the algorithm as a set of nested for loops. The outermost loop sequences through the array from the first element through the next-to-last element (a[n-2]). For each such element, a second for loop is entered, which starts from the element after the one currently selected by the outer loop and ranges through the last element of the array.
If the elements are out of order (that is, if a[i] is greater than a[j]), the elements are switched. The variable temp is used as a temporary storage place while the switch is being made.
When both for loops are finished, the array has been sorted into ascending order. Execution of the function is then complete.
In the main() routine, array is defined and initialized to 16 integer values. The program then displays the values of the array at the terminal and proceeds to call the sort() function, passing as arguments array and 16, the number of elements in array. After the function returns, the program once again displays the values contained in array. As you can see from the output, the function successfully sorted the array into ascending order.
The sort() function shown in Program 7.12 is fairly simple. The price that must be paid for such a simplistic approach is one of execution time. If you have to sort an extremely large array of values (arrays containing thousands of elements, for example), the sort() routine as you have implemented it here could take a considerable amount of execution time. If this happened, you would have to resort to one of the more sophisticated algorithms. The Art of Computer Programming, Volume 3, Sorting and Searching (Donald E. Knuth, Addison-Wesley) is a classic reference source for such algorithms.2
2. There is also a function called qsort() in the standard C library that can be used to sort an array containing any data type. However, before you use it, you need to understand pointers to functions, which are discussed in Chapter 10.
Multidimensional Arrays
A multidimensional array element can be passed to a function just as any ordinary variable or single-dimensional array element can. So the statement
squareRoot (matrix[i][j]);
calls the squareRoot() function, passing the value contained in matrix[i][j] as the argument.
An entire multidimensional array can be passed to a function in the same way that a single-dimensional array can: You simply list the name of the array. For example, if the matrix measured_values is declared to be a two-dimensional array of integers, the C statement
scalarMultiply (measured_values, constant);
can be used to invoke a function that multiplies each element in the matrix by the value of constant. This implies, of course, that the function itself can change the values contained inside the measured_values array. The discussion of this topic for single-dimensional arrays also applies here: An assignment made to any element of the formal parameter array inside the function makes a permanent change to the array that was passed to the function.
When declaring a single-dimensional array as a formal parameter inside a function, you learned that the actual dimension of the array is not needed; simply use a pair of empty brackets to inform the C compiler that the parameter is, in fact, an array. This does not totally apply in the case of multidimensional arrays. For a two-dimensional array, the number of rows in the array can be omitted, but the declaration must contain the number of columns in the array. So the declarations
int array_values[100][50]
and
int array_values[][50]
are both valid declarations for a formal parameter array called array_values containing 100 rows by 50 columns; but the declarations
int array_values[100][]
and
int array_values[][]
are not because the number of columns in the array must be specified.
In Program 7.13, you define a function scalarMultiply(), which multiplies a two-dimensional integer array by a scalar integer value. Assume for purposes of this example that the array is dimensioned 3 × 5. The main() routine calls the scalarMultiply() routine twice. After each call, the array is passed to the displayMatrix() routine to display the contents of the array. Pay careful attention to the nested for loops that are used in both scalarMultiply() and displayMatrix() to sequence through each element of the two-dimensional array.
Program 7.13 Using Multidimensional Arrays and Functions
#include <stdio.h>
int main (void)
{
void scalarMultiply (int matrix[3][5], int scalar);
void displayMatrix (int matrix[3][5]);
int sampleMatrix[3][5] =
{
{ 7, 16, 55, 13, 12 },
{ 12, 10, 52, 0, 7 },
{ -2, 1, 2, 4, 9 }
};
printf ("Original matrix:\n");
displayMatrix (sampleMatrix);
scalarMultiply (sampleMatrix, 2);
printf ("\nMultiplied by 2:\n");
displayMatrix (sampleMatrix);
scalarMultiply (sampleMatrix, -1);
printf ("\nThen multiplied by -1:\n");
displayMatrix (sampleMatrix);
return 0;
}
// Function to multiply a 3 x 5 array by a scalar
void scalarMultiply (int matrix[3][5], int scalar)
{
int row, column;
for ( row = 0; row < 3; ++row )
for ( column = 0; column < 5; ++column )
matrix[row][column] *= scalar;
}
void displayMatrix (int matrix[3][5])
{
int row, column;
for ( row = 0; row < 3; ++row) {
for ( column = 0; column < 5; ++column )
printf ("%5i", matrix[row][column]);
printf ("\n");
}
}
Program 7.13 Output
Original matrix:
7 16 55 13 12
12 10 52 0 7
-2 1 2 4 9
Multiplied by 2:
14 32 110 26 24
24 20 104 0 14
-4 2 4 8 18
Then multiplied by -1:
-14 -32 -110 -26 -24
-24 -20 -104 0 -14
4 -2 -4 -8 -18
The main() routine defines the matrix sampleValues and then calls the displayMatrix() function to display its initial values at the terminal. Inside the displayMatrix() routine, notice the nested for statements. The first or outermost for statement sequences through eachrow in the matrix, so the value of the variable row varies from 0 through 2. For each value of row, the innermost for statement is executed. This for statement sequences through each column of the particular row, so the value of the variable column ranges from 0 through 4.
The printf() statement displays the value contained in the specified row and column using the format characters %5i to ensure that the elements line up in the display. After the innermost for loop has finished execution—meaning that an entire row of the matrix has been displayed—a newline character is displayed so that the next row of the matrix is displayed on the next line.
The first call to the scalarMultiply() function specifies that the sampleMatrix array is to be multiplied by 2. Inside the function, a simple set of nested for loops is set up to sequence through each element in the array. The element contained in matrix[row][column] is multiplied by the value of scalar in accordance with the use of the assignment operator *=. After the function returns to the main() routine, the displayMatrix() function is once again called to display the contents of the sampleMatrix() array. The program’s output verifies that each element in the array has, in fact, been multiplied by 2.
The scalarMultiply() function is called a second time to multiply the now modified elements of the sampleMatrix array by −1. The modified array is then displayed by a final call to the displayMatrix() function, and program execution is then complete.
Multidimensional Variable-Length Arrays and Functions
You can take advantage of the variable-length array feature in the C language and write functions that can take multidimensional arrays of varying sizes. For example, Program 7.13 can be rewritten so that the scalarMultiply() and displayMatrix() functions can accept matrices containing any number of rows and columns, which can be passed as arguments to the functions. See Program 7.14.
Program 7.14 Multidimensional Variable-Length Arrays
#include <stdio.h>
int main (void)
{
void scalarMultiply (int nRows, int nCols,
int matrix[nRows][nCols], int scalar);
void displayMatrix (int nRows, int nCols, int matrix[nRows][nCols]);
int sampleMatrix[3][5] =
{
{ 7, 16, 55, 13, 12 },
{ 12, 10, 52, 0, 7 },
{ -2, 1, 2, 4, 9 }
};
printf ("Original matrix:\n");
displayMatrix (3, 5, sampleMatrix);
scalarMultiply (3, 5, sampleMatrix, 2);
printf ("\nMultiplied by 2:\n");
displayMatrix (3, 5, sampleMatrix);
scalarMultiply (3, 5, sampleMatrix, -1);
printf ("\nThen multiplied by -1:\n");
displayMatrix (3, 5, sampleMatrix);
return 0;
}
// Function to multiply a matrix by a scalar
void scalarMultiply (int nRows, int nCols,
int matrix[nRows][nCols], int scalar)
{
int row, column;
for ( row = 0; row < nRows; ++row )
for ( column = 0; column < nCols; ++column )
matrix[row][column] *= scalar;
}
void displayMatrix (int nRows, int nCols, int matrix[nRows][nCols])
{
int row, column;
for ( row = 0; row < nRows; ++row) {
for ( column = 0; column < nCols; ++column )
printf ("%5i", matrix[row][column]);
printf ("\n");
}
}
Program 7.14 Output
Original matrix:
7 16 55 13 12
12 10 52 0 7
-2 1 2 4 9
Multiplied by 2:
14 32 110 26 24
24 20 104 0 14
-4 2 4 8 18
Then multiplied by -1:
-14 -32 -110 -26 -24
-24 -20 -104 0 -14
4 -2 -4 -8 -18
The function declaration for scalarMultiply() looks like this:
void scalarMultiply (int nRows, int nCols, int matrix[nRows][nCols], int scalar)
The rows and columns in the matrix, nRows, and nCols, must be listed as arguments before the matrix itself so that the compiler knows about these parameters before it encounters the declaration of matrix in the argument list. If you try it this way instead:
void scalarMultiply (int matrix[nRows][nCols], int nRows, int nCols, int scalar)
you get an error from the compiler because it doesn’t know about nRows and nCols when it sees them listed in the declaration of matrix.
As you can see, the output shown in Program 7.14 matches that shown in Program 7.13. Now, you have two functions (scalarMultiply() and displayMatrix()) that you can use with matrices of any size. This is one of the advantages of using variable-length arrays.
Global Variables
It is now time to tie together many of the principles you have learned in this chapter, as well as learn some new ones. Take Program 6.7, which converted a positive integer to another base, and rewrite it in function form. To do this, you must conceptually divide the program into logical segments. If you glance back at that program, you see that this is readily accomplished simply by looking at the three comment statements inside main(). They suggest the three primary functions that the program is performing: getting the number and base from the user, converting the number to the desired base, and displaying the results.
You can define three functions to perform an analogous task. The first function you call is getNumberAndBase(). This function prompts the user to enter the number to be converted and the base, and reads these values. Here, you make a slight improvement over what was done inProgram 6.7. If the user types in a value of base that is less than 2 or greater than 16, the program displays an appropriate message at the terminal and sets the value of the base to 10. In this manner, the program ends up redisplaying the original number to the user. (Another approach might be to let the user reenter a new value for the base, but this is left as an exercise.)
The second function you call is convertNumber(). This function takes the value as typed in by the user and converts it to the desired base, storing the digits resulting from the conversion process inside the convertedNumber array.
The third and final function you call is displayConvertedNumber(). This function takes the digits contained inside the convertedNumber array and displays them to the user in the correct order. For each digit to be displayed, a lookup is made inside the baseDigits array so that the correct character is displayed for the corresponding digit.
The three functions that you define communicate with each other by means of global variables. As noted previously, one of the fundamental properties of a local variable is that its value can be accessed only by the function in which the variable is defined. As you might expect, this restriction does not apply to global variables. That is, a global variable’s value can be accessed by any function in the program.
The distinguishing quality of a global variable declaration versus a local variable declaration is that the former is made outside of any function. This indicates its global nature—it does not belong to any particular function. Any function in the program can then access the value of that variable and can change its value if desired.
In Program 7.15, four global variables are defined. Each of these variables is used by at least two functions in the program. Because the baseDigits array and the variable nextDigit are used exclusively by the function displayConvertedNumber(), they are not defined as global variables. Instead, these variables are locally defined within the function displayConvertedNumber().
The global variables are defined first in the program. Because they are not defined within any particular function, these variables are global, which means that they can now be referenced by any function in the program.
Program 7.15 Converting a Positive Integer to Another Base
// Program to convert a positive integer to another base
#include <stdio.h>
int convertedNumber[64];
long int numberToConvert;
int base;
int digit = 0;
void getNumberAndBase (void)
{
printf ("Number to be converted? ");
scanf ("%li", &numberToConvert);
printf ("Base? ");
scanf ("%i", &base);
if ( base < 2 || base > 16 ) {
printf ("Bad base - must be between 2 and 16\n");
base = 10;
}
}
void convertNumber (void)
{
do {
convertedNumber[digit] = numberToConvert % base;
++digit;
numberToConvert /= base;
}
while ( numberToConvert != 0 );
}
void displayConvertedNumber (void)
{
const char baseDigits[16] =
{ '0', '1', '2', '3', '4', '5', '6', '7',
'8', '9', 'A', 'B', 'C', 'D', 'E', 'F' };
int nextDigit;
printf ("Converted number = ");
for (--digit; digit >= 0; --digit ) {
nextDigit = convertedNumber[digit];
printf ("%c", baseDigits[nextDigit]);
}
printf ("\n");
}
int main (void)
{
void getNumberAndBase (void), convertNumber (void),
displayConvertedNumber (void);
getNumberAndBase ();
convertNumber ();
displayConvertedNumber ();
return 0;
}
Program 7.15 Output
Number to be converted? 100
Base? 8
Converted number = 144
Program 7.15 Output (Rerun)
Number to be converted? 1983
Base? 0
Bad base - must be between 2 and 16
Converted number = 1983
Notice how the wise choice of function names makes the operation of Program 7.15 clear. Spelled out directly in the main() routine is the function of the program: to get a number and a base, convert the number, and then display the converted number. The much-improved readability of this program over the equivalent one from Chapter 6 is a direct result of the structuring of the program into separate functions that perform small, well-defined tasks. Note that you do not even need comment statements inside the main() routine to describe what the program is doing—the function names speak for themselves.
The primary use of global variables is in programs in which many functions must access the value of the same variable. Rather than having to pass the value of the variable to each individual function as an argument, the function can explicitly reference the variable instead. There is a drawback with this approach. Because the function explicitly references a particular global variable, the generality of the function is somewhat reduced. So, every time that function is to be used, you must ensure that the global variable exists, by its particular name.
For example, the convertNumber() function of Program 7.15 succeeds in converting only a number that is stored in the variable numberToConvert to a base as specified by the value of the variable base. Furthermore, the variable digit and the array convertedNumber must be defined. A far more flexible version of this function would allow the arguments to be passed to the function.
Although the use of global variables can reduce the number of arguments that need to be passed to a function, the price that must be paid is reduced function generality and, in some cases, reduced program readability. This issue of program readability stems from the fact that if you use global variables, the variables that are used by a particular function are not evident simply by examining the function’s header. Also, a call to the particular function does not indicate to the reader what types of parameters the function needs as inputs or produces as outputs.
Some programmers adopt the convention of prefixing all global variable names with the letter “g”. For example, their variable declarations for Program 7.15 might look like this:
int gConvertedNumber[64];
long int gNumberToConvert;
int gBase;
int gDigit = 0;
The reason for adopting such a convention is that it becomes easier to pick out a global variable from a local one when reading through a program. For example, the statement
nextMove = gCurrentMove + 1;
implies that nextMove is a local variable and gCurrentMove is a global one. This tells the reader of this line about the scope of these variables and where to look for their declarations.
One final thing about global variables. They do have default initial values: zero. So, in the global declaration
int gData[100];
all 100 elements of the gData array are set to zero when the program begins execution.
So remember that although global variables have default initial values of zero, local variables have no default initial value and so must be explicitly initialized by the program.
Automatic and Static Variables
When you normally declare a local variable inside a function, as in the declaration of the variables guess and epsilon in your squareRoot() function
float squareRoot (float x)
{
const float epsilon = .00001;
float guess = 1.0;
. . .
}
you are declaring automatic local variables. Recall that the keyword auto can, in fact, precede the declaration of such variables, but is optional because it is the default case. An automatic variable is, in a sense, actually created each time the function is called. In the preceding example, the local variables epsilon and guess are created whenever the squareRoot() function is called. As soon as the squareRoot() function is finished, these local variables “disappear.” This process happens automatically, hence the name automatic variables.
Automatic local variables can be given initial values, as is done with the values of epsilon and guess, previously. In fact, any valid C expression can be specified as the initial value for a simple automatic variable. The value of the expression is calculated and assigned to the automatic local variable each time the function is called. And because an automatic variable disappears after the function completes execution, the value of that variable disappears along with it. In other words, the value an automatic variable has when a function finishes execution is guaranteed not to exist the next time the function is called.
If you place the word static in front of a variable declaration, you are in an entirely new ballgame. The word static in C refers not to an electric charge, but rather to the notion of something that has no movement. This is the key to the concept of a static variable—it does not come and go as the function is called and returns. This implies that the value a static variable has upon leaving a function is the same value that variable will have the next time the function is called.
Static variables also differ with respect to their initialization. A static, local variable is initialized only once at the start of overall program execution—and not each time that the function is called. Furthermore, the initial value specified for a static variable must be a simple constant or constant expression. Static variables also have default initial values of zero, unlike automatic variables, which have no default initial value.
In the function auto_static(), which is defined as follows:
void auto_static (void)
{
static int staticVar = 100;
.
.
.
}
the value of staticVar is initialized to 100 only once when program execution begins. To set its value to 100 each time the function is executed, an explicit assignment statement is needed, as in
void auto_static (void)
{
static int staticVar;
staticVar = 100;
.
.
.
}
Of course, reinitializing staticVar this way defeats the purpose of using a static variable in the first place.
Program 7.16 should help make the concepts of automatic and static variables a bit clearer.
Program 7.16 Illustrating Static and Automatic Variables
// Program to illustrate static and automatic variables
#include <stdio.h>
void auto_static (void)
{
int autoVar = 1;
static int staticVar = 1;
printf ("automatic = %i, static = %i\n", autoVar, staticVar);
++autoVar;
++staticVar;
}
int main (void)
{
int i;
void auto_static (void);
for ( i = 0; i < 5; ++i )
auto_static ();
return 0;
}
Program 7.16 Output
automatic = 1, static = 1
automatic = 1, static = 2
automatic = 1, static = 3
automatic = 1, static = 4
automatic = 1, static = 5
Inside the auto_static() function, two local variables are declared. The first variable, called autoVar, is an automatic variable of type int with an initial value of 1. The second variable, called staticVar, is a static variable, also of type int and also with an initial value of 1. The function calls the printf() routine to display the values of these two variables. After this, the variables are each incremented by 1, and execution of the function is then complete.
The main() routine sets up a loop to call the auto_static() function five times. The output from Program 7.16 points out the difference between the two variable types. The value of the automatic variable is listed as 1 for each line of the display. This is because its value is set to 1each time the function is called. On the other hand, the output shows the value of the static variable steadily increasing from 1 through 5. This is because its value is set equal to 1 only once—when program execution begins—and because its value is retained from one function call to the next.
The choice of whether to use a static variable or automatic variable depends upon the intended use of the variable. If you want the variable to retain its value from one function call to the next (for example, consider a function that counts the number of times that it is called), use a static variable. Also, if your function uses a variable whose value is set once and then never changes, you might want to declare the variable static, as it saves the inefficiency of having the variable reinitialized each time that the function is called. This efficiency consideration is even more important when dealing with arrays.
From the other direction, if the value of a local variable must be initialized at the beginning of each function call, an automatic variable seems the logical choice.
Recursive Functions
The C language supports a capability known as recursive function. Recursive functions can be effectively used to succinctly and efficiently solve problems. They are commonly used in applications in which the solution to a problem can be expressed in terms of successively applying the same solution to subsets of the problem. One example might be in the evaluation of expressions containing nested sets of parenthesized expressions. Other common applications involve the searching and sorting of data structures called trees and lists.
Recursive functions are most commonly illustrated by an example that calculates the factorial of a number. Recall that the factorial of a positive integer n, written n!, is simply the product of the successive integers 1 through n. The factorial of 0 is a special case and is defined equal to 1. So 5! is calculated as follows:
5! = 5 x 4 x 3 x 2 x 1
= 120
And 6! is calculated like so:
6! = 6 x 5 x 4 x 3 x 2 x 1
= 720
Comparing the calculation of 6! to the calculation of 5!, observe that the former is equal to 6 times the latter; that is, 6! = 6 × 5!. In the general case, the factorial of any positive integer n greater than zero is equal to n multiplied by the factorial of n - 1:
n! = n x (n - 1)!
The expression of the value of n! in terms of the value of (n-1)! is called a recursive definition because the definition of the value of a factorial is based on the value of another factorial. In fact, you can develop a function that calculates the factorial of an integer n according to this recursive definition. Such a function is illustrated in Program 7.17.
Program 7.17 Calculating Factorials Recursively
#include <stdio.h>
int main (void)
{
unsigned int j;
unsigned long int factorial (unsigned int n);
for ( j = 0; j < 11; ++j )
printf ("%2u! = %lu\n", j, factorial (j));
return 0;
}
// Recursive function to calculate the factorial of a positive integer
unsigned long int factorial (unsigned int n)
{
unsigned long int result;
if ( n == 0 )
result = 1;
else
result = n * factorial (n - 1);
return result;
}
Program 7.17 Output
0! = 1
1! = 1
2! = 2
3! = 6
4! = 24
5! = 120
6! = 720
7! = 5040
8! = 40320
9! = 362880
10! = 3628800
The fact that the factorial() function includes a call to itself makes this function recursive. When the function is called to calculate the factorial of 3, the value of the formal parameter n is set to 3. Because this value is not zero, the following program statement
result = n * factorial (n - 1);
is executed, which, given the value of n, is evaluated as
result = 3 * factorial (2);
This expression specifies that the factorial() function is to be called, this time to calculate the factorial of 2. Therefore, the multiplication of 3 by this value is left pending while factorial (2) is calculated.
Even though you are again calling the same function, you should conceptualize this as a call to a separate function. Each time any function is called in C—be it recursive or not—the function gets its own set of local variables and formal parameters with which to work. Therefore, the local variable result and the formal parameter n that exist when the factorial() function is called to calculate the factorial of 3 are distinct from the variable result and the parameter n when the function is called to calculate the factorial of 2.
With the value of n equal to 2, the factorial() function executes the statement
result = n * factorial (n - 1);
which is evaluated as
result = 2 * factorial (1);
Once again, the multiplication of 2 by the factorial of 1 is left pending while the factorial() function is called to calculate the factorial of 1.
With the value of n equal to 1, the factorial() function once again executes the statement
result = n * factorial (n - 1);
which is evaluated as
result = 1 * factorial (0);
When the factorial() function is called to calculate the factorial of 0, the function sets the value of result to 1 and return, thus initiating the evaluation of all of the pending expressions. So the value of factorial (0), or 1, is returned to the calling function (which happens to be the factorial() function), multiplied by 1, and assigned to result. This value of 1, which represents the value of factorial (1), is then returned back to the calling function (once again the factorial() function) where it is multiplied by 2, stored into result, and returned as the value of factorial (2). Finally, the returned value of 2 is multiplied by 3, thus completing the pending calculation of factorial (3). The resulting value of 6 is returned as the final result of the call to the factorial() function, to be displayed by the printf() function.
In summary, the sequence of operations that is performed in the evaluation of factorial (3) can be conceptualized as follows:
factorial (3) = 3 * factorial (2)
= 3 * 2 * factorial (1)
= 3 * 2 * 1 * factorial (0)
= 3 * 2 * 1 * 1
= 6
It might be a good idea for you to trace through the operation of the factorial() function with a pencil and paper. Assume that the function is initially called to calculate the factorial of 4. List the values of n and result at each call to the factorial() function.
This discussion concludes this chapter on functions and variables. The program function is a powerful tool in the C programming language. Enough cannot be said about the critical importance of structuring a program in terms of small, well-defined functions. Functions are used heavily throughout the remainder of this book. At this point, you should review any topics covered in this chapter that still seem unclear. Working through the following exercises will also help reinforce the topics that have been discussed.
Exercises
1. Type in and run the 17 programs presented in this chapter. Compare the output produced by each program with the output presented after each program in the text.
2. Modify Program 7.4 so the value of triangularNumber is returned by the function. Then go back to Program 4.5 and change that program so that it calls the new version of the calculateTriangularNumber() function.
3. Modify Program 7.8 so that the value of epsilon is passed as an argument to the function. Try experimenting with different values of epsilon to see the effect that it has on the value of the square root.
4. Modify Program 7.8 so that the value of guess is printed each time through the while loop. Notice how quickly the value of guess converges to the square root. What conclusions can you reach about the number of iterations through the loop, the number whose square root is being calculated, and the value of the initial guess?
5. The criteria used for termination of the loop in the squareRoot() function of Program 7.8 is not suitable for use when computing the square root of very large or very small numbers. Rather than comparing the difference between the value of x and the value of guess2, the program should compare the ratio of the two values to 1. The closer this ratio gets to 1, the more accurate the approximation of the square root.
Modify Program 7.8 so this new termination criteria is used.
6. Modify Program 7.8 so that the squareRoot() function accepts a double precision argument and returns the result as a double precision value. Be certain to change the value of the variable epsilon to reflect the fact that double precision variables are now being used.
7. Write a function that raises an integer to a positive integer power. Call the function x_to_the_n() taking two integer arguments x and n. Have the function return a long int, which represents the results of calculating xn.
8. An equation of the form
ax2 + bx + c = 0
is known as a quadratic equation. The values of a, b, and c in the preceding example represent constant values. So
4x2 - 17x - 15 = 0
represents a quadratic equation where a = 4, b = −17, and c = −15. The values of x that satisfy a particular quadratic equation, known as the roots of the equation, can be calculated by substituting the values of a, b, and c into the following two formulas:
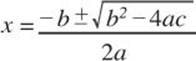
If the value of b2−4ac, called the discriminant, is less than zero, the roots of the equation, x1 and x2, are imaginary numbers.
Write a program to solve a quadratic equation. The program should allow the user to enter the values for a, b, and c. If the discriminant is less than zero, a message should be displayed that the roots are imaginary; otherwise, the program should then proceed to calculate and display the two roots of the equation. (Note: Be certain to make use of the squareRoot() function that you developed in this chapter.)
9. The least common multiple (lcm) of two positive integers u and v is the smallest positive integer that is evenly divisible by both u and v. Thus, the lcm of 15 and 10, written lcm (15, 10), is 30 because 30 is the smallest integer divisible by both 15 and 10. Write a function lcm() that takes two integer arguments and returns their lcm. The lcm() function should calculate the least common multiple by calling the gcd() function from Program 7.6 in accordance with the following identity:
lcm (u, v) = uv / gcd (u, v) u, v >= 0
10. Write a function prime() that returns 1 if its argument is a prime number and returns 0 otherwise.
11. Write a function called arraySum() that takes two arguments: an integer array and the number of elements in the array. Have the function return as its result the sum of the elements in the array.
12. A matrix M with i rows, j columns can be transposed into a matrix N having j rows and i columns by simply setting the value of Na,b equal to the value of Mb,a for all relevant values of a and b.
a. Write a function transposeMatrix() that takes as an argument a 4 × 5 matrix and a 5 × 4 matrix. Have the function transpose the 4 × 5 matrix and store the results in the 5 × 4 matrix. Also write a main() routine to test the function.
b. Using variable-length arrays, rewrite the transposeMatrix() function developed in exercise 12a to take the number of rows and columns as arguments, and to transpose the matrix of the specified dimensions.
13. Modify the sort() function from Program 7.12 to take a third argument indicating whether the array is to be sorted in ascending or descending order. Then modify the sort() algorithm to correctly sort the array into the indicated order.
14. Rewrite the functions developed in the last four exercises to use global variables instead of arguments. For example, the preceding exercise should now sort a globally defined array.
15. Modify Program 7.14 so that the user is asked again to type in the value of the base if an invalid base is entered. The modified program should continue to ask for the value of the base until a valid response is given.
16. Modify Program 7.14 so that the user can convert any number of integers. Make provision for the program to terminate when a zero is typed in as the value of the number to be converted.
All materials on the site are licensed Creative Commons Attribution-Sharealike 3.0 Unported CC BY-SA 3.0 & GNU Free Documentation License (GFDL)
If you are the copyright holder of any material contained on our site and intend to remove it, please contact our site administrator for approval.
© 2016-2025 All site design rights belong to S.Y.A.