The C++ Programming Language (2013)

Part IV: The Standard Library

32. STL Algorithms

Form is liberating.

– Engineer’s proverb

• Introduction

• Algorithms

Sequences; Policy Arguments; Complexity

• Nonmodifying Sequence Algorithms

for_each(); Sequence Predicates; count(); find(); equal() and mismatch(); search()

• Modifying Sequence Algorithms

copy(); unique(); remove() and replace(); rotate(), random_shuffle(), and partition(); Permutations; fill(); swap()

• Sorting and Searching

Binary Search; merge(); Set Algorithms; Heaps; lexcographical_compare()

• Min and Max

• Advice

32.1. Introduction

This chapter presents the STL algorithms. The STL consists of the iterator, container, algorithm, and function object parts of the standard library. The rest of the STL is presented in Chapter 31 and Chapter 33.

32.2. Algorithms

There are about 80 standard algorithms defined in <algorithm>. They operate on sequences defined by a pair of iterators (for inputs) or a single iterator (for outputs). When copying, comparing, etc., two sequences, the first is represented by a pair of iterators, [b:e), but the second by just a single iterator, b2, which is considered the start of a sequence holding sufficient elements for the algorithm, for example, as many elements as the first sequence: [b2:b2+(e–b)). Some algorithms, such as sort(), require random-access iterators, whereas many, such as find(), only read their elements in order so that they can make do with a forward iterator. Many algorithms follow the usual convention of returning the end of a sequence to represent “not found” (§4.5). I don’t mention that for each algorithm.

Algorithms, both the standard-library algorithms and the users’ own ones, are important:

• Each names a specific operation, documents an interface, and specifies semantics.

• Each can be widely used and known by many programmers.

For correctness, maintainability, and performance, these can be immense advantages compared to “random code” with less well-specified functions and dependencies. If you find yourself writing a piece of code with several loops, local variables that don’t seem to relate to each other, or complicated control structures, consider if the code could be simplified by making a part into a function/algorithm with a descriptive name, a well-defined purpose, a well-defined interface, and well-defined dependencies.

Numerical algorithms in the style of the STL algorithms are presented in §40.6.

32.2.1. Sequences

The ideal for a standard-library algorithm is to provide the most general and flexible interface to something that can be implemented optimally. The iterator-based interfaces are a good, but not perfect, approximation to that ideal (§33.1.1). For example, an iterator-based interface does not directly represent the notion of a sequence, leading to the possibility of confusion and difficulties in detecting some range errors:

void user(vector<int>& v1, vector<int>& v2)
{
copy(v1.begin(),v1.end(),v2.begin()); // may overflow v2
sort(v1.begin(),v2.end()); // oops!
}

Many such problems can be alleviated by providing container versions of the standard-library algorithms. For example:

template<typename Cont>
void sort(Cont& c)
{
static_assert(Range<Cont>(), "sort(): Cont argument not a Range");
static_assert(Sortable<Iterator<Cont>>(), "sort(): Cont argument not Sortable");

std::sort(begin(c),end(c));
}

template<typename Cont1, typename Cont2>
void copy(const Cont1& source, Cont2& target)
{
static_assert(Range<Cont1>(), "copy(): Cont1 argument not a Range");
static_assert(Range<Cont2>(), "copy(): Cont2 argument not a Range");
if (target.size()<source.size()) throw out_of_range{"copy target too small"};

std::copy(source.begin(),source.end(),target.begin());
}

This would simplify the definition of user(), make the second error impossible to express, and catch the first at run time:

void user(vector<int>& v1, vector<int>& v2)
{
copy(v1,v2); // overflows will be caught
sort(v1);
}

However, the container versions are also less general than the versions that use iterators directly. In particular, you cannot use the container sort() to sort half a container, and you cannot use the container copy() to write to an output stream.

A complementary approach is to define a “range” or “sequence” abstraction that allows us to define sequences when needed. I use the concept Range to denote anything with begin() and end() iterators (§24.4.4). That is, there is no Range class holding data – exactly as there is noIterator class or Container class in the STL. So, in the “container sort()” and “container copy()” examples, I called the template argument Cont (for “container”), but they will accept any sequence with a begin() and an end() that meets the rest of the requirements for the algorithm.

The standard-library containers mostly return iterators. In particular, they do not return containers of results (except in a few rare examples, a pair). One reason for that is that when the STL was designed, there was no direct support for move semantics. So, there was no obvious and efficient way to return a lot of data from an algorithm. Some programmers used explicit indirection (e.g., a pointer, reference, or iterator) or some clever trickery. Today, we can do better:

template<typename Cont, typename Pred>
vector<Value_type<Cont>*>
find_all(Cont& c, Pred p)
{
static_assert(Range<Cont>(), "find_all(): Cont argument not a Range");
static_assert(Predicate<Pred>(), "find_all(): Pred argument not a Predicate");

vector<Value_type<Cont>*> res;
for (auto& x : c)
if (p(x)) res.push_back(&x);
return res;
}

In C++98, this find_all() would have been a bad performance bug whenever the number of matches was large. If the choice of standard-library algorithms seems restrictive or insufficient, extension with new versions of STL algorithms or new algorithms is often a viable and superior alternative to just writing “random code” to work around the problem.

Note that whatever an STL algorithm returns, it cannot be an argument container. The arguments to STL algorithms are iterators (Chapter 33), and an algorithm has no knowledge of the data structure those iterators point into. Iterators exist primarily to isolate algorithms from the data structure on which they operate, and vice versa.

32.3. Policy Arguments

Most standard-library algorithms come in two versions:

• A “plain” version that performs its action using conventional operations, such as < and ==

• A version that takes key operations as arguments

For example:

template<class Iter>
void sort(Iter first, Iter last)
{
// ... sort using e1<e2 ...
}

template<class Iter, class Pred>
void sort(Iter first, Iter last, Pred pred)
{
// ... sort using pred(e1,e2) ...
}

This greatly increases the flexibility of the standard library and its range of uses.

The usual two versions of an algorithm can be implemented as two (overloaded) function templates or as a single function template with a default argument. For example:

template<typename Ran, typename Pred = less<Value_type<Ran>>> // use a default template argument
sort(Ran first, Ran last, Pred pred ={})
{
// ... use pred(x,y) ...
}

The difference between having two functions and having one with a default argument can be observed by someone taking pointers to functions. However, thinking of many of the variants of the standard algorithms as simply “the version with the default predicate” roughly halves the number of template functions you need to remember.

In some cases, an argument could be interpreted as either a predicate or a value. For example:

bool pred(int);

auto p = find(b,e,pred); // find element pred or apply predicate'pred()? (the latter)

In general, a compiler cannot disambiguate such examples, and programmers would get confused even in the cases where the compiler could disambiguate.

To simplify the task for the programmer, the _if suffix is often used to indicate that an algorithm takes a predicate. The reason to distinguish by using two names is to minimize ambiguities and confusion. Consider:

using Predicate = bool(*)(int);

void f(vector<Predicate>& v1, vector<int>& v2)
{
auto p1 = find(v1.begin(),v1.end(),pred); // find element with the value pred
auto p2 = find_if(v2.begin(),v2.end(),pred); // count elements for which pred() returns true
}

Some operations passed as arguments to an algorithm are meant to modify the element to which they are applied (e.g., some operations passed to for_each(); §32.4.1), but most are predicates (e.g., a comparison object for sort()). Unless otherwise stated, assume that a policy argument passed to an algorithm should not modify an element. In particular, do not try to modify elements through predicates:

int n_even(vector<int>& v) // don't do this
// count the number of even values in v
{
return find_if(v.begin(),v.end(),[](int& x) {++x; return x&1; });
}

Modifying an element through a predicate obscures what is being done. If you are really sneaky, you could even modify the sequence (e.g., by inserting or removing an element using the name of a container being iterated over), so that the iteration would fail (probably in obscure ways). To avoid accidents, you may pass arguments to predicates by const reference.

Similarly, a predicate should not carry state that changes the meaning of its operation. The implementation of an algorithm may copy a predicate, and we rarely want repeated uses of a predicate on the same value to give different results. Some function objects passed to algorithms, such as random number generators, do carry mutable state. Unless you are really sure that an algorithm doesn’t copy, keep a function object argument’s mutable state in another object and access it through a pointer or a reference.

The == and < operations on pointer elements are rarely appropriate for an STL algorithm: they compare machine addresses rather than the values pointed to. In particular, do not sort or search containers of C-style strings using the default == and < (§32.6).

32.3.1. Complexity

As for containers (§31.3), the complexity of algorithms is specified by the standard. Most algorithms are linear, O(n), for some n, which is usually the length of an input sequence.

As ever, these are asymptotic complexities, and you have to know what n measures to have an idea of the implications. For example, if n<3, a quadratic algorithm may be the best choice. The cost of each iteration can vary dramatically. For example, traversing a list can be much slower thantraversing a vector, even though the complexity in both cases is linear (O(n)). Complexity measures are not a substitute for common sense and actual time measurements; they are one tool among many to ensure quality code.

32.4. Nonmodifying Sequence Algorithms

A nonmodifying algorithm just reads the values of elements of its input sequences; it does not rearrange the sequence and does not change the values of the elements. Typically, user-supplied operations to an algorithm don’t change the values of elements either; they tend to be predicates (which may not modify their arguments).

32.4.1. for_each()

The simplest algorithm is for_each(), which just applies an operation to each element of a sequence:

When possible, prefer a more specific algorithm.

The operation passed to for_each() may modify elements. For example:

void increment_all(vector<int>& v) // increment each element of v
{
for_each(v.begin(),v.end(), [](int& x) {++x;});
}

32.4.2. Sequence Predicates

For example:

vector<double> scale(const vector<double>& val, const vector<double>& div)
{
assert(val.size()<div.size());
assert(all_of(div.begin(),div.end(),[](double x){ return 0<x; });

vector res(val.size());
for (int i = 0; i<val.size(); ++i)
res[i] = val[i]/div[i];
return res;
}

When one of these sequence predicates fails, it does not tell which element caused the failure.

32.4.3. count()

For example:

void f(const string& s)
{
auto n_space = count(s.begin(),s.end(),' ');
auto n_whitespace = count_if(s.begin(),s.end(),isspace);
// ...
}

The isspace() predicate (§36.2) lets us count all whitespace characters, rather than just space.

32.4.4. find()

The find() family of algorithms do linear searches for some element or predicate match:

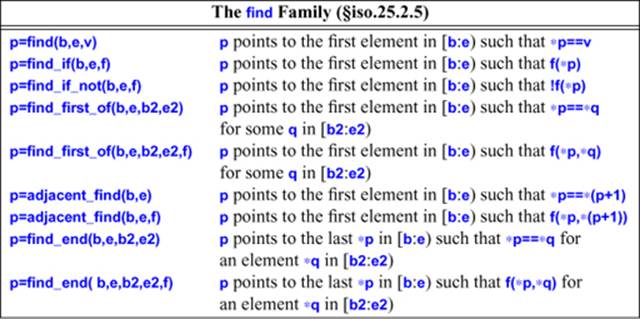
The algorithms find() and find_if() return an iterator to the first element that matches a value and a predicate, respectively.

void f(const string& s)
{
auto p_space = find(s.begin(),s.end(),' ');
auto p_whitespace = find_if(s.begin(),s.end(), isspace);
// ...
}

The find_first_of() algorithms find the first occurrence in a sequence of an element from another sequence. For example:

array<int> x = {1,3,4 };
array<int> y = {0,2,3,4,5};

void f()
{
auto p = find_first_of(x.begin(),x.end(),y.begin(),y.end); // p = &x[1]
auto q = find_first_of(p+1,x.end(),y.begin(),y.end()); // q = &x[2]
}

The iterator p will point to x[1] because 3 is the first element of x with a match in y. Similarly, q will point to x[2].

32.4.5. equal() and mismatch()

The equal() and mismatch() algorithms compare pairs of sequences:

The mismatch() looks for the first pair of elements of two sequences that compare unequal and returns iterators to those elements. No end is specified for the second sequence; that is, there is no last2. Instead, it is assumed that there are at least as many elements in the second sequence as in the first, and first2+(last–first) is used as last2. This technique is used throughout the standard library, where pairs of sequences are used for operations on pairs of elements. We could implement mismatch() like this:

template<class In, class In2, class Pred = equal_to<Value_type<In>>>
pair<In, In2> mismatch(In first, In last, In2 first2, Pred p ={})
{
while (first != last && p(*first,*first2)) {
++first;
++first2;
}
return {first,first2};
}

I used the standard function object equal_to (§33.4) and the type function Value_type (§28.2.1).

32.4.6. search()

The search() and search_n() algorithms find one sequence as a subsequence in another:

The search() algorithm looks for its second sequence as a subsequence of its first. If that second sequence is found, an iterator for the first matching element in the first sequence is returned. As usual, the end of the sequence is used to represent “not found.” For example:

string quote {"Why waste time learning, when ignorance is instantaneous?"};

bool in_quote(const string& s)
{
auto p = search(quote.begin(),quote.end(),s.begin(),s.end()); // find s in quote
return p!=quote.end();
}

void g()
{
bool b1 = in_quote("learning"); // b1 = true
bool b2 = in_quote("lemming"); // b2 = false
}

Thus, search() is a useful algorithm for finding a substring generalized to all sequences.

Use find() or binary_search() (§32.6) to look for just a single element.

32.5. Modifying Sequence Algorithms

The modifying algorithms (also called mutating sequence algorithms) can (and often do) modify elements of their argument sequences.

Somewhat confusingly, transform() doesn’t necessarily change its input. Instead, it produces an output that is a transformation of its input based on a user-supplied operation. The one-input-sequence version of transform() may be defined like this:

template<class In, class Out, class Op>
Out transform(In first, In last, Out res, Op op)
{
while (first!=last)
*res++ = op(*first++);
return res;
}

The output sequence may be the same as the input sequence:

void toupper(string& s) // remove case
{
transform(s.begin(),s.end(),s.begin(),toupper);
}

This really transforms the input s.

32.5.1. copy()

The copy() family of algorithms copy elements from one sequence into another. The following sections list versions of copy() combined with other algorithms, such as replace_copy() (§32.5.3).

The target of a copy algorithm need not be a container. Anything that can be described by an output iterator (§38.5) will do. For example:

void f(list<Club>& lc, ostream& os)
{
copy(lc.begin(),lc.end(),ostream_iterator<Club>(os));
}

To read a sequence, we need a pair of iterators describing where to begin and where to end. To write, we need only an iterator describing where to write to. However, we must take care not to write beyond the end of the target. One way to ensure that we don’t do this is to use an inserter (§33.2.2) to grow the target as needed. For example:

void f(const vector<char>& vs, vector<char>& v)
{
copy(vs.begin(),vs.end(),v.begin()); // might overwrite end of v
copy(vs.begin(),vs.end(),back_inserter(v)); // add elements from vs to end of v
}

The input sequence and the output sequence may overlap. We use copy() when the sequences do not overlap or if the end of the output sequence is in the input sequence.

We use copy_if() to copy only elements that fulfill some criterion. For example:

void f(list<int>&ld, int n, ostream& os)
{
copy_if(ld.begin(),ld.end(),
ostream_iterator<int>(os),
[](int x) { return x>n); });
}

See also remove_copy_if().

32.5.2. unique()

The unique() algorithm removes adjacent duplicate elements from a sequence:

The unique() and unique_copy() algorithms eliminate adjacent duplicate values. For example:

void f(list<string>& ls, vector<string>& vs)
{
ls.sort(); // list sort (§31.4.2)
unique_copy(ls.begin(),ls.end(),back_inserter(vs));
}

This copies ls to vs, eliminating duplicates in the process. I used sort() to get equal strings adjacent.

Like other standard algorithms, unique() operates on iterators. It does not know which container these iterators point into, so it cannot modify that container. It can only modify the values of the elements. This implies that unique() does not eliminate duplicates from its input sequence in the way we naively might expect. Therefore, this does not eliminate duplicates in a vector:

void bad(vector<string>& vs) // warning: doesn't do what it appears to do!
{
sort(vs.begin(),vs.end()); // sort vector
unique(vs.begin(),vs.end()); // eliminate duplicates (no it doesn't!)
}

Rather, unique() moves unique elements toward the front (head) of a sequence and returns an iterator to the end of the subsequence of unique elements. For example:

int main()
{
string s ="abbcccde";

auto p = unique(s.begin(),s.end());
cout << s << ' ' << p–s.begin() << '\n';
}

produces

abcdecde 5

That is, p points to the second c (that is, the first of the duplicates).

Algorithms that might have removed elements (but can’t) generally come in two forms: the “plain” version that reorders elements in a way similar to unique() and a _copy version that produces a new sequence in a way similar to unique_copy().

To eliminate duplicates from a container, we must explicitly shrink it:

template<class C>
void eliminate_duplicates(C& c)
{
sort(c.begin(),c.end()); // sort
auto p = unique(c.begin(),c.end()); // compact
c.erase(p,c.end()); // shrink
}

I could equivalently have written c.erase(unique(c.begin(),c.end()),c.end()), but I don’t think such terseness improves readability or maintainability.

32.5.3. remove() and replace()

The remove() algorithm “removes” elements to the end of a sequence:

The replace() algorithm assigns new values to selected elements:

These algorithms cannot change the size of their input sequence, so even remove() leaves the size of its input sequence unchanged. Like unique(), it “removes” by moving elements to the left. For example:

string s {"*CamelCase*IsUgly*"};
cout << s << '\n'; // *CamelCase*IsUgly*
auto p = remove(s.begin(),s.end(),'*');
copy(s.begin(),p,ostream_iterator<char>{cout}); // CamelCaseIsUgly
cout << s << '\n'; // CamelCaseIsUglyly*

32.5.4. rotate(), random_shuffle(), and partition()

The rotate(), random_shuffle(), and partition() algorithms provide systematic ways of moving elements around in a sequence:

The movement of elements done by rotate() (and by the shuffle and partition algorithms) is done using swap().

A shuffle algorithm shuffles its sequence much in the way we would shuffle a pack of cards. That is, after a shuffle, the elements are in a random order, where “random” is defined by the distribution produced by the random number generator.

By default, random_shuffle() shuffles its sequence using a uniform distribution random number generator. That is, it chooses a permutation of the elements of the sequence so that each permutation has the same chances of being chosen. If you want a different distribution or a better random number generator, you can supply one. For a call random_shuffle(b,e,r), the generator is called with the number of elements in the sequence (or a subsequence) as its argument. For example, for a call r(e–b) the generator must return a value in the range [0,e–b). If My_rand is such a generator, we might shuffle a deck of cards like this:

void f(deque<Card>& dc, My_rand& r)
{
random_shuffle(dc.begin(),dc.end(),r);
// ...
}

The partition algorithm separates a sequence into two parts based on a partition criterion:

32.5.5. Permutations

The permutation algorithms provide a systematic way of generating all permutations of a sequence.

Permutations are used to generate combinations of elements of a sequence. For example, the permutations of abc are acb, bac, bca, cab, and cba.

The next_permutation() takes a sequence [b:e) and transforms it into the next permutation. The next permutation is found by assuming that the set of all permutations is lexicographically sorted. If such a permutation exists, next_permutation() returns true; otherwise, it transforms the sequence into the smallest permutation, that is, the ascendingly sorted one (abc in the example), and returns false. So, we can generate the permutations of abc like this:

vector<char> v {'a','b','c'};
while(next_permutation(v.begin(),v.end()))
cout << v[0] << v[1] << v[2] << ' ';

Similarly, the return value for prev_permutation() is false if [b:e) already contains the first permutation (abc in the example); in that case, it returns the last permutation (cba in the example).

32.5.6. fill()

The fill() family of algorithms provide ways of assigning to and initializing elements of a sequence:

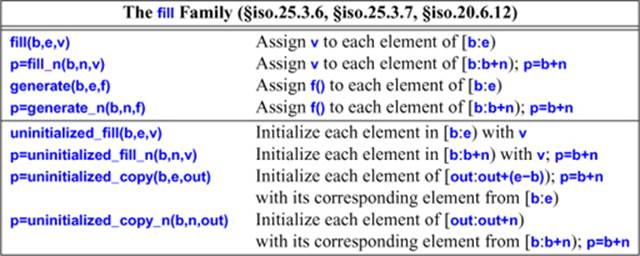
The fill() algorithm repeatedly assigns the specified value, whereas generate() assigns values obtained by calling its function argument repeatedly. For example, using the random number generators Randint and Urand from §40.7:

int v1[900];
array<int,900> v2;
vector v3;

void f()
{
fill(begin(v1),end(v1),99); // set all elements of v1 to 99
generate(begin(v2),end(v2),Randint{}); // set to random values (§40.7)

// output 200 random integers in the interval [0:100):
generate_n(ostream_iterator<int>{cout},200,Urand{100}); // see §40.7

fill_n(back_inserter{v3},20,99); // add 20 elements with the value 99 to v3
}

The generate() and fill() functions assign rather than initialize. If you need to manipulate raw storage, say, to turn a region of memory into objects of well-defined type and state, you use one of the uninitialized_ versions (presented in <memory>).

Uninitialized sequences should only occur at the lowest level of programming, usually inside the implementation of containers. Elements that are targets of uninitialized_fill() or uninitialized_copy() must be of built-in type or uninitialized. For example:

vector<string> vs {"Breugel","El Greco","Delacroix","Constable"};
vector<string> vs2 {"Hals","Goya","Renoir","Turner"};
copy(vs.begin(),vs.end(),vs2.begin()); // OK
uninitialized_copy(vs.begin(),vs.end(),vs2.begin()); // leaks!

A few more facilities for dealing with uninitialized memory are described in §34.6.

32.5.7. swap()

A swap() algorithm exchanges the values of two objects:

for example:

void use(vector<int>& v, int* p)
{
swap_ranges(v.begin(),v.end(),p); // exchange values
}

The pointer p had better point to an array with at least v.size() elements.

The swap() algorithm is possibly the simplest and arguably the most crucial algorithm in the standard library. It is used as part of the implementaton of many of the most widely used algorithms. Its implementation is used as an example in §7.7.2 and the standard-library version is presented in §35.5.2.

32.6. Sorting and Searching

Sorting and searching in sorted sequences are fundamental, and the needs of programmers are quite varied. Comparison is by default done using the < operator, and equivalence of values a and b is determined by !(a<b)&&!(b<a) rather than requiring operator ==.

In addition to the “plain sort” there are many variants:

The sort() algorithms require random-access iterators (§33.1.2).

Despite its name, is_sorted_until() returns an iterator, rather than a bool.

The standard list (§31.3) does not provide random-access iterators, so lists should be sorted using the specific list operations (§31.4.2) or by copying their elements into a vector, sorting that vector, and then copying the elements back into the list:

template<typename List>
void sort_list(List& lst)
{
vector v {lst.begin(),lst.end()}; // initialize from lst
sort(v); // use container sort (§32.2)
copy(v,lst);
}

The basic sort() is efficient (on average N*log(N)). If a stable sort is required, stable_sort() should be used, that is, an N*log(N)*log(N) algorithm that improves toward N*log(N) when the system has sufficient extra memory. The get_temporary_buffer() function may be used for getting such extra memory (§34.6). The relative order of elements that compare equal is preserved by stable_sort() but not by sort().

Sometimes, only the first elements of a sorted sequence are needed. In that case, it makes sense to sort the sequence only as far as is needed to get the first part in order, that is, a partial sort. The plain partial_sort(b,m,e) algorithms put the elements in the range [b:m) in order. Thepartial_sort_copy() algorithms produce N elements, where N is the lower of the number of elements in the output sequence and the number of elements in the input sequence. We need to specify both the start and the end of the result sequence because that’s what determines how many elements we need to sort. For example:

void f(const vector<Book>& sales) // find the top ten books
{
vector<Book> bestsellers(10);
partial_sort_copy(sales.begin(),sales.end(),
bestsellers.begin(),bestsellers.end(),
[](const Book& b1, const Book& b2) { return b1.copies_sold()>b2.copies_sold(); });
copy(bestsellers.begin(),bestsellers.end(),ostream_iterator<Book>{cout,"\n"});
}

Because the target of partial_sort_copy() must be a random-access iterator, we cannot sort directly to cout.

If the number of elements desired to be sorted by a partial_sort() is small compared to the total number of elements, these algorithms can be significatly faster than a complete sort(). Then, their complexity approaches O(N) compared to sort()’s O(N*log(N)).

The nth_element() algorithm sorts only as far as is necessary to get the Nth element to its proper place with no element comparing less than the Nth element placed after it in the sequence. For example:

vector<int> v;
for (int i=0; i<1000; ++i)
v.push_back(randint(1000)); // §40.7
constexpr int n = 30;
nth_element(v.begin(), v.begin()+n, v.end());
cout << "nth: " << v[n] < '\n';
for (int i=0; i<n; ++i)
cout << v[i] << ' ';

This produces:

nth: 24
10 8 15 19 21 15 8 7 6 17 21 2 18 8 1 9 3 21 20 18 10 7 3 3 8 11 11 22 22 23

The nth_element() differs from partial_sort() in that the elements before n are not necessarily sorted, just all less than the nth element. Replacing nth_element with partial_sort in that example (and using the same seed for the random number generator to get the same sequence), I got:

nth: 995
1 2 3 3 3 6 7 7 8 8 8 8 9 10 10 11 11 15 15 17 18 18 19 20 21 21 21 22 22 23

The nth_element() algorithm is particularly useful for people – such as economists, sociologists, and teachers – who need to look for medians, percentiles, etc.

Sorting C-style strings requires an explicit sorting criterion. The reason is that C-style strings are simply pointers with a set of conventions for their use, so < on pointers compares machine addresses rather than character sequences. For example:

vector<string> vs = {"Helsinki","Copenhagen","Oslo","Stockholm"};
vector<char*> vcs = {"Helsinki","Copenhagen","Oslo","Stockholm"};

void use()
{
sort(vs); // I have defined a range version of sort()
sort(vcs);

for (auto& x : vs)
cout << x << ' '
cout << '\n';
for (auto& x : vcs)
cout << x << ' ';

This prints:

Copenhagen Helsinki Stockholm Oslo
Helsinki Copenhagen Oslo Stockholm

Naively, we might have expected the same output from both vectors. However, to sort C-style strings by string value rather than by address we need a proper sort predicate. For example:

sort(vcs, [](const char* p, const char* q){ return strcmp(p,q)<0; });

The standard-library function strcmp() is described in §43.4.

Note that I did not have to supply a == to sort C-style strings. To simplify the user interface, the standard library uses !(x<y>||y<x) rather than x==y to compare elements (§31.2.2.2).

32.6.1. Binary Search

The binary_search() family of algorithms provide binary searches of ordered (sorted) sequences:

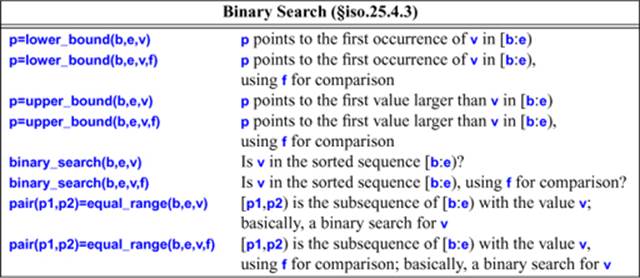
A sequential search such as find() (§32.4) is terribly inefficient for large sequences, but it is about the best we can do without sorting or hashing (§31.4.3.2). Once a sequence is sorted, however, we can use a binary search to determine whether a value is in a sequence. For example:

void f(vector<int>& c)
{
if (binary_search(c.begin(),c.end(),7)){ // is 7 in c?
// ...
}
// ...
}

A binary_search() returns a bool indicating whether a value is present. As with find(), we often also want to know where the elements with that value are in that sequence. However, there can be many elements with a given value in a sequence, and we often need to find either the first or all such elements. Consequently, algorithms are provided for finding a range of equal elements, equal_range(), and algorithms for finding the lower_bound() and upper_bound() of that range. These algorithms correspond to the operations on multimaps (§31.4.3). We can think oflower_bound() as a fast find() and find_if() for sorted sequences. For example:

void g(vector<int>& c)
{
auto p = find(c.begin(),c.end(),7); // probably slow: O(N); c needn't be sorted
auto q = lower_bound(c.begin(),c.end(),7); // probably fast: O(log(N)); c must be sorted
// ...
}

If lower_bound(first,last,k) doesn’t find k, it returns an iterator to the first element with a key greater than k, or last if no such greater element exists. This way of reporting failure is also used by upper_bound() and equal_range(). This means that we can use these algorithms to determine where to insert a new element into a sorted sequence so that the sequence remains sorted: just insert before the second of the returned pair.

Curiously enough, the binary search algorithms do not require random-access iterators: a forward iterator suffices.

32.6.2. merge()

The merge algorithms combine two ordered (sorted) sequences into one:

The merge() algorithm can take different kinds of sequences and elements of different types. For example:

vector<int> v {3,1,4,2};
list<double> lst {0.5,1.5,2,2.5}; // lst is in order

sort(v.begin(),v.end()); // put v in order

vector<double> v2;
merge(v.begin(),v.end(),lst.begin(),lst.end(),back_inserter(v2)); // merger v and lst into v2
for (double x : v2)
cout << x << ", ";

For inserters, see §33.2.2. The output is:

0.5, 1, 1.5, 2, 2, 2.5, 3, 4,

32.6.3. Set Algorithms

These algorithms treat a sequence as a set of elements and provide the basic set operations. The input sequences are supposed to be sorted and the output sequences are also sorted.

For example:

string s1 = "qwertyasdfgzxcvb";
string s2 = "poiuyasdfg/.,mnb";
sort(s1.begin(),s1.end()); // the set algorithms require sorted sequences
sort(s2.begin(),s2.end());

string s3(s1.size()+s2.size(),'*'); // set aside enough space for the largest possible result
cout << s3 << '\n';
auto up = set_union(s1.begin(),s1.end(),s2.begin(),s2.end(),s3.begin());
cout << s3 << '\n';
for (auto p = s3.begin(); p!=up; ++p)
cout << *p;
cout << '\n';

s3.assign(s1.size()+s2.size(),'+');
up = set_difference(s1.begin(),s1.end(),s2.begin(),s2.end(),s3.begin());
cout << s3 << '\n';
for (auto p = s3.begin(); p!=up; ++p)
cout << *p;
cout << '\n';

This little test produces:

*******************************
,./abcdefgimnopqrstuvxyz
ceqrtvwxz++++++++++++++++++++++
ceqrtvwxz

32.6.4. Heaps

A heap is a compact data structure that keeps the element with the highest value first. Think of a heap as a representation of a binary tree. The heap algorithms allow a programmer to treat a random-access sequence as a heap:

Think of the end, e, of a heap [b:e) as a pointer, which it decremented by pop_heap() and incremented by push_heap(). The largest element is extracted by reading through b (e.g., x=*b) and then doing a pop_heap(). A new element is inserted by writing through e (e.g., *e=x) and then doing a push_heap(). For example:

string s = "herewego";
make_heap(s.begin(),s.end()); // rogheeew
pop_heap(s.begin(),s.end()); // rogheeew
pop_heap(s.begin(),s.end()–1); // ohgeeerw
pop_heap(s.begin(),s.end()–2); // hegeeorw

*(s.end()–3)='f';
push_heap(s.begin(),s.end()–2); // hegeefrw
*(s.end()–2)='x';
push_heap(s.begin(),s.end()–1); // xeheefge
*(s.end()–1)='y';
push_heap(s.begin(),s.end()); // yxheefge
sort_heap(s.begin(),s.end()); // eeefghxy
reverse(s.begin(),s.end()); // yxhgfeee

The way to understand the changes to s is that a user reads only s[0] and writes only s[x] where x is the index of the current end of the heap. The heap removes an element (always s[0]) by swapping it with s[x].

The point of a heap is to provide fast addition of elements and fast access to the element with the highest value. The main use of heaps is to implement priority queues.

32.6.5. lexicographical_compare()

A lexicographical compare is the rule we use to order words in dictionaries.

We might implement lexicographical_compare(b,e,b2,e2) like this:

template<class In, class In2>
bool lexicographical_compare(In first, In last, In2 first2, In2 last2)
{
for (; first!=last && first2!=last2; ++first,++last) {
if (*first<*first2)
return true; // [first:last)<[first2:last2)
if (*first2<*first)
return false; // [first2:last2)<[first:last)
}
return first==last && first2!=last2; // [first:last)<[first2:last2) if [first:last) is shorter
}

That is, a string compares as a sequence of characters. For example:

string n1 {"10000"};
string n2 {"999"};

bool b1 = lexicographical_compare(n1.begin(),n1.end(),n2.begin(),n2.end()); // b1 == true

n1 = "Zebra";
n2 = "Aardvark";
bool b2 = lexicographical_compare(n1.begin(),n1.end(),n2.begin(),n2.end()); // b2 == false

32.7. Min and Max

Value comparisons are useful in many contexts:

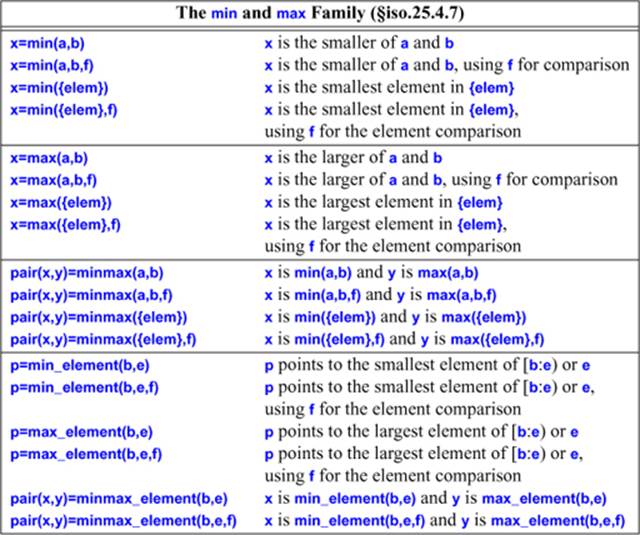
If we compare two lvalues, the result is a reference to the result; otherwise, an rvalue is returned. Unfortunately, the versions that take lvalues take const lvalues, so you can never modify the result of one of these functions. For example:

int x = 7;
int y = 9;

++min(x,y); // the result of min(x,y) is a const int&
++min({x,y}); // error: the result of min({x,y}) is an rvalue (an initializer_list is immutable)

The _element functions return iterators and the minmax function returns pairs, so we can write:

string s = "Large_Hadron_Collider";
auto p = minmax_element(s.begin(),s.end(),
[](char c1,char c2) { return toupper(c1)<toupper(c2); });
cout << "min==" << *(p.first) << ' ' << "max==" << *(p.second) << '\n';

With the ACSII character set on my machine, this little test produces:

min==a max==_

32.8. Advice

[1] An STL algorithm operates on one or more sequences; §32.2.

[2] An input sequence is half-open and defined by a pair of iterators; §32.2.

[3] When searching, an algorithm usually returns the end of the input sequence to indicate “not found”; §32.2.

[4] Prefer a carefully specified algorithm to “random code”; §32.2.

[5] When writing a loop, consider whether it could be expressed as a general algorithm; §32.2.

[6] Make sure that a pair of iterator arguments really do specify a sequence; §32.2.

[7] When the pair-of-iterators style becomes tedious, introduce a container/range algorithm; §32.2.

[8] Use predicates and other function objects to give standard algorithms a wider range of meanings; §32.3.

[9] A predicate must not modify its argument; §32.3.

[10] The default == and < on pointers are rarely adequate for standard algorithms; §32.3.

[11] Know the complexity of the algorithms you use, but remember that a complexity measure is only a rough guide to performance; §32.3.1.

[12] Use for_each() and transform() only when there is no more-specific algorithm for a task; §32.4.1.

[13] Algorithms do not directly add or subtract elements from their argument sequences; §32.5.2, §32.5.3.

[14] If you have to deal with uninitialized objects, consider the uninitialized_* algorithms; §32.5.6.

[15] An STL algorithm uses an equality comparison generated from its ordering comparison, rather than ==; §32.6.

[16] Note that sorting and searching C-style strings requires the user to supply a string comparison operation; §32.6.