Learning JavaScript Data Structures and Algorithms (2014)
Chapter 3. Stacks
You learned in the previous chapter how to create and use arrays, which are the most common type of data structure in Computer Science. As you learned, we can add and remove elements from an array at any index desired. However, sometimes we need some form of data structure where we have more control over adding and removing items. There are two data structures that have some similarities to arrays but give us more control over the addition and removal of elements. These data structures are stacks and queues. In this chapter, we will cover stacks.
A stack is an ordered collection of items that follows the LIFO (short for Last In First Out) principle. The addition of new items or the removal of existing items takes place at the same end. The end of the stack is known as the top and the opposite is known as the base. The newest elements are near the top, and the oldest elements are near the base.
We have several examples of stacks in real life, for example, a pile of books, as we can see in the following image, or a stack of trays from a cafeteria or food court:

A stack is also used by compilers in programming languages and by computer memory to store variables and method calls.
Creating a stack
We are going to create our own class to represent a stack. Let's start from the basics and declare our class:
function Stack() {
//properties and methods go here
}
First, we need a data structure that will store the elements of the stack. We can use an array to do this:
var items = [];
Next, we need to declare the methods available for our stack:
· push(element(s)): This adds a new item (or several items) to the top of the stack.
· pop(): This removes the top item from the stack. It also returns the removed element.
· peek(): This returns the top element from the stack. The stack is not modified (it does not remove the element; it only returns the element for information purposes).
· isEmpty(): This returns true if the stack does not contain any elements and false if the size of the stack is bigger than 0.
· clear(): This removes all the elements of the stack.
· size(): This returns how many elements the stack contains. It is similar to the length property of an array.
The first method we will implement is the push method. This method will be responsible for adding new elements to the stack with one very important detail: we can only add new items to the top of the stack, meaning at the end of the stack. The push method is represented as follows:
this.push = function(element){
items.push(element);
};
As we are using an array to store the elements of the stack, we can use the push method from the JavaScript array class that we covered in the previous chapter.
Next, we are going to implement the pop method. This method will be responsible for removing the items from the stack. As the stack uses the LIFO principle, the last item that we added is the one that is removed. For this reason, we can use the pop method from the JavaScript array class that we also covered in the previous chapter. The pop method is represented as follows:
this.pop = function(){
return items.pop();
};
With the push and pop methods being the only methods available for adding and removing items from the stack, the LIFO principle will apply to our own Stack class.
Now, let's implement some additional helper methods for our class. If we would like to know what the last item added to our stack was, we can use the peek method. This method will return the item from the top of the stack:
this.peek = function(){
return items[items.length-1];
};
As we are using an array to store the items internally, we can obtain the last item from an array using length - 1 as follows:
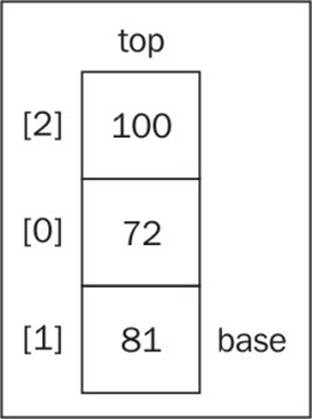
For example, in the previous diagram, we have a stack with three items; therefore, the length of the internal array is 3. The last position used in the internal array is 2. As a result, the length - 1 (3 - 1) is 2!
The next method is the isEmpty method, which returns true if the stack is empty (no item has been added) and false otherwise:
this.isEmpty = function(){
return items.length == 0;
};
Using the isEmpty method, we can simply verify whether the length of the internal array is 0.
Similar to the length property from the array class, we can also implement length for our Stack class. For collections, we usually use the term "size" instead of "length." And again, as we are using an array to store the items internally, we can simply return its length:
this.size = function(){
return items.length;
};
Finally, we are going to implement the clear method. The clear method simply empties the stack, removing all its elements. The simplest way of implementing this method is as follows:
this.clear = function(){
items = [];
};
An alternative implementation would be calling the pop method until the stack is empty.
And we are done! Our Stack class is implemented. Just to make our lives easier during the examples, to help us inspect the contents of our stack, let's implement a helper method called print that is going to output the content of the stack on the console:
this.print = function(){
console.log(items.toString());
};
And now we are really done!
The complete Stack class
Let's take a look at how our Stack class looks after its full implementation:
function Stack() {
var items = [];
this.push = function(element){
items.push(element);
};
this.pop = function(){
return items.pop();
};
this.peek = function(){
return items[items.length-1];
};
this.isEmpty = function(){
return items.length == 0;
};
this.size = function(){
return items.length;
};
this.clear = function(){
items = [];
};
this.print = function(){
console.log(items.toString());
};
}
Using the Stack class
Before we dive into some examples, we need to learn how to use the Stack class.
The first thing we need to do is instantiate the Stack class we just created. Next, we can verify whether it is empty (the output is true because we have not added any elements to our stack yet):
var stack = new Stack();
console.log(stack.isEmpty()); //outputs true
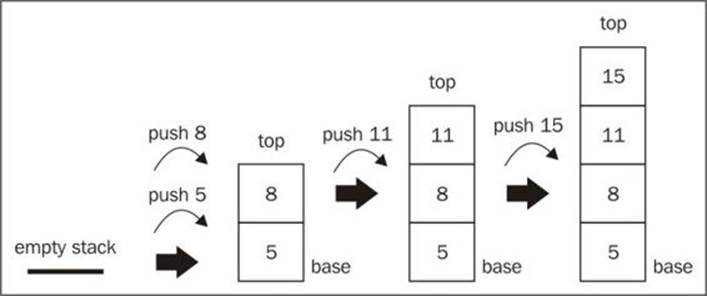
Next, let's add some elements to it (let's push the numbers 5 and 8; you can add any element type to the stack):
stack.push(5);
stack.push(8);
If we call the peek method, the output will be the number 8 because it was the last element that was added to the stack:
console.log(stack.peek()); // outputs 8
Let's also add another element:
stack.push(11);
console.log(stack.size()); // outputs 3
console.log(stack.isEmpty()); //outputs false
We added the element 11. If we call the size method, it will give the output as 3, because we have three elements in our stack (5, 8, and 11). Also, if we call the isEmpty method, the output will be false (we have three elements in our stack). Finally, let's add another element:
stack.push(15);
The following diagram shows all the push operations we have executed so far and the current status of our stack:
Next, let's remove two elements from the stack by calling the pop method twice:
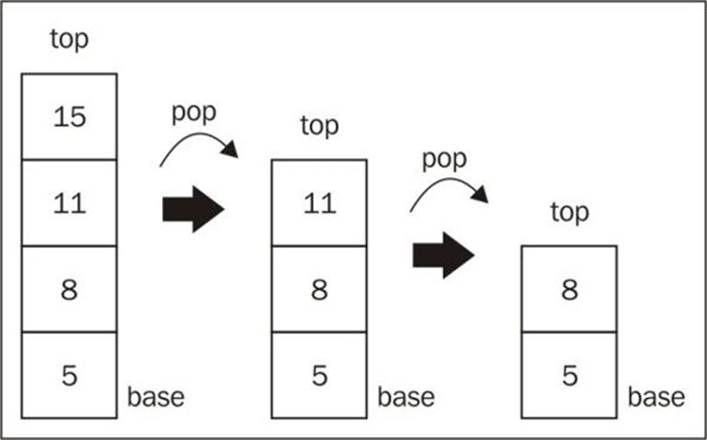
stack.pop();
stack.pop();
console.log(stack.size()); // outputs 2
stack.print(); // outputs [5, 8]
Before we called the pop method twice, our stack had four elements in it. After the execution of the pop method two times, the stack now has only two elements: 5 and 8. The following diagram exemplifies the execution of the pop method:
Decimal to binary
Now that we know how to use the Stack class, let's use it to solve some Computer Science problems.
You are probably already aware of the decimal base. However, binary representation is very important in Computer Science as everything in a computer is represented by binary digits (0 and 1). Without the ability to convert back and forth between decimal and binary numbers, it would be a little bit difficult to communicate with a computer.
To convert a decimal number to a binary representation, we can divide the number by 2 (binary is base 2 number system) until the division result is 0. As an example, we will convert the number 10 into binary digits:
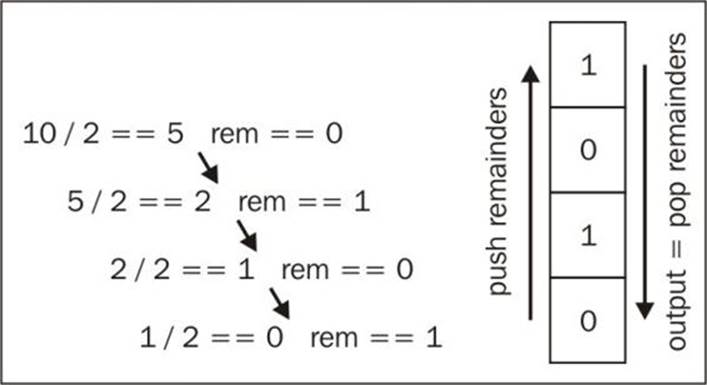
This conversion is one of the first things you learn in college (Computer Science classes). The following is our algorithm:
function divideBy2(decNumber){
var remStack = new Stack(),
rem,
binaryString = '';
while (decNumber > 0){ //{1}
rem = Math.floor(decNumber % 2); //{2}
remStack.push(rem); //{3}
decNumber = Math.floor(decNumber / 2); //{4}
}
while (!remStack.isEmpty()){ //{5}
binaryString += remStack.pop().toString();
}
return binaryString;
}
In this code, while the division result is not zero (line {1}), we get the remainder of the division (mod) and push it to the stack (lines {2} and {3}), and finally, we update the number that will be divided by 2 (line {4}). An important observation: JavaScript has a numeric data type, but it does not distinguish integers from floating points. For this reason, we need to use the Math.floor function to obtain only the integer value from the division operations. And finally, we pop the elements from the stack until it is empty, concatenating the elements that were removed from the stack into a string (line {5}).
We can try the previous algorithm and output its result on the console using the following code:
console.log(divideBy2(233));
console.log(divideBy2(10));
console.log(divideBy2(1000));
We can easily modify the previous algorithm to make it work as a converter from decimal to any base. Instead of dividing the decimal number by 2, we can pass the desired base as an argument to the method and use it in the divisions, as shown in the following algorithm:
function baseConverter(decNumber, base){
var remStack = new Stack(),
rem,
baseString = '',
digits = '0123456789ABCDEF'; //{6}
while (decNumber > 0){
rem = Math.floor(decNumber % base);
remStack.push(rem);
decNumber = Math.floor(decNumber / base);
}
while (!remStack.isEmpty()){
baseString += digits[remStack.pop()]; //{7}
}
return baseString;
}
There is one more thing we need to change. In the conversion from decimal to binary, the remainders will be 0 or 1; in the conversion from decimal to octagonal, the remainders will be from 0 to 8, but in the conversion from decimal to hexadecimal, the remainders can be 0 to 8 plus the letters A to F (values 10 to 15). For this reason, we need to convert these values as well (lines {6} and {7}).
We can use the previous algorithm and output its result on the console as follows:
console.log(baseConverter(100345, 2));
console.log(baseConverter(100345, 8));
console.log(baseConverter(100345, 16));
Note
You will also find the balanced parentheses and the Hanoi tower examples when you download the source code of this book.
Summary
In this chapter, you learned about the stack data structure. We implemented our own algorithm that represents a stack and you learned how to add and remove elements from it using the push and pop methods. We also covered a very famous example of how to use a stack.
In the next chapter, you will learn about queues, which are very similar to stacks but use a different principle than LIFO.
All materials on the site are licensed Creative Commons Attribution-Sharealike 3.0 Unported CC BY-SA 3.0 & GNU Free Documentation License (GFDL)
If you are the copyright holder of any material contained on our site and intend to remove it, please contact our site administrator for approval.
© 2016-2026 All site design rights belong to S.Y.A.