Learning JavaScript Data Structures and Algorithms (2014)
Chapter 6. Sets
So far, we have learned about sequential data structures such as arrays (lists), stacks, queues, and linked lists (and their variants). In this chapter, we will cover the data structure called a set.
A set is a collection of items that are unordered and consists of unique elements (meaning they cannot be repeated). This data structure uses the same math concept as of finite sets, but applied to a Computer Science data structure.
Let's take a look at the math concept of sets before we dive into the Computer Science implementation of it. In Mathematics, a set is a collection of distinct objects.
For example, we have a set of natural numbers, which consists of integer numbers greater than or equal to 0: N = {0, 1, 2, 3, 4, 5, 6, …}. The list of the objects within the set is surrounded by {} (curly braces).
There is also the null set concept. A set with no element is called a null set or empty set. For example, a set of prime numbers between 24 and 29. As there is no prime number (a natural number greater than 1 that has no positive divisors other than 1 and itself) between 24 and 29, the set will be empty. We represent an empty set as { }.
You can also imagine a set as an array with no repeated elements and with no concept or order.
In Mathematics, a set also has some basic operations such as union, intersection, and difference. We will also cover these operations in this chapter.
Creating a set
The current implementation of JavaScript is based on ECMAScript 5.1 (supported by modern browsers) published on June 2011. It contains the Array class implementation that we covered in earlier chapters. ECMAScript 6 (a work in progress, expected to be released in March 2015 at the time of writing this book) contains an implementation of the Set class.
Note
You can see the details of the ECMAScript 6 Set class implementation at https://developer.mozilla.org/en-US/docs/Web/JavaScript/Reference/Global_Objects/Set (or http://goo.gl/2li2a5).
The class we are going to implement in this chapter is based on the Set implementation of ECMAScript 6.
This is the skeleton of our Set class:
function Set() {
var items = {};
}
A very important detail is that we are using an object to represent our set ( items ) instead of an array. But we could also use an array to do this implementation. Let's use an object to implement things a little bit differently and learn new ways of implementing data structures that are similar. And also, objects in JavaScript do not allow you to have two different properties on the same key, which guarantees unique elements in our set.
Next, we need to declare the methods available for a set (we will try to simulate the same Set class implemented in ECMAScript 6):
· add(value): This adds a new item to the set.
· remove(value): This removes the value from the set.
· has(value): This returns true if the value exists in the set and false otherwise.
· clear(): This removes all the items from the set.
· size(): This returns how many elements the set contains. It is similar to the length property of the array.
· values(): This returns an array of all the values of the set.
The has (value) method
The first method we will implement is the has(value) method. We will implement this method first because it will be used in other methods such as add and remove. We can see its implementation here:
this.has = function(value){
return value in items;
};
As we are using an object to store all the values of the set, we can use JavaScript's in operator to verify that the given value is a property of the items object.
But there is a better way of implementing this method, which is as follows:
this.has = function(value){
return items.hasOwnProperty(value);
};
All JavaScript objects have the hasOwnProperty method. This method returns a Boolean indicating whether the object has the specified property or not.
The add method
The next method we will implement is the add method:
this.add = function(value){
if (!this.has(value)){
items[value] = value; //{1}
return true;
}
return false;
};
Given a value, we can check whether the value already exists in the set. If not, we add the value to the set (line {1}) and return true to indicate that the value was added. If the value already exists in the set, we simply return false to indicate that the value was not added.
Note
We are adding the value as key and value because it will help us search for the value if we store it as the key as well.
The remove and clear methods
Next, we will implement the remove method:
this.remove = function(value){
if (this.has(value)){
delete items[value]; //{2}
return true;
}
return false;
};
In the remove method, we will verify that the given value exists in the set. If this is positive, we remove the value from the set (line {2}) and return true to indicate the value was removed; otherwise, we return false.
As we are using an object to store the items object of the set, we can simply use the delete operator to remove the property from the items object (line {2}).
To use the Set class, we can use the following code as an example:
var set = new Set();
set.add(1);
set.add(2);
Note
Just out of curiosity, if we output the items variable on the console (console.log) after executing the previous code, this will be the output in Google Chrome:
Object {1: 1, 2: 2}
As we can see, it is an object with two properties. The property name is the value we added to the set and its value as well.
If we want to remove all the values from the set, we can use the clear method:
this.clear = function(){
items = {}; // {3}
};
All we need to do to reset the items object is assign it to an empty object again (line {3}). We could also iterate the set and remove all the values one by one using the remove method, but that is too much work as we have an easier way of doing it.
The size method
The next method we will implement is the size method (which returns how many items are in the set). There are three ways of implementing this method.
The first method is to use a length variable and control it whenever we use the add or remove method, as we used in the LinkedList class in the previous chapter.
In the second method, we use a built-in function from the built-in Object class in JavaScript (ECMAScript 5+):
this.size = function(){
return Object.keys(items).length; //{4}
};
The Object class in JavaScript contains a method called keys that returns an array of all properties of a given object. In this case, we can use the length property of this array (line {4}) to return how many properties we have in the items object. This code will work only in modern browsers (such as IE9+, FF4+, Chrome5+, Opera12+, Safari5+, and so on).
The third method is to extract each property of the items object manually and count how many properties there are and return this number. This method will work in any browser and is the equivalent of the previous code:
this.sizeLegacy = function(){
var count = 0;
for(var prop in items) { //{5}
if(items.hasOwnProperty(prop)) //{6}
++count; //{7}
}
return count;
};
So, first we iterate through all the properties of the items object (line {5}) and check whether that property is really a property (so we do not count it more than once—line {6}). If positive, we increment the count variable (line {7}) and at the end of the method we return this number.
Note
We cannot simply use the for-in statement and iterate through the properties of the items object and increment the count variable value. We also need to use the has method (to verify that the items object has that property) because the object's prototype contains additional properties for the object as well (properties are inherited from the base JavaScript Object class, but it still has properties of the object, which are not used in this data structure).
The values method
The same logic applies to the values method, using which we want to extract all the properties of the items object and return it as an array:
this.values = function(){
return Object.keys(items);
};
This code will only work in modern browsers. As we are using Google Chrome and Firefox as testing browsers in this book, the code will work.
If we want code that can be executed in any browser, we can use the following code, which is equivalent to the previous code:
this.valuesLegacy = function(){
var keys = [];
for(var key in items){ //{7}
keys.push(key); //{8}
}
return keys;
};
So, first we iterate through all the properties of the items object (line {7}), add them to an array (line {8}), and return this array.
Using the Set class
Now that we have finished implementing our data structure, let's see how we can use it. Let's give it a try and execute some commands to test our Set class:
var set = new Set();
set.add(1);
console.log(set.values()); //outputs ["1"]
console.log(set.has(1)); //outputs true
console.log(set.size()); //outputs 1
set.add(2);
console.log(set.values()); //outputs ["1", "2"]
console.log(set.has(2)); //true
console.log(set.size()); //2
set.remove(1);
console.log(set.values()); //outputs ["2"]
set.remove(2);
console.log(set.values()); //outputs []
So, now we have a very similar implementation of the Set class as in ECMAScript 6. As mentioned before, we could also have used an array instead of an object to store the elements. As we used arrays in Chapter 2, Arrays, Chapter 3, Stacks, and Chapter 4, Queues, it is nice to know there are different ways of implementing the same thing.
Set operations
We can perform the following operations on sets:
· Union: Given two sets, this returns a new set with the elements from both given sets
· Intersection: Given two sets, this returns a new set with the elements that exist in both sets
· Difference: Given two sets, this returns a new set with all elements that exist in the first set and do not exist in the second set
· Subset: This confirms whether a given set is a subset of another set
Set union
The mathematic concept of union is that the union of sets A and B, denoted by 
, is the set defined as:
This means that x (the element) exists in A or x exists in B. The following diagram exemplifies the union operation:
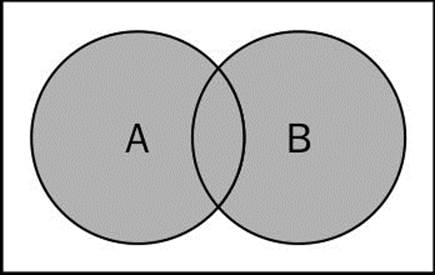
Now let's implement the union method in our Set class:
this.union = function(otherSet){
var unionSet = new Set(); //{1}
var values = this.values(); //{2}
for (var i=0; i<values.length; i++){
unionSet.add(values[i]);
}
values = otherSet.values(); //{3}
for (var i=0; i<values.length; i++){
unionSet.add(values[i]);
}
return unionSet;
};
First, we need to create a new set to represent the union of two sets (line {1}). Next, we get all the values from the first set (the current instance of the Set class), iterate through them, and add all the values to the set that represents the union (line {2}). Then, we do the exact same thing, but with the second set (line {3}). And at last, we return the result.
Let's test the previous code:
var setA = new Set();
setA.add(1);
setA.add(2);
setA.add(3);
var setB = new Set();
setB.add(3);
setB.add(4);
setB.add(5);
setB.add(6);
var unionAB = setA.union(setB);
console.log(unionAB.values());
The output will be ["1", "2", "3", "4", "5", "6"]. Note that the element 3 is present in both A and B, and it appears only once in the result set.
Set intersection
The mathematic concept of intersection is that the intersection of sets A and B, denoted by 
, is the set defined as:
This means that x (the element) exists in A and x exists in B. The following diagram exemplifies the intersection operation:
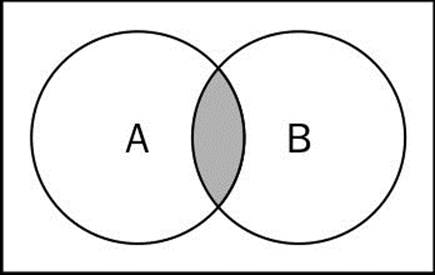
Now, let's implement the intersection method in our Set class:
this.intersection = function(otherSet){
var intersectionSet = new Set(); //{1}
var values = this.values();
for (var i=0; i<values.length; i++){ //{2}
if (otherSet.has(values[i])){ //{3}
intersectionSet.add(values[i]); //{4}
}
}
return intersectionSet;
}
For the intersection method, we need to find all elements from the current instance of the Set class that also exist in the given Set instance. So first, we create a new Set instance so that we can return it with the common elements (line {1}). Next, we iterate through all the values of the current instance of the Set class (line {2}) and we verify that the value exists in the otherSet instance as well (line {3}). We can use the has method that we implemented earlier in this chapter to verify that the element exists in the Set instance. Then, if the value exists in the other Set instance also, we add it to the created intersectionSet variable (line {4}) and return it.
Let's do some testing:
var setA = new Set();
setA.add(1);
setA.add(2);
setA.add(3);
var setB = new Set();
setB.add(2);
setB.add(3);
setB.add(4);
var intersectionAB = setA.intersection(setB);
console.log(intersectionAB.values());
The output will be ["2", "3"], as the values 2 and 3 exist in both sets.
Set difference
The mathematic concept of difference is that the difference of set A from B, denoted by A - B, is the set defined as:
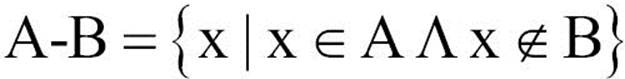
This means that x (the element) exists in A and x does not exist in B. The following diagram exemplifies the difference operation between sets A and B:
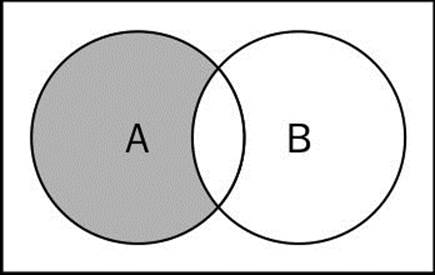
Now let's implement the difference method in our Set class:
this.difference = function(otherSet){
var differenceSet = new Set(); //{1}
var values = this.values();
for (var i=0; i<values.length; i++){ //{2}
if (!otherSet.has(values[i])){ //{3}
differenceSet.add(values[i]); //{4}
}
}
return differenceSet;
};
The intersection method will get all the values that exist in both sets. The difference method will get all the values that exist in A but not in B. So, the only difference in the implementation of the method is in line {3}. Instead of getting the values that also exist in the otherSet instance, we will get only the values that do not exist. Lines {1}, {2}, and {4} are exactly the same.
Let's do some testing (with the same sets we used in the intersection section):
var setA = new Set();
setA.add(1);
setA.add(2);
setA.add(3);
var setB = new Set();
setB.add(2);
setB.add(3);
setB.add(4);
var differenceAB = setA.difference(setB);
console.log(differenceAB.values());
The output will be ["1"] because 1 is the only element that exists only in setA.
Subset
The last set operation we will cover is the subset. The mathematic concept of subset is that A is a subset of (or is included in) B, denoted by 
, and is defined as:
This means that for every x (element) that exists in A it also needs to exist in B. The following diagram exemplifies when A is a subset of B and when it is not:
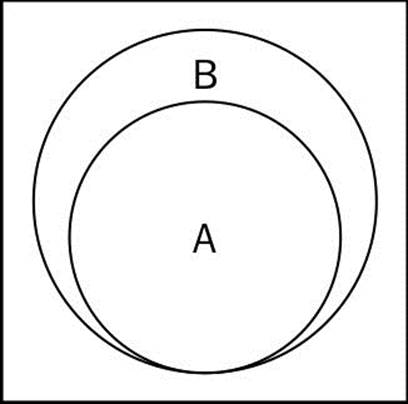
Now let's implement the subset method in our Set class:
this.subset = function(otherSet){
if (this.size() > otherSet.size()){ //{1}
return false;
} else {
var values = this.values();
for (var i=0; i<values.length; i++){ //{2}
if (!otherSet.has(values[i])){ //{3}
return false; //{4}
}
}
return true; //{5}
}
};
The first verification that we need to do is check the size of the current instance of the Set class. If the current instance has more elements than the otherSet instance, it is not a subset (line {3}). A subset needs to have fewer or the same number of elements than the compared set.
Next, we will iterate through all the set elements (line {2}) and we will verify that the element also exists in otherSet (line {3}). If any element does not exist in otherSet, it means that it is not a subset, so we return false (line {4}). If all elements also exist in otherSet, line {4} will not be executed and then we will return true (line {5}).
Let's try the previous code:
var setA = new Set();
setA.add(1);
setA.add(2);
var setB = new Set();
setB.add(1);
setB.add(2);
setB.add(3);
var setC = new Set();
setC.add(2);
setC.add(3);
setC.add(4);
console.log(setA.subset(setB));
console.log(setA.subset(setC));
We have three sets: setA is a subset of setB (so the output is true), however, setA is not a subset of setC (setC only contains value 2 from setA, and not values 1 and 2), so the output will be false.
Summary
In this chapter, we learned how to implement a Set class from scratch, which is similar to the Set class defined in the definition of ECMAScript 6. We also covered some methods that are not usually in other programming language implementations of the set data structure, such as union, intersection, difference, and subset. So, we implemented a very complete Set class compared to the current implementation of Set in other programming languages.
In the next chapter, we will cover hashes and dictionaries, which are non sequential data structures.