OpenGL ES 3.0: Programming Guide, Second Edition (2014)
Appendix B. Built-In Functions
The OpenGL ES shading language built-in functions described in this appendix are copyrighted by Khronos and are reprinted with permission from the OpenGL ES 3.00.4 Shading Language Specification. The latest OpenGL ES 3.0 Shading Language specification can be downloaded fromhttp://khronos.org/registry/gles/.
The OpenGL ES Shading Language defines an assortment of built-in convenience functions for scalar and vector operations. Many of these built-in functions can be used in more than one type of shader, but some are intended to provide a direct mapping to hardware and so are available only for a specific type of shader.
The built-in functions basically fall into three categories:
• They expose some necessary hardware functionality in a convenient way such as accessing a texture map. There is no way in the language for these functions to be emulated by a shader.
• They represent a trivial operation (clamp, mix, etc.) that is simple for the user to write, but they are very common and might have direct hardware support. It is a very hard problem for the compiler to map expressions to complex assembler instructions.
• They represent an operation graphics hardware that is likely to accelerate at some point. The trigonometry functions fall into this category.
Many of the functions are similar to the same named ones in common C libraries, but they support vector input as well as the more traditional scalar input.
Applications should be encouraged to use the built-in functions rather than do the equivalent computations in their own shader code because the built-in functions are assumed to be optimal (e.g., perhaps supported directly in hardware).
When the built-in functions are specified below, where the input arguments (and corresponding output) can be float, vec2, vec3, or vec4, genType is used as the argument. Where the input arguments (and corresponding output) can be int, ivec2, ivec3, or ivec4, genIType is used as the argument. Where the input arguments (and corresponding output) can be uint, uvec2, uvec3, or uvec4, genUType is used as the argument. Where the input arguments (or corresponding output) can be bool, bvec2, bvec3, or bvec4, genBType is used as the argument. For any specific use of a function, the actual types substituted for genType, genIType, genUType, or genBType have to have the same number of components for all arguments and for the return type. Similarly for mat, which can be any matrix basic type.
The precision of built-in functions is dependent on the function and arguments. There are three categories:
• Some functions have predefined precisions. The precision is specified; for example,
highp ivec2 textureSize (gsampler2D sampler, int lod)
• For the texture sampling functions, the precision of the return type matches the precision of the sampler type:
uniform lowp sampler2D sampler;
highp vec2 coord;
. . .
// texture() returns lowp
lowp vec4 col = texture(sampler, coord);
• For other built-in functions, a call will return a precision qualification matching the highest precision qualification of the call’s input arguments.
The built-in functions are assumed to be implemented according to the equations specified in the following sections.
Angle and Trigonometry Functions
Function parameters specified as angle are assumed to be in units of radians. In no case will any of these functions result in a divide by zero error. If the divisor of a ratio is 0, then results will be undefined.
These functions all operate component-wise. The description shown in Table B-1 is per component.
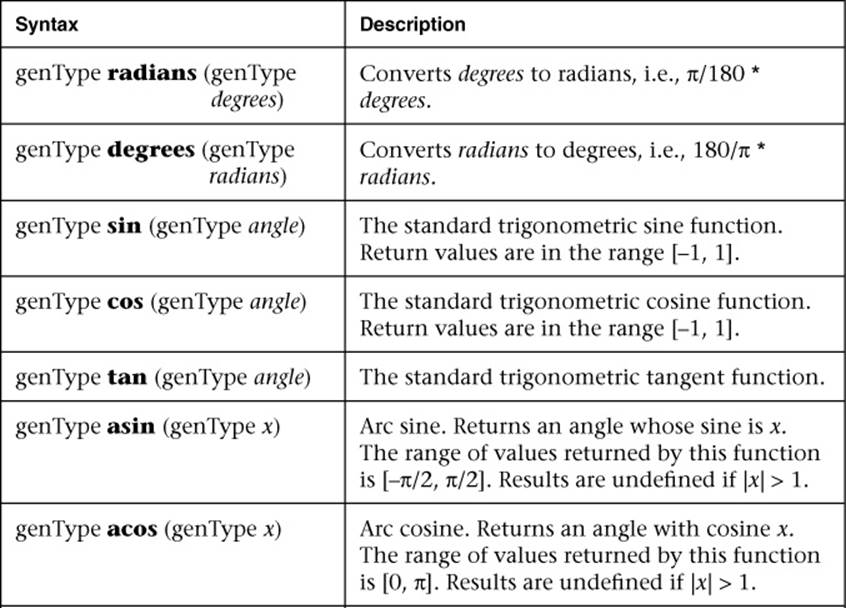
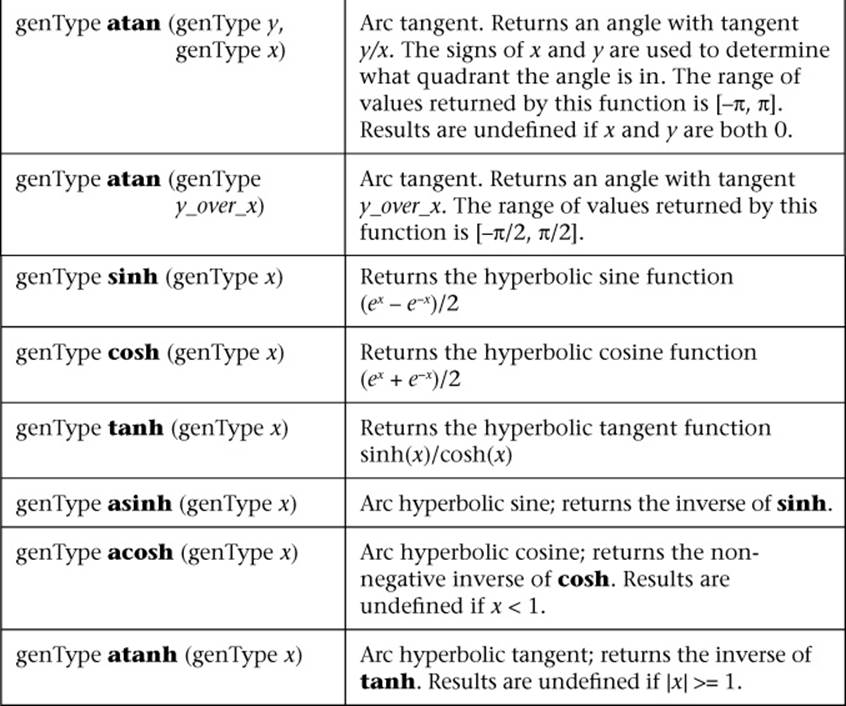
Table B-1 Angle and Trigonometry Functions
Exponential Functions
Exponential functions all operate component-wise. The description shown in Table B-2 is per component.
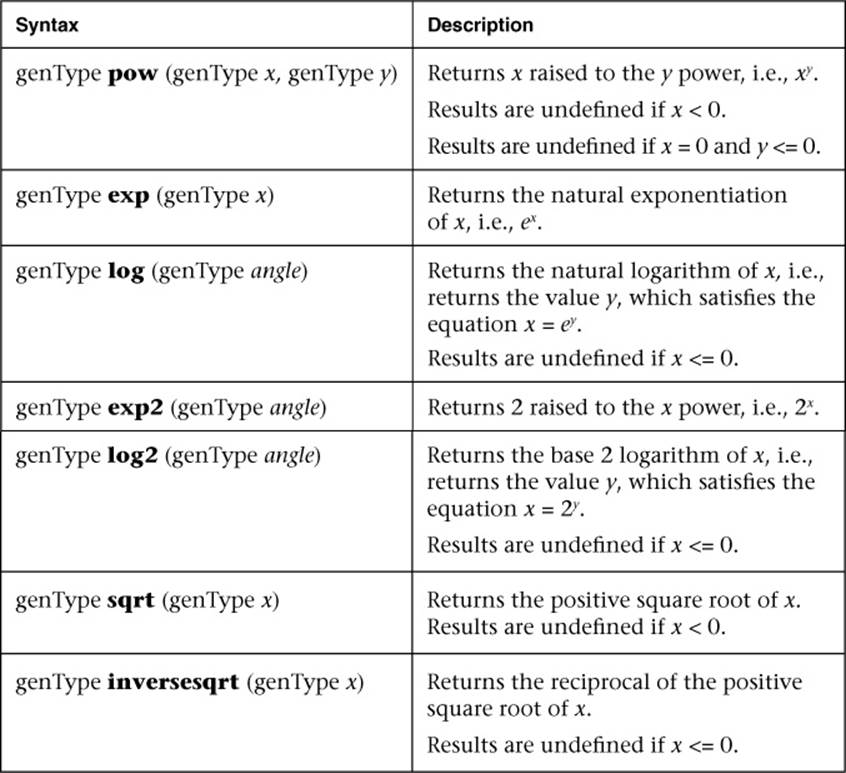
Table B-2 Exponential Functions
Common Functions
Common functions all operate component-wise. The description shown in Table B-3 is per component.






Table B-3 Common Functions
Floating-Point Pack and Unpack Functions
Floating-point pack and unpack functions do not operate component-wise, rather as described in each case (Table B-4).



Table B-4 Floating-Point Pack and Unpack Functions
Geometric Functions
Geometric functions operate on vectors as vectors, not component-wise. Table B-5 describes these functions.
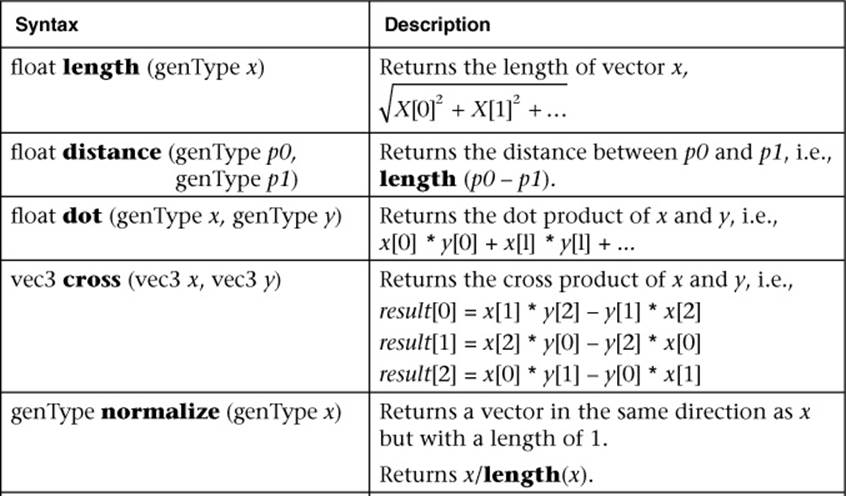

Table B-5 Geometric Functions
Matrix Functions
The built-in functions that operate on matrices are described in Table B-6.


Table B-6 Matrix Functions
Vector Relational Functions
Relational and equality operators (<, <=, >, >=, ==, !=) are defined to produce scalar boolean results. For vector results, use the following built-in functions. In Table B-7, “bvec” is a placeholder for one of bvec2, bvec3, or bvec4; “ivec” is a placeholder for one of ivec2, ivec3, or ivec4; “uvec” is a placeholder for uvec2, uvec3, or uvec4; and “vec” is a placeholder for vec2, vec3, or vec4. In all cases, the sizes of the input and return vectors for any particular call must match.
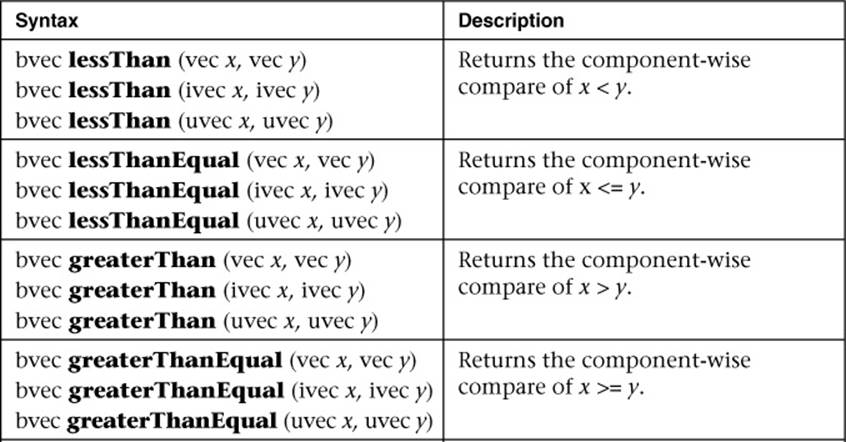

Table B-7 Vector Relational Functions
Texture Lookup Functions
Texture lookup functions are available to vertex and fragment shaders. However, level of detail is not implicitly computed for vertex shaders. The functions in Table B-8 provide access to textures through samplers, as set up through the OpenGL ES API. Texture properties such as size, pixel format, number of dimensions, filtering method, number of mipmap levels, depth comparison, and so on are also defined by OpenGL ES API calls. Such properties are taken into account as the texture is accessed via the built-in functions defined below.
Texture data can be stored by the GL as floating-point, unsigned normalized integer, unsigned integer, or signed integer data. This is determined by the type of the internal format of the texture. Texture lookups on unsigned normalized integer and floating-point data return floating-point values in the range [0, 1].
Texture lookup functions are provided that can return their result as floating-point, unsigned integer, or signed integer values, depending on the sampler type passed to the lookup function. Care must be taken to use the right sampler type for texture access. Table B-8 lists the supported combinations of sampler types and texture internal formats. Blank entries are unsupported. Doing a texture lookup will return undefined values for unsupported combinations.
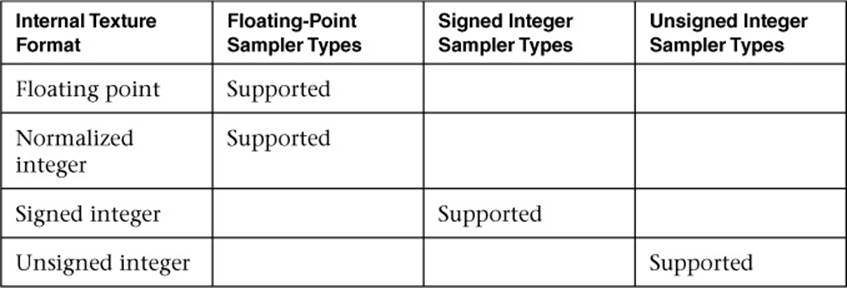
Table B-8 Supported Combinations of Sampler and Internal Texture Formats
If an integer sampler type is used, the result of a texture lookup is an ivec4. If an unsigned integer sampler type is used, the result of a texture lookup is a uvec4. If a floating-point sampler type is used, the result of a texture lookup is a vec4, where each component is in the range [0, 1].
In the prototypes below, the “g” in the return type “gvec4” is used as a placeholder for nothing; “i” or “u” making a return type of vec4, ivec4, or uvec4. In these cases, the sampler argument type also starts with “g”, indicating the same substitution done on the return type; it is either a floating-point, signed integer, or unsigned integer sampler, matching the basic type of the return type, as described above.
For shadow forms (the sampler parameter is a shadow type), a depth comparison lookup on the depth texture bound to sampler is done as described in section 3.8.16, “Texture Comparison Modes,” of the OpenGL ES Graphics System Specification. See the table below for which component specifies Dref. The texture bound to sampler must be a depth texture, or results are undefined. If a non-shadow texture call is made to a sampler that represents a depth texture with depth comparisons turned on, then results are undefined. If a shadow texture call is made to a sampler that represents a depth texture with depth comparisons turned off, then results are undefined. If a shadow texture call is made to a sampler that does not represent a depth texture, then results are undefined.
In all functions below, the bias parameter is optional for fragment shaders. The bias parameter is not accepted in a vertex shader. For a fragment shader, if bias is present, it is added to the implicit level of detail prior to performing the texture access operation.
The implicit level of detail is selected as follows: For a texture that is not mipmapped, the texture is used directly. If it is mipmapped and running in a fragment shader, the LOD computed by the implementation is used to do the texture lookup. If it is mipmapped and running on the vertex shader, then the base texture is used.
Some texture functions (non-“Lod” and non-“Grad” versions) may require implicit derivatives. Implicit derivatives are undefined within non-uniform control flow and for vertex texture fetches.
For Cube forms, the direction of P is used to select which face to do a two-dimensional texture lookup in, as described in section 3.8.10, “Cube Map Texture Selection,” in the OpenGL ES Graphics System Specification.
For Array forms, the array layer used will be
max(0,min(d − 1, floor(layer + 0.5)))
where d is the depth of the texture array and layer comes from the component indicated in Table B-9.




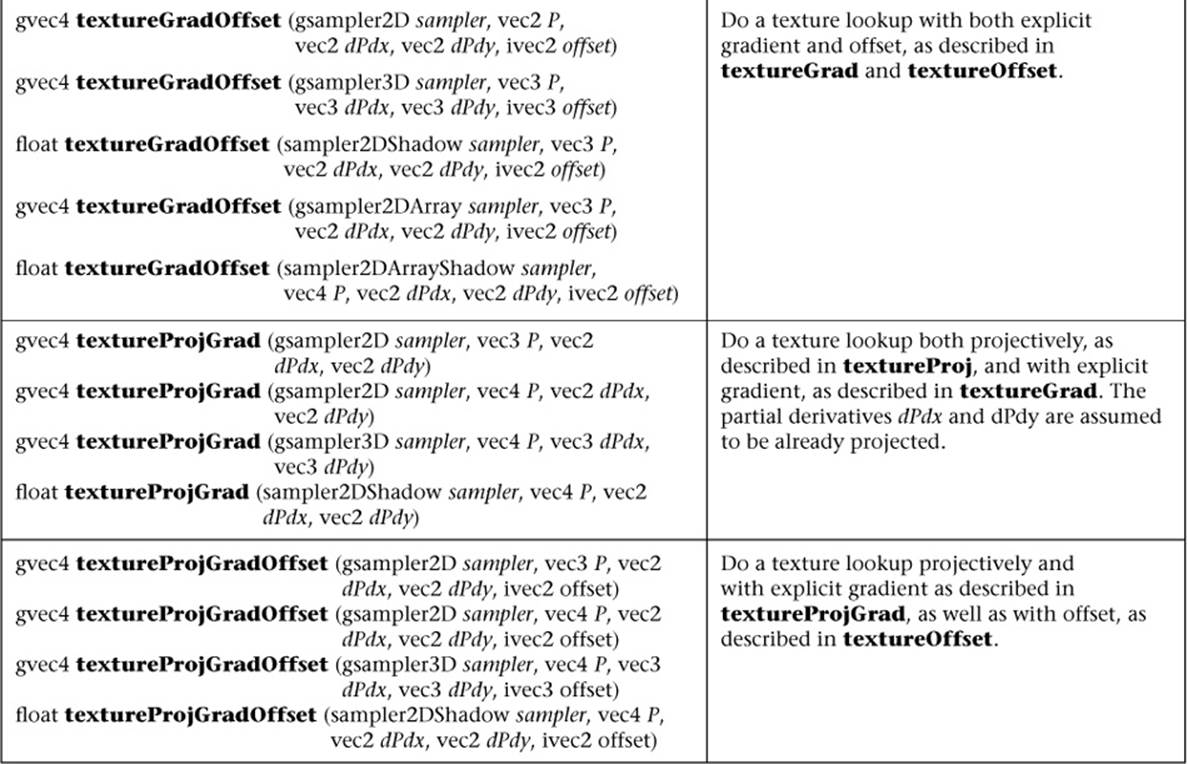
Table B-9 Texture Lookup Functions
Fragment Processing Functions
Fragment processing functions are only available in fragment shaders.
Derivatives may be computationally expensive and/or numerically unstable. Therefore, an OpenGL ES implementation may approximate the true derivatives by using a fast but not entirely accurate derivative computation. Derivatives are undefined within non-uniform control flow.
The expected behavior of a derivative is specified using forward–backward differencing.
Forward differencing:
F(x + dx) – F(x) ~ dFdx(x) * dx
dFdx ~ (F(x + dx) – F(x) )/dx
Backward differencing:
F(x – dx) – F(x) ~ –dFdx(x) * dx
dFdx ~ ( F(x) – F(x – dx) )/dx
With single-sample rasterization, dx <= 1.0 in the preceding equations. For multisample rasterization, dx < 2.0 in the preceding equations.
dFdy is approximated similarly, with y replacing x.
An OpenGL ES implementation can use the preceding or other methods to perform the calculation, subject to the following conditions:
• The method can use piecewise linear approximations. Such linear approximations imply that higher-order derivatives, dFdx(dFdx(x)) and above, are undefined.
• The method can assume that the function evaluated is continuous. Therefore derivatives within the body of a non-uniform conditional are undefined.
• The method can differ per fragment, subject to the constraint that the method can vary by window coordinates, not screen coordinates. The invariance requirement is relaxed for derivative calculations, because the method can be a function of fragment location.
Other properties that are desirable, but not required, are
• Functions should be evaluated within the interior of a primitive (interpolated, not extrapolated).
• Functions for dFdx should be evaluated while holding y constant. Functions for dFdy should be evaluated while holding x constant. However, mixed higher-order derivatives, like dFdx(dFdy(y)) and dFdy(dFdx(x)), are undefined.
• Derivatives of constant arguments should be 0.
In some implementations, varying degrees of derivative accuracy can be obtained by providing hints using glHint(GL_FRAGMENT_SHADER_DERIVATIVE_HINT), allowing a user to make an image quality versus speed trade-off.
Table B-10 describes the fragment processing functions.
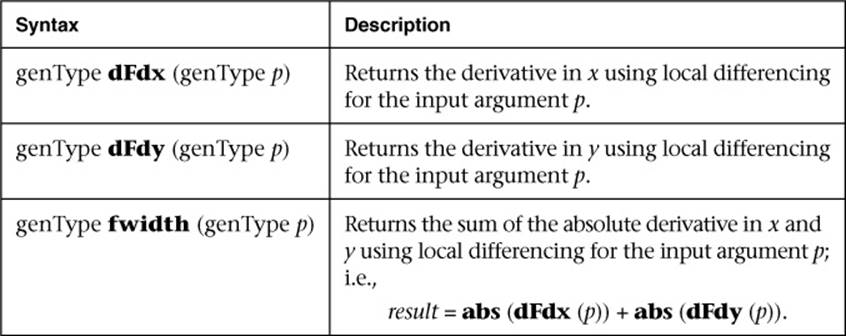
Table B-10 Fragment Processing Functions
All materials on the site are licensed Creative Commons Attribution-Sharealike 3.0 Unported CC BY-SA 3.0 & GNU Free Documentation License (GFDL)
If you are the copyright holder of any material contained on our site and intend to remove it, please contact our site administrator for approval.
© 2016-2026 All site design rights belong to S.Y.A.