Algorithms (2014)

One. Fundamentals

1.1 Basic Programming Model

OUR STUDY OF ALGORITHMS is based upon implementing them as programs written in the Java programming language. We do so for several reasons:

• Our programs are concise, elegant, and complete descriptions of algorithms.

• You can run the programs to study properties of the algorithms.

• You can put the algorithms immediately to good use in applications.

These are important and significant advantages over the alternatives of working with English-language descriptions of algorithms.

A potential downside to this approach is that we have to work with a specific programming language, possibly making it difficult to separate the idea of the algorithm from the details of its implementation. Our implementations are designed to mitigate this difficulty, by using programming constructs that are both found in many modern languages and needed to adequately describe the algorithms.

We use only a small subset of Java. While we stop short of formally defining the subset that we use, you will see that we make use of relatively few Java constructs, and that we emphasize those that are found in many modern programming languages. The code that we present is complete, and our expectation is that you will download it and execute it, on our test data or test data of your own choosing.

We refer to the programming constructs, software libraries, and operating system features that we use to implement and describe algorithms as our programming model. In this section and SECTION 1.2, we fully describe this programming model. The treatment is self-contained and primarily intended for documentation and for your reference in understanding any code in the book. The model we describe is the same model introduced in our book An Introduction to Programming in Java: An Interdisciplinary Approach, which provides a slower-paced introduction to the material.

For reference, the figure on the facing page depicts a complete Java program that illustrates many of the basic features of our programming model. We use this code for examples when discussing language features, but defer considering it in detail to page 46 (it implements a classic algorithm known as binary search and tests it for an application known as whitelist filtering). We assume that you have experience programming in some modern language, so that you are likely to recognize many of these features in this code. Page references are included in the annotations to help you find answers to any questions that you might have. Since our code is somewhat stylized and we strive to make consistent use of various Java idioms and constructs, it is worthwhile even for experienced Java programmers to read the information in this section.

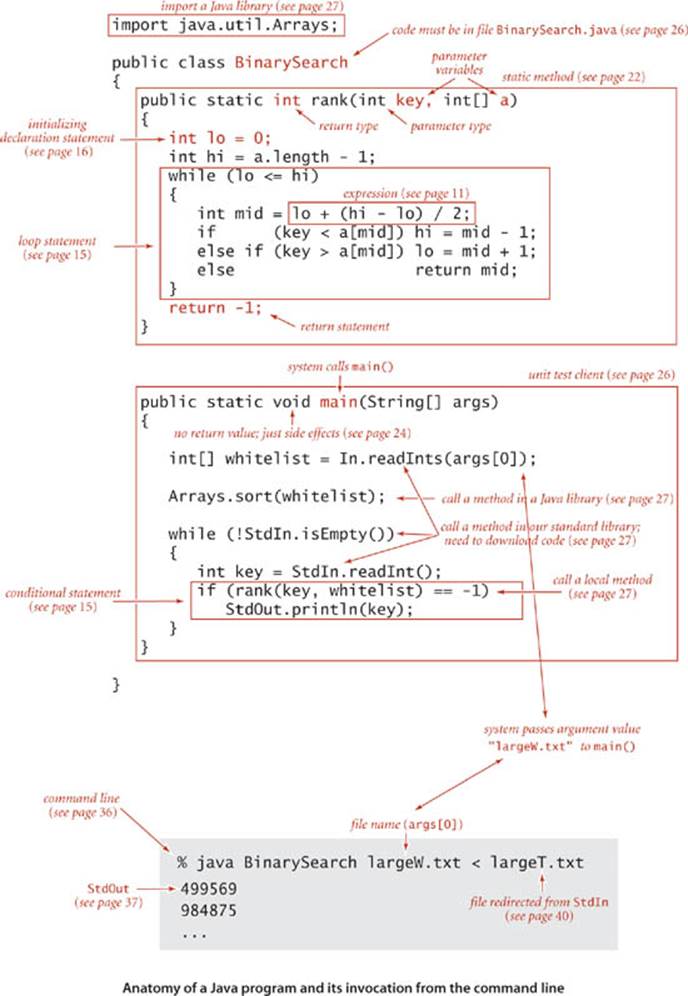
Basic structure of a Java program

A Java program (class) is either a library of static methods (functions) or a data type definition. To create libraries of static methods and data-type definitions, we use the following seven components, the basis of programming in Java and many other modern languages:

• Primitive data types precisely define the meaning of terms like integer, real number, and boolean value within a computer program. Their definition includes the set of possible values and operations on those values, which can be combined into expressions like mathematical expressions that define values.

• Statements allow us to define a computation by creating and assigning values to variables, controlling execution flow, or causing side effects. We use six types of statements: declarations, assignments, conditionals, loops, calls, and returns.

• Arrays allow us to work with multiple values of the same type.

• Static methods allow us to encapsulate and reuse code and to develop programs as a set of independent modules.

• Strings are sequences of characters. Some operations on them are built into Java.

• Input/output sets up communication between programs and the outside world.

• Data abstraction extends encapsulation and reuse to allow us to define non-primitive data types, thus supporting object-oriented programming.

In this section, we will consider the first five of these in turn. Data abstraction is the topic of the next section.

Running a Java program involves interacting with an operating system or a program development environment. For clarity and economy, we describe such actions in terms of a virtual terminal, where we interact with programs by typing commands to the system. See the booksite for details on using a virtual terminal on your system, or for information on using one of the many more advanced program development environments that are available on modern systems.

For example, BinarySearch is two static methods, rank() and main(). The first static method, rank(), is four statements: two declarations, a loop (which is itself an assignment and two conditionals), and a return. The second, main(), is three statements: a declaration, a call, and a loop (which is itself an assignment and a conditional).

To invoke a Java program, we first compile it using the javac command, then run it using the java command. For example, to run BinarySearch, we first type the command javac BinarySearch.java (which creates a file BinarySearch.class that contains a lower-level version of the program in Java bytecode). Then we type java BinarySearch (followed by a whitelist file name) to transfer control to the bytecode version of the program. To develop a basis for understanding the effect of these actions, we next consider in detail primitive data types and expressions, the various kinds of Java statements, arrays, static methods, strings, and input/output.

Primitive data types and expressions

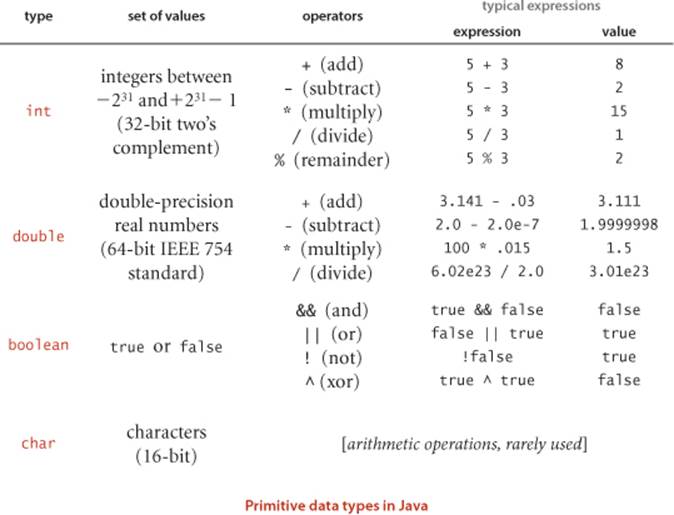
A data type is a set of values and a set of operations on those values. We begin by considering the following four primitive data types that are the basis of the Java language:

• Integers, with arithmetic operations (int)

• Real numbers, again with arithmetic operations (double)

• Booleans, the set of values { true, false } with logical operations (boolean)

• Characters, the alphanumeric characters and symbols that you type (char)

Next we consider mechanisms for specifying values and operations for these types.

A Java program manipulates variables that are named with identifiers. Each variable is associated with a data type and stores one of the permissible data-type values. In Java code, we use expressions like familiar mathematical expressions to apply the operations associated with each type. For primitive types, we use identifiers to refer to variables, operator symbols such as + - * / to specify operations, literals such as 1 or 3.14 to specify values, and expressions such as (x + 2.236)/2 to specify operations on values. The purpose of an expression is to define one of the data-type values.

To define a data type, we need only specify the values and the set of operations on those values. This information is summarized in the table below for Java’s int, double, boolean, and char data types. These data types are similar to the basic data types found in many programming languages. Forint and double, the operations are familiar arithmetic operations; for boolean, they are familiar logical operations. It is important to note that +, -, *, and / are overloaded—the same symbol specifies operations in multiple different types, depending on context. The key property of these primitive operations is that an operation involving values of a given type has a value of that type. This rule highlights the idea that we are often working with approximate values, since it is often the case that the exact value that would seem to be defined by the expression is not a value of the type. For example, 5/3 has the value 1 and 5.0/3.0 has a value very close to 1.66666666666667 but neither of these is exactly equal to 5/3. This table is far from complete; we discuss some additional operators and various exceptional situations that we occasionally need to consider in the Q&A at the end of this section.

Expressions

As illustrated in the table at the bottom of the previous page, typical expressions are infix: a literal (or an expression), followed by an operator, followed by another literal (or another expression). When an expression contains more than one operator, the order in which they are applied is often significant, so the following precedence conventions are part of the Java language specification: The operators * and / (and %) have higher precedence than (are applied before) the + and - operators; among logical operators, ! is the highest precedence, followed by && and then ||. Generally, operators of the same precedence are applied left to right. As in standard arithmetic expressions, you can use parentheses to override these rules. Since precedence rules vary slightly from language to language, we use parentheses and otherwise strive to avoid dependence on precedence rules in our code.

Type conversion

Numbers are automatically promoted to a more inclusive type if no information is lost. For example, in the expression 1 + 2.5, the 1 is promoted to the double value 1.0 and the expression evaluates to the double value 3.5. A cast is a type name in parentheses within an expression, a directive to convert the following value into a value of that type. For example (int) 3.7 is 3 and (double) 3 is 3.0. Note that casting to an int is truncation instead of rounding—rules for casting within complicated expressions can be intricate, and casts should be used sparingly and with care. A best practice is to use expressions that involve literals or variables of a single type.

Comparisons

The following operators compare two values of the same type and produce a boolean value: equal (==), not equal (!=), less than (<), less than or equal (<=), greater than (>), and greater than or equal (>=). These operators are known as mixed-type operators because their value is boolean, not the type of the values being compared. An expression with a boolean value is known as a boolean expression. Such expressions are essential components in conditional and loop statements, as we will see.

Other primitive types

Java’s int has 2³² different values by design, so it can be represented in a 32-bit machine word (many machines have 64-bit words nowadays, but the 32-bit int persists). Similarly, the double standard specifies a 64-bit representation. These data-type sizes are adequate for typical applications that use integers and real numbers. To provide flexibility, Java has five additional primitive data types:

• 64-bit integers, with arithmetic operations (long)

• 16-bit integers, with arithmetic operations (short)

• 16-bit characters, with arithmetic operations (char)

• 8-bit integers, with arithmetic operations (byte)

• 32-bit single-precision real numbers, again with arithmetic operations (float)

We most often use int and double arithmetic operations in this book, so we do not consider the others (which are very similar) in further detail here.

Statements

A Java program is composed of statements, which define the computation by creating and manipulating variables, assigning data-type values to them, and controlling the flow of execution of such operations. Statements are often organized in blocks, sequences of statements within curly braces.

• Declarations create variables of a specified type and name them with identifiers.

• Assignments associate a data-type value (defined by an expression) with a variable. Java also has several implicit assignment idioms for changing the value of a data-type value relative to its current value, such as incrementing the value of an integer variable.

• Conditionals provide for a simple change in the flow of execution—execute the statements in one of two blocks, depending on a specified condition.

• Loops provide for a more profound change in the flow of execution—execute the statements in a block as long as a given condition is true.

• Calls and returns relate to static methods (see page 22), which provide another way to change the flow of execution and to organize code.

A program is a sequence of statements, with declarations, assignments, conditionals, loops, calls, and returns. Programs typically have a nested structure: a statement among the statements in a block within a conditional or a loop may itself be a conditional or a loop. For example, the while loop in rank() contains an if statement. Next, we consider each of these types of statements in turn.

Declarations

A declaration statement associates a variable name with a type at compile time. Java requires us to use declarations to specify the names and types of variables. By doing so, we are being explicit about any computation that we are specifying. Java is said to be a strongly typed language, because the Java compiler checks for consistency (for example, it does not permit us to multiply a boolean and a double). Declarations can appear anywhere before a variable is first used—most often, we put them at the point of first use. The scope of a variable is the part of the program where it is defined. Generally the scope of a variable is composed of the statements that follow the declaration in the same block as the declaration.

Assignments

An assignment statement associates a data-type value (defined by an expression) with a variable. When we write c = a + b in Java, we are not expressing mathematical equality, but are instead expressing an action: set the value of the variable c to be the value of a plus the value of b. It is true that c is mathematically equal to a + b immediately after the assignment statement has been executed, but the point of the statement is to change the value of c (if necessary). The left-hand side of an assignment statement must be a single variable; the right-hand side can be an arbitrary expression that produces a value of the type.

Conditionals

Most computations require different actions for different inputs. One way to express these differences in Java is the if statement:

if (<boolean expression>) { <block statements> }

This description introduces a formal notation known as a template that we use occasionally to specify the format of Java constructs. We put within angle brackets (< >) a construct that we have already defined, to indicate that we can use any instance of that construct where specified. In this case, <boolean expression> represents an expression that has a boolean value, such as one involving a comparison operation, and <block statements> represents a sequence of Java statements. It is possible to make formal definitions of <boolean expression> and <block statements>, but we refrain from going into that level of detail. The meaning of an if statement is self-explanatory: the statement(s) in the block are to be executed if and only if the boolean expression is true. The if-else statement:

if (<boolean expression>) { <block statements> }
else { <block statements> }

allows for choosing between two alternative blocks of statements.

Loops

Many computations are inherently repetitive. The basic Java construct for handling such computations has the following format:

while (<boolean expression>) { <block statements> }

The while statement has the same form as the if statement (the only difference being the use of the keyword while instead of if), but the meaning is quite different. It is an instruction to the computer to behave as follows: if the boolean expression is false, do nothing; if the boolean expression istrue, execute the sequence of statements in the block (just as with if) but then check the boolean expression again, execute the sequence of statements in the block again if the boolean expression is true, and continue as long as the boolean expression is true. We refer to the statements in the block in a loop as the body of the loop.

Break and continue

Some situations call for slightly more complicated control flow than provided by the basic if and while statements. Accordingly, Java supports two additional statements for use within while loops:

• The break statement, which immediately exits the loop

• The continue statement, which immediately begins the next iteration of the loop

We rarely use these statements in the code in this book (and many programmers never use them), but they do considerably simplify code in certain instances.

Shortcut notations

There are several ways to express a given computation; we seek clear, elegant, and efficient code. Such code often takes advantage of the following widely used shortcuts (that are found in many languages, not just Java).

Initializing declarations

We can combine a declaration with an assignment to initialize a variable at the same time that it is declared (created). For example, the code int i = 1; creates an int variable named i and assigns it the initial value 1. A best practice is to use this mechanism close to first use of the variable (to limit scope).

Implicit assignments

The following shortcuts are available when our purpose is to modify a variable’s value relative to its current value:

• Increment/decrement operators: ++i is the same as i = i + 1; both have the value i in an expression. Similarly, --i is the same as i = i - 1. The code i++ and i-- are the same except that the expression value is the value before the increment/decrement, not after.

• Other compound operators: Prepending a binary operator to the = in an assignment is equivalent to using the variable on the left as the first operand. For example, the code i/=2; is equivalent to the code i = i/2; Note that i += 1; has the same effect as i = i+1; (and i++).

Single-statement blocks

If a block of statements in a conditional or a loop has only a single statement, the curly braces may be omitted.

For notation

Many loops follow this scheme: initialize an index variable to some value and then use a while loop to test a loop continuation condition involving the index variable, where the last statement in the while loop increments the index variable. You can express such loops compactly with Java’s fornotation:

for (<initialize>; <boolean expression>; <increment>)
{
<block statements>
}

This code is, with only a few exceptions, equivalent to

<initialize>;
while (<boolean expression>)
{
<block statements>
<increment>;
}

We use for loops to support this initialize-and-increment programming idiom.

Arrays

An array stores a sequence of values that are all of the same type. We want not only to store values but also to access each individual value. The method that we use to refer to individual values in an array is numbering and then indexing them. If we have N values, we think of them as being numbered from 0 to N−1. Then, we can unambiguously specify one of them in Java code by using the notation a[i] to refer to the ith value for any value of i from 0 to N-1. This Java construct is known as a one-dimensional array.

Creating and initializing an array

Making an array in a Java program involves three distinct steps:

• Declare the array name and type.

• Create the array.

• Initialize the array values.

To declare the array, you need to specify a name and the type of data it will contain. To create it, you need to specify its length (the number of values). For example, the “long form” code shown at right makes an array of N numbers of type double, all initialized to 0.0. The first statement is the array declaration. It is just like a declaration of a variable of the corresponding primitive type except for the square brackets following the type name, which specify that we are declaring an array. The keyword new in the second statement is a Java directive to create the array. The reason that we need to explicitly create arrays at run time is that the Java compiler cannot know how much space to reserve for the array at compile time (as it can for primitive-type values). The for statement initializes the N array values. This code sets all of the array entries to the value 0.0. When you begin to write code that uses an array, you must be sure that your code declares, creates, and initializes it. Omitting one of these steps is a common programming mistake.

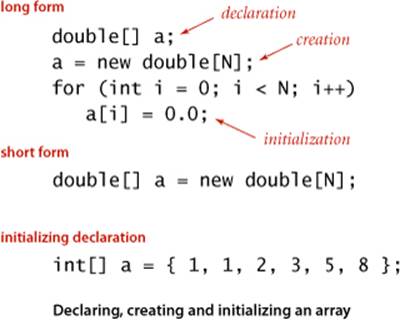
Default array initialization

For economy in code, we often take advantage of Java’s default array initialization convention and combine all three steps into a single statement, as in the “short form” code in our example. The code to the left of the equal sign constitutes the declaration; the code to the right constitutes the creation. The for loop is unnecessary in this case because the default initial value of variables of type double in a Java array is 0.0, but it would be required if a nonzero value were desired. The default initial value is zero for numeric types and false for type boolean.

Initializing declaration

The third option shown for our example is to specify the initialization values at compile time, by listing literal values between curly braces, separated by commas.

Using an array

Typical array-processing code is shown on page 21. After declaring and creating an array, you can refer to any individual value anywhere you would use a variable name in a program by enclosing an integer index in square brackets after the array name. Once we create an array, its size is fixed. A program can refer to the length of an array a[] with the code a.length. The last element of an array a[] is always a[a.length-1]. Java does automatic bounds checking—if you have created an array of size N and use an index whose value is less than 0 or greater than N-1, your program will terminate with an ArrayOutOfBoundsException runtime exception.

Aliasing

Note carefully that an array name refers to the whole array—if we assign one array name to another, then both refer to the same array, as illustrated in the following code fragment.

int[] a = new int[N];
...
a[i] = 1234;
...
int[] b = a;
...
b[i] = 5678; // a[i] is now 5678.

This situation is known as aliasing and can lead to subtle bugs. If your intent is to make a copy of an array, then you need to declare, create, and initialize a new array and then copy all of the entries in the original array to the new array, as in the third example on page 21.

Two-dimensional arrays

A two-dimensional array in Java is an array of one-dimensional arrays. A two-dimensional array may be ragged (its arrays may all be of differing lengths), but we most often work with (for appropriate parameters M and N) M-by-N two-dimensional arrays that are arrays of M rows, each an array of length N (so it also makes sense to refer to the array as having N columns). Extending Java array constructs to handle two-dimensional arrays is straightforward. To refer to the entry in row i and column j of a two-dimensional array a[][], we use the notation a[i][j]; to declare a two-dimensional array, we add another pair of square brackets; and to create the array, we specify the number of rows followed by the number of columns after the type name (both within square brackets), as follows:

double[][] a = new double[M][N];

We refer to such an array as an M-by-N array. By convention, the first dimension is the number of rows and the second is the number of columns. As with one-dimensional arrays, Java initializes all entries in arrays of numeric types to zero and in arrays of boolean values to false. Default initialization of two-dimensional arrays is useful because it masks more code than for one-dimensional arrays. The following code is equivalent to the single-line create-and-initialize idiom that we just considered:

double[][] a;
a = new double[M][N];
for (int i = 0; i < M; i++)
for (int j = 0; j < N; j++)
a[i][j] = 0.0;

This code is superfluous when initializing to zero, but the nested for loops are needed to initialize to other value(s).

Static methods

Every Java program in this book is either a data-type definition (which we describe in detail in SECTION 1.2) or a library of static methods (which we describe here). Static methods are called functions in many programming languages, since they can behave like mathematical functions, as described next. Each static method is a sequence of statements that are executed, one after the other, when the static method is called, in the manner described below. The modifier static distinguishes these methods from instance methods, which we discuss in SECTION 1.2. We use the wordmethod without a modifier when describing characteristics shared by both kinds of methods.

Defining a static method

A method encapsulates a computation that is defined as a sequence of statements. A method takes arguments (values of given data types) and computes a return value of some data type that depends upon the arguments (such as a value defined by a mathematical function) or causes a side effect that depends on the arguments (such as printing a value). The static method rank() in BinarySearch is an example of the first; main() is an example of the second. Each static method is composed of a signature (the keywords public static followed by a return type, the method name, and a sequence of arguments, each with a declared type) and a body (a statement block: a sequence of statements, enclosed in curly braces). Examples of static methods are shown in the table on the facing page.

Invoking a static method

A call on a static method is its name followed by expressions that specify argument values in parentheses, separated by commas. When the method call is part of an expression, the method computes a value and that value is used in place of the call in the expression. For example the call onrank() in BinarySearch() returns an int value. A method call followed by a semicolon is a statement that generally causes side effects. For example, the call Arrays.sort() in main() in BinarySearch is a call on the system method Arrays.sort() that has the side effect of putting the entries in the array in sorted order. When a method is called, its argument variables are initialized with the values of the corresponding expressions in the call. A return statement terminates a static method, returning control to the caller. If the static method is to compute a value, that value must be specified in a returnstatement (if such a static method can reach the end of its sequence of statements without a return, the compiler will report the error).

Properties of methods

A complete detailed description of the properties of methods is beyond our scope, but the following points are worth noting:

• Arguments are passed by value. You can use argument variables anywhere in the code in the body of the method in the same way you use local variables. The only difference between an argument variable and a local variable is that the argument variable is initialized with the argument value provided by the calling code. The method works with the value of its arguments, not the arguments themselves. One consequence of this approach is that changing the value of an argument variable within a static method has no effect on the calling code. Generally, we do not change argument variables in the code in this book. The pass-by-value convention implies that array arguments are aliased (see page 19)—the method uses the argument variable to refer to the caller’s array and can change the contents of the array (though it cannot change the array itself). For example, Arrays.sort() certainly changes the contents of the array passed as argument: it puts the entries in order.

• Method names can be overloaded. For example, the Java Math library uses this approach to provide implementations of Math.abs(), Math.min(), and Math.max() for all primitive numeric types. Another common use of overloading is to define two different versions of a function, one that takes an argument and another that uses a default value of that argument.

• A method has a single return value but may have multiple return statements. A Java method can provide only one return value, of the type declared in the method signature. Control goes back to the calling program as soon as the first return statement in a static method is reached. You can put return statements wherever you need them. Even though there may be multiple return statements, any static method returns a single value each time it is invoked: the value following the first return statement encountered.

• A method can have side effects. A method may use the keyword void as its return type, to indicate that it has no return value. An explicit return is not necessary in a void static method: control returns to the caller after the last statement. A void static method is said to produce side effects (consume input, produce output, change entries in an array, or otherwise change the state of the system). For example, the main() static method in our programs has a void return type because its purpose is to produce output. Technically, void methods do not implement mathematical functions (and neither does Math.random(), which takes no arguments but does produce a return value).

The instance methods that are the subject of SECTION 2.1 share these properties, though profound differences surround the issue of side effects.

Recursion

A method can call itself (if you are not comfortable with this idea, known as recursion, you are encouraged to work EXERCISES 1.1.16 through 1.1.22). For example, the code at the bottom of this page gives an alternate implementation of the rank() method in BinarySearch. We often use recursive implementations of methods because they can lead to compact, elegant code that is easier to understand than a corresponding implementation that does not use recursion. For example, the comment in the implementation below provides a succinct description of what the code is supposed to do. We can use this comment to convince ourselves that it operates correctly, by mathematical induction. We will expand on this topic and provide such a proof for binary search in SECTION 3.1. There are three important rules of thumb in developing recursive programs:

• The recursion has a base case—we always include a conditional statement as the first statement in the program that has a return.

• Recursive calls must address subproblems that are smaller in some sense, so that recursive calls converge to the base case. In the code below, the difference between the values of the fourth and the third arguments always decreases.

• Recursive calls should not address subproblems that overlap. In the code below, the portions of the array referenced by the two subproblems are disjoint.

Violating any of these guidelines is likely to lead to incorrect results or a spectacularly inefficient program (see EXERCISES 1.1.19 and 1.1.27). Adhering to them is likely to lead to a clear and correct program whose performance is easy to understand. Another reason to use recursive methods is that they lead to mathematical models that we can use to understand performance. We address this issue for binary search in SECTION 3.2 and in several other instances throughout the book.

Recursive implementation of binary search

public static int rank(int key, int[] a)
{ return rank(key, a, 0, a.length - 1); }
public static int rank(int key, int[] a, int lo, int hi)
{ // Index of key in a[], if present, is not smaller than lo
// and not larger than hi.
if (lo > hi) return -1;
int mid = lo + (hi - lo) / 2;
if (key < a[mid]) return rank(key, a, lo, mid - 1);
else if (key > a[mid]) return rank(key, a, mid + 1, hi);
else return mid;
}

Basic programming model

A library of static methods is a set of static methods that are defined in a Java class, by creating a file with the keywords public class followed by the class name, followed by the static methods, enclosed in braces, kept in a file with the same name as the class and a .java extension. A basic model for Java programming is to develop a program that addresses a specific computational task by creating a library of static methods, one of which is named main(). Typing java followed by a class name followed by a sequence of strings leads to a call on main() in that class, with an array containing those strings as argument. After the last statement in main() executes, the program terminates. In this book, when we talk of a Java program for accomplishing a task, we are talking about code developed along these lines (possibly also including a data-type definition, as described inSECTION 1.2). For example, BinarySearch is a Java program composed of two static methods, rank() and main(), that accomplishes the task of printing numbers from an input stream that are not found in a whitelist file given as command-line argument.

Modular programming

Of critical importance in this model is that libraries of static methods enable modular programming where we build libraries of static methods (modules) and a static method in one library can call static methods defined in other libraries. This approach has many important advantages. It allows us to

• Work with modules of reasonable size, even in program involving a large amount of code

• Share and reuse code without having to reimplement it

• Easily substitute improved implementations

• Develop appropriate abstract models for addressing programming problems

• Localize debugging (see the paragraph below on unit testing)

For example, BinarySearch makes use of three other independently developed libraries, our StdIn and In library and Java’s Arrays library. Each of these libraries, in turn, makes use of several other libraries.

Unit testing

A best practice in Java programming is to include a main() in every library of static methods that tests the methods in the library (some other programming languages disallow multiple main() methods and thus do not support this approach). Proper unit testing can be a significant programming challenge in itself. At a minimum, every module should contain a main() method that exercises the code in the module and provides some assurance that it works. As a module matures, we often refine the main() method to be a development client that helps us do more detailed tests as we develop the code, or a test client that tests all the code extensively. As a client becomes more complicated, we might put it in an independent module. In this book, we use main() to help illustrate the purpose of each module and leave test clients for exercises.

External libraries

We use static methods from four different kinds of libraries, each requiring (slightly) differing procedures for code reuse. Most of these are libraries of static methods, but a few are data-type definitions that also include some static methods.

• The standard system libraries java.lang.*. These include Math, which contains methods for commonly used mathematical functions; Integer and Double, which we use for converting between strings of characters and int and double values; String and StringBuilder, which we discuss in detail later in this section and in CHAPTER 5; and dozens of other libraries that we do not use.

• Imported system libraries such as java.util.Arrays. There are thousands of such libraries in a standard Java release, but we make scant use of them in this book. An import statement at the beginning of the program is needed to use such libraries (and signal that we are doing so).

• Other libraries in this book. For example, another program can use rank() in BinarySearch. To use such a program, download the source from the booksite into your working directory.

• The standard libraries Std* that we have developed for use in this book (and our introductory book An Introduction to Programming in Java: An Interdisciplinary Approach). These libraries are summarized in the following several pages. Source code and instructions for downloading them are available on the booksite.

To invoke a method from another library (one in the same directory or a specified directory, a standard system library, or a system library that is named in an import statement before the class definition), we prepend the library name to the method name for each call. For example, the main()method in BinarySearch calls the sort() method in the system library java.util.Arrays, the readInts() method in our library In, and the println() method in our library StdOut.

LIBRARIES OF METHODS IMPLEMENTED BY OURSELVES AND BY OTHERS in a modular programming environment can vastly expand the scope of our programming model. Beyond all of the libraries available in a standard Java release, thousands more are available on the web for applications of all sorts. To limit the scope of our programming model to a manageable size so that we can concentrate on algorithms, we use just the libraries listed in the table at right on this page, with a subset of their methods listed in APIs, as described next.

APIs

A critical component of modular programming is documentation that explains the operation of library methods that are intended for use by others. We will consistently describe the library methods that we use in this book in application programming interfaces (APIs) that list the library name and the signatures and short descriptions of each of the methods that we use. We use the term client to refer to a program that calls a method in another library and the term implementation to describe the Java code that implements the methods in an API.

Example

The following example, the API for commonly used static methods from the standard Math library in java.lang, illustrates our conventions for APIs:

These methods implement mathematical functions—they use their arguments to compute a value of a specified type (except random(), which does not implement a mathematical function because it does not take an argument). Since they all operate on double values and compute a double result, you can consider them as extending the double data type—extensibility of this nature is one of the characteristic features of modern programming languages. Each method is described by a line in the API that specifies the information you need to know in order to use the method. The Math library also defines the precise constant values PI (for π) and E (for e), so that you can use those names to refer to those constants in your programs. For example, the value of Math.sin(Math.PI/2) is 1.0 and the value of Math.log(Math.E) is 1.0 (because Math.sin() takes its argument in radians and Math.log()implements the natural logarithm function).

Java libraries

Extensive online descriptions of thousands of libraries are part of every Java release, but we excerpt just a few methods that we use in the book, in order to clearly delineate our programming model. For example, BinarySearch uses the sort() method from Java’s Arrays library, which we document as follows:

The Arrays library is not in java.lang, so an import statement is needed to use it, as in BinarySearch. Actually, CHAPTER 2 of this book is devoted to implementations of sort() for arrays, including the mergesort and quicksort algorithms that are implemented in Arrays.sort(). Many of the fundamental algorithms that we consider in this book are implemented in Java and in many other programming environments. For example, Arrays also includes an implementation of binary search. To avoid confusion, we generally use our own implementations, although there is nothing wrong with using a finely tuned library implementation of an algorithm that you understand.

Our standard libraries

We have developed a number of libraries that provide useful functionality for introductory Java programming, for scientific applications, and for the development, study, and application of algorithms. Most of these libraries are for input and output; we also make use of the following two libraries to test and analyze our implementations. The first extends Math.random() to allow us to draw random values from various distributions; the second supports statistical calculations:

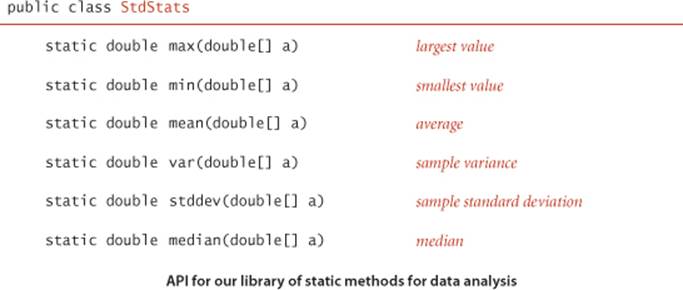
The setSeed() method in StdRandom allows us to seed the random number generator so that we can reproduce experiments involving random numbers. For reference, implementations of many of these methods are given on page 32. Some of these methods are extremely easy to implement; why do we bother including them in a library? Answers to this question are standard for well-designed libraries:

• They implement a level of abstraction that allow us to focus on implementing and testing the algorithms in the book, not generating random objects or calculating statistics. Client code that uses such methods is clearer and easier to understand than homegrown code that does the same calculation.

• Library implementations test for exceptional conditions, cover rarely encountered situations, and submit to extensive testing, so that we can count on them to operate as expected. Such implementations might involve a significant amount of code. For example, we often want implementations for various types of data. For example, Java’s Arrays library includes multiple overloaded implementations of sort(), one for each type of data that you might need to sort.

These are bedrock considerations for modular programming in Java, but perhaps a bit overstated in this case. While the methods in both of these libraries are essentially self-documenting and many of them are not difficult to implement, some of them represent interesting algorithmic exercises. Accordingly, you are well-advised to both study the code in StdRandom.java and StdStats.java on the booksite and to take advantage of these tried-and-true implementations. The easiest way to use these libraries (and to examine the code) is to download the source code from the booksite and put them in your working directory; various system-dependent mechanisms for using them without making multiple copies are also described on the booksite.

Your own libraries

It is worthwhile to consider every program that you write as a library implementation, for possible reuse in the future.

• Write code for the client, a top-level implementation that breaks the computation up into manageable parts.

• Articulate an API for a library (or multiple APIs for multiple libraries) of static methods that can address each part.

• Develop an implementation of the API, with a main() that tests the methods independent of the client.

Not only does this approach provide you with valuable software that you can later reuse, but also taking advantage of modular programming in this way is a key to successfully addressing a complex programming task.

THE PURPOSE OF AN API is to separate the client from the implementation: the client should know nothing about the implementation other than information given in the API, and the implementation should not take properties of any particular client into account. APIs enable us to separately develop code for various purposes, then reuse it widely. No Java library can contain all the methods that we might need for a given computation, so this ability is a crucial step in addressing complex programming applications. Accordingly, programmers normally think of the API as acontract between the client and the implementation that is a clear specification of what each method is to do. Our goal when developing an implementation is to honor the terms of the contract. Often, there are many ways to do so, and separating client code from implementation code gives us the freedom to substitute new and improved implementations. In the study of algorithms, this ability is an important ingredient in our ability to understand the impact of algorithmic improvements that we develop.

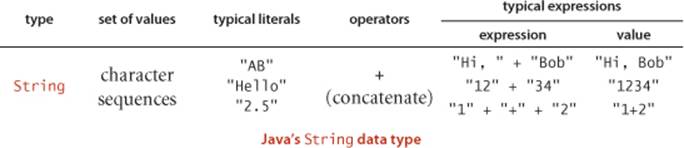
Strings

A String is a sequence of characters (char values). A literal String is a sequence of characters within double quotes, such as "Hello, World". The data type String is a Java data type but it is not a primitive type. We consider String now because it is a fundamental data type that almost every Java program uses.

Concatenation

Java has a built-in concatenation operator (+) for String like the built-in operators that it has for primitive types, justifying the addition of the row in the table below to the primitive-type table on page 12. The result of concatenating two String values is a single String value, the first string followed by the second.

Conversion

Two primary uses of strings are to convert values that we can enter on a keyboard into data-type values and to convert data-type values to values that we can read on a display. Java has built-in operations for String to facilitate these operations. In particular, the language includes libraries Integerand Double that contain static methods to convert between String values and int values and between String values and double values, respectively.

Automatic conversion

We rarely explicitly use the static toString() methods just described because Java has a built-in mechanism that allows us to convert from any data type value to a String value by using concatenation: if one of the arguments of + is a String, Java automatically converts the other argument to a String(if it is not already a String). Beyond usage like "The square root of 2.0 is " + Math.sqrt(2.0) this mechanism enables conversion of any data-type value to a String, by concatenating it with the empty string "".

Command-line arguments

One important use of strings in Java programming is to enable a mechanism for passing information from the command line to the program. The mechanism is simple. When you type the java command followed by a library name followed by a sequence of strings, the Java system invokes themain() method in that library with an array of strings as argument: the strings typed after the library name. For example, the main() method in BinarySearch takes one command-line argument, so the system creates an array of size one. The program uses that value, args[0], to name the file containing the whitelist, for use as the argument to In.readInts(). Another typical paradigm that we often use in our code is when a command-line argument is intended to represent a number, so we use parseInt() to convert to an int value or parseDouble() to convert to a double value.

COMPUTING WITH STRINGS is an essential component of modern computing. For the moment, we make use of String just to convert between external representation of numbers as sequences of characters and internal representation of numeric data-type values. In SECTION 1.2, we will see that Java supports many, many more operations on String values that we use throughout the book; in SECTION 1.4, we will examine the internal representation of String values; and in CHAPTER 5, we consider in depth algorithms that process String data. These algorithms are among the most interesting, intricate, and impactful methods that we consider in this book.

Input and output

The primary purpose of our standard libraries for input, output, and drawing is to support a simple model for Java programs to interact with the outside world. These libraries are built upon extensive capabilities that are available in Java libraries, but are generally much more complicated and much more difficult to learn and use. We begin by briefly reviewing the model.

In our model, a Java program takes input values from command-line arguments or from an abstract stream of characters known as the standard input stream and writes to another abstract stream of characters known as the standard output stream.

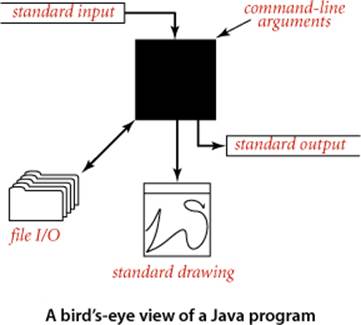
Necessarily, we need to consider the interface between Java and the operating system, so we need to briefly discuss basic mechanisms that are provided by most modern operating systems and program-development environments. You can find more details about your particular system on the booksite. By default, command-line arguments, standard input, and standard output are associated with an application supported by either the operating system or the program development environment that takes commands. We use the generic term terminal window to refer to the window maintained by this application, where we type and read text. Since early Unix systems in the 1970s this model has proven to be a convenient and direct way for us to interact with our programs and data. We add to the classical model a standard drawing that allows us to create visual representations for data analysis.

Commands and arguments

In the terminal window, we see a prompt, where we type commands to the operating system that may take arguments. We use only a few commands in this book, shown in the table below. Most often, we use the java command, to run our programs. As mentioned on page 35, Java classes have a main() static method that takes a String array args[] as its argument. That array is the sequence of command-line arguments that we type, provided to Java by the operating system. By convention, both Java and the operating system process the arguments as strings. If we intend for an argument to be a number, we use a method such as Integer.parseInt() to convert it from String to the appropriate type.

Standard output

Our StdOut library provides support for standard output. By default, the system connects standard output to the terminal window. The print() method puts its argument on standard output; the println() method adds a newline; and the printf() method supports formatted output, as described next. Java provides a similar method in its System.out library; we use StdOut to treat standard input and standard output in a uniform manner (and to provide a few technical improvements).

To use these methods, download into your working directory StdOut.java from the booksite and use code such as StdOut.println("Hello, World"); to call them. A sample client is shown at right.

Sample StdOut client

public class RandomSeq
{
public static void main(String[] args)
{ // Print N random values in (lo, hi).
int N = Integer.parseInt(args[0]);
double lo = Double.parseDouble(args[1]);
double hi = Double.parseDouble(args[2]);
for (int i = 0; i < N; i++)
{
double x = StdRandom.uniform(lo, hi);
StdOut.printf("%.2f\n", x);
}
}
}

Formatted output

In its simplest form, printf() takes two arguments. The first argument is a format string that describes how the second argument is to be converted to a string for output. The simplest type of format string begins with % and ends with a one-letter conversion code. The conversion codes that we use most frequently are d (for decimal values from Java’s integer types), f (for floating-point values), and s (for String values). Between the % and the conversion code is an integer value that specifies the field width of the converted value (the number of characters in the converted output string). By default, blank spaces are added on the left to make the length of the converted output equal to the field width; if we want the spaces on the right, we can insert a minus sign before the field width. (If the converted output string is bigger than the field width, the field width is ignored.) Following the width, we have the option of including a period followed by the number of digits to put after the decimal point (the precision) for a double value or the number of characters to take from the beginning of the string for a String value. The most important thing to remember about using printf() is that the conversion code in the format and the type of the corresponding argument must match. That is, Java must be able to convert from the type of the argument to the type required by the conversion code. The first argument of printf() is a String that may contain characters other than a format string. Any part of the argument that is not part of a format string passes through to the output, with the format string replaced by the argument value (converted to a String as specified). For example, the statement

StdOut.printf("PI is approximately %.2f\n", Math.PI);

% java RandomSeq 5 100.0 200.0
123.43
153.13
144.38
155.18
104.02

prints the line

PI is approximately 3.14

Note that we need to explicitly include the newline character \n in the argument in order to print a new line with printf(). The printf() function can take more than two arguments. In this case, the format string will have a format specifier for each additional argument, perhaps separated by other characters to pass through to the output. You can also use the static method String.format() with arguments exactly as just described for printf() to get a formatted string without printing it. Formatted printing is a convenient mechanism that allows us to develop compact code that can produce tabulated experimental data (our primary use in this book).

Standard input

Our StdIn library takes data from the standard input stream that may be empty or may contain a sequence of values separated by whitespace (spaces, tabs, newline characters, and the like). By default, the system connects standard output to the terminal window—what you type is the input stream (terminated by <ctrl-d> or <ctrl-z>, depending on your terminal window application). Each value is a String or a value from one of Java’s primitive types. One of the key features of the standard input stream is that your program consumes values when it reads them. Once your program has read a value, it cannot back up and read it again. This assumption is restrictive, but it reflects physical characteristics of some input devices and simplifies implementing the abstraction. Within the input stream model, the static methods in this library are largely self-documenting (described by their signatures).

Sample StdIn client

public class Average
{
public static void main(String[] args)
{ // Average the numbers on StdIn.
double sum = 0.0;
int cnt = 0;
while (!StdIn.isEmpty())
{ // Read a number and cumulate the sum.
sum += StdIn.readDouble();
cnt++;
}
double avg = sum / cnt;
StdOut.printf("Average is %.5f\n", avg);
}
}

% java Average
1.23456
2.34567
3.45678
4.56789
<ctrl-d>
Average is 2.90123

Redirection and piping

Standard input and output enable us to take advantage of command-line extensions supported by many operating-systems. By adding a simple directive to the command that invokes a program, we can redirect its standard output to a file, either for permanent storage or for input to another program at a later time:

% java RandomSeq 1000 100.0 200.0 > data.txt

This command specifies that the standard output stream is not to be printed in the terminal window, but instead is to be written to a text file named data.txt. Each call to StdOut.print() or StdOut.println() appends text at the end of that file. In this example, the end result is a file that contains 1,000 random values. No output appears in the terminal window: it goes directly into the file named after the > symbol. Thus, we can save away information for later retrieval. Note that we do not have to change RandomSeq in any way—it is using the standard output abstraction and is unaffected by our use of a different implementation of that abstraction. Similarly, we can redirect standard input so that StdIn reads data from a file instead of the terminal application:

% java Average < data.txt

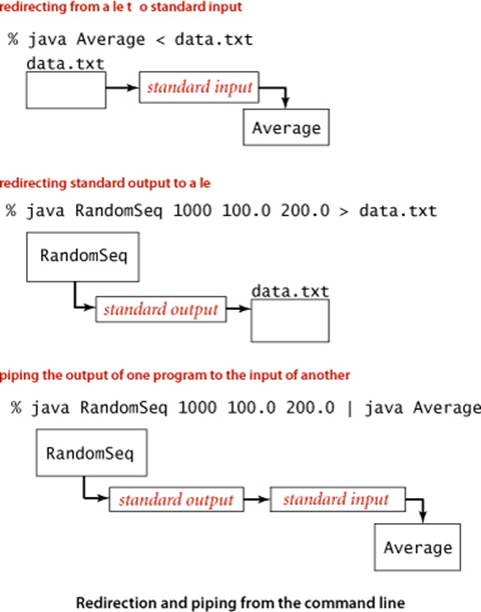
This command reads a sequence of numbers from the file data.txt and computes their average value. Specifically, the < symbol is a directive that tells the operating system to implement the standard input stream by reading from the text file data.txt instead of waiting for the user to type something into the terminal window. When the program calls StdIn.readDouble(), the operating system reads the value from the file. Combining these to redirect the output of one program to the input of another is known as piping:

% java RandomSeq 1000 100.0 200.0 | java Average

This command specifies that standard output for RandomSeq and standard input for Average are the same stream. The effect is as if RandomSeq were typing the numbers it generates into the terminal window while Average is running. This difference is profound, because it removes the limitation on the size of the input and output streams that we can process. For example, we could replace 1000 in our example with 1000000000, even though we might not have the space to save a billion numbers on our computer (we do need the time to process them). When RandomSeq calls StdOut.printf(), a string is added to the end of the stream; when Average calls StdIn.readDouble(), a string is removed from the beginning of the stream. The timing of precisely what happens is up to the operating system: it might run RandomSeq until it produces some numbers, and then run Average to consume those numbers, or it might run Average until it needs to consume a number, and then run RandomSeq until it produces the needed number. The end result is the same, but our programs are freed from worrying about such details because they work solely with the standard input and standard output abstractions.

Input and output from a file

Our In and Out libraries provide static methods that implement the abstraction of reading from and writing to a file the contents of an array of values of a primitive type (or String). We use readInts(), readDoubles(), and readStrings() in the In library and writeInts(), writeDoubles(), and writeStrings() in the Outlibrary. The named argument can be a file or a web page. For example, this ability allows us to use a file and standard input for two different purposes in the same program, as in BinarySearch. The In and Out libraries also implement data types with instance methods that allow us the more general ability to treat multiple files as input and output streams, and web pages as input streams, so we will revisit them in SECTION 1.2.

Standard drawing (basic methods)

Up to this point, our input/output abstractions have focused exclusively on text strings. Now we introduce an abstraction for producing drawings as output. This library is easy to use and allows us to take advantage of a visual medium to cope with far more information than is possible with just text. As with standard input/output, our standard drawing abstraction is implemented in a library StdDraw that you can access by downloading the file StdDraw.java from the booksite into your working directory. Standard draw is very simple: we imagine an abstract drawing device capable of drawing lines and points on a two-dimensional canvas. The device is capable of responding to the commands to draw basic geometric shapes that our programs issue in the form of calls to static methods in StdDraw, including methods for drawing lines, points, text strings, circles, rectangles, and polygons. Like the methods for standard input and standard output, these methods are nearly self-documenting: StdDraw.line() draws a straight line segment connecting the point (x₀, y₀) with the point (x₁, y₁) whose coordinates are given as arguments. StdDraw.point() draws a spot centered on the point (x, y) whose coordinates are given as arguments, and so forth, as illustrated in the diagrams at right. Geometric shapes can be filled (in black, by default). The default scale is the unit square (all coordinates are between 0 and 1). The standard implementation displays the canvas in a window on your computer’s screen, with black lines and points on a white background.

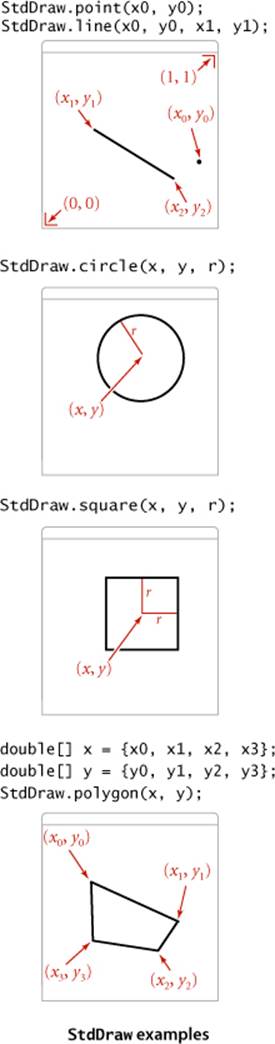
Standard drawing (control methods)

The library also includes methods to change the scale and size of the canvas, the color and width of the lines, the text font, and the timing of drawing (for use in animation). As arguments for setPenColor() you can use one of the predefined colors BLACK, BLUE, CYAN, DARK_GRAY, GRAY, GREEN, LIGHT_GRAY, MAGENTA,ORANGE, PINK, RED, BOOK_RED, WHITE, and YELLOW that are defined as constants in StdDraw (so we refer to one of them with code like StdDraw.RED). The window also includes a menu option to save your drawing to a file, in a format suitable for publishing on the web.

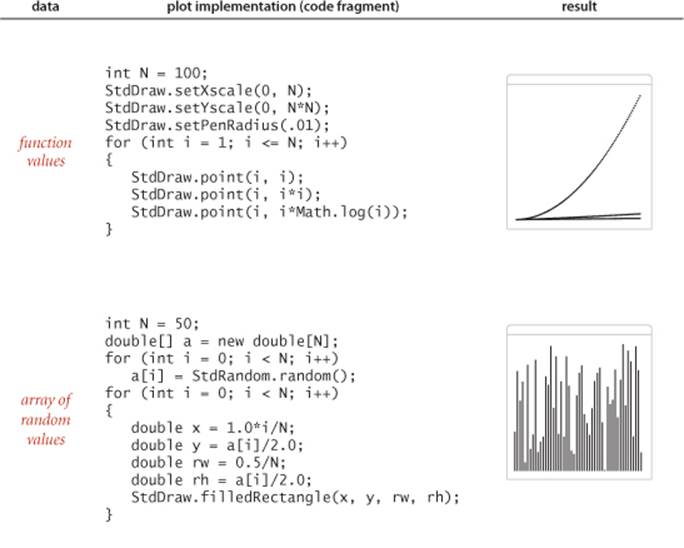
IN THIS BOOK, we use StdDraw for data analysis and for creating visual representations of algorithms in operation. The table on the opposite page indicates some possiblities; we will consider many more examples in the text and the exercises throughout the book. The library also supportsanimation—of course, this topic is treated primarily on the booksite.

Binary search

The sample Java program that we started with, shown on the facing page, is based on the famous, effective, and widely used binary search algorithm. This example is a prototype of the way in which we will examine new algorithms throughout the book. As with all of the programs we consider, it is both a precise definition of the method and a complete Java implementation that you can download from the booksite.

Binary search

We will study the binary search algorithm in detail in SECTION 3.2, but a brief description is appropriate here. The algorithm is implemented in the static method rank(), which takes an integer key and a sorted array of int values as arguments and returns the index of the key if it is present in the array, -1 otherwise. It accomplishes this task by maintaining variables lo and hi such that the key is in a[lo..hi] if it is in the array, then entering into a loop that tests the middle entry in the interval (at index mid). If the key is equal to a[mid], the return value is mid; otherwise the method cuts the interval size about in half, looking at the left half if the key is less than a[mid] and at the right half if the key is greater than a[mid]. The process terminates when the key is found or the interval is empty. Binary search is effective because it needs to examine just a few array entries (relative to the size of the array) to find the key (or determine that it is not there).

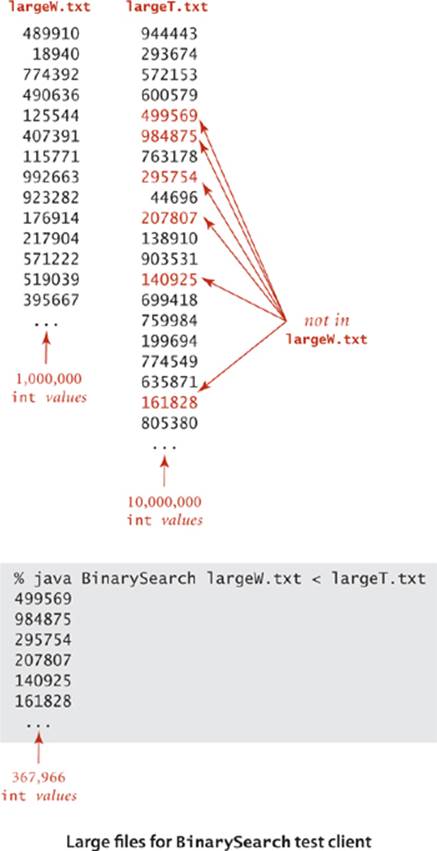
Development client

For every algorithm implementation, we include a development client main() that you can use with sample input files provided in the book and on the booksite to learn about the algorithm and to test its performance. In this example, the client reads integers from the file named on the command line, then prints any integers to standard output that do not appear in the file. We use small test files such as those shown at right to demonstrate this behavior, and as the basis for traces and examples such as those at left above. We use large test files to model real-world applications and to test performance (see page 48).