Algorithms (2014)
One. Fundamentals
1.3 Bags, Queues, and Stacks
SEVERAL FUNDAMENTAL DATA TYPES involve collections of objects. Specifically, the set of values is a collection of objects, and the operations revolve around adding, removing, or examining objects in the collection. In this section, we consider three such data types, known as the bag, thequeue, and the stack. They differ in the specification of which object is to be removed or examined next.
Bags, queues, and stacks are fundamental and broadly useful. We use them in implementations throughout the book. Beyond this direct applicability, the client and implementation code in this section serves as an introduction to our general approach to the development of data structures and algorithms.
One goal of this section is to emphasize the idea that the way in which we represent the objects in the collection directly impacts the efficiency of the various operations. For collections, we design data structures for representing the collection of objects that can support efficient implementation of the requisite operations.
A second goal of this section is to introduce generics and iteration, basic Java constructs that substantially simplify client code. These are advanced programming-language mechanisms that are not necessarily essential to the understanding of algorithms, but their use allows us to develop client code (and implementations of algorithms) that is more clear, compact, and elegant than would otherwise be possible.
A third goal of this section is to introduce and show the importance of linked data structures. In particular, a classic data structure known as the linked list enables implementation of bags, queues, and stacks that achieve efficiencies not otherwise possible. Understanding linked lists is a key first step to the study of algorithms and data structures.
For each of the three types, we consider APIs and sample client programs, then look at possible representations of the data type values and implementations of the data-type operations. This scenario repeats (with more complicated data structures) throughout this book. The implementations here are models of implementations later in the book and worthy of careful study.
APIs
As usual, we begin our discussion of abstract data types for collections by defining their APIs, shown below. Each contains a no-argument constructor, a method to add an item to the collection, a method to test whether the collection is empty, and a method that returns the size of the collection. Stack and Queue each have a method to remove a particular item from the collection. Beyond these basics, these APIs reflect two Java features that we will describe on the next few pages: generics and iterable collections.


Generics
An essential characteristic of collection ADTs is that we should be able to use them for any type of data. A specific Java mechanism known as generics, also known as parameterized types, enables this capability. The impact of generics on the programming language is sufficiently deep that they are not found in many languages (including early versions of Java), but our use of them in the present context involves just a small bit of extra Java syntax and is easy to understand. The notation <Item> after the class name in each of our APIs defines the name Item as a type parameter, a symbolic placeholder for some concrete type to be used by the client. You can read Stack<Item> as “stack of items.” When implementing Stack, we do not know the concrete type of Item, but a client can use our stack for any type of data, including one defined long after we develop our implementation. The client code provides a concrete type when the stack is created: we can replace Item with the name of any reference data type (consistently, everywhere it appears). This provides exactly the capability that we need. For example, you can write code such as
Stack<String> stack = new Stack<String>();
stack.push("Test");
...
String next = stack.pop();
to use a stack for String objects and code such as
Queue<Date> queue = new Queue<Date>();
queue.enqueue(new Date(12, 31, 1999));
...
Date next = queue.dequeue();
to use a queue for Date objects. If you try to add a Date (or data of any other type than String) to stack or a String (or data of any other type than Date) to queue, you will get a compile-time error. Without generics, we would have to define (and implement) different APIs for each type of data we might need to collect; with generics, we can use one API (and one implementation) for all types of data, even types that are implemented in the future. As you will soon see, generic types lead to clear client code that is easy to understand and debug, so we use them throughout this book.
Autoboxing
Type parameters have to be instantiated as reference types, so Java has special mechanisms to allow generic code to be used with primitive types. Recall that Java’s wrapper types are reference types that correspond to primitive types: Boolean, Byte, Character, Double, Float, Integer, Long, and Shortcorrespond to boolean, byte, char, double, float, int, long, and short, respectively. Java automatically converts between these reference types and the corresponding primitive types—in assignments, method arguments, and arithmetic/logic expressions. In the present context, this conversion is helpful because it enables us to use generics with primitive types, as in the following code:
Stack<Integer> stack = new Stack<Integer>();
stack.push(17); // auto-boxing (int -> Integer)
int i = stack.pop(); // auto-unboxing (Integer -> int)
Automatically casting a primitive type to a wrapper type is known as autoboxing, and automatically casting a wrapper type to a primitive type is known as auto-unboxing. In this example, Java automatically casts (autoboxes) the primitive value 17 to be of type Integer when we pass it to thepush() method. The pop() method returns an Integer, which Java casts (auto-unboxes) to an int before assigning it to the variable i.
Iterable collections
For many applications, the client’s requirement is just to process each of the items in some way, or to iterate through the items in the collection. This paradigm is so important that it has achieved first-class status in Java and many other modern languages (the programming language itself has specific mechanisms to support it, not just the libraries). With it, we can write clear and compact code that is free from dependence on the details of a collection’s implementation. For example, suppose that a client maintains a collection of transactions in a Queue, as follows:
Queue<Transaction> collection = new Queue<Transaction>();
If the collection is iterable, the client can print a transaction list with a single statement:
for (Transaction t : collection)
{ StdOut.println(t); }
This construct is known as the foreach statement: you can read the for statement as for each transaction t in the collection, execute the following block of code. This client code does not need to know anything about the representation or the implementation of the collection; it just wants to process each of the items in the collection. The same for loop would work with a Bag of transactions or any other iterable collection. We could hardly imagine client code that is more clear and compact. As you will see, supporting this capability requires extra effort in the implementation, but this effort is well worthwhile.
IT IS INTERESTING TO NOTE that the only differences between the APIs for Stack and Queue are their names and the names of the methods. This observation highlights the idea that we cannot easily specify all of the characteristics of a data type in a list of method signatures. In this case, the true specification has to do with the English-language descriptions that specify the rules by which an item is chosen to be removed (or to be processed next in the foreach statement). Differences in these rules are profound, part of the API, and certainly of critical importance in developing client code.
Bags
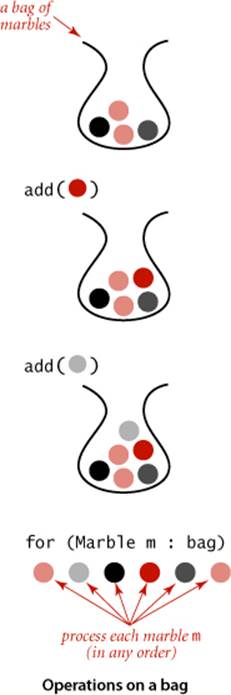
A bag is a collection where removing items is not supported—its purpose is to provide clients with the ability to collect items and then to iterate through the collected items (the client can also test if a bag is empty and find its number of items). The order of iteration is unspecified and should be immaterial to the client. To appreciate the concept, consider the idea of an avid marble collector, who might put marbles in a bag, one at a time, and periodically process all the marbles to look for one having some particular characteristic. With our Bag API, a client can add items to a bag and process them all with a foreach statement whenever needed. Such a client could use a stack or a queue, but one way to emphasize that the order in which items are processed is immaterial is to use a Bag. The class Stats at right illustrates a typical Bag client. The task is simply to compute the average and the sample standard deviation of the double values on standard input. If there are N numbers on standard input, their average is computed by adding the numbers and dividing by N; their sample standard deviation is computed by adding the squares of the difference between each number and the average, dividing by N–1, and taking the square root. The order in which the numbers are considered is not relevant for either of these calculations, so we save them in a Bag and use the foreach construct to compute each sum. Note: It is possible to compute the standard deviation without saving all the numbers (as we did for the average in Accumulator—see EXERCISE 1.2.18). Keeping the numbers in a Bag is required for more complicated statistics.

FIFO queues
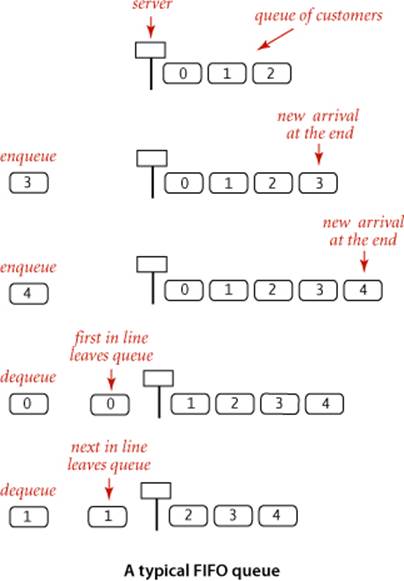
A FIFO queue (or just a queue) is a collection that is based on the first-in-first-out (FIFO) policy. The policy of doing tasks in the same order that they arrive is one that we encounter frequently in everyday life: from people waiting in line at a theater, to cars waiting in line at a toll booth, to tasks waiting to be serviced by an application on your computer. One bedrock principle of any service policy is the perception of fairness. The first idea that comes to mind when most people think about fairness is that whoever has been waiting the longest should be served first. That is precisely the FIFO discipline. Queues are a natural model for many everyday phenomena, and they play a central role in numerous applications. When a client iterates through the items in a queue with the foreach construct, the items are processed in the order they were added to the queue. A typical reason to use a queue in an application is to save items in a collection while at the same time preserving their relative order: they come out in the same order in which they were put in. For example, the client below is a possible implementation of the readInts() static method from our Inclass. The problem that this method solves for the client is that the client can get numbers from a file into an array without knowing the file size ahead of time. We enqueue the numbers from the file, use the size() method from Queue to find the size needed for the array, create the array, and thendequeue the numbers to move them to the array. A queue is appropriate because it puts the numbers into the array in the order in which they appear in the file (we might use a Bag if that order is immaterial). This code uses autoboxing and auto-unboxing to convert between the client’s intprimitive type and the queue’s Integer wrapper type.
Sample Queue client
public static int[] readInts(String name)
{
In in = new In(name);
Queue<Integer> q = new Queue<Integer>();
while (!in.isEmpty())
q.enqueue(in.readInt());
int N = q.size();
int[] a = new int[N];
for (int i = 0; i < N; i++)
a[i] = q.dequeue();
return a;
}
Pushdown stacks
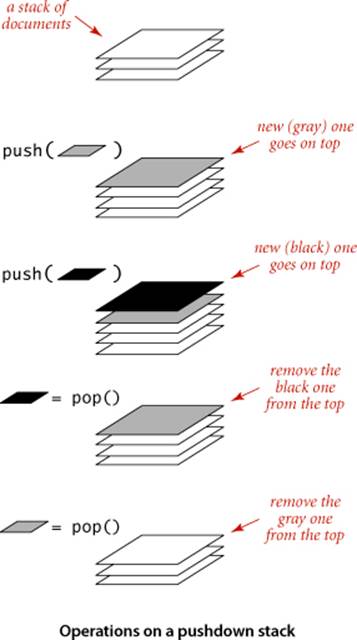
A pushdown stack (or just a stack) is a collection that is based on the last-in-first-out (LIFO) policy. When you keep your mail in a pile on your desk, you are using a stack. You pile pieces of new mail on the top when they arrive and take each piece of mail from the top when you are ready to read it. People do not process as many papers as they did in the past, but the same organizing principle underlies several of the applications that you use regularly on your computer. For example, many people organize their email as a stack—they push messages on the top when they are received and pop them from the top when they read them, with most recently received first (last in, first out). The advantage of this strategy is that we see interesting email as soon as possible; the disadvantage is that some old email might never get read if we never empty the stack. You have likely encountered another common example of a stack when surfing the web. When you click a hyperlink, your browser displays the new page (and pushes onto a stack). You can keep clicking on hyperlinks to visit new pages, but you can always revisit the previous page by clicking the back button (popping it from the stack). The LIFO policy offered by a stack provides just the behavior that you expect. When a client iterates through the items in a stack with the foreach construct, the items are processed in the reverse of the order in which they were added. A typical reason to use a stack iterator in an application is to save items in a collection while at the same time reversing their relative order. For example, the client Reverse at right reverses the order of the integers on standard input, again without having to know ahead of time how many there are. The importance of stacks in computing is fundamental and profound, as indicated in the detailed example that we consider next.
Sample Stack client
public class Reverse
{
public static void main(String[] args)
{
Stack<Integer> stack;
stack = new Stack<Integer>();
while (!StdIn.isEmpty())
stack.push(StdIn.readInt());
for (int i : stack)
StdOut.println(i);
}
}
Arithmetic expression evaluation
As another example of a stack client, we consider a classic example that also demonstrates the utility of generics. Some of the first programs that we considered in SECTION 1.1 involved computing the value of arithmetic expressions like this one:
( 1 + ( ( 2 + 3 ) * ( 4 * 5 ) ) )
If you multiply 4 by 5, add 3 to 2, multiply the result, and then add 1, you get the value 101. But how does the Java system do this calculation? Without going into the details of how the Java system is built, we can address the essential ideas by writing a Java program that can take a string as input (the expression) and produce the number represented by the expression as output. For simplicity, we begin with the following explicit recursive definition: an arithmetic expression is either a number, or a left parenthesis followed by an arithmetic expression followed by an operator followed by another arithmetic expression followed by a right parenthesis. For simplicity, this definition is for fully parenthesized arithmetic expressions, which specify precisely which operators apply to which operands—you are a bit more familiar with expressions such as 1 + 2 * 3, where we often rely on precedence rules instead of parentheses. The same basic mechanisms that we consider can handle precedence rules, but we avoid that complication. For specificity, we support the familiar binary operators *, +, -, and /, as well as a square-root operator sqrt that takes just one argument. We could easily allow more operators and more kinds of operators to embrace a large class of familiar mathematical expressions, involving trigonometric, exponential, and logarithmic functions. Our focus is on understanding how to interpret the string of parentheses, operators, and numbers to enable performing in the proper order the low-level arithmetic operations that are available on any computer. Precisely how can we convert an arithmetic expression—a string of characters—to the value that it represents? A remarkably simple algorithm that was developed by E. W. Dijkstra in the 1960s uses two stacks (one for operands and one for operators) to do this job. An expression consists of parentheses, operators, and operands (numbers). Proceeding from left to right and taking these entities one at a time, we manipulate the stacks according to four possible cases, as follows:
• Push operands onto the operand stack.
• Push operators onto the operator stack.
• Ignore left parentheses.
• On encountering a right parenthesis, pop an operator, pop the requisite number of operands, and push onto the operand stack the result of applying that operator to those operands.
After the final right parenthesis has been processed, there is one value on the stack, which is the value of the expression. This method may seem mysterious at first, but it is easy to convince yourself that it computes the proper value: any time the algorithm encounters a subexpression consisting of two operands separated by an operator, all surrounded by parentheses, it leaves the result of performing that operation on those operands on the operand stack. The result is the same as if that value had appeared in the input instead of the subexpression, so we can think of replacing the subexpression by the value to get an expression that would yield the same result. We can apply this argument again and again until we get a single value. For example, the algorithm computes the same value for all of these expressions:
( 1 + ( ( 2 + 3 ) * ( 4 * 5 ) ) )
( 1 + ( 5 * ( 4 * 5 ) ) )
( 1 + ( 5 * 20 ) )
( 1 + 100 )
101
Dijkstra’s Two-Stack Algorithm for Expression Evaluation
public class Evaluate
{
public static void main(String[] args)
{
Stack<String> ops = new Stack<String>();
Stack<Double> vals = new Stack<Double>();
while (!StdIn.isEmpty())
{ // Read token, push if operator.
String s = StdIn.readString();
if (s.equals("(")) ;
else if (s.equals("+")) ops.push(s);
else if (s.equals("-")) ops.push(s);
else if (s.equals("*")) ops.push(s);
else if (s.equals("/")) ops.push(s);
else if (s.equals("sqrt")) ops.push(s);
else if (s.equals(")"))
{ // Pop, evaluate, and push result if token is ")".
String op = ops.pop();
double v = vals.pop();
if (op.equals("+")) v = vals.pop() + v;
else if (op.equals("-")) v = vals.pop() - v;
else if (op.equals("*")) v = vals.pop() * v;
else if (op.equals("/")) v = vals.pop() / v;
else if (op.equals("sqrt")) v = Math.sqrt(v);
vals.push(v);
} // Token not operator or paren: push double value.
else vals.push(Double.parseDouble(s));
}
StdOut.println(vals.pop());
}
}
This Stack client uses two stacks to evaluate arithmetic expressions, illustrating an essential computational process: interpreting a string as a program and executing that program to compute the desired result. With generics, we can use the code in a single Stack implementation to implement one stack of String values and another stack of Double values. For simplicity, this code assumes that the expression is fully parenthesized, with numbers and characters separated by whitespace.
% java Evaluate
( 1 + ( ( 2 + 3 ) * ( 4 * 5 ) ) )
101.0
% java Evaluate
( ( 1 + sqrt ( 5.0 ) ) / 2.0 )
1.618033988749895
Evaluate on the previous page is an implementation of this algorithm. This code is a simple example of an interpreter: a program that interprets the computation specified by a given string and performs the computation to arrive at the result.

Implementing collections
To address the issue of implementing Bag, Stack and Queue, we begin with a simple classic implementation, then address improvements that lead us to implementations of the APIs articulated on page 121.
Fixed-capacity stack
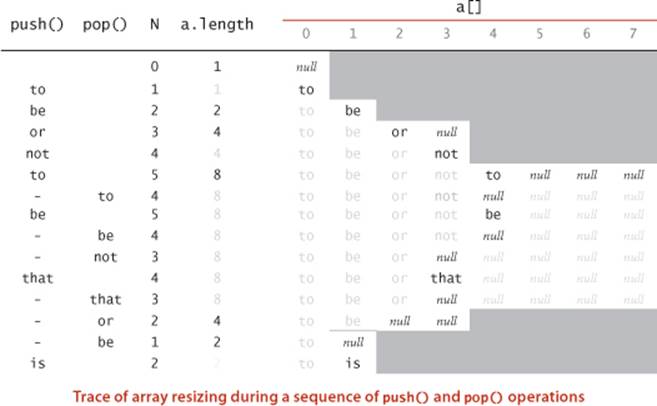
As a strawman, we consider an abstract data type for a fixed-capacity stack of strings, shown on the opposite page. The API differs from our Stack API: it works only for String values, it requires the client to specify a capacity, and it does not support iteration. The primary choice in developing an API implementation is to choose a representation for the data. For FixedCapacityStackOfStrings, an obvious choice is to use an array of String values. Pursuing this choice leads to the implementation shown at the bottom on the opposite page, which could hardly be simpler (each method is a one-liner). The instance variables are an array a[] that holds the items in the stack and an integer N that counts the number of items in the stack. To remove an item, we decrement N and then return a[N]; to insert a new item, we set a[N] equal to the new item and then increment N. These operations preserve the following properties:
• The items in the array are in their insertion order.
• The stack is empty when N is 0.
• The top of the stack (if it is nonempty) is at a[N-1].
As usual, thinking in terms of invariants of this sort is the easiest way to verify that an implementation operates as intended. Be sure that you fully understand this implementation. The best way to do so is to examine a trace of the stack contents for a sequence of operations, as illustrated at left for the test client, which reads strings from standard input and pushes each string onto a stack, unless it is "-", when it pops the stack and prints the result. The primary performance characteristic of this implementation is that the push and pop operations take time independent of the stack size. For many applications, it is the method of choice because of its simplicity. But it has several drawbacks that limit its potential applicability as a general-purpose tool, which we now address. With a moderate amount of effort (and some help from Java language mechanisms), we can develop an implementation that is broadly useful. This effort is worthwhile because the implementations that we develop serve as a model for implementations of other, more powerful, abstract data types throughout the book.



Generics
The first drawback of FixedCapacityStackOfStrings is that it works only for String objects. If we want a stack of double values, we would need to develop another class with similar code, essentially replacing String with double everywhere. This is easy enough but becomes burdensome when we consider building a stack of Transaction values or a queue of Date values, and so forth. As discussed on page 122, Java’s parameterized types (generics) are specifically designed to address this situation, and we saw several examples of client code (on pages 125, 126, 127, and 129). But how do weimplement a generic stack? The code on the facing page shows the details. It implements a class FixedCapacityStack that differs from FixedCapacityStackOfStrings only in the code highlighted in red—we replace every occurrence of String with Item (with one exception, discussed below) and declare the class with the following first line of code:
public class FixedCapacityStack<Item>
The name Item is a type parameter, a symbolic placeholder for some concrete type to be used by the client. You can read FixedCapacityStack<Item> as stack of items, which is precisely what we want. When implementing FixedCapacityStack, we do not know the actual type of Item, but a client can use our stack for any type of data by providing a concrete type when the stack is created. Concrete types must be reference types, but clients can depend on autoboxing to convert primitive types to their corresponding wrapper types. Java uses the type parameter Item to check for type mismatch errors—even though no concrete type is yet known, variables of type Item must be assigned values of type Item, and so forth. But there is one significant hitch in this story: We would like to implement the constructor in FixedCapacityStack with the code
a = new Item[cap];
which calls for creation of a generic array. For historical and technical reasons beyond our scope, generic array creation is disallowed in Java. Instead, we need to use a cast:
a = (Item[]) new Object[cap];
This code produces the desired effect (though the Java compiler gives a warning, which we can safely ignore), and we use this idiom throughout the book (the Java system library implementations of similar abstract data types use the same idiom).


Array resizing
Choosing an array to represent the stack contents implies that clients must estimate the maximum size of the stack ahead of time. In Java, we cannot change the size of an array once created, so the stack always uses space proportional to that maximum. A client that chooses a large capacity risks wasting a large amount of memory at times when the collection is empty or nearly empty. For example, a transaction system might involve billions of items and thousands of collections of them. Such a client would have to allow for the possibility that each of those collections could hold all of those items, even though a typical constraint in such systems is that each item can appear in only one collection. Moreover, every client risks overflow if the collection grows larger than the array. For this reason, push() needs code to test for a full stack, and we should have an isFull()method in the API to allow clients to test for that condition. We omit that code, because our desire is to relieve the client from having to deal with the concept of a full stack, as articulated in our original Stack API. Instead, we modify the array implementation to dynamically adjust the size of the array a[] so that it is both sufficiently large to hold all of the items and not so large as to waste an excessive amount of space. Achieving these goals turns out to be remarkably easy. First, we implement a method that moves a stack into an array of a different size:
private void resize(int max)
{ // Move stack of size N <= max to a new array of size max.
Item[] temp = (Item[]) new Object[max];
for (int i = 0; i < N; i++)
temp[i] = a[i];
a = temp;
}
Now, in push(), we check whether the array is too small. In particular, we check whether there is room for the new item in the array by checking whether the stack size N is equal to the array size a.length. If there is no room, we double the size of the array. Then we simply insert the new item with the code a[N++] = item, as before:
public void push(Item item)
{ // Add item to top of stack.
if (N == a.length) resize(2*a.length);
a[N++] = item;
}
Similarly, in pop(), we begin by deleting the item, then we halve the array size if it is too large. If you think a bit about the situation, you will see that the appropriate test is whether the stack size is less than one-fourth the array size. After the array is halved, it will be about half full and can accommodate a substantial number of push() and pop() operations before having to change the size of the array again.
public Item pop()
{ // Remove item from top of stack.
String item = a[--N];
a[N] = null; // Avoid loitering (see text).
if (N > 0 && N == a.length/4) resize(a.length/2);
return item;
}
With this implementation, the stack never overflows and never becomes less than one-quarter full (unless the stack is empty, when the array size is 2). We will address the performance analysis of this approach in more detail in SECTION 1.4.
Loitering
Java’s garbage collection policy is to reclaim the memory associated with any objects that can no longer be accessed. In our pop() implementations, the reference to the popped item remains in the array. The item is effectively an orphan—it will never be accessed again—but the Java garbage collector has no way to know this until it is overwritten. Even when the client is done with the item, the reference in the array may keep it alive. This condition (holding a reference to an item that is no longer needed) is known as loitering. In this case, loitering is easy to avoid, by setting the array entry corresponding to the popped item to null, thus overwriting the unused reference and making it possible for the system to reclaim the memory associated with the popped item when the client is finished with it.
Iteration
As mentioned earlier in this section, one of the fundamental operations on collections is to process each item by iterating through the collection using Java’s foreach statement. This paradigm leads to clear and compact code that is free from dependence on the details of a collection’s implementation. To consider the task of implementing iteration, we start with a snippet of client code that prints all of the items in a collection of strings, one per line:
Stack<String> collection = new Stack<String>();
...
for (String s : collection)
StdOut.println(s);
...
Now, this foreach statement is shorthand for a while construct (just like the for statement itself). It is essentially equivalent to the following while statement:
Iterator<String> i = collection.iterator();
while (i.hasNext())
{
String s = i.next();
StdOut.println(s);
}
This code exposes the ingredients that we need to implement in any iterable collection:
• The collection must implement an iterator() method that returns an Iterator object.
• The Iterator class must include two methods: hasNext() (which returns a boolean value) and next() (which returns a generic item from the collection).
In Java, we use the interface mechanism to express the idea that a class implements a specific method (see page 100). For iterable collections, the necessary interfaces are already defined for us in Java. To make a class iterable, the first step is to add the phrase implements Iterable<Item> to its declaration, matching the interface
public interface Iterable<Item>
{
Iterator<Item> iterator();
}
(which is in java.lang.Iterable), and to add a method iterator() to the class that returns an Iterator<Item>. Iterators are generic, so we can use our parameterized type Item to allow clients to iterate through objects of whatever type is provided by our client. For the array representation that we have been using, we need to iterate through an array in reverse order, so we name the iterator ReverseArrayIterator and add this method:
public Iterator<Item> iterator()
{ return new ReverseArrayIterator(); }
What is an iterator? An object from a class that implements the methods hasNext() and next(), as defined in the following interface (which is in java.util.Iterator):
public interface Iterator<Item>
{
boolean hasNext();
Item next();
void remove();
}
Although the interface specifies a remove() method, we always use an empty method for remove() in this book, because interleaving iteration with operations that modify the data structure is best avoided. For ReverseArrayIterator, these methods are all one-liners, implemented in a nested class within our stack class:
private class ReverseArrayIterator implements Iterator<Item>
{
private int i = N;
public boolean hasNext() { return i > 0; }
public Item next() { return a[--i]; }
public void remove() { }
}
Note that this nested class can access the instance variables of the enclosing class, in this case a[] and N (this ability is the main reason we use nested classes for iterators). Technically, to conform to the Iterator specification, we should throw exceptions in two cases: an UnsupportedOperationExceptionif a client calls remove() and a NoSuchElementException if a client calls next() when i is 0. Since we only use iterators in the foreach construction where these conditions do not arise, we omit this code. One crucial detail remains: we have to include
import java.util.Iterator;
at the beginning of the program because (for historical reasons) Iterator is not part of java.lang (even though Iterable is part of java.lang). Now a client using the foreach statement for this class will get behavior equivalent to the common for loop for arrays, but does not need to be aware of the array representation (an implementation detail). This arrangement is of critical importance for implementations of fundamental data types like the collections that we consider in this book and those included in Java libraries. For example, it frees us to switch to a totally different representationwithout having to change any client code. More important, taking the client’s point of view, it allows clients to use iteration without having to know any details of the class implementation.
ALGORITHM 1.1 is an implementation of our Stack API that resizes the array, allows clients to make stacks for any type of data, and supports client use of foreach to iterate through the stack items in LIFO order. This implementation is based on Java language nuances involving Iterator andIterable, but there is no need to study those nuances in detail, as the code itself is not complicated and can be used as a template for other collection implementations.
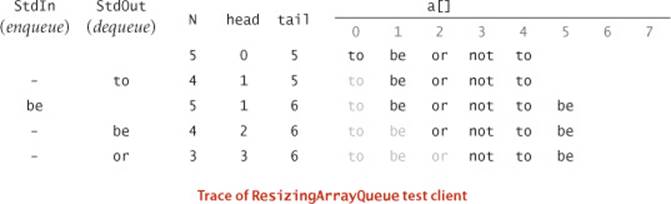
For example, we can implement the Queue API by maintaining two indices as instance variables, a variable head for the beginning of the queue and a variable tail for the end of the queue. To remove an item, use head to access it and then increment head; to insert an item, use tail to store it, and then increment tail. If incrementing an index brings it past the end of the array, reset it to 0. Developing the details of checking when the queue is empty and when the array is full and needs resizing is an interesting and worthwhile programming exercise (see EXERCISE 1.3.14).
In the context of the study of algorithms, ALGORITHM 1.1 is significant because it almost (but not quite) achieves optimum performance goals for any collection implementation:
• Each operation should require time independent of the collection size.
• The space used should always be within a constant factor of the collection size.
The flaw in ResizingArrayStack is that some push and pop operations require resizing: this takes time proportional to the size of the stack. Next, we consider a way to correct this flaw, using a fundamentally different way to structure data.
Algorithm 1.1 Pushdown (LIFO) stack (resizing array implementation)
import java.util.Iterator;
public class ResizingArrayStack<Item> implements Iterable<Item>
{
private Item[] a = (Item[]) new Object[1]; // stack items
private int N = 0; // number of items
public boolean isEmpty() { return N == 0; }
public int size() { return N; }
private void resize(int max)
{ // Move stack to a new array of size max.
Item[] temp = (Item[]) new Object[max];
for (int i = 0; i < N; i++)
temp[i] = a[i];
a = temp;
}
public void push(Item item)
{ // Add item to top of stack.
if (N == a.length) resize(2*a.length);
a[N++] = item;
}
public Item pop()
{ // Remove item from top of stack.
Item item = a[--N];
a[N] = null; // Avoid loitering (see text).
if (N > 0 && N == a.length/4) resize(a.length/2);
return item;
}
public Iterator<Item> iterator()
{ return new ReverseArrayIterator(); }
private class ReverseArrayIterator implements Iterator<Item>
{ // Support LIFO iteration.
private int i = N;
public boolean hasNext() { return i > 0; }
public Item next() { return a[--i]; }
public void remove() { }
}
}
This generic, iterable implementation of our Stack API is a model for collection ADTs that keep items in an array. It resizes the array to keep the array size within a constant factor of the stack size.
Linked lists
Now we consider the use of a fundamental data structure that is an appropriate choice for representing the data in a collection ADT implementation. This is our first example of building a data structure that is not directly supported by the Java language. Our implementation serves as a model for the code that we use for building more complex data structures throughout the book, so you should read this section carefully, even if you have experience working with linked lists.
Definition. A linked list is a recursive data structure that is either empty (null) or a reference to a node having a generic item and a reference to a linked list.
The node in this definition is an abstract entity that might hold any kind of data, in addition to the node reference that characterizes its role in building linked lists. As with a recursive program, the concept of a recursive data structure can be a bit mindbending at first, but is of great value because of its simplicity.
Node record
With object-oriented programming, implementing linked lists is not difficult. We start with a nested class that defines the node abstraction:
private class Node
{
Item item;
Node next;
}
A Node has two instance variables: an Item (a parameterized type) and a Node. We define Node within the class where we want to use it, and make it private because it is not for use by clients. As with any data type, we create an object of type Node by invoking the (no-argument) constructor with new Node(). The result is a reference to a Node object whose instance variables are both initialized to the value null. The Item is a placeholder for any data that we might want to structure with a linked list (we will use Java’s generic mechanism so that it can represent any reference type); the instance variable of type Node characterizes the linked nature of the data structure. To emphasize that we are just using the Node class to structure the data, we define no methods and we refer directly to the instance variables in code: if first is a variable associated with an object of type Node, we can refer to the instance variables with the code first.item and first.next. Classes of this kind are sometimes called records. They do not implement abstract data types because we refer directly to instance variables. However, Node and its client code are in the same class in all of our implementations and not accessible by clients of that class, so we still enjoy the benefits of data abstraction.
Building a linked list
Now, from the recursive definition, we can represent a linked list with a variable of type Node simply by ensuring that its value is either null or a reference to a Node whose next field is a reference to a linked list. For example, to build a linked list that contains the items to, be, and or, we create aNode for each item:
Node first = new Node();
Node second = new Node();
Node third = new Node();
and set the item field in each of the nodes to the desired value (for simplicity, these examples assume that Item is String):
first.item = "to";
second.item = "be";
third.item = "or";
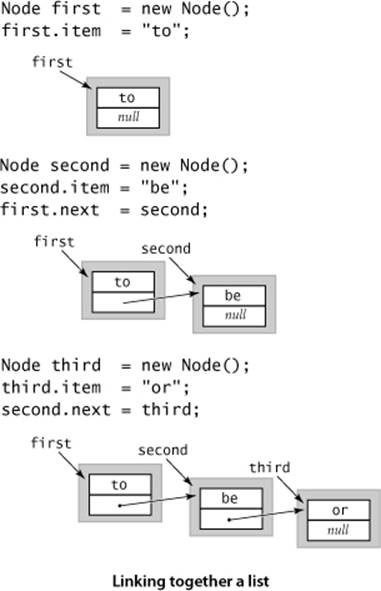
and set the next fields to build the linked list:
first.next = second;
second.next = third;
(Note that third.next remains null, the value it was initialized to at the time of creation.) As a result, third is a linked list (it is a reference to a node that has a reference to null, which is the null reference to an empty linked list), and second is a linked list (it is a reference to a node that has a reference to third, which is a linked list), and first is a linked list (it is a reference to a node that has a reference to second, which is a linked list). The code that we will examine does these assignment statements in a different order, depicted in the diagram on this page.
A LINKED LIST REPRESENTS A SEQUENCE of items. In the example just considered, first represents the sequence to be or. We can also use an array to represent a sequence of items. For example, we could use
String[] s = { "to", "be", "or" };
to represent the same sequence of strings. The difference is that it is easier to insert items into the sequence and to remove items from the sequence with linked lists. Next, we consider code to accomplish these tasks.
When tracing code that uses linked lists and other linked structures, we use a visual representation where
• We draw a rectangle to represent each object
• We put the values of instance variables within the rectangle
• We use arrows that point to the referenced objects to depict references
This visual representation captures the essential characteristic of linked lists. For economy, we use the term links to refer to node references. For simplicity, when item values are strings (as in our examples), we put the string within the object rectangle rather than the more accurate rendition depicting the string object and the character array that we discussed in SECTION 1.2. This visual representation allows us to focus on the links.
Insert at the beginning
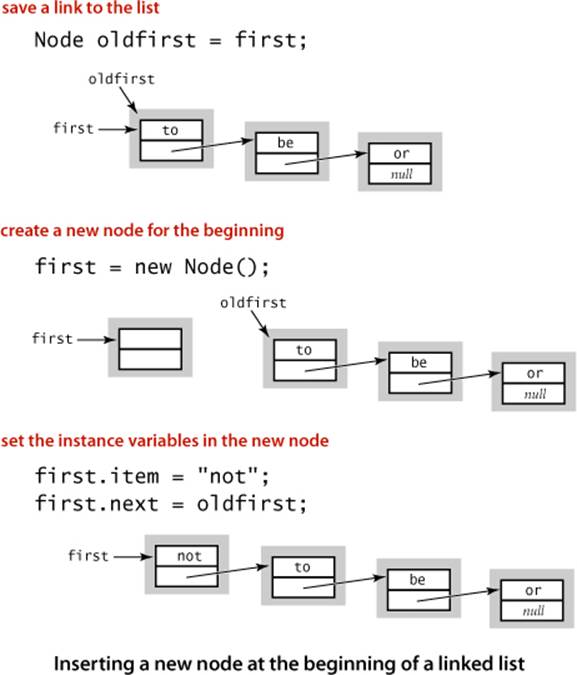
First, suppose that you want to insert a new node into a linked list. The easiest place to do so is at the beginning of the list. For example, to insert the string not at the beginning of a given linked list whose first node is first, we save first in oldfirst, assign to first a new Node, and assign its itemfield to not and its next field to oldfirst. This code for inserting a node at the beginning of a linked list involves just a few assignment statements, so the amount of time that it takes is independent of the length of the list.
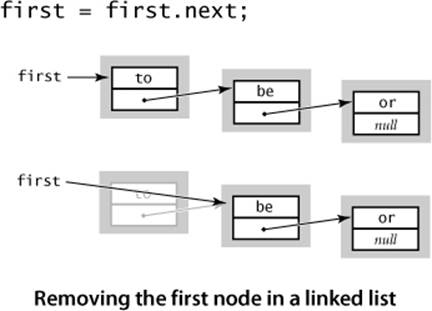
Remove from the beginning
Next, suppose that you want to remove the first node from a list. This operation is even easier: simply assign to first the value first.next. Normally, you would retrieve the value of the item (by assigning it to some variable of type Item) before doing this assignment, because once you change the value of first, you may not have any access to the node to which it was referring. Typically, the node object becomes an orphan, and the Java memory management system eventually reclaims the memory it occupies. Again, this operation just involves one assignment statement, so its running time is independent of the length of the list.
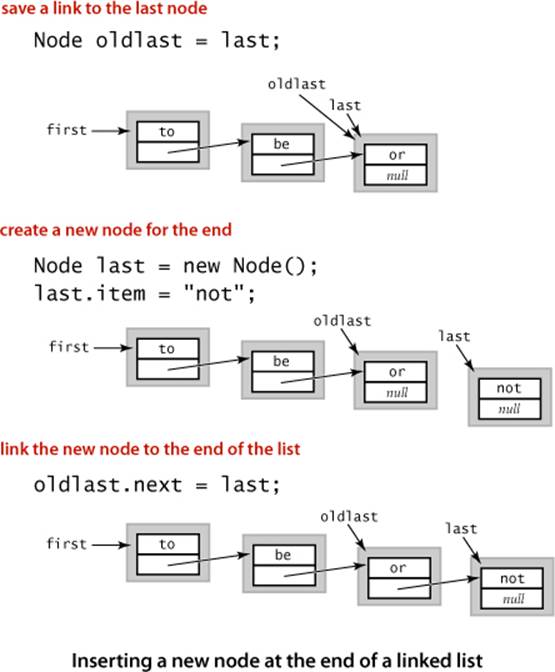
Insert at the end
How do we add a node to the end of a linked list? To do so, we need a link to the last node in the list, because that node’s link has to be changed to reference a new node containing the item to be inserted. Maintaining an extra link is not something that should be taken lightly in linked-list code, because every method that modifies the list needs code to check whether that variable needs to be modified (and to make the necessary modifications). For example, the code that we just examined for removing the first node in the list might involve changing the reference to the last node in the list, since when there is only one node in the list, it is both the first one and the last one! Also, this code does not work (it follows a null link) in the case that the list is empty. Details like these make linked-list code notoriously difficult to debug.
Insert/remove at other positions
In summary, we have shown that we can implement the following operations on linked lists with just a few instructions, provided that we have access to both a link first to the first element in the list and a link last to the last element in the list:
• Insert at the beginning.
• Remove from the beginning.
• Insert at the end.
Other operations, such as the following, are not so easily handled:
• Remove a given node.
• Insert a new node before a given node.
For example, how can we remove the last node from a list? The link last is no help, because we need to set the link in the previous node in the list (the one with the same value as last) to null. In the absence of any other information, the only solution is to traverse the entire list looking for the node that links to last (see below and EXERCISE 1.3.19). Such a solution is undesirable because it takes time proportional to the length of the list. The standard solution to enable arbitrary insertions and deletions is to use a doubly-linked list, where each node has two links, one in each direction. We leave the code for these operations as an exercise (see EXERCISE 1.3.31). We do not need doubly linked lists for any of our implementations.
Traversal
To examine every item in an array, we use familiar code like the following loop for processing the items in an array a[]:
for (int i = 0; i < N; i++)
{
// Process a[i].
}
There is a corresponding idiom for examining the items in a linked list: We initialize a loop index variable x to reference the first Node of the linked list. Then we find the item associated with x by accessing x.item, and then update x to refer to the next Node in the linked list, assigning to it the value of x.next and repeating this process until x is null (which indicates that we have reached the end of the linked list). This process is known as traversing the list and is succinctly expressed in code like the following loop for processing the items in a linked list whose first item is associated with the variable first:
for (Node x = first; x != null; x = x.next)
{
// Process x.item.
}
This idiom is as natural as the standard idiom for iterating through the items in an array. In our implementations, we use it as the basis for iterators for providing client code the capability of iterating through the items, without having to know the details of the linked-list implementation.
Stack implementation
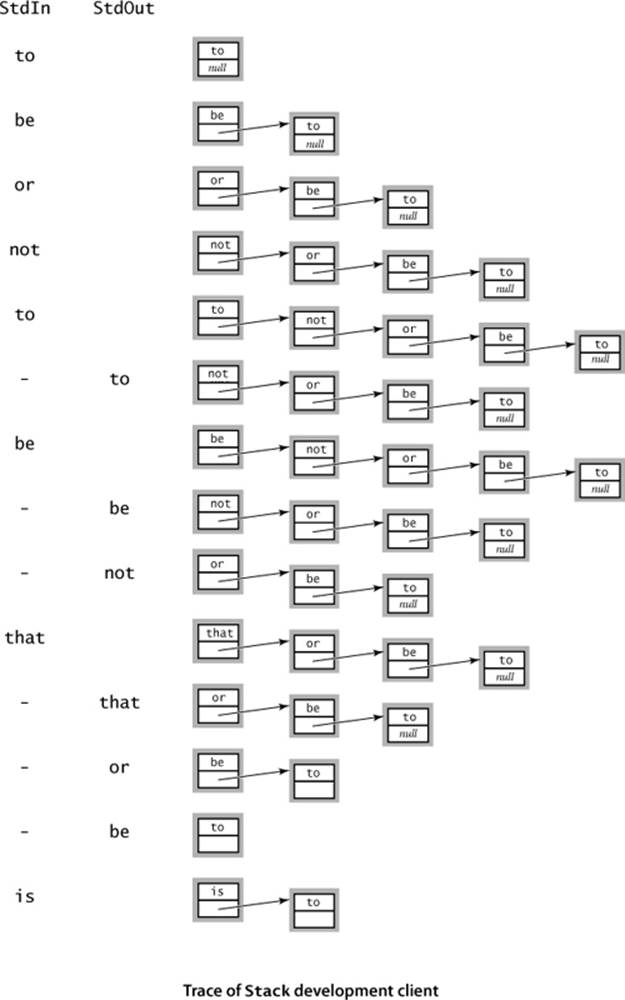
Given these preliminaries, developing an implementation for our Stack API is straightforward, as shown in ALGORITHM 1.2 on page 149. It maintains the stack as a linked list, with the top of the stack at the beginning, referenced by an instance variable first. Thus, to push() an item, we add it to the beginning of the list, using the code discussed on page 144 and to pop() an item, we remove it from the beginning of the list, using the code discussed on page 145. To implement size(), we keep track of the number of items in an instance variable N, incrementing N when we push and decrementing N when we pop. To implement isEmpty() we check whether first is null (alternatively, we could check whether N is 0). The implementation uses the generic type Item—you can think of the code <Item> after the class name as meaning that any occurrence of Item in the implementation will be replaced by a client-supplied data-type name (see page 134). For now, we omit the code to support iteration, which we consider on page 155. A trace for the test client that we have been using is shown on the next page. This use of linked lists achieves our optimum design goals:
• It can be used for any type of data.
• The space required is always proportional to the size of the collection.
• The time per operation is always independent of the size of the collection.
This implementation is a prototype for many algorithm implementations that we consider. It defines the linked-list data structure and implements the client methods push() and pop() that achieve the specified effect with just a few lines of code. The algorithms and data structure go hand in hand. In this case, the code for the algorithm implementations is quite simple, but the properties of the data structure are not at all elementary, requiring explanations on the past several pages. This interaction between data structure definition and algorithm implementation is typical and is our focus in ADT implementations throughout this book.
Test client for Stack
public static void main(String[] args)
{ // Create a stack and push/pop strings as directed on StdIn.
Stack<String> s = new Stack<String>();
while (!StdIn.isEmpty())
{
String item = StdIn.readString();
if (!item.equals("-"))
s.push(item);
else if (!s.isEmpty()) StdOut.print(s.pop() + " ");
}
StdOut.println("(" + s.size() + " left on stack)");
}
Algorithm 1.2 Pushdown stack (linked-list implementation)
public class Stack<Item> implements Iterable<Item>
{
private Node first; // top of stack (most recently added node)
private int N; // number of items
private class Node
{ // nested class to define nodes
Item item;
Node next;
}
public boolean isEmpty() { return first == null; }
public int size() { return N; }
public void push(Item item)
{ // Add item to top of stack.
Node oldfirst = first;
first = new Node();
first.item = item;
first.next = oldfirst;
N++;
}
public Item pop()
{ // Remove item from top of stack.
Item item = first.item;
first = first.next;
N--;
return item;
}
// See page 155 for iterator() implementation.
// See page 147 for test client main().
}
This generic Stack implementation is based on a linked-list data structure. It can be used to create stacks containing any type of data. To support iteration, add the highlighted code described for Bag on page 155.
% more tobe.txt
to be or not to - be - - that - - - is
% java Stack < tobe.txt
to be not that or be (2 left on stack)
Queue implementation
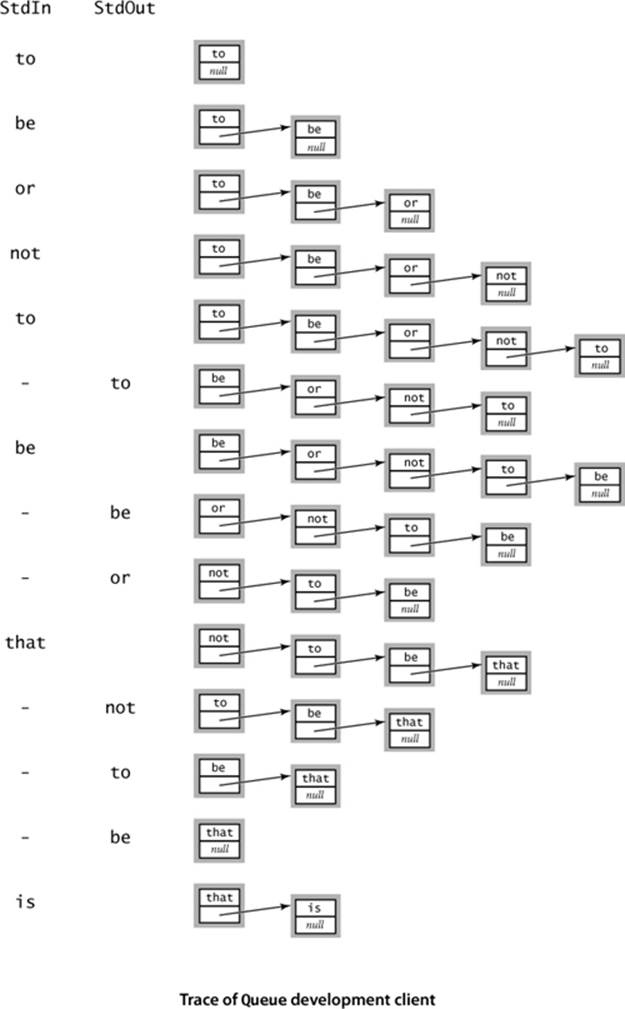
An implementation of our Queue API based on the linked-list data structure is also straightforward, as shown in ALGORITHM 1.3 on the facing page. It maintains the queue as a linked list in order from least recently to most recently added items, with the beginning of the queue referenced by an instance variable first and the end of the queue referenced by an instance variable last. Thus, to enqueue() an item, we add it to the end of the list (using the code discussed on page 145, augmented to set both first and last to refer to the new node when the list is empty) and to dequeue() an item, we remove it from the beginning of the list (using the same code as for pop() in Stack, augmented to update last when the list becomes empty). The implementations of size() and isEmpty() are the same as for Stack. As with Stack the implementation uses the generic type parameter Item, and we omit the code to support iteration, which we consider in our Bag implementation on page 155. A development client similar to the one we used for Stack is shown below, and the trace for this client is shown on the following page. This implementation uses the same data structure as does Stack—a linked list—but it implements different algorithms for adding and removing items, which make the difference between LIFO and FIFO for the client. Again, the use of linked lists achieves our optimum design goals: it can be used for any type of data, the space required is proportional to the number of items in the collection, and the time required per operation is always independent of the size of the collection.
Test client for Queue
public static void main(String[] args)
{ // Create a queue and enqueue/dequeue strings.
Queue<String> q = new Queue<String>();
while (!StdIn.isEmpty())
{
String item = StdIn.readString();
if (!item.equals("-"))
q.enqueue(item);
else if (!q.isEmpty()) StdOut.print(q.dequeue() + " ");
}
StdOut.println("(" + q.size() + " left on queue)");
}
% more tobe.txt
to be or not to - be - - that - - - is
% java Queue < tobe.txt
to be or not to be (2 left on queue)
Algorithm 1.3 FIFO queue
public class Queue<Item> implements Iterable<Item>
{
private Node first; // link to least recently added node
private Node last; // link to most recently added node
private int N; // number of items on the queue
private class Node
{ // nested class to define nodes
Item item;
Node next;
}
public boolean isEmpty() { return first == null; }
public int size() { return N; }
public void enqueue(Item item)
{ // Add item to the end of the list.
Node oldlast = last;
last = new Node();
last.item = item;
last.next = null;
if (isEmpty()) first = last;
else oldlast.next = last;
N++;
}
public Item dequeue()
{ // Remove item from the beginning of the list.
Item item = first.item;
first = first.next;
N--;
if (isEmpty()) last = null;
return item;
}
// See page 155 for iterator() implementation.
// See page 150 for test client main().
}
This generic Queue implementation is based on a linked-list data structure. It can be used to create queues containing any type of data. To support iteration, add the highlighted code described for Bag on page 155.
LINKED LISTS ARE A FUNDAMENTAL ALTERNATIVE to arrays for structuring a collection of data. From a historical perspective, this alternative has been available to programmers for many decades. Indeed, a landmark in the history of programming languages was the development of LISP by John McCarthy in the 1950s, where linked lists are the primary structure for programs and data. Programming with linked lists presents all sorts of challenges and is notoriously difficult to debug, as you can see in the exercises. In modern code, the use of safe pointers, automatic garbage collection (see page 111), and ADTs allows us to encapsulate list-processing code in just a few classes such as the ones presented here.
Bag implementation
Implementing our Bag API using a linked-list data structure is simply a matter of changing the name of push() in Stack to add() and removing the implementation of pop(), as shown in ALGORITHM 1.4 on the facing page (doing the same for Queue would also be effective but requires a bit more code). This implementation also highlights the code needed to make Stack, Queue, and Bag all iterable, by traversing the list. For Stack the list is in LIFO order; for Queue it is in FIFO order; and for Bag it happens to be in LIFO order, but the order is not relevant. As detailed in the highlighted code inALGORITHM 1.4, to implement iteration in a collection, the first step is to include
import java.util.Iterator;
so that our code can refer to Java’s Iterator interface. The second step is to add
implements Iterable<Item>
to the class declaration, a promise to provide an iterator() method. The iterator() method itself simply returns an object from a class that implements the Iterator interface:
public Iterator<Item> iterator()
{ return new ListIterator(); }
This code is a promise to implement a class that implements the hasNext(), next(), and remove() methods that are called when a client uses the foreach construct. To implement these methods, the nested class ListIterator in ALGORITHM 1.4 maintains an instance variable current that keeps track of the current node on the list. Then the hasNext() method tests if current is null, and the next() method saves a reference to the current item, updates current to refer to the next node on the list, and returns the saved reference.
Algorithm 1.4 Bag
import java.util.Iterator;
public class Bag<Item> implements Iterable<Item>
{
private Node first; // first node in list
private class Node
{
Item item;
Node next;
}
public void add(Item item)
{ // same as push() in Stack
Node oldfirst = first;
first = new Node();
first.item = item;
first.next = oldfirst;
}
public Iterator<Item> iterator()
{ return new ListIterator(); }
private class ListIterator implements Iterator<Item>
{
private Node current = first;
public boolean hasNext()
{ return current != null; }
public void remove() { }
public Item next()
{
Item item = current.item;
current = current.next;
return item;
}
}
}
This Bag implementation maintains a linked list of the items provided in calls to add(). Code for isEmpty() and size() is the same as in Stack and is omitted. The iterator traverses the list, maintaining the current node in current. We can make Stack and Queue iterable by adding the code highlighted in red to ALGORITHMS 1.2 and ALGORITHMS 1.3, because they use the same underlying data structure and Stack and Queue maintain the list in LIFO and FIFO order, respectively.
Overview
The implementations of bags, queues, and stacks that support generics and iteration that we have considered in this section provide a level of abstraction that allows us to write compact client programs that manipulate collections of objects. Detailed understanding of these ADTs is important as an introduction to the study of algorithms and data structures for three reasons. First, we use these data types as building blocks in higher-level data structures throughout this book. Second, they illustrate the interplay between data structures and algorithms and the challenge of simultaneously achieving natural performance goals that may conflict. Third, the focus of several of our implementations is on ADTs that support more powerful operations on collections of objects, and we use the implementations here as starting points.
Data structures
We now have two ways to represent collections of objects, arrays and linked lists. Arrays are built into Java; linked lists are easy to build with standard Java records. These two alternatives, often referred to as sequential allocation and linked allocation, are fundamental. Later in the book, we develop ADT implementations that combine and extend these basic structures in numerous ways. One important extension is to data structures with multiple links. For example, our focus in SECTIONS 3.2 and 3.3 is on data structures known as binary trees that are built from nodes that each have two links. Another important extension is to compose data structures: we can have a bag of stacks, a queue of arrays, and so forth. For example, our focus in CHAPTER 4 is on graphs, which we represent as arrays of bags. It is very easy to define data structures of arbitrary complexity in this way: one important reason for our focus on abstract data types is an attempt to control such complexity.

OUR TREATMENT OF BAGS, QUEUES, AND STACKS in this section is a prototypical example of the approach that we use throughout this book to describe data structures and algorithms. In approaching a new applications domain, we identify computational challenges and use data abstraction to address them, proceeding as follows:
• Specify an API.
• Develop client code with reference to specific applications.
• Describe a data structure (representation of the set of values) that can serve as the basis for the instance variables in a class that will implement an ADT that meets the specification in the API.
• Describe algorithms (approaches to implementing the set of operations) that can serve as the basis for implementing the instance methods in the class.
• Analyze the performance characteristics of the algorithms.
In the next section, we consider this last step in detail, as it often dictates which algorithms and implementations can be most useful in addressing real-world applications.
Q&A
Q. Not all programming languages have generics, even early versions of Java. What are the alternatives?
A. One alternative is to maintain a different implementation for each type of data, as mentioned in the text. Another is to build a stack of Object values, then cast to the desired type in client code for pop(). The problem with this approach is that type mismatch errors cannot be detected until run time. But with generics, if you write code to push an object of the wrong type on the stack, like this:
Stack<Apple> stack = new Stack<Apple>();
Apple a = new Apple();
...
Orange b = new Orange();
...
stack.push(a);
...
stack.push(b); // compile-time error
you will get a compile-time error:
push(Apple) in Stack<Apple> cannot be applied to (Orange)
This ability to discover such errors at compile time is reason enough to use generics.
Q. Why does Java disallow generic arrays?
A. Experts still debate this point. You might need to become one to understand it! For starters, learn about covariant arrays and type erasure.
Q. How do I create an array of stacks of strings?
A. Use a cast, such as the following:
Stack<String>[] a = (Stack<String>[]) new Stack[N];
Warning: This cast, in client code, is different from the one described on page 134. You might have expected to use Object instead of Stack. When using generics, Java checks for type safety at compile time, but throws away that information at run time, so it is left with Stack<Object>[] or just Stack[], for short, which we must cast to Stack<String>[].
Q. What happens if my program calls pop() for an empty stack?
A. It depends on the implementation. For our implementation on page 149, you will get a NullPointerException. In our implementations on the booksite, we throw a runtime exception to help users pinpoint the error. Generally, including as many such checks as possible is wise in code that is likely to be used by many people.
Q. Why do we care about resizing arrays, when we have linked lists?
A. We will see several examples of ADT implementations that need to use arrays to perform other operations that are not easily supported with linked lists. ResizingArrayStack is a model for keeping their memory usage under control.
Q. Why declare Node as a nested class? Why private?
A. By declaring the nested class Node to be private, we restrict its access to methods and instance variables within the enclosing class. One characteristic of a private nested class is that its instance variables can be directly accessed from within the enclosing class but nowhere else, so there is no need to declare the instance variables public or private. Note for experts: A nested class that is not static is known as an inner class, so technically our Node classes are inner classes.
Q. When I type javac Stack.java to compile ALGORITHM 1.2 and similar programs, I find Stack.class and a file Stack$Node.class. What is the purpose of that second one?
A. That file is for the inner class Node. Java’s naming convention is to use $ to separate the name of the outer class from the inner class.
Q. Are there Java libraries for stacks and queues?
A. Yes and no. Java has a built-in library called java.util.Stack, but you should avoid using it when you want a stack. It has several additional operations that are not normally associated with a stack, e.g., getting the ith element. It also allows adding an element to the bottom of the stack (instead of the top), so it can implement a queue! Although having such extra operations may appear to be a bonus, it is actually a curse. We use data types not just as libraries of all the operations we can imagine, but also as a mechanism to precisely specify the operations we need. The prime benefit of doing so is that the system can prevent us from performing operations that we do not actually want. The java.util.Stack API is an example of a wide interface, which we generally strive to avoid.
Q. Should a client be allowed to insert null items onto a stack or queue?
A. This question arises frequently when implementing collections in Java. Our implementation (and Java’s stack and queue libraries) do permit the insertion of null values.
Q. What should the Stack iterator do if the client calls push() or pop() during iterator?
A. Throw a java.util.ConcurrentModificationException to make it a fail-fast iterator. See Exercise 1.3.50.
Q. Can I use a foreach loop with arrays?
A. Yes (even though arrays do not implement the Iterable interface). The following one-liner prints out the command-line arguments:
public static void main(String[] args)
{ for (String s : args) StdOut.println(s); }
Q. Can I use a foreach loop with strings?
A. No. String does not implement Iterable.
Q. Why not have a single Collection data type that implements methods to add items, remove the most recently inserted, remove the least recently inserted, remove random, iterate, return the number of items in the collection, and whatever other operations we might desire? Then we could get them all implemented in a single class that could be used by many clients.
A. Again, this is an example of a wide interface. Java has such implementations in its java.util.ArrayList and java.util.LinkedList classes. One reason to avoid them is that there is no assurance that all operations are implemented efficiently. Throughout this book, we use APIs as starting points for designing efficient algorithms and data structures, which is certainly easier to do for interfaces with just a few operations as opposed to an interface with many operations. Another reason to insist on narrow interfaces is that they enforce a certain discipline on client programs, which makes client code much easier to understand. If one client uses Stack<String> and another uses Queue<Transaction>, we have a good idea that the LIFO discipline is important to the first and the FIFO discipline is important to the second.
Exercises
1.3.1 Add a method isFull() to FixedCapacityStackOfStrings.
1.3.2 Give the output printed by java Stack for the input
it was - the best - of times - - - it was - the - -
1.3.3 Suppose that a client performs an intermixed sequence of (stack) push and pop operations. The push operations put the integers 0 through 9 in order onto the stack; the pop operations print out the return values. Which of the following sequence(s) could not occur?
a. 4 3 2 1 0 9 8 7 6 5
b. 4 6 8 7 5 3 2 9 0 1
c. 2 5 6 7 4 8 9 3 1 0
d. 4 3 2 1 0 5 6 7 8 9
e. 1 2 3 4 5 6 9 8 7 0
f. 0 4 6 5 3 8 1 7 2 9
g. 1 4 7 9 8 6 5 3 0 2
h. 2 1 4 3 6 5 8 7 9 0
1.3.4 Write a stack client Parentheses that reads in a text stream from standard input and uses a stack to determine whether its parentheses are properly balanced. For example, your program should print true for [()]{}{[()()]()} and false for [(]).
1.3.5 What does the following code fragment print when N is 50? Give a high-level description of what it does when presented with a positive integer N.
Stack<Integer> stack = new Stack<Integer>();
while (N > 0)
{
stack.push(N % 2);
N = N / 2;
}
for (int d : stack) StdOut.print(d);
StdOut.println();
Answer: Prints the binary representation of N (110010 when N is 50).
1.3.6 What does the following code fragment do to the queue q?
Stack<String> stack = new Stack<String>();
while (!q.isEmpty())
stack.push(q.dequeue());
while (!stack.isEmpty())
q.enqueue(stack.pop());
1.3.7 Add a method peek() to Stack that returns the most recently inserted item on the stack (without popping it).
1.3.8 Give the contents and size of the array for ResizingArrayStackOfStrings with the input
it was - the best - of times - - - it was - the - -
1.3.9 Write a program that takes from standard input an expression without left parentheses and prints the equivalent infix expression with the parentheses inserted. For example, given the input:
1 + 2 ) * 3 - 4 ) * 5 - 6 ) ) )
your program should print
( ( 1 + 2 ) * ( ( 3 - 4 ) * ( 5 - 6 ) ) )
1.3.10 Write a filter InfixToPostfix that converts an arithmetic expression from infix to postfix.
1.3.11 Write a program EvaluatePostfix that takes a postfix expression from standard input, evaluates it, and prints the value. (Piping the output of your program from the previous exercise to this program gives equivalent behavior to Evaluate.)
1.3.12 Write an iterable Stack client that has a static method copy() that takes a stack of strings as argument and returns a copy of the stack. Note: This ability is a prime example of the value of having an iterator, because it allows development of such functionality without changing the basic API.
1.3.13 Suppose that a client performs an intermixed sequence of (queue) enqueue and dequeue operations. The enqueue operations put the integers 0 through 9 in order onto the queue; the dequeue operations print out the return value. Which of the following sequence(s) could not occur?
a. 0 1 2 3 4 5 6 7 8 9
b. 4 6 8 7 5 3 2 9 0 1
c. 2 5 6 7 4 8 9 3 1 0
d. 4 3 2 1 0 5 6 7 8 9
1.3.14 Develop a class ResizingArrayQueueOfStrings that implements the queue abstraction with a fixed-size array, and then extend your implementation to use array resizing to remove the size restriction.
1.3.15 Write a Queue client that takes a command-line argument k and prints the kth from the last string found on standard input (assuming that standard input has k or more strings).
1.3.16 Using readInts() on page 126 as a model, write a static method readDates() for Date that reads dates from standard input in the format specified in the table on page 119 and returns an array containing them.
1.3.17 Do EXERCISE 1.3.16 for Transaction.
Linked-List Exercises
This list of exercises is intended to give you experience in working with linked lists. Suggestion: make drawings using the visual representation described in the text.
1.3.18 Suppose x is a linked-list node and not the last node on the list. What is the effect of the following code fragment?
x.next = x.next.next;
Answer: Deletes from the list the node immediately following x.
1.3.19 Give a code fragment that removes the last node in a linked list whose first node is first.
1.3.20 Write a method delete() that takes an int argument k and deletes the kth element in a linked list, if it exists.
1.3.21 Write a method find() that takes a linked list and a string key as arguments and returns true if some node in the list has key as its item field, false otherwise.
1.3.22 Suppose that x is a linked list Node. What does the following code fragment do?
t.next = x.next;
x.next = t;
Answer: Inserts node t immediately after node x.
1.3.23 Why does the following code fragment not do the same thing as in the previous question?
x.next = t;
t.next = x.next;
Answer: When it comes time to update t.next, x.next is no longer the original node following x, but is instead t itself!
1.3.24 Write a method removeAfter() that takes a linked-list Node as argument and removes the node following the given one (and does nothing if the argument or the next field in the argument node is null).
1.3.25 Write a method insertAfter() that takes two linked-list Node arguments and inserts the second after the first on its list (and does nothing if either argument is null).
1.3.26 Write a method remove() that takes a linked list and a string key as arguments and removes all of the nodes in the list that have key as its item field.
1.3.27 Write a method max() that takes a reference to the first node in a linked list as argument and returns the value of the maximum key in the list. Assume that all keys are positive integers, and return 0 if the list is empty.
1.3.28 Develop a recursive solution to the previous question.
1.3.29 Write a Queue implementation that uses a circular linked list, which is the same as a linked list except that no links are null and the value of last.next is first whenever the list is not empty. Keep only one Node instance variable (last).
1.3.30 Write a function that takes the first Node in a linked list as argument and (destructively) reverses the list, returning the first Node in the result.
Iterative solution: To accomplish this task, we maintain references to three consecutive nodes in the linked list, reverse, first, and second. At each iteration, we extract the node first from the original linked list and insert it at the beginning of the reversed list. We maintain the invariant that first is the first node of what’s left of the original list, second is the second node of what’s left of the original list, and reverse is the first node of the resulting reversed list.
public Node reverse(Node x)
{
Node first = x;
Node reverse = null;
while (first != null)
{
Node second = first.next;
first.next = reverse;
reverse = first;
first = second;
}
return reverse;
}
When writing code involving linked lists, we must always be careful to properly handle the exceptional cases (when the linked list is empty, when the list has only one or two nodes) and the boundary cases (dealing with the first or last items). This is usually much trickier than handling the normal cases.
Recursive solution: Assuming the linked list has N nodes, we recursively reverse the last N–1 nodes, and then carefully append the first node to the end.
public Node reverse(Node first)
{
if (first == null) return null;
if (first.next == null) return first;
Node second = first.next;
Node rest = reverse(second);
second.next = first;
first.next = null;
return rest;
}
1.3.31 Implement a nested class DoubleNode for building doubly-linked lists, where each node contains a reference to the item preceding it and the item following it in the list (null if there is no such item). Then implement static methods for the following tasks: insert at the beginning, insert at the end, remove from the beginning, remove from the end, insert before a given node, insert after a given node, and remove a given node.
Creative Problems
1.3.32 Steque. A stack-ended queue or steque is a data type that supports push, pop, and enqueue. Articulate an API for this ADT. Develop a linked-list-based implementation.
1.3.33 Deque. A double-ended queue or deque (pronounced “deck”) is like a stack or a queue but supports adding and removing items at both ends. A deque stores a collection of items and supports the following API:

Write a class Deque that uses a doubly-linked list to implement this API and a class ResizingArrayDeque that uses a resizing array.
1.3.34 Random bag. A random bag stores a collection of items and supports the following API:

Write a class RandomBag that implements this API. Note that this API is the same as for Bag, except for the adjective random, which indicates that the iteration should provide the items in random order (all N! permutations equally likely, for each iterator). Hint: Put the items in an array and randomize their order in the iterator’s constructor.
1.3.35 Random queue. A random queue stores a collection of items and supports the following API:

Write a class RandomQueue that implements this API. Hint: Use an array representation (with resizing). To remove an item, swap one at a random position (indexed 0 through N-1) with the one at the last position (index N-1). Then delete and return the last object, as in ResizingArrayStack. Write a client that deals bridge hands (13 cards each) using RandomQueue<Card>.
1.3.36 Random iterator. Write an iterator for RandomQueue<Item> from the previous exercise that returns the items in random order.
1.3.37 Josephus problem. In the Josephus problem from antiquity, N people are in dire straits and agree to the following strategy to reduce the population. They arrange themselves in a circle (at positions numbered from 0 to N–1) and proceed around the circle, eliminating every Mth person until only one person is left. Legend has it that Josephus figured out where to sit to avoid being eliminated. Write a Queue client Josephus that takes M and N from the command line and prints out the order in which people are eliminated (and thus would show Josephus where to sit in the circle).
% java Josephus 2 7
1 3 5 0 4 2 6
1.3.38 Delete kth element. Implement a class that supports the following API:

First, develop an implementation that uses an array implementation, and then develop one that uses a linked-list implementation. Note: the algorithms and data structures that we introduce in CHAPTER 3 make it possible to develop an implementation that can guarantee that both insert() anddelete() take time prortional to the logarithm of the number of items in the queue—see EXERCISE 3.5.27.
1.3.39 Ring buffer. A ring buffer, or circular queue, is a FIFO data structure of a fixed size N. It is useful for transferring data between asynchronous processes or for storing log files. When the buffer is empty, the consumer waits until data is deposited; when the buffer is full, the producer waits to deposit data. Develop an API for a RingBuffer and an implementation that uses an array representation (with circular wrap-around).
1.3.40 Move-to-front. Read in a sequence of characters from standard input and maintain the characters in a linked list with no duplicates. When you read in a previously unseen character, insert it at the front of the list. When you read in a duplicate character, delete it from the list and reinsert it at the beginning. Name your program MoveToFront: it implements the well-known move-to-front strategy, which is useful for caching, data compression, and many other applications where items that have been recently accessed are more likely to be reaccessed.
1.3.41 Copy a queue. Create a new constructor so that
Queue<Item> r = new Queue<Item>(q);
makes r a reference to a new and independent copy of the queue q. You should be able to enqueue and pop from either q or r without influencing the other. Hint: Delete all of the elements from q and add these elements to both q and r.
1.3.42 Copy a stack. Create a new constructor for the linked-list implementation of Stack so that
Stack<Item> t = new Stack<Item>(s);
makes t a reference to a new and independent copy of the stack s.
1.3.43 Listing files. A folder is a list of files and folders. Write a program that takes the name of a folder as a command-line argument and prints out all of the files contained in that folder, with the contents of each folder recursively listed (indented) under that folder’s name. Hint: Use a queue, and see java.io.File.
1.3.44 Text editor buffer. Develop a data type for a buffer in a text editor that implements the following API:

Hint: Use two stacks.
1.3.45 Stack generability. Suppose that we have a sequence of intermixed push and pop operations as with our test stack client, where the integers 0, 1, ..., N-1 in that order (push directives) are intermixed with N minus signs (pop directives). Devise an algorithm that determines whether the intermixed sequence causes the stack to underflow. (You may use only an amount of space independent of N—you cannot store the integers in a data structure.) Devise a linear-time algorithm that determines whether a given permutation can be generated as output by our test client (depending on where the pop directives occur).
Solution: The stack does not overflow unless there exists an integer k such that the first k pop operations occur before the first k push operations. If a given permutation can be generated, it is uniquely generated as follows: if the next integer in the output permutation is in the top of the stack, pop it; otherwise, push it onto the stack.
1.3.46 Forbidden triple for stack generability. Prove that a permutation can be generated by a stack (as in the previous question) if and only if it has no forbidden triple (a, b, c) such that a < b < c with c first, a second, and b third (possibly with other intervening integers between c and a and between a and b).
Partial solution: Suppose that there is a forbidden triple (a, b, c). Item c is popped before a and b, but a and b are pushed before c. Thus, when c is pushed, both a and b are on the stack. Therefore, a cannot be popped before b.
1.3.47 Catenable queues, stacks, or steques. Add an extra operation catenation that (destructively) concatenates two queues, stacks, or steques (see EXERCISE 1.3.32). Hint: Use a circular linked list, maintaining a pointer to the last item.
1.3.48 Two stacks with a deque. Implement two stacks with a single deque so that each operation takes a constant number of deque operations (see EXERCISE 1.3.33).
1.3.49 Queue with a constant number of stacks. Implement a queue with a constant number of stacks so that each queue operation takes a constant (worst-case) number of stack operations. Warning: high degree of difficulty.
1.3.50 Fail-fast iterator. Modify the iterator code in Stack to immediately throw a java.util.ConcurrentModificationException if the client modifies the collection (via push() or pop()) during iteration?
Solution: Maintain a counter that counts the number of push() and pop() operations. When creating an iterator, store this value as an Iterator instance variable. Before each call to hasNext() and next(), check that this value has not changed since construction of the iterator; if it has, throw the exception.
All materials on the site are licensed Creative Commons Attribution-Sharealike 3.0 Unported CC BY-SA 3.0 & GNU Free Documentation License (GFDL)
If you are the copyright holder of any material contained on our site and intend to remove it, please contact our site administrator for approval.
© 2016-2026 All site design rights belong to S.Y.A.