Algorithms (2014)
Five. Strings
5.1 String Sorts 702
5.2 Tries 730
5.3 Substring Search 758
5.4 Regular Expressions 788
5.5 Data Compression 810
We communicate by exchanging strings of characters. Accordingly, numerous important and familiar applications are based on processing strings. In this chapter, we consider classic algorithms for addressing the underlying computational challenges surrounding applications such as the following:
Information processing
When you search for web pages containing a given keyword, you are using a string-processing application. In the modern world, virtually all information is encoded as a sequence of strings, and the applications that process it are string-processing applications of crucial importance.
Genomics
Computational biologists work with a genetic code that reduces DNA to (very long) strings formed from four characters (A, C, T, and G). Vast databases giving codes describing all manner of living organisms have been developed in recent years, so that string processing is a cornerstone of modern research in computational biology.
Communications systems
When you send a text message or an email or download an ebook, you are transmitting a string from one place to another. Applications that process strings for this purpose were an original motivation for the development of string-processing algorithms.
Programming systems
Programs are strings. Compilers, interpreters, and other applications that convert programs into machine instructions are critical applications that use sophisticated string-processing techniques. Indeed, all written languages are expressed as strings, and another motivation for the development of string-processing algorithms was the theory of formal languages, the study of describing sets of strings.
This list of a few significant examples illustrates the diversity and importance of string-processing algorithms.
The plan of this chapter is as follows: After addressing basic properties of strings, we revisit in SECTIONS 5.1 AND 5.2 the sorting and searching APIs from CHAPTERS 2 and 3. Algorithms that exploit special properties of string keys are faster and more flexible than the algorithms that we considered earlier. In SECTION 5.3 we consider algorithms for substring search, including a famous algorithm due to Knuth, Morris, and Pratt. In SECTION 5.4 we introduce regular expressions, the basis of the pattern-matching problem, a generalization of substring search, and a quintessential search tool known as grep. These classic algorithms are based on the related conceptual devices known as formal languages and finite automata. SECTION 5.5 is devoted to a central application: data compression, where we try to reduce the size of a string as much as possible.
Rules of the game
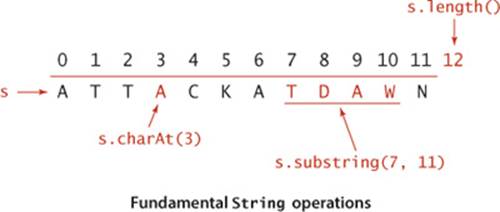
For clarity and efficiency, our implementations are expressed in terms of the Java String class, but we intentionally use as few operations as possible from that class to make it easier to adapt our algorithms for use on other string-like types of data and to other programming languages. We introduced strings in detail in SECTION 1.2 but briefly review here their most important characteristics.
Characters
A String is a sequence of characters. Characters are of type char and can have one of 216 possible values. For many decades, programmers restricted attention to characters encoded in 7-bit ASCII (see page 815 for a conversion table) or 8-bit extended ASCII, but many modern applications call for 16-bit Unicode.
Immutability
String objects are immutable, so that we can use them in assignment statements and as arguments and return values from methods without having to worry about their values changing.
Indexing
The operation that we perform most often is extract a specified character from a string that the charAt() method in Java’s String class provides. We expect charAt() to complete its work in constant time, as if the string were stored in a char[] array. As discussed in CHAPTER 1, this expectation is quite reasonable.
Length
In Java, the find the length of a string operation is implemented in the length() method in String. Again, we expect length() to complete its work in constant time, and again, this expectation is reasonable, although some care is needed in some programming environments.
Substring
Java’s substring() method implements the extract a specified substring operation. Its running time depends on the underlying representation. It takes constant time and space in typical Java 6 (and earlier) implementations but linear time and space in typical Java 7 implementations (see page 202).
Concatenation
In Java, the create a new string formed by appending one string to another operation is a built-in operation (using the + operator) that takes time proportional to the length of the result. For example, we avoid forming a string by appending one character at a time because that is a quadraticprocess in Java. (Java has a StringBuilder class for that use.)
Character arrays
The Java String is decidedly not a primitive type. The standard implementation provides the operations just described to facilitate client programming. By contrast, many of the algorithms that we consider can work with a low-level representation such as an array of char values, and many clients might prefer such a representation, because it consumes less space and takes less time. For several of the algorithms that we consider, the cost of converting from one representation to the other would be higher than the cost of running the algorithm. As indicated in the table below, the differences in code that processes the two representations are minor (substring() is more complicated and is omitted), so use of one representation or the other is no barrier to understanding the algorithm.
UNDERSTANDING THE EFFICIENCY OF THESE OPERATIONS is a key ingredient in understanding the efficiency of several string-processing algorithms. Not all programming languages provide String implementations with these performance characteristics. For example, determining the length of a string take time proportional to the number of characters in the string in the widely used C programming language. Adapting the algorithms that we describe to such languages is always possible (implement an ADT like Java’s String), but also might present different challenges and opportunities.
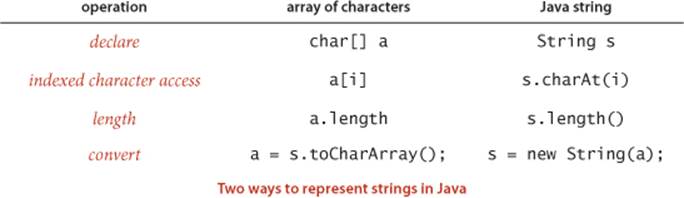
We primarily use the String data type in the text, with liberal use of indexing and length and occasional use of substring extraction and concatenation. When appropriate, we also provide on the booksite the corresponding code for char arrays. In performance-critical applications, the primary consideration in choosing between the two for clients is often the cost of accessing a character (a[i] is likely to be much faster than s.charAt(i) in typical Java implementations).
Alphabets
Some applications involve strings taken from a restricted alphabet. In such applications, it often makes sense to use an Alphabet class with the following API:

This API is based on a constructor that takes as argument an R-character string that specifies the alphabet and the toChar() and toIndex() methods for converting (in constant time) between string characters and int values between 0 and R-1. It also includes a contains() method for checking whether a given character is in the alphabet, the methods R() and lgR() for finding the number of characters in the alphabet and the number of bits needed to represent them, and the methods toIndices() and toChars() for converting between strings of characters in the alphabet and int arrays. For convenience, we also include the built-in alphabets in the table at the top of the next page, which you can access with code such as Alphabet.UNICODE16. Implementing Alphabet is a straightforward exercise (see EXERCISE 5.1.12). We will examine a sample client on page 699.
Character-indexed arrays
One of the most important reasons to use Alphabet is that many algorithms gain efficiency through the use of character-indexed arrays, where we associate information with each character that we can retrieve with a single array access. With a Java String, we have to use an array of size 65,536; with Alphabet, we just need an array with one entry for each alphabet character. Some of the algorithms that we consider can produce huge numbers of such arrays, and in such cases, the space for arrays of size 65,536 can be prohibitive. As an example, consider the class Count at the bottom of the previous page, which takes a string of characters from the command line and prints a table of the frequency of occurrence of those characters that appear on standard input. The count[] array that holds the frequencies in Count is an example of a character-indexed array. This calculation may seem to you to be a bit frivolous; actually, it is the basis for a family of fast sorting methods that we will consider in SECTION 5.1.
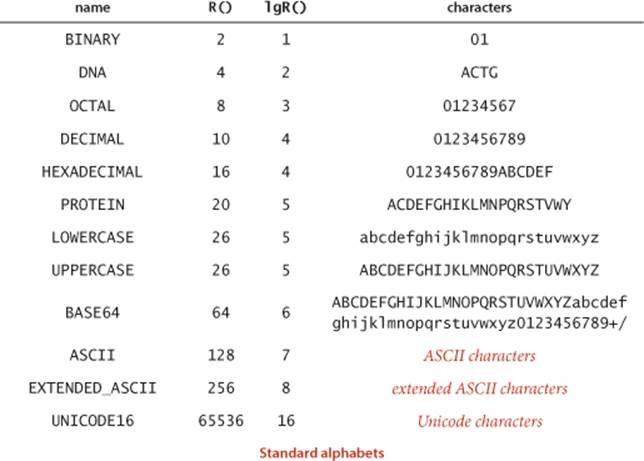

Numbers
As you can see from several of the standard Alphabet examples, we often represent numbers as strings. The method toIndices() converts any String over a given Alphabet into a base-R number represented as an int[] array with all values between 0 and R − 1. In some situations, doing this conversion at the start leads to compact code, because any digit can be used as an index in a character-indexed array. For example, if we know that the input consists only of characters from the alphabet, we could replace the inner loop in Count with the more compact code
int[] a = alpha.toIndices(s);
for (int i = 0; i < N; i++)
count[a[i]]++;
In this context, we refer to R as the radix, the base of the number system. Several of the algorithms that we consider are often referred to as “radix” methods because they work with one digit at a time.
% more pi.txt
3141592653
5897932384
6264338327
9502884197
... [100,000 digits of pi]
% java Count 0123456789 < pi.txt
0 9999
1 10137
2 9908
3 10026
4 9971
5 10026
6 10028
7 10025
8 9978
9 9902
DESPITE THE ADVANTAGES of using a data type such as Alphabet in string-processing algorithms (particularly for small alphabets), we do not develop our implementations in the book for strings taken from a general Alphabet because
• The preponderance of clients just use String
• Conversion to and from indices tends to fall in the inner loop and slow down implementations considerably
• The code is more complicated, and therefore more difficult to understand
Accordingly we use String, use the constant R = 256 in the code and R as a parameter in the analysis, and discuss performance for general alphabets when appropriate. You can find full Alphabet-based implementations on the booksite.
5.1 String Sorts
FOR MANY SORTING APPLICATIONS, the keys that define the order are strings. In this section, we look at methods that take advantage of special properties of strings to develop sorts for string keys that are more efficient than the general-purpose sorts that we considered in CHAPTER 2.
We consider two fundamentally different approaches to string sorting. Both of them are venerable methods that have served programmers well for many decades.
The first approach examines the characters in the keys in a right-to-left order. Such methods are generally referred to as least-significant-digit (LSD) string sorts. Use of the term digit instead of character traces back to the application of the same basic method to numbers of various types. Thinking of a string as a base-256 number, considering characters from right to left amounts to considering first the least significant digits. This approach is the method of choice for string-sorting applications where all the keys are the same length.
The second approach examines the characters in the keys in a left-to-right order, working with the most significant character first. These methods are generally referred to as most-significant-digit (MSD) string sorts—we will consider two such methods in this section. MSD string sorts are attractive because they can get a sorting job done without necessarily examining all of the input characters. MSD string sorts are similar to quicksort, because they partition the array to be sorted into independent pieces such that the sort is completed by recursively applying the same method to the subarrays. The difference is that MSD string sorts use just the first character of the sort key to do the partitioning, while quicksort uses comparisons that could involve examining the whole key. The first method that we consider creates a partition for each character value; the second always creates three partitions, for sort keys whose first character is less than, equal to, or greater than the partitioning key’s first character.
The number of characters in the alphabet is an important parameter when analyzing string sorts. Though we focus on extended ASCII strings (R = 256), we will also consider strings taken from much smaller alphabets (such as genomic sequences) and from much larger alphabets (such as the 65,536-character Unicode alphabet that is an international standard for encoding natural languages).
Key-indexed counting
As a warmup, we consider a simple method for sorting that is effective whenever the keys are small integers. This method, known as key-indexed counting, is useful in its own right and is also the basis for two of the three string sorts that we consider in this section.
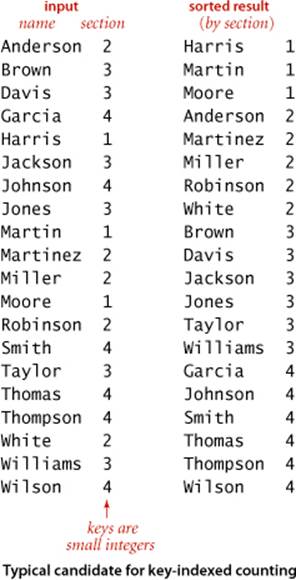
Consider the following data-processing problem, which might be faced by a teacher maintaining grades for a class with students assigned to sections, which are numbered 1, 2, 3, and so forth. On some occasions, it is necessary to have the class listed by section. Since the section numbers are small integers, sorting by key-indexed counting is appropriate. To describe the method, we assume that the information is kept in an array a[] of items that each contain a name and a section number, that section numbers are integers between 0 and R-1, and that the code a[i].key() returns the section number for the indicated student. The method breaks down into four steps, which we describe in turn.
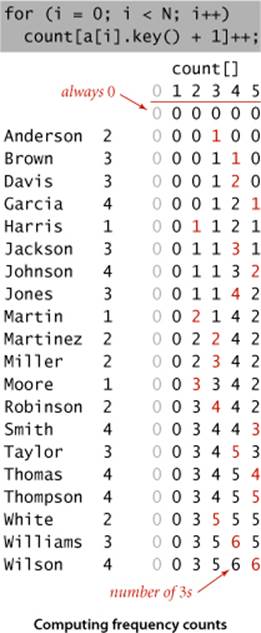
Compute frequency counts
The first step is to count the frequency of occurrence of each key value, using an int array count[]. For each item, we use the key to access an entry in count[] and increment that entry. If the key value is r, we increment count[r+1]. (Why +1? The reason for that will become clear in the next step.) In the example at left, we first increment count[3] because Anderson is in section 2, then we increment count[4] twice because Brown and Davis are in section 3, and so forth. Note that count[0] is always 0, and that count[1] is 0 in this example (no students are in section 0).
Transform counts to indices
Next, we use count[] to compute, for each key value, the starting index positions in the sorted order of items with that key. In our example, since there are three items with key 1 and five items with key 2, then the items with key 3 start at position 8 in the sorted array. In general, to get the starting index for items with any given key value we sum the frequency counts of smaller values. For each key value r, the sum of the counts for key values less than r+1 is equal to the sum of the counts for key values less than r plus count[r], so it is easy to proceed from left to right to transform count[] into an index table that we can use to sort the data.

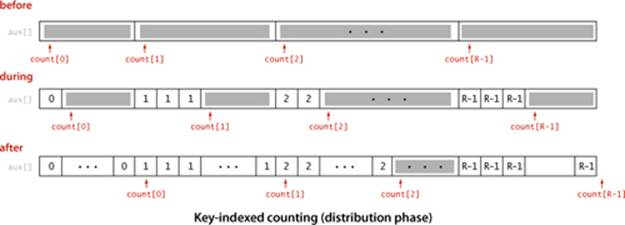
Distribute the data
With the count[] array transformed into an index table, we accomplish the actual sort by moving the items to an auxiliary array aux[]. We move each item to the position in aux[] indicated by the count[] entry corresponding to its key, and then increment that entry to maintain the following invariant for count[]: for each key value r, count[r] is the index of the position in aux[] where the next item with key value r (if any) should be placed. This process produces a sorted result with one pass through the data, as illustrated at left. Note: In one of our applications, the fact that this implementation is stable is critical: items with equal keys are brought together but kept in the same relative order.
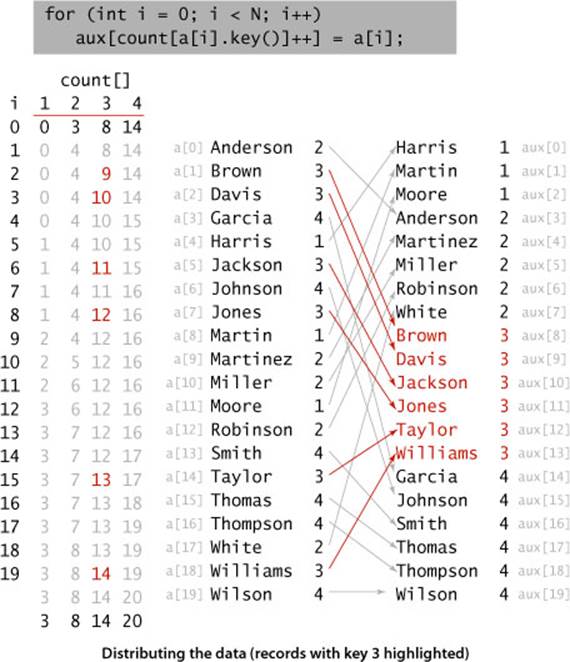
Copy back
Since we accomplished the sort by moving the items to an auxiliary array, the last step is to copy the sorted result back to the original array.
Proposition A. Key-indexed counting uses 11N + 4 R + 1 array accesses to stably sort N items whose keys are integers between 0 and R − 1.
Proof: Immediate from the code. Initializing the arrays uses N + R + 1 array accesses. The first loop increments a counter for each of the N items (3N array accesses); the second loop does R additions (3R array accesses); the third loop does N counter increments and N data moves (5Narray accesses); and the fourth loop does N data moves (2N array accesses). Both moves preserve the relative order of equal keys.
KEY-INDEXED COUNTING is an extremely effective and often overlooked sorting method for applications where keys are small integers. Understanding how it works is a first step toward understanding string sorting. PROPOSITION A implies that key-indexed counting breaks through the N log Nlower bound that we proved for sorting. How does it manage to do so? PROPOSITION I in SECTION 2.2 is a lower bound on the number of compares needed (when data is accessed only through compareTo())—key-indexed counting does no compares (it accesses data only through key()). When R is within a constant factor of N, we have a linear-time sort.
Key-indexed counting (a[i].key() is an int in [0, R)).
int N = a.length;
[] aux = new String[N];
int[] count = new int[R+1];
// Compute frequency counts.
for (int i = 0; i < N; i++)
count[a[i].key() + 1]++;
// Transform counts to indices.
for (int r = 0; r < R; r++)
count[r+1] += count[r];
// Distribute the records.
for (int i = 0; i < N; i++)
aux[count[a[i].key()]++] = a[i];
// Copy back.
for (int i = 0; i < N; i++)
a[i] = aux[i];
LSD string sort
The first string-sorting method that we consider is known as least-significant-digit first (LSD) string sort. Consider the following motivating application: Suppose that a highway engineer sets up a device that records the license plate numbers of all vehicles using a busy highway for a given period of time and wants to know the number of different vehicles that used the highway. As you know from SECTION 2.1, one easy way to solve this problem is to sort the numbers, then make a pass through to count the different values, as in Dedup (page 490). License plates are a mixture of numbers and letters, so it is natural to represent them as strings. In the simplest situation (such as the California license plate examples at right) the strings all have the same number of characters. This situation is often found in sort applications—for example, telephone numbers, bank account numbers, and IP addresses are typically fixed-length strings.

Sorting such strings can be done with key-indexed counting, as shown in ALGORITHM 5.1 (LSD) and the example below it on the facing page. If the strings are each of length W, we sort the strings W times with key-indexed counting, using each of the positions as the key, proceeding from right to left. It is not easy, at first, to be convinced that the method produces a sorted array—in fact, it does not work at all unless the key-indexed count implementation is stable. Keep this fact in mind and refer to the example when studying this proof of correctness:
Proposition B. LSD string sort stably sorts fixed-length strings.
Proof: This fact depends crucially on the key-indexed counting implementation being stable, as indicated in PROPOSITION A. After sorting keys on their i trailing characters (in a stable manner), we know that any two keys appear in proper order in the array (considering just those characters) either because the first of their i trailing characters is different, in which case the sort on that character puts them in order, or because the first of their i trailing characters is the same, in which case they are in order because of stability (and by induction, for i-1).
Another way to state the proof is to think about the future: if the characters that have not been examined for a pair of keys are identical, any difference between the keys is restricted to the characters already examined, so the keys have been properly ordered and will remain so because of stability. If, on the other hand, the characters that have not been examined are different, the characters already examined do not matter, and a later pass will correctly order the pair based on the more significant differences.
Algorithm 5.1 LSD string sort
public class LSD
{
public static void sort(String[] a, int W)
{ // Sort a[] on leading W characters.
int N = a.length;
int R = 256;
String[] aux = new String[N];
for (int d = W-1; d >= 0; d--)
{ // Sort by key-indexed counting on dth char.
int[] count = new int[R+1]; // Compute frequency counts.
for (int i = 0; i < N; i++)
count[a[i].charAt(d) + 1]++;
for (int r = 0; r < R; r++) // Transform counts to indices.
count[r+1] += count[r];
for (int i = 0; i < N; i++) // Distribute.
aux[count[a[i].charAt(d)]++] = a[i];
for (int i = 0; i < N; i++) // Copy back.
a[i] = aux[i];
}
}
}
To sort an array a[] of strings that each have exactly W characters, we do W key-indexed counting sorts: one for each character position, proceeding from right to left.

LSD radix sorting is the method used by the old punched-card-sorting machines that were developed at the beginning of the 20th century and thus predated the use of computers in commercial data processing by several decades. Such machines had the capability of distributing a deck of punched cards among 10 bins, according to the pattern of holes punched in the selected columns. If a deck of cards had numbers punched in a particular set of columns, an operator could sort the cards by running them through the machine on the rightmost digit, then picking up and stacking the output decks in order, then running them through the machine on the next-to-rightmost digit, and so forth, until getting to the first digit. The physical stacking of the cards is a stable process, which is mimicked by key-indexed counting sort. Not only was this version of LSD radix sorting important in commercial applications up through the 1970s, but it was also used by many cautious programmers (and students!), who would have to keep their programs on punched cards (one line per card) and would punch sequence numbers in the final few columns of a program deck so as to be able to put the deck back in order mechanically if it were accidentally dropped. This method is also a neat way to sort a deck of playing cards: deal them into thirteen piles (one for each value), pick up the piles in order, then deal into four piles (one for each suit). The (stable) dealing process keeps the cards in order within each suit, so picking up the piles in suit order yields a sorted deck.

In many string-sorting applications (even license plates, for some states), the keys are not all be the same length. It is possible to adapt LSD string sort to work for such applications, but we leave this task for exercises because we will next consider two other methods that are specifically designed for variable-length keys.
From a theoretical standpoint, LSD string sort is significant because it is a linear-time sort for typical applications. No matter how large the value of N, it makes W passes through the data. Specifically:
Proposition B. LSD string sort uses ~7WN + 3WR array accesses and extra space proportional to N + R to sort N items whose keys are W-character strings taken from an R-character alphabet.
Proof: The method is W passes of key-indexed counting, except that the aux[] array is initialized just once. The total is immediate from the code and PROPOSITION A.
For typical applications, R is far smaller than N, so PROPOSITION B implies that the total running time is proportional to WN. An input array of N strings that each have W characters has a total of WN characters, so the running time of LSD string sort is linear in the size of the input.
MSD string sort
To implement a general-purpose string sort, where strings are not necessarily all the same length, we consider the characters in left-to-right order. We know that strings that start with a should appear before strings that start with b, and so forth. The natural way to implement this idea is a recursive method known as most-significant-digit-first (MSD) string sort. We use key-indexed counting to sort the strings according to their first character, then (recursively) sort the subarrays corresponding to each character (excluding the first character, which we know to be the same for each string in each subarray). Like quicksort, MSD string sort partitions the array into subarrays that can be sorted independently to complete the job, but it partitions the array into one subarray for each possible value of the first character, instead of the two or three partitions in quicksort.

End-of-string convention
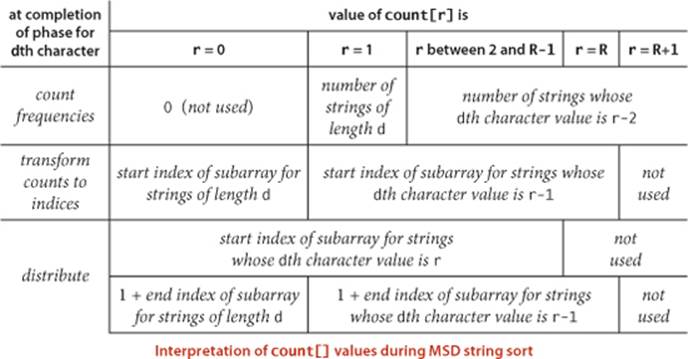
We need to pay particular attention to reaching the ends of strings in MSD string sort. For a proper sort, we need the sub-array for strings whose characters have all been examined to appear as the first subarray, and we do not want to recursively sort this subarray. To facilitate these two parts of the computation we use a private two-argument charAt() method to convert from an indexed string character to an array index that returns -1 if the specified character position is past the end of the string. This convention means that we have R+1 different possible character values at each string position: -1 to signify end of string, 0 fot the first alphapet character, 1, for the second alphapet character, and so forth. Then, we just add 1 to each returned value, to get a nonnegative int that we can use to index count[]. Since key-indexed counting already needs one extra position, we use the code int count[] = new int[R+2]; to create the array of frequency counts (and set all of its values to 0). Note: Some languages, notably C and C++, have a built-in end-of-string convention, so our code needs to be adjusted accordingly for such languages.


WITH THESE PREPARATIONS, the implementation of MSD string sort, in ALGORITHM 5.2, requires very little new code. We add a test to cutoff to insertion sort for small subarrays (using a specialized insertion sort that we will consider later), and we add a loop to key-indexed counting to do the recursive calls. As summarized in the table at the bottom of this page, the values in the count[] array (after serving to count the frequencies, transform counts to indices, and distribute the data) give us precisely the information that we need to (recursively) sort the subarrays corresponding to each character value.
Specified alphabet
The cost of MSD string sort depends strongly on the number of possible characters in the alphabet. It is easy to modify our sort method to take an Alphabet as argument, to allow for improved efficiency in clients involving strings taken from relatively small alphabets. The following changes will do the job:
• Save the alphabet in an instance variable alpha in the constructor.
• Set R to alpha.R() in the constructor.
• Replace s.charAt(d) with alpha.toIndex(s.charAt(d)) in charAt().
Algorithm 5.2 MSD string sort
public class MSD
{
private static int R = 256; // radix
private static final int M = 15; // cutoff for small subarrays
private static String[] aux; // auxiliary array for distribution
private static int charAt(String s, int d)
{ if (d < s.length()) return s.charAt(d); else return -1; }
public static void sort(String[] a)
{
int N = a.length;
aux = new String[N];
sort(a, 0, N-1, 0);
}
private static void sort(String[] a, int lo, int hi, int d)
{ // Sort from a[lo] to a[hi], starting at the dth character.
if (hi <= lo + M)
{ Insertion.sort(a, lo, hi, d); return; }
int[] count = new int[R+2]; // Compute frequency counts.
for (int i = lo; i <= hi; i++)
count[charAt(a[i], d) + 2]++;
for (int r = 0; r < R+1; r++) // Transform counts to indices.
count[r+1] += count[r];
for (int i = lo; i <= hi; i++) // Distribute.
aux[count[charAt(a[i], d) + 1]++] = a[i];
for (int i = lo; i <= hi; i++) // Copy back.
a[i] = aux[i - lo];
// Recursively sort for each character value.
for (int r = 0; r < R; r++)
sort(a, lo + count[r], lo + count[r+1] - 1, d+1);
}
}
To sort an array a[] of strings, we sort them on their first character using key-indexed counting, then (recursively) sort the subarrays corresponding to each first-character value.
In our running examples, we use strings made up of lowercase letters. It is also easy to extend LSD string sort to provide this feature, but typically with much less impact on performance than for MSD string sort.
THE CODE IN ALGORITHM 5.2 is deceptively simple, masking a rather sophisticated computation. It is definitely worth your while to study the trace of the top level at the bottom of this page and the trace of recursive calls on the next page, to be sure that you understand the intricacies of the algorithm. This trace uses a cutoff-for-small-subarrays threshold value (M) of 0, so that you can see the sort to completion for this small example. The strings in this example are taken from Alphabet.LOWERCASE, with R = 26; bear in mind that typical applications might use Alphabet.EXTENDED_ASCII, with R = 256, or Alphabet.UNICODE16, with R = 65536. For large alphabets, MSD string sort is so simple as to be dangerous—improperly used, it can consume outrageous amounts of time and space. Before considering performance characteristics in detail, we shall discuss three important issues (all of which we have considered before, in CHAPTER 2) that must be addressed in any application.
Small subarrays
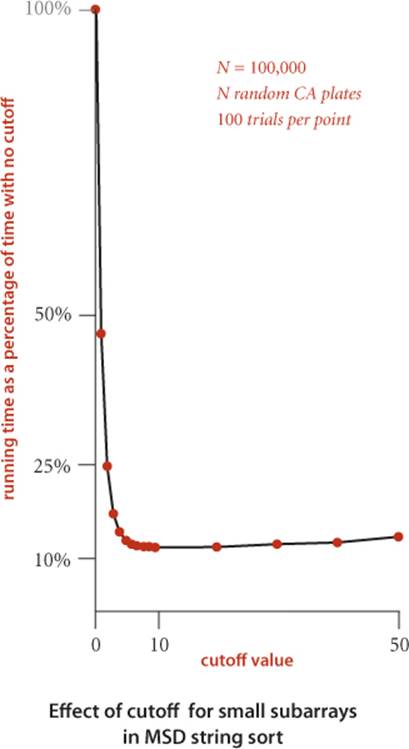
The basic idea behind MSD string sort is quite effective: in typical applications, the strings will be in order after examining only a few characters in the key. Put another way, the method quickly divides the array to be sorted into small subarrays. But this is a double-edged sword: we are certain to have to handle huge numbers of tiny subarrays, so we had better be sure that we handle them efficiently. Small subarrays are of critical importance in the performance of MSD string sort. We have seen this situation for other recursive sorts (quicksort and mergesort), but it is much more dramatic for MSD string sort. For example, suppose that you are sorting millions of ASCII strings (R = 256) that are all different, with no cutoff for small subarrays. Each string eventually finds its way to its own subarray, so you will sort millions of subarrays of size 1. But each such sort involves initializing the 258 entries of the count[] array to 0 and transforming them all to indices. This cost is likely to dominate the rest of the sort. With Unicode (R = 65536) the sort might be thousands of times slower. Indeed, many unsuspecting sort clients have seen their running times explode from minutes to hours on switching from ASCII to Unicode, for precisely this reason. Accordingly, the switch to insertion sort for small subarrays is a must for MSD string sort. To avoid the cost of reexamining characters that we know to be equal, we use the version of insertion sort given at the top of the page, which takes an extra argument d and assumes that the first d characters of all the strings to be sorted are known to be equal. As with quicksort and mergesort, most of the benefit of this improvement is achieved with a small value of the cutoff, but the savings here are much more dramatic. The diagram at right shows the results of experiments where using a cutoff to insertion sort for subarrays of size 10 or less decreases the running time by a factor of 10 for a typical application.


Insertion sort for strings whose first d characters are equal
public static void sort(String[] a, int lo, int hi, int d)
{ // Sort from a[lo] to a[hi], starting at the dth character.
for (int i = lo; i <= hi; i++)
for (int j = i; j > lo && less(a[j], a[j-1], d); j--)
exch(a, j, j-1);
}
private static boolean less(String v, String w, int d)
{
for (int i = d; i < Math.min(v.length(), w.length()); i++)
if (v.charAt(i) < w.charAt(i)) return true;
else if (v.charAt(i) > w.charAt(i)) return false;
return v.length() < w.length();
}
Equal keys
A second pitfall for MSD string sort is that it can be relatively slow for subarrays containing large numbers of equal keys. If a substring occurs sufficiently often that the cutoff for small subarrays does not apply, then a recursive call is needed for every character in all of the equal keys. Moreover, key-indexed counting is an inefficient way to determine that the characters are all equal: not only does each character need to be examined and each string moved, but all the counts have to be initialized, converted to indices, and so forth. Thus, the worst case for MSD string sorting is when all keys are equal. The same problem arises when large numbers of keys have long common prefixes, a situation often found in applications.
Extra space
To do the partitioning, MSD uses two auxiliary arrays: the temporary array for distributing keys (aux[]) and the array that holds the counts that are transformed into partition indices (count[]). The aux[] array is of size N and can be created outside the recursive sort() method. This extra space can be eliminated by sacrificing stability (see EXERCISE 5.1.17), but it is often not a major concern in practical applications of MSD string sort. Space for the count[] array, on the other hand, can be an important issue (because it cannot be created outside the recursive sort() method) as addressed inPROPOSITION D below.
Random string model
To study the performance of MSD string sort, we use a random string model, where each string consists of (independently) random characters, with no bound on their length. Long equal keys are essentially ignored, because they are extremely unlikely. The behavior of MSD string sort in this model is similar to its behavior in a model where we consider random fixed-length keys and also to its performance for typical real data; in all three, MSD string sort tends to examine just a few characters at the beginning of each key, as we will see.
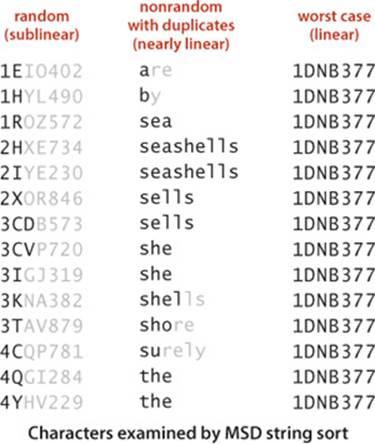
Performance
The running time of MSD string sort depends on the data. For compare-based methods, we were primarily concerned with the order of the keys; for MSD string sort, the order of the keys is immaterial, but we are concerned with the values of the keys.
• For random inputs, MSD string sort examines just enough characters to distinguish among the keys, and the running time is sublinear in the number of characters in the data (it examines a small fraction of the input characters).
• For nonrandom inputs, MSD string sort still could be sublinear but might need to examine more characters than in the random case, depending on the data. In particular, it has to examine all the characters in equal keys, so the running time is nearly linear in the number of characters in the data when significant numbers of equal keys are present.
• In the worst case, MSD string sort examines all the characters in the keys, so the running time is linear in the number of characters in the data (like LSD string sort). A worst-case input is one with all strings equal.
Some applications involve distinct keys that are well-modeled by the random string model; others have significant numbers of equal keys or long common prefixes, so the sort time is closer to the worst case. Our license-plate-processing application, for example, can fall anywhere between these extremes: if our engineer takes an hour of data from a busy interstate, there will not be many duplicates and the random model will apply; for a week’s worth of data on a local road, there will be numerous duplicates and performance will be closer to the worst case.
Proposition C. To sort N random strings from an R-character alphabet, MSD string sort examines about N logR N characters, on average.
Proof sketch: We expect the subarrays to be all about the same size, so the recurrence CN = RCN/R + N approximately describes the performance, which leads to the stated result, generalizing our argument for quicksort in CHAPTER 2. Again, this description of the situation is not entirely accurate, because N/R is not necessarily an integer, and the subarrays are the same size only on the average (and because the number of characters in real keys is finite). These effects turn out to be less significant for MSD string sort than for standard quicksort, so the leading term of the running time is the solution to this recurrence. The detailed analysis that proves this fact is a classical example in the analysis of algorithms, first done by Knuth in the early 1970s.
As food for thought and to indicate why the proof is beyond the scope of this book, note that key length does not play a role. Indeed, the random-string model allows key length to approach infinity. There is a nonzero probability that two keys will match for any specified number of characters, but this probability is so small as to not play a role in our performance estimates.
As we have discussed, the number of characters examined is not the full story for MSD string sort. We also have to take into account the time and space required to count frequencies and turn the counts into indices.
Proposition D. MSD string sort uses between 8N + 3R and ~7wN + 3WR array accesses to sort N strings taken from an R-character alphabet, where w is the average string length.
Proof: Immediate from the code, PROPOSITION A, and PROPOSITION B. In the best case MSD sort uses just one pass; in the worst case, it performs like LSD string sort.
When N is small, the factor of R dominates. Though precise analysis of the total cost becomes difficult and complicated, you can estimate the effect of this cost just by considering small subarrays when keys are distinct. With no cutoff for small subarrays, each key appears in its own subarray, so NR array accesses are needed for just these subarrays. If we cut off to small subarrays of size M, we have about N/M subarrays of size M, so we are trading off NR/M array accesses with NM/4 compares, which tells us that we should choose M to be proportional to the square root of R.
Proposition D. To sort N strings taken from an R-character alphabet, the amount of space needed by MSD string sort is proportional to R times the length of the longest string (plus N), in the worst case.
Proof: The count[] array must be created within sort(), so the total amount of space needed is proportional to R times the depth of recursion (plus N for the auxiliary array). Precisely, the depth of the recursion is the length of the longest string that is a prefix of two or more of the strings to be sorted.
As just discussed, equal keys cause the depth of the recursion to be proportional to the length of the keys. The immediate practical lesson to be drawn from PROPOSITION D is that it is quite possible for MSD string sort to run out of time or space when sorting long strings taken from large alphabets, particularly if long equal keys are to be expected. For example, with Alphabet.UNICODE16 and more than M equal 1,000-character strings, MSD.sort() would require space for over 65 million counters!
THE MAIN CHALLENGE in getting maximum efficiency from MSD string sort on keys that are long strings is to deal with lack of randomness in the data. Typically, keys may have long stretches of equal data, or parts of them might fall in only a narrow range. For example, an information-processing application for student data might have keys that include graduation year (4 bytes, but one of four different values), state names (perhaps 10 bytes, but one of 50 different values), and gender (1 byte with one of two given values), as well as a person’s name (more similar to random strings, but probably not short, with nonuniform letter distributions, and with trailing blanks in a fixed-length field). Restrictions like these lead to large numbers of empty subarrays during the MSD string sort. Next, we consider a graceful way to adapt to such situations.
Three-way string quicksort
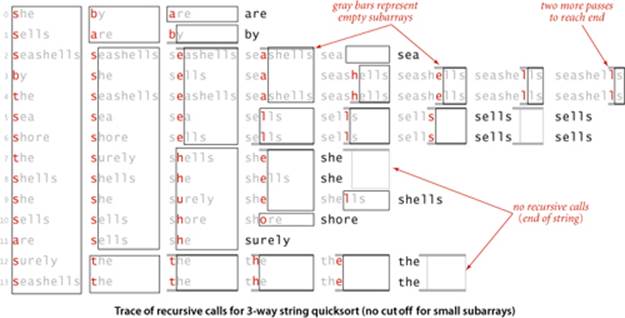
We can also adapt quicksort to MSD string sorting by using 3-way partitioning on the leading character of the keys, moving to the next character on only the middle subarray (keys with leading character equal to the partitioning character). This method is not difficult to implement, as you can see in ALGORITHM 5.3: we just add an argument to the recursive method in ALGORITHM 2.5 that keeps track of the current character, adapt the 3-way partitioning code to use that character, and appropriately modify the recursive calls.
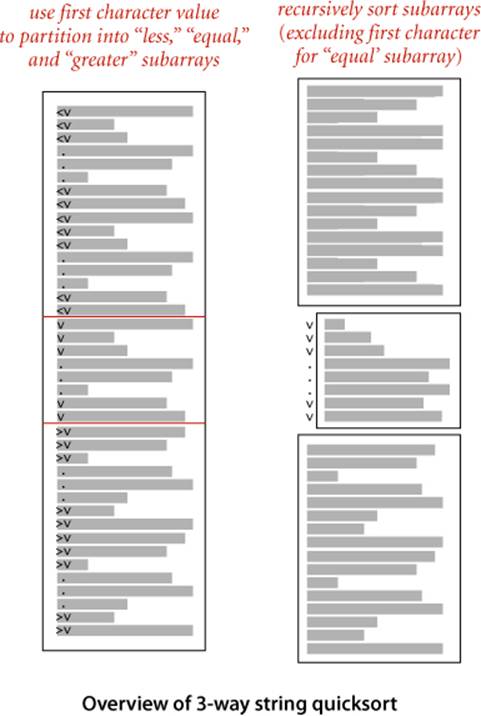
Although it does the computation in a different order, 3-way string quicksort amounts to sorting the array on the leading characters of the keys (using quicksort), then applying the method recursively on the remainder of the keys. For sorting strings, the method compares favorably with normal quicksort and with MSD string sort. Indeed, it is a hybrid of these two algorithms.
Three-way string quicksort divides the array into only three parts, so it involves more data movement than MSD string sort when the number of nonempty partitions is large because it has to do a series of 3-way partitions to get the effect of the multiway partition. On the other hand, MSD string sort can create large numbers of (empty) subarrays, whereas 3-way string quicksort always has just three. Thus, 3-way string quicksort adapts well to handling equal keys, keys with long common prefixes, keys that fall into a small range, and small arrays—all situations where MSD string sort runs slowly. Of particular importance is that the partitioning adapts to different kinds of structure in different parts of the key. Also, like quicksort, 3-way string quicksort does not use extra space (other than the implicit stack to support recursion), which is an important advantage over MSD string sort, which requires space for both frequency counts and an auxiliary array.
Algorithm 5.3 Three-way string quicksort
public class Quick3string
{
private static int charAt(String s, int d)
{ if (d < s.length()) return s.charAt(d); else return -1; }
public static void sort(String[] a)
{ sort(a, 0, a.length - 1, 0); }
private static void sort(String[] a, int lo, int hi, int d)
{
if (hi <= lo) return;
int lt = lo, gt = hi;
int v = charAt(a[lo], d);
int i = lo + 1;
while (i <= gt)
{
int t = charAt(a[i], d);
if (t < v) exch(a, lt++, i++);
else if (t > v) exch(a, i, gt--);
else i++;
}
// a[lo..lt-1] < v = a[lt..gt] < a[gt+1..hi]
sort(a, lo, lt-1, d);
if (v >= 0) sort(a, lt, gt, d+1);
sort(a, gt+1, hi, d);
}
}
To sort an array a[] of strings, we 3-way partition them on their first character, then (recursively) sort the three resulting subarrays: the strings whose first character is less than the partitioning character, the strings whose first character is equal to the partitioning character (excluding their first character in the sort), and the strings whose first character is greater than the partitioning character.
The figure at the bottom of this page shows all of the recursive calls that Quick3string makes for our example. Each subarray is sorted using precisely three recursive calls, except when we skip the recursive call on reaching the ends of the (equal) string(s) in the middle subarray.
As usual, in practice, it is worthwhile to consider various standard improvements to the implementation in ALGORITHM 5.3:
Small subarrays
In any recursive algorithm, we can gain efficiency by treating small subarrays differently. In this case, we use the insertion sort from page 715, which skips the characters that are known to be equal. The improvement due to this change is likely to be significant, though not nearly as important as for MSD string sort.
Restricted alphabet
To handle specialized alphabets, we could add an Alphabet argument alpha to each of the methods and replace s.charAt(d) with alpha.toIndex(s.charAt(d)) in charAt(). In this case, there is no benefit to doing so, and adding this code is likely to substantially slow the algorithm down because this code is in the inner loop.
Randomization
As with any quicksort, it is generally worthwhile to shuffle the array beforehand or to use a random paritioning item by swapping the first item with a random one. The primary reason to do so is to protect against worst-case performance in the case that the array is already sorted or nearly sorted.
For string keys, standard quicksort and all the other sorts in CHAPTER 2 are actually MSD string sorts, because the compareTo() method in String accesses the characters in left-to-right order. That is, compareTo() accesses only the leading characters if they are different, the leading two characters if the first characters are the same and the second different, and so forth. For example, if the first characters of the strings are all different, the standard sorts will examine just those characters, thus automatically realizing some of the same performance gain that we seek in MSD string sorting. The essential idea behind 3-way quicksort is to take special action when the leading characters are equal. Indeed, one way to think of ALGORITHM 5.3 is as a way for standard quicksort to keep track of leading characters that are known to be equal. In the small subarrays, where most of the compares in the sort are done, the strings are likely to have numerous equal leading characters. The standard algorithm has to scan over all those characters for each compare; the 3-way algorithm avoids doing so.
Performance
Consider a case where the string keys are long (and are all the same length, for simplicity), but most of the leading characters are equal. In such a situation, the running time of standard quicksort is proportional to the string length times 2N ln N, whereas the running time of 3-way string quicksort is proportional to N times the string length (to discover all the leading equal characters) plus 2N ln N character comparisons (to do the sort on the remaining short keys). That is, 3-way string quicksort requires up to a factor of 2lnN fewer character compares than normal quicksort. It is not unusual for keys in practical sorting applications to have characteristics similar to this artificial example.
Proposition E. To sort an array of N random strings, 3-way string quicksort uses ~2Nln N character compares, on the average.
Proof: There are two instructive ways to understand this result. First, considering the method to be equivalent to quicksort partitioning on the leading character, then (recursively) using the same method on the subarrays, we should not be surprised that the total number of operations is about the same as for normal quicksort—but they are single-character compares, not full-key compares. Second, considering the method as replacing key-indexed counting by quicksort, we expect that the N logR N running time from PROPOSITION C should be multiplied by a factor of 2 lnR because it takes quicksort 2R ln R steps to sort R characters, as opposed to R steps for the same characters in the MSD string sort. We omit the full proof.
As emphasized on page 716, considering random strings is instructive, but more detailed analysis is needed to predict performance for practical situations. Researchers have studied this algorithm in depth and have proved that no algorithm can beat 3-way string quicksort (measured by number of character compares) by more than a constant factor, under very general assumptions. To appreciate its versatility, note that 3-way string quicksort has no direct dependencies on the size of the alphabet.
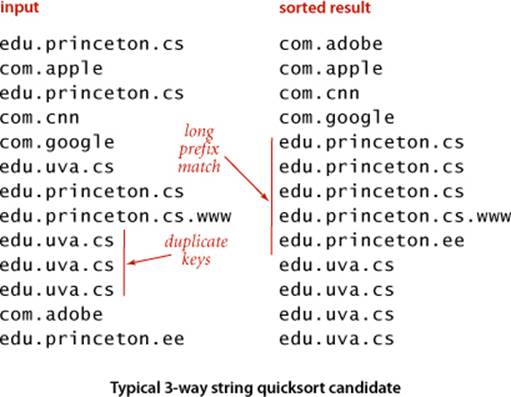
Example: web logs
As an example where 3-way string quicksort shines, we can consider a typical modern data-processing task. Suppose that you have built a website and want to analyze the traffic that it generates. You can have your system administrator supply you with a web log of all transactions on your site. Among the information associated with a transaction is the domain name of the originating machine. For example, the file week.log.txt on the booksite is a log of one week’s transactions on our booksite. Why does 3-way string quicksort do well on such a file? Because the sorted result is replete with long common prefixes that this method does not have to reexamine.
Which string-sorting algorithm should I use?
Naturally, we are interested in how the string-sorting methods that we have considered compare to the general-purpose methods that we considered in CHAPTER 2. The following table summarizes the important characteristics of the string-sort algorithms that we have discussed in this section (the rows for quicksort, mergesort, and 3-way quicksort are included from CHAPTER 2, for comparison).
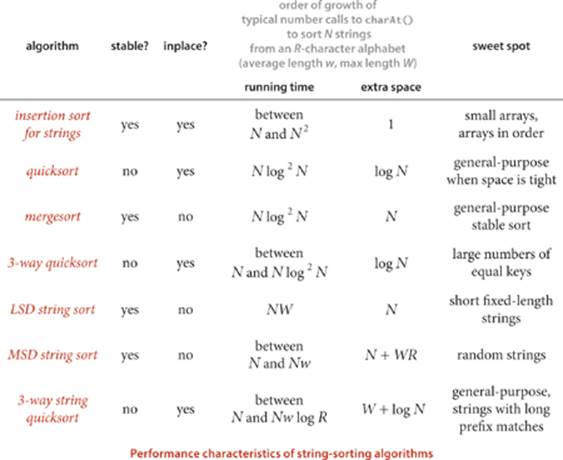
As in CHAPTER 2, multiplying these growth rates by appropriate algorithm- and data-dependent constants gives an effective way to predict running time.
As explored in the examples that we have already considered and in many other examples in the exercises, different specific situations call for different methods, with appropriate parameter settings. In the hands of an expert (maybe that’s you, by now), dramatic savings can be realized for certain situations.
Q&A
Q. Does the Java system sort use one of these methods for String sorts?
A. No, but the standard implementation includes a fast string compare that makes standard sorts competitive with the methods considered here.
Q. So, I should just use the system sort for String keys?
A. Probably yes in Java, though if you have huge numbers of strings or need an exceptionally fast sort, you may wish to switch to char arrays instead of String values and use a radix sort.
Q. What is explanation of the log2N factors on the table in the previous page?
A. They reflect the idea that most of the comparisons for these algorithms wind up being between keys with a common prefix of length log N. Recent research has established this fact for random strings with careful mathematical analysis (see booksite for reference).
Exercises
5.1.1 Develop a sort implementation that counts the number of different key values, then uses a symbol table to apply key-indexed counting to sort the array. (This method is not for use when the number of different key values is large.)
5.1.2 Give a trace for LSD string sort for the keys
no is th ti fo al go pe to co to th ai of th pa
5.1.3 Give a trace for MSD string sort for the keys
no is th ti fo al go pe to co to th ai of th pa
5.1.4 Give a trace for 3-way string quicksort for the keys
no is th ti fo al go pe to co to th ai of th pa
5.1.5 Give a trace for MSD string sort for the keys
now is the time for all good people to come to the aid of
5.1.6 Give a trace for 3-way string quicksort for the keys
now is the time for all good people to come to the aid of
5.1.7 Develop an implementation of key-indexed counting that makes use of an array of Queue objects.
5.1.8 Give the number of characters examined by MSD string sort and 3-way string quicksort for a file of N keys a, aa, aaa, aaaa, aaaaa, . . .
5.1.9 Develop an implementation of LSD string sort that works for variable-length strings.
5.1.10 What is the total number of characters examined by 3-way string quicksort when sorting N fixed-length strings (all of length W), in the worst case?
Creative Problems
5.1.11 Queue sort. Implement MSD string sorting using queues, as follows: Keep one queue for each bin. On a first pass through the items to be sorted, insert each item into the appropriate queue, according to its leading character value. Then, sort the sublists and stitch together all the queues to make a sorted whole. Note that this method does not involve keeping the count[] arrays within the recursive method.
5.1.12 Alphabet. Develop an implementation of the Alphabet API that is given on page 698 and use it to develop LSD and MSD sorts for general alphabets.
5.1.13 Hybrid sort. Investigate the idea of using standard MSD string sort for large arrays, in order to get the advantage of multiway partitioning, and 3-way string quicksort for smaller arrays, in order to avoid the negative effects of large numbers of empty bins.
5.1.14 Array sort. Develop a method that uses 3-way string quicksort for keys that are arrays of int values.
5.1.15 Sublinear sort. Develop a sort implementation for int values that makes two passes through the array to do an LSD sort on the leading 16 bits of the keys, then does an insertion sort.
5.1.16 Linked-list sort. Develop a sort implementation that takes a linked list of nodes with String key values as argument and rearranges the nodes so that they appear in sorted order (returning a link to the node with the smallest key). Use 3-way string quicksort.
5.1.17 In-place key-indexed counting. Develop a version of key-indexed counting that uses only a constant amount of extra space. Prove that your version is stable or provide a counterexample.
Experiments
5.1.18 Random decimal keys. Write a static method randomDecimalKeys that takes int values N and W as arguments and returns an array of N string values that are each W-digit decimal numbers.
5.1.19 Random CA license plates. Write a static method randomPlatesCA that takes an int value N as argument and returns an array of N String values that represent CA license plates as in the examples in this section.
5.1.20 Random fixed-length words. Write a static method randomFixedLengthWords that takes int values N and W as arguments and returns an array of N string values that are each strings of W characters from the alphabet.
5.1.21 Random items. Write a static method randomItems that takes an int value N as argument and returns an array of N string values that are each strings of length between 15 and 30 made up of three fields: a 4-character field with one of a set of 10 fixed strings; a 10-char field with one of a set of 50 fixed strings; a 1-character field with one of two given values; and a 15-byte field with random left-justified strings of letters equally likely to be 4 through 15 characters long.
5.1.22 Timings. Compare the running times of MSD string sort and 3-way string quicksort, using various key generators. For fixed-length keys, include LSD string sort.
5.1.23 Array accesses. Compare the number of array accesses used by MSD string sort and 3-way string sort, using various key generators. For fixed-length keys, include LSD string sort.
5.1.24 Rightmost character accessed. Compare the position of the rightmost character accessed for MSD string sort and 3-way string quicksort, using various key generators.
All materials on the site are licensed Creative Commons Attribution-Sharealike 3.0 Unported CC BY-SA 3.0 & GNU Free Documentation License (GFDL)
If you are the copyright holder of any material contained on our site and intend to remove it, please contact our site administrator for approval.
© 2016-2026 All site design rights belong to S.Y.A.