Algorithms (2014)
Five. Strings
5.2 Tries
As with sorting, we can take advantage of properties of strings to develop search methods (symbol-table implementations) that can be more efficient than the general-purpose methods of CHAPTER 3 for typical applications where search keys are strings.
Specifically, the methods that we consider in this section achieve the following performance characteristics in typical applications, even for huge tables:
• Search hits take time proportional to the length of the search key.
• Search misses involve examining only a few characters.
On reflection, these performance characteristics are quite remarkable, one of the crowning achievements of algorithmic technology and a primary factor in enabling the development of the computational infrastructure we now enjoy that has made so much information instantly accessible. Moreover, we can extend the symbol-table API to include character-based operations defined for string keys (but not necessarily for all Comparable types of keys) that are powerful and quite useful in practice, as in the following API:

This API differs from the symbol-table API introduced in CHAPTER 3 in the following aspects:
• We replace the generic type Key with the concrete type String.
• We add three new methods, longestPrefixOf(), keysWithPrefix() and keysThatMatch().
We retain the basic conventions of our symbol-table implementations in CHAPTER 3 (no duplicate or null keys and no null values).
As we saw for sorting with string keys, it is often quite important to be able to work with strings from a specified alphabet. Simple and efficient implementations that are the method of choice for small alphabets turn out to be useless for large alphabets because they consume too much space. In such cases, it is certainly worthwhile to add a constructor that allows clients to specify the alphabet. We will consider the implementation of such a constructor later in this section but omit it from the API for now, in order to concentrate on string keys.
The following descriptions of the three new methods use the keys { she, sells, sea, shells, by, the, sea, shore } to give examples:
• longestPrefixOf() takes a string as argument and returns the longest key in the symbol table that is a prefix of that string. For the keys above, longestPrefixOf("shell") is she and longestPrefixOf("shellsort") is shells.
• keysWithPrefix() takes a string as argument and returns all the keys in the symbol table having that string as prefix. For the keys above, keysWithPrefix("she") is she and shells, and keysWithPrefix("se") is sells and sea.
• keysThatMatch() takes a string as argument and returns all the keys in the symbol table that match that string, in the sense that a period (.) in the argument string matches any character. For the keys above, keysThatMatch(".he") returns she and the, and keysThatMatch("s..") returns she and sea.
We will consider in detail implementations and applications of these operations after we have seen the basic symbol-table methods. These particular operations are representative of what is possible with string keys; we discuss several other possibilities in the exercises.
To focus on the main ideas, we concentrate on put(), get(), and the new methods; we assume (as in CHAPTER 3) default implementations of contains() and isEmpty(); and we leave implementations of size() and delete() for exercises. Since strings are Comparable, extending the API to also include the ordered operations defined in the ordered symbol-table API in CHAPTER 3 is possible (and worthwhile); we leave those implementations (which are generally straightforward) to exercises and booksite code.
Tries
In this section, we consider a search tree known as a trie, a data structure built from the characters of the string keys that allows us to use the characters of the search key to guide the search. The name “trie” is a bit of wordplay introduced by E. Fredkin in 1960 because the data structure is used for retrieval, but we pronounce it “try” to avoid confusion with “tree.” We begin with a high-level description of the basic properties of tries, including search and insert algorithms, and then proceed to the details of the representation and Java implementation.
Basic properties
As with search trees, tries are data structures composed of nodes that contain links that are either null or references to other nodes. Each node is pointed to by just one other node, which is called its parent (except for one node, the root, which has no nodes pointing to it), and each node has Rlinks, where R is the alphabet size. Often, tries have a substantial number of null links, so when we draw a trie, we typically omit null links. Although links point to nodes, we can view each link as pointing to a trie, the trie whose root is the referenced node. Each link corresponds to a character value—since each link points to exactly one node, we label each node with the character value corresponding to the link that points to it (except for the root, which has no link pointing to it). Each node also has a corresponding value, which may be null or the value associated with one of the string keys in the symbol table. Specifically, we store the value associated with each key in the node corresponding to its last character. It is very important to bear in mind the following fact: nodes with null values exist to facilitate search in the trie and do not correspond to keys.An example of a trie is shown at right.
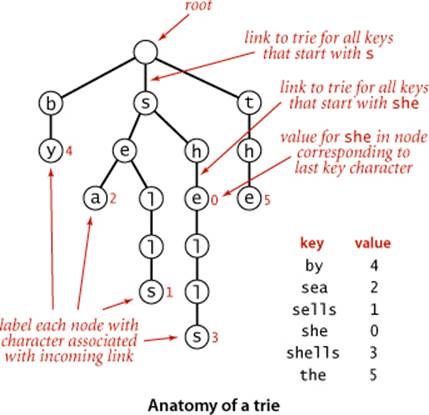
Search in a trie
Finding the value associated with a given string key in a trie is a simple process, guided by the characters in the search key. Each node in the trie has a link corresponding to each possible string character. We start at the root, then follow the link associated with the first character in the key; from that node we follow the link associated with the second character in the key; from that node we follow the link associated with the third character in the key and so forth, until reaching the last character of the key or a null link. At this point, one of the following three conditions holds (refer to the figure above for examples):
• The value at the node corresponding to the last character in the key is not null (as in the searches for shells and she depicted at left above). This result is a search hit—the value associated with the key is the value in the node corresponding to its last character.
• The value in the node corresponding to the last character in the key is null (as in the search for shell depicted at top right above). This result is a search miss: the key is not in the table.
• The search terminated with a null link (as in the search for shore depicted at bottom right above). This result is also a search miss.
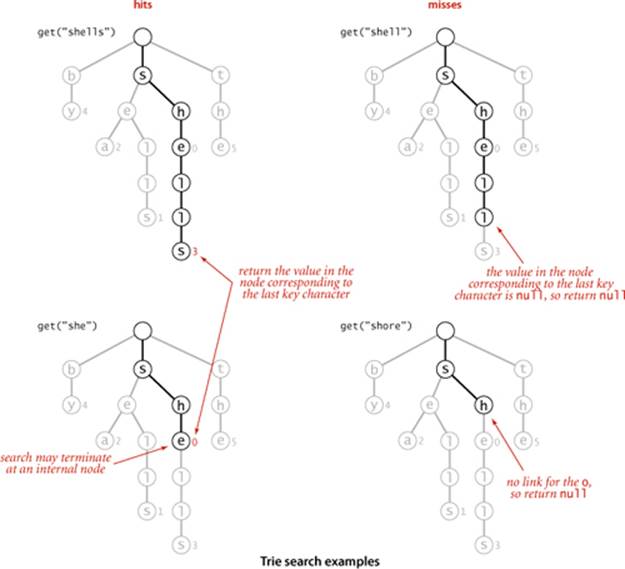
In all cases, the search is accomplished just by examining nodes along a path from the root to another node in the trie.
Insertion into a trie
As with binary search trees, we insert by first doing a search: in a trie that means using the characters of the key to guide us down the trie until reaching the last character of the key or a null link. At this point, one of the following two conditions holds:
• We encountered a null link before reaching the last character of the key. In this case, there is no trie node corresponding to the last character in the key, so we need to create nodes for each of the characters in the key not yet encountered and set the value in the last one to the value to be associated with the key.
• We encountered the last character of the key before reaching a null link. In this case, we set that node’s value to the value to be associated with the key (whether or not that value is null), as usual with our associative array convention.
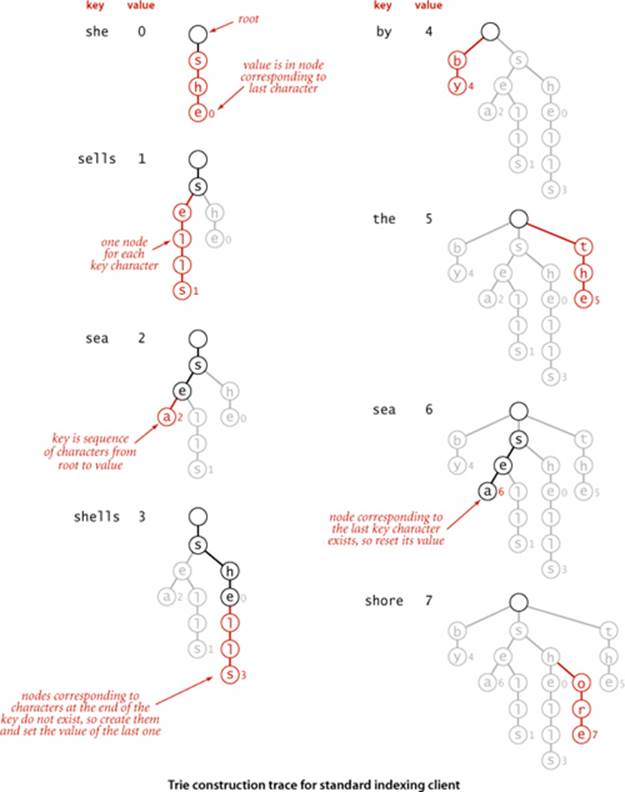
In all cases, we examine or create a node in the trie for each key character. The construction of the trie for our standard indexing client from CHAPTER 3 with the input
she sells sea shells by the sea shore
is shown on the facing page.
Node representation
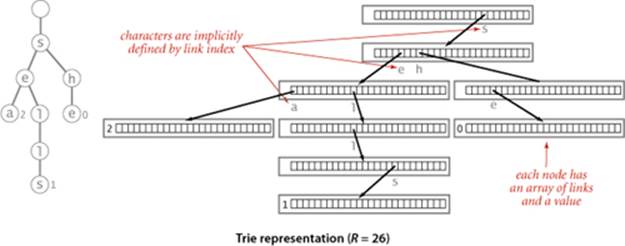
As mentioned at the outset, our trie diagrams do not quite correspond to the data structures our programs will build, because we do not draw null links. Taking null links into account emphasizes the following important characteristics of tries:
• Every node has R links, one for each possible character.
• Characters and keys are implicitly stored in the data structure.
For example, the figure below depicts a trie for keys made up of lowercase letters, with each node having a value and 26 links. The first link points to a subtrie for keys beginning with a, the second points to a subtrie for substrings beginning with b, and so forth. Keys in the trie are implicitly represented by paths from the root that end at nodes with non-null values. For example, the string sea is associated with the value 2 in the trie because the 19th link in the root (which points to the trie for all keys that start with s) is not null and the 5th link in the node that link refers to (which points to the trie for all keys that start with se) is not null, and the first link in the node that link refers to (which points to the trie for all keys that starts with sea) has the value 2. Neither the string sea nor the characters s, e, and a are stored in the data structure. Indeed, the data structure contains no characters or strings, just links and values. Since the parameter R plays such a critical role, we refer to a trie for an R-character alphabet as an R-way trie.
WITH THESE PREPARATIONS, the symbol-table implementation TrieST on the facing page is straightforward. It uses recursive methods like those that we used for search trees in CHAPTER 3, based on a private Node class with instance variable val for client values and an array next[] of Node references. The methods are compact recursive implementations that are worthy of careful study. Next, we discuss implementations of the constructor that takes an Alphabet as argument and the methods size(), keys(), longestPrefixOf(), keysWithPrefix(), keysThatMatch(), and delete(). These are also easily understood recursive methods, each slightly more complicated than the last.
Size
As for the binary search trees of CHAPTER 3, three straightforward options are available for implementing size():
• An eager implementation where we maintain the number of keys in an instance variable N.
• A very eager implementation where we maintain the number of keys in a subtrie as a node instance variable that we update after the recursive calls in put() and delete().
• A lazy recursive implementation like the one at right. It traverses all of the nodes in the trie, counting the number having a non-null value.
Lazy recursive size() for tries
public int size()
{ return size(root); }
private int size(Node x)
{
if (x == null) return 0;
int cnt = 0;
if (x.val != null) cnt++;
for (char c = 0; c < R; c++)
cnt += size(next[c]);
return cnt;
}
As with binary search trees, the lazy implementation is instructive but should be avoided because it can lead to performance problems for clients. The eager implementations are explored in the exercises.
Algorithm 5.4 Trie symbol table
public class TrieST<Value>
{
private static int R = 256; // radix
private Node root = new Node(); // root of trie
private static class Node
{
private Object val;
private Node[] next = new Node[R];
}
public Value get(String key)
{
Node x = get(root, key, 0);
if (x == null) return null;
return (Value) x.val;
}
private Node get(Node x, String key, int d)
{ // Return node associated with key in the subtrie rooted at x.
if (x == null) return null;
if (d == key.length()) return x;
char c = key.charAt(d); // Use dth key char to identify subtrie.
return get(x.next[c], key, d+1);
}
public void put(String key, Value val)
{ root = put(root, key, val, 0); }
private Node put(Node x, String key, Value val, int d)
{ // Change value associated with key if in subtrie rooted at x.
if (x == null) x = new Node();
if (d == key.length()) { x.val = val; return x; }
char c = key.charAt(d); // Use dth key char to identify subtrie.
x.next[c] = put(x.next[c], key, val, d+1);
return x;
}
}
This code uses an R-way trie to implement a symbol table. Additional methods in the string symbol-table API of page 730 are presented in the next several pages. Modifying this code to handle keys from specialized alphabets is straighforward (see page 741). The value in Node has to be an Object because Java does not support arrays of generics; we cast values back to Value in get().
Collecting keys
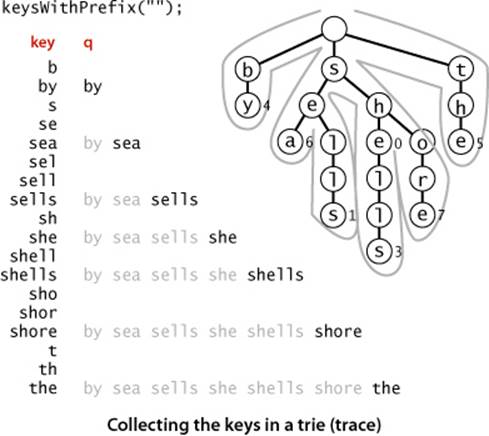
Because characters and keys are represented implicitly in tries, providing clients with the ability to iterate through the keys presents a challenge. As with binary search trees, we accumulate the string keys in a Queue, but for tries we need to create explicit representations of all of the string keys, not just find them in the data structure. We do so with a recursive private method collect() that is similar to size() but also maintains a string with the sequence of characters on the path from the root. Each time that we visit a node via a call to collect() with that node as first argument, the second argument is the string associated with that node (the sequence of characters on the path from the root to the node). To visit a node, we add its associated string to the queue if its value is not null, then visit (recursively) all the nodes in its array of links, one for each possible character. To create the key for each call, we append the character corresponding to the link to the current key. We use this collect() method to collect keys for both the keys() and the keysWithPrefix() methods in the API. To implement keys() we call keysWithPrefix() with the empty string as argument; to implementkeysWithPrefix(), we call get() to find the trie node corresponding to the given prefix (null if there is no such node), then use the collect() method to complete the job. The diagram at left shows a trace of collect() (or keysWithPrefix("")) for an example trie, giving the value of the second argument key and the contents of the queue for each call to collect(). The diagram at the top of the facing page illustrates the process for keysWithPrefix("sh").
Collecting the keys in a trie
public Iterable<String> keys()
{ return keysWithPrefix(""); }
public Iterable<String> keysWithPrefix(String pre)
{
Queue<String> q = new Queue<String>();
collect(get(root, pre, 0), pre, q);
return q;
}
private void collect(Node x, String pre,
Queue<String> q)
{
if (x == null) return;
if (x.val != null) q.enqueue(pre);
for (char c = 0; c < R; c++)
collect(x.next[c], pre + c, q);
}
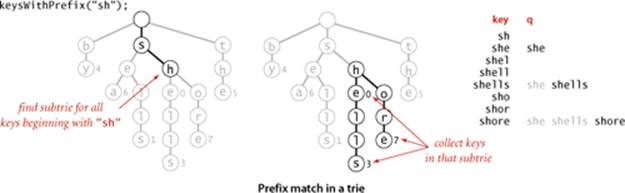
Wildcard match
To implement keysThatMatch(), we use a similar process, but add an argument specifying the pattern to collect() and add a test to make a recursive call for all links when the pattern character is a wildcard or only for the link corresponding to the pattern character otherwise, as in the code below. Note also that we do not need to consider keys longer than the pattern.
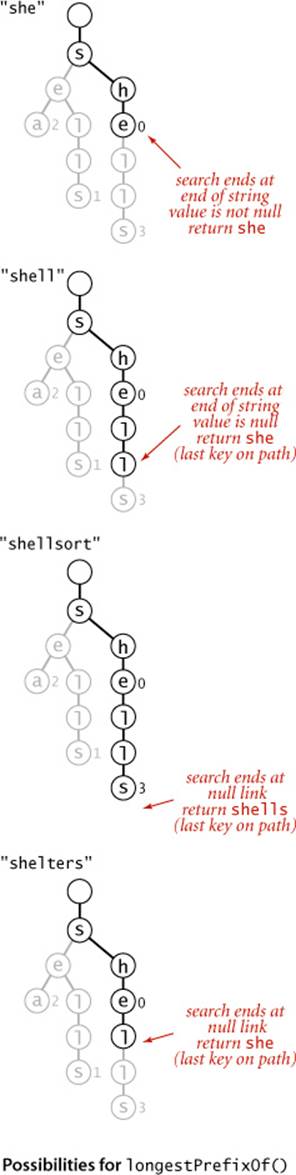
Longest prefix
To find the longest key that is a prefix of a given string, we use a recursive method like get() that keeps track of the length of the longest key found on the search path (by passing it as a parameter to the recursive method, updating the value whenever a node with a non-null value is encountered). The search ends when the end of the string or a null link is encountered, whichever comes first.
Wildcard match in a trie
public Iterable<String> keysThatMatch(String pat)
{
Queue<String> q = new Queue<String>();
collect(root, "", pat, q);
return q;
}
private void collect(Node x, String pre, String pat, Queue<String> q)
{
int d = pre.length();
if (x == null) return;
if (d == pat.length() && x.val != null) q.enqueue(pre);
if (d == pat.length()) return;
char next = pat.charAt(d);
for (char c = 0; c < R; c++)
if (next == '.' || next == c)
collect(x.next[c], pre + c, pat, q);
}
Matching the longest prefix of a given string
public String longestPrefixOf(String s)
{
int length = search(root, s, 0, 0);
return s.substring(0, length);
}
private int search(Node x, String s, int d, int length)
{
if (x == null) return length;
if (x.val != null) length = d;
if (d == s.length()) return length;
char c = s.charAt(d);
return search(x.next[c], s, d+1, length);
}
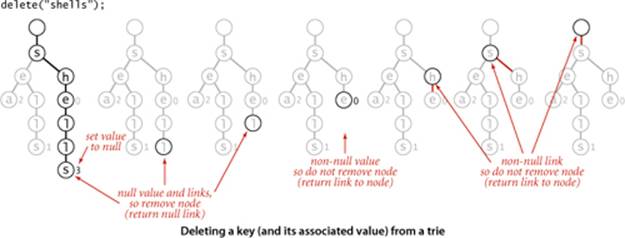
Deletion
The first step needed to delete a key-value pair from a trie is to use a normal search to find the node corresponding to the key and set the corresponding value to null. If that node has a non-null link to a child, then no more work is required; if all the links are null, we need to remove the node from the data structure. If doing so leaves all the links null in its parent, we need to remove that node, and so forth. The implementation on the facing page demonstrates that this action can be accomplished with remarkably little code, using our standard recursive setup: after the recursive calls for a node x, we return null if the client value and all of the links in a node are null; otherwise we return x.
Alphabet
As usual, ALGORITHM 5.4 is coded for Java String keys, but it is a simple matter to modify the implementation to handle keys taken from any alphabet, as follows:
• Implement a constructor that takes an Alphabet as argument, which sets an Alphabet instance variable to that argument value and the instance variable R to the number of characters in the alphabet.
• Use the toIndex() method from Alphabet in get() and put() to convert string characters to indices between 0 and R − 1.
• Use the toChar() method from Alphabet to convert indices between 0 and R − 1 to char values. This operation is not needed in get() and put() but is important in the implementations of keys(), keysWithPrefix(), and keysThatMatch().
Deleting a key (and its associated value) from a trie
public void delete(String key)
{ root = delete(root, key, 0); }
private Node delete(Node x, String key, int d)
{
if (x == null) return null;
if (d == key.length())
x.val = null;
else
{
char c = key.charAt(d);
x.next[c] = delete(x.next[c], key, d+1);
}
if (x.val != null) return x;
for (char c = 0; c < R; c++)
if (x.next[c] != null) return x;
return null;
}
With these changes, you can save a considerable amount of space (use only R links per node) when you know that your keys are taken from a small alphabet, at the cost of the time required to do the conversions between characters and indices.
THE CODE THAT WE HAVE CONSIDERED is a compact and complete implementation of the string symbol-table API that has broadly useful practical applications. Several variations and extensions are discussed in the exercises. Next, we consider basic properties of tries, and some limitations on their utility.
Properties of tries
As usual, we are interested in knowing the amount of time and space required to use tries in typical applications. Tries have been extensively studied and analyzed, and their basic properties are relatively easy to understand and to apply.
Proposition F. The linked structure (shape) of a trie is independent of the key insertion/deletion order: there is a unique trie for any given set of keys.
Proof: Immediate, by induction on the subtries.
This fundamental fact is a distinctive feature of tries: for all of the other search tree structures that we have considered so far, the tree that we construct depends both on the set of keys and on the order in which we insert those keys.
Worst-case time bound for search and insert
How long does it take to find the value associated with a key? For BSTs, hashing, and other methods in CHAPTER 3, we needed mathematical analysis to study this question, but for tries it is very easy to answer:
Proposition G. The number of array accesses when searching in a trie or inserting a key into a trie is at most 1 plus the length of the key.
Proof: Immediate from the code. The recursive get() and put() implementations carry an argument d that starts at 0, increments for each call, and is used to stop the recursion when it reaches the key length.
From a theoretical standpoint, the implication of PROPOSITION G is that tries are optimal for search hit—we could not expect to do better than search time proportional to the length of the search key. Whatever algorithm or data structure we are using, we cannot know that we have found a key that we seek without examining all of its characters. From a practical standpoint this guarantee is important because it does not depend on the number of keys: when we are working with 7-character keys like license plate numbers, we know that we need to examine at most 8 nodes to search or insert; when we are working with 20-digit account numbers, we only need to examine at most 21 nodes to search or insert.
Expected time bound for search miss
Suppose that we are searching for a key in a trie and find that the link in the root node that corresponds to its first character is null. In this case, we know that the key is not in the table on the basis of examining just one node. This case is typical: one of the most important properties of tries is that search misses typically require examining just a few nodes. If we assume that the keys are drawn from the random string model (each character is equally likely to have any one of the R different character values) we can prove this fact:
Proposition H. The average number of nodes examined for search miss in a trie built from N random keys over an alphabet of size R is ~logR N.
Proof sketch (for readers who are familiar with probabilistic analysis): The probability that each of the N keys in a random trie differs from a random search key in at least one of the leading t characters is (1 − R−t)N. Subtracting this quantity from 1 gives the probability that one of the keys in the trie matches the search key in all of the leading t characters. In other words, 1 − (1 − R−t)N is the probability that the search requires more than t character compares. From probabilistic analysis, the sum for t = 0, 1, 2, ... of the probabilities that an integer random variable is >tis the average value of that random variable, so the average search cost is
1 − (1 − R−1)N + 1 − (1 − R−2)N + ... + 1 − (1 − R−t)N + ...
Using the elementary approximation (1−1/x)x ~ e−1, we find the search cost to be approximately
(1 − e−N/R1) + (1 − e−N/R2) + ... + (1 − e−N/Rt) + ...
The summand is extremely close to 1 for approximately logR N terms with Rt substantially smaller than N; it is extremely close to 0 for all the terms with Rt substantially greater than N; and it is somewhere between 0 and 1 for the few terms with Rt ≈ N. So the grand total is about logR N.
From a practical standpoint, the most important implication of this proposition is that search miss does not depend on the key length. For example, it says that unsuccessful search in a trie built with 1 million random keys will require examining only three or four nodes, whether the keys are 7-digit license plates or 20-digit account numbers. While it is unreasonable to expect truly random keys in practical applications, it is reasonable to hypothesize that the behavior of trie algorithms for keys in typical applications is described by this model. Indeed, this sort of behavior is widely seen in practice and is an important reason for the widespread use of tries.
Space
How much space is needed for a trie? Addressing this question (and understanding how much space is available) is critical to using tries effectively.
Proposition I. The number of links in a trie is between RN and RNw, where w is the average key length.
Proof: Every key in the trie has a node containing its associated value that also has R links, so the number of links is at least RN. If the first characters of all the keys are different, then there is a node with R links for every key character, so the number of links is R times the total number of key characters, or RNw.
The table on the facing page shows the costs for some typical applications that we have considered. It illustrates the following rules of thumb for tries:
• When keys are short, the number of links is close to RN.
• When keys are long, the number of links is close to RNw.
• Therefore, decreasing R can save a huge amount of space.
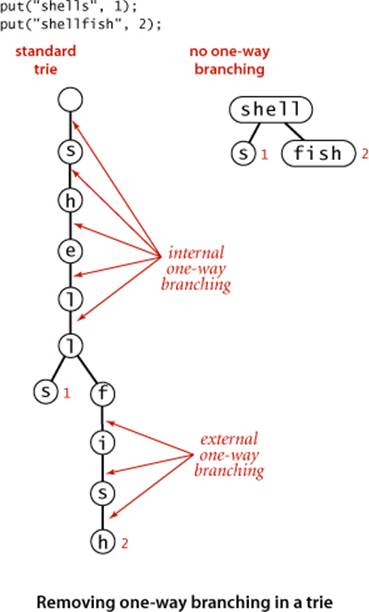
A more subtle message of this table is that it is important to understand the properties of the keys to be inserted before deploying tries in an application.
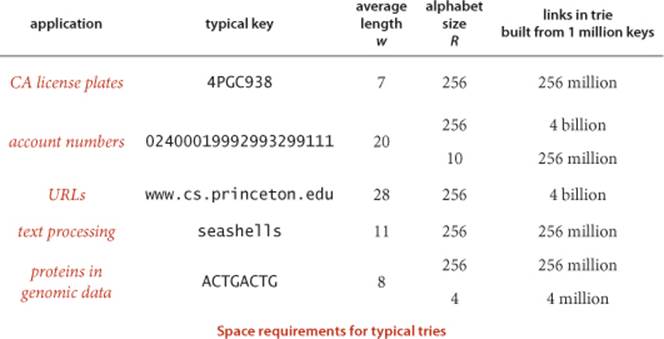
One-way branching
The primary reason that trie space is excessive for long keys is that long keys tend to have long tails in the trie, with each node having a single link to the next node (and, therefore, R−1 null links). This situation known as external one-way branching is not difficult to correct (see EXERCISE 5.2.11). A trie might also have internal one-way branching. For example, two long keys may be equal except for their last character. This situation is a bit more difficult to address (see EXERCISE 5.2.12). These changes can make trie space usage a less important factor than for the straightforward implementation that we have considered, but they are not necessarily effective in practical applications. Next, we consider an alternative approach to reducing space usage for tries.
THE BOTTOM LINE is this: do not try to use ALGORITHM 5.4 for large numbers of long keys taken from large alphabets, because it will require space proportional to R times the total number of key characters. Otherwise, if you can afford the space, trie performance is difficult to beat.
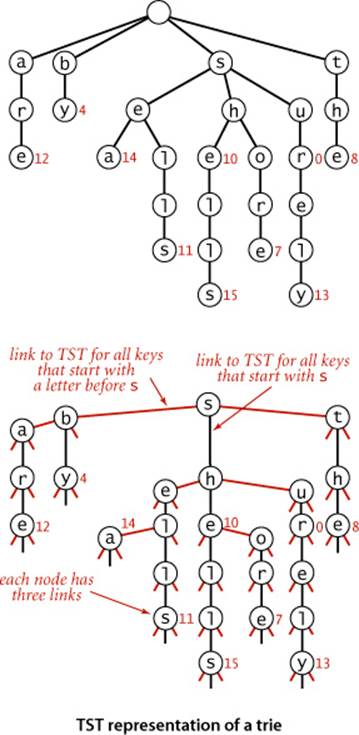
Ternary search tries (TSTs)
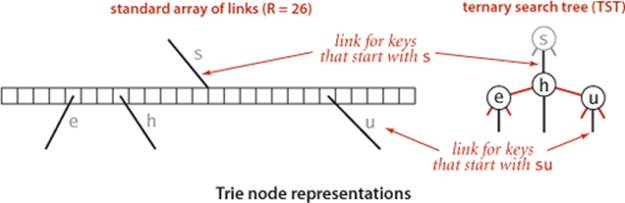
To help us avoid the excessive space cost associated with R-way tries, we now consider an alternative representation: the ternary search trie (TST). In a TST, each node has a character, three links, and a value. The three links correspond to keys whose current characters are less than, equal to, or greater than the node’s character. In the R-way tries of ALGORITHM 5.4, trie nodes are represented by R links, with the character corresponding to each non-null link implictly represented by its index. In the corresponding TST, characters appear explicitly in nodes—we find characters corresponding to keys only when we are traversing the middle links.
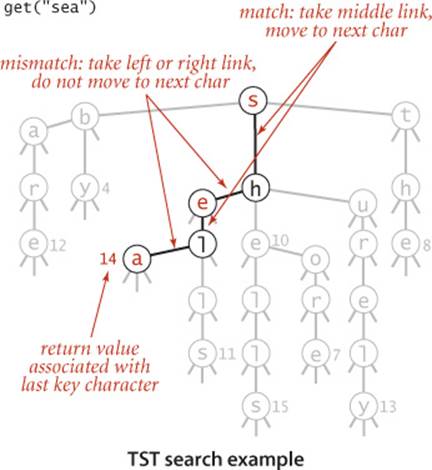
Search and insert
The search and insert code for implementing our symbol-table API with TSTs writes itself. To search, we compare the first character in the key with the character at the root. If it is less, we take the left link; if it is greater, we take the right link; and if it is equal, we take the middle link and move to the next search key character. In each case, we apply the algorithm recursively. We terminate with a search miss if we encounter a null link or if the node where the search ends has a null value, and we terminate with a search hit if the node where the search ends has a non-null value. To insert a new key, we search, then add new nodes for the characters in the tail of the key, just as we did for tries. ALGORITHM 5.5 gives the details of the implementation of these methods.
Using this arrangement is equivalent to implementing each R-way trie node as a binary search tree that uses as keys the characters corresponding to non-null links. By contrast, ALGORITHM 5.4 uses a key-indexed array. A TST and its corresponding trie are illustrated above. Continuing the correspondence described in CHAPTER 3 between binary search trees and sorting algorithms, we see that TSTs correspond to 3-way string quicksort in the same way that BSTs correspond to quicksort and tries correspond to MSD sorting. The figures on page 714 and 721, which show the recursive call structure for MSD and 3-way string quicksort (respectively), correspond precisely to the trie and TST drawn on page 746 for that set of keys. Space for links in tries corresponds to the space for counters in string sorting; 3-way branching provides an effective solution to both problems.
Algorithm 5.5 TST symbol table
public class TST<Value>
{
private Node root; // root of trie
private class Node
{
char c; // character
Node left, mid, right; // left, middle, and right subtries
Value val; // value associated with string
}
public Value get(String key) // same as for tries (See page 737).
private Node get(Node x, String key, int d)
{
if (x == null) return null;
char c = key.charAt(d);
if (c < x.c) return get(x.left, key, d);
else if (c > x.c) return get(x.right, key, d);
else if (d < key.length() - 1)
return get(x.mid, key, d+1);
else return x;
}
public void put(String key, Value val)
{ root = put(root, key, val, 0); }
private Node put(Node x, String key, Value val, int d)
{
char c = key.charAt(d);
if (x == null) { x = new Node(); x.c = c; }
if (c < x.c) x.left = put(x.left, key, val, d);
else if (c > x.c) x.right = put(x.right, key, val, d);
else if (d < key.length() - 1)
x.mid = put(x.mid, key, val, d+1);
else x.val = val;
return x;
}
}
This implementation uses a char value c and three links per node to build string search tries where subtries have keys whose first character is less than c (left), equal to c (middle), and greater than c (right).
Properties of TSTs
A TST is a compact representation of an R-way trie, but the two data structures have remarkably different properties. Perhaps the most important difference is that PROPOSITION F does not hold for TSTs: the BST representations of each trie node depend on the order of key insertion, as with any other BST.
Space
The most important property of TSTs is that they have just three links in each node, so a TST requires far less space than the corresponding trie.
Proposition J. The number of links in a TST built from N string keys of average length w is between 3N and 3Nw.
Proof. Immediate, by the same argument as for PROPOSITION I.
Actual space usage is generally less than the upper bound of three links per character, because keys with common prefixes share nodes at high levels in the tree.
Search cost
To determine the cost of search (and insert) in a TST, we multiply the cost for the corresponding trie by the cost of traversing the BST representation of each trie node.
Proposition K. A search miss in a TST built from N random string keys requires ~ln N character compares, on the average. A search hit or an insertion in a TST uses ~ln N character compare for each character in the search key.
Proof: The search hit/insertion cost is immediate from the code. The search miss cost is a consequence of the same arguments discussed in the proof sketch of PROPOSITION H. We assume that all but a constant number of the nodes on the search path (a few at the top) act as random BSTs on R character values with average path length ln R, so we multiply the time cost logR N = ln N / ln R by ln R.
In the worst case, a node might be a full R-way node that is unbalanced, stretched out like a singly linked list, so we would need to multiply by a factor of R. More typically, we might expect to do ln R or fewer character compares at the first level (since the root node behaves like a random BST on the R different character values) and perhaps at a few other levels (if there are keys with a common prefix and up to R different values on the character following the prefix), and to do only a few compares for most characters (since most trie nodes are sparsely populated with non-null links). Search misses are likely to involve only a few character compares, ending at a null link high in the trie, and search hits involve only about one compare per search key character, since most of them are in nodes with one-way branching at the bottom of the trie.
Alphabet
The prime virtue of using TSTs is that they adapt gracefully to irregularities in search keys that are likely to appear in practical applications. In particular, note that there is no reason to allow for strings to be built from a client-supplied alphabet, as was crucial for tries. There are two main effects. First, keys in practical applications come from large alphabets, and usage of particular characters in the character sets is far from uniform. With TSTs, we can use a 256-character ASCII encoding or a 65,536-character Unicode encoding without having to worry about the excessive costs of nodes with 256- or 65,536-way branching, and without having to determine which sets of characters are relevant. Unicode strings in non-Roman alphabets can have thousands of characters—TSTs are especially appropriate for standard Java String keys that consist of such characters. Second, keys in practical applications often have a structured format, differing from application to application, perhaps using only letters in one part of the key, only digits in another part of the key. In our CA license plate example, the second, third, and fourth characters are uppercase letter (R = 26) and the other characters are decimal digits (R = 10). In a TST for such keys, some of the trie nodes will be represented as 10-node BSTs (for places where all keys have digits) and others will be represented as 26-node BSTs (for places where all keys have letters). This structure develops automatically, without any need for special analysis of the keys.
Prefix match, collecting keys, and wildcard match
Since a TST represents a trie, implementations of longestPrefixOf(), keys(), keysWithPrefix(), and keysThatMatch() are easily adapted from the corresponding code for tries in the previous section, and a worthwhile exercise for you to cement your understanding of both tries and TSTs (see EXERCISE 5.2.9). The same tradeoff as for search (linear memory usage but an extra ln R multiplicative factor per character compare) holds.
Deletion
The delete() method for TSTs requires more work. Essentially, each character in the key to be deleted belongs to a BST. In a trie, we could remove the link corresponding to a character by setting the corresponding entry in the array of links to null; in a TST, we have to use BST node deletion to remove the node corresponding to the character.
Hybrid TSTs
An easy improvement to TST-based search is to use a large explicit multiway node at the root. The simplest way to proceed is to keep a table of R TSTs: one for each possible value of the first character in the keys. If R is not large, we might use the first two letters of the keys (and a table of size R2). For this method to be effective, the leading digits of the keys must be well-distributed. The resulting hybrid search algorithm corresponds to the way that a human might search for names in a telephone book. The first step is a multiway decision (“Let’s see, it starts with ‘A’,”), followed perhaps by some two-way decisions (“It’s before ‘Andrews,’ but after ‘Aitken,’”), followed by sequential character matching (“‘Algonquin,’ ... No, ‘Algorithms’ isn’t listed, because nothing starts with ‘Algor’!”). These programs are likely to be among the fastest available for searching with string keys.
One-way branching
Just as with tries, we can make TSTs more efficient in their use of space by putting keys in leaves at the point where they are distinguished and by eliminating one-way branching between internal nodes.
Proposition L. A search or an insertion in a TST built from N random string keys with no external one-way branching and Rt-way branching at the root requires roughly ln N − t ln R character compares, on the average.
Proof: These rough estimates follow from the same argument we used to prove PROPOSITION K. We assume that all but a constant number of the nodes on the search path (a few at the top) act as random BSTs on R character values, so we multiply the time cost by ln R.
DESPITE THE TEMPTATION to tune the algorithm to peak performance, we should not lose sight of the fact that one of the most attractive features of TSTs is that they free us from having to worry about application-specific dependencies, often providing good performance without any tuning.
Which string symbol-table implementation should I use?
As with string sorting, we are naturally interested in how the string-searching methods that we have considered compare to the general-purpose methods that we considered in CHAPTER 3. The following table summarizes the important characteristics of the algorithms that we have discussed in this section (the rows for BSTs, red-black BSTs and hashing are included from CHAPTER 3, for comparison). For a particular application, these entries must be taken as indicative, not definitive, since so many factors (such as characteristics of keys and mix of operations) come into play when studying symbol-table implementations.
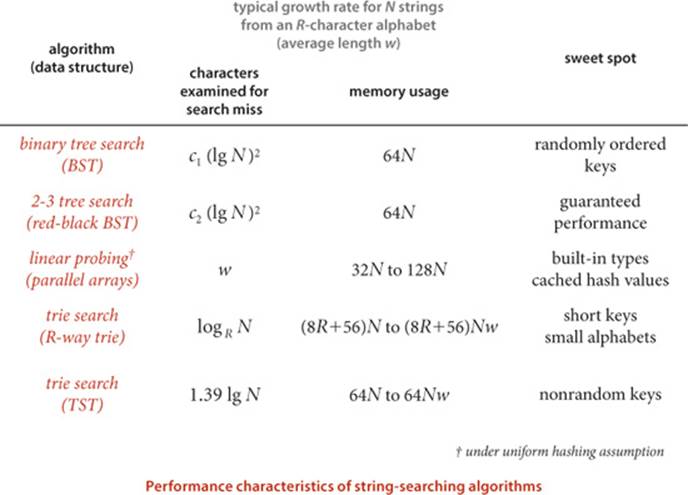
If space is available, R-way tries provide the fastest search, essentially completing the job with a constant number of character compares. For large alphabets, where space may not be available for R-way tries, TSTs are preferable, since they use a logarithmic number of character compares, while BSTs use a logarithmic number of key compares. Hashing can be competitive, but, as usual, cannot support ordered symbol-table operations or extended character-based API operations such as prefix or wildcard match.
Q&A
Q. Does the Java system sort use one of these methods for searching with String keys?
A. No.
Exercises
5.2.1 Draw the R-way trie that results when the keys
no is th ti fo al go pe to co to th ai of th pa
are inserted in that order into an initially empty trie (do not draw null links).
5.2.2 Draw the TST that results when the keys
no is th ti fo al go pe to co to th ai of th pa
are inserted in that order into an initially empty TST.
5.2.3 Draw the R-way trie that results when the keys
now is the time for all good people to come to the aid of
are inserted in that order into an initially empty trie (do not draw null links).
5.2.4 Draw the TST that results when the keys
now is the time for all good people to come to the aid of
are inserted in that order into an initially empty TST.
5.2.5 Develop nonrecursive versions of TrieST and TST.
5.2.6 Implement the following API, for a StringSET data type:

Creative Problems
5.2.7 Empty string in TSTs. The code in TST does not handle the empty string properly. Explain the problem and suggest a correction.
5.2.8 Ordered operations for tries. Implement the floor(), ceiling(), rank(), and select() (from our standard ordered ST API from CHAPTER 3) for TrieST.
5.2.9 Extended operations for TSTs. Implement keys() and the extended operations introduced in this section—longestPrefixOf(), keysWithPrefix(), and keysThatMatch()—for TST.
5.2.10 Size. Implement very eager size() (that keeps in each node the number of keys in its subtree) for TrieST and TST.
5.2.11 External one-way branching. Add code to TrieST and TST to eliminate external one-way branching.
5.2.12 Internal one-way branching. Add code to TrieST and TST to eliminate internal one-way branching.
5.2.13 Hybrid TST with R2-way branching at the root. Add code to TST to do multiway branching at the first two levels, as described in the text.
5.2.14 Unique substrings of length L. Write a TST client that reads in text from standard input and calculates the number of unique substrings of length L that it contains. For example, if the input is cgcgggcgcg, then there are five unique substrings of length 3: cgc, cgg, gcg, ggc, and ggg. Hint: Use the string method substring(i, i + L) to extract the ith substring, then insert it into a symbol table.
5.2.15 Unique substrings. Write a TST client that reads in text from standard input and calculates the number of distinct substrings of any length. This can be done very efficiently with a suffix tree—see CHAPTER 6.
5.2.16 Document similarity. Write a TST client with a static method that takes an int value k and two file names as command-line arguments and computes the k-similarity of the two documents: the Euclidean distance between the frequency vectors defined by the number of occurrences of each k-gram divided by the number of trigrams. Include a static method main() that takes an int value k as command-line argument and a list of file names from standard input and prints a matrix showing the k-similarity of all pairs of documents.
5.2.17 Spell checking. Write a TST client SpellChecker that takes as command-line argument the name of a file containing a dictionary of words in the English language, and then reads a string from standard input and prints out any word that is not in the dictionary. Use a string set.
5.2.18 Whitelist. Write a TST client that solves the whitelisting problem presented in SECTION 1.1 and revisited in SECTION 3.5 (see page 491).
5.2.19 Random phone numbers. Write a TrieST client (with R = 10) that takes as command line argument an int value N and prints N random phone numbers of the form (xxx) xxx-xxxx. Use a symbol table to avoid choosing the same number more than once. Use the file AreaCodes.txt from the booksite to avoid printing out bogus area codes.
5.2.20 Contains prefix. Add a method containsPrefix() to StringSET (see EXERCISE 5.2.6) that takes a string s as input and returns true if there is a string in the set that contains s as a prefix.
5.2.21 Substring matches. Given a list of (short) strings, your goal is to support queries where the user looks up a string s and your job is to report back all strings in the list that contain s. Design an API for this task and develop a TST client that implements your API. Hint: Insert the suffixes of each word (e.g., string, tring, ring, ing, ng, g) into the TST.
5.2.22 Typing monkeys. Suppose that a typing monkey creates random words by appending each of 26 possible letter with probability p to the current word and finishes the word with probability 1 − 26p. Write a program to estimate the frequency distribution of the lengths of words produced. If "abc" is produced more than once, count it only once.
Experiments
5.2.23 Duplicates (revisited again). Redo EXERCISE 3.5.30 using StringSET (see EXERCISE 5.2.6) instead of HashSET. Compare the running times of the two approaches. Then use Dedup to run the experiments for N = 107, 108, and 109, repeat the experiments for random long values and discuss the results.
5.2.24 Spell checker. Redo EXERCISE 3.5.31, which uses the file dictionary.txt from the booksite and the BlackFilter client on page 491 to print all misspelled words in a text file. Compare the performance of TrieST and TST for the file WarAndPeace.txt with this client and discuss the results.
5.2.25 Dictionary. Redo EXERCISE 3.5.32: Study the performance of a client like LookupCSV (using TrieST and TST) in a scenario where performance matters. Specifically, design a query-generation scenario instead of taking commands from standard input, and run performance tests for large inputs and large numbers of queries.
5.2.26 Indexing. Redo EXERCISE 3.5.33: Study a client like LookupIndex (using TrieST and TST) in a scenario where performance matters. Specifically, design a query-generation scenario instead of taking commands from standard input, and run performance tests for large inputs and large numbers of queries.
All materials on the site are licensed Creative Commons Attribution-Sharealike 3.0 Unported CC BY-SA 3.0 & GNU Free Documentation License (GFDL)
If you are the copyright holder of any material contained on our site and intend to remove it, please contact our site administrator for approval.
© 2016-2026 All site design rights belong to S.Y.A.