Algorithms (2014)
Five. Strings
5.4 Regular Expressions
IN MANY APPLICATIONS, we need to do substring searching with somewhat less than complete information about the pattern to be found. A user of a text editor may wish to specify only part of a pattern, or to specify a pattern that could match a few different words, or to specify that any one of a number of patterns would do. A biologist might search for a genomic sequence satisfying certain conditions. In this section we will consider how pattern matching of this type can be done efficiently.
The algorithms in the previous section fundamentally depend on complete specification of the pattern, so we have to consider different methods. The basic mechanisms we will consider make possible a very powerful string-searching facility that can match complicated M-character patterns inN-character text strings in time proportional to MN in the worst case, and much faster for typical applications.
First, we need a way to describe the patterns: a rigorous way to specify the kinds of partial-substring-searching problems suggested above. This specification needs to involve more powerful primitive operations than the “check if the ith character of the text string matches the jth character of the pattern” operation used in the previous section. For this purpose, we use regular expressions, which describe patterns in combinations of three natural, basic, and powerful operations.
Programmers have used regular expressions for decades. With the explosive growth of search opportunities on the web, their use is becoming even more widespread. We will discuss a number of specific applications at the beginning of the section, not only to give you a feeling for their utility and power, but also to enable you to become more familiar with their basic properties.
As with the KMP algorithm in the previous section, we consider the three basic operations in terms of an abstract machine that can search for patterns in a text string. Then, as before, our pattern-matching algorithm will construct such a machine and then simulate its operation. Naturally, pattern-matching machines are typically more complicated than KMP DFAs, but not as complicated as you might expect.
As you will see, the solution we develop to the pattern-matching problem is intimately related to fundamental processes in computer science. For example, the method we will use in our program to perform the string-searching task implied by a given pattern description is akin to the method used by the Java system to transform a given Java program into a machine-language program for your computer. We also encounter the concept of nondeterminism, which plays a critical role in the search for efficient algorithms (see CHAPTER 6).
Describing patterns with regular expressions
We focus on pattern descriptions made up of characters that serve as operands for three fundamental operations. In this context, we use the word language specifically to refer to a set of strings (possibly infinite) and the word pattern to refer to a language specification. The rules that we consider are quite analogous to familiar rules for specifying arithmetic expressions.
Concatenation
The first fundamental operation is the one used in the last section. When we write AB, we are specifying the language {AB} that has one two-character string, formed by concatenating A and B.
Or
The second fundamental operation allows us to specify alternatives in the pattern. If we have an or between two alternatives, then both are in the language. We will use the vertical bar symbol | to denote this operation. For example, A|B specifies the language {A, B} and A|E|I|O|U specifies the language {A, E, I, O, U}. Concatenation has higher precedence than or, so AB|BCD specifies the language {AB, BCD}.
Closure
The third fundamental operation allows parts of the pattern to be repeated arbitrarily. The closure of a pattern is the language of strings formed by concatenating the pattern with itself any number of times (including zero). We denote closure by placing a * after the pattern to be repeated. Closure has higher precedence than concatenation, so AB* specifies the language consisting of strings with an A followed by 0 or more Bs, while A*B specifies the language consisting of strings with 0 or more As followed by a B. The empty string, which we denote by ![]() , is found in every text string (and in A*).
, is found in every text string (and in A*).
Parentheses
We use parentheses to override the default precedence rules. For example, C(AC|B)D specifies the language {CACD, CBD}; (A|C)((B|C)D) specifies the language {ABD, CBD, ACD, CCD}; and (AB)* specifies the language of strings formed by concatenating any number of occurrences of AB, including no occurrences: {![]() , AB, ABAB, . . .}.
, AB, ABAB, . . .}.

These simple rules allow us to write down REs that, while complicated, clearly and completely describe languages (see the table at right for a few examples). Often, a language can be simply described in some other way, but discovering such a description can be a challenge. For example, the RE in the bottom row of the table specifies the subset of (A|B)* with an even number of Bs.
REGULAR EXPRESSIONS ARE EXTREMELY SIMPLE formal objects, even simpler than the arithmetic expressions that you learned in grade school. Indeed, we will take advantage of their simplicity to develop compact and efficient algorithms for processing them. Our starting point will be the following formal definition:
Definition. A regular expression (RE) is either
• The empty set Ø.
• The empty string ![]()
• A single character
• A regular expression enclosed in parentheses
• Two or more concatenated regular expressions
• Two or more regular expressions separated by the or operator (|)
• A regular expression followed by the closure operator (*)
This definition describes the syntax of regular expressions, telling us what constitutes a legal regular expression. The semantics that tells us the meaning of a given regular expression is the point of the informal descriptions that we have given in this section. For review, we summarize these by continuing the formal definition:
Definition. Each RE represents a set of strings, defined as follows:
• The empty set Ørepresents the set of strings with 0 elements.
• The empty string ![]() represents the set of strings with one element, the string with zero characters.
represents the set of strings with one element, the string with zero characters.
• A single character represents the set of strings with one element, itself.
• An RE enclosed in parentheses represents the same set of strings as the RE without the parentheses.
• The RE consisting of two concatenated REs represents the cross product of the sets of strings represented by the individual components (all possible strings that can be formed by taking one string from each and concatenating them, in the same order as the REs).
• The RE consisting of the or of two REs represents the union of the sets represented by the individual components.
• The RE consisting of the closure of an RE represents ![]() or the union of the sets represented by the concatenation of any number of copies of the RE.
or the union of the sets represented by the concatenation of any number of copies of the RE.
There are many different ways to describe each language: we must try to specify succinct patterns just as we try to write compact programs and implement efficient algorithms.
Shortcuts
Typical applications adopt various additions to these basic rules to enable us to develop succinct descriptions of languages of practical interest. From a theoretical standpoint, these are each simply a shortcut for a sequence of operations involving many operands; from a practical standpoint, they are a quite useful extention to the basic operations that enable us to develop compact patterns.
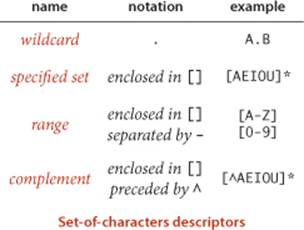
Set-of-characters descriptors
It is often convenient to be able to use a single character or a short sequence to directly specify sets of characters. The dot character (.) is a wildcard that represents any single character. A sequence of characters within square brackets represents any one of those characters. The sequence may also be specified as a range of characters. If preceded by a ^, a sequence within square brackets represents any character but one of those characters. These notations are simply shortcuts for a sequence of or operations.
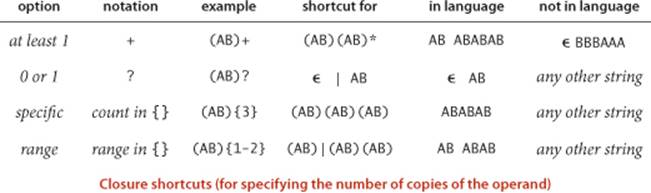
Closure shortcuts
The closure operator specifies any number of copies of its operand. In practice, we want the flexibility to specify the number of copies, or a range on the number. In particular, we use the plus sign (+) to specify at least one copy, the question mark (?) to specify zero or one copy, and a count or a range within braces ({}) to specify a given number of copies. Again, these notations are shortcuts for a sequence of the basic concatenation, or, and closure operations.
Escape sequences
Some characters, such as \, ., |, *, (, and ), are metacharacters that we use to form regular expressions. We use escape sequences that begin with a backslash character \ separating metacharacters from characters in the alphabet. An escape sequence may be a \ followed by a single metacharacter (which represents that character). For example, \\ represents \. Other escape sequences represent special characters and whitespace. For example, \t represents a tab character, \n represents a newline, and \s represents any whitespace character.
REs in applications
REs have proven to be remarkably versatile in describing languages that are relevant in practical applications. Accordingly, REs are heavily used and have been heavily studied. To familiarize you with regular expressions while at the same time giving you some appreciation for their utility, we consider a number of practical applications before addressing the RE pattern-matching algorithm. REs also play an important role in theoretical computer science. Discussing this role to the extent it deserves is beyond the scope of this book, but we sometimes allude to relevant fundamental theoretical results.
Substring search
Our general goal is to develop an algorithm that determines whether a given text string is in the set of strings described by a given regular expression. If a text is in the language described by a pattern, we say that the text matches the pattern. Pattern matching with REs vastly generalizes the substring search problem of SECTION 5.3. Precisely, to search for a substring pat in a text string txt is to check whether txt is in the language described by the pattern .*pat.* or not.
Validity checking
You frequently encounter RE matching when you use the web. When you type in a date or an account number on a commercial website, the input-processing program has to check that your response is in the right format. One approach to performing such a check is to write code that checks all the cases: if you were to type in a dollar amount, the code might check that the first symbol is a $, that the $ is followed by a set of digits, and so forth. A better approach is to define an RE that describes the set of all legal inputs. Then, checking whether your input is legal is precisely the pattern-matching problem: is your input in the language described by the RE? Libraries of REs for common checks have sprung up on the web as this type of checking has come into widespread use. Typically, an RE is a much more precise and concise expression of the set of all valid strings than would be a program that checks all the cases.

Programmer’s toolbox
The origin of regular expression pattern matching is the Unix command grep, which prints all lines matching a given RE. This capability has proven invaluable for generations of programmers, and REs are built into many modern programming systems, from awk and emacs to Perl, Python, and JavaScript. For example, suppose that you have a directory with dozens of .java files, and you want to know which of them has code that uses StdIn. The command
% grep StdIn *.java
will immediately give the answer. It prints all lines that match .*StdIn.* for each file.
Genomics
Biologists use REs to help address important scientific problems. For example, the human gene sequence has a region that can be described with the RE gcg(cgg)*ctg, where the number of repeats of the cgg pattern is highly variable among individuals, and a certain genetic disease that can cause mental retardation and other symptoms is known to be associated with a high number of repeats.
Search
Web search engines support REs, though not always in their full glory. Typically, if you want to specify alternatives with | or repetition with *, you can do so.
Possibilities
A first introduction to theoretical computer science is to think about the set of languages that can be specified with an RE. For example, you might be surprised to know that you can implement the modulus operation with an RE: for example, (0 | 1(01*0)*1)* describes all strings of 0s and 1s that are the binary representations of numbers that are multiples of three (!): 11, 110, 1001, and 1100 are in the language, but 10, 1011, and 10000 are not.
Limitations
Not all languages can be specified with REs. A thought-provoking example is that no RE can describe the set of all strings that specify legal REs. Simpler versions of this example are that we cannot use REs to check whether parentheses are balanced or to check whether a string has an equal number of As and Bs.
THESE EXAMPLES JUST SCRATCH THE SURFACE. Suffice it to say that REs are a useful part of our computational infrastructure and have played an important role in our understanding of the nature of computation. As with KMP, the algorithm that we describe next is a byproduct of the search for that understanding.
Nondeterministic finite-state automata
Recall that we can view the Knuth-Morris-Pratt algorithm as a finite-state machine constructed from the search pattern that scans the text. For regular expression pattern matching, we will generalize this idea.
The finite-state automaton for KMP changes from state to state by looking at a character from the text string and then changing to another state, depending on the character. The automaton reports a match if and only if it reaches the accept state. The algorithm itself is a simulation of the automaton. The characteristic of the machine that makes it easy to simulate is that it is deterministic: each state transition is completely determined by the next character in the text.
To handle regular expressions, we consider a more powerful abstract machine. Because of the or operation, the automaton cannot determine whether or not the pattern could occur at a given point by examining just one character; indeed, because of closure, it cannot even determine how manycharacters might need to be examined before a mismatch is discovered. To overcome these problems, we will endow the automaton with the power of nondeterminism: when faced with more than one way to try to match the pattern, the machine can “guess” the right one! This power might seem to you to be impossible to realize, but we will see that it is easy to write a program to build a nondeterministic finite-state automaton (NFA) and to efficiently simulate its operation. The overview of our RE pattern matching algorithm is the nearly same as for KMP:
• Build the NFA corresponding to the given RE.
• Simulate the operation of that NFA on the given text.
Kleene’s Theorem, a fundamental result of theoretical computer science, asserts that there is an NFA corresponding to any given RE (and vice versa). We will consider a constructive proof of this fact that will demonstrate how to transform any RE into an NFA; then we simulate the operation of the NFA to complete the job.
Before we consider how to build pattern-matching NFAs, we will consider an example that illustrates their properties and the basic rules for operating them. Consider the figure below, which shows an NFA that determines whether a text string is in the language described by the RE ((A*B|AC)D). As illustrated in this example, the NFAs that we define have the following characteristics:
• The NFA corresponding to an RE of length M has exactly one state per pattern character, starts at state 0, and has a (virtual) accept state M.

• States corresponding to a character from the alphabet have an outgoing edge that goes to the state corresponding to the next character in the pattern (black edges in the diagram).
• States corresponding to the metacharacters (, ), |, and * have at least one outgoing edge (red edges in the diagram), which may go to any other state.
• Some states have multiple outgoing edges, but no state has more than one outgoing black edge.
By convention, we enclose all patterns in parentheses, so the first state corresponds to a left parenthesis and the final state corresponds to a right parenthesis (and has a transition to the accept state).
As with the DFAs of the previous section, we start the NFA at state 0, reading the first character of a text. The NFA moves from state to state, sometimes reading text characters, one at a time, from left to right. However, there are some basic differences from DFAs:
• Characters appear in the nodes, not the edges, in the diagrams.
• Our NFA recognizes a text string only after explicitly reading all its characters, whereas our DFA recognizes a pattern in a text without necessarily reading all the text characters.
These differences are not critical—we have picked the version of each machine that is best suited to the algorithms that we are studying.
Our focus now is on checking whether the text matches the pattern—for that, we need the machine to reach its accept state and consume all the text. The rules for moving from one state to another are also different than for DFAs—an NFA can do so in one of two ways:
• If the current state corresponds to a character in the alphabet and the current character in the text string matches the character, the automaton can scan past the character in the text string and take the (black) transition to the next state. We refer to such a transition as a match transition.
• The automaton can follow any red edge to another state without scanning any text character. We refer to such a transition as an ![]() -transition, referring to the idea that it corresponds to “matching” the empty string
-transition, referring to the idea that it corresponds to “matching” the empty string ![]() .
.
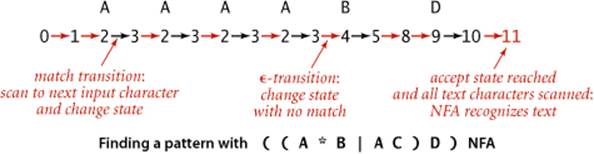
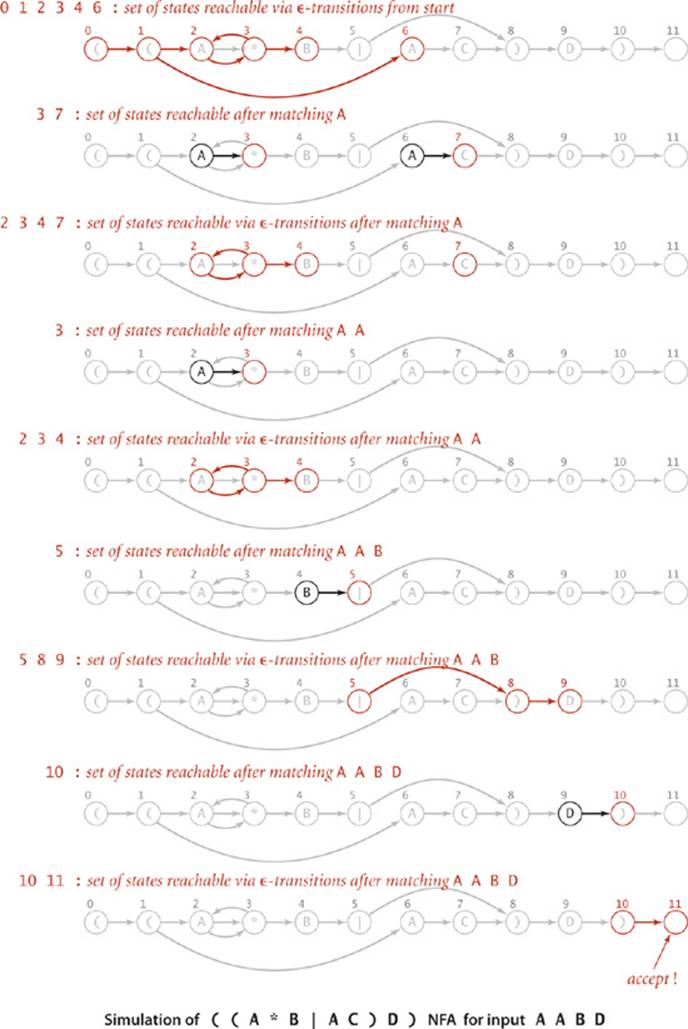
For example, suppose that our NFA for ( ( A * B | A C ) D ) is started (at state 0) with the text A A A A B D as input. The figure at the bottom of the previous page shows a sequence of state transitions ending in the accept state. This sequence demonstrates that the text is in the set of strings described by the RE—the text matches the pattern. With respect to the NFA, we say that the NFA recognizes that text.
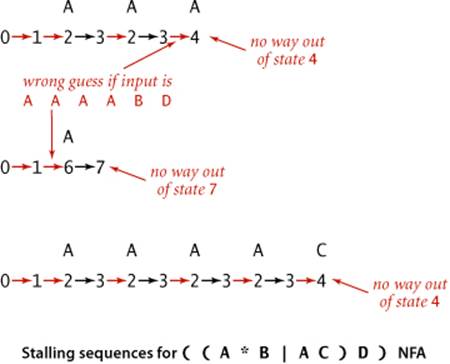
The examples shown at left illustrate that it is also possible to find transition sequences that cause the NFA to stall, even for input text such as A A A A B D that it should recognize. For example, if the NFA takes the transition to state 4 before scanning all the As, it is left with nowhere to go, since the only way out of state 4 is to match a B. These two examples demonstrate the nondeterministic nature of the automaton. After scanning an A and finding itself in state 3, the NFA has two choices: it could go on to state 4 or it could go back to state 2. The choices make the difference between getting to the accept state (as in the first example just discussed) or stalling (as in the second example just discussed). This NFA also has a choice to make at state 1 (whether to take an ![]() -transition to state 2 or to state 6).
-transition to state 2 or to state 6).
These examples illustrate the key difference between NFAs and DFAs: since an NFA may have multiple edges leaving a given state, the transition from such a state is not deterministic—it might take one transition at one point in time and a different transition at a different point in time, without scanning past any text character. To make some sense of the operation of such an automaton, imagine that an NFA has the power to guess which transition (if any) will lead to the accept state for the given text string. In other words, we say that an NFA recognizes a text string if and only if there is some sequence of transitions that scans all the text characters and ends in the accept state when started at the beginning of the text in state 0. Conversely, an NFA does not recognize a text string if and only if there is no sequence of match transitions and ![]() -transitions that can scan all the text characters and lead to the accept state for that string.
-transitions that can scan all the text characters and lead to the accept state for that string.
As with DFAs, we have been tracing the operation of the NFA on a text string simply by listing the sequence of state changes, ending in the final state. Any such sequence is a proof that the machine recognizes the text string (there may be other proofs). But how do we find such a sequence for a given text string? And how do we prove that there is no such sequence for another given text string? The answers to these questions are easier than you might think: we systematically try all possibilities.
Simulating an NFA
The idea of an automaton that can guess the state transitions it needs to get to the accept state is like writing a program that can guess the right answer to a problem: it seems ridiculous. On reflection, you will see that the task is conceptually not at all difficult: we make sure that we check all possible sequences of state transitions, so if there is one that gets to the accept state, we will find it.
Representation
To begin, we need an NFA representation. The choice is clear: the RE itself gives the state names (the integers between 0 and M, where M is the number of characters in the RE). We keep the RE itself in an array re[] of char values that defines the match transitions (if re[i] is in the alphabet, then there is a match transition from i to i+1). The natural representation for the ![]() -transitions is a digraph—they are directed edges (red edges in our diagrams) connecting vertices between 0 and M (one for each state). Accordingly, we represent all the
-transitions is a digraph—they are directed edges (red edges in our diagrams) connecting vertices between 0 and M (one for each state). Accordingly, we represent all the ![]() -transitions as a digraph G. We will consider the task of building the digraph associated with a given RE after we consider the simulation process. For our example, the digraph consists of the nine edges
-transitions as a digraph G. We will consider the task of building the digraph associated with a given RE after we consider the simulation process. For our example, the digraph consists of the nine edges
0 → 1 1 → 2 1 → 6 2 → 3 3 → 2 3 → 4 5 → 8 8 → 9 10 → 11
NFA simulation and reachability
To simulate an NFA, we keep track of the set of states that could possibly be encountered while the automaton is examining the current input character. The key computation is the familiar multiple-source reachability computation that we addressed in ALGORITHM 4.4 (page 571). To initialize this set, we find the set of states reachable via ![]() -transitions from state 0. For each such state, we check whether a match transition for the first input character is possible. This check gives us the set of possible states for the NFA just after matching the first input character. To this set, we add all states that could be reached via
-transitions from state 0. For each such state, we check whether a match transition for the first input character is possible. This check gives us the set of possible states for the NFA just after matching the first input character. To this set, we add all states that could be reached via ![]() -transitions from one of the states in the set. Given the set of possible states for the NFA just after matching the first character in the input, the solution to the multiple-source reachability problem in the
-transitions from one of the states in the set. Given the set of possible states for the NFA just after matching the first character in the input, the solution to the multiple-source reachability problem in the ![]() -transition digraph gives the set of states that could lead to match transitions for the second character in the input. For example, the initial set of states for our example NFA is 0 1 2 3 4 6; if the first character is an A, the NFA could take a match transition to 3 or 7; then it could take
-transition digraph gives the set of states that could lead to match transitions for the second character in the input. For example, the initial set of states for our example NFA is 0 1 2 3 4 6; if the first character is an A, the NFA could take a match transition to 3 or 7; then it could take ![]() -transitions from 3 to 2 or 3 to 4, so the set of possible states that could lead to a match transition for the second character is 2 3 4 7. Iterating this process until all text characters are exhausted leads to one of two outcomes:
-transitions from 3 to 2 or 3 to 4, so the set of possible states that could lead to a match transition for the second character is 2 3 4 7. Iterating this process until all text characters are exhausted leads to one of two outcomes:
• The set of possible states contains the accept state.
• The set of possible states does not contain the accept state.
The first of these outcomes indicates that there is some sequence of transitions that takes the NFA to the accept state, so we report success. The second of these outcomes indicates that the NFA always stalls on that input, so we report failure. With our SET data type and the DirectedDFS class just described for computing multiple-source reachability in a digraph, the NFA simulation code given below is a straightforward translation of the English-language description just given. You can check your understanding of the code by following the trace on the facing page, which illustrates the full simulation for our example.
Proposition Q. Determining whether an N-character text string is recognized by the NFA corresponding to an M-character RE takes time proportional to NM in the worst case.
Proof: For each of the N text characters, we iterate through a set of states of size no more than M and run a DFS on the digraph of ![]() -transitions. The construction that we will consider next establishes that the number of edges in that digraph is no more than 2M, so the worst-case time for each DFS is proportional to M.
-transitions. The construction that we will consider next establishes that the number of edges in that digraph is no more than 2M, so the worst-case time for each DFS is proportional to M.
Take a moment to reflect on this remarkable result. This worst-case cost, the product of the text and pattern lengths, is the same as the worst-case cost of finding an exact substring match using the elementary algorithm that we started with at the beginning of SECTION 5.3.
NFA simulation for pattern matching
public boolean recognizes(String txt)
{ // Does the NFA recognize txt?
Bag<Integer> pc = new Bag<Integer>();
DirectedDFS dfs = new DirectedDFS(G, 0);
for (int v = 0; v < G.V(); v++)
if (dfs.marked(v)) pc.add(v);
for (int i = 0; i < txt.length(); i++)
{ // Compute possible NFA states for txt[i+1].
Bag<Integer> match = new Bag<Integer>();
for (int v : pc)
if (v < M)
if (re[v] == txt.charAt(i) || re[v] == '.')
match.add(v+1);
pc = new Bag<Integer>();
dfs = new DirectedDFS(G, match);
for (int v = 0; v < G.V(); v++)
if (dfs.marked(v)) pc.add(v);
}
for (int v : pc) if (v == M) return true;
return false;
}
Building an NFA corresponding to an RE
From the similarity between regular expressions and familiar arithmetic expressions, you may not be surprised to find that translating an RE to an NFA is somewhat similar to the process of evaluating an arithmetic expression using Dijkstra’s two-stack algorithm, which we considered inSECTION 1.3. The process is a bit different because
• REs do not have an explicit operator for concatenation
• REs have a unary operator, for closure (*)
• REs have only one binary operator, for or (|)
Rather than dwell on the differences and similarities, we will consider an implementation that is tailored for REs. For example, we need only one stack, not two.
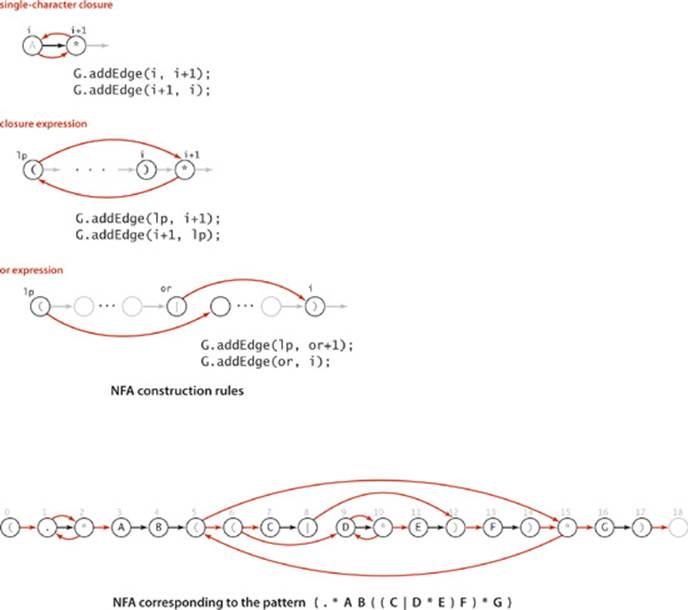
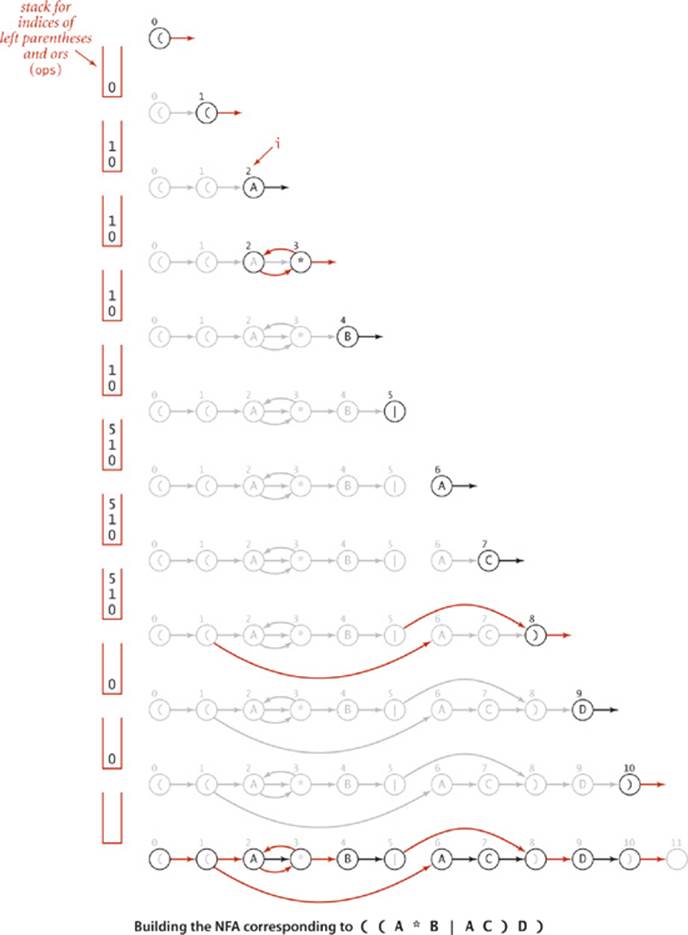
From the discussion of the representation at the beginning of the previous subsection, we need only build the digraph G that consists of all the ![]() -transitions. The RE itself and the formal definitions that we considered at the beginning of this section provide precisely the information that we need. Taking a cue from Dijkstra’s algorithm, we will use a stack to keep track of the positions of left parentheses and or operators.
-transitions. The RE itself and the formal definitions that we considered at the beginning of this section provide precisely the information that we need. Taking a cue from Dijkstra’s algorithm, we will use a stack to keep track of the positions of left parentheses and or operators.
Concatenation
In terms of the NFA, the concatenation operation is the simplest to implement. Match transitions for states corresponding to characters in the alphabet explicitly implement concatenation.
Parentheses
We push the RE index of each left parenthesis on the stack. Each time we encounter a right parenthesis, we eventually pop the corresponding left parentheses from the stack in the manner described below. As in Dijkstra’s algorithm, the stack enables us to handle nested parentheses in a natural manner.
Closure
A closure (*) operator must occur either (i) after a single character, when we add ![]() -transitions to and from the character, or (ii) after a right parenthesis, when we add
-transitions to and from the character, or (ii) after a right parenthesis, when we add ![]() -transitions to and from the corresponding left parenthesis, the one at the top of the stack.
-transitions to and from the corresponding left parenthesis, the one at the top of the stack.
Or expression
We process an RE of the form (A | B) where A and B are both REs by adding two ![]() -transitions: one from the state corresponding to the left parenthesis to the state corresponding to the first character of B and one from the state corresponding to the | operator to the state corresponding to the right parenthesis. We push the RE index corresponding the | operator onto the stack (as well as the index corresponding to the left parenthesis, as described above) so that the information we need is at the top of the stack when needed, at the time we reach the right parenthesis. These
-transitions: one from the state corresponding to the left parenthesis to the state corresponding to the first character of B and one from the state corresponding to the | operator to the state corresponding to the right parenthesis. We push the RE index corresponding the | operator onto the stack (as well as the index corresponding to the left parenthesis, as described above) so that the information we need is at the top of the stack when needed, at the time we reach the right parenthesis. These ![]() -transitions allow the NFA to choose one of the two alternatives. We do not add an
-transitions allow the NFA to choose one of the two alternatives. We do not add an ![]() -transition from the state corresponding to the | operator to the state with the next higher index, as we have for all other states—the only way for the NFA to leave such a state is to take a transition to the state corresponding to the right parenthesis.
-transition from the state corresponding to the | operator to the state with the next higher index, as we have for all other states—the only way for the NFA to leave such a state is to take a transition to the state corresponding to the right parenthesis.
THESE SIMPLE RULES SUFFICE TO build NFAs corresponding to arbitrarily complicated REs. ALGORITHM 5.9 is an implementation whose constructor builds the ![]() -transition digraph corresponding to a given RE, and a trace of the construction for our example appears on the following page. You can find other examples at the bottom of this page and in the exercises and are encouraged to enhance your understanding of the process by working your own examples. For brevity and for clarity, a few details (handling metacharacters, set-of-character descriptors, closure shortcuts, and multiway or operations) are left for exercises (see EXERCISES 5.4.16 through 5.4.21). Otherwise, the construction requires remarkably little code and represents one of the most ingenious algorithms that we have seen.
-transition digraph corresponding to a given RE, and a trace of the construction for our example appears on the following page. You can find other examples at the bottom of this page and in the exercises and are encouraged to enhance your understanding of the process by working your own examples. For brevity and for clarity, a few details (handling metacharacters, set-of-character descriptors, closure shortcuts, and multiway or operations) are left for exercises (see EXERCISES 5.4.16 through 5.4.21). Otherwise, the construction requires remarkably little code and represents one of the most ingenious algorithms that we have seen.
Algorithm 5.9 Regular expression pattern matching (grep)
public class NFA
{
private char[] re; // match transitions
private Digraph G; // epsilon transitions
private int M; // number of states
public NFA(String regexp)
{ // Create the NFA for the given regular expression.
Stack<Integer> ops = new Stack<Integer>();
re = regexp.toCharArray();
M = re.length;
G = new Digraph(M+1);
for (int i = 0; i < M; i++)
{
int lp = i;
if (re[i] == '(' || re[i] == '|')
ops.push(i);
else if (re[i] == ')')
{
int or = ops.pop();
if (re[or] == '|')
{
lp = ops.pop();
G.addEdge(lp, or+1);
G.addEdge(or, i);
}
else lp = or;
}
if (i < M-1 && re[i+1] == '*') // lookahead
{
G.addEdge(lp, i+1);
G.addEdge(i+1, lp);
}
if (re[i] == '(' || re[i] == '*' || re[i] == ')')
G.addEdge(i, i+1);
}
}
public boolean recognizes(String txt)
// Does the NFA recognize txt? (See page 799.)
}
This constructor builds an NFA corresponding to a given RE by creating a digraph of ![]() -transitions.
-transitions.
Proposition R. Building the NFA corresponding to an M-character RE takes time and space proportional to M in the worst case.
Proof. For each of the M RE characters in the regular expression, we add at most three ![]() -transitions and perhaps execute one or two stack operations.
-transitions and perhaps execute one or two stack operations.
The classic GREP client for pattern matching, illustrated in the code at left, takes an RE as argument and prints the lines from standard input having some substring that is in the language described by the RE. This client was a feature in the early implementations of Unix and has been an indispensable tool for generations of programmers.
Classic Generalized Regular Expression Pattern-matching NFA client
public class GREP
{
public static void main(String[] args)
{
String regexp = "(.*" + args[0] + ".*)";
NFA nfa = new NFA(regexp);
while (StdIn.hasNextLine())
{
String txt = StdIn.readLine();
if (nfa.recognizes(txt))
StdOut.println(txt);
}
}
}
% more tinyL.txt
AC
AD
AAA
ABD
ADD
BCD
ABCCBD
BABAAA
BABBAAA
% java GREP "(A*B|AC)D" < tinyL.txt
ABD
ABCCBD
% java GREP StdIn < GREP.java
while (StdIn.hasNextLine())
String txt = StdIn.hasNextLine();
Q&A
Q. What is the difference between Ø and ![]() ?
?
A. The former denotes an empty set; the latter denotes an empty string. You can have a set that contains one element, ![]() , and is therefore not an empty set Ø.
, and is therefore not an empty set Ø.
Exercises
5.4.1 Give regular expressions that describe all strings that contain
• Exactly four consecutive As
• No more than four consecutive As
• At least one occurrence of four consecutive As
5.4.2 Give a brief English description of each of the following REs:
a. .*
b. A.*A | A
c. .*ABBABBA.*
d. .* A.*A.*A.*A.*
5.4.3 What is the maximum number of different strings that can be described by a regular expression with M or operators and no closure operators (parentheses and concatenation are allowed)?
5.4.4 Draw the NFA corresponding to the pattern (((A|B)*|CD*|EFG)*)*.
5.4.5 Draw the digraph of ![]() -transitions for the NFA from EXERCISE 5.4.4.
-transitions for the NFA from EXERCISE 5.4.4.
5.4.6 Give the sets of states reachable by your NFA from EXERCISE 5.4.4 after each character match and susbsequent ![]() -transitions for the input ABBACEFGEFGCAAB.
-transitions for the input ABBACEFGEFGCAAB.
5.4.7 Modify the GREP client on page 804 to be a client GREPmatch that encloses the pattern in parentheses but does not add .* before and after the pattern, so that it prints out only those lines that are strings in the language described by the given RE. Give the result of typing each of the following commands:
a. % java GREPmatch "(A|B)(C|D)" < tinyL.txt
b. % java GREPmatch "A(B|C)*D" < tinyL.txt
c. % java GREPmatch "(A*B|AC)D" < tinyL.txt
5.4.8 Write a regular expression for each of the following sets of binary strings:
a. Contains at least three consecutive 1s
b. Contains the substring 110
c. Contains the substring 1101100
d. Does not contain the substring 110
5.4.9 Write a regular expression for binary strings with at least two 0s but not consecutive 0s.
5.4.10 Write a regular expression for each of the following sets of binary strings:
a. Has at least 3 characters, and the third character is 0
b. Number of 0s is a multiple of 3
c. Starts and ends with the same character
d. Odd length
e. Starts with 0 and has odd length, or starts with 1 and has even length
f. Length is at least 1 and at most 3
5.4.11 For each of the following regular expressions, indicate how many bitstrings of length exactly 1,000 match:
a. 0(0 | 1)*1
b. 0*101*
c. (1 | 01)*
5.4.12 Write a Java regular expression for each of the following:
a. Phone numbers, such as (609) 555-1234
b. Social Security numbers, such as 123-45-6789
c. Dates, such as December 31, 1999
d. IP addresses of the form a.b.c.d where each letter can represent one, two, or three digits, such as 196.26.155.241
e. License plates that start with four digits and end with two uppercase letters
Creative Problems
5.4.13 Challenging REs. Construct an RE that describes each of the following sets of strings over the binary alphabet:
a. All strings except 11 or 111
b. Strings with 1 in every odd-number bit position
c. Strings with at least two 0s and at most one 1
d. Strings with no two consecutive 1s
5.4.14 Binary divisibility. Construct an RE that describes all binary strings that when interpreted as a binary number are
a. Divisible by 2
b. Divisible by 3
c. Divisible by 123
5.4.15 One-level REs. Construct a Java RE that describes the set of strings that are legal REs over the binary alphabet, but with no occurrence of parentheses within parentheses. For example, (0.*1)* | (1.*0)* is in this language, but (1(0 | 1)1)* is not.
5.4.16 Multiway or. Add multiway or to NFA. Your code should produce the machine drawn below for the pattern (.*AB((C|D|E)F)*G).

5.4.17 Wildcard. Add to NFA the capability to handle wildcards.
5.4.18 One or more. Add to NFA the capability to handle the + closure operator.
5.4.19 Specified set. Add to NFA the capability to handle specified-set descriptors.
5.4.20 Range. Add to NFA the capability to handle range descriptors.
5.4.21 Complement. Add to NFA the capability to handle complement descriptors.
5.4.22 Proof. Develop a version of NFA that prints a proof that a given string is in the language recognized by the NFA (a sequence of state transitions that ends in the accept state).
All materials on the site are licensed Creative Commons Attribution-Sharealike 3.0 Unported CC BY-SA 3.0 & GNU Free Documentation License (GFDL)
If you are the copyright holder of any material contained on our site and intend to remove it, please contact our site administrator for approval.
© 2016-2026 All site design rights belong to S.Y.A.