Algorithms in a Nutshell 2E (2015)

Chapter 11. Emerging Algorithm Categories

Earlier book chapters describe algorithms that solve common problems. Obviously, you will encounter challenges in your programming career that do not fit into any common category, so this chapter presents four algorithmic approaches to solve problems.

Another change in this chapter is its focus on randomness and probability. These were used in previous chapters when analyzing the average-case behavior of algorithms. Here the randomness can become an essential part of an algorithm. Indeed, the probabilistic algorithms we describe are interesting alternatives to deterministic algorithms. Running the same algorithm on the same input at two different times may provide very different answers. Sometimes we will tolerate wrong answers or even claims that there is no solution.

Variations on a Theme

The earlier algorithms in this book solve instances of a problem by giving an exact answer on a sequential, deterministic computer. Much interesting research has been done by relaxing these three assumptions:

Approximation algorithms

Instead of seeking an exact answer for a problem, accept solutions that are close to, but not necessarily as good as, the true answer.

Parallel algorithms

Instead of being restricted to sequential computation, create multiple computational processes to work simultaneously on sub-problem instances.

Probabilistic algorithms

Instead of computing the same result for a problem instance, use randomized computations to compute an answer. When run multiple times, the answers often converge on the true answer.

Approximation Algorithms

Approximation algorithms trade off accuracy for more efficient performance. As an example where a “good enough” answer is sufficient, consider the Knapsack Problem, which arises in a variety of computational domains. The goal is to determine the items to add to a backpack that maximizes the value of the entire backpack while not exceeding some maximum weight, W. This problem, known as Knapsack 0/1, can be solved using Dynamic Programming.

KNAPSACK 0/1 SUMMARY

Best, Average, Worst: O(n*W)

Knapsack 0/1 (weights, values, W):

n = number of items

m = empty (n+1) x (W+1) matrix

for i=1 to n do

for j=0 to W do

if weights[i-1] <= j then

remaining = j - weights[i-1]

m[i][j] = max(m[i-1][j], m[i-1][remaining] + values[i-1])

else

m[i][j] = m[i-1][j]

return m[n][W]

end

Knapsack unbounded(weights, values, W):

n = number of items

m = (W+1) vector

for j=1 to W+1 do

best = m[j-1]

for i=0 to n-1 do

remaining = j - weights[i]

if remaining >= 0 andm[remaining] + values[i] > best:

best = m[remaining] + values[i]

m[j] = best

m[i][j] records maximum value using first i items without exceeding j weight

Can we increase value by adding item i to previous solution with weight (j - item i’s weight)

Item i exceeds weight limit

Returns computed best value

For unbounded, m[j] records maximum value without exceeding weight j

Input/Output

You are given a set of items (each with an integer weight and value) and a maximum weight, W. The problem is to determine which items to pack into the knapsack so the total weight is less than or equal to W and the total value of the packed items is as large as possible.

For the Knapsack 0/1 problem, there is only one instance of each item. A variation named Knapsack unbounded allows you to pack as many copies of a particular item that you desire. In both cases, the algorithm must return the maximum value.

Context

This is a type of resource allocation problem with constraints, which is quite common in computer science, mathematics, and economics. It has been studied extensively for over a century and has numerous variations. Often you need to know the actual selection of items, not just the maximum value, so the solution must also return the items selected to put into the knapsack.

Solution

We use Dynamic Programming which works by storing the results of simpler sub-problems. For Knapsack 0/1, the two-dimensional matrix m[i][j] records the result of the maximum value using the first i items without exceeding j weight. The structure of the solution in Example 11-1matches the expected double loops of Dynamic Programming.

Example 11-1. Python Implementation of Knapsack 0/1

class Item:

def __init__(self, value, weight):

"""Create item with given value and weight."""

self.value = value

self.weight = weight

def knapsack_01 (items, W):

"""

Compute 0/1 knapsack solution (just one of each item is available)

for set of items with corresponding weights and values. Return total weight

and selection of items.

"""

n = len(items)

m = [None] * (n+1)

for i inrange(n+1):

m[i] = [0] * (W+1)

for i inrange(1,n+1):

for j inrange(W+1):

if items[i-1].weight <= j:

m[i][j] = max(m[i-1][j], m[i-1][j-items[i-1].weight] + items[i-1].value)

else:

m[i][j] = m[i-1][j]

selections = [0] * n

i = n

w = W

while i > 0 andw >= 0:

if m[i][w] != m[i-1][w]:

selections[i-1] = 1

w -= items[i-1].weight

i -= 1

return (m[n][W], selections)

The Python code follows the Dynamic Programming structure by computing each sub-problem in order. Once the nested loops compute the maximum value, m[n][W], the subsequent while loop shows how to recover the actual items selected by “walking” over the m matrix. It starts at the lower right-hand corner, m[n][W], and determines whether the i^th item was selected, based on whether m[i][w] is different from m[i-1][w]. If this is the case, it records the selection and then moves left in m by removing the weight of i and continuing until it hits the first row (no more items) or the left column (no more weight).

The Knapsack unbounded problem uses a one-dimensional vector m[j] to record the result of the maximum value not exceeding j weight. Its Python implementation is shown in Example 11-2.

Example 11-2. Python Implementation of Knapsack Unbounded

def knapsack_unbounded (items, W):

"""

Compute unbounded knapsack solution (any number of each item is

available) for set of items with corresponding weights and values.

Return total weight and selection of items.

"""

n = len(items)

progress = [0] * (W+1)

progress[0] = -1

m = [0] * (W + 1)

for j inrange(1, W+1):

progress[j] = progress[j-1]

best = m[j-1]

for i inrange(n):

remaining = j - items[i].weight

if remaining >= 0 andm[remaining] + items[i].value > best:

best = m[remaining] + items[i].value

progress[j] = i

m[j] = best

selections = [0] * n

i = n

w = W

while w >= 0:

choice = progress[w]

if choice == -1:

break

selections[choice] += 1

w -= items[progress[w]].weight

return (m[W], selections)

Analysis

These solutions are not polynomial with regard to the input, but actually depend upon W as well. That is, in both cases, the solution is O(n*W), as clearly shown by the nested for loops. Recovering the selections is O(n), so this doesn’t change the overall performance.

Why does this observation matter? In Knapsack 0/1, when W is much larger than the weights of the individual items, the algorithm must repeatedly perform wasted iterations, because each item is only chosen once. There are similar inefficiencies for Knapsack unbounded.

In 1957, George Dantzig proposed an approximate solution to Knapsack Unbounded, shown in Example 11-3. The intuition behind this approximation is that you should first insert items into the knapsack that maximize the value-to-weight ratio. In fact, this approach is guaranteed to find an approximation that is no worse than half of the maximum value that would have been found by Dynamic Programming. In practice, the results are actually quite close to the real value, but the code is noticeably faster.

Example 11-3. Python Implementation of Knapsack Unbounded Approximation

class ApproximateItem(Item):

"""

Extends Item by storing the normalized value and the original position

of the item before sorting.

"""

def __init__(self, item, idx):

Item.__init__(self, item.value, item.weight)

self.normalizedValue = item.value/item.weight

self.index = idx

def knapsack_approximate (items, W):

"""Compute approximation to knapsack problem using Dantzig approach."""

approxItems = []

n = len(items)

for idx inrange(n):

approxItems.append(ApproximateItem(items[idx], idx))

approxItems.sort(key=lambda x:x.normalizedValue, reverse=True)

selections = [0] * n

w = W

total = 0

for idx inrange(n):

item = approxItems[idx]

if w == 0:

break

# find out how many fit

numAdd = w // item.weight

if numAdd > 0:

selections[item.index] += numAdd

w -= numAdd * item.weight

total += numAdd * item.value

return (total, selections)

The implementation iterates over the items in reverse order by their normalized value (i.e., the ratio of value to weight). The cost of this algorithm is O(n log n) because it must sort the items first. The following table compares the performance of the Knapsack Unbounded Approximationwith Knapsack Unbounded as W grows in size. Each of the items in the set of n=53 items has a different weight and an item’s value is set to its weight. The weights range from 103 to 407. As you can see, as the size of W doubles, the time to execute Knapsack Unbounded also doubles, because of its O(n*W) performance. However, the performance of Knapsack Approximate doesn’t change as W gets larger because its performance is determined only by O(n log n).

Reviewing the final two columns, you can see that for W = 175, the approximate solution is 60% of the actual answer. As W increases, the approximate solution converges to be closer to the actual number.

Table 11-1. Performance on small set

Parallel Algorithms

Parallel algorithms take advantage of existing computational resources by creating and managing different threads of execution.

Quicksort, presented in Chapter 4, can be implemented in Java as follows, assuming the existence of a partition function to divide the original list into two subsequent problems to complete.

Example 11-4. Quicksort Implementation in Java

public class MultiThreadQuickSort<E extends Comparable<E>>

final E[] ar; /** Elements to be sorted. */

IPivotIndex pi; /** Partition function. */

/** Construct an instance to solve quicksort. */

public MultiThreadQuickSort (E ar[]) {

this.ar = ar;

}

/** Set the partition method. */

public void setPivotMethod (IPivotIndex ipi) { this.pi = ipi; }

/** Single-thread sort of ar[left,right]. */

public void qsortSingle (int left, int right) {

if (right <= left) { return; }

int pivotIndex = pi.selectPivotIndex (ar, left, right);

pivotIndex = partition (left, right, pivotIndex);

qsortSingle (left, pivotIndex-1);

qsortSingle (pivotIndex+1, right);

}

}

The two subproblems qsortSingle (left, pivotIndex-1) and qsortSingle(pivotIndex+1, right) are independent problems and, theoretically, can be solved at the same time. The immediate question is how to use multiple threads to solve this problem. You cannot simply spawn a helper thread with each recursive call since that would overwhelm the resources of the operating system. Consider the following rewrite, qsort2:

Example 11-5. Multithreaded Java Quicksort Implementation in Java

/** Multi-thread sort of ar[left,right]. */

void qsort2 (int left, int right) {

if (right <= left) { return; }

int pivotIndex = pi.selectPivotIndex (ar, left, right);

pivotIndex = partition (left, right, pivotIndex);

qsortThread(left, pivotIndex-1);

qsortThread(pivotIndex+1, right);

}

/**

* Spawn thread to sort ar[left,right] or use existing thread

* if problem size is too big or all helpers are being used.

*/

private void qsortThread(final int left, final int right) {

// are all helper threads working OR is problem too big?

// Continue with recursion if so.

int n = right + 1 - left;

if (helpersWorking == numThreads || n >= threshold) {

qsort2 (left, right);

} else {

// otherwise, complete in separate thread

synchronized(helpRequestedMutex) {

helpersWorking++;

}

new Thread () {

public void run () {

// invoke single-thread qsort

qsortSingle (left, right);

synchronized(helpRequestedMutex) {

helpersWorking--;

}

}

}.start();

}

}

For each of the two qsortThread subproblems, there is a simple check to see whether the primary thread should continue the recursive qsortThread function call. As you can see, the separate helper thread is dispatched to compute a subproblem only if (a) a thread is available; and (b) the size of the subproblem is smaller than the specified threshold value. This logic is applied when sorting the left sub-array as well as the right sub-array. The threshold value is computed by calling setThresholdRatio(r), which sets the threshold problem size to be n/r where n is the number of elements to be sorted. The default ratio is 5, which means a helper thread is only invoked on sub-problems that are smaller than 20% of the original problem size.

The helpersWorking class attribute stores the number of active helper threads. Whenever a thread is spawned, the helpersWorking variable is incremented, and the thread itself will decrement this same value upon completion. Using the mutex variable, helpRequestedMutex, and the ability in Java to synchronize a block of code for exclusive access, this implementation safely updates the helpersWorking variable. qsort2 invokes the single-threaded qsortSingle method within its helper threads. This ensures that only the primary thread is responsible for spawning new threads of computation.

For this design, helper threads cannot spawn additional helper threads. If this were allowed to happen, the “first” helper thread would have to synchronize with these “second” threads, so the “second” threads would only begin to execute after the “first” helper thread had properly partitioned the array.

Let’s now consider how well this solution works. The following graphs compare the Java single-helper solution against a single-threaded solution sorting random integers from the range [0, 16777216]. We have several parameters that we consider:

§ Size n of the array being sorted: This falls in the range {65,536 to 1,048,576}.

§ Threshold n/r: this determines the maximum size of the problem for which a helper thread is spawned. We experimented with values of r in the range {1 to 20} and MAXINT, which effectively denies using helper threads.

§ Number of helper threads available: we experimented with 0 to 9 helper threads.

§ Partition method to use: we tried both “select a random element” and “select the rightmost element.”

The parameter space thus amounts to 2,000 unique combinations of these parameters. In general, we found there is a noticeable performance slowdown of about 5% in using the random number generator across all experiments, so we now focus only on the “rightmost” partition method. In addition, for Quicksort, having more than one helper thread available did not improve the performance, so we focus only on having a single helper thread.

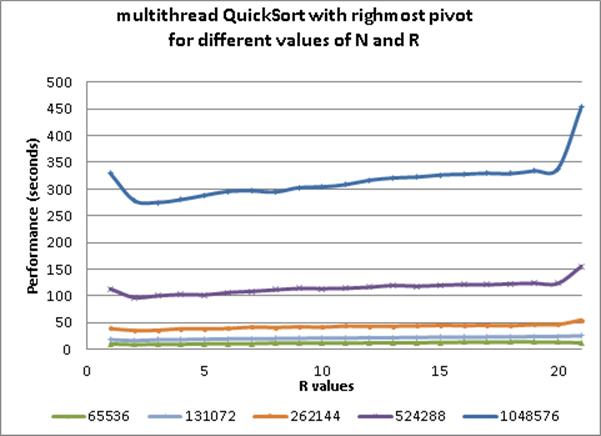
Figure 11-1. Performance of Multi-Threaded Quicksort for varying n and r

Reading the graph from left to right, you can see that the first data point (r=1) reports the performance that tries to immediately begin using the helper thread, while the last data point (r=21) reports the result when no helper thread is ever used. When we compute the speedup factor from time T1 to a smaller time T2, we use the equation T1/T2. Simply using an extra thread shows a speedup factor of about 1.3. This is a very nice return on investment for a small programming change!

Table 11-2. Speedup of having one helper thread for (r=1) vs. (r=MAXINT)

Returning to Figure 11-1, you can see that the best improvement occurs near where r=2, and as n increases in size, it appears that the best result appears when r=3 or r=4. There is a built-in overhead to using threads, and one shouldn’t automatically dispatch a new thread of execution without some assurance that the primary thread will not have to wait and block until the helper thread completes its execution. It seems the “sweet spot” is near where r=4.

In many cases, the speed up is affected by the number of CPUs on the computing platform. To investigate, we generated the following speed up tables on two different computing platforms—a dual core CPU and a quad core CPU. In Figure 11-2, each row represents the potential number of available threads while each column represents a threshold value r. The total number of elements sorted is fixed at n=1,048,576. The quad core results demonstrate the effectiveness of allowing multiple threads, achieving a speed up of 1.5; the same cannot be said of the dual core execution, whose performance increases by no more than 5% when allowing multiple threads.

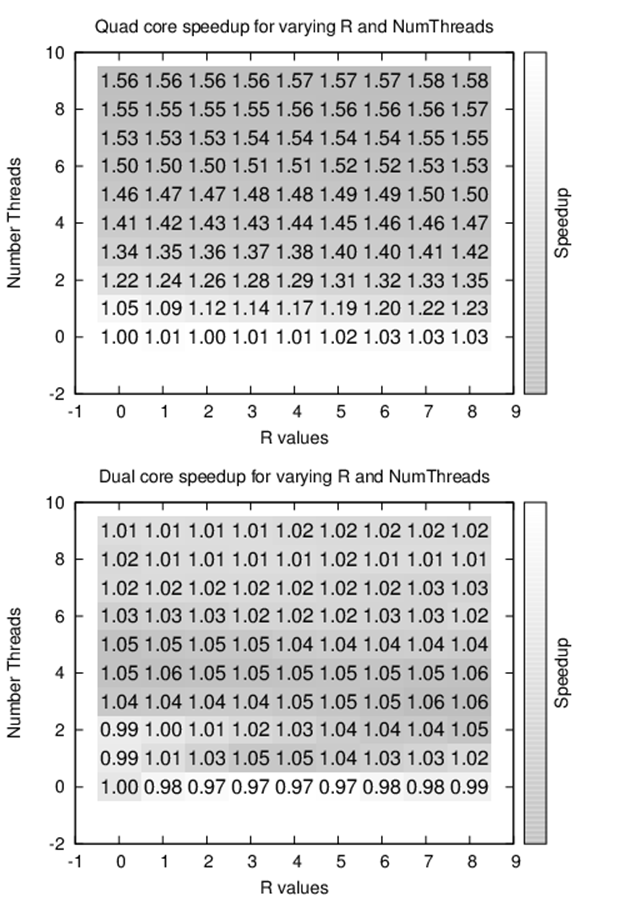
Figure 11-2. Performance of Multi-Threaded Quicksort with fixed n and varying r and number of threads

Research in speedup factors for parallel algorithms shows there are inherent limitations to how much extra threading or extra processing will actually help a specific algorithmic implementation. Here the multi-threaded Quicksort implementation achieves a nice speedup factor because the individual subproblems of recursive Quicksort are entirely independent; there will be no contention for shared resources by the multiple threads. If other problems share this same characteristic, they should also be able to benefit from our multi-threaded approach.

Probabilistic Algorithms

The implementation of many algorithms requires the assumption that they have access to a stream of random bits. It is hard to define randomness, though we’ll look at several tests that a sequence of random bits must satisfy. It is also hard to generate a sequence of bits that satisfy these tests.

A probabilistic algorithm uses a stream of random bits (i.e., random numbers) as part of the process for computing an answer, so you will get different results when running the algorithm on the same problem instance. Often, assuming access to a stream of random bits leads to algorithms that are faster than any current alternatives.

For practical purposes, one should be aware that streams of random bits are very difficult to generate on deterministic computers. Though we may generate streams of quasi-random bits that are virtually indistinguishable from streams of truly random bits, the cost of generating these streams should not be ignored.

Estimating the Size of a Set

As an example of the speedup that can be obtained in allowing probabilistic algorithms, assume we want to estimate the size of a set of n distinct objects. That is, we want to estimate the value n. It would be straightforward to count all the objects, at a cost of O(n). Clearly this process is guaranteed to yield an exact answer. But if an incorrect estimate of the value of n is tolerable, assuming it could be computed more quickly, the algorithm described in Example 10-1 is a faster alternative. This algorithm is similar to the mark-and-recapture experiments biologists use to estimate the size of a spatially limited population of organisms. The approach here is to use a generator function that returns a random individual in the population.

Example 11-6. Implementation of probabilistic counting algorithm

def computeK(generator):

"""

Compute estimate of using probabilistic counting algorithm.

Doesn't know value of n, the size of the population.

"""

seen = set()

while True:

item = generator()

if item inseen:

k = len(seen)

return 2.0*k*k/math.pi

else:

seen.add(item)

As long as the generator function returns an individual that has already been seen (which it must do because the population is finite) the while loop will terminate. In statistics, this behavior is known as “sampling with replacement” and the expected number of executions of the while loop is √π*n/2 or O(√n). Clearly, the algorithm can never give the exact value of n, because 2*k²/π can never be an integer. But the value 2*k²/π is an unbiased estimate of n; that is, the expected value of 2*k²/π approximates n.

In Table 10-1 we show a sample run of the algorithm that records the results of performing the computation repeatedly for a number of trials, k = {32, 64, 128, 256}. From these trials, the lowest and highest estimates were discarded, and the average of the remaining k-2 trials is shown in the each column.

Table 11-3. Sample execution of probabilistic counting algorithm

Because of the random nature of the trials, it is not at all guaranteed that the final accurate result can be achieved simply by averaging over an increasing number of independent random trials. Even increasing the number of trials does little to improve the accuracy, but that misses the point; this probabilistic algorithm efficiently returns an estimate based on a small sample size.

Estimating the Size of a Search Tree

Mathematicians have long studied the “Eight Queens Problem,” which asks whether it is possible to place eight queens on a chessboard so that no two queens threaten each other. This was expanded to the more general problem of counting the number of unique solutions to placing n non-threatening queens on an n by n chessboard. No one has yet been able to devise a way to mathematically compute this answer; instead you can write a brute force program that checks all possible board configurations to determine the answer. Table 10-2 contains some of the computed values taken from the On-Line Encyclopedia of Integer Sequences ^[7^]. As you can see, the number of solutions grows extremely rapidly.

Table 11-4. Known count of solutions for n-Queens Problem with our computed estimates

To count the number of exact solutions to the 4-Queens Problem, we expand a search tree (shown in Figure 11-3) based upon the fact that each solution will have one queen on each row. Such an exhaustive elaboration of the search tree permits us to see that there are two solutions to the 4-Queens Problem. Trying to compute the number of solutions to the 19-Queens Problem is much harder because there are 4,968,057,848 nodes at level 19 of the search tree. It is simply prohibitively expensive to generate each and every solution.

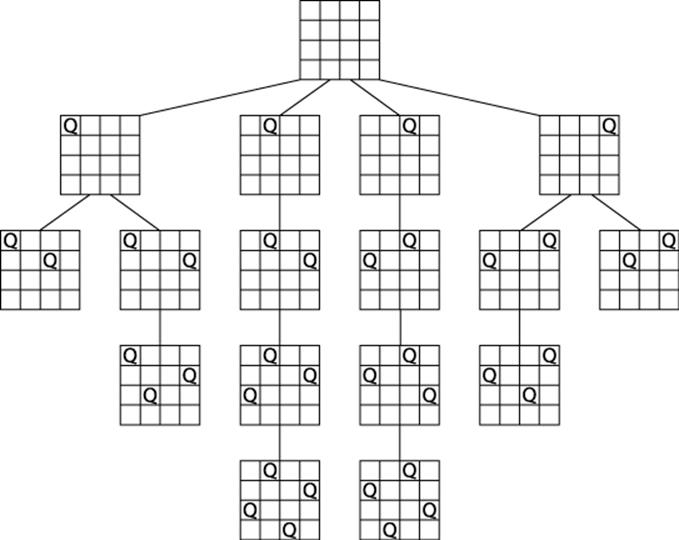
Figure 11-3. Final solution for 4-Queens Problem with four rows extended

However, what if you were interested only in approximating the number of solutions, or in other words, the number of potential board states on level n? Donald Knuth (1975) developed a novel alternative approach to estimate the size and shape of a search tree. His method corresponds to taking a random walk down the search tree. For the sake of brevity, we illustrate his technique for the 4-Queens Problem, but clearly it could just as easily be applied to approximate the number of solutions to the 19-Queens Problem. Instead of counting all possible solutions, try to create a single board state containing n queens and estimate the overall count by totaling the potential board states not followed, assuming that each of these directions would be equally productive.

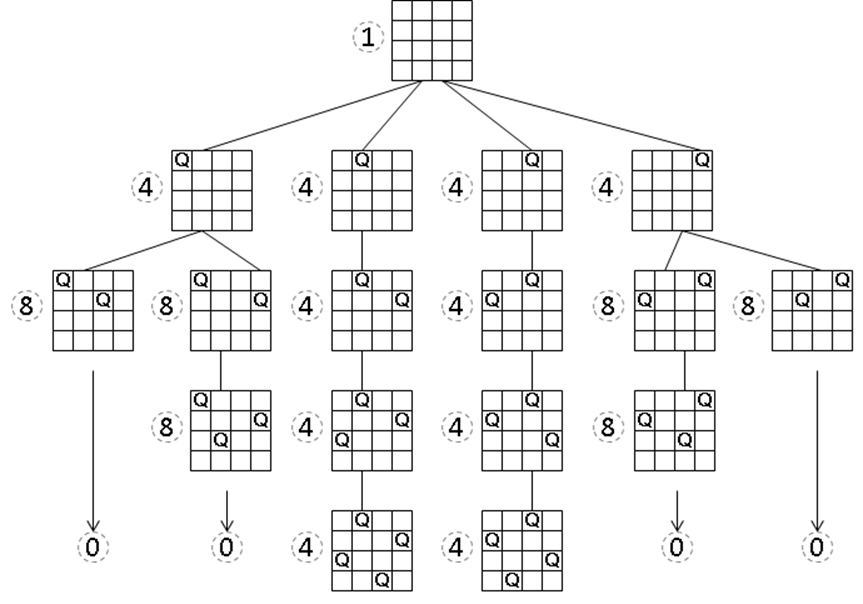
Figure 11-4. Estimating number of solutions of 4-Queens Problem

Figure 11-4 demonstrates Knuth’s approach on a 4x4 chessboard. Each of the board states has an associated estimate in a small dashed circle for the number of board states at that level. Starting with the root of the search tree (no queens placed), we estimate that there is one board state at that level 0. Each board state expands to a new level based on its number of children. We will conduct a large number of random walks over this search tree, which will never be constructed during the process. Let’s perform two possible walks starting from the root:

§ Choose the leftmost board state in the first level. Because there are four children, our best estimate for the total number of solutions is 4. Now again, choose the leftmost child from its two children, resulting in a board state on level 2. From its perspective, it still might lead to two solutions, and assuming each of the other three children of the root node are similarly productive, it guesses the total number of solutions to be 4*2=8. However, at this point, there are no more possible moves, so from its perspective, it assumes no other branch is productive, so it estimates there are 0 solutions.

§ Choose the second-to-left board state in the first level. Its best estimate for the number of solutions is 4. Now, in each of the subsequent levels there is only one valid board state, which leads to the estimate of 4*1=4, assuming all of the other original paths were similarly productive. Upon reaching the lowest level, it estimates there are 4 solutions.

Neither of these estimates is correct, and it is typical of this approach that different walks lead to under- and overestimates of the actual count. However, if we perform a large number of random walks, the average of the estimates will converge on the value. Each estimate can be computed quickly, thus this refined (averaged) estimate can also be computed quickly.

If you refer back to Table 10-2, we show the computed results from our implementation for 1,024, 8,192, and 65,536 trials. No timing information is included, because all results were computed in less than a minute. The final estimate for the 19-Queens problem with T=65,536 trials is within 3% of the actual answer. Indeed, all of the estimates for T=65,536 are within 5.8% of the actual answer. This algorithm has the desirable property that the computed value is more accurate as more random trials are run. Example 10-2 shows the implementation in Java for a single estimate of the n-Queens problem.

Example 11-7. Implementation of Knuth’s randomized estimation of n-Queens problem

/**

* For an n-by-n board, store up to n non-threatening queens and support

* search along the lines of Knuth's random walk. It is assumed the

* queens are being added row by row starting from 0.

*/

public class Board {

boolean [][] board; /** The board. */

final int n; /** board size. */

/** Temporary store for last valid positions. */

ArrayList<Integer> nextValidRowPositions = new ArrayList<Integer>();

public Board (int n) {

board = new boolean[n][n];

this.n = n;

}

/** Start with row and work upwards to see if still valid. */

private boolean valid (int row, int col) {

// another queen in same column, left diagonal, or right diagonal?

int d = 0;

while (++d <= row) {

if (board[row-d][col]) { return false; } // column

if (col >= d && board[row-d][col-d]) { return false; } // left-d

if (col+d < n && board[row-d][col+d]) { return false; } // right-d

}

return true; // OK

}

/**

* Find out how many valid children states are found by trying to add

* a queen to the given row. Returns a number from 0 to n.

*/

public int numChildren(int row) {

int count = 0;

nextValidRowPositions.clear();

for (int i = 0; i < n; i++) {

board[row][i] = true;

if (valid(row, i)) {

count++;

nextValidRowPositions.add(i);

}

board[row][i] = false;

}

return count;

}

/** If no board is available at this row then return false. */

public boolean randomNextBoard(int r) {

int sz = nextValidRowPositions.size();

if (sz == 0) { return false; }

// select one randomly

int c = ((int)(Math.random()*sz));

board[r][nextValidRowPositions.get(c)] = true;

return true;

}

}

public class SingleQuery {

public static void main (String []args) {

for (int i = 0; i < 100; i++) {

System.out.println(i + ": " + estimate(19));

}

}

public static long estimate(int n) {

Board b = new Board(n);

int r = 0;

long lastEstimate = 1;

while (r < n) {

int numChildren = b.numChildren(r);

// no more to go, so no solution found.

if (!b.randomNextBoard(r)) {

lastEstimate = 0;

break;

}

// compute estimate based on ongoing tally and advance

lastEstimate = lastEstimate*numChildren;

r++;

}

return lastEstimate;

}

}

References

Armstrong, Joe, Programming Erlang: Software for a Concurrent World. Pragmatic Bookshelf, 2007.

Berman, Kenneth and Jerome Paul, Algorithms: Sequential, Parallel, and Distributed. Course Technology, 2004.

Christofides, Nicos, “Worst-case analysis of a new heuristic for the travelling salesman problem,” Report 388, Graduate School of Industrial Administration, CMU, 1976.

Knuth, Donald, “Estimating the efficiency of backtrack programs,” Mathematics of Computation 29: 121-136, 1975.