Modern Cryptography: Applied Mathematics for Encryption and Informanion Security (2016)
PART II. Symmetric Ciphers and Hashes
Chapter 9. Cryptographic Hashes
In this chapter we will cover the following:
![]() What is a cryptographic hash?
What is a cryptographic hash?
![]() Specific algorithms
Specific algorithms
![]() Message authentication codes (MACs)
Message authentication codes (MACs)
![]() Applications of cryptographic hashes
Applications of cryptographic hashes
In the preceding eight chapters, we examined cryptography as a means of keeping information confidential. Cryptographic hashes are not concerned with protecting confidentiality, however; instead, they are concerned with ensuring integrity. Computer security has a handful of bedrock concepts upon which it is built. The CIA triangle, consisting of confidentiality, integrity, and availability, is one such concept. Different technologies support different aspects of the CIA triangle. For example, backups, disaster recovery plans, and redundant equipment support availability. Certainly encrypting a message so others cannot read it supports confidentiality. Cryptographic hashes are about supporting integrity.
As with previous chapters, some algorithms in this chapter will be discussed in depth, while others will be briefly described. The goal is not necessarily for you to memorize every major cryptographic hashing function, but to gain a general familiarity with cryptographic hashes. It is also important that you understand how cryptographic hashing algorithms are used to support security.
What Is a Cryptographic Hash?
A cryptographic hash is a special type of algorithm. William Stallings, in his book Network Security Essentials, describes a hash as follows:
1. H can be applied to a block of data of variable size.
2. H produces a fixed-length output.
3. H(x) is relatively easy to compute for any given x, making both hardware and software implementations practical. X is whatever you input into the hash.
4. For any given value h, it is computationally infeasible to find x such that H(x) = h. This is sometimes referred to in the literature as the one-way property.
5. For any given block x, it is computationally infeasible to find y !=x such that H(y) = H(x). This is sometimes referred to as weak collision resistance.
6. It is computationally infeasible to find any pair x, y such that H(x) = H(y). This is sometimes referred to as strong collision resistance.1
Note
William Stallings received his Ph.D. in computer science from the Massachusetts Institute of Technology. He has authored several computer science and security textbooks as well as a number of scientific articles.
Stallings’s definition is accurate, but it may be a bit technical for the novice. Allow me to explain the properties of a cryptographic hash in a manner that is a bit less technical, but no less true. In order to be a cryptographic hash function, an algorithm needs to have three properties.
First, the function must be one way. That means it cannot be “unhashed.” This may seem a bit odd at first—an algorithm that is not reversible? In fact, it is not simply difficult to reverse, but it is literally impossible to reverse—like trying to unscramble a scrambled egg and put it back in the shell. When we examine specific hashing algorithms later in this chapter, you’ll understand why a cryptographic hash is irreversible.
Second, a variable-length input must produce a fixed-length output. That means that no matter what size of input you have, you will get the same sized output. Each particular cryptographic hash algorithm has a specific sized output. For example, the Secure Hash Algorithm (SHA-1) produces a 160-bit hash. It does not matter whether you input 1 byte or 1 terabyte; you’ll still get out 160 bits. How do you get fixed-length output regardless of the size of the input? Different algorithms will each use its own specific approach, but in general, it involves compressing all the data into a block of a specific size. If the input is smaller than the block, you can pad it.
Consider the following example, which is trivial and for demonstrative purposes. It would not suffice as a secure cryptographic hash. We will call this the trivial hashing algorithm (THA):
1. If the input is less than 64 bits, pad it with 0’s until you achieve 64 bits. If it is greater than 64 bits, divide it into 64-bit segments. Make sure the last segment is exactly 64 bits, even if you need to pad it with 0’s.
2. Divide each 64-bit block into two halves.
3. XOR the left half of each block with the right half.
4. If there is more than one block, start at the first block, XOR’ing it with the next block. Continue this until you reach the last block. The output from the final XOR operation is your hash. If you had only one block, the result of XOR’ing the left half with the right half is your hash.
Note
I cannot emphasize enough that this would not be secure. It is very easy to envision collisions occurring in this scenario—quite easily, in fact. However, this does illustrate a rather primitive way in which the input text can be condensed (or padded) to reach a specific size.
Third, there should be few or no collisions. That means if you hash two different inputs, you should not get the same output. Why “few or no” rather than no collisions, when the preference is for no collisions? If you use SHA-1, then you have a 160-bit output, and that means about 1.461 × 1048 possible outputs. Clearly, you could have trillions of different inputs and never see a collision. For most people, this qualifies as “no collisions.” In the interest of being accurate, however, I cannot help but note that it is at least theoretically possible that two inputs could produce the same output, even though that has never yet occurred and the possibility is incredibly remote. Thus the caveat “few or no collisions.”
How Are Cryptographic Hashes Used?
Cryptographic hashes can be used in many ways, and this section discusses some of the most common uses. Each will depend on one or more of the three key properties of a cryptographic hash, as discussed in the previous section. Reading this section should help you understand the importance of cryptographic hashes in computer security.
Message Integrity
One common use of hashing algorithms is to ensure message integrity. Obviously, messages can be altered in transit, either intentionally or accidentally. You can use hashing algorithms to detect any alterations that have occurred. Consider, for example, an e-mail message. If you put the body of the message into a hashing algorithm—say, SHA-1—the output is a 160-bit hash. That hash can be appended at the end of the message.
Note
Another term for hash is message digest, or just digest.
When the mail is received, the recipient can recalculate the cryptographic hash of the message and compare that result to the hash that was attached to the message. If the two do not match exactly, this indicates that some alteration in the message has occurred and that the message contents are no longer reliable.
Cryptographic hashes are also used in file integrity systems. For example, the popular Tripwire product (both the open source Linux version and the Windows version) creates a cryptographic hash of key files (as designated by the Tripwire administrator). At any time, a hash of the current file can be compared to the previously computed cryptographic hash to determine whether there has been any change in the file. This can detect anything from a simple edit of a file such as a spreadsheet to an executable that has been infected with a Trojan horse.
Note
A Trojan horse is a program or file that has malware attached to it. Often, attackers use wrapper programs to tie a virus or spyware to a legitimate program. A user who executes the legitimate program may inadvertently launch the malware.
Password Storage
Cryptographic hashes also provide a level of security against insider threats. Consider the possibility, for example, that someone with access to a system, such as a network administrator, has malicious intentions. This person may simply read a user’s password from the database, and then use that user’s login credentials to accomplish some attack on the system. Then, should the attack become known, it is the end user who will be a suspect, not the administrator who actually perpetrated the breach. One way to avoid this is to store passwords in a cryptographic hash. When the user logs into the system, whatever password is typed in is hashed and then compared to the hash in the database. If they match exactly, the user is logged into the system.
Given that the database stores only a hash of the password, and hashes are not reversible, even a network administrator or database administrator cannot retrieve the password from the database. If someone attempts to type in the hash as a password, the system will hash whatever input is placed into the password field, thus yielding a hash different from the one stored in the database. The storing of passwords as a hash is widely used and strongly recommended.
Hashing is, in fact, how Windows stores passwords. For example, if your password is password, then Windows will first hash it producing something like this:
![]()
That hash will be stored in the Security Accounts Manager (SAM) file in the Windows System directory. When you log on, Windows cannot “un-hash” your password. Instead, it hashes whatever password you type in and compares that result with what is stored in the SAM file. If they match (exactly), then you can log in.
Forensic Integrity
When you conduct a forensic examination of a hard drive, one of your first steps is to create an image of the drive and perform the analysis on the image. After creating an image, you must verify that the imaging process was accurate. To do this, you create a hash of the original and a hash of the image and compare the two. This is where the “variable-length input produces fixed-length output” and “few or no collisions” comes in. If you have a terabyte drive, for example, and you image it, you must ensure that your image is an exact copy. The fact that the hash is only a fixed size, such as 160 bits for SHA-1, is very useful. It would be quite unwieldy if the hash itself was the size of the input. Comparing terabyte-sized hashes would be problematic at best.
If you make a hash of the original and the image, and then compare them, you can verify that everything is copied exactly into the image. If the variable-length input produced a fixed-length output, then you would have hashes that were humongous and that took forever to compute. Also, if two different inputs could produce the same output, you could not verify that the image was an exact copy.
Merkle-Damgård
Before we delve into specific hashing algorithms, it is worthwhile to examine a function that is key to many commonly used cryptographic hashes. A Merkle-Damgård function (also called a Merkle-Damgård construction) is a method used to build hash functions. Merkle-Damgård functions form the basis for MD5, SHA1, SHA2, and other hashing algorithms.
Note
To read more about Merkle-Damgård functions, see the article “Merkle-Damgård Revisited: How to Construct a Hash Function,” at http://www.cs.nyu.edu/~puniya/papers/merkle.pdf.
Computer scientist Ralph Merkle co-invented cryptographic hashing and published his findings in his 1979 doctoral dissertation. The function starts by applying some padding function to create an output that is of some particular size (256, 512, or 1024 bits, and so on). The specific size will vary from one algorithm to another, but 512 bits is a common size used by many algorithms. The function then processes blocks one at a time, combining the new block of input with the block from the previous round (recall our earlier THA example that took output from one block and combined it with the next). Put another way, if you break up a 1024-bit message into four 256-bit blocks, block 1 will be processed, and then its output will be combined with block 2 before block 2 is processed. Then that output will be combined with block 3 before it is processed. And, finally, that output is combined with block 4 before that block is processed. Merkle-Damgård is often referred to as a “compression function,” because it compresses the entire message into a single output block.
The algorithm starts with some initial value or initialization vector that is specific to the implementation. The final message block is always padded to the appropriate size (256, 512 bits, and so on) and includes a 64-bit integer that indicates the size of the original message.
Specific Algorithms
You can use a variety of specific algorithms to create cryptographic hashes. Remember that to be a viable cryptographic hash, an algorithm needs three properties:
1. Variable-length input produces fixed-length output
2. Few or no collisions
3. Not reversible
A variety of cryptographic hashing functions meet these three criteria. In the United States as well as much of the world, the MD5 and SHA algorithms are the most widely used, and thus will be prominently covered in this chapter.
Checksums
A checksum is a much simpler algorithm than a cryptographic hash and can serve similar purposes—for example, a checksum can check for message integrity. The word checksum is often used as a generic term for the actual output of a specific algorithm. The algorithms are often called achecksum function or checksum algorithm.
Longitudinal Parity Check
One of the simplest checksum algorithms is the longitudinal parity check. It breaks data into segments (called words) with a fixed number of bits. Then the algorithm computes the XOR of all of these words, with the final result being a single word or checksum. Here’s an example: Assume a text that says this:
![]()
Then convert that to binary (first converting to ASCII codes, and then converting that to binary):

The segments can be any size, but let’s assume a 2-byte (16-bit) word. So this text is now divided into nine words (shown here separated with brackets):

The next step is to XOR the first word with the second:
![]()
Then that result is XOR’d with the next word:
![]()
This process is continued with the result of the previous XOR, which is then XOR’d with the next word until a result is achieved. That result is called the longitudinal parity check.
This type of checksum (as well as others) works well for error detection. The checksum of a message can be appended to a message. The recipient then recalculates the checksum and compares it. Checksums are usually much faster than cryptographic hashes. However, collisions are possible (different inputs producing identical outputs).
Fletcher Checksum
The Fletcher checksum is an algorithm for computing a position-dependent checksum. Devised by John G. Fletcher at Lawrence Livermore Labs in the late 1970s, this checksum’s objective was to provide error-detection properties that were those of a cyclic redundancy check but with the lower computational effort associated with summation techniques. The Fletcher checksum works by dividing the input into words and computing the modular sum of those words. Any modulus can be used for computing the modular sum. The checksum is appended to the original message, and the recipient recalculates the checksum and compares it to the original.
MD5
This 128-bit hash is specified by RFC 1321. Designed by Ron Rivest in 1991 to replace and improve on the MD4 hash function, MD5 produces a 128-bit hash, or digest. As early as 1996, a flaw was found in MD5 and by 2004 it was shown that MD5 was not collision resistant.
The first step in the algorithm is to break the message to be encrypted into 512-bit segments, each consisting of sixteen 32-bit words. If the last segment is less than 512 bits, it is padded to reach 512 bits. The final 64 bits represents the length of the original message.
Because MD5 ultimately seeks to create a 128-bit output, it works on a 128-bit state that consists of four 32-bit words labeled A, B, C, and D. These 32-bit words are initialized to some fixed constant. The algorithm has four rounds consisting of a number of rotations and binary operations, with a different round function for each round. Since MD5 is a Merkle-Damgård function, the following steps are taken for each 512-bit block. If the message is more than 512 bits, final output of a given block is then combined with the next block until the last block is reached.
1. Round 1: B is XOR’d with C. The output of that operation is OR’d with the output of the negation of B XOR’d with D.
2. Round 2: B is XOR’d with D. The output of that operation is OR’d with the output of C XOR’d with the negation of D.
3. Round 3: B is XOR’d with C. The output is XOR’d with D.
4. Round 4: C is XOR’d with the output of B, which is OR’d with the negation of D.
Note
These round functions are often denoted as F, G, H, and I, with F being round 1, G being round 2, H being round 3, and I being round 4.
The algorithm is illustrated in Figure 9-1. The blocks A–D have already been explained. The F in Figure 9-1 represents the round function for that given round (F, G, H, or I depending on the round in question). The message word is Mi and Ki is a constant. The <<< denotes a binary left shift by s bits. After all rounds are done, the A, B, C, and D words contain the digest, or hash, of the original message.
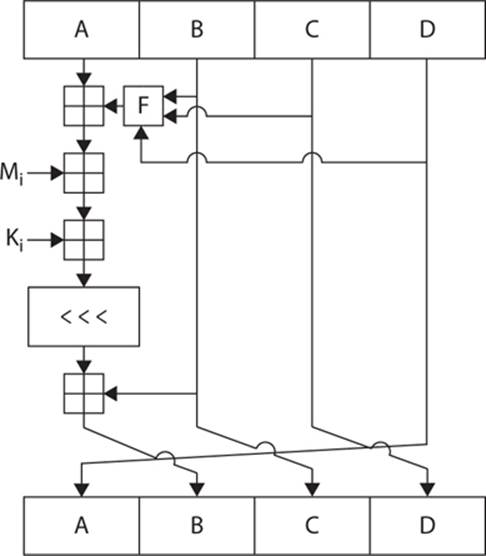
FIGURE 9-1 The MD5 algorithm
SHA
The Secure Hash Algorithm is perhaps the most widely used hash algorithm today, with several versions, all of which are considered secure and collision free:
![]() SHA-1 This 160-bit hash function resembles the earlier MD5 algorithm. It was designed by the National Security Agency (NSA) to be part of the Digital Signature Algorithm (DSA).
SHA-1 This 160-bit hash function resembles the earlier MD5 algorithm. It was designed by the National Security Agency (NSA) to be part of the Digital Signature Algorithm (DSA).
![]() SHA-2 These are two similar hash functions with different block sizes and are known as SHA-256 and SHA-512. They differ in the word size; SHA-256 uses 32-byte (256-bit) words, and SHA-512 uses 64-byte (512-bit) words. Truncated versions of each standard are known as SHA-224 and SHA-384; these were also designed by the NSA.
SHA-2 These are two similar hash functions with different block sizes and are known as SHA-256 and SHA-512. They differ in the word size; SHA-256 uses 32-byte (256-bit) words, and SHA-512 uses 64-byte (512-bit) words. Truncated versions of each standard are known as SHA-224 and SHA-384; these were also designed by the NSA.
![]() SHA-3 The latest version of SHA was adopted in October 2012.
SHA-3 The latest version of SHA was adopted in October 2012.
SHA-1
Much like MD5, SHA-1 uses some padding and 512-bit blocks. The final block must be 448 bits, followed by a 64-bit unsigned integer that represents the size of the original message. Because SHA-1 is also a Merkle-Damgård function, each 512-bit block undergoes a step-by-step process (shown a bit later). If the message is more than 512 bits, final output of a given block is combined with the next block until the last block is reached.
Unlike MD5, SHA1 uses five blocks, often denoted as h1, h2, h3, h4, and h5. These are initialized to some constant value. The message to be hashed is changed into characters and converted to binary format. The message is padded so it evenly breaks into 512-bit segments with the 64-bit original message length at the end.
Each 512-bit segment is divided into sixteen 32-bit words. The first step after preparing the message is a process that will create 80 words from the 16 in the block. This is a loop that will be executed until a given condition is true. First, the 16 words in the 512-bit block are put into the first 16 words of the 80-word array. The other words are generated by XOR’ing previous words and shifting 1 bit to the left.
Then you loop 80 times through a process that does the following:
1. Calculates the SHA function and a constant K, both based on the current round.
2. Sets word E = D, word D = C, word C = B after rotating B left 30 bits; word B = 1, word A = word A rotated left 5 bits + the SHA function + E + K + word [i], where i is the current round.
3. Concatenates the final hash as A, B, C, D, and E; this has five final words (each 32-bit), whereas MD5 only had four, because MD5 produces a 128-bit digest and SHA-1 produces a 160-bit digest.
This process is depicted in Figure 9-2.
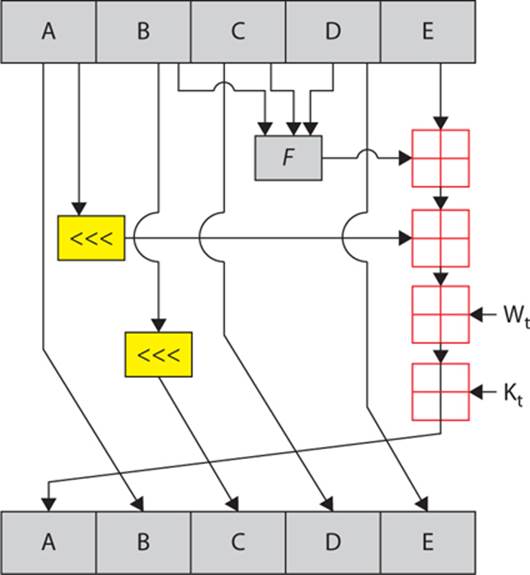
FIGURE 9-2 The SHA-1 algorithm
Notice the round function in Figure 9-2. Like MD5, SHA-1 has a varying round function that changes slightly each round:
Variation 1: f(t;B,C,D) = (B AND C) OR ((NOT B) AND D) ( 0 <= t <= 19)
Variation 2: f(t;B,C,D) = B XOR C XOR D (20 <= t <= 39)
Variation 3: f(t;B,C,D) = (B AND C) OR (B AND D) OR (C AND D) (40 <= t <=59)
Variation 4: f(t;B,C,D) = B XOR C XOR D (60 <= t <= 79)
Note
At this point, you may find both MD5 and SHA-1 to be a bit convoluted, and that’s OK. Remember the goal is to have a nonreversible algorithm. So the convoluted steps are designed simply to scramble the message so that it cannot be unscrambled.
If you have a programming background or are simply familiar with algorithm analysis, you may find the following pseudo-code helpful in understanding SHA-1:

SHA-2
SHA-2 is similar in structure and function to SHA-1, and it is also a Merkle-Damgård construction. However, it has a variety of sizes, the most common of which are SHA-256 (which uses 32-bit words) and SHA-512 (which uses 64-bit words); there is also SHA-224 and SHA-384. In the United States, FIPS PUB 180-2 defines SHA-2 as a standard.
While SHA-1 is one of the most widely used hashing algorithms in existence today, SHA-2 is widely used in Pretty Good Privacy (PGP), Secure Sockets Layer (SSL), Transport Layer Security (TLS), Secure Shell (SSH), IPsec, and other security protocols. Certain Linux distributions, such as Debian, use SHA-2 variations to authenticate software packages, and some implementations of Bitcoin also use SHA-2 to verify transactions.
SHA-3
SHA-3 is an interesting algorithm in that it was not designed to replace SHA-2. (There are no known significant flaws with SHA-2, but there are issues with MD-5 and at least theoretical issues with SHA-1.) SHA-3 was the result of a contest to find a new hashing algorithm. The original algorithm family, named Keccak, was designed by Guido Bertoni, Joan Daemen, Michaël Peeters, and Gilles Van Assche. The U.S. National Institute of Standards and Technology (NIST) published FIPS 202,2 which standardized the use of SHA-3.
Unlike SHA-1 and SHA-2 that use a Merkle-Damgård construction, SHA-3 uses a sponge construction (also known as a sponge function), which is a type of algorithm that uses an internal state and takes input of any size to produce a specific-sized output. This makes it a good fit for cryptographic hashes that need to take variable-length input to produce fixed-length output.
Any sponge construction uses three components: a state, usually called S, that is of some fixed size; some function, f, that transforms the state; and a padding function to ensure the output is of the proper size.
The state is usually divided into two sections, denoted R and C. The R represents the size bitrate and the C is the size of the capacity. The bitrate is simply the base size for the algorithm. Just as Merkle-Damgård constructions might use 512-bit blocks, sponge constructions have a certain base size, and the entire input must be a multiple of that size. The padding function ensures that the input is a multiple of R.
The sponge function consists of iterations of the following steps:
1. The state (S) is initialized to 0.
2. The input string is padded using the padding function.
3. R is XOR’d with the first r-bit block of padded input. (Remember R is the bit size being used as a base for this implementation.)
4. S is replaced by F(S). The function F is specific to a particular sponge function.
5. R is then XOR’d with the next r-bit block of padded input.
6. Steps 4 and 5 continue until the end of the input, at which time, the output is produced as follows:
A. The R portion of the state memory is the first r-bits of output.
B. If more output bits are desired, S is replaced by F(S).
C. The R portion of the state memory is the next r-bits of output.
Note
This is a generic overview of the essentials of a sponge construction; there can be variations on this process. The details of the function F will vary with specific implementations. In SHA-3, the state consists of a 5 × 5 array of 64-bit words, 1600 bits total. The authors claim 12.5 cycles per byte on an Intel Core 2 CPU. In hardware implementations, it was notably faster than all other finalists. The permutations of SHA-3 that were approved by the NIST include 224-, 256-, 384-, and 512-bit outputs.
RIPEMD
RACE Integrity Primitives Evaluation Message Digest is a 160-bit hash algorithm developed in Belgium by Hans Dobbertin, Antoon Bosselaers, and Bart Preneel. This algorithm has 128-, 256-, and 320-bit versions, called RIPEMD-128, RIPEMD-256, and RIPEMD-320, respectively.
RIPEMD-160 replaces the original RIPEMD, which was found to have collision issues. The larger bit sizes make this far more secure that MD5 or RIPEMD. RIPEMD-160 was developed in Europe as part of the RIPE project and is recommended by the German Security Agency. The authors of the algorithm describe RIPEMD as follows:
RIPEMD-160 is a fast cryptographic hash function that is tuned towards software implementations on 32-bit architectures. It has evolved from the 256-bit extension of MD4, which was introduced in 1990 by Ron Rivest. Its main design feature[s] are two different and independent parallel chains, the result of which are combined at the end of every application of the compression function.3
The RIPEMD-160 algorithm is slower than SHA-1 but perhaps more secure (at least according to some experts). The general algorithm uses two parallel lines of processing, each consisting of five rounds and 16 steps.
Note
Because the five rounds are in parallel, some sources describe RIPEMD as using ten rounds. Either description is accurate, depending on your perspective.
As with many other hashing algorithms, RIPEMD works with 512-bit segments of input text. It must first pad, so that the final message block is 448 bits plus a 64-bit value that is the length of the original message. (You may have noticed by now that padding is a very common approach to creating hashing algorithms.)
The initial five-word buffer (each word being 32 bits, for a total of 160 bits) is initialized to a set value. The buffers are labeled A, B, C, D, and E (as you have seen with previous algorithms). The message being hashed is processed in 512-bit segments, and the final output is the last 160 bits left in the buffer when the algorithm has completed all rounds.
Tiger
Tiger is designed using the Merkle-Damgård construction. Tiger produces a 192-bit digest. This cryptographic hash was invented by Ross Anderson and Eli Biham and published in 1995.
Note
You were introduced to Ross Anderson and Eli Biham in Chapter 7. These very prominent cryptographers are individually quite accomplished, and they have frequently collaborated in their work. Anderson is currently Cambridge University’s head of cryptography and professor in security engineering. Biham is a prominent Israeli cryptographer who has done extensive work in symmetric ciphers, hashing algorithms, and cryptanalysis.
The one-way compression function operates on 64-bit words, maintaining three words of state and processing eight words of data.4 There are 24 rounds, using a combination of operation mixing with XOR and addition/subtraction, rotates, and S-box lookups, and a fairly intricate key scheduling algorithm for deriving 24 round keys from the eight input words.
HAVAL
HAVAL is a cryptographic hash function. Unlike MD5, but like most other modern cryptographic hash functions, HAVAL can produce hashes of different lengths—128, 160, 192, 224, and 256 bits. HAVAL enables users to specify the number of rounds (three, four, or five) to be used to generate the hash. HAVAL was invented by Yuliang Zheng, Josef Pieprzyk, and Jennifer Seberry in 1992.
Note
Yuilang Zheng is, as of this writing, a professor at the University of North Carolina who has also worked in ciphers such as SPEED and the STRANDOM pseudorandom-number generator. Josef Pieprzyk is a professor at Queensland University of Technology in Australia and is known for his work on the LOKI family of block ciphers. Jennifer Seberry is currently a professor at the University of Wollongong in Australia and is notable not only for her work in cryptography, but for being the first female professor of computer science in Australia. She also has worked on the LOKI family of ciphers as well as the Py stream cipher.
Whirlpool
Whirlpool, invented by Paulo Barreto and Vincent Rijmen, was chosen as part of the NESSIE project (mentioned in Chapter 7) and has been adopted by the International Organization for Standardization (ISO) as a standard. Whirlpool is interesting because it is a modified block cipher. It is a common practice to create a hashing algorithm from a block cipher. In this case, the square cipher (precursor to Rijndael) was used as the basis. Whirlpool produces a 512-bit digest and can take in inputs up to 2256 bits in size.5 The algorithm is not patented and can be used free of charge.
Note
Vincent Rijmen was one of the creators of the Rijndael cipher, which was chosen to become AES. Paulo Barreto is a Brazilian cryptographer who also worked on the Anubis and KHAZAD ciphers. He has worked on various projects with Rijmen and published papers on elliptic curve cryptography, discussed in Chapter 11.
Skein
The Skein cryptographic hash function was one of the five finalists in the NIST competition. Entered as a candidate to become the SHA-3 standard, it lost to Keccak. Skein was created by Bruce Schneier, Stefan Lucks, Niels Ferguson, Doug Whiting, Mihir Bellare, Tadayoshi Kohno, Jon Callas, and Jesse Walker. It is based on the Threefish block cipher, which is compressed using the Unique Block Iteration (UBI) chaining mode while leveraging an optional low overhead argument system for flexibility.
Note
Both Bruce Schneier and Niels Ferguson are well-known cryptographic researchers. Stefan Lucks is primarily known for his work on cryptanalysis. Mihir Bellare is a professor at University of California San Diego and has published several papers on cryptography as well as earning the 2003 RSA’s Sixth Annual Conference Award for outstanding contributions in the field of mathematics. Jon Callas is known primarily for his work with the Internet Engineering Task Force in establishing standards such as OpenPGP. Whiting also worked on the Twofish algorithm. Tadayoshi Kohno is an adjunct professor at the University of Washington and has published various computer security–related papers. Jesse Walker has published a number of cryptography-related papers and been a guest speaker on cryptography.
FSB
The Fast Syndrome-Based (FSB) hash functions are a family of cryptographic hash functions introduced in 2003 by Daniel Augot, Matthieu Finiasz, and Nicolas Sendrier.6
Note
Daniel Augot is a French researcher known for work in cryptography as well as algebraic coding theory. Matthieu Finiasz has numerous publications covering a wide variety of cryptographic topics. Nicolas Sendrier is a French researcher with extensive publications in both cryptography and computer security.
FSB is distinctive in that it can, at least to a certain extent, be proven to be secure. Breaking FSB is at least as difficult as solving a certain NP-complete problem known as Regular Syndrome Decoding. What this means, in practical terms, is that FSB is provably secure. (You read about NP-complete problems in Chapter 5.)
Security and efficiency are often conflicting goals, and provably secure algorithms are often a bit slower. Therefore, as you might expect, FSB is slower than many traditional hash functions and uses a lot of memory. There have been various versions of FSB, one of which was submitted to the SHA-3 competition, which was rejected.
GOST
This hash algorithm was initially defined in the Russian government standard GOST R 34.11-94 Information Technology – Cryptographic Information Security – Hash Function. The GOST algorithm produces a fixed-length output of 256 bits. The input message is broken up into chunks of 256-bit blocks. If a block is less than 256 bits, the message is padded to bring the length of the message up to 256 bits. The remaining bits are filled up with a 256-bit integer arithmetic sum of all previously hashed blocks, and then a 256-bit integer representing the length of the original message, in bits, is produced. It is based on the GOST block cipher period.
Attacks on Hashes
How does someone go about attacking a hash? Of particular interest are hashes used for password storage. The most common attack on hashed passwords is a preimage attack. In the security community, this is often done using a rainbow table, which reverses cryptographic hash functions.
In 1980, Martin Hellman described a cryptanalytic technique that reduces the time of cryptanalysis by using precalculated data stored in memory. This technique was improved by Rivest before 1982. Basically, these types of password crackers are working with precalculated hashes of all passwords available within a certain character space, be that a-z, a-zA-z, or a-zA-Z0-9, and so on. If you search a rainbow table for a given hash, whatever plain text you find must be the text that was input into the hashing algorithm to produce that specific hash.
A rainbow table can get very large very fast. Assume that the passwords must be limited to keyboard characters, and that leaves 52 letters (26 uppercase and 26 lowercase), 10 digits, and roughly 10 symbols, or about 72 characters. As you can imagine, even a six-character password has a large number of possible combinations. (Recall the discussion of combinatorics in Chapter 4.) There is a limit to how large a rainbow table can be, and this is why longer passwords are more secure that shorter passwords.
Note
As a practical matter, some utilities were designed to crack Windows passwords that include rainbow tables on a Linux live CD. The utility will boot to Linux and then attempt to grab the Windows SAM file, where hashes of passwords are stored, and run those through rainbow tables to get the passwords. This is another reason why longer passwords are a good security measure.
Salt
In hashing, the term salt refers to random bits that are used as one of the inputs to the hash. Essentially, the salt is intermixed with the message that is to be hashed. Consider this example password:
![]()
In binary, that is
![]()
A salt algorithm inserts bits periodically. Suppose we insert bits every fourth bit, giving us the following:
![]()
If you convert that to text you would get
![]()
Someone using a rainbow table to try and derive salted passwords would get the incorrect password back and would not be able to log in to the system. Salt data makes rainbow tables harder to implement. The rainbow table must account for the salting algorithm as well as the hashing algorithm.
MAC and HMAC
As you know, hashing algorithms are often used to ensure message integrity. If a message is altered in transit, the recipient can compare the hash received against the hash computed and detect the error in transmission. But what about intentional alteration of messages? What happens if someone alters a message intentionally, deletes the original hash, and recomputes a new one? Unfortunately, a simple hashing algorithm cannot account for this scenario. A message authentication code (MAC), however—specifically a keyed-hash message authentication code (HMAC)—can detect intentional alterations in a message. A MAC is also often called a keyed cryptographic hash function,7 and its name should tell you how it works.
Let’s assume you are using MD5 to verify message integrity. To detect an intercepting party intentionally altering a message, both the sender and recipient must previously exchange a key of the appropriate size (in this case, 128 bits). The sender will hash the message and then XOR that hash with this key. The recipient will hash what she receives and XOR that computed hash with the key. Then the two hashes are exchanged. Should an intercepting party simply recompute the hash, he will not have the key to XOR that with (and may not even be aware that it should be XOR’d) and thus the hash the interceptor creates won’t match the hash the recipient computes and the interference will be detected.
Another common way of accomplishing a MAC is called a cipher block chaining MAC (CBC-MAC). In this case, a block cipher is used (any cipher will do) rather than a hash. The algorithm is used in CBC mode. Only the final block is used for the MAC. You can use any block cipher you choose.
Note
Recall that CBC mode XOR’s the cipher text from each block with that of the next block before encrypting it.
Conclusions
This chapter offered a broad overview of cryptographic hashes. The first important things you should absolutely commit to memory are the three criteria for an algorithm to be a cryptographic hash. You should also be familiar with the practical applications of cryptographic hashes.
You have also been exposed to several cryptographic hashing algorithms, some in more detail than others. The SHA family of hashing algorithms is the most widely used, and thus is the most important for you to be familiar with. The other algorithms presented in this chapter are widely used and warrant some study—perhaps in depth. You can find a great deal of information, including research papers, on the Internet.
Test Your Knowledge
1. __________ is a message authentication code that depends on a block cipher wherein only the final block is used.
2. The __________ works by first dividing the input into words and computing the modular sum of those words.
3. What hashing algorithm that uses a modified block cipher was chosen as part of the NESSIE project?
4. What algorithm was ultimately chosen as SHA-3?
5. What are the three properties all cryptographic hash functions must exhibit?
6. What is the compression function used as a basis for MD5, SHA1, and SHA2?
7. __________ was developed in Europe and is recommended by the German Security Agency.
8. Which algorithm discussed in this chapter was published in 1995 and produces a 192-bit digest?
9. ___________ was one of the five finalists in the SHA-3 competition (but did not win) and is based on the Threefish block cipher.
10. Which hash functions introduced in this chapter have provable security?
Answers
1. CBC-MAC
2. Fletcher checksum
3. Whirlpool
4. Keccak
5. a) Variable-length input produces fixed-length output; b) no collisions; c) not reversible
6. Merkle-Damgård
7. RIPEMD-160
8. Tiger
9. Skein
10. Fast Syndrome-Based (FSB) hash functions
Endnotes
1. William Stallings, Network Security Essentials: Applications and Standards, 5th ed. (Prentice Hall, 2013).
2. National Institute of Standards and Technology, SHA-3 Standard: Permutation-Based Hash and Extendable-Output Functions, 2014, http://csrc.nist.gov/publications/drafts/fips-202/fips_202_draft.pdf.
3. B. Preneel, H. Dobbertin, and A. Bosselaers, “The Cryptographic Hash Function RIPEMD-160,” 1997, www.cosic.esat.kuleuven.be/publications/article-317.pdf.
4. For more information, see “Tiger: A Fast New Hash Function,” at www.cl.cam.ac.uk/~rja14/Papers/tiger.pdf.
5. For more information, see “The Whirlpool Secure Hash Function” by William Stallings, at www.seas.gwu.edu/~poorvi/Classes/CS381_2007/Whirlpool.pdf.
6. For more information, see “A Family of Fast Syndrome Based Cryptographic Hash Functions,” at http://lasec.epfl.ch/pub/lasec/doc/AFS05.pdf.
7. RFC 2104, “HMAC: Keyed-Hashing for Message Authentication,” describes HMAC in detail. See https://tools.ietf.org/html/rfc2104.
All materials on the site are licensed Creative Commons Attribution-Sharealike 3.0 Unported CC BY-SA 3.0 & GNU Free Documentation License (GFDL)
If you are the copyright holder of any material contained on our site and intend to remove it, please contact our site administrator for approval.
© 2016-2025 All site design rights belong to S.Y.A.