Modern Cryptography: Applied Mathematics for Encryption and Informanion Security (2016)
PART III. Asymmetric Ciphers
Chapter 10. Common Algorithms
In this chapter we will cover the following:
![]() What is asymmetric cryptography?
What is asymmetric cryptography?
![]() RSA
RSA
![]() Diffie-Hellman
Diffie-Hellman
![]() ElGamal
ElGamal
![]() MQV
MQV
![]() Homomorphic encryption
Homomorphic encryption
![]() Applications
Applications
In this chapter we will discuss asymmetric cryptography, including its general concepts and usage, as well as an in-depth discussion of the more common asymmetric algorithms. You will apply the mathematics you learned about in Chapters 4 and 5.
Note
Where necessary, I will provide a brief reminder of the mathematical principles covered earlier in the book. However, if those chapters were new or difficult for you, you may want to review them before proceeding with this chapter.
What Is Asymmetric Cryptography?
In asymmetric cryptography, as the name suggests, one key is used to encrypt a message and a different (but related) key is used to decrypt it. This concept often baffles those new to cryptography and students in network security courses. How can it be that a key used to encrypt will not also decrypt? This will be clearer to you once we examine a few algorithms and you see the actual mathematics involved. For now, set that issue to one side and simply accept that one key encrypts but cannot decrypt the message; another key is used to decrypt it.
Asymmetric cryptography is a powerful concept because symmetric cryptography (which you studied in Chapters 6 and 7) has a serious problem. That problem is key exchange and the potential for compromise. Let’s look at an example to demonstrate. For some reason, all security and cryptography books like to use the fictitious characters Alice, Bob, and Eve to explain how asymmetric cryptography works, and I will continue that tradition here.
Let’s assume, then, that Alice would like to send Bob a message. But Alice is concerned that Eve might eavesdrop (thus her name!) on the communication. Now let’s further assume that they don’t have asymmetric cryptography—all they have are the symmetric ciphers (which you learned about in Chapters 6 and 7). Further, Bob and Alice do not live in the same location, so how can they exchange a key so that they might encrypt messages? Any method (other than asymmetric cryptography) has the very real chance of being compromised, short of a secure/trusted courier manually taking the keys to the two parties. (If a courier was needed to exchange keys every time secure communication was required, then we would not have online banking, e-commerce, or a host of other useful technologies.)
With public key/asymmetric cryptography, Alice will get Bob’s public key and use that to encrypt the message she sends to Bob. If Eve intercepts the message and gains access to Bob’s public key, that’s OK, because that key won’t decrypt the message. Only Bob’s private key will do so, and this he safeguards. You can see the process in Figure 10-1.

FIGURE 10-1 Alice sends Bob a message with asymmetric cryptography.
If Bob wants to respond to Alice, he reverses the process. He gets Alice’s public key and encrypts a message to her—a message that only her private key will decrypt.
Asymmetric cryptography solves the problem of key exchange. It does not impede security, even if literally every person on the planet has both Bob’s and Alice’s public keys. Those keys can be used only to encrypt messages to Bob and Alice (respectively) and cannot decrypt the messages. So as long as Bob and Alice keep their private keys secret, secure communication is achieved with no problems in key exchange.
This basic concept of two keys—one key being public and another being private—is why this is often called public key cryptography. The term asymmetric cryptography is also used because the two keys are not the same—they are not symmetrical. Unfortunately, this is as far as many security courses go in explaining asymmetric cryptography—but, of course, we will be delving into the actual algorithms.
RSA
RSA may be the most widely used asymmetric algorithm, and it is certainly one of the most well-known. This public key method was developed in 1977 by three mathematicians—Ron Rivest, Adi Shamir, and Leonard Adleman. The name RSA is derived from the first letter of each mathematician’s last name. The algorithm is based on prime numbers and the difficulty of factoring a large number into its prime factors.
Note
The three inventors of RSA are very well-known and respected cryptographers. Ron Rivest has been a professor at MIT and invented several algorithms including RC2, RC4, RC5, MD2, MD4, MD5, and MD6. Adi Shamir is an Israeli cryptographer and one of the inventors of differential cryptanalysis. Leonard Adleman has made significant contributions to using DNA as a computational system.
As often happens in the history of cryptography, it turns out that a similar system was developed earlier in England, but it was classified. In 1973, Clifford Cocks developed a system that remained classified until the late 1990s. Cocks worked for the English government, specifically the Government Communications Headquarters (GCHQ). He went on to develop other, nonclassified cryptographic innovations. In 2001 he invented one of the early identity-based encryption methodologies using aspects of number theory.
The RSA Algorithm
To create the public and private key pair, you start by generating two large random primes, p and q, of approximately equal size. You need to select two numbers so that when multiplied together, the product will be the size you want (such as 2048 bits, 4096 bits, and so on).
Next, multiply p and q to get n:
Let n = pq
The next step is to multiply Euler’s totient for each of these primes.
Tip
You’ll recall reading about Euler’s totient in Chapter 4. Two numbers are considered co-prime if they have no common factors. For example, if the original number is 8, then 8 and 9 would be co-prime—8’s factors are 2 and 4, and 9’s factors are 3. Euler asked a few questions about co-prime integers. Given a number X, how many numbers smaller than X are co-prime to X? We call that number Euler’s totient, or just the totient. It just so happens that for prime numbers, this is always the number minus 1. So, for example 7 has 6 numbers that are co-prime to it.
When you multiply two primes together, you get a composite number, and there is no easy way to determine the Euler’s totient of a composite number. Recall that Euler found that if you multiply any two prime numbers together, the Euler’s totient of that product is the Euler’s totient of each prime multiplied together. So here’s our next step:
Let m = (p – 1)(q – 1)
So m is the Euler’s totient of n.
Now we are going to select another number—we will call this number e. The number e should be co-prime to m. Frequently, a prime number is chosen for e; that way, if e does not evenly divide m, then we are confident that e and m are co-prime, because e does not have any factors to consider.
Note
Many RSA implementations use e = 216 + 1 = 65537. This is considered large enough to be effective but small enough to still be fast.
At this point, we have almost completed generating the key. Now we must find a number d that, when multiplied by e and modulo m, would yield a 1. (Note that modulo means to divide two numbers and return the remainder—for example, 8 modulo 3 would be 2.) In other words,
Find d, such that de % m = 1
Now you will publish e and n as the public key. Keep d as the secret key. To encrypt, you simply take your message raised to the e power and modulo n.
C = Me % n
To decrypt, you take the cipher text and raise it to the d power modulo n.
P = Cd % n
RSA Example 1
Let’s look at an example that might help you better understand. Of course, RSA would be done with very large integers, but to make the math easy to follow, small integers are used in this example. (Note that this example is from Wikipedia.)
1. Choose two distinct prime numbers, such as p = 61 and q = 53.
2. Compute n = pq, giving n = 61 × 53 = 3233.
3. Compute the totient of the product as φ(n) = (p – 1)(q – 1) giving φ(3233) = (61 – 1) × (53 – 1) = 3120.
4. Choose any number 1 < e < 3120 that is co-prime to 3120. Choosing a prime number for e leaves us only to check that e is not a divisor of 3120. Let e = 17.
5. Compute d, the modular multiplicative inverse of e, yielding d = 2753.
The public key is (n = 3233, e = 17). For a padded plaintext message m, the encryption function is m17 (mod 3233).
The private key is (n = 3233, d = 2753). For an encrypted cipher text c, the decryption function is c2753 (mod 3233).
RSA Example 2
For those of you who are new to RSA, or new to cryptography in general, it might be helpful to see one more example, with even smaller numbers.
1. Select primes: p = 17 and q = 11.
2. Compute n = pq = 17 × 11 = 187.
3. Compute ø(n) = (p – 1)(q – 1) = 16 × 10 = 160.
4. Select e: gcd(e,160) = 1; choose e = 7.
5. Determine d: de = 1 mod 160 and d < 160. Value is d = 23 since 23 × 7 = 161 = 10 × 160 + 1.
6. Publish public key (7 and 187).
7. Keep secret private key 23.
If you are struggling with the concepts of RSA key generation, I suggest you first work through these two examples. Because the complete process as well as the answers are provided for you, it will be easy for you to check your work. You may also want to work through a few more examples. Start with any two prime numbers that are small enough to make the calculations feasible.
Factoring RSA Keys
You may be thinking, couldn’t someone take the public key and use factoring to derive the private key? Well, hypothetically yes. However, it turns out that factoring really large numbers into their prime factors is extremely difficult—a more technical description would be that it is computationally infeasible, because there is no efficient algorithm for doing it. And when I say large numbers, RSA can use 1024-, 2048-, 4096-, 8192-bit and larger keys—those are extremely large numbers. Here’s an example of a 2048-bit number represented in decimal format:

In most modern implementations, at least as of this writing, 2048 bits is the smallest RSA key used. Reflect on the rather large number above and contemplate attempting to factor that number.
There are mathematical techniques that will improve the process, but nothing that makes factoring such large numbers a feasible endeavor. Of course, should anyone ever invent an efficient algorithm that will factor a large number into its prime factors, RSA would be dead.
There certainly have been incidents where someone was able to factor a small RSA key. In 2009, Benjamin Moody factored a 512-bit RSA key in 73 days. In 2010, researchers were able to factor a 768-bit RSA key. Due to these advances in factorization, modern implementations of RSA are using larger key sizes.1 In Chapter 17 we will examine cryptanalysis techniques used on RSA.
Tip
This section provides a basic introduction to RSA. A great resource for delving deeper into RSA is the book Cryptanalysis of RSA and Its Variants by M. Jason Hinek (Chapman and Hall/CRC, 2009). You also might find it interesting to read the paper “Fast Variants of RSA” by Dan Boneh and Hovav Shacham, at https://cseweb.ucsd.edu/~hovav/dist/survey.pdf.
The Rabin Cryptosystem
This algorithm was created in 1979 by Israeli cryptographer Michael Rabin, who is a recipient of the Turing Award. You can think of the Rabin cryptosystem as an RSA cryptosystem in which the value of e and d are fixed.
e = 2 and d = 1/2
The encryption is C ≡ P2 (mod n) and the decryption is P ≡ C1/2 (mod n).
Here is a very trivial example to show the idea:
1. Bob selects p = 23 and q = 7.
2. Bob calculates n = p × q = 161.
3. Bob announces n publicly; he keeps p and q private.
4. Alice wants to send the plain text message M = 24. Note that 161 and 24 are relatively prime; 24 is in the group selected, Z161*.
Encryption: C ≡ 242 mod 161 = 93, and sends the cipher text 93 to Bob.
Note
This algorithm is not as widely used as RSA or Diffie-Hellman, but I present it here to give you a general overview of alternative asymmetric algorithms.
The Turing Award
The Turing award is a prize given every year by the Association for Computing Machinery (ACM) to a computer scientist whose contributions are lasting and of major importance. Some people call this award the Nobel Prize for computing. It is named after Alan Turing. Some notable recipients are Edgar F. Codd, who won the award for creating the concept of relational databases; Niklaus Wirth, who developed several programming languages, including Pascal and ALGOL-w; and Alan Kay, for his work in object-oriented programming, including leading the team that developed the Smalltalk programming language.
Diffie-Hellman
Although some security textbooks state that RSA was the “first asymmetric algorithm,” this is not accurate. In fact, Diffie-Hellman was the first publically described asymmetric algorithm. This cryptographic protocol allows two parties to establish a shared key over an insecure channel. In other words, Diffie-Hellman is often used to allow parties to exchange a symmetric key through some unsecure medium, such as the Internet. It was developed by Whitfield Diffie and Martin Hellman in 1976.
Note
As you already saw with RSA, one problem with working in cryptology is that much of the work is classified. You could labor away and create something wonderful…that you cannot tell anyone about. Then, to make matters worse, years later someone else might develop something similar and release it, getting all the credit. This is exactly the situation with Diffie-Hellman. It turns out that a similar method had been developed a few years earlier by Malcolm J. Williamson of the British Intelligence Service, but it was classified.
The system has two parameters called p and g. Parameter p is a prime number and parameter g (usually called a generator) is an integer less than p, with the following property: for every number n between 1 and p – 1 inclusive, there is a power k of g such that n = gk mod p.
Let’s revisit our old friends Alice and Bob to illustrate this:
1. Alice generates a random private value a and Bob generates a random private value b. Both a and b are drawn from the set of integers.
2. They derive their public values using parameters p and g and their private values. Alice’s public value is ga mod p and Bob’s public value is gb mod p.
3. They exchange their public values.
4. Alice computes gab = (gb)a mod p, and Bob computes gba = (ga)b mod p.
5. Since gab = gba = k, Alice and Bob now have a shared secret key k.
This process is shown in Figure 10-2.

FIGURE 10-2 Diffie-Hellman process
ElGamal
First described by Egyptian cryptographer Taher ElGamal in 1984, ElGamal is based on the Diffie-Hellman key exchange algorithm and is used in some versions of Pretty Good Privacy (PGP). The ElGamal algorithm has three components: the key generator, the encryption algorithm, and the decryption algorithm.
Here’s an example, with Alice and Bob:
1. Alice generates an efficient description of a multiplicative cyclic group G of order q with generator g.
Note
You should remember groups from Chapter 5. A cyclic group is generated by a single element—in this case, that is the generator g. With a multiplicative cyclic group, each element can be written as some power of g.
2. Next Alice chooses a random number x from a set of numbers {0, …, q – 1).
3. Then Alice computes h = gx. Remember g is the generator for the group and x is a random number from within the group.
4. h, G, q, and g are the public key, and x is the private key.
5. If Bob wants to encrypt a message m with the public key Alice generated, the following process occurs:
A. Bob generates a random number y chosen from {0, …, q – 1}. Y is often called an ephemeral key.
B. Next Bob will calculate c1: c1 = gy.
C. Next a shared secret, s = hy, is computed.
D. The message m is converted to m′ of G.
E. Next Bob must calculate c2: c2 = m′ * s.
F. Bob can now send c1 and c2 = as the encrypted text.
6. To decrypt a message m with the public key the first person generated, the following process occurs:
A. The recipient calculates s = c1x.
B. The recipient calculates m′ = c2 * s–1.
C. Finally, m′ is converted back to the plain text m.
Note
This structure should look similar to Diffie-Hellman.
MQV
Like ElGamal, MQV (Menezes–Qu–Vanstone) is a protocol for key agreement that is based on Diffie-Hellman. It was first proposed by Alfred Menezes, Minghua Qu, and Scott Vanstone in 1995 and then modified in 1998. MQV is incorporated in the public-key standard IEEE P1363. HQMV is an improved version. The specific algorithm is related to elliptic curves, and we will address those specifics in Chapter 11.
Note
Alfred Menezes is a professor of mathematics at the University of Waterloo in Canada and the author of several books on cryptography.
Optimal Asymmetric Encryption Padding
OAEP (Optimal Asymmetric Encryption Padding) was introduced in 1994 by M. Bellare and P. Rogaway and is standardized in RFC 2437. OAEP processes the plain text prior to encryption with an asymmetric algorithm. When used with an algorithm such as RSA, it gives a cryptography scheme that is proven to be secure against a chosen plain text attack.
OAEP satisfies the following two goals:
![]() Adds an element of randomness that can be used to convert a deterministic encryption scheme such as RSA into a probabilistic scheme.
Adds an element of randomness that can be used to convert a deterministic encryption scheme such as RSA into a probabilistic scheme.
![]() Prevents partial decryption of cipher texts (or other information leakage) by ensuring that an adversary cannot recover any portion of the plain text without being able to invert the trapdoor one-way permutation f.
Prevents partial decryption of cipher texts (or other information leakage) by ensuring that an adversary cannot recover any portion of the plain text without being able to invert the trapdoor one-way permutation f.
Cramer-Shoup
The Cramer-Shoup system is an asymmetric key encryption algorithm that was developed by Ronald Cramer and Victor Shoup in 1998. It is an extension of the ElGamal cryptosystem and was the first efficient algorithm proven to be secure against an adaptive chosen cipher text attack.
Applications
By this point, you should have a general understanding of several asymmetric algorithms and a very good understanding of at least RSA and Diffie-Hellman. Now for a thorough discussion of how asymmetric algorithms are used. In this section we will look at common applications for asymmetric algorithms.
Key Exchange
As you know, symmetric algorithms are much faster than asymmetric, and they achieve the same security with much smaller keys. However, asymmetric algorithms overcome the issue of key exchange. Therefore, it is common for asymmetric algorithms to be used for exactly that purpose. For example, in Secure Sockets Layer (SSL) and Transport Layer Security (TLS), an asymmetric algorithm (such as RSA) is used to exchange a symmetric key (such as AES, Advanced Encryption Standard). This is a common way to use asymmetric algorithms.
Digital Signatures
I am sure you are familiar with the term “digital signatures,” but do you know what they are and how they work? Remember that cryptographic algorithms are about protecting confidentiality, ensuring that only the intended recipient can read the message. Essentially, digital signatures reverse asymmetric cryptography, so that they can protect integrity. A digital signature uses the sender’s private key and encrypts either the entire message or a portion of it (such as the signature block) so anyone with the sender’s public key can decrypt that. A digital signature verifies that the sender really is who he or she claims to be and is an important aspect of message security.
Put another way, assume your boss sends you an e-mail telling you that you have done such a great job, he thinks you should take next week off with pay. It would probably be a good thing to verify that this is legitimate, that he really sent it, and that it’s not a prank. What a digital signature does is to take the sender’s private key and encrypt either the entire message or a portion (like the signature block). Now anyone with the sender’s public key can decrypt that. So let’s return to Alice and Bob to see how this works.
Bob wants to send Alice a message and make certain she knows it’s from him, so he signs it with his private key. When Alice uses Bob’s public key, the message decrypts and she can read it. Now suppose that Bob didn’t really send this message. Instead, Eve sent it, pretending to be Bob. Because Eve does not have Bob’s private key, she had to use some other key to sign the message. So when Alice tries to decrypt it (that is, verify the signature) with Bob’s public key, she will get back gibberish and nonsense, such as that shown in Figure 10-3.

FIGURE 10-3 Without having the appropriate key, all you get is gibberish.
In essence, to have total security for a message, you would execute the following steps:
1. Use a hash, message authentication code (MAC), or hash MAC (HMAC) on the message and put the digest at the end of the message.
2. Digitally sign the message—usually just a portion such as the hash or signature block—with your own private key.
3. Encrypt the message with the recipient’s public key.
This process is depicted in Figure 10-4.
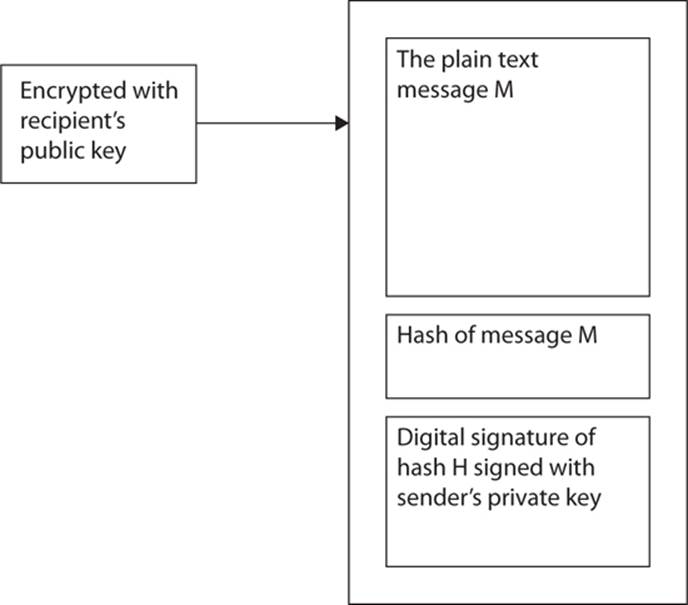
FIGURE 10-4 Message security with digital signatures
The recipient then reverses the process:
1. Decrypts the message with the recipient’s private key.
2. Verifies the signature with the sender’s public key.
3. Recalculates the hash, MAC, or HMAC and compares it to the one received to ensure that there were no errors in transmission.
More than one type of digital signature exists. The type I just described is the most common and is referred to as a direct digital signature. A second type is the arbitrated digital signature. It is similar to the process just described, but instead of the sender digitally signing each message, a trusted third party digitally signs the message, attesting to the sender’s identity.
A third type of digital signature also exists—the blind signature. Basically, a sender makes a signer to sign a message m without knowing m; therefore, this is considered a blind signature. Blind signing can be achieved by a two-party protocol between the sender and the signer that has the following properties.
![]() In order to sign (by a signer) a message m, the sender computes, using a blinding procedure, from m and m* from which m cannot be obtained without knowing a secret, and sends m* to the signer.
In order to sign (by a signer) a message m, the sender computes, using a blinding procedure, from m and m* from which m cannot be obtained without knowing a secret, and sends m* to the signer.
![]() The signer signs m* to get a signature sm* (of m*) and sends sm* to the sender. Signing is done in such a way that the sender can afterward compute, using an unblinding procedure, from signer’s signature sm* of m*—the signer signature sm of m.
The signer signs m* to get a signature sm* (of m*) and sends sm* to the sender. Signing is done in such a way that the sender can afterward compute, using an unblinding procedure, from signer’s signature sm* of m*—the signer signature sm of m.
This allows the arbiter to sign the message, confirming that it was created on a given date by a specific sender, without knowing the contents of the message.
Digital Signature Algorithm
A digital signature can be done with any asymmetric algorithm; however, some algorithms have been created specifically for digitally signing messages. The Digital Signature Algorithm (DSA) described in U.S. Patent 5,231,668 was filed July 26, 1991, and attributed to David W. Kravitz. It was adopted by the U.S. government in 1993 with FIPS 186. The actual algorithm functions as follows:
1. Choose a hash function (traditionally this has been SHA1, but the stronger the hash the better).
2. Select a key length L and N.
Note that the original Digital Signature Standard constrained L to be a multiple of 64 between 512 and 1024. Now lengths of 2048 are recommended. U.S. government documents now specify L and N length pairs of (1024,160), (2048,224), (2048,256), and (3072,256).
3. Choose a prime number q that is less than or equal to the hash output length.
4. Choose a prime number p such that p – 1 is a multiple of q.
5. Choose g, which must be a number whose multiplicative order modulo p is q.
6. Choose a random number x, where 0 < x < q.
7. Calculate y = gx mod p.
Public key is (p, q, g, y).
Private key is x.
To use DSA to digitally sign, follow these steps:
1. Let H be the hashing function and m the message.
2. Generate a random value for each message k where 0 < k < q.
3. Calculate r = (gk mod p) mod q.
4. Calculate s = (k–1(H(m) + x*r)) mod q.
5. If r or s = 0, then recalculate for a non-zero result (that is, pick a different k).
6. The signature is (r, s).
DSA is a commonly used digital signature algorithm. In Chapter 11 you will see an elliptic curve variation of DSA.
Digital Certificates
A digital certificate is a digital document that contains information about the certificate holder and (if it is an X.509 certificate) the method to verify this information with a trusted third party. Digital certificates are how web sites distribute their public keys to end users, and they are how web sites can be authenticated.
The most common type of certificates is X.509. Before we go further into this topic, you should first get acquainted with the contents of an X.509 certificate:
![]() Version What version of the X.509 standard is this certificate using.
Version What version of the X.509 standard is this certificate using.
![]() Certificate holder’s public key One of the reasons we use digital certificates is so that the recipient can get the certificate holder’s public key. If you visit a web site that uses SSL/TLS (discussed later in this chapter), your browser gets the web site’s public key from the site’s digital certificate.
Certificate holder’s public key One of the reasons we use digital certificates is so that the recipient can get the certificate holder’s public key. If you visit a web site that uses SSL/TLS (discussed later in this chapter), your browser gets the web site’s public key from the site’s digital certificate.
![]() Serial number This identifies the specific certificate.
Serial number This identifies the specific certificate.
![]() Certificate holder’s distinguished name Something to identify the certificate holder uniquely, often an e-mail address or domain name.
Certificate holder’s distinguished name Something to identify the certificate holder uniquely, often an e-mail address or domain name.
![]() Certificate’s validity period How long this certificate is good for.
Certificate’s validity period How long this certificate is good for.
![]() Unique name of certificate issuer The preceding items identify the certificate, the certificate holder, and provide the certificate holder’s public key. But how do you know this certificate really belongs to who claims it? How do you know it is not a fake? You verify the certificate with a trusted certificate issuer, such as Verisign.
Unique name of certificate issuer The preceding items identify the certificate, the certificate holder, and provide the certificate holder’s public key. But how do you know this certificate really belongs to who claims it? How do you know it is not a fake? You verify the certificate with a trusted certificate issuer, such as Verisign.
![]() Digital signature of issuer To prove this certificate was issued by a trusted certificate issuer, that issuer signs the certificate.
Digital signature of issuer To prove this certificate was issued by a trusted certificate issuer, that issuer signs the certificate.
![]() Signature algorithm identifier Indicates what digital signing algorithm the certificate issuer used in this process.
Signature algorithm identifier Indicates what digital signing algorithm the certificate issuer used in this process.
For example, when you visit a web site that uses SSL/TLS, your browser will first retrieve the web site’s certificate. Then it notes the unique name of the certificate issuer. The browser then retrieves that issuer’s public key from the issuer to verify the digital signature. If it is verified, secure communications can proceed. You can see this process in Figure 10-5.
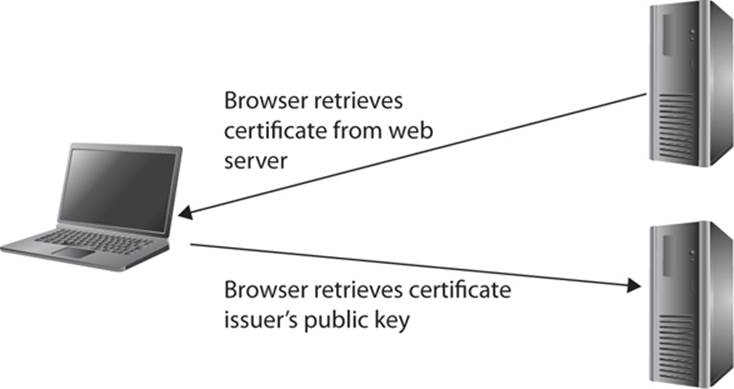
FIGURE 10-5 Retrieving a digital signature
Following are some general terms associated with digital certificates that you should be familiar with:
![]() PKI (public key infrastructure) Uses asymmetric key pairs and combines software, encryption, and services to provide a means of protecting the security of business communication and transactions.
PKI (public key infrastructure) Uses asymmetric key pairs and combines software, encryption, and services to provide a means of protecting the security of business communication and transactions.
![]() PKCS (Public Key Cryptography Standards) Put in place by RSA to ensure uniform certificate management throughout the Internet.
PKCS (Public Key Cryptography Standards) Put in place by RSA to ensure uniform certificate management throughout the Internet.
![]() CA (certification authority) An entity trusted by one or more users to issue and manage certificates.
CA (certification authority) An entity trusted by one or more users to issue and manage certificates.
![]() RA (registration authority) Takes the burden off a CA by handling verification prior to certificates being issued. The RA acts as a proxy between the user and the CA—receiving a request, authenticating it, and forwarding it to the CA.
RA (registration authority) Takes the burden off a CA by handling verification prior to certificates being issued. The RA acts as a proxy between the user and the CA—receiving a request, authenticating it, and forwarding it to the CA.
![]() X.509 The international standard for the format and information contained in a digital certificate. X.509 is the most common type of digital certificate in the world. It is a digital document that contains a public key signed by a trusted third party known as a certificate authority.
X.509 The international standard for the format and information contained in a digital certificate. X.509 is the most common type of digital certificate in the world. It is a digital document that contains a public key signed by a trusted third party known as a certificate authority.
![]() CRL (certificate revocation list) A list of certificates issued by a CA that are no longer valid. CRLs are distributed in two main ways: via a PUSH model, in which the CA automatically sends out the CRL at regular intervals, and via a pull model, in which the CRL is downloaded from the CA by those who want to see it to verify a certificate.
CRL (certificate revocation list) A list of certificates issued by a CA that are no longer valid. CRLs are distributed in two main ways: via a PUSH model, in which the CA automatically sends out the CRL at regular intervals, and via a pull model, in which the CRL is downloaded from the CA by those who want to see it to verify a certificate.
![]() Online Certificate Status Protocol (OCSP) An Internet protocol used for obtaining the revocation status of an X.509 digital certificate. It is described in RFC 2560 and is on the Internet standards track. It was created as an alternative to CRLs, specifically to address certain problems associated with using CRLs in a PKI. The OCSP allows the authenticity of a certificate to be verified immediately.
Online Certificate Status Protocol (OCSP) An Internet protocol used for obtaining the revocation status of an X.509 digital certificate. It is described in RFC 2560 and is on the Internet standards track. It was created as an alternative to CRLs, specifically to address certain problems associated with using CRLs in a PKI. The OCSP allows the authenticity of a certificate to be verified immediately.
Although X.509 certificates are the most common certificate type, they are not the only type. Usually web sites will use an X.509 certificate, but for e-mail some people use PGP, or Pretty Good Privacy, software that provides encryption as well as integrity. PGP was created by Phil Zimmerman in 1991. PGP software defines its own certificate. It does not have CAs that issue certificates, so there is no third-party verification of the certificate holder’s identity. But PGP certificates can be used to exchange public keys. Here are some basic fields found in most PGP certificates:
![]() PGP version number
PGP version number
![]() Certificate holder’s public key
Certificate holder’s public key
![]() Certificate holder’s information
Certificate holder’s information
![]() Digital signature of certificate owner
Digital signature of certificate owner
![]() Certificate’s validity period
Certificate’s validity period
![]() Preferred symmetric encryption algorithm for the key
Preferred symmetric encryption algorithm for the key
The critical issue to keep in mind with PGP certificates is that they do not include any trusted third-party verification. Therefore, they are not used in applications where such verification is important, such as e-commerce. However, PGP is often used to encrypt e-mail.
SSL/TLS
Chapter 13 covers SSL and TLS fully. This section is meant as a basic introduction to the topic. If you ever use a secure web site—for example, to check your bank account, shop on Amazon.com, or for any sort of e-commerce—you have used SSL/TLS. The Secure Sockets Layer is a technology employed to allow for transport-layer security via public-key encryption. Most web sites now use TLS (the successor to SSL) but the term SSL stuck, so many people simply refer to SSL to mean either SSL or TLS. The SSL/TLS protocol was developed by Netscape for transmitting private documents via the Internet. URLs that require an SSL connection start with https: instead of http:. SSL/TLS works by using X.509 certificates so the browser can get the web server’s public key, and then that public key is used to exchange a symmetric key. There have been several versions as of this writing:
![]() Unreleased v1 (Netscape)
Unreleased v1 (Netscape)
![]() Version 2, released in 1995 with many flaws
Version 2, released in 1995 with many flaws
![]() Version 3, released in 1996, RFC 6101
Version 3, released in 1996, RFC 6101
![]() Standard TLS1.0, RFC 2246, released in 1999
Standard TLS1.0, RFC 2246, released in 1999
![]() TLS 1.1 defined in RFC 4346 in April 2006
TLS 1.1 defined in RFC 4346 in April 2006
![]() TLS 1.2 defined in RFC 5246 in August 2008, based on the earlier TLS 1.1 spec
TLS 1.2 defined in RFC 5246 in August 2008, based on the earlier TLS 1.1 spec
![]() TLS 1.3 as of July 2014, TLS 1.3
TLS 1.3 as of July 2014, TLS 1.3
The process of establishing an SSL/TLS connection is actually somewhat straightforward:
1. When the client browser first encounters a web site that indicates the use of SSL/TLS, the client sends the server the client’s SSL version number, cipher settings (that is, what algorithms the client is capable of), and some session-specific data.
2. The server responds to the client with similar information from the server: the server’s SSL version number, cipher settings, and some session-specific data. The server also sends its X.509 certificate. If mutual authentication is being used, or if the client is requesting a server resource that requires client authentication, the server requests the client’s certificate.
3. The client browser first uses the X.509 certificate from the server to authenticate the server. If the server cannot be authenticated, the user is warned of the problem and informed that an encrypted and authenticated connection cannot be established. If the server can be successfully authenticated, the client proceeds to the next step, using the server’s public key that the client retrieved from the X.509 certificate.
4. Using all data generated in the handshake thus far, the client creates the premaster secret for the session. Then the client encrypts this premaster secret with the server’s public key and sends the encrypted premaster secret to the server.
5. In this optional step, if the server has requested client authentication, the client will also send its own X.509 certificate so that the server can authenticate the client. The server attempts to authenticate the client. If the client cannot be authenticated, the session ends. If the client can be successfully authenticated, the server uses its private key to decrypt the premaster secret, and then performs a series of steps to generate the master secret. These are the exact steps the client will use on the premaster secret to generate the same master secret on the client side.
6. Both the client and the server use the master secret to generate the session keys, which are symmetric keys (using whatever algorithm the client and server agreed upon). All communication between the client and the server after this point will be encrypted with that session key.
7. The client sends a message to the server informing it that future messages from the client will be encrypted with the session key. It then sends a message indicating that the client portion of the handshake is finished. The server responds with a similar message, telling the client that all future messages from the server will be encrypted, and the server portion of the handshake is complete.
This handshake process may seem a bit complex, but it serves several purposes. First, it allows the client to authenticate the server and get the server’s public key. It then allows the client and server both to generate the same symmetric key, and then use that key to encrypt all communication between the two parties. This provides a very robust means of secure communication.
Homomorphic Encryption
Homomorphic encryption is about allowing mathematical operations to be performed on data that is still encrypted. In other words, analysis can be conducted on the cipher text itself, without the need to decipher the text first. Before I delve into how this is accomplished, you may find it useful to understand why this is done. In some situations, you may want a third party to calculate some value regarding data, without exposing the party to the actual plain text data. In such situations, homomorphic encryption is the solution.
Homomorphic encryption plays an important part in cloud computing by allowing companies to store encrypted data in a public cloud and still use the cloud provider’s analytic tools. The cloud provider can analyze aspects of the data without decrypting the data.
The Pallier cryptosystem is an example of a homomorphic cryptography system. This asymmetric algorithm was invented by Pascal Paillier in 1999 and is one of the modern homomorphic cryptographic algorithms.
Conclusions
This chapter provided an overview of asymmetric cryptography. RSA is the most important algorithm for you to understand from this chapter, which is why you were shown two different examples of RSA. It is imperative that you fully understand RSA before proceeding to the next chapter. The next most important algorithm discussed is Diffie-Hellman. The other algorithms are interesting, and if you proceed further in cryptography you will, undoubtedly, delve deeper into those algorithms.
This chapter also introduced you to applications of cryptography. Digital certificates and SSL/TLS are commonly used, and you need to have a strong understanding of these applications before proceeding. Homomorphic encryption is a relatively new topic, and at this point you need only have a general understanding of what it is.
Test Your Knowledge
1. Which algorithm based on Diffie-Hellman was first described in 1984 and is named after its inventor?
2. U.S. Patent 5,231,668 was filed July 26, 1991, and attributed to David W. Kravitz. The __________ was adopted by the U.S. government in 1993 with FIPS 186.
3. The __________ can be thought of as an RSA cryptosystem in which the value of e and d are fixed: e = 2 and d = 1/2.
4. Explain the basic setup of Diffie-Hellman (the basic math including key generation).
5. Explain RSA key generation.
6. What is the formula for encrypting with RSA?
7. ____________ was introduced by Bellare and Rogaway and is standardized in RFC 2437.
8. What does PKCS stand for?
9. What is the most widely used digital certificate standard?
10. X.509 certificates contain the digital signature of who?
Answers
1. ElGamal
2. Digital Signature Algorithm (DSA)
3. Rabin cryptosystem
4. The system has two parameters called p and g. Parameter p is a prime number and parameter g (usually called a generator) is an integer less than p, with the following property: for every number n between 1 and p – 1 inclusive, there is a power k of g such that n = gk mod p. One public key is ga and the other is gb.
5. Let n = pq. Let m = (p – 1)(q – 1). Choose a small number e, co-prime to m.
(Note: Two numbers are co-prime if they have no common factors.) Find d, such that de % m = 1. Publish e and n as the public key. Keep d and n as the secret key.
6. C = Me % n
7. OAEP (Optimal Asymmetric Encryption Padding)
8. Public Key Cryptography Standards
9. X.509
10. The issuer of the certificate
Endnote
1. For more information, see “Factorization of a 768-bit RSA Modulus,” by Kleinjung, Aoki, Franke, et al., at https://eprint.iacr.org/2010/006.pdf.
All materials on the site are licensed Creative Commons Attribution-Sharealike 3.0 Unported CC BY-SA 3.0 & GNU Free Documentation License (GFDL)
If you are the copyright holder of any material contained on our site and intend to remove it, please contact our site administrator for approval.
© 2016-2025 All site design rights belong to S.Y.A.