Modern Cryptography: Applied Mathematics for Encryption and Informanion Security (2016)
PART IV. Applications
Chapter 12. Random Number Generators
In this chapter we will cover the following:
Properties of pseudo-random numbers
Tests of randomness
Algorithmic random number generators
The Marsaglia CD-ROM
Random numbers are a key part of cryptography. When you generate a key for a symmetric algorithm such as Advanced Encryption Standard (AES), Blowfish, or GOST, you need that key to be very random. Random numbers are also required for initialization vectors used with a variety of algorithms. A truly random number is impossible to generate from a computer algorithm. It is possible to generate a truly random number using other means, including hardware, but not strictly in a software algorithm. Certain naturally occurring phenomena such as radioactive decay can form the basis for true random-number generation. However, this is not a practical source of random numbers for use in cryptographic applications.
Algorithms called pseudo-random-number generators (PRNGs) are normally used in cryptography. These algorithms can be used to create long runs of numbers with good random properties, but eventually the sequence repeats.
The need to generate random numbers is nothing new; in fact, many methods of generating random numbers have been around for centuries, though they are usually not sufficient for cryptographic purposes. We will explore some of these in this chapter.
There are three types of PRNGs:
Table look-up generators Literally a table of precomputed pseudo-random numbers is compiled and numbers are extracted from it as needed.
Hardware generators Some hardware process, perhaps packet loss on the network card, or fluctuations from a chip, are used to produce pseudo-random numbers.
Algorithmic (software) generators This type is most commonly used in cryptography, and it’s what we will focus our attention on in this chapter.
What Makes a Good PRNG?
You know that a true random-number generator is impractical, but what makes a particular PRNG good enough? Is the output of a given algorithm random enough?
There are some specific properties and standards you can look for in a PRNG, and you can use some tests to measure for randomness. In this section we will look at all three of these items. This information should inform your evaluation of specific algorithms we will explore later in this chapter.
(Desirable) Properties of Pseudo-random Numbers
Before you consider actual algorithms and attempt to evaluate the efficacy of each for cryptographic purposes, it is important that you understand what you are looking for in a cryptographic algorithm. Any good PRNG will generate a sequence of numbers that have the following properties:
Uncorrelated sequences The sequences are not correlated—there, quite literally, is no correlation between one section of output bits and another. So you cannot take a given stretch of numbers (say 16 bits) and use that to predict subsequent bits.
Long period Ideally the series of digits (usually bits) should never have any repeating pattern. However, the reality is that some repetition will eventually occur. The distance (in digits or bits) between repetitions is the period of that sequence of numbers. The longer the period, the better. Put another way: we can accept that there will be repeated sequences, but those should be as far apart as possible.
Uniformity Pseudo-random numbers are usually represented in binary format, with an equal number of 1’s and 0’s that are not distributed in any discernable pattern. The sequence of random numbers should be uniform and unbiased. If you have significantly more (or significantly less) 1’s than 0’s, then the output is biased. This category is the one most often used in cryptography. It does not produce a truly random number, but rather a pseudo-random number.
Computational indistinguishability Any subsection of numbers taken from the output of a given PRNG should not be distinguishable from any other subset of numbers in polynomial time by any efficient procedure. The two sequences are indistinguishable. That does not, however, mean they are identical—it means there is no efficient way to determine specific differences.
Tests of Randomness
How do you know if a PRNG is “random enough”? You can apply a variety of tests to the output of any algorithm to determine the degree of randomness—to determine whether that algorithm is suitable for cryptographic purposes. Let’s start with relatively simple tests that you can easily execute. Then I’ll provide an overview of more sophisticated statistical tests.
1-D Test
The 1-D frequency test is a simple test that is used as a first pass. In other words, simply passing the 1-D test does not mean an algorithm is suitable for cryptographic purposes. However, if a PRNG fails the 1-D test, there is no need for further testing.
Imagine a number line stretching from 0 to 1, with decimal points in between. Use the random-number generator to plot random points on this line. First, divide the line into a number of “bins” of any size. In the following graph, there are four bins, each with a size of 0.25:
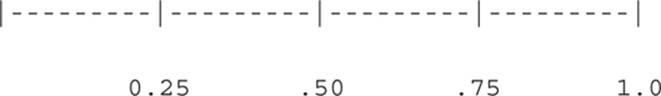
As random numbers (between 0 and 1.0) are generated, count how many fit into each bin. If the bins fill evenly, that is a good sign that you have random dispersal. If there is a significant preference for one bin over another, then the PRNG is not sufficiently random and has a bias; further testing is not required to determine that it is not useful for cryptographic purposes.
Equidistribution
The equidistribution test, sometimes called the Monobit frequency test, is used to determine whether there is an equal distribution of 1’s and 0’s throughout the output of the PRNG. It seeks to verify that the arithmetic mean of the sequence approaches 0.5. This can be applied to the entire output of a PRNG or to a given segment, though the larger the segment, the more meaningful the test. The further the arithmetic mean is from 0.5, the more of a bias the algorithm is displaying and therefore the less suitable this PRNG is for cryptographic purposes.
This test is described by the National Institute of Standards (NIST) as follows:
The focus of the test is the proportion of zeroes and ones for the entire sequence. The purpose of this test is to determine whether the number of ones and zeros in a sequence are approximately the same as would be expected for a truly random sequence. The test assesses the closeness of the fraction of ones to zeroes, that is, the number of ones and zeroes in a sequence should be about the same. All subsequent tests depend on the passing of this test; there is no evidence to indicate that the tested sequence is non-random.1
This test (also sometimes just called the frequency test) has similarities to the 1-D test in that the purpose is to determine whether there is bias in the output of a given PRNG. The focus of the test is the proportion of 0’s and 1’s for the entire sequence.
Note
Throughout this chapter, I will use a tool named CrypTool to demonstrate PRNGs as well as randomness tests. This is a free and open source tool you can download from https://www.cryptool.org/en/.
Runs Test
A run is an uninterrupted sequence of identical bits. The focus of the runs test is the total number of runs in the sequence. A run of length k consists of exactly k identical bits and is bounded before and after with a bit of the opposite value. The purpose of the runs test is to determine whether the number of runs of 1’s and 0’s of various lengths is as expected for a random sequence. This test determines whether the oscillation between such 0’s and 1’s is too fast or too slow. In other words, are the 1’s and 0’s alternating quickly or slowly?
Fast oscillation occurs when there are a lot of changes, e.g., 010101010 oscillates with every bit.
Note
A p-value is a statistical test. A small p-value (typically ≤ 0.05) indicates strong evidence against the null hypothesis, so you reject the null hypothesis. A large p-value (> 0.05) indicates weak evidence against the null hypothesis, so you do not reject the null hypothesis.
You can use CrypTool to apply the runs test to a sequence of numbers. You can find the various randomness tests by choosing Analysis | Analyze Randomness, as shown in Figure 12-1.
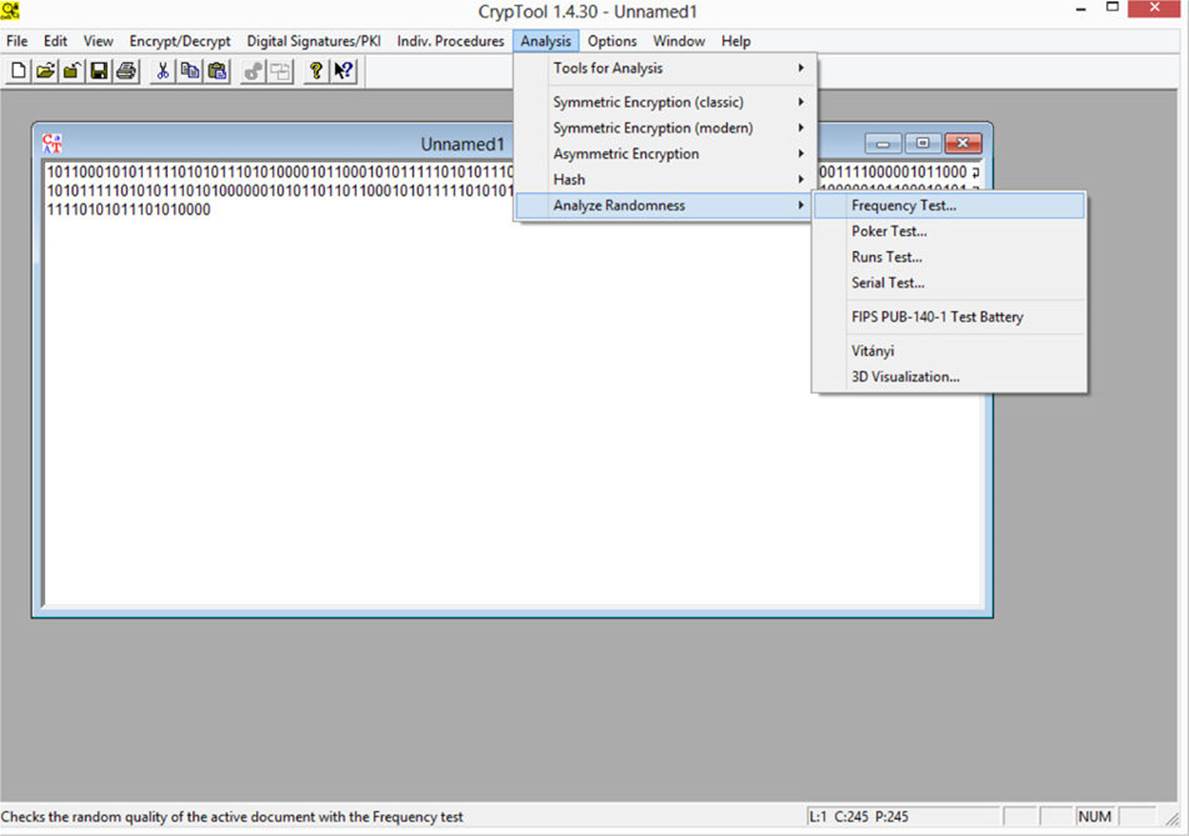
FIGURE 12-1 CrypTool randomness analysis
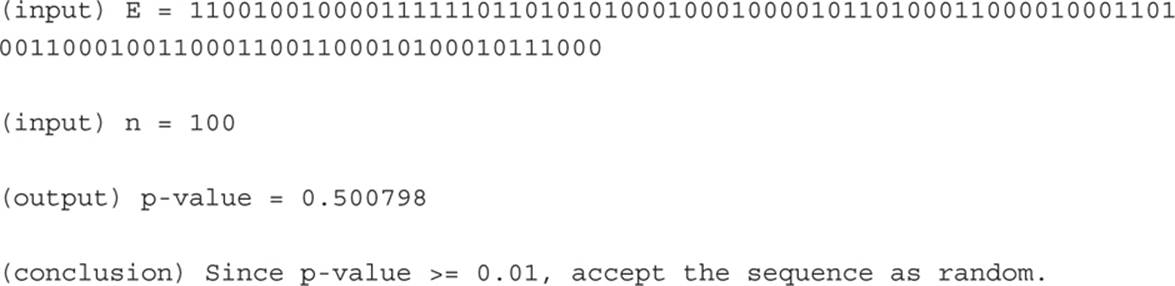
In the output shown previously (11001001000011111101101010100010001000010110100 01100001000110100110001001100011001100010100010111000), there is a seemingly random series of 1’s and 0’s. To apply the runs test to this, you will first be prompted to select some test parameters, as shown in Figure 12-2. For this example, simply use the default parameters. To test this you, select Analysis | Analyze Randomness | Runs Test.
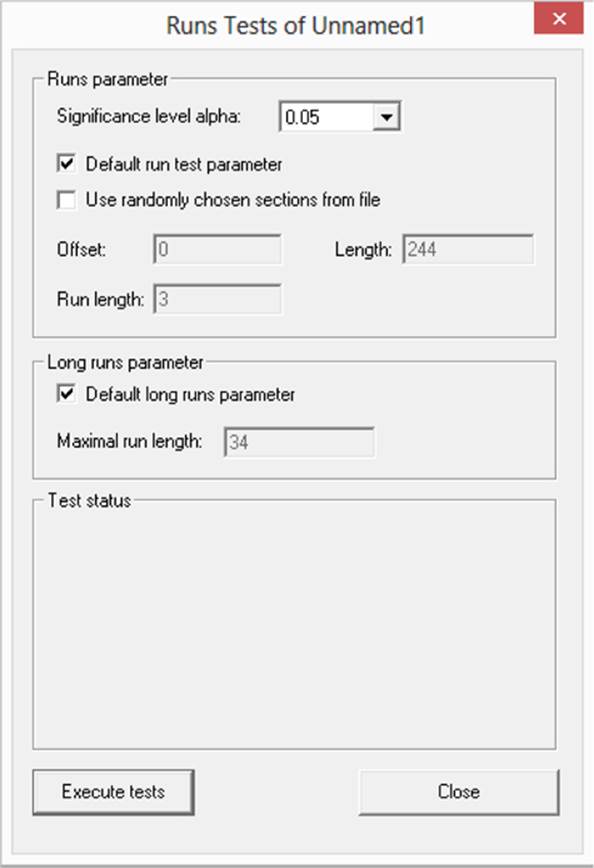
FIGURE 12-2 Runs test parameters
The test results, shown in Figure 12-3, are relatively simple to interpret—and, in this case, the sequence of numbers did not pass a key part of the runs test. If subsequent tests also cast doubt on the particular algorithm used, it should definitely be rejected.
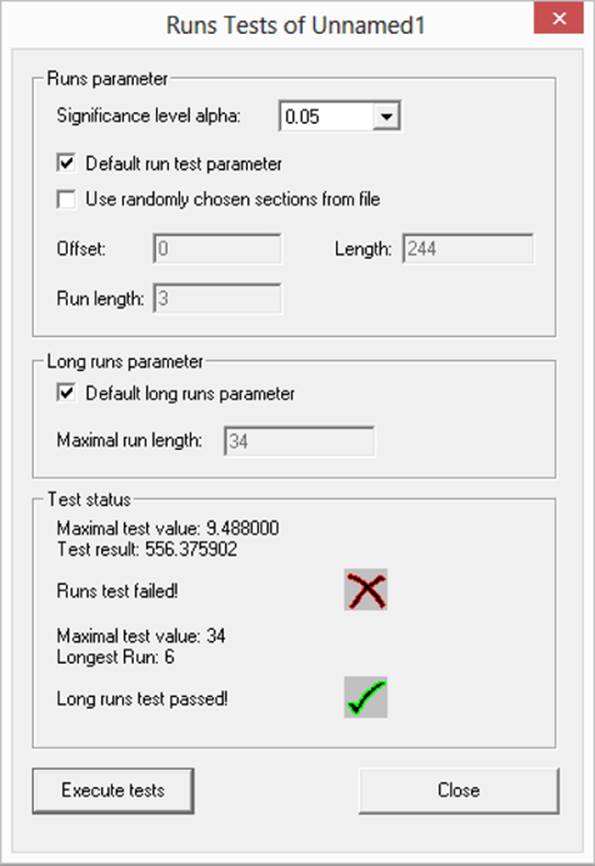
FIGURE 12-3 Runs test results
Test for Longest Run of 1’s
This test is very similar to the runs test. It tests for the longest uninterrupted series of 1’s within a given output for a given PRNG. The purpose of this test is to determine whether the length of the longest run of 1’s within the tested sequence is consistent with the length of the longest run of 1’s that would be expected in a random sequence.
Poker Test
The poker test for PRNGs is based on the frequency in which certain digits are repeated in a series of numbers. Let’s consider a trivial example—a three-digit number. In a three-digit number, there are only three possibilities.
All three digits are the same.
The three digits are all different.
One digit is different from the other two.
The poker test actually assumes sequences of five numbers (there are five cards in a hand of poker). The five numbers are analyzed to determine whether any sequence appears more frequently than the other possible sequences. This is a rather primitive test. When using CrypTool to execute this test, you will need to select a few simple parameters. For our purposes use the default settings. You can see the results in Figure 12-4.
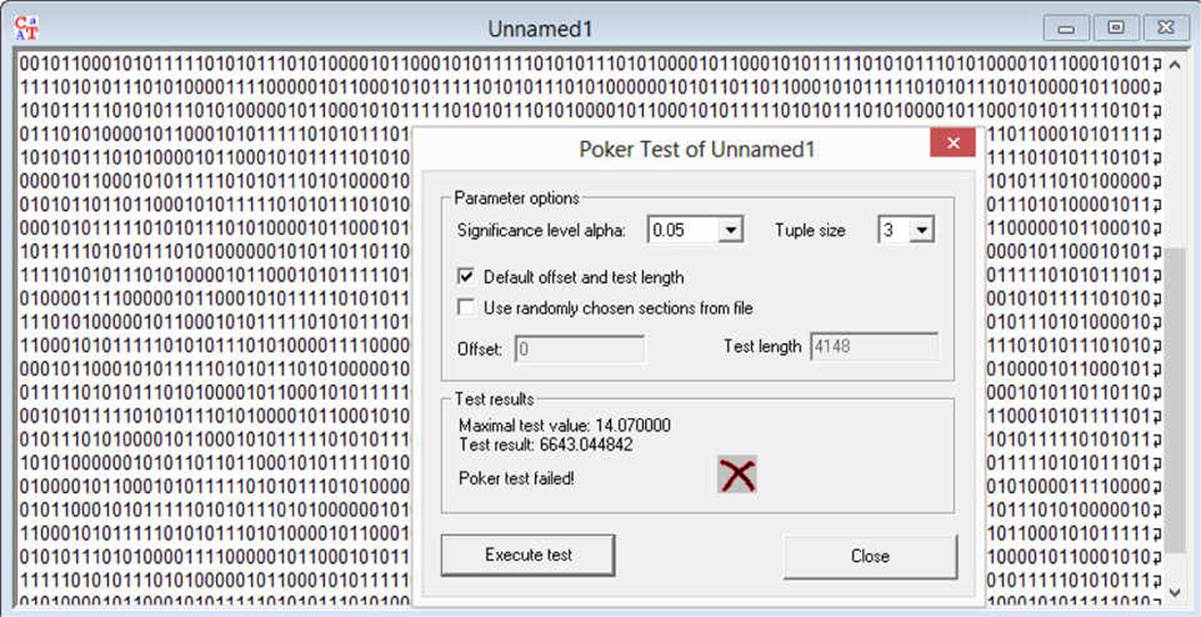
FIGURE 12-4 The poker test
Chi-Squared Statistical Test
Many statistical tests can be applied to a sequence of numbers to determine how random that sequence is.
Chi Squared The chi-squared test is a common statistical test used to test a sampling distribution. It is often used to compare observed data with data you would expect to obtain according to a specific hypothesis.
Note
My purpose is not to evaluate all of the possible tests, but to give you some insight into how you might apply a common statistical test to determining how random a PRNG’s output is. If you are not familiar with statistical testing, consult any elementary statistics textbook.
Chi-squared test results are usually reported as a chi2 measure. A chi2 measure of ±2 is probably random noise, ±3 probably means the generator is biased, and ±4 almost certainly means the generator is biased. The lower the value, the more random the number sequence; the higher the value, the less random the sequence.
Note
NIST recommends a number of statistical tests for testing a PRNG. These tests are documented in “Statistical Testing of Random Number Generators” at http://csrc.nist.gov/groups/ST/toolkit/rng/documents/nissc-paper.pdf.
Standards for PRNG
The German Federal Office for Information Security (BSI) has established four criteria for quality of random number generators:
K1 A sequence of random numbers with a low probability of containing identical consecutive elements.
K2 A sequence of numbers that is indistinguishable from “true random” numbers according to specified statistical tests.
K3 It should be impossible for any attacker to calculate, or otherwise guess, from any given subsequence, any previous or future values in the sequence.
K4 It should be impossible for an attacker to calculate, or guess from an inner state of the generator, any previous numbers in the sequence or any previous inner generator states.
To be suitable for cryptography, any PRNG should meet K3 and K4 standards.
Obviously, K4 is inclusive of K3 and would be the ideal level to achieve; however, K3 should be suitable for cryptographic purposes.
Specific Algorithms
In this section, I’ll start with older algorithms that produce a pseudo-random number, but perhaps one that is not sufficient for cryptographic purposes. Just as I did in Chapters 1 and 2 with historical ciphers, I will start here with historical PRNGs.
Middle-Square Algorithm
The middle-square, or mid-square, is a very old algorithm that was first described by a Franciscan friar in the 13th century. It was reintroduced by John Von Neumann in the 1940s. It is a rather simple method and easy to follow.
Here’s a step by step description of the middle-square method:
1. Start with an initial seed (for example, a four-digit integer).
2. Square the number.
3. The middle four digits become the new seed.
4. Divide this value by 10,000 to produce the random number, and go back to step 2.
The following is a concrete example:
1. x0 = 1234
2. x1: 12342 = 01522756 → x1 = 5227, R1 = 0. 5227
3. x2: 52272 = 27321529 → x2 = 3215, R2 = 0.3215
4. x3: 32152 = 10336225 → x3 = 3362, R3 = 0.3362
The process is repeated indefinitely, generating a new random number each time. The middle 4 bits of each output is the seed for the next iteration of the algorithm.
This algorithm has some definite limitations. The initial starting value is very important. If you start with all 0’s, for example, then you will continue with all 0’s. However, if you start with leading 0’s followed by some number, the subsequent values produced by the algorithm will be reducing to 0. Certain seed numbers are known to generate short periods of repeating cycles. In fact, the best that you can get from any mid-square implementation of n-digit numbers is a period of 8n. And some have far shorter periods.
This algorithm makes an excellent introduction to PRNGs, and it is easy to understand and easy to code should you be interested in implementing this in a program. However, it is not adequate for modern cryptographic purposes.
Linear Congruential Generator
A linear congruential generator (LCG) is an algorithm that depends on a linear equation to generate a pseudo-random sequence. More specifically, it depends on a piecewise linear congruence equation.
Note
A piecewise linear function is a linear function that produces different results depending on input. In other words, it functions in pieces. Here is a simple example:
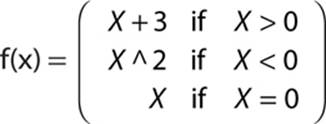
This function performs one of three operations on X, depending on the value of X.
There are a variety of LCGs, but the most common form is
Xn+1 = (aXn + C) mod m
a is the multiplier.
C is the increment.
m is the modulus.
X0 is the initial value of X.
The period of a general LCG is at most m, so the choice of m is quite critical. Some linear congruential generators have a smaller period than m.
Note
Not all LCGs are created equal; some are quite good, others depend heavily on initial conditions, and others are very bad. The RANDU LCG was used in the 1970s. It has a rather poor design and has widely been considered so bad at generating pseudo-random numbers that it caused some to question the efficacy of LCGs in general.
A number of LCGs are built into the random-number generators of various libraries. Each has a value of m sufficient for most random-number purposes. The following table provides details on some of these implementations.
LCGs Implemented in Code
LCGs are fast and easy to code. And as you can see, many programming tools, libraries, and languages have LCGs built in, so you need not even code the algorithm itself. Keep in mind, however, that LCGs are not considered random enough for many cryptographic applications. They are a great place to start learning about PRNGs, and for less rigorous applications they might be used in some limited cryptographic scenarios, but in general they are not sufficient for secure cryptography.
Note
One of the major issues with cryptography is the implementation. Many common hard drive and file encryption products use sound algorithms such as AES and Blowfish, but they use substandard PRNGs to generate the cipher key for the chosen algorithm. Many programmers are not even aware that the library they are using may not have an adequate PRNG.
CrypTool
CrypTool can also be used to generate random numbers. You can find a few common random number generators in CrypTool by choosing Individual Procedures | Tools | Generate Random Numbers, as shown in Figure 12-5.
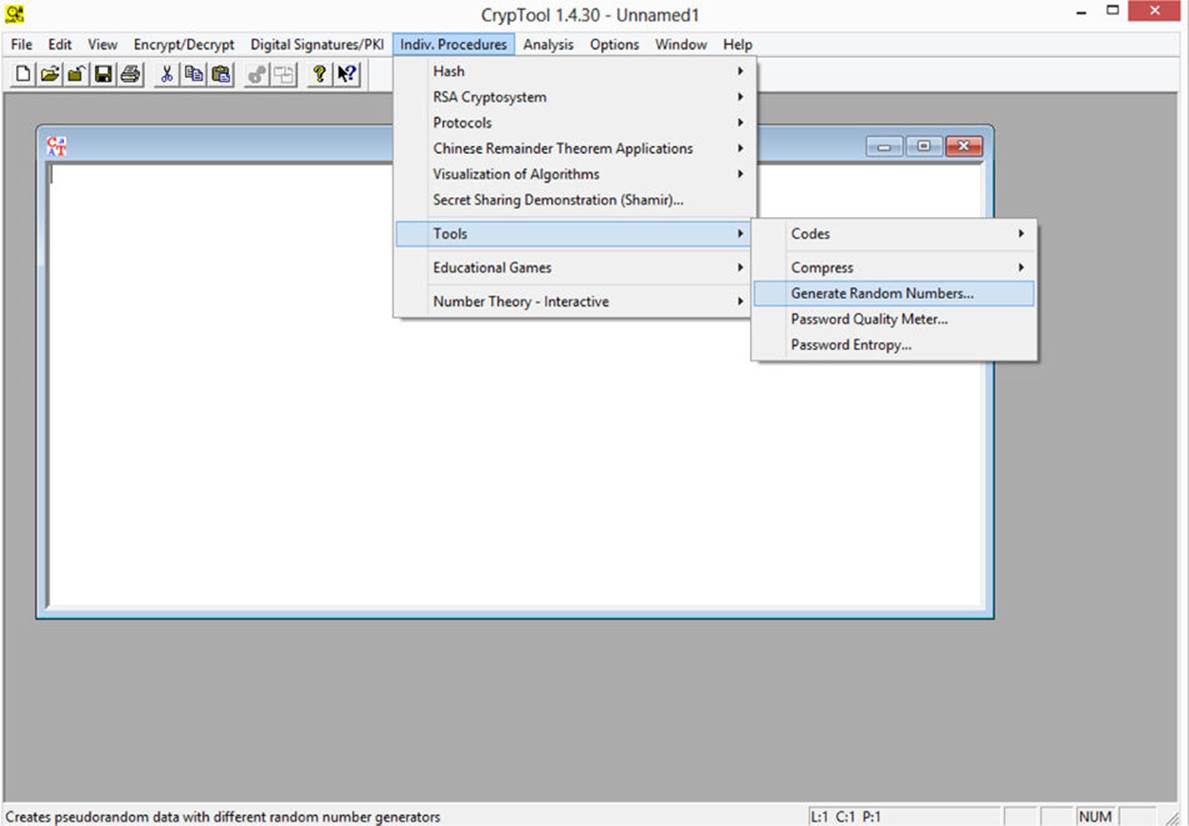
FIGURE 12-5 CrypTool random number generation
As you can see in Figure 12-6, LCG is one of the PRNGs available. It starts with a preset seed of 314149, but you can change that if you want. Using default settings, it produces 1200 bytes of pseudo-random numbers, as shown in the figure.
FIGURE 12-6 CrypTool random numbers from LCG
Note
Feel free to test this random number with the randomness tests mentioned earlier in this chapter, which are also available in CrypTool.
Lagged Fibonacci Generators
The Lagged Fibonacci Generator (LFG) is a particular type of LCG that uses the Fibonacci sequence as a base.
Note
Recall that the Fibonacci sequence is Sn = Sn – 1 + Sn – 2, so that the sequence is 1, 1, 2, 3, 5, 8, 13, 21, 35, and so on.
LFGs come in a variety of forms. If addition is used, it is referred to as an Additive Lagged Fibonacci Generator (ALFG). If multiplication is used, it is referred to as a Multiplicative Lagged Fibonacci Generator or (MLFG). If the XOR operation is used, it is called a Two-tap generalized feedback shift register (GFS).
The basic formula is
y = xk + xj + 1
or
y = xk * xj + 1 (multiplicative LCG)
or
y = xkXORxj + 1 (GFS)
The indices j, k are the lags of the generator.
When the modulus is prime, a maximum period of mk – 1 is possible. It is, however, more common to use a modulus which is a power of two, m = 2p, with p being some prime number.2 In this case, the maximum periods are
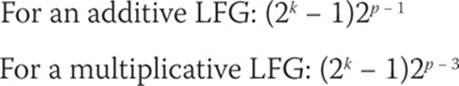
Any LFG must be seeded with the initial k elements of the sequence.
Lehmer Algorithm
This PRNG is named after D.H. Lehmer (and sometimes referred to as the Park-Miller random number generator, after S.K. Park and K.W. Miller). It is the classic example of a linear congruential generator. This algorithm produces a sequence of numbers {Xn} using a standard LCG format:
Xn+1 = (a × Xn + c) mod m
Here is a relatively simple example:
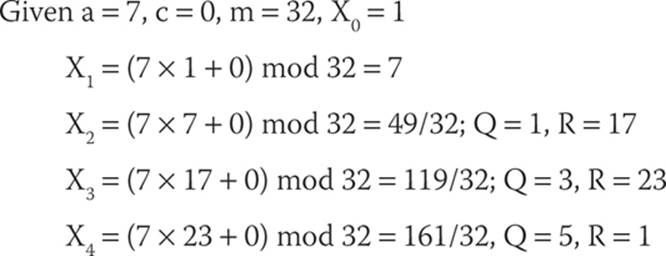
However, with the small m you would expect a repetition at some point, and indeed you find one:
X5 = (7 × 1 + 0) mod 32 = 7/32; Q = 0, R = 7
Oops!
X6 = obviously, we are at the same point as X2 again.
The sequence repeats with a period of 4, and that is clearly unacceptable. Let’s consider a few things that can be done to make this acceptable. For a range of m numbers 0 < m < 2m, the function should generate all the numbers up to 2m before repeating. So clearly a large value of m is important. Even a good algorithm with poorly chosen inputs will produce bad results.
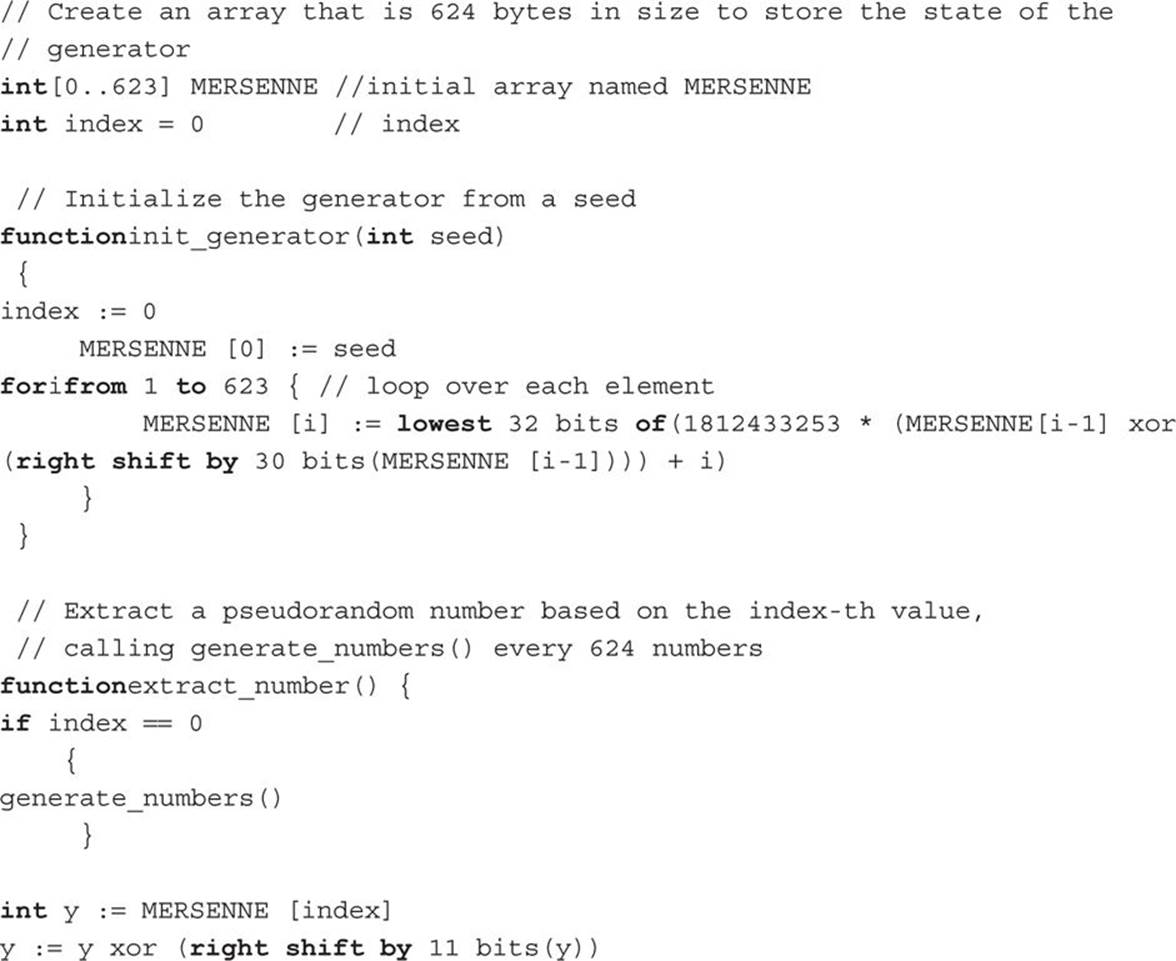
Mersenne Twister
The original Mersenne Twister is not suitable for cryptographic purposes, but permutations of it are. This PRNG was invented by Makoto Matsumoto and Takuji Nishimura. It has a very large period, 219937–1, which is greater than the many other generators. Its name derives from the fact that its period length is chosen to be a Mersenne prime.
The most commonly used version of the Mersenne Twister algorithm is based on the Mersenne prime 219937–1 and uses a 32-bit word. It is often called MT 19937. There is a 64-bit word version called MT 199937-64. The Mersenne Twister is widely used and is implemented in PHP, MATLAB,3 Microsoft Visual C++,4 and Ruby.5
The algorithm itself can be a bit complex to describe, but the following pseudo-code may help you understand this algorithm if you have even a rudimentary programming background:
Blum Blum Shub
This algorithm was proposed in 1986 by Lenore Blum, Manuel Blum, and Michael Shub.
Note
Lenore Blum is a professor of computer science at Carnegie Mellon University. Manuel Blum is the recipient of the 1995 Turing Award for his work in complexity theory. Michael Shub is a mathematician known for his work in dynamical systems and in the complexity of real number algorithms.
The format of Blum Blum Shub is as follows:
Xn+1 = Xn2 mod M
M = pq is the product of two large primes, p and q (this should remind you of the RSA algorithm). At each step of the algorithm, some output is derived from Xn+1. The main difficulty of predicting the output of Blum Blum Shub lies in the difficulty of the “quadratic residuosity problem”: given a composite number n, find whether x is a perfect square modulo n. It has been proven that this is as difficult as breaking the RSA public-key cryptosystem, which involves the factoring of a large composite. This makes Blum Blum Shub a quite effective PRNG.
Yarrow
This algorithm was invented by Bruce Schneier, John Kelsey, and Niels Ferguson. Like all of Schneier’s inventions, this algorithm is unpatented and open source. Yarrow is no longer recommended by its inventors and has been supplanted by Fortuna.6 However, it is still an excellent algorithm to study, because it is generally easy to implement, and it does a good job of generating sufficiently random numbers. The general structure of Yarrow is relatively simple to understand. Yarrow has four parts:
An entropy accumulator Collects semi-random samples from various sources and accumulates them in two pools
A generation mechanism Generates the PRNG outputs
Reseed mechanism Periodically reseeds the key with new entries from the entropy pools
Reseed control Determines when reseeding should occur
The two pools are called the fast pool and slow pool. The fast pool, as the name suggests, is used frequently to reseed the key, while the slow pool provides very conservative reseeds of the key. Both pools contain a hash of all inputs to that point in time, and both use Secure Hash Algorithm (SHA-1), so they produce a 160-bit hash output. Put more simply, each pool is fed some semi-random source, and that source is then put into a hash. As new data is fed to the pool, the hash is updated. This way, there is a constantly changing hash value that could be used as a key.
The SHA-1 outputs are used to create keys for 3-DES. The outputs from 3-DES are the pseudo-random numbers. Periodically the reseed mechanism goes back to the entropy accumulator to get a new SHA-1 hash so that a new key is used with the 3-DES algorithm. Essentially, the algorithm consists of accumulating semi-random input, hashing that output, and using the hash as a seed/key for a block cipher (in this case, 3-DES).
One reason this algorithm is worthy of study is that the same concepts could be easily modified. Allow me to illustrate with a simple but effective variation:
1. Begin with a poor PRNG such as mid-square. Use that to generate a pool of semi-random numbers. You can seed the PRNG with any value, even a current date/time stamp.
2. Subject each number in the pool to a hashing algorithm of your choice (SHA-1, RIPEMD, and so on).
3. From that pool, select two hashes: one will be the seed, the other will be the input or plain text value subjected to a cipher.
4. Use a block cipher of your choice (Blowfish, AES, Serpent, and so on) in cipher-block chaining mode. The output of that cipher is your random number.
This is provided as an example of how you can take existing cryptographic functions and combine them to produce numbers that should be sufficiently random for cryptographic purposes.
Fortuna
Fortuna is actually a group of PRNGs and has many options for whoever implements the algorithm. It has three main components (note that this is similar to Yarrow):
A generator, which is seeded and will produced pseudo-random data
The entropy accumulator, which collects random data from various sources and uses that to reseed the generator
The seed file, which has initial seed values
The algorithm uses a generator that is based on any good block cipher—DES, AES, Twofish, and so on. The algorithm is run in counter mode. The generator is just a block cipher in counter mode. The counter mode generates a random stream of data, which will be the output of Fortuna. Because it is possible that a sequence would eventually repeat, it is recommended that the key used for the block cipher be periodically replaced.
Note
Counter mode is usually used to turn a block cipher into a stream cipher. It generates the next key-stream block by encrypting successive values of the counter.
After each number is generated, the algorithm generates a fresh new key that is used for the next PRNG. This is done so that if an attacker were to compromise the PRNG and learn the state of the algorithm when generating a given PRNG, this will not compromise previous or subsequent numbers generated by this algorithm.
Reseeding the algorithm is done with some arbitrary string. A hashing algorithm is often used for this purpose, because it produces a somewhat random number itself, making it an excellent seed for Fortuna.
Dual_EC_DRBG
The Dual Elliptic Curve Deterministic Random Bit Generator became well known outside of cryptographic circles when Edward Snowden revealed that the algorithm contained a backdoor inserted by the National Security Agency. The algorithm itself is based on elliptic curve mathematics and was standardized in NIST SP 800-90A.
According to John Kelsey, the possibility of the backdoor by carefully chosen P and Q values was brought up at a meeting of the ANSI X9.82 committee. As a result, a way was specified for implementers to choose their own P and Q values.
In 2007, Bruce Schneier’s article, “Did NSA Put a Secret Backdoor in New Encryption Standard?” appeared in Wired Magazine. It is based on an earlier presentation by Dan Shumow and Niels Ferguson.
Given that Dual_EC_DRBG is clearly not secure, the details of the algorithm are not important; however, the story of this algorithm illustrates an important point about the relationship between cryptography and network security. Most network security professionals learn only the most elementary facts about cryptography. Major industry security certifications such as the Certified Information Systems Security Professional (CISSP from ISC2), Certified Advanced Security Practitioner (CASP from the Computer Technology Industry Association), and even many university security textbooks contribute only a surface view of cryptography. This is dramatically illustrated by the story of Dual_EC_DRBG. When Snowden revealed, in 2013, that there was a backdoor in this algorithm, the network security community was stunned. However, the cryptography community had been discussing this possibility for many years. This is, in fact, one of the major purposes of this book you are reading now—to present the world of cryptography in a manner that even general security practitioners can understand.
The Marsaglia CD-ROM
As mentioned earlier in this chapter, you can use tables of pseudo-random numbers as sources for random numbers. George Marsaglia produced a CD-ROM containing 600 MB of random numbers. These were produced using various dependable pseudo-random-number generators, but they were then combined with bytes from a variety of random sources or semi-random sources to produce quality random numbers.
The theory behind combining random numbers to create new random numbers can be described as follows: Suppose X and Y are independent random bytes, and at least one of them is uniformly distributed over the values 0 to 255 (the range found in a single byte when expressed in decimal format). Then both the bitwise exclusive-or of X and Y, and X+Y mod 256, are uniformly distributed over 0 to 255. If both X and Y are approximately uniformly distributed, then the combination will be more closely uniformly distributed.
In the Marsaglia CD-ROM, the idea is to get the excellent properties of the pseudo-random-number generator but to further “randomize” the numbers by disrupting any remaining patterns with the combination operation.
Improving PRNGs
There are a number of ways to improve any given PRNG algorithm. You might think that simply creating new PRNG algorithms would be the ideal way to improve randomness; however, that approach can be difficult. You’d then need to subject the new algorithm to lengthy peer review to ensure that a new problem had not been introduced. Furthermore, the more complex an algorithm, the more computationally intensive it will be. So in some cases it is desirable to take an existing algorithm and simply improve it. A few simple methods can be applied to any PRNG to improve randomness.
Shuffling
One of the simplest methods for improving a PRNG is to shuffle the output. Consider the following example:
1. Start with an array of 100 bytes (you can actually use any size, but we will use 100 for this example).
2. Fill that array with the output of the PRNG algorithm you are trying to improve.
3. When a random number is required, combine any two random numbers from the array.
This combination, as described earlier in reference to specific PRNGs, will increase the randomness. You can make it even more random by combining nonsequential elements of the array.
Cryptographic Hash
This method is sometimes used to generate a reasonably secure random number from a PRNG that is not cryptographically secure—such as a simple mid-square method. The methodology is quite simple. You use the PRNG output as the input to a well-known cryptographic hash such as SHA-1. The output should be reasonably random.
Conclusions
In this chapter you were introduced to pseudo-random-number generators. We have looked at specific algorithms, the desirable properties of a PRNG, and specific tests for randomness. It cannot be overstated how important PRNGs are in the creation of cryptographic keys for symmetric algorithms and in the creation of initialization vectors. Even if you use a secure algorithm, if the PRNG used to create the key is not sufficiently random, it will weaken the cryptographic implementation.
Test Your Knowledge
1. What does K3 of the German standard for PRNG state?
2. What is the basic formula for a linear congruential generator?
3. Briefly describe the 1-D test?
4. What is shuffling?
5. Provide a general overview of Yarrow (the major steps).
Answers
1. Given any stream of bits in the output, you cannot predict previous or subsequent bits.
2. xn+1 = P1xn + P2 (mod N)
3. In the 1-D test, you take 0 to 1.0 and divide it into “bins” and fill the bins with output from the PRNG and see if they fill evenly.
4. In shuffling, you mix the output of a PRNG in some fashion to increase entropy.
5. 1) Generate a seed from semi-random sources; 2) hash the output (SHA-1); and 3) feed that output into 3DES.
Endnotes
1. NIST Special Publication 800-22, http://csrc.nist.gov/groups/ST/toolkit/rng/documents/SP800-22b.pdf.
2. S. Aluru, “Lagged Fibonacci Random Number Generators for Distributed Memory Parallel Computers,” Journal of Parallel and Distributed Computing 45 (1997), 1–12.
3. MathWorks Random Number Generator, www.mathworks.com/help/matlab/ref/randstream.list.html.
4. Microsoft Developer Network, https://msdn.microsoft.com/en-us/library/bb982398.aspx.
5. PHP Manual, http://php.net/manual/en/function.mt-srand.php.
6. B. Schneier, J. Kelsey, and N. Ferguson, “Yarrow-160: Notes on the Design and Analysis of the Yarrow Cryptographic Pseudorandom Number Generator,” www.schneier.com/paper-yarrow.pdf.