Modern Cryptography: Applied Mathematics for Encryption and Informanion Security (2016)
PART I. Foundations
Chapter 1. History of Cryptography to the 1800s
In this chapter we will cover the following:
![]() Single substitution ciphers
Single substitution ciphers
![]() Multi-alphabet substitution
Multi-alphabet substitution
![]() Devices
Devices
![]() Transposition ciphers
Transposition ciphers
The desire to send secret communications is almost as old as written communication itself. For centuries, it often involved military secrets or political intrigue. Generals needed to communicate about troop movements to ensure that if a message was intercepted it wouldn’t be intelligible to the enemy. Political intrigue, such as a palace coup, required surreptitious communications.
Modern cryptography still includes military communications as well as political scheming, but it has expanded into more mundane areas as well. Online banking and shopping, for example, have made cryptography a part of most people’s daily lives, whether they are aware of it or not. Many people also choose to encrypt their computer hard drives or files. Others encrypt their e-mail transmissions. Today, cryptography permeates our lives.
Note
The release of Apple’s iOS 6.0 was interesting because it changed how the iPhone would implement cryptography.
Why Study Cryptography?
It is an unfortunate fact that most people have almost no knowledge of cryptography. Even within the discipline of computer science, and more specifically the profession of computer security, a dearth of cryptographic knowledge plagues the industry. Most computer security professionals have only the most basic understanding of cryptography. Some would even argue that a deeper knowledge of cryptography is unnecessary. It can be assumed that since you are reading this book, you feel a need to deepen and broaden your knowledge of cryptography, and there are clearly practical reasons to do so, particularly for those in the computer security profession.
By understanding cryptology, you can select the most appropriate cryptographic implementations to suit your needs. Even if you have no desire to be a cryptographer, you still have to choose which tool to use to encrypt a hard drive, for example. Should you use the Data Encryption Standard (DES)? Triple DES (3DES)? Blowfish? The Advanced Encryption Standard (AES)? If you use AES, then what key size do you use, and why? If you are interested in message integrity for e-mail, should you use the Secure Hash Algorithm (SHA-2)? Perhaps a message authentication code (MAC) or hash message authentication code (HMAC)? Which will provide the most appropriate solution to your particular problem, and why?
In addition, knowing about cryptology helps you understand issues that occur when cryptographic incidents broadly impact computer security. A good example occurred in 2013, when the New York Times reported that among the documents released by National Security Agency subcontractor Edward Snowden was evidence that the NSA had placed a cryptographic backdoor in the random number generator known as Dual_EC_DRBG (Elliptic Curve Deterministic Random Bit Generator). This news story generated a flurry of activity in the computer security community. But what is a cryptographic backdoor? What does this mean for privacy and security? Does this mean that the NSA could read anyone’s e-mail as if it were published on a billboard?
We will be examining these very issues as well as random number generators and cryptographic backdoors later in this book. For now, it is enough for you to realize that you cannot answer any questions about this particular news story without having some knowledge of cryptography. This story, in fact, was not news to the informed cryptographic community. As early as 2006, papers had been published that suggested the possibility of a backdoor in this random number generator. Well-known and respected cryptographer Bruce Schneier, for example, blogged about this issue in 2007.1 Had the security community a deeper knowledge of cryptography, this backdoor would have been a non-story.
I could continue with other reasons—very practical reasons—why learning cryptography is important, and you will see some of those reasons in later chapters. Cryptography is not merely a mathematical endeavor to be engaged in by a select few mathematicians and cryptologists. In this chapter, you will begin your journey into the world of cryptography by learning some essential terms and then exploring some historical ciphers.
What Is Cryptography?
Before you can begin studying cryptography, you need to know what exactly cryptography is. A number of people seem to have some misconceptions about what cryptography and related terms actually mean. The Merriam-Webster online dictionary defines cryptography as follows: “1) secret writing 2) the enciphering and deciphering of messages in secret code or cipher; also: the computerized encoding and decoding of information.”2 This definition does not seem overly helpful and may not provide you with much insight into the topic. Columbia University provides a slightly better definition in its “Introduction to Cryptography” course: to “process data into unintelligible form, reversibly, without data loss—typically digitally.”3
The Columbia University definition adds the important element of not losing information, certainly a critical component in secure communications. However, I cannot help but think that the definition could be a bit clearer on the issue of exactly what cryptography is. So allow me to try my hand at defining cryptography:
Cryptography is the study of how to alter a message so that someone intercepting it cannot read it without the appropriate algorithm and key.
This definition is certainly not radically different from that of either Merriam-Webster or Columbia University. However, I think it is a good, concise definition, and one we will use throughout this book.
Note that cryptography and cryptology are not synonyms, though many people mistakenly use the terms as if they were. I’ll define and differentiate these two terms, as well as some other common terms you will need throughout your study of cryptography. These terms are used in both ancient and modern cryptography.
![]() Cipher A synonym for the algorithm used in transforming plain text to cipher text.
Cipher A synonym for the algorithm used in transforming plain text to cipher text.
![]() Cipher text The coded or encrypted message. If your encryption is sufficiently strong, your cipher text should be secure.
Cipher text The coded or encrypted message. If your encryption is sufficiently strong, your cipher text should be secure.
![]() Cryptanalysis Also known as code breaking; the study of principles and methods of deciphering cipher text without knowing the key. This is more difficult than movies or television would indicate, as you will see in Chapter 17.
Cryptanalysis Also known as code breaking; the study of principles and methods of deciphering cipher text without knowing the key. This is more difficult than movies or television would indicate, as you will see in Chapter 17.
![]() Cryptography The study of how to alter a message so that someone intercepting it cannot read it without the appropriate algorithm and key.
Cryptography The study of how to alter a message so that someone intercepting it cannot read it without the appropriate algorithm and key.
![]() Cryptology Although some people, including more than a few computer security books, use the terms cryptography and cryptology interchangeably, that is inaccurate. Cryptology is more comprehensive and includes both cryptography and cryptanalysis.
Cryptology Although some people, including more than a few computer security books, use the terms cryptography and cryptology interchangeably, that is inaccurate. Cryptology is more comprehensive and includes both cryptography and cryptanalysis.
![]() Decipher (decrypt) Decipher and decrypt are synonyms. Both terms mean to convert the cipher text to plain text.
Decipher (decrypt) Decipher and decrypt are synonyms. Both terms mean to convert the cipher text to plain text.
![]() Encipher (encrypt) Encipher and encrypt are synonyms. Both words mean to convert the plain text into cipher text.
Encipher (encrypt) Encipher and encrypt are synonyms. Both words mean to convert the plain text into cipher text.
![]() Key The information, usually some sort of number, used with the algorithm to encrypt or decrypt the message. Think of the key as the fuel the algorithm requires in order to function.
Key The information, usually some sort of number, used with the algorithm to encrypt or decrypt the message. Think of the key as the fuel the algorithm requires in order to function.
![]() Key space The total number of possible keys that could be used. For example, DES uses a 56-bit key; thus the total number of possible keys, or the key space, is 256.
Key space The total number of possible keys that could be used. For example, DES uses a 56-bit key; thus the total number of possible keys, or the key space, is 256.
![]() Plain text The original message—the information you want to secure.
Plain text The original message—the information you want to secure.
These are some of the most basic terms that permeate the study of cryptology and cryptography. In any discipline, it is important that you know, understand, and use the correct vocabulary of that field of study. These terms are essential for your understanding.
If you suppose that you cannot study cryptography without a good understanding of mathematics, to some extent you are correct. Modern methods of cryptography, particularly asymmetric cryptography, depend on mathematics. We will examine those algorithms later in this book, along with the mathematics you need to understand modern cryptography. It is often easier for students first to grasp the concepts of cryptography within the context of simpler historical ciphers, however. These ciphers don’t require any substantive mathematics at all, but they do use the same concepts you will encounter later in this book. It is also good to have an historical perspective on any topic before you delve deeper into it. In this chapter we will examine a history of cryptography, looking at specific ciphers that have been used from the earliest days of cryptography to the 1800s.
Let us begin our study of historical cryptography by examining the most common historical ciphers. These are fascinating to study and illustrate the fundamental concepts you need in order to understand cryptography. Each one will demonstrate an algorithm, plain text, cipher text, and a key. The implementations, however, are far simpler than those of modern methods and make it relatively easy for you to master these ancient methods. Keep in mind that these ciphers are totally inadequate for modern security methods. They would be cracked extremely quickly with a modern computer, and many can be analyzed and cracked with a pen, paper, and the application of relatively simple cryptanalysis legerdemain.
Substitution Ciphers
The first ciphers in recorded history are substitution ciphers. With this method, each letter of plain text is substituted for some letter of cipher text according to some algorithm. There are two types of substitution ciphers: single-alphabet (or mono-alphabet) and multi-alphabet (or poly-alphabet). In a single-alphabet substitution cipher, a given letter of plain text is always substituted for the corresponding letter of cipher text. For example, an a in the plain text would always be a k in the cipher text. Multi-alphabet substitution uses multiple substitutions, so that, for example, an a in the plain text is sometimes a k and sometimes a j in the cipher text. You will see examples of both in this section.
The Caesar Cipher
One of the most widely known historical encryption methods is the Caesar cipher. According to the Roman historian Gaius Suetonius Tranquillus (c. 70–130 CE), Julius Caesar used this cipher to encrypt military messages, shifting all letters of the plain text three places to the right. So, for example, the message
![]()
becomes
![]()
As you can see, the a in the plain text is shifted to the right three letters to become a d in the cipher text. Then the t in the plain text is shifted three letters to the right to become a w in the cipher text. This process continues for all the letters in the plain text. In our example, none of the shifts went beyond the letter z. What would happen if we shifted the letter y to the right three? The process would wrap around the alphabet, starting back at letter a. So the letter y would be shifted to a letter b in the cipher text.
Note
Decryption is trivial if the recipient knows the shift that was used and reverses it. For example, if the sender shifts three to the right to encrypt the message, the recipient can shift three to the left to decrypt the message.
Although Caesar was reputed to have used a shift of three to the right, any shifting pattern will work with this method, shifting either to the right or left by any number of spaces. Because this is a very simple method to understand, it’s a good place to start our study of encryption. It is, however, extremely easy to crack. You see, any language has a certain letter and word frequency, meaning that some letters are used more frequently than others. In the English language, the most common single-letter word is a, followed closely by the word I. The most common three-letter word is the, followed closely by the word and. Those two facts alone could help you decrypt a Caesar cipher. However, you can apply additional rules. For example, in the English language, the most common two letter sequences are oo and ee.4 Examining the frequency of letter and letter combination occurrences is called frequency analysis.
It is claimed that other Caesars, such as Augustus, used variations of the Caesar cipher, such as one shift to the right. It should be obvious that any shift, left or right, of more than 26 (at least in English) would simply loop around the alphabet. So a shift to the right of 27 is really just a shift of one.
Although the Caesar cipher is certainly not appropriate for modern cryptographic needs, it does contain all the items needed for a cryptography algorithm. First, we have the plain text message—in our current example, Attack at dawn. Then we have an algorithm—shift every letter. And then a key, in this case +3, or three to the right (–3 would be three to the left). And finally we have cipher text, Dwwdfn dw gdzq. This is, essentially, the same structure used by all modern symmetric algorithms. The only differences between the Caesar cipher and modern symmetric ciphers are the complexity of the algorithm and the size of the key.
The size of the key brings us to one significant problem with the Caesar cipher—its small key space. Recall that key space is the total number of possible keys. Because there are only 26 letters in the English alphabet, the key space is 26 (that is, +–26). It would be relatively easy for a person working with pen and paper to check all possible keys, and it would be ridiculously trivial for a computer to do so. In the cyber security world, a malicious person who checks all possible keys to decipher an encrypted message is conducting what is called a brute-force attack. The smaller the key space, the easier a brute-force attack will be. Compare the Caesar cipher, with a key space of 26, to AES 128-bit, with a key space of 2128, or about 3.4 × 1038. Clearly, the larger key space makes a cipher more resistant to brute-force attacks. Note, however, that simply having a long key is not sufficient for security. You will learn more about this when we discuss cryptanalysis in Chapter 17.
Mathematical Notation of the Caesar Cipher
With the various ancient ciphers we will be using, the math is trivial. However, it is a good idea for you to become accustomed to mathematical notation, at least with those algorithms where such notation is appropriate. It is common to use a capital letter P to represent plain text and a capital letter C to represent cipher text. We can also use a capital letter K to represent the key. This gives us the following mathematical representation of a Caesar cipher:
C ≡ P + K (mod 26)
Don’t be overly concerned about the mod 26. We will explore modulus operations in detail in Chapter 4. For now, I just use the modulus operation to denote dividing by a given number (in this case, 26, because there are 26 letters in the alphabet) and listing only the remainder.
Decryption can also be represented via mathematical symbols:
P ≡ C – K (mod 26)
The mathematical representation of Caesar’s method of shifting three to the right is
C ≡ P + 3 (mod 26)
According to the book The Lives of the Caesars, written by Suetonius, Julius Caesar used this cipher extensively:
There are also the letters of his to Cicero, as well as to his intimates on private affairs, and in the latter, if he had anything confidential to say, he wrote it in cipher, that is by so changing the order of the letters of the alphabet, that not a word could be made out. If anyone wishes to decipher these, and get at their meaning, he must substitute the fourth letter of the alphabet, namely D, for A, and so with the others.5
If the plain text is the 24th letter of the alphabet (which is the letter X), then the cipher text is (24 + 3)/26, listing only the remainder. Thus, 27/26 = 1, or the letter A.
Note
We cannot know how effective the Caesar cipher was at concealing messages. However, at the time of Julius Caesar, illiteracy was widespread and cryptography was not widely known. So what may seem a trivial cipher today—in fact, child’s play—may well have been effective enough more than 2000 years ago.
The Caesar cipher is probably the most widely known substitution cipher, but it is not the only one. All substitution ciphers operate the same way: by substituting each letter in the plain text for some letter in the cipher text, with a one-to-one relationship between the plain text and cipher text. Let’s look at a few other substitution ciphers.
Atbash Cipher
Hebrew scribes copying the biblical book of Jeremiah used the Atbash substitution cipher. Applying the Atbash cipher is fairly simple: just reverse the order of the letters of the alphabet. This is, by modern standards, a very primitive cipher that is easy to break. For example, in English, abecomes z, b becomes y, c becomes x, and so on. Of course, the Hebrews used the Hebrew alphabet, with aleph being the first letter and tav the last letter. However, I will use English examples to demonstrate the cipher:
![]()
becomes
![]()
As you can see, the A (the first letter in the alphabet) is switched with Z (the last letter), and the t is the 19th letter (or 7th from the end) and gets swapped with g, the 7th letter from the beginning. This process is continued until the entire message is enciphered.
To decrypt the message, you simply reverse the process so that z becomes a, b becomes y, and so on. This is obviously a simple cipher and is not used in modern times. However, like the Caesar cipher example, it illustrates the basic concept of cryptography—to perform some permutation on the plain text to render it difficult to read by those who don’t have the key to “unscramble” the cipher text. The Atbash cipher, like the Caesar cipher, is a single-substitution cipher (each letter in the plain text has a direct, one-to-one relationship with each letter in the cipher text). The same letter and word frequency issues that can be used to crack the Caesar cipher can be used to crack the Atbash cipher.
Affine Ciphers
Affine ciphers are any single-substitution alphabet ciphers (also called mono-alphabet substitution) in which each letter in the alphabet is mapped to some numeric value, permuted with some relatively simple mathematical function, and then converted back to a letter. For example, using the Caesar cipher, each letter is converted to a number, shifted by some amount, and then converted back to a letter.
The basic formula for any affine cipher is
ax + b (mod m)
M is the size of the alphabet—so in English that would be 26. The x represents the plain text letter’s numeric equivalent, and the b is the amount to shift. The letter a is some multiple—in the case of the Caesar cipher, a is 1. So the Caesar cipher would be
1x + 3 (mod 26)
You could obviously use any shift amount you want, as well as any multiplier. The ax value could be 1x, as with Caesar, or it could be 2x, 3x, or any other value. For example, let’s create a simple affine cipher:
2x + 4 (mod 26)
To encrypt the phrase Attack at dawn, we first convert each letter to a number, then multiply that number by 2 and calculate that result mod 26. So A is 1, 2 multiplied by 1 is 2, add 4, gives us 6 mod 26 yielding 6, or F.
Then we have t, which is 20, and 2 multiplied by 20 is 40, add 4, which gives us 44, and 44 mod 26 yields 18, or r. Ultimately we get this:

Notice that the letter k did not convert to a letter; instead, a 0 (zero) appears. K is the 11th letter of the alphabet, and 2x + 4, where x = 11, equals 26. And 26 mod 26 is 0.
This is one example of an affine cipher, and there are quite a few others. As you have just seen, you can easily create one of your own. You would want to limit your selection of a to values that produce only integer results, rather than decimals. A value of 1.3x, for example, would lead to decimal values, which could not easily be converted to letters. We know that 1 is a and 2 is b, but what letter is 1.3?
All affine ciphers have the same weaknesses as any single-substitution cipher. They all preserve the letter and word frequencies found in the underlying language and are thus susceptible to frequency analysis. In fact, no matter how complex you make the permutation, any single-substitution cipher is going to be vulnerable to frequency analysis.
ROT 13
ROT 13 is a trivial single-substitution cipher that also happens to be an affine cipher. ROT is short for rotate: each letter is rotated to the right by 13. So the affine representation of the ROT 13 (in English) is
1x + 13 (mod 26)
Since the Latin alphabet has 26 letters, simply applying ROT 13 a second time will decrypt the message. As you can probably guess, this is not at all secure by modern standards. However, it is actually used in some situations. For example, some of the keys in the Microsoft Windows Registry are encrypted using ROT 13.6 In this case, the reasoning is likely to be that, first and foremost, you need access to the system before you can explore the Windows Registry, and second, most people are not well versed in the Windows Registry and would have difficulty finding specific items there even if they were not encrypted at all, so ROT 13 may be secure enough for this scenario. I am not necessarily in agreement with that outlook, but it is a fact that the Windows Registry uses ROT 13.
Note
ROT 13 has been used in online forums and web pages to obfuscate the answer to some quiz, so that it is not readily apparent without applying ROT 13 to the answer. Some people have chosen to publish their e-mail encoded with ROT 13 so that it is easy for a human to decrypt, but difficult for an automated spam bot to decrypt and send spam e-mail.
It has also been reported that in the late 1990s Netscape Communicator used ROT 13 to store e-mail passwords. ROT 13 has actually become somewhat of a joke in the cryptology community. For example, cryptologists will jokingly refer to “ROT 26,” which would effectively be no encryption at all. Another common joke is to refer to “triple ROT 13.” Just a brief reflection should demonstrate to you that the second application of ROT 13 returns to the original plain text, and the third application of ROT 13 is just the same as the first.
Homophonic Substitution
Over time, the flaws in single-substitution ciphers became more apparent. Homophonic substitution was one of the earlier attempts to make substitution ciphers more robust by masking the letter frequencies, as plain text letters were mapped to more than one cipher text symbol, and usually the higher frequency plain text letters were given more cipher text equivalents. For example, a might map either to x or y. This had the effect of disrupting frequencies, making analysis more difficult. It was also possible to use invented symbols in the cipher text and to have a variety of mappings. For example, a maps to x, but z maps to ¥.
Tip
Having a single character of plain text map to more than one character of cipher text makes homophonic substitution ciphers more difficult to analyze. Using symbols other than characters can make them even more challenging to analyze.
There are variations of this cipher, and one of the most notable versions is called the nomenclator cipher, which used a codebook with a table of homophonic substitutions. Originally the codebook used only the names of people, thus the term nomenclator. So, for example, Mr. Smith might be XX and Mr. Jones would be XYZ. Eventually, nomenclators were created that used a variety of words rather than just names. The codes could be random letters, such as those already described, or code words. Thus, Mr. Jones might be enciphered as poodle and Mr. Smith enciphered as catfish. Such codebooks with nomenclator substitutions where quite popular in espionage for a number of years. The advantage of a nomenclator is that it does not provide any frequencies to analyze. However, should the codebook become compromised, all messages encoded with it will also be compromised.
The Great Cipher
The Great Cipher is one famous nomenclator used by the French government until the early 1800s. This cipher was invented by the Rossignol family, a French family with several generations of cryptographers, all of whom served the French court. The first, a 26-year-old Rossignol mathematician, served under Louis XIII, creating secure codes.
The Great Cipher used 587 different numbers that stood for syllables (note that there where variations on this theme, some with a different number of codes). To help prevent frequency analysis, the cipher text would include nulls, or numbers that meant nothing. There were also traps, or codes that indicated the recipient should ignore the previous coded message.
Polybius Cipher
The Polybius cipher (also known as the Polybius square) was invented by the Greek historian Polybius (c. 200–118 B.C.E.). Obviously, his work used the Greek alphabet, but we will use it with English here. As shown in the following grid, in the Polybius cipher, each letter is represented by two numbers. Those two numbers being the x and y coordinates of that letter on the grid. For example, A is 1 1, T is 4 4, C is 1 3, and K is 2 5. So to encrypt the word attack, you would use 114444111325.
Despite the use of two numbers to represent a single letter, this is a substitution cipher and still maintains the letter and word frequencies found in the underlying language of the plain text. If you used the standard Polybius square, which is a widely known cipher, it would be easily cracked, even without any frequency analysis. If you wanted to use a different encoding for letters in the square, that would require the sending and receiving parties share the particular Polybius square in advance, so that they could send and read messages.
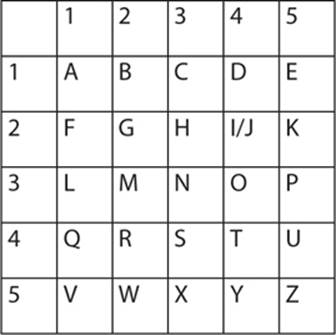
It is interesting to note that the historian Polybius actually established this cipher as a means of sending codes via torches. Messengers standing on hilltops could hold up torches to represent letters, and thus send messages. Establishing a series of such messengers on hilltops, each relaying the message to the next, allowed communications over a significant distance, much faster than any messenger on foot or horseback could travel.
Ancient Cryptography in Modern Wars
Here is a very interesting story that does not necessarily fit with the timeline of this chapter (pre-20th century), but it does concern the Polybius square. The Polybius square was used by prisoners of war in Vietnam, who communicated via tapping on a wall to signal letters. So, for example, four taps, a pause, and then two taps would be the letter R. When used in this fashion, it is referred to as a tap code.7 This cipher was introduced into the POW camps in 1965 by Captain Carlyle Harris, Lieutenant Phillip Butler, Lieutenant Robert Peel, and Lieutenant Commander Robert Shumaker, all imprisoned at the Hoa Lo prisoner of war camp. It is reported that Harris recalled being introduced to the Polybius square by an instructor during his training. He then applied the Polybius square to a tap code so that he and his fellow prisoners could communicate. This technique was taught to new prisoners and became widespread in the POW camp. Vice Admiral James Stockdale wrote about using the tap code, stating, “Our tapping ceased to be just an exchange of letters and words; it became conversation. Elation, sadness, humor, sarcasm, excitement, depression—all came through.”8 This is a poignant example of cryptography being applied to very practical purposes.
Null Cipher
The null cipher is a very old cipher—in fact, by today’s standards, it might be considered more steganography than cipher (you’ll read about steganography in Chapter 16). Essentially, the message is hidden in unrelated text. So, in a message such as
We are having breakfast at noon at the cafe, would that be okay?
the sender and recipient have prearranged to use some pattern, taking certain letters from the message. So, for example, the numbers
![]()
would signify the letters in the sentence and provide the message
![]()
The pattern can be complex or simple—such as always using the second letter of each word or any other pattern. In addition, punctuation and spaces could be counted as characters (our example ignored punctuation and spaces).
Multi-Alphabet Substitution
As you know, any single-alphabet substitution cipher is susceptible to frequency analysis. The most obvious way to improve such ciphers would be to find some mechanism whereby the frequency of letters and words could be disrupted. Eventually, a slight improvement on the single-substitution cipher was developed, called multi-alphabet substitution. In this scheme, you select multiple numbers by which to shift letters (that is, multiple substitution alphabets). For example, if you select three substitution alphabets (+1, +2, and +3), then
![]()
becomes
![]()
In this example, the first letter was shifted forward by one, so A became B; the second letter was shifted forward by two, so t became v; the third letter was shifted forward by three, so in this case t became w. Then you start over with one shift forward. As you can see, the use of multiple alphabets changes letter and word frequency. The first letter t became v, but the second letter t became w. This disrupts the letter and word frequency of the underlying plain text. The more alphabets you use, the more disruption there will be to the letter and word frequency of the plain text. This disruption of the letter and word frequency overcomes the weaknesses of traditional single-substitution ciphers. There are a variety of methods for making a multi-alphabet substitution cipher. We will examine a few of the most common multi-alphabet ciphers in the following sections.
Tabula Recta
Tabula recta is one of the earliest major multi-alphabet substitution ciphers. It was invented in the 16th century by Johannes Trithemius. A tabula recta is a square table of alphabets made by shifting the previous alphabet to the right, as shown in Figure 1-1.

FIGURE 1-1 Tabula recta
This essentially creates 26 different Caesar ciphers. Trithemius described this in his book Polygraphia, which is presumed to be the first published book on cryptology. To encrypt a message using this cipher, you substitute the plain text letter for the letter that appears beneath it in the table. Basically, the first letter of the plain text (denoting the row) is matched with the first letter of the keyword (denoting the column), and the intersection of the two forms the cipher text. This is repeated with each letter. When the end of the keyword is reached, you start over at the beginning of the keyword. Trithemius used a fixed keyword, so although this did change the frequency distributions found in single-substitution ciphers, it still had a significant flaw when compared to later developments such as Vigenère.
Vigenère
Perhaps the most widely known multi-alphabet cipher is the Vigenère cipher. This cipher was first described in 1553 by Giovan Battista Bellaso, though it is misattributed to 19th-century cryptographer Blaise de Vigenère. It is a method of encrypting alphabetic text by using a series of different mono-alphabet ciphers selected based on the letters of a keyword. Bellaso also added the concept of using any keyword, thereby making the choice of substitution alphabets difficult to calculate.
Note
For many years, Vigenère was considered very strong—even unbreakable. However, in the 19th century, Friedrich Kasiski published a technique for breaking the Vigenère cipher. We will revisit that when we discuss cryptanalysis later in this book.
It is important that you get accustomed to mathematical notation. Here, using P for plain text, C for cipher text, and K for key, we can view Vigenère very similarly to Caesar, with one important difference: the value K changes.
Ci ≡ Pi + Ki (mod 26)
The i denotes the current key with the current letter of plain text and the current letter of cipher text. Note that many sources use M (for message) rather than P (for plain text) in this notation.
A variation of the Vigenère, the running key cipher, simply uses a long string of random characters as the key, which makes it even more difficult to decipher.
The Beaufort Cipher
The Beaufort cipher uses a tabula recta to encipher the plain text. A keyword is preselected by the involved parties. This cipher was created by Sir Francis Beaufort (1774–1857) and is very similar to the Vigenère cipher. A typical tabula recta was shown earlier in this chapter in Figure 1-1.
When using the Beaufort cipher, you select a keyword, except unlike Vigenère, you locate the plain text in the top row, move down until you find the matching letter of the keyword, and then choose the letter farthest to the left in the row as the cipher text.
For example, using the tabula recta in Figure 1-1, and the keyword falcon, you would encrypt the message Attack at dawn in the following manner:
1. Find the letter A on the top row.
2. Go straight down that column until you find the letter F (the first letter of the keyword).
3. Use the letter in the far left column as the cipher text letter. In this case, that would be F.
4. Repeat this, except this time use the next letter of the keyword, a. Locate the second letter of the plain text t in the top row.
5. Move down that column until you find an a, and then we select the letter on the far left of that row, which would be h.
6. When you reach the last letter of the keyword, you start over at the first letter of the keyword, so that
![]()
becomes
![]()
Devices
In modern times, devices are almost always used with cryptography. For example, computers are used to encrypt e-mail, web traffic, and so on. In ancient times, there were also ciphers based on the use of specific devices to encrypt and decrypt messages.
Scytale Cipher
The Scytale cipher is one such ancient cipher. Often mispronounced (it actually rhymes with “Italy”), this cipher used a cylinder with a strip of parchment wrapped around it. If you had the correct diameter cylinder, then when the parchment was wrapped around it, the message could be read. You can see the concept shown in Figure 1-2.
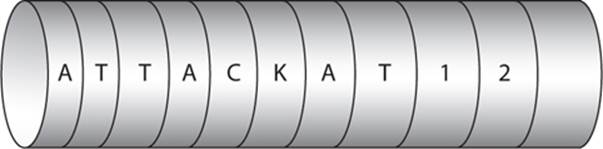
FIGURE 1-2 Scytale
If you did not have the correct size of cylinder, however, or if you simply found the parchment and no cylinder, the message would appear to be a random string of letters. This method was first used by the Spartans and later throughout Greece. The earliest mention of Scytale was by the Greek poet Archilochus in the seventh century B.C.E. However, the first mention of how it actually worked was by Plutarch in the first century B.C.E., in his work Parallel Lives:
The dispatch-scroll is of the following character. When the ephors send out an admiral or a general, they make two round pieces of wood exactly alike in length and thickness, so that each corresponds to the other in its dimensions, and keep one themselves, while they give the other to their envoy. These pieces of wood they call “scytalae.” Whenever, then, they wish to send some secret and important message, they make a scroll of parchment long and narrow, like a leathern strap, and wind it round their “scytale,” leaving no vacant space thereon, but covering its surface all round with the parchment. After doing this, they write what they wish on the parchment, just as it lies wrapped about the “scytale”; and when they have written their message, they take the parchment off, and send it, without the piece of wood, to the commander. He, when he has received it, cannot other get any meaning of it—since the letters have no connection, but are disarranged—unless he takes his own “scytale” and winds the strip of parchment about it, so that, when its spiral course is restored perfectly, and that which follows is joined to that which precedes, he reads around the staff, and so discovers the continuity of the message. And the parchment, like the staff, is called “scytale,” as the thing measured bears the name of the measure.9
Alberti Cipher Disk
The Alberti cipher disk, created by Leon Battista Alberti, is an example of a multi-alphabet substitution. Alberti wrote about this cipher in 1467 in his book De Cifris. It is said to be the first multi-alphabet cipher. It consists of two disks attached in the center with a common pin. Each disk had 24 equal cells. The larger, outer disk, called the stabilis, displayed an uppercase Latin alphabet used for the plain text. The smaller, inner disk, called the mobilis, displayed a lowercase alphabet for the cipher text.
To encrypt a message, a letter on the inner disk was lined up with a letter on the outer disk as a key. If you knew what letter to line up with, you would know which key to use. This has the effect of offering multiple substitution alphabets. You can see an example of the cipher disk, with the English alphabet, in Figure 1-3.
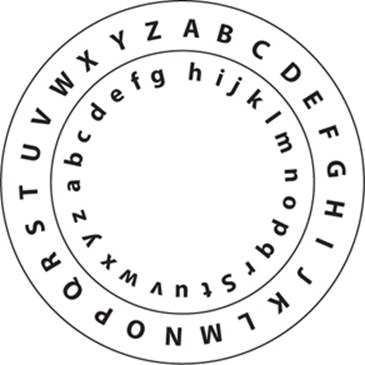
FIGURE 1-3 Cipher disk
In Alberti’s original cipher disk, he used the Latin alphabet. So the outer disk had the Latin alphabet minus a few English letters, as well as numbers 1 through 4 for use with a codebook that had phrases and words assigned four-digit values.
The Jefferson Disk
The Jefferson disk, which was called a “wheel cipher” by its inventor, Thomas Jefferson, is a rather complex device, at least for its time. Invented in 1795, the disk is a set of wheels or disks, each displaying the 26 letters of the English alphabet. The disks are all on a central axle and can be rotated about the axle. The order of the disks is the key, and both sender and receiver had to order their disks according to the key. An example of the Jefferson disk is shown in Figure 1-4.

FIGURE 1-4 Jefferson disk
When using the Jefferson disk, the sender would rotate the letters on the disks until the message was spelled out in a single row. The sender would then copy down any row of text on the disks other than the one that contained the plain text message. That enciphered message would then be sent to the recipient. The recipient then arranged the disk letters according to the predefined order and then rotated the disk until the message was displayed.
Note
This device was independently invented by Étienne Bazeries (1846–1931), a French cryptographer, although Jefferson improved on the disk in his version. Bazeries was known for being a very skilled cryptographer and cryptanalyst. After he broke several transposition systems used by the French military, the French government hired him to work for the Ministry of Foreign Affairs. During World War I, he worked on breaking German ciphers.
Stories such as this are not uncommon in cryptography. Two different parties may independently invent the same or remarkably similar ciphers. This often occurs from time to time in modern times, when at least some work in cryptography is classified by various governments. You will see other examples of this in later chapters on modern ciphers.
Book Ciphers
Book ciphers have probably been around for as long as books have been available. Essentially, the sender and receiver agree to use a particular book as its basis. The simplest implementation is to send coordinates for words. So, for example, 3 3 10 means “go to page 3, line 3, tenth word.” In this way, the sender can specify words with coordinates and write out entire sentences. There are numerous variations of this cipher. For example you could combine book ciphers with Vigenère and use the book coordinates to denote the keyword for Vigenère.
Beale Ciphers
In 1885, a pamphlet was published describing treasure buried in the 1820s by one Thomas J. Beale in Virginia. The Beale ciphers are three cipher texts that allegedly give the location, contents, and names of the owners of the buried treasure. The first Beale cipher, which has not been solved, provides the location. The second cipher provides details of the contents of the treasure and has been solved. The second cipher was a book cipher that used the US Declaration of Independence as the book. Each number in the cipher represents a word in the document. They are presented here simply as an example of a book cipher.
Transposition Ciphers
So far, we have looked at ciphers in which some sort of substitution is performed. However, this is not the only way to encrypt a message. It is also possible to transpose parts of a message. Transposition ciphers provide yet another avenue for encryption.
Reverse Order
The simplest implementation of a transposition cipher is to reverse the plain text. In this way
![]()
becomes
![]()
Obviously, this is not a particularly difficult cipher to break, but it demonstrates a simple transposition.
Rail Fence Cipher
The rail fence cipher may be the most widely known transposition cipher. You encrypt the message by alternating each letter on a different row. So
![]()
is written like this:
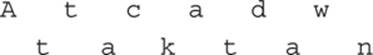
Next you write down the text on both lines, reading from left to right, as you normally would, thus producing
![]()
To decrypt the message, the recipient must write it out on rows:
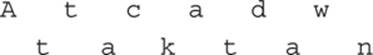
Then the recipient reconstructs the original message. Most texts use two rows as examples, but any number of rows can be used.
Geometric Shape Cipher
In the geometric shape cipher, the sender writes out the plain text in rows and then maps a path (that is, a shape) through it to create the cipher text. So if the plain text is
![]()
this message would be written in rows like this:

Then the sender chooses some path through the message to create the cipher text, as shown in Figure 1-5.
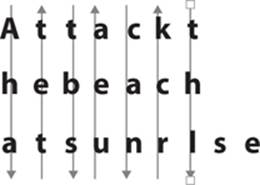
FIGURE 1-5 Geometric shape cipher
Using the path depicted in Figure 1-5, the cipher text reads
![]()
For this example, I used a very simple geometric path through the plain text, but you could use other, more complex patterns as well. This method is sometimes called a route cipher, as it is encrypted using a specific route through the plain text.
Columnar Cipher
The columnar cipher is an intriguing type of transposition cipher. In this cipher, the text you want to encrypt is written in rows usually of a specific length and determined by some keyword. For example, if the keyword is falcon, which is six characters long, you would write out your messages in rows of six characters each. So you would write out

Notice the added q at the end. That was added because the last row is only five characters long. In a regular columnar cipher, you pad the last row so that all rows are of equal length.
If you leave the blank spaces intact, this would be an irregular columnar cipher, and the order of columns would be based on the letters in the keyword as they appear in the alphabet. So if the keyword is falcon, the order is 3 1 4 2 6 5 as f is the third lowest letter in the alphabet, a is the lowest, l is the fourth lowest, and so on. So if we apply 3 1 4 2 6 5 to encrypt the message, we first write out the letters down column 3, then column 1, then column 4, then column 2, then column 6, and then column 5. So the message

is encrypted like so:
![]()
Many variations of the columnar cipher, such as the Myskowski variation, have been created over the years, each adding some subtle twist to the concept.
Myskowski Variation
When using a columnar cipher, what happens if the keyword includes the same letter twice? Normally, you treat the second occurrence as if it were the next letter. For example, if babe is the keyword, the second b is treated as if it were a c, so the order would be 2 1 3 4.
In 1902, Emile Myskowski proposed a variation that did something different. The repeated letters were numbered identically, so babe would be 2 1 2 3. Any plain text columns that had unique numbers (in this case 1 and 3) would be transcribed downward as usual. However, the recurring numbers (in this case 2) would be transcribed left to right.
Combinations
One of the first thoughts that may occur when you’re first learning cryptography is to combine two or more of the classic ciphers, such as those covered in this chapter. For example, you might use a Vigenère cipher first, and then put the message through a columnar transposition or a rail fence cipher. Combining some substitution cipher with a transposition cipher would increase the difficulty a human would have in breaking the cipher. You can think of this in mathematical terms as a function of a function:
f(g(x))
Where g is the first cipher, x is the plain text, and f is the second cipher. And you could apply them in any order—first a substitution and then a transposition, or vice versa.
When you’re exploring this train of thought, be aware that if you simply apply two monoalphabet substitution ciphers, you have not improved secrecy at all. The cipher text will still preserve the same letter and word frequencies. In fact, the best improvement will come from combining transposition and substitution ciphers. As you will see beginning in Chapter 6, modern block ciphers combine substitution and transposition, albeit in a more complex fashion. Don’t think, however, that such innovations will lead to ciphers that are sufficient for modern security needs. Performing such combinations is an intriguing intellectual exercise and will hone your cryptography knowledge, but these methods would not provide much security against modern computerized cryptanalysis.
Conclusions
In this chapter, you have been exposed to a variety of historical ciphers. You were shown single-substitution ciphers such as Caesar and Atbash and multi-alphabet ciphers such as Vigenère. You learned about the weaknesses of mono-alphabet substitution ciphers and how multi-alphabet methods attempt to overcome those issues. You were introduced to a variety of transposition ciphers, including the rail fence and columnar ciphers. This chapter also introduced you to devices such as Scytale and the Jefferson disk. It is important that you get very comfortable with these ciphers before proceeding on.
You were also introduced to some basic mathematical notation to symbolize some of the ciphers in this chapter as well as some general cryptographic terminology such as cipher text and key space. That notation and those terms should be very familiar to you because they will help form the basis for modern symmetric ciphers you’ll read about, beginning in Chapter 6.
Test Your Knowledge
A few questions are provided here to aid you in testing your knowledge before you proceed.
1. What is the most obvious weakness in a mono-alphabet cipher?
A. It preserves word frequency.
B. It can be cracked with modern computers.
C. It is actually quite strong.
D. It doesn’t use complex mathematics.
2. The total number of possible keys for a given cipher is referred to as the ___________.
A. key group
B. key domain
C. key space
D. key range
3. Which of the following methods used a cylinder with text wrapped around it?
A. Vigenère cipher
B. Jefferson disk
C. Cipher disk
D. Scytale
4. What is an affine cipher?
A. Any cipher of the form ax + b (mod m)
B. Only single substitution ciphers
C. Any single substitution cipher
D. A multi-alphabet cipher
5. What is the key feature of homophonic substitution?
A. Multiple substitution alphabets are used.
B. A single plain text letter may have several cipher text representations.
C. The cipher text is phonically similar to the plain text.
D. It combines substitution with transposition.
Answers
1. A
2. C
3. D
4. A
5. B
Endnotes
1. Bruce Schneier, “The Strange Story of DUAL_EC_DRBG,” www.schneier.com/blog/archives/2007/11/the_strange_sto.html.
2. Merriam-Webster Dictionary, www.merriam-webster.com/dictionary/cryptography.
3. Columbia University “Introduction to Cryptography” course, www.cs.columbia.edu/~hgs/teaching/security/slides/crypto2.pdf.
4. For more about word and letter frequencies, see “Puzzle Barron’s Cryptograms,” www.cryptograms.org/letter-frequencies.php; “Cornell University Letter Frequency,” www.math.cornell.edu/~mec/2003-2004/cryptography/subs/frequencies.html; and “Letter Frequencies in English,”www.letterfrequency.org/.
5. Suetonius, Lives of the Caesars (Oxford University Press, 2009).
6. Ken Harthun discusses the use of ROT 13 in the Windows Registry in “How to Use the Windows Registry for Cyber Forensics: Part 2,” at http://itknowledgeexchange.techtarget.com/security-corner/how-to-use-the-windows-registry-for-cyberforensics-part-2/.
7. Tap codes were discussed in “Return with Honor,” an episode of American Experience on PBS television. For information on the POWs’ use of the tap code, see www.pbs.org/wgbh/amex/honor/sfeature/sf_tap.html.
8. Jim and Sybil Stockdale, In Love and War: The Story of a Family’s Ordeal and Sacrifice During the Vietnam Years (Harper & Row, 1984).
9. From Plutarch’s Parallel Lives, “The Life of Lysander”: http://penelope.uchicago.edu/Thayer/E/Roman/Texts/Plutarch/Lives/Lysander*.html.
All materials on the site are licensed Creative Commons Attribution-Sharealike 3.0 Unported CC BY-SA 3.0 & GNU Free Documentation License (GFDL)
If you are the copyright holder of any material contained on our site and intend to remove it, please contact our site administrator for approval.
© 2016-2026 All site design rights belong to S.Y.A.