Modern Cryptography: Applied Mathematics for Encryption and Informanion Security (2016)

PART I. Foundations

Chapter 2. History of Cryptography from the 1800s

In this chapter we will cover the following:

Playfair cipher

Two-square and four-square ciphers

Hill cipher

ADFGX and ADFGVX ciphers

Bifid ciphers

Gronsfeld cipher

Vernam cipher

Enigma

Historical figures in cryptography

In Chapter 1, you were introduced to several relatively simple ciphers that were widely used for many centuries. Beginning in the 1800s, the art of cryptography entered an age of growth as more complex ciphers were developed. In this chapter we will look at the end of the classical (pre-computer) days of cryptography and continue on to the 20th century. The ciphers in this chapter are, for the most part, more complex than those of Chapter 1. You may find yourself having to reread the descriptions of some. If you have any difficulty with a cipher, I urge you to take a pencil and paper and experiment with it until you are comfortable.

Cryptography Marches On

Although these ciphers are more complex than those in Chapter 1, they are still not adequate for the modern computer age, so it would be an egregious mistake to attempt to implement one of these, perhaps via computer code, and then presume your data is secure. Modern computers can utilize brute-force methods, and, in fact, noncomputerized cryptanalysis methods have been developed to attack many of these ciphers. I examine those methods in Chapter 17, when we explore cryptanalysis in general.

Tip

Most people have some level of difficulty with cryptography when they first encounter it. In this chapter, as well as the rest of this book, keep in mind that some topics will require some hands-on practice and others will require reading the text more than once. But make sure you fully understand a topic before moving on to the next topic.

Playfair Cipher

The Playfair cipher was invented in 1854 by Charles Wheatstone, but it was popularized by Scottish politician and scientist Lord Playfair, thus it bears his name. This cipher works by encrypting pairs of letters, also called digraphs, at a time. Although it was first rejected by the British government as being too complex, it was actually used by the British military in World War I and to some extent in World War II. It was also used by the government of New Zealand as late as the early 1940s for non-military communications.

Note

Charles Wheatstone (1802–1875) was an accomplished inventor and scientist. Among his various contributions to science was the Wheatstone bridge, an electrical circuit that is used to measure electrical resistance. The original bridge was invented by Samuel Hunter Christie, but Wheatstone improved it. Wheatstone also made a number of contributions to our knowledge and application of electricity.

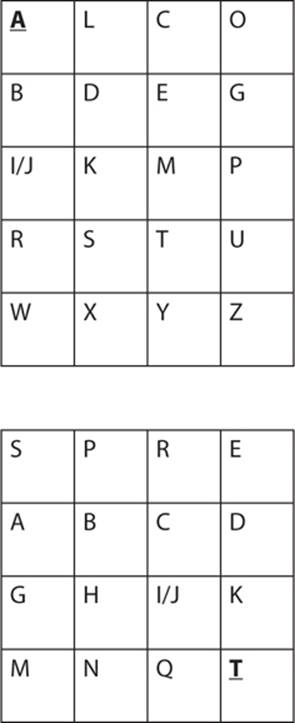
The Playfair cipher depends on a 5-by-5 table, or matrix, that contains a keyword or key phrase. To use the Playfair cipher, you need to memorize that keyword and four rules. Any square of 5-by-5 letters can be used. You first fill in the keyword, and then start, in order, adding in letters that did not appear in the keyword. Note that the letters I and J are combined. You can see this in the table below. In this example the keyword is falcon.

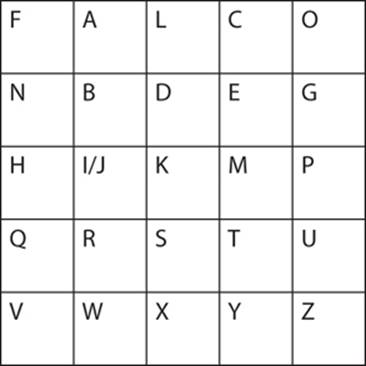
Since the 5-by-5 matrix is created by starting with a keyword, and then filling in letters that did not appear in the keyword, the matrix will be different when different keywords are used.

The next step is to divide the plain text into digraphs (combinations of two letters). In this case, Attack at dawn becomes At ta ck at da wn. If the final digraph is incomplete (a single letter), you can pad it with a letter z. If there are any duplicate letters, replace the second letter with an x. For example, puppet would be pu px et. Playfair does not account for numbers or punctuation marks, so you must remove any punctuation from the plain text and spell out any numbers.

Next, you look at the plain text digraph—in our case At ta ck at da wn—and find the pairs of letters in the table. Look to the rectangle formed by those letters. In our example, the first two letters, AT, form the rectangle in the table as shown next, with A in the upper-left corner and T in the lower-right corner.

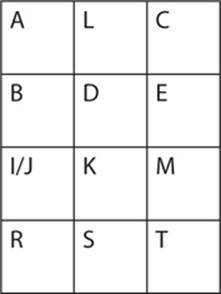
Use the letters at the opposite ends of the rectangle to create the cipher text. The letter A is in the upper-left corner, so you replace it with whatever appears in the upper-right corner, which in this case is the letter C. The letter T is in the lower-right corner, so you replace it with the letter in the lower-left corner, which is R. So the letters AT are enciphered as CR.

Just to make sure you’re clear, let’s continue with a few more examples. The next digraph is TA and will form the same rectangle in the table. However, since T is the first letter of the plain text, R will be the first letter of the cipher text, yielding RC. Next we have CK. Those letters form the rectangle shown here:

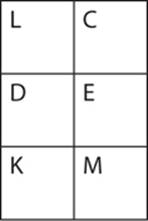
C becomes L, and K becomes M, so the enciphered letters are LM. If you continue this process to the end of the plain text,

is encrypted to yield

Yes, this cipher does take some practice to master.

Note that the cipher disrupts the letter and word frequencies found in single-substitution ciphers, merely by encrypting digraphs instead of single letters.

Two-Square Cipher

The two-square cipher is also often referred to as a double Playfair, for reasons that will soon become clear. Like the Playfair, it works on digraphs. There are two variations of the two-square cipher, the horizontal and the vertical, which refer to how the table’s squares are arranged. In the horizontal method, they are side-by-side, and in the vertical, the squares are arranged one on top of the other. Each square requires its own keyword, so the two-square cipher is based on using two keywords as well as two matrices.

Let’s consider an example of a vertical two-square cipher with the keywords falcon and osprey, shown here:

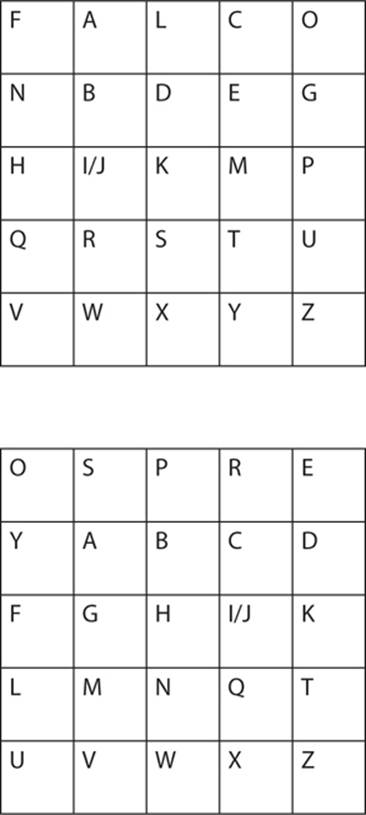
As with the Playfair, you divide the plain text into digraphs. So Attack at dawn becomes At ta ck at da wn.

Next, you form a rectangle, as with Playfair, but the rectangle bridges both tables. Find the first letter of plain text in the top table and the second letter in the bottom table. In this case, A in the top table and T in the bottom forms the rectangle shown here:

The letter A is in the upper-left corner, so you replace it with the letter in the upper-right corner, which is the letter O. The letter T is in the lower-right corner, so you replace it with the letter in the lower-left corner, M, providing the cipher text OM.

If you continue this process through the entire plain text, you will generate the cipher text shown here:

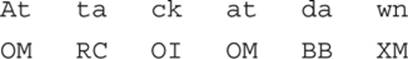
Note that if the two letters in the digraph line up (that is, they appear in the same column in the two tables), the cipher text is the same as the plain text. If you are using the horizontal two-square cipher, the same rule applies if the two plain text characters are in the same row.

Four-Square Cipher

As you can probably surmise, the four-square cipher takes the Playfair concept and expands it to use four squares. This cipher was invented by Félix Marie Delastelle (1840–1902), a Frenchman who invented several ciphers including the bifid, trifid, and four-square ciphers.

Note

Delastelle’s contributions to cryptography during the 1800s are numerous. He finished work on a book on cryptography, Traité Élémentaire de Cryptographie (Elementary Treatise on Cryptography) just 11 months before he died in April 1902, and the book was published 3 months after his death. Most notable is that Delastelle was an amateur cryptographer with no formal training in math.

To create a four-square cipher, you first create four matrices of 5-by-5 letters; usually, either the Q is omitted or the letters I and J are combined to account for all 26 letters in the alphabet. Notice that in the matrices shown next, in some cases I omitted the Q, and in others I combined I andJ. Also note that the letters may, or may not, be in alphabetical order. In this cipher, the two uppercase matrices are for the cipher text, and the two lowercase matrices are for the plain text. This is why the two uppercase matrices are not in alphabetical order.

You then split the message into digraphs, so that Attack at dawn becomes at ta ck at da wn.

The next part may seem a bit complex, so follow along carefully. First, find the first letter in the upper-left plain text matrix. In this case, the letter a is in the first row. Then find the second letter of the digraph in the lower-right plain text matrix. The letter t is in the fourth column. These two letters are in boldface and underlined here:

Because we are dealing with a digraph, we need to encrypt both the a and the t. To find the first letter of the cipher text, use the upper-left matrix’s row of the first letter of plain text—in this case, a is in row 1—and the lower-right matrix’s column of the second letter of cipher text—t is incolumn 4. Look in the upper-right cipher text matrix and find that letter—row 1, column 4 is R. This is the first letter of the cipher text.

Then, to find the second letter of the cipher text, use the row of the second letter of plain text—in this case, t is in row 4—and the column of the first letter—a is in column 1. Then find that letter in the lower-left cipher text matrix—row 4, column 1 is the letter L. You can see this in the next four matrices, where the plain text letters are in boldface and the cipher text letters are in boldface and underlined.

So, the first two letters, at, in plain text become RL in cipher text. You’d continue this process throughout the entire plain text phrase, yielding

Hill Cipher

The Hill cipher was invented by mathematician Lester S. Hill in 1929. It is a bit more complex than other ciphers we have studied thus far. It is based in linear algebra and uses matrix mathematics. To encrypt a message, you break the plain text into a block of n letters (called an n-component vector). Each letter is represented by a number (a = 1, b = 2, c = 3, and so on); note that the number assignment is not critical—for example, some implementations start with a = 0. That block of numbers representing the block of plain text forms a matrix that is multiplied by some invertiblen-by-n matrix, mod 26. (If you don’t have some math background, this may seem rather intimidating—not to worry, it will all be made clear.)

Note

Lester Hill was a mathematician who received his bachelor’s degree from Columbia in 1911 and his Ph.D. from Yale in 1926. He was a professor at several colleges including Princeton and Yale. His research interest included application of mathematics to communications, as evidenced by the Hill cipher. He also worked on methods to find errors in telegraph communications.

The matrix used is the key for this cipher. It should be selected randomly and be mod 26 (26 for the letters of the English alphabet; other alphabets would require a different mod). For our discussions on this cipher, we will use the following matrix as a key:

Note

Although I am showing you a 3-by-3 matrix, you can use any size as long as it is a square.

For those readers not familiar with matrix math, I will show you just enough to allow you to understand the Hill cipher. Chapters 4 and 5 will give you a better introduction to mathematics for cryptography. To understand multiplying a matrix by a vector, examine this example using letters:

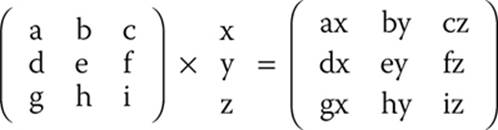
Each row of the original matrix is multiplied by each item in the vector to provide a resulting matrix.

In the case of the Hill cipher, the vector is simply numbers representing a block of text. Note that this conversion assumes 1 = a, 2 = b, and so on:

is

Now let’s break this down into three-character blocks:

We multiply each vector times the numbers in the key. So the first line goes like this:

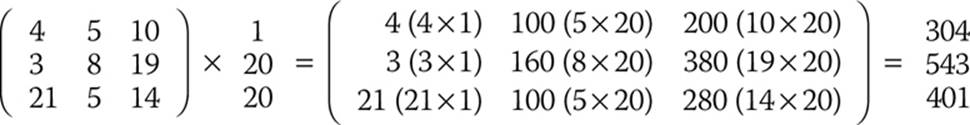
That resulting vector (304, 543, 401) has to be mod 26, which produces

Next, you convert these numbers back to letters. The letters ATT in plain text encrypts to TXM (if we assume a = 1). Repeat this process for each block of letters until the entire message is encrypted. To decrypt a message, you need to convert the letters of the cipher text back to numbers, and then, taking blocks of cipher text, multiply them by the inverse of the key matrix.

ADFGX and ADFGVX Ciphers

The ADFGVX cipher is an improvement on a previous cipher, the ADFGX. We will look at both ciphers.

ADFGVX was invented by Colonel Fritz Nebel in 1918 and was used by the German Army during World War I. It is essentially a modified Polybius square combined with a columnar transposition. (Recall from Chapter 1 that you can combine ciphers to create a new cipher.) It is interesting to note that ADFGVX was designed to work well when transmitted by Morse code.

Let us start by examining the first cipher, the ADFGX cipher.

First, create a modified Polybius square. Rather than number coordinates, however, the letters A, D, F, G, and X are used (the letter V is not used to create the modified Polybius square).

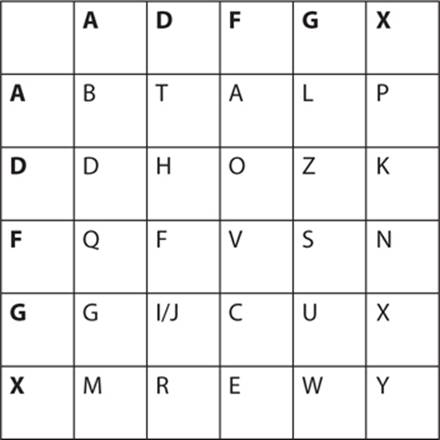
Notice that the letters are not in alphabetic order in the Polybius square. This is a common variation to help make the cipher more secure. Again, the letters I and J are combined in one square.

The next step is to encrypt the message using this modified Polybius square. Let’s assume the message is Attack at dawn. As with the traditional Polybius square, each letter is represented by its coordinates, in this case by two letters:

Next, you write out the message in columns under some keyword; let’s again use falcon as our keyword:

Next, we re-sort the columns after rearranging the letters of the keyword in alphabetic order, so FALCON becomes ACFLNO, like so:

To create cipher text, write down each column in sequence:

Obviously, you can use any transposition keyword of any size. In practice, longer keywords were frequently used to make the ciphers more secure.

In 1918, the ADFGX cipher was expanded to add the letter V, making a 6-by-6 cipher, which allowed for all 26 letters of the English alphabet (no need to combine I and J) and the digits 0 to 9. Otherwise, the ADFGVX works exactly the same as the ADFGX cipher.

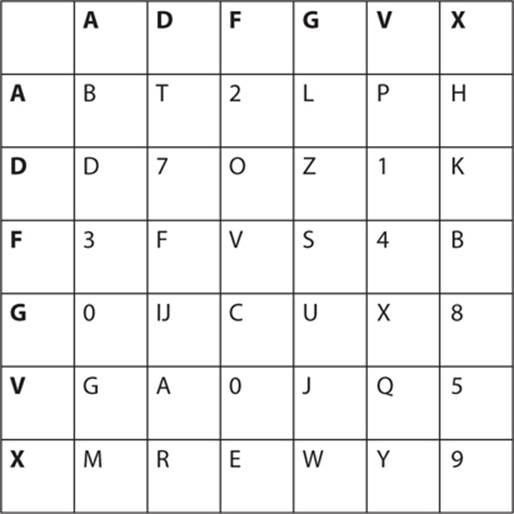
Compared to various classical ciphers, and prior to the computer age, the ADFGVX was a very strong cipher and difficult to break. A French army officer, Lieutenant Georges Painvin, worked on analyzing this cipher and was eventually able to break it. However, his method required large amounts of cipher text to cryptanalyze. This was a forerunner to modern cipher text–only attacks that we will examine in Chapter 17.

Bifid Cipher

The bifid cipher is another cipher that combines the Polybius square with a transposition cipher. It was invented in 1901 by Félix Delastelle (who also created the four-square cipher, discussed earlier in the chapter).

The first step is, of course, to create a Polybius square, as shown here:

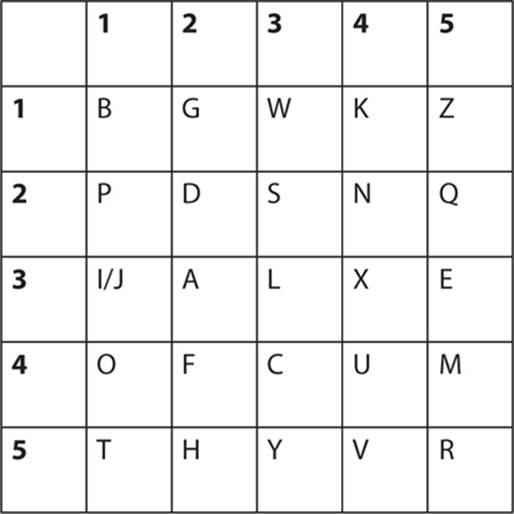
As you can see, the letters in the square are not necessarily in alphabetical order.

The coordinates are written down, as with the traditional Polybius cipher, except each coordinate is written vertically in a column. With this cipher, the phrase Attack at dawn is written in 12 columns in two rows, like so:

When the numbers are spread out, much like a rail fence cipher, you create the following stream of numbers:

Next, those numbers are paired and converted back to letters:

To decrypt a message, the process is reversed.

Gronsfeld Cipher

The Gronsfeld cipher is a variant of the Vigenère cipher discussed in Chapter 1. It uses 10 different alphabet orderings that correspond to the numbers 0 to 9. The numbers can be picked at random, which is more secure but more difficult to remember, unless the numbers had some significance to the sender and recipient.

For this cipher, you select each letter of plain text and substitute it for the cipher text corresponding to the appropriate alphabet. So you’d use alphabet 0 for the first letter, then alphabet 1 for the next letter, then alphabet 2, and so on. After you use alphabet 9, you start over with alphabet 0.

To encrypt the plain text Attack at dawn, you find the letter corresponding to A in alphabet 0, yielding A as the cipher text. Then you find the letter corresponding to T in alphabet 1, yielding U as the cipher text. Then you find the second T, and the third alphabet (alphabet 2) yields V. Continuing this process move down the rows of alphabets until

is encrypted as

As an interesting historical note, as late as 1892, the Gronsfeld cipher was still being used: the French government arrested several anarchists who were using it for communications.

Vernam Cipher

The Vernam cipher is a one-time pad cipher, in which the plain text is somehow altered by a random string of data so that the resulting cipher text is truly random. Gilbert Vernam (1890–1960) first proposed a stream cipher that would be used with teleprinters (teletype machines). It would combine character-by-character a prepared key that was stored on a paper tape, with the characters of the plain text used to produce the cipher text. The recipient would apply the same key to read the plain text.

In 1919, Vernam patented his idea (U.S. Patent 1,310,719). In Vernam’s method he used the binary XOR (exclusive OR) operation applied to the bits of the message. (We will be examining binary operations, including XOR, in Chapter 3.) (Note that Vernam also patented three other cryptographic inventions: U.S. Patent 1,416,765; U.S. Patent 1,584,749; and U.S. Patent 1,613,686.)

To be a true one-time pad, by modern standards, a cipher needs two properties. The first is suggested by the name: the key is used only once. After a message is enciphered with a particular key, that key is never used again. This makes the one-time pad quite secure, but it is also very impractical for ongoing communications, such as those encountered in modern e-commerce. The second property is that the key be as long as the message, which prevents any patterns from emerging in the cipher text.

Note

One-time pads are used for communications today, but only for the most sensitive communications. The keys must be stored in a secure location, such as a safe, and used only once for very critical messages. The keys for modern one-time pads are simply strings of random numbers sufficiently large enough to account for whatever message might be sent.

Edgar Allen Poe

Although Edgar Allen Poe is most known for his literary works, he also was an accomplished amateur cryptographer. In 1841, Poe wrote an essay entitled “A Few Words on Secret Writing” that was published in Graham’s Magazine. In addition, in his short story “The Gold-Bug,” cryptography plays a central role in the plot. Poe is not known to have researched cryptography, nor did he create any ciphers, but he did play a key role in increasing public interest in the field of cryptography. In fact, cryptographer William Friedman (1891–1969) credited his interest in cryptography to Poe’s “The Gold-Bug.” Friedman was the director of research for the Army Signals Intelligence Service in the 1930s and is credited with coining the term cryptanalysis.

In December 1839, Poe published a challenge in the Philadelphia periodical Alexander’s Weekly Messenger. In that challenge, he stated that he could solve any single-substitution cipher than readers could submit. His challenge stated

It would be by no means a labor lost to show how great a degree of rigid method enters into enigma-guessing. This may sound oddly; but it is not more strange than the well known fact that rules really exist, by means of which it is easy to decipher any species of hieroglyphical writing—that is to say writing where, in place of alphabetical letters, any kind of marks are made use of at random. For example, in place of A put % or any other arbitrary character—in place of B, a *, etc., etc. Let an entire alphabet be made in this manner, and then let this alphabet be used in any piece of writing. This writing can be read by means of a proper method. Let this be put to the test. Let any one address us a letter in this way, and we pledge ourselves to read it forthwith—however unusual or arbitrary may be the characters employed.¹

From December 1839 to May 1840, Poe was able to solve all the ciphers that readers submitted—except one. Since that time, however, various analysts have determined that this cipher was simply a set of random characters and not a legitimate example of cipher text.

Cryptography Comes of Age

The various ciphers used in the 19th through the early 20th centuries were certainly more complex than the ciphers of earlier times. However, they were still ciphers that could be decrypted manually, with pencil and paper. The 20th century moved cryptography toward encryption related to devices and alternative methods of encryption.

Enigma

Contrary to popular misconceptions, the Enigma is not a single machine, but a family of machines. The first version was invented by German engineer Arthur Scherbius near the end of World War I. It was also used by several different militaries, not only the Nazi Germans.

Some military texts encrypted using a version of Enigma were broken by Polish cryptanalysts Marian Rejewski, Jerzy Różycki, and Henryk Zygalski. The three basically reverse-engineered a working Enigma machine and then developed tools for breaking Enigma ciphers, including one tool called the cryptologic bomb.

The rotors were the core of the Enigma machine—disks that included 26 letters arranged in a circle, with several rotors aligned with one another. Essentially, each rotor represented a different single-substitution cipher—you can think of the Enigma as a sort of mechanical poly-alphabet cipher. After the operator was given a message in plain text, he typed the message into the Enigma. For each letter that was typed in, Enigma would provide a different cipher text based on a different substitution alphabet. The recipient would type in the cipher text to retrieve the plain text, but only if both Enigma machines had the same rotor settings. Figure 2-1 shows an Enigma machine.

FIGURE 2-1 An Enigma machine

Enigma Variations

The Enigma models included several variations:

Enigma A, the first public Enigma

Enigma B

Enigma C

Enigma B, used by United Kingdom, Japan, Sweden, and others

Navy Cipher D, used by the Italian Navy

Funkschlüssel C, used by the German Navy beginning in 1926

Enigma G, used by the German Army

Wehrmacht Enigma I, a modification to the Enigma G, used extensively by the German military

M3, an improved Enigma introduced in 1930 for the German military

Other systems were either derived from Enigma or were similar in concept, including the Japanese system codenamed GREEN by American cryptographers, the SIGABA system, NEMA, and others.

Alan Turing

I cannot tell the story of Enigma without at least mentioning Alan Turing, who is famous for leading the team that was able to crack the Enigma version used by the German Navy during World War II—a story that has been immortalized in the book Alan Turing: The Enigma and the movieThe Imitation Game. During World War II, Turing worked for the Government Code and Cipher School that operated out of Bletchley Park, located 50 miles northwest of London. The mansion and 58 acres were purchased by MI6 (British Intelligence) for use by the Code and Cipher School. A number of prominent people worked at Bletchley Park, including mathematicians Derek Taunt and Max Newman, and chess champion Hugh Alexander.

Turing’s impact on the field of cryptography is profound. He led the British team responsible for attempting to break the German naval Enigma. He worked to improve the pre-war Polish machine that would find Enigma settings. He was successful, and MI6 was able to decipher German naval messages. This work was considered highly classified. They feared that if the Germans realized that the Enigma had been compromised, they would change how they communicated. So intelligence gathered via Turing’s team was kept a closely guarded secret, and when it needed to be shared with others (such as military commanders), a cover story was given to account for the source of the information. Many sources claim that Turing’s work at Bletchley Park shortened the war by at least two years, saving millions of lives.

Note

Alan Turing was a mathematician and an accomplished marathon runner as well. He also was a key figure in the development of computer science. Among his most notable achievements, he developed a test to determine if a machine was indeed sentient—that test is known as the Turing Test.

The work at Bletchley Park was kept in strict secrecy, but in the decades since the war, many details have been declassified and are now available to the public. Turing’s team was by no means the only team working at Bletchley Park. Various “huts,” or buildings, on the grounds were used for various purposes. Turing and his team worked on the Naval Enigma in Hut 8. In Hut 6, a team worked on the Army and Air Force Enigmas. Hut 7 concentrated on Japanese codes and intelligence. Other huts were used for intelligence work and support work (such as communications and engineering), and Hut 2 was a recreational hut where the workers at Bletchley could enjoy beer, tea, and relaxation.

The work at Hut 8 centered on use of a bombe, an electromechanical device that helped to determine what settings the Enigma machine was using. The initial design used at Bletchley was created by Turing and later refined by others such as Gordon Welchman, a British mathematician.

The work at Bletchley was kept top secret, and much of the equipment and documents were destroyed at the end of the war. Even close relatives did not know what their family at Bletchley worked on. Today it is home to a museum with extensive displays of cryptography history, including Enigma machines.

SIGABA

SIGABA was an encryption machine used by the U.S. military from World War II through the 1950s. The machine, a joint effort of the U.S. Army and Navy, was developed specifically to overcome weaknesses found in other rotor systems, such as Enigma. You can find detailed specifications for this machine today, but some of the operating principles remained classified until the year 2000. SIGABA was patented (6,175,625), filed on December 15, 1944, but the patent remained classified until 2001. Figure 2-2 shows a picture of a SIGABA machine.

FIGURE 2-2 SIGABA machine

Several similar devices were used during the mid-20th century, including the British Air Ministry device Mercury, used in the early 1960s. Mercury was designed by E.W. Smith and F. Rudd and was in wide use in the British military by 1950. Other rotor-based machines were in wide use, including the M-325, or SIGFOY (U.S. Patent 2,877,565), which was used in the early 1940s by the U.S. Foreign Service. The French government also used a rotor machine in the 1950s, the HX-63, which was designed by a Swiss communications equipment manufacturer, Crypto AG. In the 1940s the U.S. Army used a device known as M-228, or SIGCUM, to encrypt communications. This device was designed by William Friedman, who later served as director of research for the Army Signals Intelligence Service.

Lorenz Cipher

The Lorenz cipher is actually a group of three machines—SZ40, SZ42A, and SZ42B—that were used by the German Army during World War II. These machines were rotor stream cipher machines. They were attached to standard teleprinters to encrypt and decrypt messages sent via teleprinter.

Navajo Code Talkers

Although code talkers are not considered ciphers, they are important to include in any history of cryptography. Phillip Johnston was raised on a Navajo reservation and was one of the few non-Navajo people who spoke the Navajo language. At the beginning of World War II, he proposed to the U.S. Marine Corps that the Navajo language be used to encode important tactical messages—very few non-Navajo knew the language, and it was an unwritten language, making it difficult for someone to learn it.

Johnston’s system was tested and proved that Navajo men could encode, transmit, and decode a three-line message in 20 seconds or less. Time was a critical factor—the machines being used at the time required 30 seconds for the same steps to be accomplished, and in the heat of battle, time is of the essence.

In both World Wars I and II, hundreds of Navajo code talkers were used for secure communications by the U.S. military, specifically by the Marines in World War I. Indigenous code talking was pioneered by Cherokee and Choctaw code talkers during World War I.

IFF Systems

Identify Friend or Foe, or IFF, was developed during World War II. These systems allowed a friendly aircraft to be identified and thus differentiated from an enemy, or foe. As aircraft have become faster and missile systems reach further, waiting for visual confirmation of friend or foe status is no longer feasible. Most modern systems use cryptographic functions to identify friendly aircraft.

Britain was the first to work out an IFF system. The most primitive of these systems simply sent a prearranged signal at specific intervals. With the advent of radar, it was important to identify what aircraft the radar system had detected. The IFF Mark I was first used in 1939. It was an active transponder that would receive a query (called an interrogation) from the radar system. The query consisted of a distinctive pulse using a specific frequency. The transponder would then respond with a signal that used a steadily increasing amplitude, thus identifying the aircraft as friendly.

By 1940, the Mark III was in use by Western Allies and continued to be used throughout World War II. The Mark III expanded the types of communications that could be accomplished, including a coded Mayday response.

In Germany, IFF systems were also being developed. The first widely implemented system was the FuG 25a. Before a plane took off, two mechanical keys were inserted, each with 10 bits. These provided the keys to encode the IFF transmissions. British scientists, however, were able to build a device that would trigger a response from any FuG 25a system within range, thus revealing the position of German planes flying at night.

Since World War II, IFF systems have been used for a variety of purposes, operating in four primary modes:

Mode 1 is not secure and is used to track the position of aircraft and ships.

Mode 2 is used for landings on aircraft carriers.

Mode 3 is a standard system used by commercial (non-military) aircraft around the world to communicate their position for air traffic control.

Mode 4 is encrypted and thus secure.

In modern times, secure IFF systems are a part of military air defense operations. Cryptography is critical in ensuring that these systems are secure and reliable.² In some cases, the cryptographic key used is changed daily. These systems represent one very practical application of cryptography, whose primary goal is to ensure that friendly aircraft are not shot down.

The NSA: The Early Years

It is impossible to discuss the history of cryptography without including the history of the U.S. National Security Agency (NSA). A large organization, the NSA is often reported to be the single largest employer of mathematicians in the world. The history of cryptography in the latter half of the 20th century, and beyond, is closely intertwined with the history of the NSA.

Although the NSA formally was founded in 1952, it had many precursors. As early as 1919, the U.S. Department of State created the Cipher Bureau, often simply called the “Black Chamber,” which operated in an office in Manhattan. Its main purpose was to crack communications of foreign governments. The operation persuaded Western Union to allow it to monitor telegraphs transmitted by Western Union customers. Although the group had significant initial successes, it was shut down in 1929 by Secretary of State Henry Stimson, who felt that spying was not a gentlemanly or honorable activity.

In 1924, the U.S. Navy formed its Radio Intelligence office with the purpose of developing intelligence from monitoring radio communications. By 1942, the U.S. Army renamed its Signal Intelligence Service to Signal Security Service. At this time, each military branch had its own initiatives on communications, radio intelligence, and cryptography, and cooperation was at a minimum.

In 1949, various military agencies coordinated cryptology activities with a new, centralized organization named the Armed Forces Security Agency, which was part of the Department of Defense rather than a specific branch of the military. In 1951, President Harry Truman set up a panel to investigate the shortcomings of the AFSA, including its failure to predict the outbreak of the Korean War. From this investigation came the National Security Agency. President Truman issued a classified directive entitled “Communications Intelligence Activities” that, among other things, established the NSA.

For much of its early history, the existence of the NSA was not acknowledged, and those who did know of it jokingly referred to the NSA as “No Such Agency.” Obviously, the history of any intelligence agency is not completely public, but let’s examine some highlights that are.

After World War II, Soviet encryption was unbreakable and thus posed a significant issue for U.S. intelligence agencies. This fact, coupled with the discovery of Soviet spies in various western governments, led to a renewed emphasis on signals intelligence (SIGINT) and cryptanalysis.

The NSA had two primary roles, the first being to monitor and decipher the communications of other nations to gather important intelligence. The second role was the protection of U.S. communications from other eavesdropping nations. This led the NSA to develop a standard now known as TEMPEST, an acronym for Transient Electromagnetic Pulse Emanation Standard. This standard applies both to equipment used and deployment and configuration of communications equipment.

During the Cold War, the NSA grew and had some significant successes. As one prominent example, in 1964 the NSA intercepted and decrypted communications regarding China’s first nuclear weapons test. There were many other important communications captured by the NSA, and some are still classified today. In 2013, the Washington Times reported that NSA programs have foiled terrorist plots in more than 20 different countries.³

We will revisit the NSA in later chapters, particularly when we study modern cryptographic ciphers such as DES and AES in Chapters 6 and 7, and then when we discuss cryptographic backdoors in Chapter 18.

Conclusions

In this chapter you were introduced to more complex ciphers, many of which used tables and matrices to encrypt and decrypt text. You saw variations of the Polybius square you learned about in Chapter 1. The Hill cipher introduced you to the basics of matrix algebra, which you will see more of in Chapter 5. You also learned about contributions to cryptography made by historical figures such as Edgar Allen Poe and Allen Turing.

We examined some significant developments in the history of cryptography, including the famous Navajo code talkers and IFF systems that are critical to air traffic control and air defense. We ended the chapter with a discussion of the history of the National Security Agency and its impact on the history of cryptography.

Test Your Knowledge

A few questions are provided here to aid you in testing your knowledge before you proceed.

1. The __________ is based on using a matrix as the key and using n-letter groups.

2. Which of the following is a variation of Vigenère that uses ten alphabets, one for each decimal numeral 0 through 9?

A. Playfair

B. Hill

C. Bifid

D. Gronsfeld

3. What was Edgar Allen Poe’s main contribution to cryptography?

A. Popularizing cryptography

B. Creating the Hill cipher

C. Creating SIGABA

D. Breaking the Hill cipher

4. What did Alan Turing work on?

A. Breaking the German Naval Enigma

B. Breaking the German Army Enigma

C. Breaking all Enigma variations

D. Breaking the SIGABA system

5. The __________ cipher works by modifying a Polybius square. Rather than number coordinates, letters are used.

Answers

1. Hill cipher

2. D

3. A

4. A

5. ADFGVX

Endnotes

1. This citation was included in the article “Edgar Allen Poe and Cryptography,” by R. Morelli, at www.cs.trincoll.edu/~crypto/historical/poe.html.

2. In 2009, General Dynamics awarded a $37 million contract for a modern IFF system: www.generaldynamics.com/news/press-releases/detail.cfm?customel_dataPageID_1811=6123. In addition, a paper written in 2010 by E.A. El-Badawy, W.A. El-Masry, M.A Mokhtar, and A.S. Hafez, “A secured chaos encrypted mode-S aircraft identification friend or foe (IFF) system” (DOI 10.1109/ICSPCS.2010.5709756), discussed a new technique for IFF.

3. Kimberly Dozier, “NSA programs broke plots in 20 nations,” www.washingtontimes.com/news/2013/jun/16/nsa-programs-broke-plots-20-nations-officials/.