Modern Cryptography: Applied Mathematics for Encryption and Informanion Security (2016)

PART I. Foundations

Chapter 3. Basic Information Theory

In this chapter we will cover the following:

Information theory basics

Claude Shannon’s theorems

Information entropy

Confusing and diffusion

Hamming distance and hamming weight

Scientific and mathematical theories

Binary math

In this chapter we are going to explore the fundamentals of information theory, which is very important to modern cryptography. Of course, entire books have been written on the topic, so in this chapter we’ll provide just enough information to help you understand the cryptography we will discuss in subsequent chapters. For some readers, this will be a review. We will also explore the essentials of mathematical and scientific theories. This chapter also provides an introduction to basic binary mathematics, which should be a review for most readers.

Although information theory is relevant to cryptography, that is not the only application of information theory. At its core, information theory is about quantifying information. This will involve understanding how to code information, information compression, information transmission, and information security (that is, cryptography).

The Information Age

It is often stated that we live in the “information age.” This would clearly make information theory pertinent not only to understanding cryptography, but also to understanding modern society. First, however, we must be clear on what is meant by the phrase “information age.” To a great extent, the information age and the digital age go hand-in-hand. Some might argue the degree of overlap, but it is definitely the case that without modern computers, the information age would be significantly stifled. Claude Shannon, who is considered the father of information theory, wrote his famous paper, “A Mathematical Theory of Communication,” in 1948—long before digital computers even existed.

From one perspective, the information age is marked by the information itself, which has become a primary commodity. Obviously, information has always been of value, but it was historically just a means to a more concrete end. For example, even prehistoric people needed information, such as locations for finding food and game. However, that information was peripheral to the tangible commodity of food. In this example, the food was the goal—the actual commodity. In the information age, the information itself is the commodity.

If you reflect on this even briefly, I think you will concur that in modern times information itself is a product. Consider, for example, this book you now hold in your hands. Certainly the paper and ink used was not worth the price of the book. It is the information encoded on the pages that you pay for. In fact, you may have an electronic copy and not actually have purchased any pages and ink at all. If you are reading this book as part of a class, you paid tuition for the class. The commodity you purchased was the information transmitted to you by the professor or instructor (and, of course, augmented by the information in this book). So, clearly, information as a commodity can exist separately from computer technology. The efficient and effective transmission and storage of information, however, requires computer technology.

Yet another perspective on the information age is the proliferation of information. Just a few decades ago, news meant a daily paper, or perhaps a 30-minute evening news broadcast. Now news is 24 hours a day on several cable channels and on various Internet sites. In my own childhood, research meant going to the local library and consulting a limited number of books that were, hopefully, not more than ten years out of date. Now, with the click of a mouse button, you have access to scholarly journals, research web sites, almanacs, dictionaries, encyclopedias—an avalanche of information. So we could view the information age as the age in which most people have ready access to a wide range of information.

Younger readers who have grown up with the Internet and cell phones and who have been immersed in a sea of instant information may not fully comprehend how much information has exploded. Once you appreciate the magnitude of the information explosion, the more you can fully appreciate the need for information theory. To give you some perspective on just how much information is being transmitted and consumed in our modern civilization, consider the following facts: As early as 2003, experts estimated that humanity had accumulated a little over 12 exabytes of data during the entire course of human history. Modern media, such as magnetic storage, print, and film, had produced 5 exabytes in just the first two years of the 21st century. In 2009, researchers claim that in a single year, Americans consumed more than 3 zettabytes of information.¹ As of 2013, the World Wide Web is said to hold 4 zettabytes, or 4,000 exabytes, of data.

Measuring Data

Such large numbers can be difficult to comprehend. Most readers understand kilobytes, megabytes, and gigabytes, but you may not be as familiar with larger sizes. Here are the various sizes of data:

Kilobyte = 1000 bytes

Megabyte = 1,000,000 bytes

Gigabyte = 1,000,000,000 bytes

Terabyte = 1,000,000,000,000 bytes

Petabyte = 1,000,000,000,000,000 bytes

Exabyte = 1,000,000,000,000,000,000 bytes

Zettabyte = 1,000,000,000,000,000,000,000 bytes

These incredible scales of data can be daunting to grasp but should give you an idea as to why information theory is so important. It should also clearly demonstrate that whether you measure data by the amount of information we access, or the fact that we value information itself as a commodity, we are truly in the Information Age.

Claude Shannon

It is impossible to discuss information theory thoroughly without including Claude Shannon, who is often called the “father of information theory.” He was a mathematician and engineer who lived from April 30, 1916, until February, 24, 2001. He did a lot of work on electrical applications of mathematics and on cryptanalysis. His research interests included using Boolean algebra (we will discuss various algebras at length in Chapter 5) and binary math (which we will introduce you to later in this chapter) in conjunction with electrical relays. This use of electrical switches working with binary numbers and Boolean algebra is the basis of digital computers.

Note

During World War II, Shannon worked for Bell Labs on defense applications. Part of his work involved cryptography and cryptanalysis. It should be no surprise that his most famous work, information theory, has been applied to modern developments in cryptography. In 1943, Shannon became acquainted with Alan Turing, whom we discussed in Chapter 2. Turing was in the United States to work with the U.S. Navy’s cryptanalysis efforts, sharing with the United States some of the methods that the British had developed.

Information theory was introduced by Shannon in 1948 with the publication of his article “A Mathematical Theory of Communication.” He was interested in information, specifically in relation to signal processing operations. Information theory now encompasses the entire field of quantifying, storing, transmitting, and securing information. Shannon’s landmark paper was expanded into a book entitled The Mathematical Theory of Communication, which he co-authored with Warren Weaver.

In his original paper, Shannon laid out some basic concepts that might seem very elementary today, particularly for those readers with engineering or mathematics backgrounds. At the time, however, no one had ever attempted to quantify information or the process of communicating information. The relevant concepts he outlined are provided here with a brief explanation of their significance to cryptography:

An information source produces a message. This is perhaps the most elementary concept Shannon developed. There must be some source that produces a given message. In reference to cryptography, that source takes plain text and applies some cipher to create cipher text.

A transmitter operates on the message to create a signal that can be sent through a channel. A great deal of Shannon’s work was about the transmitter and channel, the mechanisms that send a message—in our case an encrypted message—to its destination.

A channel is the medium over which the signal carrying the information that composes the message is sent. Modern cryptographic communications often take place over the Internet. However, encrypted radio and voice transmissions are often used. In Chapter 2, you were introduced to Identify Friend or Foe (IFF) systems.

A receiver transforms the signal back into the message intended for delivery. For our purposes, the receiver will also decrypt the message, producing plain text from the cipher text that is received.

A destination can be a person or a machine for whom or which the message is intended. This is relatively straightforward. As you might suspect, sometimes the receiver and destination are one and the same.

Information entropy is a concept that was very new with Shannon’s paper, and it’s one we delve into in a separate section of this chapter.

In addition to these concepts, Shannon also developed some general theorems that are important to communicating information. Some of this information applies primarily to electronic communications, but it does have relevance to cryptography.

Theorem 1: Shannon’s Source Coding Theorem

It is impossible to compress the data such that the code rate is less than the Shannon entropy of the source, without it being virtually certain that information will be lost.

In information theory, entropy is a measure of the uncertainty associated with a random variable. We will discuss this in detail later in this chapter. This theorem states that if you compress data in a way that the rate of coding is less than the information content, then it is very likely that you will lose some information. It is frequently the case that messages are both encrypted and compressed. Compression is used to reduce transmission time and bandwidth. Shannon’s coding theorem is important when compressing data.

Theorem 2: Noisy Channel Theorem

For any given degree of noise contamination of a communication channel, it is possible to communicate discrete data (digital information) nearly error-free up to a computable maximum rate through the channel.

This theorem addresses the issue of noise on a given channel. Whether it be a radio signal or a network signal traveling through a twisted pair cable, noise is usually involved in signal transmission. This theorem essentially states that even if there is noise, you can communicate digital information. However, there is some maximum rate at which you can compute information, and that rate is computable and is related to how much noise there is in the channel.

Core Concepts of Cryptography

Some key concepts of information theory are absolutely pivotal in your study of cryptography. You have been given a brief overview of information theory and those concepts have some relevance to cryptography. In this section, you will learn core concepts that are essential to cryptography.

Information Entropy

Shannon thought information entropy was a critical topic in information theory. His landmark paper included an entire section entitled “Choice, Uncertainty and Entropy” that rigorously explored this topic. Here we’ll cover just enough about information entropy for you to move forward in your study of cryptography.

Entropy has a different meaning in information theory than it does in physics. In the context of information, entropy is a way of measuring information content. People often encounter two difficulties in mastering this concept. The first difficulty lies in confusing information entropy with the thermodynamic entropy that you may have encountered in elementary physics courses. In such courses, entropy is often described as “the measure of disorder in a system.” This is usually followed by a discussion of the second law of thermodynamics, which states that “in a closed system, entropy tends to increase.” In other words, without the addition of energy, a close system will become more disordered over time. Before you can understand information entropy, however, you need to firmly understand that information entropy and thermodynamic entropy are not the same thing. So you can take the entropy definition you received in freshman physics courses and put it out of your mind—at least for the time being.

The second problem you might have with understanding information theory is that many references define the concept in different ways, some of which can seem contradictory. In this section, I will demonstrate some of the common ways that information entropy is described so that you can gain a complete understanding of these seemingly disparate explanations.

In information theory, entropy is the amount of information in a given message. This is simple, easy to understand, and, as you will see, essentially synonymous with other definitions you may encounter. Information entropy is sometimes described as “the number of bits required to communicate information.” So if you wish to communicate a message that contains information, if you represent the information in binary format, entropy is how many bits of information the message contains. It is entirely possible that a message might contain some redundancy, or even data you already have (which, by definition, would not be information); thus the number of bits required to communicate information could be less than the total bits in the message.

Note

This is actually the basis for lossless data compression. Lossless data compression seeks to remove redundancy in a message to compress the message. The first step is to determine the minimum number of bits required to communicate the information in the message—or, put another way, to calculate the information entropy.

Many texts describe entropy as “the measure of uncertainty in a message.” You may be wondering, how can both of these definitions be true? Actually, they are both saying the same thing, as I’ll explain.

Let’s examine the definition that is most likely causing you some consternation: entropy as a measure of uncertainty. It might help you to think of it in the following manner: only uncertainty can provide information. For example, if I tell you that right now you are reading this book, this does not provide you with any new information. You already knew that, and there was absolutely zero uncertainty regarding that issue. However, the content you are about to read in remaining chapters is uncertain, and you don’t know what you will encounter—at least, not exactly. There is, therefore, some level of uncertainty, and thus information content. Put even more directly, uncertainty is information. If you are already certain about a given fact, no information is communicated to you. New information clearly requires uncertainty that the information you received cleared up. Thus, the measure of uncertainty in a message is the measure of information in a message.

Now let’s move to a more mathematical expression of this concept. Let’s assume X is some random variable. The amount of entropy measured in bits that X is associated with is usually denoted by H(X). We’ll further assume that X is the answer to a simple yes or no question. If you already know the answer, then there is no information. It is the uncertainty of the value of X that provides information. Put mathematically, if you already know the outcome, then H(X) = 0. If you do not know the outcome, you will get 1 bit of information from this variable X. That bit could be a 1 (a yes) or a 0 (a no) so H(X) = 1.

Hopefully, you now have a good grasp of the concept of information entropy, so let’s try to make it more formal and include the concept of probability.

Note

I am purposefully avoiding a rigorous discussion of probability here. At some point in your cryptographic studies, you’ll find it wise to take a rigorous statistics course. However, that is not necessary to understand the fundamentals of cryptography.

What is the information content of a variable X? First, we know X has some number of possible values; we will call that number n. With a binary variable that is 1 single bit, then n = 2 (values 0 or 1). However, if you have more than 1 bit, then you have n > 2. For example, 2 bits has n = 2². Let’s consider each possible value of X to be i. Of course, all possible values of X might not have the same probability, and some might be more likely than others. For example, if X is a variable giving the height of your next-door neighbor in inches, a value of 69 (5 feet 9 inches) is a lot more probable than a value of 89 (7 feet 5 inches). So consider the probability of each given i to be P_i. Now we can write an equation that will provide the entropy (that is, the information contained) in the variable X, taking into account the probabilities of individual values of X. That equation is shown in Figure 3-1.

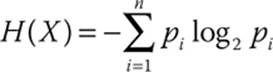
FIGURE 3-1 The information entropy of X

As stated earlier in this chapter, we won’t be examining proofs in this text. In fact, for our purposes, you can simply accept the math as a given. A number of excellent mathematics books and courses delve into the proofs for these topics. The equation shown in Figure 3-1 provides a way of calculating the information contained in (that is, the information entropy) of some variable X, assuming you know the probabilities of each possible value of X. If you do not know those probabilities, you can still get at least a range for the information contained in X with the equation shown in Figure 3-2.

FIGURE 3-2 Range of information contained in X

This equation assumes that there is some information, or some level of uncertainty, so we set the lower range at greater than zero. Hopefully, this gives you a clear understanding of the concept of information entropy.

In addition to information entropy are a few closely related concepts that you should understand:

Joint entropy This is the entropy of two variables or two messages. If the two messages are truly independent, their joint entropy is just the sum of the two entropies. Here is the equation:

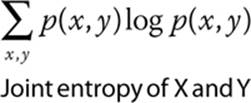
Conditional entropy If the two variables are not independent, but rather variable Y depends on variable X, then instead of joint entropy you have conditional entropy.

Differential entropy This is a more complex topic and involves extending Shannon’s concept of entropy to cover continuous random variables, rather than discrete random variables. The equation for differential entropy is shown next:

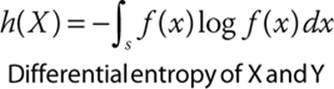
The basic concept of information entropy, often called Shannon entropy, is essential to cryptography, and you will encounter it later in this book. Joint entropy and differential entropy are more advanced topics and are introduced here for readers who want to delve deeper, beyond the scope of this book.

Quantifying Information

Understanding information entropy is essential to your understanding of how we quantify information. If you have any doubts about your understanding of entropy, please reread the preceding section before moving on. Quantifying information can be a difficult task. For those new to information theory, even understanding what is meant by “quantifying information” can be daunting. Usually it is done in the context of binary information (bits). In fact, although you can find many different definitions for what information is, within the context of information theory, we look at information as bits of data. This works nicely with computer science, since computers store data as bits. A bit can have only one of two values: 0 or 1, which can be equivalent to yes or no. Of course, several bits together can contain several yes or no values, thus accumulating more information.

Once we have defined information as a single bit of data, the next issue becomes quantifying that data. One method often used to explain the concept is to imagine how many guesses it would take to ascertain the contents of a sealed envelope. Let me walk you through this helpful thought experiment.

Suppose someone hands you a sealed envelope that contains a message. You are not allowed to open the envelope. Instead, you have to ascertain the contents merely by asking a series of yes or no questions (binary information: 1 being yes, 0 being no). What is the smallest number of questions required to identify the contents of the enclosed message accurately?

Notice that the scenario is “how many questions, on average, will it take?” Clearly, if you try the same scenario with different people posing the queries, even with the same message, you will get a different number of questions needed. The game could be repeated with different messages. We can enumerate messages, with any given message as M_i and the probability of getting that particular message as P_i. This leaves us with the question of what, exactly, is the probability of guessing a specific message. The actual equation takes us back to Figure 3-1. Computing the entropy of a given message is quantifying the information content of that message.

Confusion and Diffusion

The concept of confusion, as relates to cryptography, was outlined in Shannon’s 1948 paper. In general, this concept attempts to make the relationship between the statistical frequencies of the cipher text and the actual key as complex as possible. Put another way, the relationship between the plain text, cipher text, and the key should be complex enough that it is not easy to determine what that relationship is.

If you don’t have sufficient confusion, then someone could simply examine a copy of plain text and the associated cipher text and determine what the key is. This would allow the person to decipher all other messages that are encrypted with that same key.

Diffusion literally means “having changes to one character in the plain text affect multiple characters in the cipher text.” This is unlike historical algorithms (such as the Caesar cipher, Atbash, and Vigenère), where each plain text character affected only one cipher text character.

Shannon thought the related concepts of confusion and diffusion were both needed to create an effective cipher:

Two methods (other than recourse to ideal systems) suggest themselves for frustrating a statistical analysis. These we may call the methods of diffusion and confusion. In the method of diffusion the statistical structure of M which leads to its redundancy is “dissipated” into long range statistics—i.e., into statistical structure involving long combinations of letters in the cryptogram. The effect here is that the enemy must intercept a tremendous amount of material to tie down this structure, since the structure is evident only in blocks of very small individual probability. Furthermore, even when he has sufficient material, the analytical work required is much greater since the redundancy has been diffused over a large number of individual statistics.²

These two goals are achieved through a complex series of substitution and permutation. Although the historic ciphers you studied in Chapters 1 and 2 are not secure enough to withstand modern cryptanalysis, we can make an example using them. Let’s assume you have a simple Caesar cipher in which you shift each letter three to the right. This will provide a small degree of confusion, but no diffusion. Now assume you swap every three letters. This transposition will provide another small degree of confusion. Next, let’s apply a second substitution—this time two letters to the right. The two substitutions, separated by a transposition, provide minimal diffusion. Consider the following example:

Let’s try changing just one letter of plain text (though it will make for a misspelled plain text word). Change attack at dawn to attack an dawn:

Now compare this cipher text to the one originally produced. You can see that only one letter has changed—the last letter—and instead of sfy you now have sfs. This provides only minimal confusion and still no diffusion! What is missing? Two things: The first is that, at least by modern standards, this simply is not complex enough. It is certainly an improvement on the basic Caesar cipher, but still it is not enough. The second problem is that there is no mechanism to have a change in one character of plain text change multiple characters in the cipher text. In modern ciphers, operations are at the bit level, not the character level. Furthermore, in modern ciphers, there are mechanisms to propagate a change, and we will see those beginning in Chapter 6. However, this example should give you the general idea of combining substitution and permutation.

Avalanche

A small change can yield a large effect in the output, like an avalanche. This is Horst Fiestel’s variation on Shannon’s concept of diffusion. Fiestel’s ideas are used in many of the block ciphers we explore in Chapter 6. Obviously, a high avalanche impact is desirable in any cryptographic algorithm. Ideally, a change in 1 bit in the plain text would affect all the bits of the cipher text. This would be considered a complete avalanche, but that has not been achieved in any current algorithm.

Hamming Distance

The Hamming distance is the number of characters that are different between two strings. This can be expressed mathematically as follows:

h(x, y)

Hamming distance is used to measure the number of substitutions that would be required to turn one string into another. In modern cryptography, we usually deal with binary representations rather than text. In that context, Hamming distance can be defined as the number of 1’s if you exclusive or (XOR) two strings.

Note

The concept of Hamming distance was developed by Richard Hamming, who first described the concept in his paper “Error Detecting and Error Correcting Codes.” The concept is used widely in telecommunications, information theory, and cryptography.

Hamming distance works only when the strings being compared are of the same length. One application is to compare plain text to cipher text to determine how much has changed. However, if two strings of different lengths are compared, another metric must be used. One such metric is the Levenshtein distance, a measurement of the number of single-character edits required to change one word into another. Edits can include substitutions (as with Hamming distance) but can also include insertions and deletions. The Levenshtein distance was first described by Vladimir Levenshtein in 1965.

Hamming Weight

The concept of Hamming weight is closely related to Hamming distance. It is essentially comparing the string to a string of all 0’s. Put more simply, it is how many 1’s are in the binary representation of a message. Some sources call this the population count, or pop count. There are actually many applications for Hamming weight both within cryptography and in other fields. For example, the number of modular multiplications required for some exponent e is computed by log2 e + hamming weight (e). (You will see modular arithmetic in Chapter 4. Later in this book, when the RSA algorithm is examined at length, you will find that the e value in RSA is chosen due to low Hamming weight.)

Note

Richard Hamming was not the first to describe the concept of Hamming weight. The concept was first introduced by Irving S. Reed, though he used a different name. Hamming later described an almost identical concept to the one Reed had described, and this latter description was more widely known, thus the term Hamming weight.

Kerckhoffs’s Principle/Shannon’s Maxim

Kerckhoffs’s principle is an important concept in cryptography. Auguste Kerckhoffs’s first articulated this in the 1800s, stating that “the security of a cipher depends only on the secrecy of the key, not the secrecy of the algorithm.” Shannon rephrased this, stating that “One ought to design systems under the assumption that the enemy will ultimately gain full familiarity with them.”³ This is referred to as Shannon’s maxim and states essentially the same thing Kerckhoffs’s principle states.

Let me attempt to restate and expound this in terms you might find more verbose, but hopefully easier to understand. Both Kerckhoffs’s principle and Shannon’s maxim state that the only thing that you must keep secret is the key. You don’t need to keep the algorithm secret. In fact, in subsequent chapters, this book will provide intimate details of most modern algorithms, and that in no way compromises their security. As long as you keep your key secret, it does not matter that I know you are using AES 256 bit, or Serpent, or Blowfish, or any other algorithm you could think of.

I would add to Kerckhoffs’s principle/Shannon’s maxim something I will humbly call Easttom’s corollary:

You should be very wary of any cryptographic algorithm that has not been published and thoroughly reviewed. Only after extensive peer review should you consider the use of any cryptographic algorithm.

Consider that you have just created your own new algorithm. I mean no offense, but the most likely scenario is that you have mistaken ignorance for fresh perspective, and your algorithm has some serious flaw. You can find many examples on the Internet of amateur cryptographers believing they have invented some amazing new algorithm. Often their “discovery” is merely some permutation on the polyalphabetic ciphers you studied in Chapter 1. But even if you are an accomplished cryptographic researcher with a proven track record, it is still possible you could make an error.

To demonstrate this fact, consider Ron Rivest. You will hear a great deal about Dr. Rivest in coming chapters. His name is the R in RSA and he has been involved in other significant cryptographic developments. He submitted an algorithm to the SHA-3 competition (which we will discuss in detail in Chapter 9); however, after several months of additional analysis, a flaw was found and he withdrew his algorithm from consideration. If such a cryptographic luminary as Ron Rivest can make a mistake, certainly you can, too.

The purpose of publishing an algorithm is so that experts in the field can review it, examine it, and analyze it. This is the heart of the peer review process. Once an algorithm is published, other cryptographers get to examine it. If it withstands a significant amount of time (usually years) of such analysis, then and only then should it be considered for use.

Note

This issue has serious practical implications. In September 2011, I was interviewed by CNN Money reporter David Goldman regarding a company that claimed to have an “unbreakable code.” The reporter also interviewed cryptography experts from Symantec and Kaspersky labs. All of us agreed that the claim was nonsense. The algorithm was being kept “secret” and not open to peer review.

There is, of course one, very glaring exception to publishing an algorithm. The United States National Security Agency (NSA) organizes algorithms into two groups. The suite B group algorithms are published, which includes algorithms such as Advanced Encryption Standard (AES). You can find the complete details of that algorithm in many sources, including Chapter 7 of this book. The second group, the suite A algorithms, are classified and not published. This seems to violate the spirit of Kerckhoffs’s principle and peer review. However, keep in mind that the NSA is the single largest employer of mathematicians in the world, and this means that they can subject an algorithm to a thorough peer review entirely via their own internal staff, all of whom have clearance to view classified material.

Scientific and Mathematical Theories

We have discussed information theory, but we have not discussed what constitutes a theory within the scientific and mathematical world. Mathematics and science are closely related, but the processes are slightly different. We will examine and compare both in this section.

Many words can mean different things in specific situations. For example the word “bug” usually refers to an insect, but in computer programming it refers to a flaw in a program. Even a simple and common word such as “love” can mean different things in different situations. For example, you may “love” your favorite TV show, “love” your spouse, and “love” chocolate ice cream, but you probably don’t mean the same thing in each case. When you are attempting to define a term, it is important that you consider the context in which it is being used.

This is even truer when a word is being used in a specific technical or professional context. Various professions use very specific definitions for certain words. Consider the legal community, for example. Many words have very specific meanings within the context of law that might not exactly match their ordinary daily use.

It is also true that scientists as well as mathematicians have some very specific meanings for words they use. The term theory is such a word. This word has a very different meaning in a scientific context than it does in everyday language. In the day-to-day vernacular, a theory is often synonymous with a guess. For example, if your favorite sports team is on a losing streak, you might have a theory about why they are losing. And in this case, by theory you probably mean just a guess. You may or may not have a shred of data to support your theory. In fact it may be little more than a “gut feeling.”

In science and mathematics, however, a theory is not a guess or gut feeling—it is not even an educated guess. Theories in mathematics and science are actually closely related, as you will see.

What Is a Mathematical Theory?

Theories in math flow from axioms. An axiom is a single fact that is assumed to be true without proof. I think it should be obvious to all readers that only the most basic facts can be taken on an a priori basis as axioms.

There are a number of interesting math theories. For example, graph theory studies mathematical structures that represent objects and the relationships between them. It does this by using vertices (the objects) and edges (the connections between objects). Set theory studies collections of objects or sets. It governs combining sets, overlapping sets, subsets, and related topics.

Unlike science, mathematics deals with proofs rather than experiments. So the hypothesis that applies in the scientific process (discussed next) is not strictly applicable to mathematics. That is why we begin with axioms. The statements are derived from those axioms, and the veracity of those statements can be objectively determined. This is sometimes taught using truth tables.

Individual mathematical theories address a particular system. They begin with a foundation that is simply the data describing what is known or what is assumed (that is, axioms). New concepts are logically derived from this foundation and are (eventually) proven mathematically.

Formal mathematics courses will discuss first-order theories, syntactically consistent theories, deductive theories, and other nuances of mathematical theory. However, this book is focused on applied mathematics, and more narrowly on a single narrow subtopic in applied mathematics: cryptography. We won’t be delving into the subtleties of mathematical theory, and you won’t be exposed to proofs in this book. We will simply apply mathematics that others have rigorously proven.

The Scientific Process

The scientific process is primarily about experimentation. Nothing is really considered “true” until some experiment proves it is true. Usually, multiple experiments are needed to confirm that something is indeed true. The first step is to create a hypothesis—an educated guess that can be tested. Then facts are developed from that. The key part is that a hypothesis is a testable guess. In fact, a guess that is untestable has no place in science at all. Once you have tested your hypothesis you have a fact. The fact may be that the test results confirm or reject your hypothesis. Usually, you repeat the test several times to make sure the results were not an error. But even a hypothesis is more than a wild guess or a hunch. It is an educated estimate that must be testable. If it is not testable it is not even a hypothesis.

Testing, experimentation, and forming hypotheses are all important parts of the scientific process. However, the pinnacle of the scientific process is the theory.

Note

This was not always the case. In ancient times, it was far more common for philosophers to simply formulate compelling arguments for their ideas, without any experimentation. Ptolemy, in the 2nd century, was one of the early proponents of experimentation and what is today known as the “scientific method.” Roger Bacon, who lived in the 13th century, is often considered the father of the modern scientific method. His experimentation in optics was a framework for the modern approach to science.

A Scientific Theory

You know that a hypothesis is a testable guess. You also know that after conducting a number of tests, one or more facts will be confirmed. Eventually, a number of facts are collected, requiring some explanation. The explanation of those facts is called a theory. Or put another way,

A theory is an explanation of a set of related observations or events based upon proven hypotheses and verified multiple times by detached groups of researchers. How does a scientific theory compare to a scientific law? In general, both a scientific theory and a scientific law are accepted to be true by the scientific community as a whole. Both are used to make predictions of events. Both are used to advance technology.⁴

Now think about this definition for the word theory for just a moment. “A theory is an explanation.” That is the key part of this definition. After you have accumulated data, you must have some sort of explanation. A string of facts with no connection, no explanation, is of little use. This is not only true in science, but in other fields as well. Think about how a detective works, for example. Anyone can notice a string of facts, but the detective’s job is to put those facts together in a manner that is consistent with all the facts. This is very similar to what scientists do when trying to formulate a theory. With both the scientist and the detective, the theory must match all the facts.

It is sometimes difficult for non-scientists to become accustomed to this use of the word theory. A basic dictionary usually includes multiple definitions, and some of those are synonymous with guess. However, even a standard dictionary such as Merriam-Webster online offers alternative definitions for the word theory. Those applicable to science’s use of the word theory follow:

1: the analysis of a set of facts in their relation to one another

3: the general or abstract principles of a body of fact, a science, or an art <music theory>

5: a plausible or scientifically acceptable general principle or body of principles offered to explain phenomena <wave theory of light>⁵

As you can see, these three definitions are not synonymous with guess or gut feeling. An even better explanation of theory was provided by Scientific American magazine:

Many people learned in elementary school that a theory falls in the middle of a hierarchy of certainty—above a mere hypothesis but below a law. Scientists do not use the terms that way, however. According to the National Academy of Sciences (NAS), a scientific theory is “a well-substantiated explanation of some aspect of the natural world that can incorporate facts, laws, inferences, and tested hypotheses.” No amount of validation changes a theory into a law, which is a descriptive generalization about nature. So when scientists talk about the theory of evolution—or the atomic theory or the theory of relativity, for that matter—they are not expressing reservations about its truth.⁶

The point to keep in mind is that a theory is an explanatory model. It explains the facts we know and gives us context for expanding our knowledge base. Although scientific theories are based on experimentation and mathematical theories are based on proofs and axioms, the issue of being an explanatory model is the same for a scientific theory and a mathematical theory. Putting it in the context of information theory, a theory provides a conceptual model of information and provides the framework to continue adding to our knowledge of information.

A Look at Successful Scientific Theories

Examining in general terms what a theory is and is not may not provide an adequate explanation for all readers. So let’s look at a concrete example of a very well-accepted theory, the theory of gravity, and how it relates to specific facts. Sir Isaac Newton observed that things tend to fall. In a very general way, this is the essence of his law of gravity: Gravity makes things fall downward. Of course, he expressed that law mathematically with this equation:

F = Gm₁m₂/d²

In this equation, F is the force of gravity, G is a constant (the Gravitational Constant) that can be measured, m₁ and m₂ are the masses of the two objects (such as the Earth and a falling apple), and d is the distance between them. This law of gravity can be measured and verified thousands of times, and in fact it has been.

But this law, by itself, is incomplete. It does not provide an adequate explanation for why this occurs. We know there is gravity and we all feel its pull, but what is it? Why does gravity work according to this formula? Einstein’s Theory of General Relativity was an explanation for why gravity exists. He proposed that matter causes time and space to curve, much like a ball sitting on a stretched-out sheet causes a curve in the sheet. Objects that get close enough to the ball will tend to fall toward it because of this curvature.

Clearly Einstein’s theory explains all the observed facts. But there is still yet another component to qualify it as a scientific theory: It must make some predictions. By predictions, I don’t mean that it foretells the future. What I mean is that if this theory is valid, then you would expect other things also to be true. If those predictions turn out not to be true, then Einstein’s theory must either be modified or rejected. Whether you choose to modify a theory or reject it depends on how well its predictions work out. If it is 90 percent accurate, then you would probably just look to adjust the theory so it matched the facts. However, if it was accurate less than half the time, you would probably consider rejecting the theory outright.

So what predictions can we make from the Theory of General Relativity?

Gravity can bend light. This has been reconfirmed literally hundreds of times with more precision each time. In 2003, the Cassini Satellite once again confirmed this prediction—and this 2003 test was just one among many that all confirmed that gravity can bend light.

Light loses energy escaping from a gravitational field. Because the energy of light is proportional to its frequency, a shift toward lower energy means a shift to lower frequency and longer wavelength. This causes a “red shift,” or shift toward the red end of the visible spectrum. This was experimentally verified on Earth using gamma-rays at the Jefferson Tower Physics Laboratories.

Light is deflected by gravity. General relativity predicts that light should be deflected, or bent, by gravity. This was first confirmed by observations and measurements of a solar eclipse in 1919. It has since been confirmed by hundreds of experiments over decades.

Other predictions relating to the General Theory of Relativity have been confirmed by dozens, and in some cases hundreds, of independent experiments. Note the word independent. These experiments were carried out by people with no particular vested interest in proving Einstein correct. And in a few cases, they really wanted to prove him wrong. Yet in every case the data confirmed Einstein’s theory. You would be hard put to find any physicist who does not agree that the General Theory of Relativity is valid and is true. Some may argue it is not yet complete, but none will argue that it is not true. Hundreds of experiments spanning many decades and literally thousands of scientists have confirmed every aspect of general relativity. Now that this theory is well established, it can be used to guide future experiments and a deeper understanding of gravity as well as related topics.

Binary Math

Binary math is not actually a part of information theory, but it is critical information you will need to be able to understand cryptography in later chapters. Many readers will already be familiar with binary math, and this will be a review for you. However, if your background does not include binary math, this section will teach you the essentials you need.

Defining binary math is actually rather simple: It is mathematics that uses a base 2 rather than the more familiar base 10. The only reason you find base 10 (that is, the decimal number system) to be more “natural” is because most of us have 10 fingers and 10 toes. (As least most people have 10 fingers and toes—but even if you have a different number of fingers and toes, you understand that 10 is normal for humans.)

Once we introduce the concept of 0, we have 10 digits in the base 10 system: 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9. Keep in mind there is not really a number 10 in the base 10 system. There is a 1 in the 10’s place and a 0 in the 1’s place. The same thing is true with binary, or base 2 numbers. There is not actually a number 2. There is a 1 in the 2’s place and a 0 in the 1’s place. This chart comparing the two might be helpful:

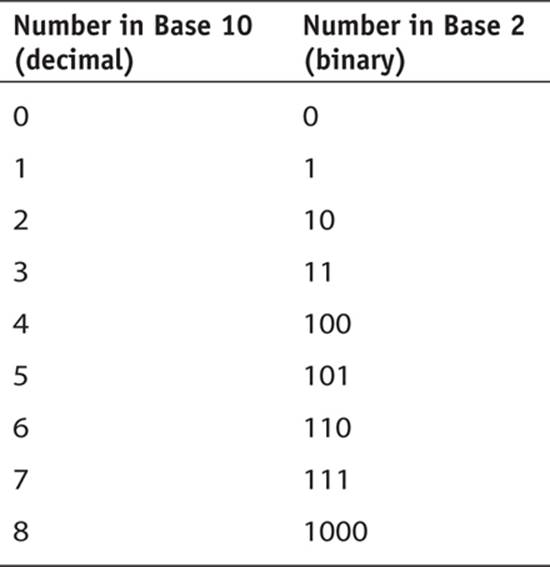
Binary numbers are important because that is, ultimately, what computers understand. You can, of course, represent numbers in any system you wish. And a number system can be based on any integer value. Historically, a few have been widely used. Hexadecimal (base 16) and octal (base 8) are sometimes used in computer science because they are both powers of 2 (2⁴ and 2³, respectively) and thus are easily converted to and from binary. The Babylonians used a base 60 number system, which you still see today in representation of degrees in a geographic coordinate system. For example, 60 seconds makes a minute and 60 minutes makes a degree, so you can designate direction by stating “45 degrees, 15 minutes, and 4 seconds.”

Note

The modern concept of binary numbers traces back to Gottfried Leibniz, who wrote an article entitled “Explanation of the Binary Arithmetic.” Leibniz noted that the Chinese I Ching hexagrams correspond to binary numbers ranging from 0 to 1111111 (or 0 to 63 in decimal numbers).

Converting

Because humans tend to be more comfortable with decimal numbers, you will frequently want to convert from binary to decimal, and you may need to make the inverse conversion as well. You can use many methods to do this, and a common one takes advantage of the fact that the various “places” in a binary number are powers of 2. So consider for a moment a binary number 10111001 and break it down into the powers of 2. If there is a 1 in a given place, then you have that value. If not, you have a 0. For example, if there is a 1 in the 2⁷ place, then you have 128; if not, you have a 0.

Now just add the values you have: 128 + 32 + 16 + 8 + 1 = 185.

This may not be the fastest method, but it works and it is easy to understand.

Binary Operations

You can do all the mathematical operations with binary that you can do with decimal numbers. Fortunately, with cryptography you will be primarily concerned with three operations, AND, OR, and XOR, and these are relatively easy to understand. For all of our examples, we will consider two 4-bit binary numbers: 1101 and 1100. We will examine how the AND, OR, and XOR operations work on these two numbers.

Binary AND

The binary AND operation combines two binary numbers, 1 bit at a time. It asks, “Is there a 1 in the same place in both numbers?” If the answer is yes, then the resulting number is a 1. If no, then the resulting number is a 0. Here, you can see the comparison of the rightmost digit in two 4-digit binary numbers:

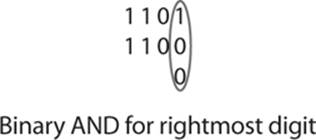
Because the first number has a 1 in this place and the second has a 0, the resultant number is a 0. You continue this process from right to left. Remember that if both numbers have a 1, then the resulting number is a 1. Otherwise, the resulting number is a 0. You can see this here:

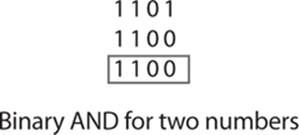
Binary OR

The binary OR operation is just a little different. It is asking the question, “Is there a 1 in the first number or the second number, or even in both numbers?” In other words, “Is there a 1 in the first number and/or the second number?” So, basically, if either number has a 1, then the result is a 1. The result will be a 0 only if both numbers are a zero. You can see this here:

Binary XOR

The binary XOR is the one that really matters for cryptography. This is the operation that provides us with interesting results we can use as part of cryptographic algorithms. With the binary exclusive or (usually denoted XOR), we ask the question, “Is there a 1 in the first number or second number, but not in both?” In other words, we are exclusively asking the “OR” question, rather than asking the “AND/OR” question that the OR operation asks. You can see this operation next:

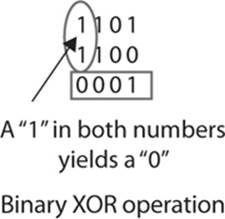
What makes this operation particularly interesting is that it is reversible. If you perform the XOR operation again, this time taking the result of the first operation and XOR’ing it with the second number, you will get back the first number. You can see this here:

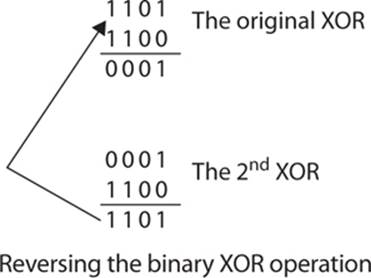
This is particularly useful in cryptographic algorithms. Our example used 4-bit numbers, but extrapolate from that. Assume instead of 4 bits, the first number was a lengthy message of, for example, 768 bits. And the second number was a randomly generated 128-bit number that we use as the key. You could then break the 768-bit plain text into blocks of 128 bits each (that would produce six blocks). Then you XOR the 128-bit key with each 128-bit block of plain text, producing a block of cipher text. The recipient could then XOR each 128-bit block of cipher text with the 128-bit key and get back the plain text.

Before you become overly excited with this demonstration, this simple XOR process is not robust enough for real cryptography. However, you will see, beginning in Chapter 6, that the XOR operation is a part of most modern symmetric ciphers. It cannot be overly stressed, however, that it is only a part of modern ciphers. The XOR operation is not, in and of itself, sufficient.

Conclusions

In this chapter you were introduced to a number of concepts that will be critical for your understanding of modern ciphers, particularly symmetric ciphers, which we begin studying in Chapter 6. Information entropy is a critical concept that you must understand. You were also introduced to confusion and diffusion, Hamming distance, and Hamming weight. These concepts are frequently used in later chapters. You also learned about mathematical and scientific theory. The chapter ended with a basic coverage of binary math.

Test Your Knowledge

1. The difference in bits between two strings X and Y is called ____________.

2. If you take 1110 XOR 0101, the answer is ____________.

3. A change in 1 bit of plain text leading to changes in multiple bits of cipher text is called ____________.

4. The amount of information that a given message or variable contains is referred to as ____________.

5. ____________ refers to significant differences between plain text, key, and cipher text that make cryptanalysis more difficult.

Answers

1. Hamming distance

2. 1011

3. diffusion

4. information entropy

5. Diffusion

Endnotes

1. Roger Bohn and James Short, “How Much Information?” http://hmi.ucsd.edu/pdf/HMI_2009_ConsumerReport_Dec9_2009.pdf.

2. Claude Shannon, “Communication Theory of Secrecy Systems,” http://netlab.cs.ucla.edu/wiki/files/shannon1949.pdf.

3. Kerckhoffs’s principle is discussed at Crytpo-IT, http://www.crypto-it.net/eng/theory/kerckhoffs.html.

4. Bohn and Short, “How Much Information?”

5. Merriam-Webster, http://www.merriam-webster.com/.

6. John Rennie, “Answers to Creationist Nonsense,” Scientific American, June 2002.