Modern Cryptography: Applied Mathematics for Encryption and Informanion Security (2016)
PART II. Symmetric Ciphers and Hashes
Chapter 6. Feistel Networks
In this chapter we will cover the following:
![]() Cryptographic keys
Cryptographic keys
![]() Feistel functions
Feistel functions
![]() Pseudo-Hadamard transforms
Pseudo-Hadamard transforms
![]() MDS matrix
MDS matrix
![]() S-boxes and P-boxes
S-boxes and P-boxes
![]() Symmetric algorithms
Symmetric algorithms
![]() Methods for improving symmetric algorithms
Methods for improving symmetric algorithms
This chapter is the first of two chapters regarding symmetric ciphers. Before I dive into the topic of this chapter, Feistel networks, you need to understand what a symmetric cipher is and the different types of symmetric ciphers. A symmetric cipher is an algorithm that uses the same key to decrypt the message that was used to encrypt the message, as demonstrated in Figure 6-1.
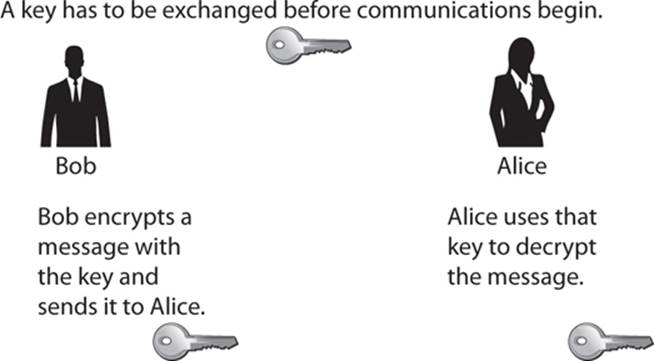
FIGURE 6-1 Symmetric cryptography
The process is rather straightforward, and a decryption key functions much like a key in a physical door—that is, the same key used to lock the door is used to unlock it. This is probably the modality of cryptography that is easiest for cryptography novices to learn. Symmetric cryptography offers some significant advantages over asymmetric cryptography (which we will examine in Chapters 10 and 11). For example, symmetric cryptography is faster than asymmetric and it is just as secure though it uses a smaller key.
Although the classic cryptography discussed in Chapters 1 and 2 could be considered symmetric ciphers, for the purposes of our current discussion we are contemplating only modern ciphers. With that in mind, symmetric algorithms can be classified in two major ways: block ciphers and stream ciphers. A block cipher literally encrypts the data in blocks—64-bit blocks are common, although some algorithms use larger blocks (for example, AES uses a 128-bit block). Stream ciphers encrypt the data as a stream, 1 bit at a time.
Modern block ciphers use a combination of substitution and transposition to achieve both confusion and diffusion (recall those concepts from Chapter 3). Remember that substitution is changing some part of the plain text for some matching part of cipher text. The Caesar and Atbash ciphers are simple substitution ciphers. Transposition is the swapping of blocks of cipher text. For example, for the text I like icecream, you could transpose or swap every three-letter sequence (or block) with the next and get ikeI l creiceam. (Of course, modern block ciphers accomplish substitution and transposition at the level of bits, or rather blocks of bits, and this example uses characters. However, the example illustrates the concept.)
There are two major types of block ciphers: Feistel networks (such as the Data Encryption Standard, DES) and substitution-permutation networks (Advanced Encryption Standard, AES). In this chapter we will examine several Feistel ciphers. Some, such as DES, will be discussed in thorough detail; others will be describe in general terms. Chapter 7 discusses substitution-permutation networks as well as stream ciphers.
It is not critical that you memorize every algorithm in this chapter, even those that are described in detail. It is recommended, however, that you pay particular attention to DES and Blowfish. Then study the other algorithms just enough to understand how they differ from DES and Blowfish. The goal of this chapter is to provide you with a solid understanding of Feistel ciphers.
Note
As with previous chapters, I will also provide sources of more information, such as books and web sites. I am aware that web sites may not always be up and available, but they are also easy and free to access. If a given URL is no longer available, I suggest you simply use your favorite search engine to search the topic. My web site, www.cryptocorner.com/, will always include links if you want to explore these topics.
Cryptographic Keys
Before we start looking at Feistel ciphers, you need to have a basic understanding of cryptographic keys and how they are used. With all block ciphers, there are two types of keys: cipher keys and round keys.
The cipher key is a random string of bits that is generated and exchanged between parties that want to send encrypted messages to each other. When someone says a particular algorithm has a certain key size, they are referring to this cipher key. For example, DES uses a 56-bit cipher key. How that key is exchanged between the two parties is not relevant at this point. Later in the chapter, when I discuss asymmetric cryptography and Secure Sockets Layer/Transport Layer Security (SSL/TLS), you’ll read about key exchange.
Note
The cipher key is actually a pseudo-random number, but we will discuss that in more detail in Chapter 12. For now, just understand that the cipher key is a number generated by some algorithm, such that it is at least somewhat random. The more random it is, the better.
In addition to the cipher key, all block ciphers have a second algorithm called a key schedule which derives a unique key, called a round key, from the cipher key for each round of the cipher. For example, DES has a 56-bit cipher key, but it derives 48-bit round keys for each of its 16 rounds. The key schedule is usually rather simple, mostly consisting of shifting bits. Using a key schedule, each round uses a key that is slightly different from the previous round. Because both the sender (who encrypts the message) and the receiver (who must decrypt the message) are using the same cipher key as a starting point and are using the same key schedule, they will generate the same round keys.
Why do it this way? If you wanted a different key for each round, why not just generate that many cipher keys? For example, why not create 16 DES keys? There are two answers. The first concerns the time needed. Using pseudo-random-number generators to generate keys is computationally more intensive than most key scheduling algorithms and thus much slower. And there is the issue of key exchange: If you generate multiple cipher keys, you have to exchange all of those keys. It is much easier to generate a single cipher key, exchange that key, and then derive round keys from the cipher key.
Feistel Function
At the heart of most block ciphers is a Feistel function, also known as a Feistel network or a Feistel cipher. Because this particular class of block cipher forms the basis for so many symmetric ciphers, it is one of the most influential developments in symmetric block ciphers.
It is named after its inventor, German-born physicist and cryptographer Horst Feistel. Although most known for his contributions to DES, Feistel made other important contributions to cryptography. He invented the Lucifer cipher, the precursor to DES. He also worked for the U.S. Air Force on Identify Friend or Foe (IFF) devices. Feistel held a bachelor’s degree from MIT and a master’s from Harvard, both in physics.
A simple view of the Feistel function is shown in Figure 6-2. The process is not too difficult to understand if you take it one step at a time. Trying to grasp the entire process at once, however, might prove difficult if this is new to you.
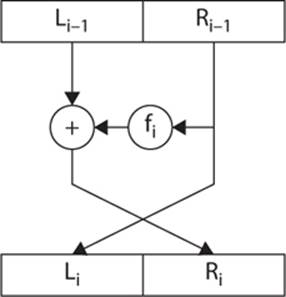
FIGURE 6-2 Feistel—a simple view
Note
Often when I am teaching cryptography, I stop at each step and inquire if the class understands so far. You might do this as you read this section. You can apply that same technique to all the algorithms you will read about from this point forward in the book.
The function starts by splitting the block of plain text data into two parts, traditionally termed L0 and R0. The specific size of the plain text block varies from one algorithm to another: 64-bit and 128-bit sizes are commonly used in many block ciphers. If you are using a 64-bit block, you have 32 bits in L0 and 32 bits in R0. The 0 subscript simply indicates that this is the initial round. The next round is L1 and R1, and then L2 and R2, and so on, for as many rounds as that particular cipher uses.
After the initial bock of plain text is split into two halves, the round function F is applied to one of the two halves. (The round function is a function performed with each iteration, or round, of the Feistel cipher.) The details of the round function F can vary with different implementations. They are usually simple functions that allow for increased speed of the algorithm. (For now, simply treat the round function as a “black box”; I will get to the details of each round function in the specific algorithms I examine—DES, Blowfish, and so on.) In every case, however, at some point in the round function, the round key is XOR’d with the block of text input into the round function—this is, in fact, usually the first step of the round function.
The output of the round function F is then XOR’d with the other half (the half that was not subjected to the round function). What this means is that, for example, L0 is passed through the round function F, and the result is XOR’d with R0. Then the halves are transposed. So L0 gets moved to the right and R0 gets moved to the left.
This process is repeated a given number of times. The main difference between various Feistel functions is the exact nature of the round function F and the number of iterations. You can see this process in Figure 6-3.
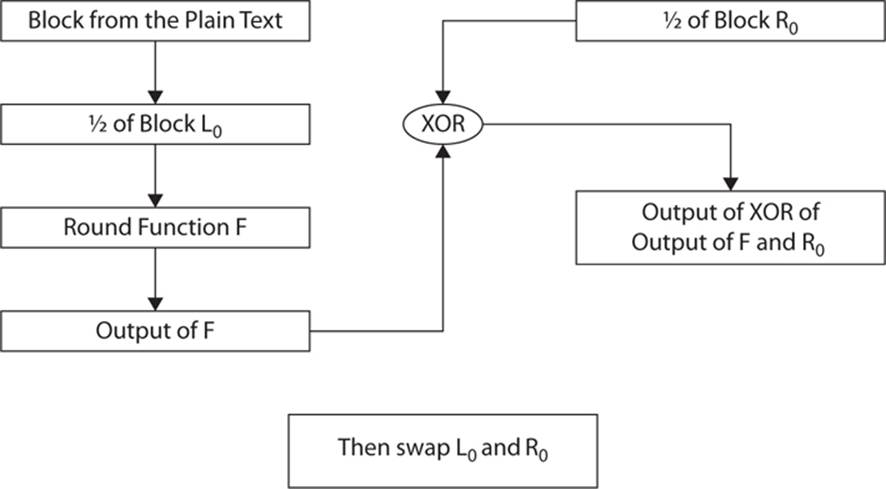
FIGURE 6-3 Feistel function process
This basic structure can provide a very robust basis for cryptographic algorithms. The swapping of the two halves guarantees that some transposition occurs, regardless of what happens in the round function. The Feistel function is the basis for many algorithms, including DES, CAST-128, Blowfish, Twofish, RC5, FEAL (Fast data Encipherment ALgorithm), MARS, TEA (Tiny Encryption Algorithm), and others. But it was first used in IBM’s Lucifer algorithm (the precursor to DES).
Note
How many rounds do you need to make a Feistel secure? Famed computer scientists Michael Luby and Charles Rackoff analyzed the Feistel cipher construction and showed that if the round function is a cryptographically secure pseudo-random function, three rounds is sufficient to make the block cipher a pseudo-random permutation, while four rounds is sufficient to make it a “strong” pseudo-random permutation.
Unbalanced Feistel
A variation of the Feistel network, the Unbalanced Feistel cipher, uses a modified structure, where L0 and R0 are not of equal lengths. So L0 might be 32 bits and R0 could be 64 bits (making a 96-bit block of text). This variation is used in the Skipjack algorithm. You can see this process inFigure 6-4.
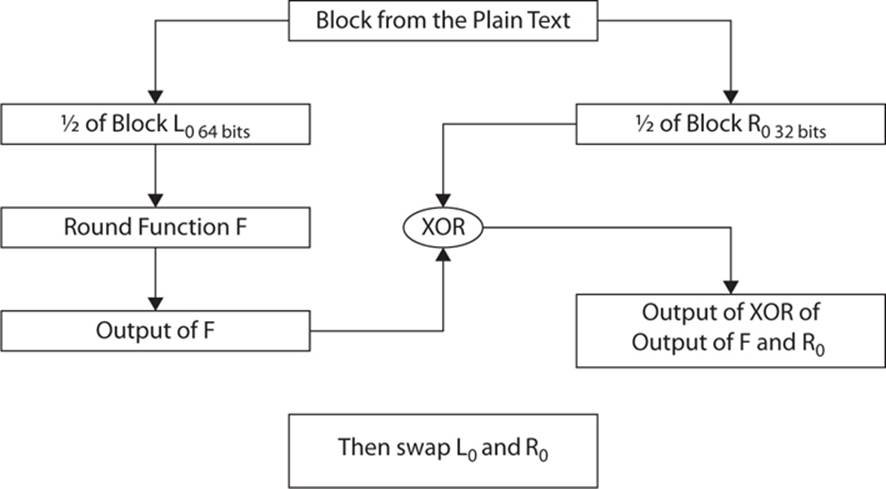
FIGURE 6-4 Unbalanced Feistel function
Pseudo-Hadamard Transform
The pseudo-Hadamard transform (PHT) is a technique applied in several symmetric ciphers. Fortunately, it is simple to understand. A PHT is a transformation of a bit string that is designed to produce diffusion in the bit string. The bit string must be an even length because it is split into two equal halves—so, for example, a 64-bit string is divided into two 32-bit halves. To compute the transform of a, you add a + b (mod 2n). To compute the transform of b, you add a + 2b (mod 2n). The n is the number of bits of each half—in our example, 32. Here’s a more formal mathematical notation:
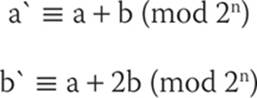
The key is that this transform is reversible, as you can see here:
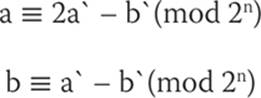
PHT is a simple transform, and because of its simplicity it is computationally fast, making it attractive for cryptographic applications.
MDS Matrix
An MDS (Maximum Distance Separable) matrix represents a function and is used in several cryptographic algorithms, including Twofish. Here’s a simplified definition of the MDS matrix: “An m × n matrix over a finite field is an MDS matrix if it is the transformation matrix of a linear transformation.” This definition is adequate for you to understand how algorithms like Twofish are designed. If you are seeking a more mathematically rigorous definition of MDS matrices, consider this quote:
MDS code over a field is a linear mapping from a field elements to b field elements, producing a composite vector of a+b elements with the property that the minimum number of non-zero elements in any non-zero vector is at least b+1. Put another way, the “distance” (i.e., the number of elements that differ) between any two distinct vectors produced by the MDS mapping is at least b+1. It can easily be shown that no mapping can have a larger minimum distance between two distinct vectors, hence the term maximum distance separable. MDS mappings can be represented by an MDS matrix consisting of a × b elements.1
Lucifer
The Lucifer cipher was the first incarnation of a Feistel cipher. The original description by Horst Feistel had a 48-bit cipher key applied to a 48-bit block. There are variations, and perhaps the most widely known variation used a 128-bit cipher key and operated on 128-bit blocks. Another variant used a 64-bit cipher key on a 32-bit block. Regardless of the key or block size, Lucifer operated exactly as the Feistel cipher operated: the 128-bit block of plain text is separated into two 64-bit blocks (L and R). The R block is subjected to the round function. Unlike DES, Lucifer does not have initial or final permutations (I will discuss those in the section on DES).
The round function has only a few, relatively simple steps. The key schedule algorithm produces a 64-bit round key (often called a subkey) for each round as well as 8 bits called interchange control bits (ICBs). The 64-bit block to be encrypted is treated as a series of 8 bytes. The 8 bits of the ICB is matched to each of the bytes of the 64-bit block. If the first bit of the ICB is a 0, then the left nibble and right nibble of the first byte of the block are swapped. If the first bit of the ICB is a 1, then the two nibbles are left unchanged. Next, if the second bit of the ICB is a 0, the nibbles of the second byte of the block are swapped. This continues through all 8 bits of the ICB and all 8 bytes of the block. Because the ICB is generated each round with the round key, it changes each round. This gives a transposition in the round function that is based on the key. After swapping based on the ICB is completed, the output bits are XOR’d again with the round key. The output of that is input into the substitution boxes, or S-boxes—tables that take input and produce output based on that input. In other words, an S-box is a substitution box that substitutes new values for the input.
Note
Several block ciphers have key-dependent functionality. In some cases, such as Lucifer, the cipher is simply deciding whether or not to execute a basic transposition. In other algorithms, the round key can be used to generate the S-boxes. Key dependency does make an algorithm more resistant to some types of cryptanalysis.
The key-scheduling algorithm is simple. Each round, the 128-bit cipher key is shifted in a shift register. The left 64 bits form the round key and the right 8 bits form the ICB. After each round, the 128 bits are shifted 56 bits to the left.
Note
Some sources say that Feistel first suggested the simple name DEMONSTRATION cipher, and then shortened it to DEMON. From that, the Lucifer cipher name evolved.
As you can see, Lucifer is relatively simple; however, consider how much change is actually taking place. First, individual bytes of plain text have their nibbles (4-byte halves) swapped based on the ICB. Then the result is XOR’d with the round key. Then that output is subjected to an S-box. In these three steps, the text is subjected to transposition as well as multiple substitutions. Then consider that the most widely known variant of Lucifer (the 128-bit key and 128-bit block variant) uses 16 rounds. So the aforementioned transposition and substitutions will be executed on a block of plain text 16 times.
To get a good idea of just how much this alters the plain text, consider a simplified example. In this case, we won’t have any S-boxes—just transposition and an XOR operation. Let’s begin with a single word of plain text:
![]()
If we convert that to ASCII codes, and then convert those to binary, we get this:
![]()
Now let’s assume we have a cipher key that is just 8 random bits. We are not even going to alter this each round, as most real algorithms do. Our key for this example is this:
![]()
Furthermore, to make this similar to Lucifer but simpler, we will swap nibbles on every other byte, and we will do the entire text at once, instead of one block at a time. So round one is like this:
Plain text: 01000001 01110100 01110100 01100001 01100011 01101011
Swapped: 00010100 01110100 01000111 01100001 00110110 01101011
(Only every other block is swapped.)
XOR with key produces this:
![]()
Converted to ASCII is
![]()
You can find ASCII tables on the Internet (such as www.asciitable.com/) to convert this to actual text, which yields the following:
199 = a symbol, not even a letter or number
66 = B
148 = a symbol, not even a letter or number
87 = W
229 = a symbol, not even a letter or number
93 = ]
Consider that this is the output after one round—and it was an overly simplified round at that. This should give you some indication of how effective such encryption can be.
DES
The Data Encryption Standard is a classic in the annals of cryptography. It was selected by the National Bureau of Standards as an official Federal Information Processing Standard (FIPS) for the United States in 1976. Although it is now considered outdated and is not recommended for use, it was the premier block cipher for many years and is worthy of study. The primary reason it is no longer considered secure is because of its small key size, though the algorithm is quite sound. Many cryptography textbooks and university courses use DES as the basic template for studying all block ciphers. We will do the same and give this algorithm more attention than most of the others do.
Tip
For a thorough discussion of the technical details of DES, refer to the actual government standard documentation: U.S. Department of Commerce/National Institute of Standards and Technology FIPS Publication 46-3, at http://csrc.nist.gov/publications/fips/fips46-3/fips46-3.pdf. For a less technical but interesting animation of DES, you can try http://kathrynneugent.com/animation.html.
DES uses a 56-bit cipher key applied to a 64-bit block. There is actually a 64-bit key, but 1 bit of every byte is used for error correction, leaving just 56 bits for actual key operations.
DES is a Feistel cipher with 16 rounds and a 48-bit round key for each round. Recall from the earlier discussion on keys that a round function is a subkey that is derived from the cipher key each round, according to a key schedule algorithm. DES’s general functionality follows the Feistel method of dividing the 64-bit block into two halves (of 32 bits each, as this is not an unbalanced Feistel cipher), applying the round function to one half, and then XOR’ing that output with the other half.
The first issue to address is the key schedule. How does DES generate a new subkey each round? The idea is to take the original 56-bit key and to permute it slightly each round, so that each round is applying a slightly different key, but one that is based on the original cipher key. To generate the round keys, the 56-bit key is split into two 28-bit halves, and those halves are circularly shifted after each round by 1 or 2 bits. This will provide a different subkey each round. During the round-key generation portion of the algorithm (recall that this is referred to as the key schedule) each round, the two halves of the original cipher key (the 56 bits of key the two endpoints of encryption must exchange) are shifted a specific amount. The amount is shown in this table:

Once the round key has been generated for the current round, the next step is to address the half of the original block that will be input into the round function. Recall that the two halves are each 32 bits, and the round key is 48 bits. That means that the size of the round key does not match the size of the half block to which it is going to be applied. (You cannot really XOR a 48-bit round key with a 32-bit half block unless you simply ignore 16 bits of the round key. If you did so, you would basically be making the round key effectively shorter and thus less secure, so this is not a good option.) So the 32-bit half needs to be expanded to 48 bits before it is XOR’d with the round key. This is accomplished by replicating some bits so that the 32-bit half becomes 48 bits: The 32-bit section to be expanded is divided into 4-bit sections (eight 4-bit sections). The bits on each end are duplicated, adding 16 bits to the original 32, for a total of 48 bits. It is important that you keep in mind that the bits on each end were duplicated, because this item will be key later in the round function.
Perhaps this example will help you to understand what is occurring at this point. Let’s assume 32 bits, as shown here:
![]()
Divide that into eight sections of 4 bits each, as shown here:
![]()
Now each of these has its end bits duplicated, as shown here:

The resultant 48-bit string is next XOR’d with the 48-bit round key. That is the extent of the round key being used in each round. It is then dispensed with, and on the next round another 48-bit round key will be derived from the two 28-bit halves of the 56-bit cipher key.
Now we have the 48-bit output of the XOR operation, which is split into eight sections of 6 bits each. For the rest of this explanation, I will focus on just one of those 6-bit sections, but keep in mind that the same process is done to all eight sections.
The 6-bit section is used as the input to an S-box. The S-boxes used in DES are then published—the first of which is shown in Figure 6-5.

FIGURE 6-5 The first DES A-box
Notice that Figure 6-5 is simply a lookup table. The 2 bits on either end are shown in the leftmost column and the 4 bits in the middle are shown in the top row. They are cross-matched, and the resulting value is the output of the S-box. For example, with the previous demonstration numbers, our first block would be 111111. So you would find 1xxxx1 on the left and x1111x on the top. The resulting value is 13 in decimal or 1101 in binary.
Note
Recall that during the expansion phase we duplicated the outermost bits, so when we come to the S-box phase and drop the outermost bits, no data is lost. As you will see in Chapter 8, this is called a “compression S-box,” and they are difficult to design properly.
At the end of this, you will have produced 32 bits that are the output of the round function. Then, in keeping with the Feistel structure, they get XOR’d with the 32 bits that were not input into the round function, and the two halves would be swapped. DES is a 16-round Feistel cipher, meaning this process is repeated 16 times.
This leaves two items to discuss regarding DES: the initial permutation, or IP, and the final permutation, which is an inverse of the IP, as shown in Figure 6-6. (This figure is an excerpt from the Federal Information Processing Standards Publication 46-3.2)
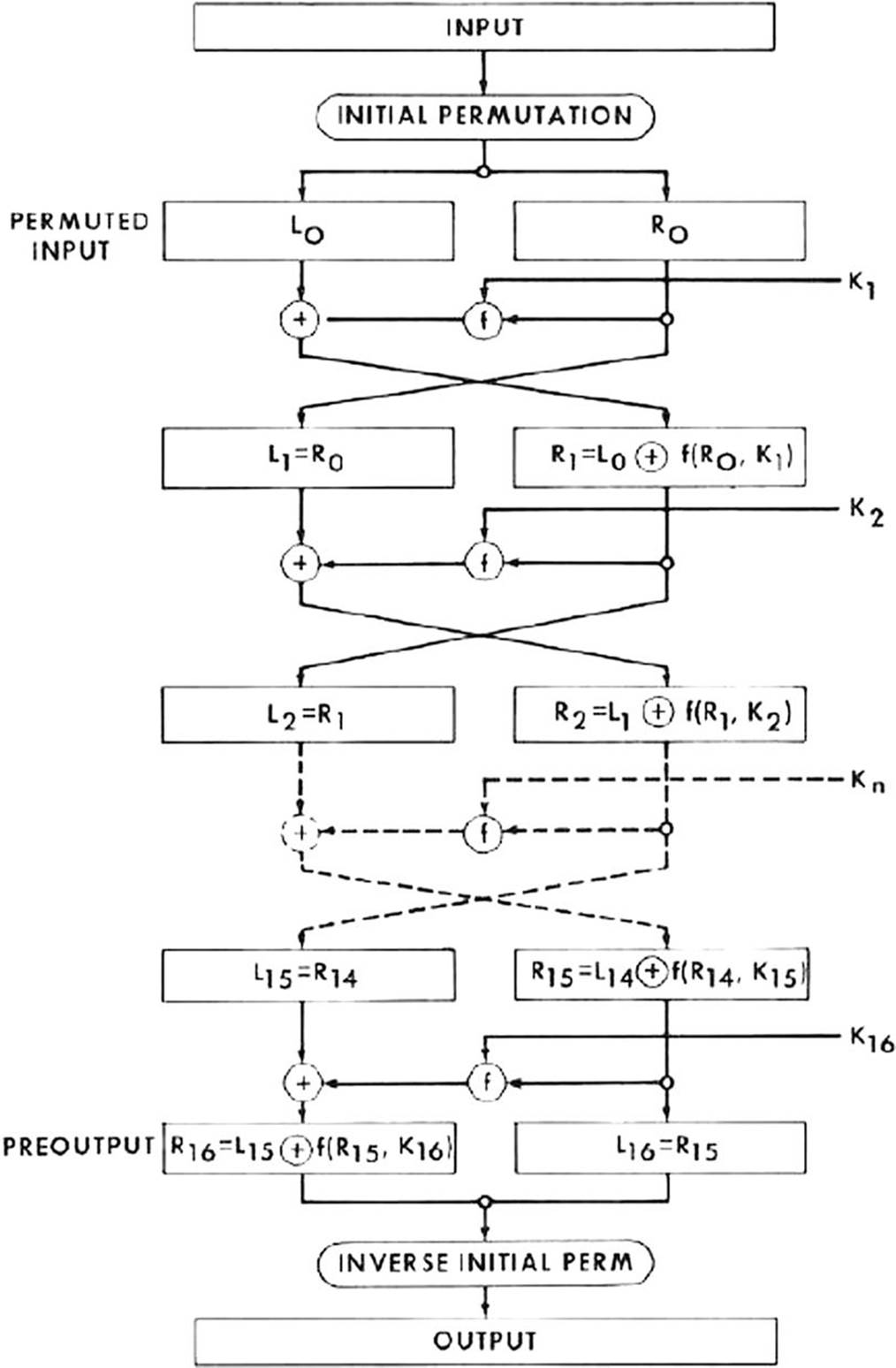
FIGURE 6-6 DES overview from FIPS 46-3
The initial permutation mentioned earlier is simply a transposition of the bits in the 64-bit plain text block. This occurs before the rounds of DES are executed, and then the reverse transposition occurs after the rounds of DES have completed. Basically, the first 58th bit is moved to the first bit spot, the 50th bit to the second bit spot, the 42nd bit to the third bit spot, and so on. The specifics are shown in Figure 6-7.
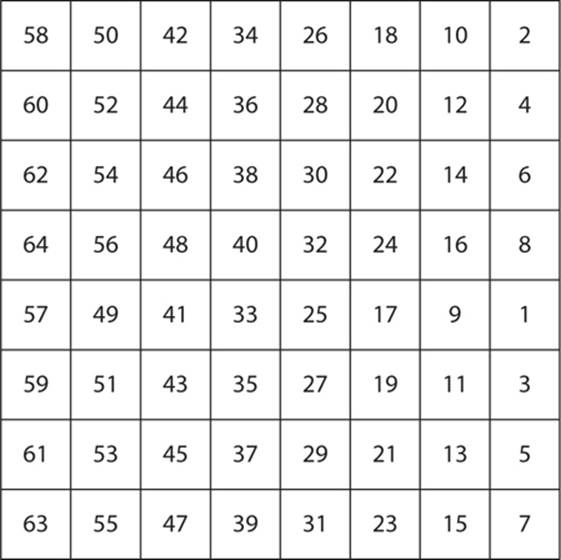
FIGURE 6-7 DES initial permutation
Note
Earlier in this chapter we looked at a very simplified version of the Lucifer cipher, and you could see that it was quite effective at altering the plain text. It should be obvious to you that DES is at least as effective as Lucifer. The small key size is the only reason DES is no longer considered secure. Furthermore, DES is probably the most widely studied symmetric cipher, and certainly the most often cited Feistel cipher. It is important that you fully understand this cipher before you move on to the rest of this chapter. You may need to re-read this section a few times to make sure you fully grasp the details of DES.
3DES
Eventually, it became obvious that DES would no longer be secure. The U.S. federal government began a contest seeking a replacement cryptography algorithm. However, in the meantime, 3DES (Triple DES) was created as an interim solution. Essentially, it “does” DES three times, with three different keys. Triple DES uses a “key bundle,” which comprises three DES keys—K1, K2, and K3. Each key is a standard 56-bit DES key. There were some variations that would use the same key for K1 and K3, but three separate keys is considered the most secure.
S-Box and P-Box
An S-box, or substitution box, is a table that substitutes some output for a given input; it defines that each of the input bits is substituted with a new bit. A P-box, or permutation box, is a variation on the S-box. Instead of each input bit being mapped to a bit found in a lookup table as with the S-box, the bits in the P-box that are input are also transposed, or permuted—that is, some may be transposed, while others are left in place. For example, a 6-bit P-box may swap the first and fourth bits, swap the second and third bit, but leave the fifth bit in place. S-boxes and P-boxes are discussed in detail in Chapter 8.
GOST
GOST is a DES-like algorithm developed by the Soviet and Russian governments in the 1970s. It was first classified but was released to the public in 1994. This 32-round Feistel cipher uses a 64-bit block and a key of 256 bits. (GOST is an acronym for gosudarstvennyy standart, which translates into English as “state standard.” The official designation is GOST 28147-89.)
GOST was meant as an alternative to the U.S. DES algorithm and has some similarities to DES. It uses a 64-bit block and a 256-bit key with 32 rounds. Like DES, GOST uses S-boxes; unlike DES, the original S-boxes were classified. The round key for GOST is relatively simple: Add a 32-bit subkey to the block, modulo 232, and then submit the output to the S-boxes. The output of the S-boxes is routed to the left by 11 bits.
The key schedule is as follows: Break the 256-bit cipher key into eight separate 32-bit keys. Each of these keys will be used four times.
Each of eight S-boxes is 4-by-4 and they are implementation dependent—that means that they are generated, for example using a pseudo-random-number generator. Because the S-boxes are not standardized, each party using GOST needs to ensure that the other party is using the same S-box implementation. The S-boxes each take in 4 bits and produce 4 bits. This is different from DES, in which the S-boxes take in 6 bits and produce 4 bits of output.
The round function is very simple, so to compensate for this, the inventors of GOST used 32 rounds (twice that of DES) and the S-boxes are secret and implementation-specific. Although the diversity of S-boxes can make certain types of cryptanalysis more difficult on GOST, it also means the individuals implementing GOST must be very careful in their creation of the S-boxes.
Blowfish
Blowfish is a symmetric block cipher that was published in 1993 by Bruce Schneier, who stated that Blowfish is unpatented and will remain so in all countries. He placed the algorithm in the public domain to be freely used by anyone, which has made Blowfish popular in open source utilities.
Note
Schneier is a very well-known American cryptographer known for his work on the Blowfish and Twofish ciphers as well as his extensive cryptanalysis of various ciphers. He is also the author of the book Applied Cryptography: Protocols, Algorithms, and Source Code in C (Wiley, 1996). Schneier maintains a security blog and writes extensively on general network security as well as cryptography-related topics.
The Blowfish cryptography algorithm was intended as a replacement for DES. Like DES, it is a 16-round Feistel cipher working on 64-bit blocks. However, unlike DES, it can have varying key sizes ranging from 32 bits to 448 bits. Early in the cipher, the cipher key is expanded. Key expansion converts a key of at most 448 bits into several subkey arrays totaling 4168 bytes.
The cipher itself is a Feistel cipher, so the first step is to divide the block into two halves. For example, a 64-bit block is divided into L0 and R0. Now there will be 16 rounds.
The S-boxes are key dependent (as you will see later in this section). That means rather than be standardized as they are in DES, they are computed based on the key. There are four S-boxes, each 32 bits in size. Each S-box has 256 entries:
s1/0, s1/1, s1/2...s1/255
s2/0, s2/1, s2/2...s2/255
s3/0, s3/1, s3/2...s3/255
s4/0, s4/1, s4/2...s4/255
Blowfish uses multiple subkeys (also called round keys). One of the first steps in the cipher is to compute those subkeys from the original cipher key. This begins with an array called the P-array. Each element of the P-array is initialized with the hexadecimal digits of pi, after the 3—in other words, only the values after the decimal point. Each element of the P-array is 32 bits in size. Here are the first few digits of pi in decimal:
![]()
Here is the same number in hexadecimal:
![]()
There are 18 elements in the P-array, each 32 bits in size. They are labeled simply P1, P2, and so on, to P18. The four S-boxes are each 32 bits in size and are also initialized with the digits of pi. Then the first 32 bits of the cipher key are XOR’d with P1, the next 32 bits are XOR’d with P2, and so on. This continues until the entire P-array has been XOR’d with bits from the cipher key. When the process is done, the P-array elements are each hexadecimal digits of pi XOR’d with segments of the cipher key.
The next step might seem confusing, so pay close attention. You take an all-zero string and encrypt it with the Blowfish algorithm using the subkeys you just generated (that is, the P-array). Then replace P1 and P2 with the output of that encryption. Encrypt that output using Blowfish, this time using the new modified keys (the P1 and P2 were modified by the last step). Then replace P3 and P4 with the output of that step. This process continues until all the entries of the P-array and all four S-boxes have been replaced with the output of this continually evolving Blowfish algorithm.3
Despite the complex key schedule, the round function itself is rather simple:
1. The 32-bit half is divided into 4 bytes, designated a, b, c, and d.
2. Then this formula is applied.4
The F function is: F(xL) = ((S1,a + S2,b mod 232) XOR S3,c) + S4,d mod 232 You can see this process in Figure 6-8.
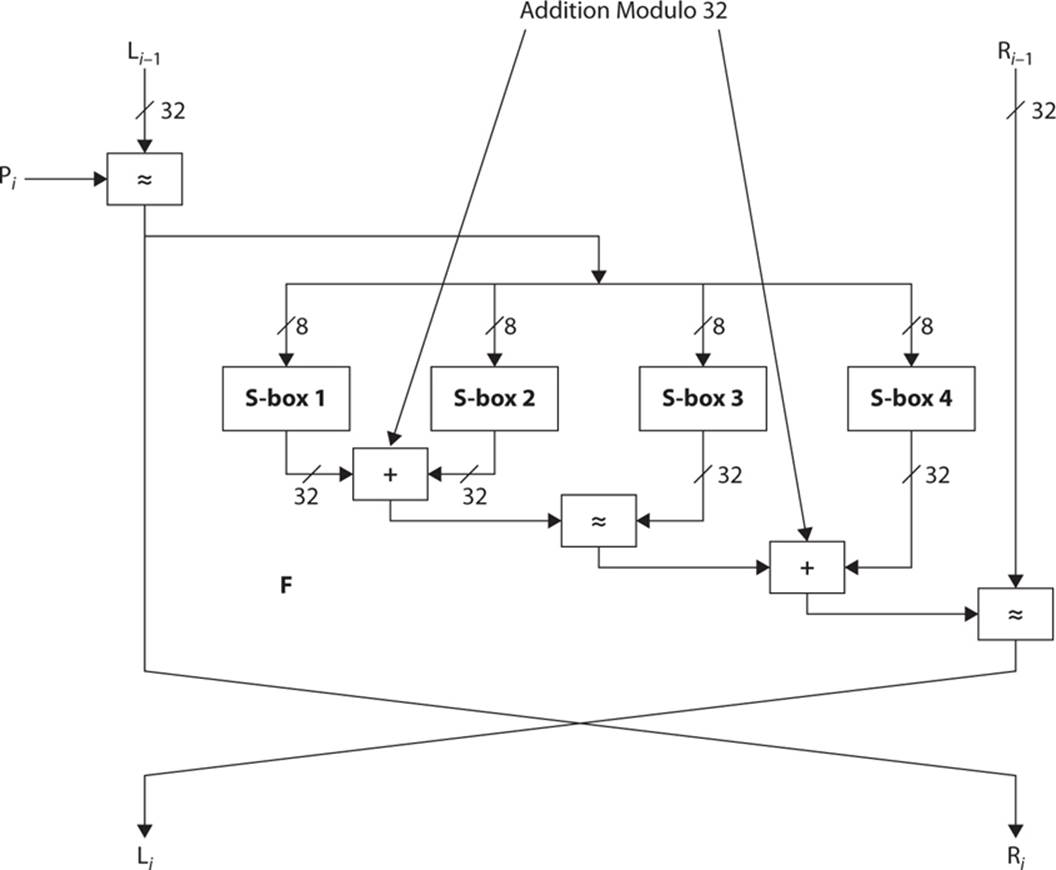
FIGURE 6-8 Blowfish round function
Twofish
Twofish was one of the five finalists of the AES contest (which we will explore in more detail in Chapter 7). It is related to the block cipher Blowfish, and Bruce Schneier was part of the team that worked on this algorithm. Twofish is a Feistel cipher that uses a 128-bit block size and key sizes of 128, 192, and 256 bits. It also has 16 rounds, like DES. Like Blowfish, Twofish is not patented and is in the public domain, so it can be used by anyone without restrictions.
Also like Blowfish, Twofish uses key-dependent S-boxes and has a fairly complex key schedule. There are four S-boxes, each 8 bit–by–8 bit. The cipher key is split in half; one half is used as a key, and the other half is used to modify the key-dependent S-boxes.
Twofish uses key whitening, a process in which a second key is generated and XOR’d with the block. This can be done before or after the round function. In the case of Twofish, it occurs both before and after. You can see this in Figure 6-9.
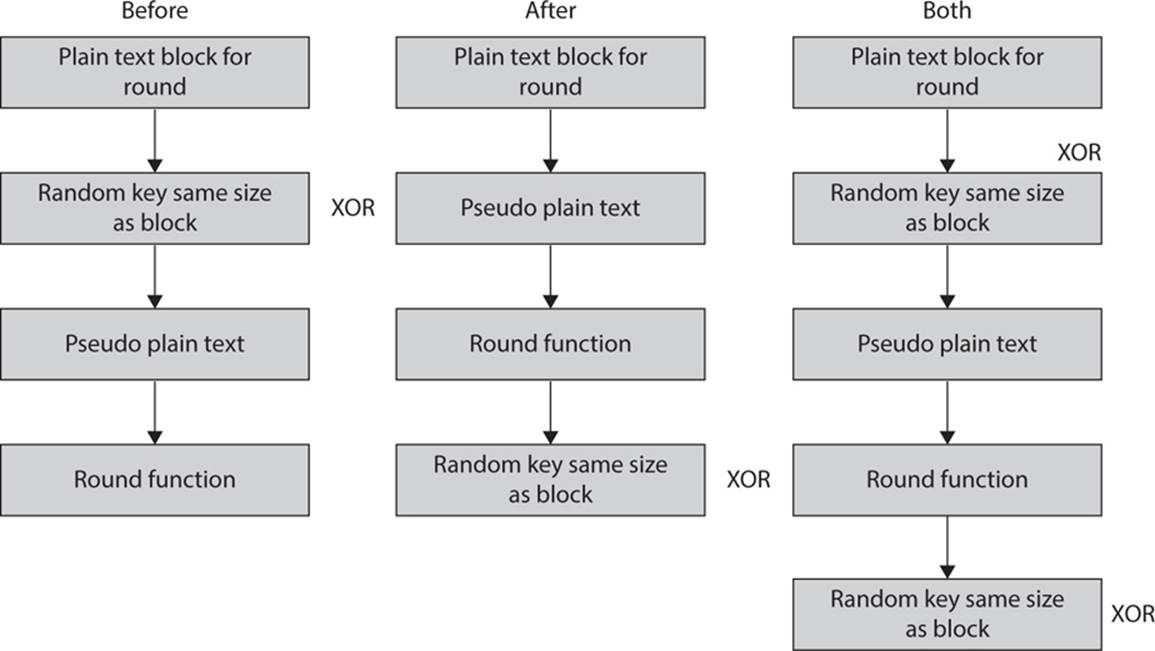
FIGURE 6-9 Key whitening in Twofish
The plain text is key whitened prior to the application of the Twofish algorithm and again after the application of the Twofish algorithm. In the Twofish documentation, this is referred to as input whitening and output whitening. With Twofish, 128 bits of key material is used for the input and output whitening.
Twofish has some aspects that are not found in most other Feistel ciphers, the first of which is the concept of the cycle. Every two rounds are considered a cycle. The design of Twofish is such that in one complete cycle (two rounds), every bit of plain text has been modified once.
The plain text is split into four 32-bit words. After the input whitening are 16 rounds of Twofish. In each round, the two 32-bit words on the left side are put into the round function (remember all Feistel ciphers divide the plain text, submitting only part of it to the round function). Those two 32-bit words are submitted to the key dependent S-boxes and then mixed using an MDS matrix. Then the results from this process are combined using the pseudo-Hadamard transform. After this is complete, the results are XOR’d with the right two 32-bit words (that were previously left untouched) and swapped for the next round.
There is one nuance to the XOR of the left and right halves. The two 32-bit words on the right are given a slight rotation. One 32-bit word is rotated 1 bit the left, and then after the XOR, the other 32-bit word is rotated 1 bit to the right.
An overview of Twofish is shown in Figure 6-10. Note that this image is the diagram originally presented in Schneier’s (et al.) paper on Twofish.5
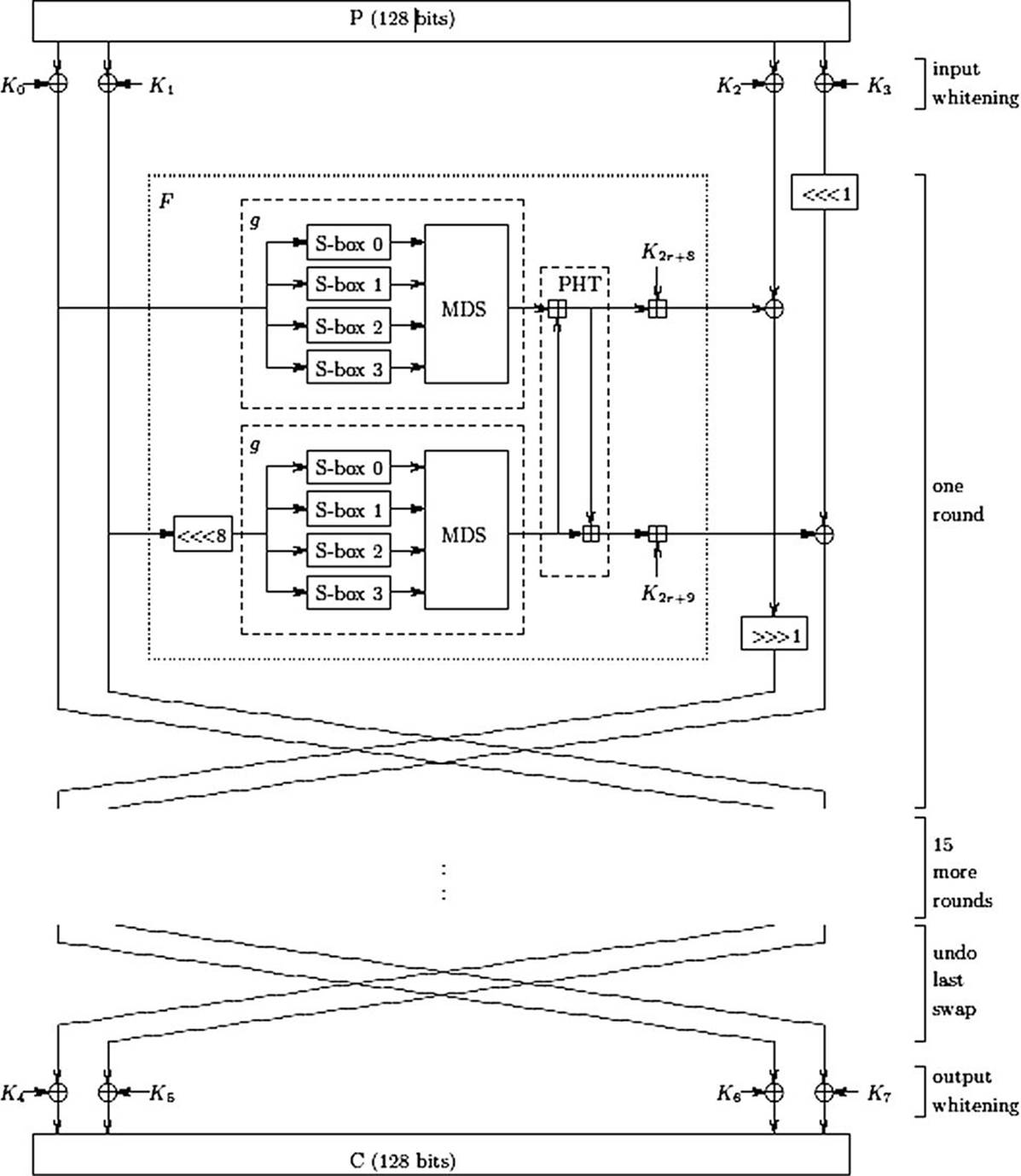
FIGURE 6-10 The original Twofish diagram
If you want to delve into more detail with Twofish, I recommend the paper that Schneier wrote on Twofish (see the Endnotes for this chapter). You may also want to consult the book The Twofish Encryption Algorithm: A 128-Bit Block Cipher by Kelsey, Whiting, Wagner, and Ferguson (Wiley, 1999).
Note
Neils Ferguson is a very well-known cryptographer who has worked on Twofish as well as the Helix cipher. He collaborated with Schneier on several projects including the Yarrow and Fortuna pseudo-random-number generators. We will examine both of those in Chapter 12. In 2007, Ferguson and Dan Shumow presented a paper that described a potential cryptographic backdoor in the Dual_EC_DRBG pseudo-random-number generator. Later disclosures by Edward Snowden (the former CIA contractor who leaked classified information) revealed that there was indeed a cryptographic backdoor in Dual_EC_DRBG. We will examine those issues in Chapter 18.
Skipjack
The Skipjack algorithm was developed by the NSA and was designed for the clipper chip. Although the algorithm was originally classified, it was eventually declassified and released to the public. The clipper chip had built-in encryption; however, a copy of the decryption key would be kept in a key escrow in case law enforcement needed to decrypt data without the device owner’s cooperation. This feature made the process highly controversial. The Skipjack algorithm was designed for voice encryption, and the clipper chip was meant for secure phones.
Skipjack uses an 80-bit key to encrypt or decrypt 64-bit data blocks. It is an unbalanced Feistel network with 32 rounds. Skipjack’s round function operates on 16-bit words. It uses two different types of rounds, called the A and B rounds. In the original specifications, A and B were termedstepping rules. First step A is applied for 8 rounds, step B for 8 rounds, and then the process is repeated, totaling 32 rounds.
Skipjack makes use of an S-box that is rather interesting. The documentation refers to it as the “G function” or “G permutation.” It takes a 16-bit word as input along with a 4-byte subkey. This G permutation includes a fixed byte S-table that is termed the “F-table” in the Skipjack documentation.
The A round is accomplished by taking the 16-bit word, called W1, and submitting it to the G box. The new W1 is produced by XOR’ing the output of the G box with the counter and then with W4. The W2 and W3 words shift one register to the right, becoming W3 and W4. This is shown in Figure 6-11, which is taken directly from the NIST specification for Skipjack.6
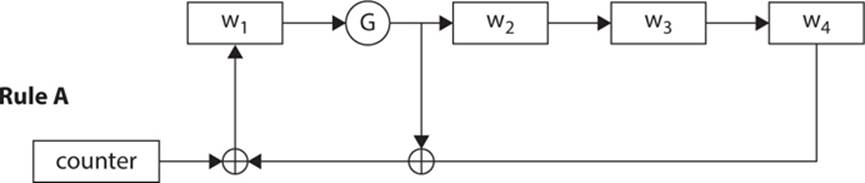
FIGURE 6-11 Skipjack A round
The B round is similar, with slight differences, shown in Figure 6-12 (also taken from the specification documentation).
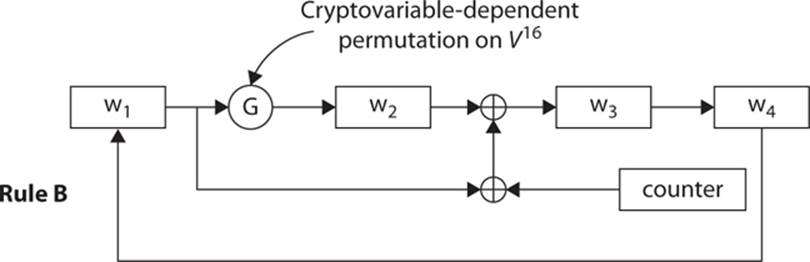
FIGURE 6-12 Skipjack B round
The Skipjack algorithm is considered to be robust. However, the key escrow issue made it unacceptable to many civilian vendors, who feared that the U.S. government would, at will, be able to eavesdrop on communications encrypted with Skipjack. For this reason, the Skipjack algorithm did not gain wide acceptance and usage.
CAST
There are two well-known versions of CAST: CAST-128 and CAST-256. CAST-256 was a candidate in the AES contest and is based on the earlier CAST-128. CAST-128 is used in some versions of PGP (Pretty Good Privacy). The algorithm was created by Carlisle Adams and Stafford Tavares. CAST-128 can use either 12 or 16 rounds, working on a 64-bit block. The key sizes are in 8-bit increments, ranging from 40 bits to 128 bits, but only in 8-bit increments. The 12-round version of CAST-128 is used with key sizes less than 80 bits, and the 16-round version is used with key sizes of 80 bits or longer. CAST-128 has 8 S-boxes, each 32 bits in size.
FEAL
FEAL (Fast data Encipherment ALgorithm) was designed by Akihrio Shimizu and Shoji Miyaguchi and published in 1987. There are variations of the FEAL cipher, but all use a 64-bit block and essentially the same round function. FEAL-4 uses 4 rounds, FEAL-8 uses 8 rounds, FEAL-N uses N rounds, chosen by the implementer. This algorithm has not done well under cryptanalysis. Because several weaknesses have been found in the algorithm, it is not considered secure.
MARS
MARS was IBM’s submission to the AES contest and was one of the final five finalists. It was designed by a team of cryptographers that included Don Coppersmith, a mathematician who was involved in the creation of DES and worked on various other cryptological topics such as cryptanalysis of RSA. The algorithm uses a 128-bit block with a key size that varies between 128 and 448 bits, in 32-bit increments.
MARS divides the input into the round function into four 32-bit words labeled A, B, C, and D. The algorithm has three phases: an 8-round phase that does forward mixing, a 16-round phase that is the core of the algorithm, then an 8-round phase that does backward mixing.
A general overview of MARS is shown in Figure 6-13.
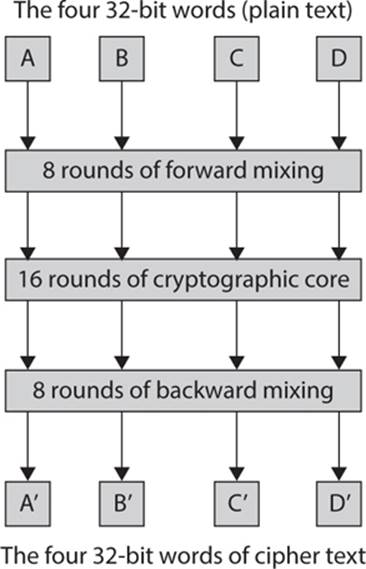
FIGURE 6-13 General overview of MARS
As mentioned, MARS can use a cipher key of 128 to 448 bits, divided into four to fourteen 32-bit words. MARS uses a key schedule that expands the user-supplied cipher key into a key array of forty 32-bit words.
MARS uses a single but very large S-box, a table of 512, 32-bit words to which the operations are applied. The original specification for MARS7 actually described the algorithm entirely in an image, which is shown in Figure 6-14.

FIGURE 6-14 MARS in detail
In Figure 6-14, you can see that A, B, C, and D are the 32-bit words that are input, and R and M are intermediate steps in the algorithm. Most of the algorithm consists of bit-shifting (denoted by the >>> and <<< symbols) and XOR’ing. The S represents the S-box (or a portion thereof). Even though it was not chosen in the AES contest, MARS, like the other five finalists, is a secure algorithm that you should feel confident using.
TEA
TEA, or Tiny Encryption Algorithm, was created by David Wheeler and Roger Needham and first publicly presented in 1994. This simple algorithm is easy to implement in code. It is a Feistel cipher that uses 64 rounds (note that this is a suggestion, and it can be implemented with fewer or more rounds). The rounds should be even in number, however, since they are implemented in pairs called cycles.
TEA uses a 128-bit key operating on a 64-bit block. It also uses a constant that is defined as 232/the golden ratio. This constant is referred to as Delta, and in each round a multiple of Delta is used.8 The 128-bit key is split into four 32-bit subkeys labeled K[0], K[1], K[2], and K[3]. Rather than use the XOR operation, TEA uses addition and subtraction, but done mod 232. The block is divided into two halves, R and L, and R is put through the round function.
The round function takes the R half and performs a left shift of 4. The result of that operation is added to K[0] (keep in mind that all addition is being done mod 232). The result of that operation is added to Delta (recall that Delta is the current multiple of the 232/the golden ratio). The result of that operation is then shifted right 5 and added to K[1]. That is the round function. As with all Feistel ciphers, the result of the round function is XOR’d with L, and then L and R are swapped for the next round.
Note
If you are not familiar with the golden ratio (also called the golden mean and divine proportion), it is a very interesting number. Two quantities are said to be in the golden ratio if their ratio is the same as the ratio of their sum to the larger of the two quantities. This can be expressed as (a + b)/a = a/b. The ratio is 1.6180339887.... It is an irrational number and appears in many places, including the paintings of Salvador Dali. Mathematicians throughout history including Pythagoras and Euclid have been fascinated by the golden ratio.
TEA is a simple Feistel cipher and is often included in programming courses because writing it in code is relatively simple. You can find numerous examples of TEA in various programming languages, including Java, C, and C++, on the Internet.
LOKI97
LOKI97, another candidate in the AES contest, was developed by Lawrie Brown. There have been other incarnations of the LOKI cipher, namely LOKI89 and LOKI91. The earlier versions used a 64-bit block.
LOKI97 uses 16 rounds (like DES) and a 128-bit block. It operates with key sizes of 128, 192, or 256 bits (as does AES). It has a complex round function, and the key schedule is accomplished via an unbalanced Feistel cipher. The algorithm is freely available.
The key schedule is treated as four 64-bit words: K40, K30, K20, K10. Depending on the key size used, the four 64-bit words may need to be generated from the key provided. In other words, if there is a cipher key less than 256 bits, then there is not enough material for four 64-bit words, but the missing material for 192- and 128-bit cipher keys is generated. The key schedule itself uses 48 rounds to generate the subkeys.
The round function is probably one of the most complex for a Feistel cipher, certainly more complex than the algorithms we have examined in this chapter. More detail can be found on the Internet in the 1998 paper “Introducing the New LOKI97 Block Cipher,” by Lawrie Brown and Josef Pieprzyk.
Camellia
Camellia is a Japanese cipher that uses a block size of 128 bits and key sizes of 128, 192, or 256 bits (like AES). With a 128-bit key, Camellia uses 18 rounds, but with the 192- or 256-bit key it uses 24 rounds—note that both of these rounds are multiples of 6 (18 and 24). Every six rounds, a transformation layer is applied called the “FL function.” Camellia uses four S-boxes, and uses key whitening on the input and output.
Note
Some browsers, such as Chrome, prefer to use Camellia for encryption. They will attempt to negotiate with the server, and if the server can support Camellia, the browser will select it over AES.
ICE
ICE, or Information Concealment Engine, was developed in 1997. It is similar to DES, but it uses a bit permutation during its round function that is key dependent. ICE works with 64-bit blocks using a 64-bit key and 16 rounds. The algorithm is in the public domain and not patented. A faster variant of ICE, called Thin-ICE, uses only 8 rounds.
Simon
Simon is actually a group of block ciphers. What makes it interesting is that it was released by the NSA in 2013. It has many variations—including, for example, a variation that uses 32-bit blocks with a 64-bit key and 32 rounds. However, if you use a 64-bit block, you can choose between 96- and 128-bit keys and either 42 or 44 rounds. The largest block size, 128 bits, can use key sizes of 128, 192, or 256 bits with either 68, 69, or 72 rounds.
Symmetric Methods
Several methods can be used to alter the way a symmetric cipher works. Some of these are meant to increase the security of the cipher.
ECB
The most basic encryption mode is the electronic codebook (ECB) mode, in which the message is divided into blocks, and each block is encrypted separately. The problem, however, is that if you submit the same plain text more than once, you always get the same cipher text. This gives attackers a place to begin analyzing the cipher to attempt to derive the key. Put another way, ECB is simply using the cipher exactly as it is described without any attempts to improve its security.
CBC
When using cipher-block chaining (CBC) mode, each block of plain text is XOR’d with the previous cipher text block before being encrypted. This means there is significantly more randomness in the final cipher text. This is much more secure than ECB mode and is the most common mode. This process is shown in Figure 6-15.
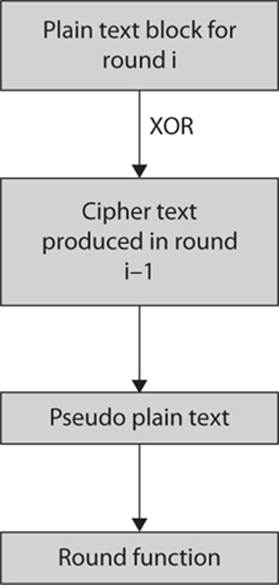
FIGURE 6-15 Cipher-block chaining mode
Tip
There really is no good reason to use ECB over CBC, if both ends of communication can support CBC. CBC is a strong deterrent to known plain text attacks and is a cryptanalysis method we will examine in Chapter 17.
The only issue with CBC is the first block. There is no preceding block of cipher text with which to XOR the first plain text block. It is common to add an initialization vector to the first block so that it has something to be XOR’d with. The initialization vector (IV) is basically a pseudo-random number, much like the cipher key. Usually an IV is used only once, so it is called a nonce (number only used once). The CBC mode is fairly old—it was introduced by IBM in 1976.9
PCBC
The propagating cipher-block chaining (PCBC) mode was designed to cause small changes in the cipher text to propagate indefinitely when decrypting and encrypting. This method is sometimes called plain text cipher-block chaining. The PCBC mode is a variation on the CBC mode of operation. It is important to keep in mind that the PCBC mode of encryption has not been formally published as a federal standard.
CFB
In cipher feedback (CFB) mode, the previous cipher text block is encrypted, and then the cipher text produced is XOR’d back with the plain text to produce the current cipher text block. Essentially, it loops back on itself, increasing the randomness of the resultant cipher text. Although CFB is very similar to CBC, its purpose is a bit different. The goal is to take a block cipher and turn it into a stream cipher. Output feedback mode is another method used to transform a block cipher into a synchronous stream cipher. We will examine both of these in more detail in Chapter 7.
Conclusions
In this chapter you have seen the different types of symmetric ciphers and studied Feistel ciphers in detail. It is critical that you fully understand the general Feistel structure and important that you have a strong understanding of DES and Blowfish before proceeding to the next chapter. Other algorithms were presented in this chapter. Although you need not memorize every single algorithm, the more algorithms you are familiar with, the better.
You have also learned some new mathematics in this chapter, such as the pseudo-Hadamard transform. Just as important, you have seen improvements to symmetric ciphers with techniques such as cipher block chaining.
Test Your Knowledge
1. __________ has an 80-bit key and is an unbalanced cipher.
2. __________ is a Feistel cipher using variable length key sizes from 32 bits to 448 bits.
3. The following formulas describe the __________.
A. a` ≡ a + b (mod 2n)
B. b` ≡ a + 2b (mod 2n)
4. Which of the following is a Russian cipher much like DES?
A. Blowfish
B. CAST
C. FEAL
D. GOST
5. What is the proper term for the algorithm used to derive subkeys (round keys) from the cipher key?
A. Key algorithm
B. Sub key generator
C. Key schedule
D. Round key generator
6. Which algorithm described in this chapter was an unbalanced Feistel cipher used with the clipper chip?
7. ___________ used input whitening and output whitening as well as a pseudo-Hadamard transform.
8. ___________ divides the input into the round function into four 32-bit words labeled A, B, C, and D, and then uses three phases: the 16-round phase that is the core of the algorithm, and pre- and post-phases of forward and backward mixing.
9. With a 128-bit key, Camellia uses ___________ rounds, but with the 192- or 256-bit key it uses ___________ rounds.
10. With ___________, each block of plain text is XOR’d with the previous cipher text block before being encrypted.
Answers
1. Skipjack
2. Blowfish
3. pseudo-Hadamard transform
4. D
5. C
6. Skipjack
7. Twofish
8. MARS
9. 18 and 24
10. cipher-block chaining
Endnotes
1. Lan Luo, Zehui Qu, and Chaoming Song, “Precise Transformation of Feistel to SP Fuse into LFSR,” http://image.sciencenet.cn/olddata/kexue.com.cn/upload/blog/file/2010/4/2010421154425312167.pdf.
2. FIPS, Federal Information Processing Standards Publication: Data Encryption Standard (DES), http://csrc.nist.gov/publications/fips/fips46-3/fips46-3.pdf.
3. For more information on Blowfish and the variable-length key, 64-bit block cipher, see “Fast Software Encryption,” by Bruce Schneier, at www.schneier.com/paper-blowfish-fse.html.
4. For more information on the equation, see “Blowfish,” by Kevin Allison, Keith Feldman, and Ethan Mick at www.cs.rit.edu/~ksf6458/cryptography/Final.pdf.
5. B. Schneier, J. Kelsey, D. Whiting, D. Wagner, C. Hall, and N. Ferguson, “Twofish: A 128-Bit Block Cipher,” 1998, www.schneier.com/paper-twofish-paper.pdf.
6. NIST Skipjack and KEA Algorithm Specifications, 1998, http://csrc.nist.gov/groups/ST/toolkit/documents/skipjack/skipjack.pdf.
7. C. Burwick, D. Coppersmith, E. Avignon, R. Gennaro, S. Halevi, C. Jutla, S. Matyas, L. O’Connor, M. Peyravian, D. Safford, and N. Zunic, “The MARS Encryption Algorithm,” 1999, http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.35.5887&rep=rep1&type=pdf.
8. D. Wheeler and R. Needham, “TEA, a Tiny Encryption Algorithm,” www.cix.co.uk/~klockstone/tea.pdf.
9. The CBC mode was introduced by IBM in 1976. (US Patent 4074066. W. Ehrsam, C. Meyer, J. Smith, and W. Tuchman, “Message verification and transmission error detection by block chaining,” 1976, www.google.com/patents/US4074066.)
All materials on the site are licensed Creative Commons Attribution-Sharealike 3.0 Unported CC BY-SA 3.0 & GNU Free Documentation License (GFDL)
If you are the copyright holder of any material contained on our site and intend to remove it, please contact our site administrator for approval.
© 2016-2025 All site design rights belong to S.Y.A.