Modern Cryptography: Applied Mathematics for Encryption and Informanion Security (2016)

PART II. Symmetric Ciphers and Hashes

Chapter 7. Substitution-Permutation Networks

In this chapter we will cover the following:

Advanced Encryption Standard

Serpent algorithm

SAFER ciphers

Stream ciphers

Asubstitution-permutation network (SPM) is a series of operations linked together. The most notable difference between an SPM and a Feistel cipher is that in SPM, the plain text block is not split in half but is operated on as a whole. The block is subjected to alternating rounds or layers of operations, including substitution or permutation boxes (S-boxes or P-boxes), in order to generate the cipher text.

Replacing DES

DES (Data Encryption Standard) is a solid cipher with a robust algorithm, but with a key that was too small. Certainly in the late 1970s and early 1980s it was adequate, but, eventually, as computing power increased, it became clear that a replacement was needed for DES. A contest was undertaken spanning from 1997 to 2000 to find a replacement for DES.

On January 2, 1997, when the National Institute of Standards and Technology (NIST) announced the contest, the search was on to find a replacement for DES. However, it was not until September 12 of that year that NIST announced the general criteria: Contestant algorithms had to be block ciphers that supported a block size of 128 bits as well as key sizes of 128, 192, and 256 bits. For the next several months, 15 different algorithms were submitted from a variety of countries: CAST-256, CRYPTON, DEAL (Data Encryption ALgorithm), DFC (Decorrelated Fast Cipher), E2, FROG (Frequency-Resolved Optical Gating), HPC (Hasty Pudding Cipher), LOKI97, MAGENTA (Multifunctional Algorithm for General-purpose Encryption and Network Telecommunication Applications), MARS (Multivariate Adaptive Regression Splines), RC6, Rijndael, SAFER+, Serpent, and Twofish. Many of these, while not ultimately selected, were solid algorithms. In Chapter 6 we examined MARS and CAST-256. In this chapter you will learn about a few of the others, though our primary focus will be on AES itself.

The algorithms where subjected to a variety of tests, including common cryptanalysis attacks. The ES1 Candidate Conference was held in August 1998 and the AES2 was in March 1999. In August 1999 the process had narrowed down the candidate list to five algorithms: MARS, RC6, Rijndael, Serpent, and Twofish. These are often referred to in the literature as the AES finalists. All five of these are robust algorithms and are widely used today. Then in October 2000, the NIST announced that the Rijndael cipher had been chosen. In computer security literature, you will see the same algorithm referred to as Rijndael or AES, but cryptography literature usually refers to Rijndael.

Advanced Encryption Standard

The Advanced Encryption Standard (AES), the Rijndael block cipher, was ultimately chosen as a replacement for DES in 2001 after a five-year process. AES is designated as Federal Information Processing Standard (FIPS) 197. The importance of AES cannot be overstated. It is widely used around the world and is perhaps the most widely used symmetric cipher. Of all the algorithms discussed in this chapter, AES is the one you should give the most attention to.

AES can have three different key sizes: 128, 192, or 256 bits. The three different implementations of AES are AES 128, AES 192, and AES 256. The block size can also be 128, 192, or 256 bits. The original Rijndael cipher allowed for variable block and key sizes in 32-bit increments; however, the U.S. government uses these three key sizes with a 128-bit block as the standard for AES.

This algorithm was developed by two Belgian cryptographers, Vincent Rijmen and Joan Daemen. Rijmen helped design the Whirlpool cryptographic hash (which we will study in Chapter 9) and worked on ciphers such as KHAZAD, Square, and SHARK. Daemen has worked extensively on the cryptanalysis of block ciphers, stream ciphers, and cryptographic hash functions.

Rijndael Steps

Rijndael uses a substitution-permutation matrix rather than a Feistel network. The Rijndael cipher works by first putting the 128-bit block of plain text into a 4-by-4–byte matrix. This matrix is termed the state, and it will change as the algorithm proceeds through its steps. The first step is to convert the plain text block into binary, and then put it into a matrix, as shown in Figure 7-1.

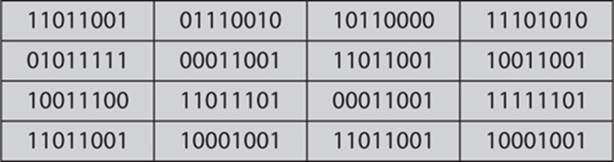
FIGURE 7-1 The Rijndael matrix first step

The algorithm consists of a few relatively simple steps that are used during various rounds.

1. AddRoundKey Each byte of the state is combined with the round key using bitwise XOR. This is where Rijndael applies the round key generated from the key schedule.

2. SubBytes In this nonlinear substitution step, each byte is replaced with another according to a lookup table. This is where the contents of the matrix are put through the S-boxes. Each S-box is 8 bits.

3. ShiftRows In this transposition step, each row of the state is shifted cyclically a certain number of steps. The first row is left unchanged. Every byte in the second row is shifted 1 byte to the left (with the far left wrapping around). Every byte of the third row is shifted 2 to the left, and every byte of the fourth row is shifted 3 to the left (again wrapping around). This is shown next. Notice that the bytes are simply labeled by their row and then a letter, such as 1a, 1b, 1c, 1d.

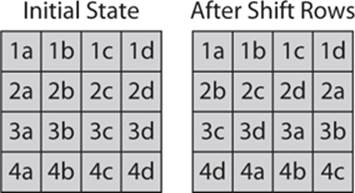
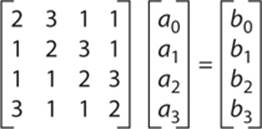
4. MixColumns A mixing operation operates on the columns of the state, combining the 4 bytes in each column. Each column of the state is multiplied with a fixed polynomial. Each column (remember the matrix we are working with) is treated as a polynomial within the Galois field (2⁸). The result is multiplied with a fixed polynomial c(x) = 3x³ + x² + x + 2 modulo x⁴ + 1. This step can also be viewed as a multiplication by the particular matrix in the finite field GF(2⁸). This is often shown as matrix multiplication, as shown next. In other words, you take the 4 bytes and multiply them by the matrix, yielding a new set of 4 bytes:

Rijndael Outline

With the aforementioned steps in mind, the following information shows how those steps are executed in the Rijndael cipher. For 128-bit keys, there are 10 rounds; for 192-bit keys, there are 12 rounds; and for 256-bit keys, there are 14 rounds.

Key Expansion The round keys are derived from the cipher key using the Rijndael key schedule, which is described in more detail later in this chapter.

Initial Round The initial round executes the AddRoundKey step—simply XOR’ing with the round key. This initial round is executed once, and then the subsequent rounds are executed.

In the AddRoundKey step, the subkey is XOR’d with the state. For each round that follows, a subkey is derived from the main key using the Rijndael key schedule; each subkey is the same size as the state.

Rounds This phase of the algorithm executes several steps in the following order:

1. SubBytes

2. ShiftRows

3. MixColumns

4. AddRoundKey

Final Round This round includes everything the rounds phase includes, except no MixColumns:

1. SubBytes

2. ShiftRows

3. AddRoundKey

Rijndael S-Box

The S-box of Rijndael is fascinating to study. (We will look more deeply into S-boxes in Chapter 8. However, a brief description is warranted here.) The S-box is generated by determining the multiplicative inverse for a given number in GF(2⁸) = GF(2)[x]/(x⁸ + x⁴ + x³ + x + 1), Rijndael’s finite field (zero, which has no inverse, is set to zero). In other words, the S-boxes are based on a mathematical formula. In fact, there are variations of the standard Rijndael S-box. It will still operate as any other S-box, taking in bits as input and substituting them for some other bits. You can see the standard Rijndael S-box in Figure 7-2.

FIGURE 7-2 Rijndael S-box

Rijndael Key Schedule

As with other ciphers we have examined, Rijndael uses a key schedule to generate round keys from the original cipher key. The key schedule uses three operations that are combined to create the key schedule:

Rotate The first operation is simply to take a 32-bit word (in hexadecimal) and to rotate it 8 bits (1 byte) to the left.

Rcon This is the term that the Rijndael documentation uses for the exponentiation of 2 to a user-specified value. However, this operation is not performed with regular integers, but in Rijndael’s finite field. In polynomial form, 2 is 2 = 00000010 = 0 x^7 + 0 x^6 + 0 x^5 + 0 x^4 + 0 x^3 + 0 x^2 + 1 x + 0.

Inner loop The key schedule has an inner loop that consists of the following steps:

1. The input is a 32-bit word and at an iteration number i. The output is a 32-bit word.

2. Copy the input over to the output.

3. Use the previously described rotate operation to rotate the output 8 bits to the left.

4. Apply Rijndael’s S-box on all 4 individual bytes in the output word.

5. On only the first (leftmost) byte of the output word, XOR the byte with 2 to the power of (i-1). In other words, perform the rcon operation with i as the input, and exclusive or the rcon output with the first byte of the output word.

The key schedule for Rijndael is one of the more complex key schedules found in symmetric ciphers. Because the key schedules for 128-bit, 192-bit, and 256-bit encryption are very similar, with only some constants changed, the following key size constants are defined here:

n has a value of 16 for 128-bit keys, 24 for 192-bit keys, and 32 for 256-bit keys.

b has a value of 176 for 128-bit keys, 208 for 192-bit keys, and 240 for 256-bit keys (with 128-bit blocks as in AES, it is correspondingly larger for variants of Rijndael with larger block sizes).

Once you have the appropriate constants, the steps of the Rijndael key schedule can be executed:

1. The first n bytes of the expanded key are the encryption key.

2. Set the rcon iteration value i to 1.

3. When the desired b bytes of expanded key are reached, do the following to generate n more bytes of expanded key:

4. Do the following to create 4 bytes of expanded key:

A. Create a 4-byte temporary variable, t.

B. Assign the value of the previous 4 bytes in the expanded key to t.

C. Perform the key schedule core (see above) on t, with i as the rcon iteration value.

D. Increment i by 1.

E. XOR t with the 4-byte block n bytes before the new expanded key. This becomes the next 4 bytes in the expanded key.

5. Then do the following three times to create the next 12 bytes of expanded key:

A. Assign the value of the previous 4 bytes in the expanded key to t.

B. XOR t with the 4-byte block n bytes before the new expanded key. This becomes the next 4 bytes in the expanded key.

6. If you are processing a 256-bit key, do the following to generate the next 4 bytes of expanded key:

A. Assign the value of the previous 4 bytes in the expanded key to t.

B. Run each of the 4 bytes in t through Rijndael’s S-box.

C. XOR t with the 4-byte block n bytes before the new expanded key. This becomes the next 4 bytes in the expanded key.

7. If you are processing a 128-bit key, do not perform the following steps. If you are processing a 192-bit key, run the following steps twice. If you are processing a 256-bit key, run the following steps three times:

A. Assign the value of the previous 4 bytes in the expanded key to t.

B. XOR t with the 4-byte block n bytes before the new expanded key. This becomes the next 4 bytes in the expanded key.

Serpent Algorithm

The Serpent algorithm, invented by Ross Anderson, Eli Biham, and Lars Knudsen, was submitted to the AES competition but was not selected because its performance is slower than AES. However, in the ensuing years since the AES competition, computational power has increased dramatically, which has led some experts to reconsider the use of Serpent on modern systems.

Anderson worked with Biham on the Tiger cryptographic hash and other algorithms. He also designed the PIKE stream cipher. Biham is an Israeli cryptographer who is well known for his extensive contributions to cryptography, including inventing the topic of differential cryptanalysis with Adi Shamir (we will study differential cryptanalysis in Chapter 17).

Note

Throughout this book, you will read brief biographies of people who have made significant contributions to cryptography. I recommend you take a bit more time, when you can spare it, to delve more deeply into the biographies of the people mentioned. They can provide significant insights into the field of cryptography.

Serpent has a block size of 128 bits and can have a key size of 128, 192, or 256 bits, much like AES. The algorithm is also a substitution-permutation network like AES. It uses 32 rounds working with a block of four 32-bit words. Each round applies one of eight 4-bit-to-4-bit S-boxes 32 times in parallel. Serpent was designed so that all operations can be executed in parallel.¹

Serpent S-Boxes and Key Schedule

The inventors of DES stated in the original proposal that they had initially considered using the S-boxes from DES, because those S-boxes had been thoroughly studied. However, they abandoned that idea in favor of using S-boxes optimized for more modern processors.

There are 33 subkeys or round keys, each 128 bits in size. The key length could have been variable, but for the purposes of the AES competition, the key sizes were fixed at 128, 192, and 256 bits.

The Serpent Algorithm

The Serpent cipher begins with an initial permutation (IP), much as DES does. It then has 32 rounds, each consisting of a key-mixing operation (simply XOR’ing the round key with the text), S-boxes, and a linear transformation (except for the last round). In the final round, the linear transformation is replaced with a key-mixing step. Then there is a final permutation (FP). The IP and FP do not have any cryptographic significance; instead, they simply optimize the cipher.

The cipher uses one S-box per round, so during R₀, the S₀ S-box is used, and then during R₁, the S₁ S-box is used. Because there are only eight S-boxes, each is used four times, so that R₁₆ reuses S₀.

It should be obvious that Serpent and Rijndael have some similarities. The following table shows a comparison of the two algorithms.

Clearly, Serpent has more rounds than Rijndael, but the round functions of the two algorithms are different enough that simply having more rounds does not automatically mean Serpent is more secure.

Square

The Square cipher was the forerunner to the Rijndael cipher. It was invented by Joan Daemen, Vincent Rijmen, and Lars Knudsen and first published in 1997.² It uses a 128 block size with a 128-bit key working in eight rounds. Given the success of AES, the Square cipher has largely become a footnote in the history of cryptography.

You have already become acquainted with Rijmen and Daemen earlier in this book. Lars Knudsen is a well-known Danish cryptographer who has done extensive work with analyzing block ciphers, cryptographic hash functions, and message authentication codes. He received his doctorate from Aarhus University in 1994.

SHARK

SHARK was invented by a team of cryptographers including Rijmen, Daemen, Bart Preneel, Antoon Bosselaers, and Erik De Win.³ SHARK uses a 64-bit block with a 128-bit key and operates in six rounds (the original SHARK used six rounds). It has some similarities to the Rijndael cipher, including the use of S-boxes that are based on GF(2⁸). (Remember that GF is a Galois field defined by a particular prime number raised to some power.) Like Rijndael (and unlike DES) the S-boxes take a fixed number of bits and put out the same number of bits. (Recall that DES S-boxes took in 6 bits and produced 4 bits.)

The original paper for SHARK described two different ways to create a key schedule algorithm (recall that the key schedule creates round keys from the cipher key). The first method took n bits of the round input that were XOR’d with n bits of the cipher key. The result was the round key. The second method used an affine transformation.

Note

An affine transformation is a function between affine spaces that preserves points, straight lines, and planes. This is often applied to geometry but works well with matrix mathematics. For more details on affine transformations, the textbook chapter “Matrix Algebra and Affine Transformations” from Clemson University is a good resource: http://people.cs.clemson.edu/~dhouse/courses/401/notes/affines-matrices.pdf.

The specific affine transformation used in SHARK is as follows: Let K_i be a key-dependent invertible (n × n) matrix over GF(2^m). The operation on that matrix is shown here:

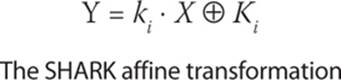
The general flow of the SHARK algorithm is shown in Figure 7-3, which is a figure from the original SHARK paper.

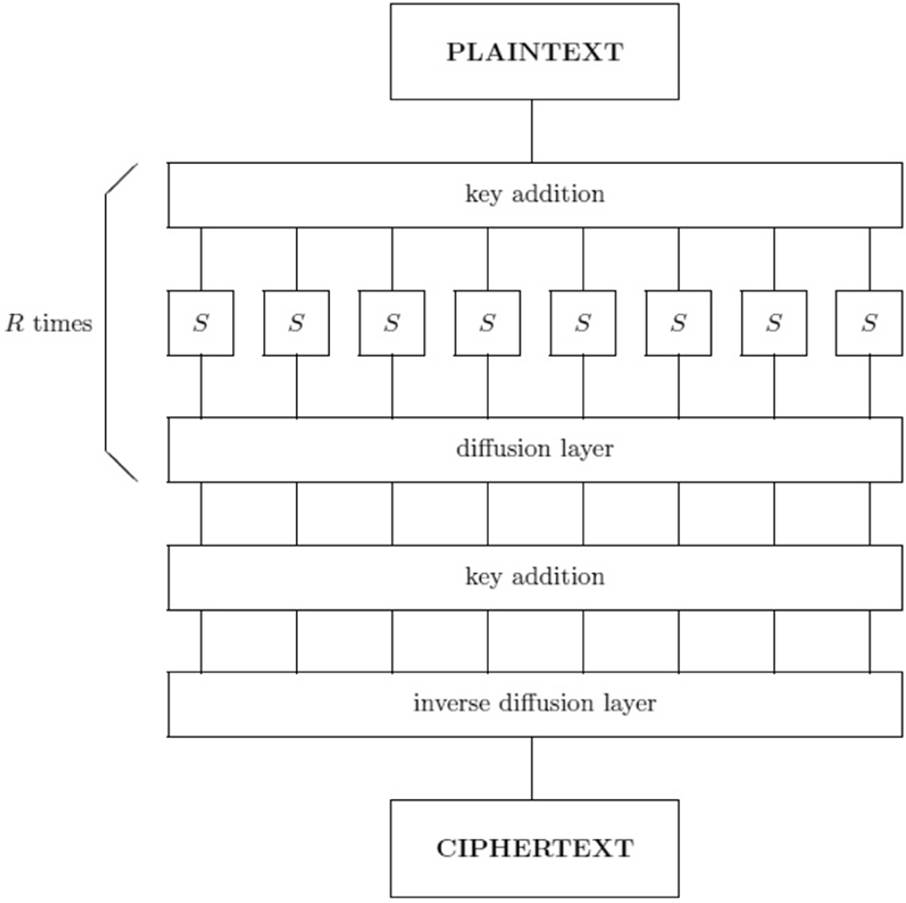
FIGURE 7-3 The SHARK cipher from the original paper

SAFER Ciphers

SAFER (Secure And Fast Encryption Routine) is actually a family of ciphers invented by a team that included James Massey (one of the creators of IDEA, a well-known block cipher). The older versions include SAFER K and SAFER SK, and the newer versions are SAFER+ and SAFER++. The first SAFER cipher was published in 1993 and used a key size of 64 bits. It was eponymously named SAFER K-64. There was also a 128-bit version named SAFER K-128.

Cryptanalysis uncovered weaknesses in the original design, specifically in the key schedule. Thus an improved key schedule was designed and the variants were named SAFER SK-64 and SAFER SK-128. (The SK stands for Safer Key schedule.)

SAFER+ was an improvement published in 1998 and submitted to the AES competition. Some Bluetooth implementations used SAFER+ for generating keys and as a message authentication code, but not for encrypting traffic.

The key size used with SAFER obviously depends on the particular variant of SAFER in use. The number of rounds can range from 6 to 10, with more rounds being used with larger key sizes. However, all the various SAFER variations use the same round function. They differ in key size, key schedule, and total number of rounds.

The Round Function

The 64-bit block of plain text is converted into eight blocks, each with 8 bits. Each round consists of an XOR with the round key, the output of which is submitted to the S-boxes, and the output of that is subjected to another XOR with a different round key. This is shown in Figure 7-4.

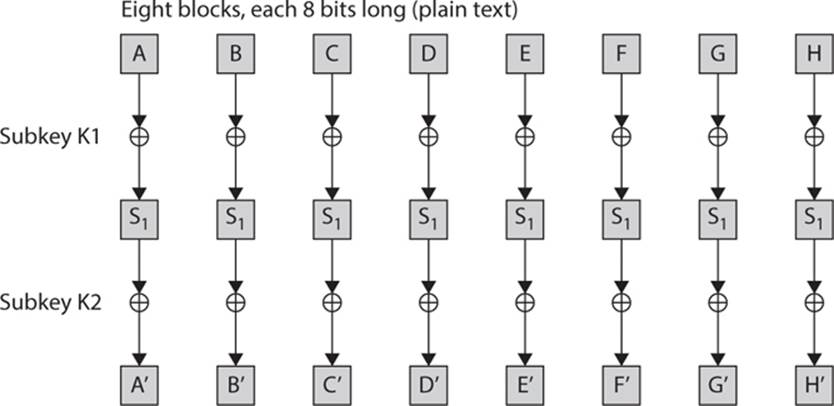
FIGURE 7-4 The SAFER round function

After the XOR’ing and S-boxes, the text is subjected to three pseudo-Hadamard transforms. This is shown in Figure 7-5.

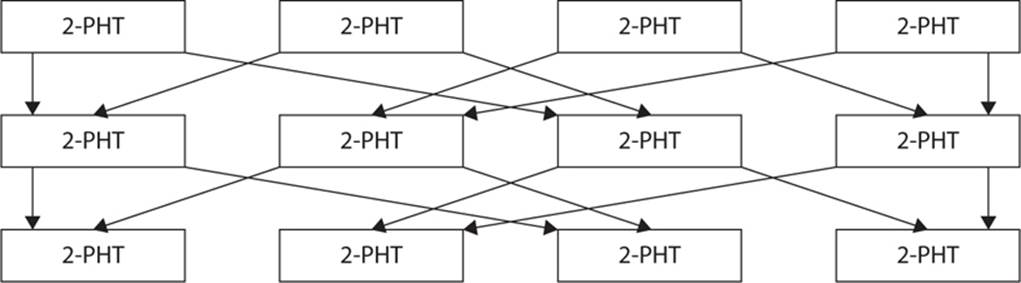
FIGURE 7-5 The SAFER pseudo-Hadamard transforms

Key Schedule

Each of the SAFER variations has a different key scheduling algorithm. For example, SAFER+ expands a 16-, 24-, or 32-byte cipher key into 272, 400, or 528 subkey bytes (these are bytes, not bits). An overview of the SAFER structure is shown in Figure 7-6, from the original SAFER paper.

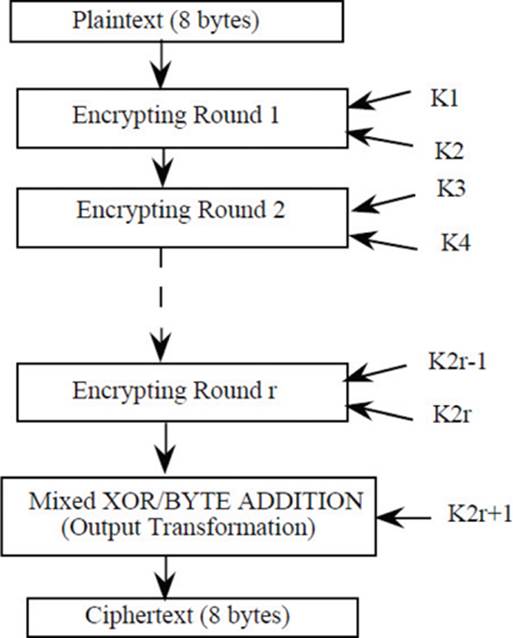
FIGURE 7-6 Overview of the SAFER function from the original paper

Note

You can find the original SAFER K-64 paper by James Massey at http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.3.4781&rep=rep1&type=pdf.

KHAZAD

The KHAZAD algorithm was designed by Rijmen (one of the creators of the Rijndael cipher) and Paulo Barreto. The name is not an acronym but is derived from a fictional Dwarven kingdom from J.R.R. Tolkien’s books called Khazad-dûm. KHAZAD uses eight rounds on a 64-bit block, applying a 128-bit key. This algorithm is not patented and is free to anyone who wants to use it.

NESSIE

In Europe, a project similar to the AES competition, named NESSIE (New European Schemes for Signatures, Integrity, and Encryption), lasted from 2000 to 2003, with the goal of not only finding a new standard symmetric cipher, but also finding secure cryptographic primitives. Cryptographic primitives are discussed frequently in this book.

Note

Cryptographic primitives are basic cryptographic algorithms used to build cryptographic protocols. Cryptographic hashes, symmetric algorithms, and asymmetric algorithms all qualify as cryptographic primitives. These primitives are combined to create cryptographic protocols such as Secure Sockets Layer (SSL) and Transport Layer Security (TLS), which you will study in Chapter 13.

Several algorithms of various types were selected in the competition, including the block ciphers MISTY1, Camellia, SHACAL-2, and AES/Rijndael. RSA was also one of the three asymmetric algorithms selected. For cryptographic hashes and message authentication codes, HMAC and SHA were chosen as well as Whirlpool.

Stream Ciphers

A stream cipher is a special type of symmetric cipher. Both Feistel ciphers and SPMs break the plain text into blocks and then encrypt each block. Stream ciphers take each bit of plain text and encrypt it with the key stream to produce the cipher text stream. The combination is usually done via XOR operations.

There are two types of stream ciphers: synchronous and self-synchronizing. In a synchronous stream cipher (sometimes called a binary additive stream cipher), the key is a stream of bits produced by some pseudo-random number generator. The production of this key stream is completely independent of the plain text. The key stream is XOR’d with the plain text to produce the cipher text. This is called a synchronous cipher because the sender and receiver need to be in synch. If digits are added or removed from the message during transmission (such as by an attacker), that synchronization is lost and needs to be restored.

Self-synchronizing ciphers use parts of the current cipher text to compute the rest of the key stream. In other words, the algorithm starts with an initial key stream, like an initialization vector, and then creates the rest of the key stream based on the cipher text already produced. These types of ciphers are sometimes called cipher text autokeys. The idea was patented in 1946, long before the advent of modern computer systems. With self-synchronizing ciphers, if digits are added or removed in transit, the receiving end can still continue to decrypt.

LFSR

There are multiple ways to create the pseudo-random key stream. One of these is to use linear feedback shift registers (LFSRs). A shift register is a type of register found in digital circuits—basically a chain of flip-flops that shifts the data stored in it by 1 bit, thus the name. LFSRs are chosen because they are easy to implement in hardware. An LFSR uses its previous state to form the input for the current state.

Usually a linear function is used to modify the data in each round, and most often an XOR is used. The LFSR is given an initial value, or seed. Then the register will shift that value and then XOR it with the previous value. Consider this rather simplified example:

Input: 0101110

First, it is shifted by the LFSR:

Then that value is XOR’d with the previous state:

This can be repeated with yet another shift and another XOR operation. You will see LSFRs used later in the book when we discuss pseudo-random number generators.

RC4

RC4, designed by Ron Rivest, is a widely known and used stream cipher, perhaps the most widely known. The RC stands for Ron’s cipher or Rivest cipher. Ron Rivest is a name that is very familiar in cryptography. He is the R in RSA, which we will explore in Chapter 10. RC4 is widely used in many security situations, including WEP (Wired Equivalent Privacy) and TLS. However, the algorithm was designed in 1987, and some experts have expressed concerns about its security. Some speculate that it can be broken, and many people recommend no longer using it in TLS. Nevertheless, it is the most widely known of stream ciphers and has a similar place in the history and study of stream ciphers as DES has in block ciphers.

RC4 Key Scheduling

The key scheduling algorithm is rather simple. It begins with an internal state that is denoted by a capital S. This state is a 256-byte array. (Although most of what you have seen so far involves bits, not bytes, this is not a typo.) There are two indexes, usually named i and j. These indexes are used to point to individual elements in the array. The key scheduling algorithm involves shuffling this array.

The first step in this algorithm involves initializing the state with what is termed the identity permutation. This means that the first element is initialized to 0, the second element to 1, the third to 0, and so on. Now, obviously, this is not very random at all, and in fact it is the antithesis of randomness. So the next step consists of shuffling, which involves iterating 256 times, performing the following actions:

1. Compute j = j + S[i] + key[i mod keylength].

2. Swap S[i] and S[j].

3. Increment i.

After 256 iterations of this, the array should be shuffled well. If you happen to have some programming experience, the following pseudo-code may assist you in understanding the shuffling:

You may argue that this is too predictable, because it would generate the same key each time. And if the algorithm stopped here, you would be correct. This is generating a state that will be used to create the key stream. But we are not done yet.

The rest of the algorithm allows for the generation of a key stream of any size. The goal is to create a key stream of the same size as the message you want to encrypt.

The first step is to initialize the two pointers i and j, and then generate the key stream 1 byte at a time. For each new byte, the algorithm takes the following steps:

1. Compute new value of i and j:

i := (i + 1) % 256

j := (j + S[i]) % 256

2. Swap S[i] and S[j].

3. Retrieve the next byte of the key stream from the S array at the index:

S[i]+S[j]% 256

Again, if you have some background in programming, you may find it easier to understand this using pseudo code:

Once you have generated the key stream, you XOR it with the plain text to encrypt, or XOR it with the cipher text to decrypt. One of the security issues with RC4 is that it does not use a nonce (a number only used once) along with the key. This means that if a key is being used repeatedly, it can be compromised. More modern stream ciphers, such as eSTREAM, specify the use of a nonce.

In 1994, Rivest published RC5 and then later, working with Matt Robshaw, Ray Sidney, and Yiqun Yin, he released RC6. However, both RC5 and RC6 are block ciphers, not stream ciphers. In fact, RC6 was designed for the AES competition.

FISH

The FISH (FIbonacci SHrinking) algorithm was published by the German engineering firm Siemens in 1993. It is a software-based stream cipher using a Lagged Fibonacci generator along with a concept borrowed from the shrinking generator ciphers.

A Lagged Fibonacci generator (LFG) is a particular type of pseudo-random-number generator. It is based on the Fibonacci sequence. Recall that the Fibonacci sequence is essentially this:

F_n = F_n–1 + F_n–2

This can be generalized to

X_n = X_n–l + X_n–k (mod m) where 0 < k < l

For most cryptographic applications, the m is some power of 2. Lagged Fibonacci generators have a maximum period of (2^k – 1)*2^m–1. This brings us to the topic of the period of a pseudo-random-number generator (PRNG). With any PRNG, if you start with the same seed you will get the same sequence. The period of a PRNG is the maximum of the length of the repetition-free sequence.

Note

Ross Anderson’s paper “On Fibonacci Keystream Generators” (http://www.cl.cam.ac.uk/~rja14/Papers/fibonacci.pdf) provides a very good discussion of Fibonacci-based key generation.

PIKE

The PIKE algorithm was published in a paper by Ross Anderson as an improvement on FISH. In that paper, Anderson showed that FISH was vulnerable to known plain-text attacks. PIKE is both faster and stronger than FISH. The name PIKE is not an acronym, but a humorous play on FISH, a pike being a type of fish.

eSTREAM

The eSTREAM project was a European search for new stream ciphers that ran from 2004 until 2008. It began with a list of forty ciphers and used three phases to narrow that list to seven ciphers. Four were meant for software implementations (HC-128, Rabbit, Salsa20/12, and SOSEMANUK) and three (Grain v1, MICKEY v2, and Trivium) for hardware. Brief descriptions of some of these ciphers are provided here:

SNOW

SNOW 1.0 was submitted to the NESSIE project and has since been supplanted by SNOW 2.0 and SNOW 3G. The SNOW cipher works on 32-bit words and can use either a 128-or 256-bit key. The cipher uses an LFSR along with a Finite State Machine (FSM).

Rabbit

Rabbit was designed by Martin Boesgaard, Mette Vesterager, Thomas Pederson, Jesper Christiansen, and Ove Scavenius. It is a stream cipher that uses a 128-bit key along with a 64-bit initialization vector. The cipher uses an internal state that is 513 bits. That consists of eight variables, each 32 bits in size; eight counters that are also 32 bits in size; and 1 counter bit. The variables are denoted as x_j,i, meaning the state of the variable of subsystem j at iteration i. The counter variables are denoted by c_j,i.

Note

The entire algorithm is described in the original paper, “The Stream Cipher Rabbit,” which can be found online at http://cr.yp.to/streamciphers/rabbit/desc.pdf.⁴

HC-128

HC-128 was invented by Hongjun Wu. It uses a 128-bit key with a 128-bit initialization vector. HC-128 consists of two secret tables, each with 512, 32-bit elements. At each step, one element of a table is updated with a nonlinear feedback function. All the elements of the two tables will get updated every 1024 steps. At each step, one 32-bit output is generated from the nonlinear output filtering function.

Note

The algorithm is described in detail in the paper, “The Stream Cipher HC-128,” at www.ecrypt.eu.org/stream/p3ciphers/hc/hc128_p3.pdf. In 2004, Wu published HC-256, which uses a 256-bit key and a 256-bit initialization vector.

MICKEY

MICKEY (Mutual Irregular Clocking KEYstream) generator was invented by Steve Babbage and Mathew Dodd. It uses an 80-bit key and a variable-length initialization vector (up to 80 bits in length).

MISTY1

MISTY1 (Mitsubishi Improved Security Technology) was invented by Matsue Mitsuru, Ichikawa Tetsuya, Sorimachi Toru, Tokita Toshio, and Yamagishi Atsurhio (note that the initials of the inventors’ first names also spell MISTY). It is a patented algorithm but can be used for free for academic purposes. MISTY1 is a Feistel network that uses 64-bit blocks and a key size of 128 bits. Its round function is a three-round Feistel network, so it is essentially a Feistel within a Feistel.

A5

A5/1 is a stream cipher that was used in GSM (Global System for Mobile Communications, also known as 2g) cell phones. It was originally a secret but eventually was made public. A variation, A5/2, was developed specifically to be weaker for export purposes.

Note

U.S. law prevents exporting cryptographic tools greater than a certain strength.

The KASUMI algorithm is used in A5/3, and it is also used in UMTS (Universal Mobile Telecommunications System, also known as 3G). In January 2010, Orr Dunkelman, Nathan Keller, and Adi Shamir released a paper showing that they could break KASUMI with a related key attack—the attack, however, was not effective against MISTY1.

Note

You can read their paper, “A Practical-Time Attack on the A5/3 Cryptosystem Used in Third Generation GSM Telephony,” at https://eprint.iacr.org/2010/013.pdf.

One-Time Pad

If used properly, the one-time pad is the only truly uncrackable encryption technique. It should be clear that this is true only if used properly. This idea was first described in 1882, but it was later rediscovered and patented in the early 20th century. In this technique, a random key is used that is as long as the actual message. If the key is sufficiently random, there will be no periods in the key, and periods in keys are used as part of cryptanalysis. The second aspect of this technique is actually in the name: the key is used for a single message and then discarded and never used again. Should the encryption somehow be broken and the key discovered (and this has never been done), it would cause minimal damage because that key will never be used again.

The patented version of this was invented in 1917 by Gilbert Vernam working at AT&T. It was patented in 1919 (U.S. Patent 1,310,719) and was called a Vernam cipher. It worked with teleprinter technology (the state of the art at that time). It combined each character of the message with a character on a paper tape key.

One-time pads are often described as being “information-theoretically secure.” This is because the cipher text provides no information about the original plain text. Claude Shannon, the father of information theory, said that the one-time pad provided “perfect secrecy.”

It should be obvious, however, that there are logistical issues with the one-time pad, since each message needs a new key. As you will see in Chapter 12, generating random numbers can be computationally intensive, with the issue of key exchange. Imagine for a moment that secure web site traffic was conducted with a one-time pad. That would require that a key be generated and exchanged for each and every packet sent between the web browser and the server. The overhead would make communication impractical. For this reason, one-time pads are used only in highly sensitive communications wherein the need for security makes the cumbersome nature of key generation and exchange worth the effort.

Conclusions

In this chapter you have learned about substitution-permutation networks as well as stream ciphers. The most important algorithm to know well is AES/Rijndael. The other algorithms are interesting, but the focus was on AES because it is widely used around the world, and within the United States it is a national standard.

Pseudo-random-number generators were also discussed, in relation to creating stream ciphers. PRNGs will be covered in much more detail in Chapter 12.

Test Your Knowledge

1. AES using a 192-bit key uses ___________ rounds.

2. What happens in the rotate phase of the Rijndael key schedule?

3. ___________ is a 32-round substitution-permutation matrix algorithm using key sizes of 128, 192, or 256 bits.

4. The ___________ algorithm is a stream cipher developed by Siemens that uses the Lagged Fibonacci generator for random numbers.

5. What are the two types of stream ciphers?

6. ___________ uses a 64-bit block with a 128-bit key and operates in six rounds.

7. In ___________, there are 33 subkeys or round keys, each 128 bits in size.

8. The ___________ key scheduling algorithm begins with a 256-byte array called the state.

9. Briefly describe the Rijndael shift rows step.

10. Which of the following steps does not occur in the final round of Rijndael?

A. SubBytes

B. ShiftRows

C. MixColumns

D. AddRoundKey

Answers

1. 12

2. The rotate operation rotates a 32-bit word (in hexadecimal) 8 bits to the left.

3. Serpent

4. FISH

5. synchronous and self-synchronizing

6. SHARK

7. Serpent

8. RC4

9. Each row of the state is shifted cyclically a certain number of steps. The first row is unchanged, the second row shifted 1 byte to the left, the third row 2 bytes to the left, and the fourth row 3 bytes to the left.

10. C

Endnotes

1. For more information, see “Serpent: A Proposal for the Advanced Encryption Standard,” by Anderson, Biham, and Knudsen, at www.cl.cam.ac.uk/~rja14/Papers/serpent.pdf.

2. For more information, see the article “The Block Cipher SQUARE,” at http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.55.6109.

3. See “The Cipher Shark,” at www.cosic.esat.kuleuven.be/publications/article-55.pdf.

4. M. Boesgaard, M. Vesterager, T. Christensen, and Erik Zenner, “The Stream Cipher Rabbit,” http://cr.yp.to/streamciphers/rabbit/desc.pdf.