Modern Cryptography: Applied Mathematics for Encryption and Informanion Security (2016)
PART II. Symmetric Ciphers and Hashes
Chapter 8. S-Box Design
In this chapter we will cover the following:
![]() The purpose of studying S-boxes
The purpose of studying S-boxes
![]() Types of S-boxes
Types of S-boxes
![]() Design criteria for S-boxes
Design criteria for S-boxes
![]() The DES S-box
The DES S-box
![]() The AES S-box
The AES S-box
![]() AES S-box variations
AES S-box variations
You’ll recall that a substitution box (S-box) is an integral part of many ciphers. In fact, it is often the key to the overall security of a given cipher. From the Data Encryption Standard (DES) to more modern ciphers, S-boxes have provided a means of altering the cipher text, and even transposing text, that goes far beyond simple XOR operations. An S-box is a lookup table in which m number of input bits are replaced with n number of output bits.
In his paper “A New Method for Generating High Non-linearity S-Boxes,” Petr Tesař states, “All modern block and stream ciphers have one or more non-linear elements. S-box is one of the most used non-linear cornerstones of modern ciphers.”1
Nonlinearity is an important concept in cryptography. The goal of any cipher is to have the output look as much like a random number as possible, and still be something we can decrypt later to get back the original plain text. Unfortunately, operations such as XOR are linear. S-boxes provide a very good source of nonlinearity in any block cipher.
Why Study S-Box Design?
Many cryptography textbooks provide scant, if any, coverage of S-box design. Usually the S-boxes used in DES or AES are explained in varying levels of detail, but that is the extent of the coverage. And many texts don’t go into any real depth on AES S-box design. So why devote an entire chapter to the study of S-boxes? Why not follow the de facto standard in cryptography texts and simply gloss over this topic? Put another way, why should you devote time to studying this topic? There are actually three primary reasons you should study S-box design. Each is explained in detail in the following sections.
Critical to Block Ciphers
You are already aware that S-boxes form a major part of most block ciphers and that they are the primary source for nonlinearity in modern block ciphers. It would be impossible to study symmetric cryptography thoroughly without knowing a bit about S-boxes. If you do not understand S-boxes, you will be forced to treat a portion of most block ciphers as simply a “black box,” having no real understanding of what happens inside or why. This fact should be readily apparent from the algorithms you studied in Chapters 6 and 7.
Consider the Feistel ciphers you studied in Chapter 6. The XOR operation forms a part of every Feistel cipher. In most round functions, there is an XOR with the round key, and of course there is a transposition of the two halves of the block each round. But the real substance of encrypting comes from the S-box. Without it, Feistel ciphers would be extremely weak and would not be acceptable for modern use. In fact, without the S-boxes, many block ciphers would not be much better than combining a substitution cipher such as Caesar with a transposition cipher such as rail-fence, and executing it several times.
Designing Ciphers
Should you ever be involved in the design of a symmetric cipher, you will need to design S-boxes. These are often key to the security of a symmetric cipher. It will be important that you understand the principles of S-box design.
Note
Usually designing your own cipher is a bad idea. It is most likely that in attempting such a task, you will create a cipher that is, at best, weak. However, someone must create the new ciphers that appear from time to time, so clearly some people do create new ciphers that are secure. My recommendation is that you carefully study cryptography for several years, looking at existing ciphers in detail. Before considering developing your own cipher, you must thoroughly understand a wide range of existing ciphers. Consider the inventors of the algorithms you have read about in Chapters 6 and 7. All had extensive related education, such as in mathematics, and all have worked in the field of cryptography for many years. This is not a field in which a novice is likely to make a substantive contribution. Becoming a cryptographer is a lengthy process. This book may be the first step on that journey. Then, if after careful and in-depth study, you are compelled to create a new cipher, submit it to the peer review process so that experts in the field can evaluate your idea.
It is difficult to overemphasize the importance of the S-box in designing a block cipher. Anna Grocholewska-Czurylo, in her paper “Cryptographic Properties of Modified AES-Like S-Boxes,” describes the importance of S-boxes as follows:
S-box design is usually the most important task while designing a new cipher. This is because an S-box is the only nonlinear element of the cipher upon which the whole cryptographic strength of the cipher depends. New methods of attacks are constantly being developed by researchers, so S-box design should always be one step ahead of those pursuits to ensure cipher’s security.2
Altering S-Boxes
Finally, there are some organizations, primarily governments, who want the security of well-known algorithms such as Advanced Encryption Standard (AES), but also want an implementation that is private to their organization. One reason this may be desirable in some situations is that it provides an extra layer of security. Should an outside party obtain the symmetric key being used, but apply it to intercepted cipher text using the standard Rijndael cipher, the message will not be decrypted. The interest in this topic has increased as awareness of cryptographic backdoors has increased, particularly when such backdoors are used in random-number generators that generate keys for algorithms such as AES. We will study cryptographic backdoors in detail in Chapter 18.
In 2013, then CIA employee Edward Snowden released classified documents that indicated that the U.S. National Security Agency (NSA) had placed backdoors in some random-number generators. This prompted some concern as to the dependability of widely used random-number generators. Some governments considered simply redesigning the S-boxes of AES so that their specific AES implementation was not standard, so that even if the key were generated from a backdoor, an attacker would still have to know the specifics of the organization’s AES implementation to compromise their security.
General Facts about S-Boxes
The core of most block ciphers (including Blowfish, AES, DES, Serpent, GOST, and so on) is the S-box. An S-box provides the source of nonlinearity for a given cryptographic algorithm. Other facets of the algorithm are typically just various swapping mechanisms and exclusive or (XOR) operations. The XOR, in particular, provides no diffusion or confusion in the resulting cipher text. (Recall that these concepts were discussed in Chapter 3.) In fact, the basis of differential cryptanalysis is the fact that the XOR operation maintains the characteristics found in the plain text to cipher text. We will closely examine differential cryptanalysis in Chapter 17.
According to Grocholewska-Czurylo,3 “S-box design is usually the most important task while designing a new cipher. This is because an S-box is the only nonlinear element of the cipher upon which the whole cryptographic strength of the cipher depends.” Although other aspects of a given S-box clearly have an impact on the security and efficiency of a given block cipher, the S-box is the core of the security. For this reason, proper S-box design is imperative.
Types of S-Boxes
S-boxes can be grouped into two types: substitution boxes and permutation boxes. A substitution box substitutes input bits for output bits. A permutation box (sometimes called a P-box) transposes the bits. It is often the case that cryptologists use “S-box” to refer to either type.
Let’s first consider a simple 3-bit S-box that performs substitution. Each 3 bits of input are mapped to the 3 bits of output. This S-box is shown in Figure 8-1. The first bit of input is on the left, the second 2 bits are on the top. By matching those you will identify the output bits.
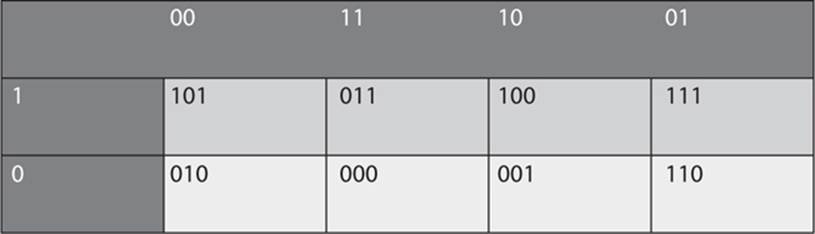
FIGURE 8-1 A 3-bit S-box
For example, with this S-box, an input of 110 would produce an output of 100. An input of 100 would produce an output of 101. This S-box is very simple and does not perform any transposition. (Note that the values of output were chosen at random.)
A P-box is an S-box that transposes, or permutes, the input bits. It may, or may not, also perform substitution. Figure 8-2 shows a P-box.
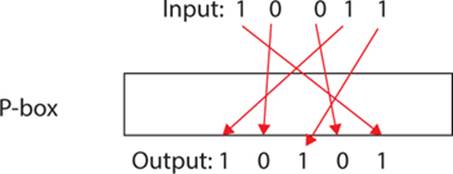
FIGURE 8-2 A P-box
Of course, in the process of permutation, the bit is also substituted. For example, if the least significant bit in the input is transposed with some other bit, then the least significant bit in the output is likely to have been changed. In the literature, you will often see the term S-box used to denote either a substitution box or a permutation box. This makes complete sense when you consider that, regardless of which type it is, one inputs some bits and the output is different bits. So for the remainder of this chapter, I will use the term S-box to denote either a substitution or permutation box.
Whether an S-box or a P-box, there are three subclassifications: straight, compressed, and expansion. A straight S-box takes in a given number of bits and puts out the same number of bits. This is the design approach used with the Rijndael cipher and is frankly the easiest and most common form of S-box.
A compression S-box puts out fewer bits than it takes in. A good example of this is the S-box used in DES, in which each S-box takes in 6 bits but outputs only 4 bits. Keep in mind, however, that in the DES algorithm, there is a bit expansion phase earlier in the round function. In that case, the 32 input bits are expanded by 16 bits to create 48 bits. So when eight inputs of 6 bits each are put into each DES S-box, and only four are produced, the difference is 16 (8 × 2). So the bits being dropped off are those that were previously added. You can see a compression S-box inFigure 8-3.
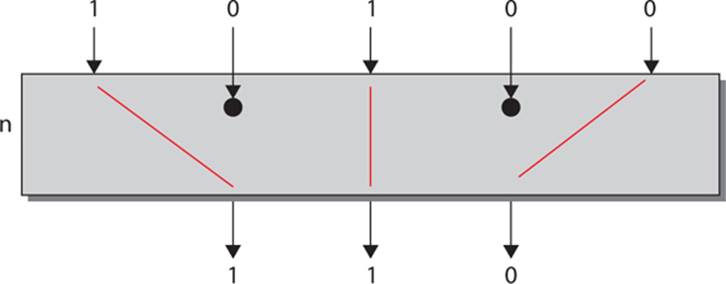
FIGURE 8-3 A compression S-box
The third type of S-box, similar to a compression S-box, is the expansion S-box. This S-box puts out more bits than it takes in. This can be accomplished by simply duplicating some of the input bits. This is shown in Figure 8-4.
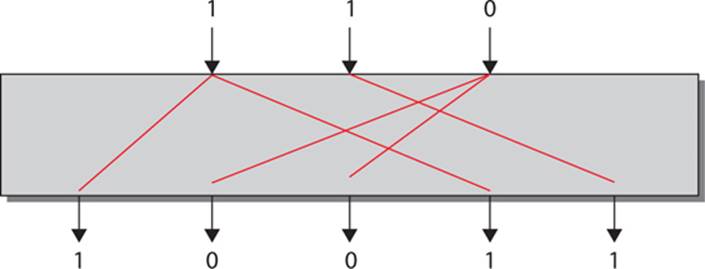
FIGURE 8-4 An expansion S-box
Significant issues are associated with both compression and expansion S-boxes. The first issue is reversibility, or decryption. Since either type of S-box alters the total number of bits, reversing the process is difficult. You have to be very careful in the design of such an algorithm, or it is likely that decryption will not be possible. The second issue is a loss of information, particularly with compression S-boxes. In the case of DES, prior to the S-box, certain bits are replicated. Thus what is lost in the compression step are duplicate bits and no information is lost. In general, working with either compression or expansion S-boxes will introduce significant complexities in your S-box design. Therefore, straight S-boxes are far more common.
Design Considerations
Regardless of the type or category of S-box that is being created, any S-box must exhibit certain features in order to be effective. You cannot simply put together any substitution scheme you want and create a good S-box. It is not enough that it simply substitutes values; an S-box must also provide confusion and diffusion. The efficacy of an S-box is usually measured by examining three separate criteria that contribute to its security: strict avalanche criterion, balance, and bit independence criterion.
Strict Avalanche Criterion
Strict avalanche criterion (SAC) is an important feature of an S-box.4 Remember from Chapter 3 that avalanche is a term that indicates that when 1 bit in the plain text is changed, multiple bits in the resultant cipher text are changed. Consider the following example:
1. We begin with a plain text, 10110011.
2. Then after applying our cipher, we have 11100100.
But what if, prior to encrypting the plain text, we change just 1 bit of the plain text—for example, the third bit from the left, so we have 10010011? In an cipher with no avalanche, the resulting cipher text would change by only 1 bit, perhaps 11100101. Notice that the only difference between this cipher text and the first cipher text is the last, or least significant, bit. This shows that a change of 1 bit in the plain text changed only 1 bit in the cipher text. That is no avalanche. However, if our algorithm has some avalanche, then changing the plain text from
![]()
to
![]()
will change more than 1 bit in the cipher text. In this case, before the change in plain text, remember our cipher text was
![]()
Now, if our cipher has some avalanche, we expect more than 1 bit in the cipher text to change, perhaps 2 bits:
![]()
Notice that the second and last bits are different. So a change in 1 bit of the plain text produced a change in 2 bits in the cipher text. Ideally, we would like to get more avalanche than this, as much as having a change in a single bit of plain text change half the cipher text bits. Without some level of avalanche, a cryptanalyst can examine changes in input and the corresponding changes in output and make predictions about the key. It is therefore critical that any cipher exhibit at least some avalanche.
In most block ciphers, the primary way to achieve avalanche is to use an S-box. SAC is one way of measuring this phenomena; it requires that for any input bit, the output bit should be changed with a probability of 0.5. In other words, if you change any given input bit, there is a 50/50 chance that the corresponding output bit will change.
One measurement of strict avalanche criteria is the hamming weight. Recall from Chapter 3 that the hamming weight of a specific binary vector, denoted by hwt(x), is the number of 1’s in that vector. Therefore, if you have an input of 8 bits with three 1’s and an output of four 1’s, the hamming weight of the output is 4. Simply measuring the hamming weight of the input and the output and comparing them will give one indication of whether or not SAC is satisfied. This is a simple test that you should subject any S-box to.
Balance
Balance is also important in effective S-box design. Various papers provide slightly different definitions of balance.5 However, in the current context, perhaps the best definition is that each output symbol should appear an equal number of times when the input is varied over all possible values. Some sources address S-boxes with unequal input and output, though it’s safe to say that an S-box with n input bits and m output bits, m < n, is balanced if every output occurs 2n–m times. So an S-box with a 6-bit input and 4-bit output would need each output bit to occur four times (26–4).
Bit Independence Criterion
The bit independence criterion (BIC) is the third criteria for good S-box design.6 Bit independence criterion states that output bits j and k should change independently when any single input bit i is inverted, for all i, j, and k. The output bits change independently of each other. They are, of course, dependent on the input bits.
Approaches to S-Box Design
A number of approaches to S-box design are currently in use:
![]() One method simply uses a pseudo-random number generator for each entry in the S-box. The problem with this approach, however, is that you will not be able to predict whether or not your S-box actually fulfills the three criteria for an effective S-box. Instead, you will have to test extensively.
One method simply uses a pseudo-random number generator for each entry in the S-box. The problem with this approach, however, is that you will not be able to predict whether or not your S-box actually fulfills the three criteria for an effective S-box. Instead, you will have to test extensively.
![]() A second approach is the human-made approach, in which some person (or persons) manually selects the values for the S-box—hopefully based on sound criteria. This was the method used in DES, and, in fact, the details of how the S-box for DES was designed are not public information. The actual S-boxes for DES are public, but the methodology for designing them is not. These S-boxes were designed in cooperation with the NSA.
A second approach is the human-made approach, in which some person (or persons) manually selects the values for the S-box—hopefully based on sound criteria. This was the method used in DES, and, in fact, the details of how the S-box for DES was designed are not public information. The actual S-boxes for DES are public, but the methodology for designing them is not. These S-boxes were designed in cooperation with the NSA.
![]() Another approach uses some mathematical-based method to generate the values for the S-box. This is the method used in AES.
Another approach uses some mathematical-based method to generate the values for the S-box. This is the method used in AES.
The DES S-Box
As discussed in Chapter 6, the NSA was involved in the creation of DES—specifically in the S-box design. In fact, Alan Konheim, one of the IBM designers who worked on DES, is quoted as saying, “We sent the S-boxes off to Washington. They came back and were all different.”7 This led many people to believe that there might be a cryptographic backdoor embedded in the DES S-boxes, which would allow the NSA to break DES-encrypted communications easily. However, many years of study and analysis have not revealed any such backdoor.
The DES S-boxes convey a resistance to differential cryptanalysis, which we will study in Chapter 17. In fact, it has been discovered that even a small change to the DES S-box can significantly weaken its resistance to differential cryptanalysis. Differential cryptanalysis was unknown to the public at the time DES was invented (differential cryptanalysis was introduced—at least publically—by Eli Biham and Adi Shamir in the late 1980s). It is interesting to note that both Biham and Shamir noticed that DES is very resistant to differential cryptanalysis.8 It therefore seems most likely that the NSA was aware of differential cryptanalysis long before it was publically known, and DES was created to be resistant to that attack.
The Actual S-Boxes for DES
Although the DES S-box design choices themselves have not been made public, we can derive some knowledge from studying them. As far as is publically known, the S-boxes are not derived from a mathematical formula, as the S-boxes in AES are. It seems that each substitution was specifically and manually chosen. Figure 8-5 shows DES S-boxes 1 through 8.
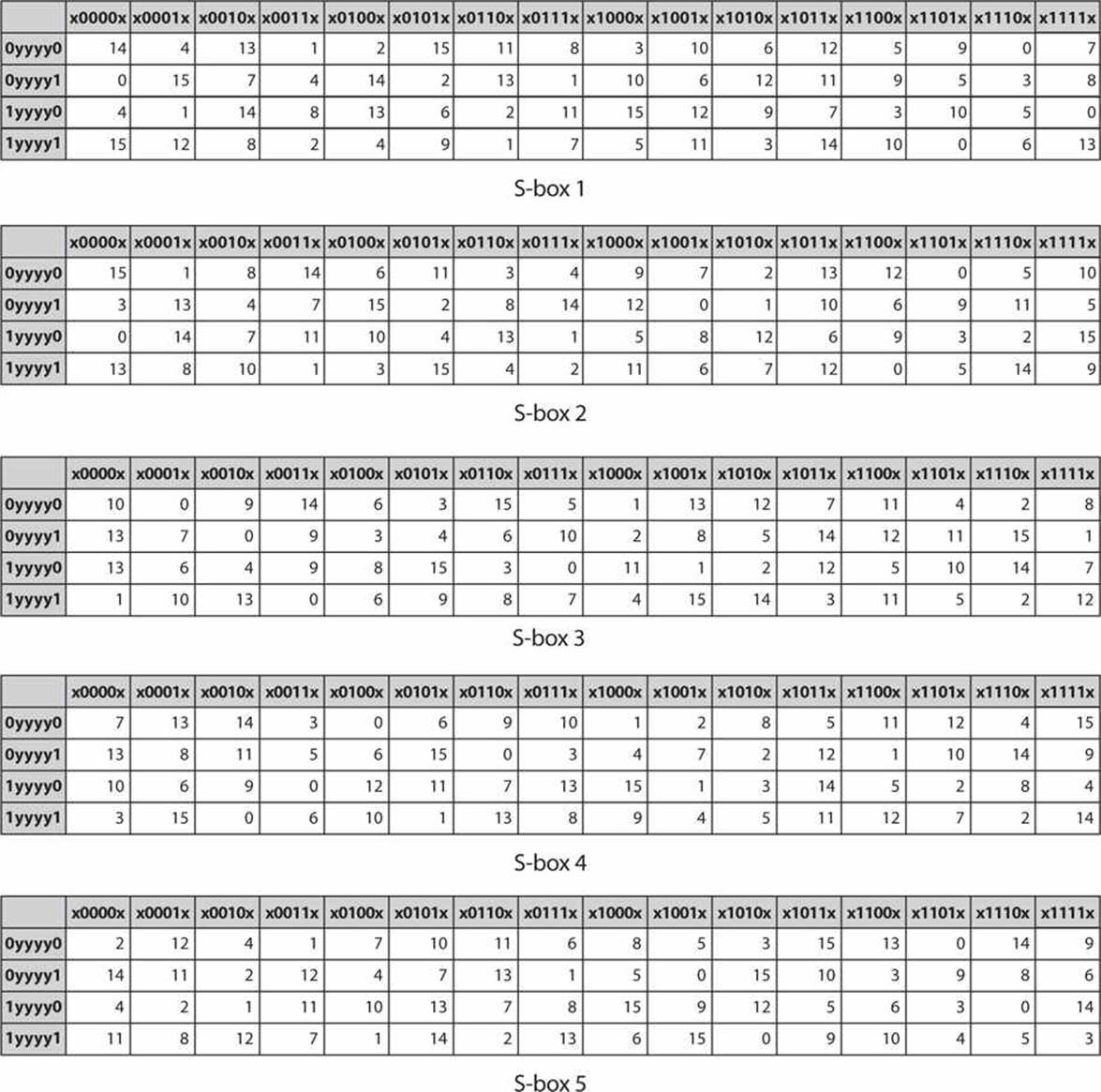
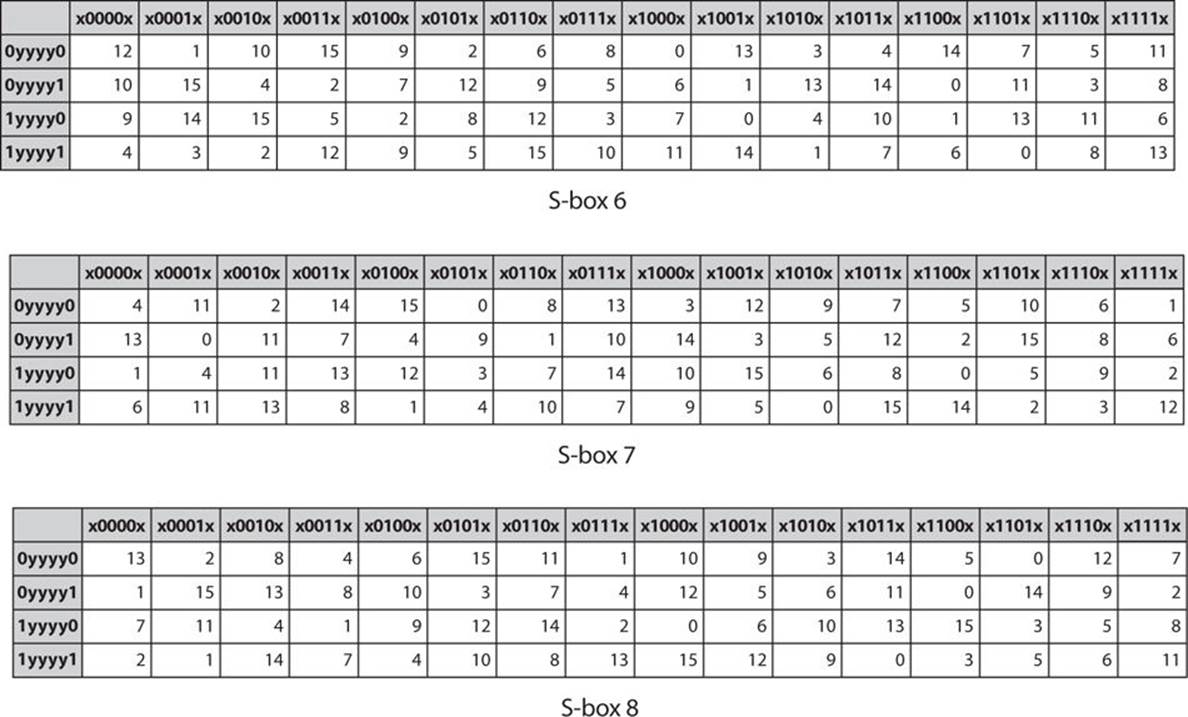
FIGURE 8-5 S-boxes 1 through 8
As you know, DES S-boxes are compression S-boxes. They take in 6 input bits and produce 4 output bits. Examine S-box 1, and you can see how this is done. All possible combinations of the middle 4 bits of the input are listed on the top row of the S-box. All possible combinations of the outer 2 bits are listed on the far left column. By matching the outer bits on the left with the inner bits on the top, you can find the output bits. Some substitutions change several bits. For example, in S-box 1, an input of all 0’s, 000000 produces 1110. However, others produce far less change—for example, again focusing on S-box 1, an input of 001000 produces 0010. A simple shift of the 1 to the right.
Although most of the S-boxes provide a different substitution for any input, there is some overlap. For example, inputting 000110 in either S-box 2 or S-box 3 will produce 1110. In several cases, different inputs to an S-box produce the same output. For example, in S-box 5, notice that an input of 000001 produces 1110. However, an input of 111110 also produces 1110.
There has been no public disclosure as to why the specific design choices for DES S-boxes were made. As mentioned, resistance to differential cryptanalysis appears to have played a significant role. However, another factor is the nature of these S-boxes as compression boxes. It is difficult to design an S-box that uses compression without losing data. In the case of DES, it is possible only because an earlier step in the algorithm expanded bits. At least some of the design choices in DES are related to providing the compression without losing data.
The Rijndael S-Box
Given the prominence of AES, the Rijndael S-box is a good candidate for analysis. In fact, this is probably the most important portion of this chapter. Before we delve deeply into the S-boxes for Rijndael, let’s look at some of the mathematics behind the S-box design. The actual Rijndael S-box is shown in Figure 8-6.

FIGURE 8-6 Rijndael S-box
The Irreducible Polynomial
The Rijndael S-box is based on a specific irreducible polynomial in a specific Galois field:
GF(28) = GF(2)[x]/(x8 + x4 + x3 + x + 1)
In hexadecimal, this is 11B; in binary, it is 100011011.
Note
An irreducible polynomial cannot be factored into the product of two other polynomials; in other words, it cannot be reduced. This is in reference to a specific field—with the irreducible polynomial we are considering, it is in reference to the Galois field GF(28). Put more formally, a polynomial is irreducible in GF(p) if it does not factor over GF(p). Otherwise, it is reducible.
Why was this specific irreducible polynomial chosen? Does it have some special property that makes it more suitable for cryptography? To answer that question, let’s consider the actual words of the inventors of Rijndael: “The polynomial m(x) (‘11B’) for the multiplication in GF(28) is the first one of the list of irreducible polynomials of degree 8.”9 In other words, they looked at a list of irreducible polynomials in a specific text and chose the first one. This is important to keep in mind. Any irreducible polynomial of the appropriate size can be used.
The text that Daemen and Rijmen consulted for their list of irreducible polynomials was Introduction to Finite Fields and Their Applications, by Rudolf Lidl and Harald Niederreiter (Cambridge University Press, 1986, revised in 1994). You can check the same source that was cited by the inventors of Rijndael. Here are a few irreducible polynomials from that list (in binary form, but you can place them in polynomial or hex form if you want):

You may have noticed that all of these, and the one chosen for Rijndael, have nine digits. Why use degree 8 (nine digits)—isn’t that one too many? According to the algorithm specification, “Clearly, the result will be a binary polynomial of degree below 8. Unlike for addition, there is no simple operation at byte level.”
The reason an irreducible polynomial must be used, instead of just any polynomial (or a primitive polynomial), is that Rijndael is trying to make a nonlinear permutation function that has diffusion, spreading input bits to output bits in a nonlinear way.
Multiplicative Inverse
In mathematics, the reciprocal, or multiplicative inverse, of a number x is the number that, when multiplied by x, yields 1. The multiplicative inverse for the real numbers, for example, is 1/x. To avoid confusion by writing the inverse using set-specific notation, it is generally written as x–1.
Multiplication in a Galois field, however, requires more tedious work. Suppose f(p) and g(p) are polynomials in GF(pn), and let m(p) be an irreducible polynomial (or a polynomial that cannot be factored) of degree at least n in GF(pn). We want m(p) to be a polynomial of degree at least n so that the product of two f(p) and g(p) does not exceed 11111111 = 255, because the product needs to be stored as a byte. If h(p) denotes the resulting product, then
h(p) ≡ (f(p) * g(p))(mod m(p))
On the other hand, the multiplicative inverse of f(p) is given by a(p) such that
(f(p) * a(p))(mod m(p)) ≡ 1
Note that calculating the product of two polynomials and the multiplicative inverse of a polynomial requires both reducing coefficients modulo p and reducing polynomials modulo m(p). The reduced polynomial can be calculated easily with long division, while the best way to compute the multiplicative inverse is by using the extended Euclidean algorithm. The details on the calculations in GF(28) is best explained in the example that follows.
Finite field multiplication is more difficult than addition and is achieved by multiplying the polynomials for the two elements concerned and collecting like powers of x in the result. Since each polynomial can have powers of x up to 7, the result can have powers of x up to 14 and will no longer fit within a single byte.
This situation is handled by replacing the result with the remainder polynomial after division by a special eighth order irreducible polynomial, which, as you may recall for Rijndael, is
m(x) = x8 + x4 + x3 + x + 1
The finite field element {00000010} is the polynomial x, which means that multiplying another element by this value increases all its powers of x by 1. This is equivalent to shifting its byte representation up by 1 bit so that the bit at position i moves to position i+1. If the top bit is set prior to this move, it will overflow to create an x8 term, in which case the modular polynomial is added to cancel this additional bit, leaving a result that fits within a single byte.
For example, multiplying {11001000} by x, that is {00000010}, the initial result is 1{10010000}. The “overflow” bit is then removed by adding 1{00011011}, the modular polynomial, using an XOR operation to give a final result of {10001011}. However, you need not calculate the multiplicative inverse manually. The table in Figure 8-7 provides multiplicative inverses.

FIGURE 8-7 Multiplicative inverses
Affine Transformation
This concept originates in graphics and is also used in transforming graphics. Moving pixels in one direction or another is very similar to moving a value in a matrix, so the concept gets applied to matrices (as in AES). In geometry, an affine transformation—or affine map or an affinity—(from the Latin, affinis, “connected with”) between two vector spaces (strictly speaking, two affine spaces) consists of a linear transformation followed by a translation. In general, an affine transform is composed of linear transformations (rotation, scaling, or shear) and a translation (or shift). For our purposes, it is just a word for a linear transformation.
Generating the S-Box
The Rijndael S-box can be generated with a series of shift operations; in fact, this is exactly how it is usually implemented in programming. These shifts essentially accomplish the same process as matrix multiplication.
The matrix multiplication can be calculated by the following algorithm:
1. Store the multiplicative inverse of the input number in two 8-bit unsigned temporary variables: s and x.
2. Rotate the value s 1 bit to the left; if the value of s had a high bit (eighth bit from the right) of 1, make the low bit of s 1; otherwise the low bit of s is 0.
3. XOR the value of x with the value of s, storing the value in x.
4. For three more iterations, repeat steps 2 and 3 a total of four times.
5. The value of x will now have the result of the multiplication.
After the matrix multiplication is complete, XOR the resultant value by the decimal number 99 (the hexadecimal number 0x63, the binary number 1100011, and the bit string 11000110 representing the number in least significant bit first notation). This value is termed the translation vector. This last operation, the final XOR, is meant to prevent any situation wherein the output is the same as the input—in other words to prevent S-box(a)=a.
An Example Generating the S-Box
It may be helpful for you to see an actual example generating the S-box.
1. Take a number for GF(28)—let’s pick 7. Looking at the multiplicative inverse table gives us d1 in hex or 11010001 in binary.
2. Now we need to do four iterations of the process of affine transformation. We start by putting the multiplicative inverse into two variables s and x:
s = 11010001
x = 11010001
3. Now we simply rotate s(10001101) to the left = 00011010
![]() If the high bit is 1 make the low bit 1
If the high bit is 1 make the low bit 1
![]() Else low bit is 0
Else low bit is 0
4. Now in this case, the high bit was 1, so we change the low bit, thus
s = 00011011
5. XOR that number with x so 00011011 XOR 10001101= 10010110
s = 00011011; x = 10010110
6. Next rotate s (00011011) to the left = 00110110.
A. If this still gives us 00110110, XOR with x, so
00110110 XOR 10010110 = 10100000
s = 00110110; x = 10100000
7. Next rotate s(00110110) to the left = 01101100.
A. If this still gives us 01101100, XOR with x, so
01101100 XOR 10100000= 11001100
s = 01101100; x = 11001100
8. Next rotate s(01101100) to the left = 11011000.
A. If this still gives us 11011000, XOR with x, so
01101100 XOR 11001100= 00010100
s = 11011000; x = 00010100
9. Now x (00010100) gets XOR’d with decimal 99 (hex x63 binary 1100011) = 1110111 or 77.
Remember the output of the matrix multiplication (which we have accomplished via shift operations) is finally XOR’d with the translation vector (decimal 99). This process allows you to create the Rijndael S-box, and it is in fact how that S-box is often created in code.
Changing the Rijndael S-Box
After studying the previous section, you should realize that there are three factors in generating the AES S-box. The first is the selection of the irreducible polynomial—in this case it was P = x8 + x4 + x3 + x + 1, which is 11B in hexadecimal notation, or 100011011 in binary numbers. As I mentioned previously, the creators of the Rijndael cipher stated clearly that this number was chosen simply because it was the first on the list of irreducible polynomials of degree 8 in the reference book they chose. That means that you could choose other irreducible polynomials.
In fact, you can choose from a total of 30 irreducible polynomials of degree 8, and this gives you 29 alternatives to the traditional S-box for AES, each with well-tested security. For more details on this alternative, you can look into Rabin’s test for irreducibility (seehttp://math.stackexchange.com/questions/528552/rabins-test-for-polynomial-irreducibility-over-mathbbf-2). In their paper “Random S-Box Generation in AES by Changing Irreducible Polynomial,” Das, Sanjoy, Subhrapratim, and Subhash10 demonstrated an equally secure variation of the Rijndael, by changing the chosen irreducible polynomial. You can use any of the 30 possible irreducible polynomials; each of these is equally secure to the original Rijndael cipher S-box.
Note
Altering the Rijndael S-box is practical only if you have the ability to ensure that all parties to encrypted communication will be using your modified S-box. If you simply modify the S-box on your end, you would render communication with other parties impossible. Even though those other parties will have the same key and the same algorithm (AES), they will be using standard S-boxes. This is why altering AES S-boxes is primarily an issue for government entities that want to have secure communication with a limited number of involved parties.
A second option, one that may be the simplest to implement, is to change the translation vector (the final number you XOR with). Obviously, there are 255 possible variations. Rather than use 0x63, you can use any of the other possible variations for that final byte. Although simple to implement, it may be more difficult to test. Some variations might adversely affect one of the three criteria that you are attempting to maintain. In fact, selecting the wrong translation vector may lead to no change at all when it is applied to the product of the preceding matrix multiplication.
The third method is to change the affine transform, and this can be more difficult to implement but safe if you simply alter parameters within the existing transform. Section 5.2 of Sinha and Arya’s paper “Algebraic Construction and Cryptographic Properties of Rijndael Substitution Box”11 discusses this in detail. According to Cui, et al.,12 the choice of affine transformation matrix or irreducible polynomial has no significant impact on the security of the resultant cipher text.
Conclusions
The S-box (or in some cases, S-boxes) is a critical part of most block ciphers. To understand any block cipher fully, you need to have some understanding of S-box design. S-boxes fall into two main categories: substitution and permutation. Either of these can be divided into three subcategories: straight, compression, and expansion.
In addition to S-boxes in general, the Rijndael S-box warrants particular attention. In addition to the standard Rijndael S-box commonly used, three relatively simple methods can be used to alter the S-box used in the Rijndael cipher. This will lead to permutations of Rijndael that are equal, or very nearly equal, in security to the original cipher. Using such permutations can lead to private versions of the AES algorithm, which can be useful for certain governmental and military applications.
If you want to delve into S-box design beyond the scope of this chapter, unfortunately there are no books on S-box design. As mentioned, many cryptography texts avoid this topic altogether or provide cursory coverage. You may, however, find a few sources useful (beyond those cited in the chapter endnotes), which can be found online using a Google search:
![]() Dawson and Tavares, “An Expanded Set of S-box Design Criteria Based on Information Theory and Its Relation to Differential-Like Attacks.”
Dawson and Tavares, “An Expanded Set of S-box Design Criteria Based on Information Theory and Its Relation to Differential-Like Attacks.”
![]() Adams and Tavares, “The Use of Bent Sequences to Achieve Higher-Order Strict Avalanche Criterion in S-Box Design.”
Adams and Tavares, “The Use of Bent Sequences to Achieve Higher-Order Strict Avalanche Criterion in S-Box Design.”
Test Your Knowledge
1. In mathematics, the ____________ of a number x is the number that, when multiplied by x, yields 1.
2. What is the irreducible polynomial used in standard AES?
3. What is the strict avalanche criterion in S-box design?
4. What is the bit independence criterion in S-box design?
5. What is the value of the Rijndael translation vector?
6. How many irreducible polynomials are there for the generation of the Rijndael S-box?
7. What is the primary advantage that DES S-boxes convey on the DES cipher?
8. A ___________ provides the source of nonlinearity for a given cryptographic algorithm.
9. An S-box that transposes bits is called a ___________.
10. What are the two concerns with using a compression S-box?
Answers
1. multiplicative inverse
2. x8 + x4 + x3 + x + 1
3. The S-box must produce at least 50 percent avalanche.
4. The resulting bits must be independent of each other.
5. Decimal 99, hex x63, or binary 1100011
6. 30
7. Resistance to differential cryptanalysis
8. substitution box
9. permutation box
10. Loss of data and an inability to decrypt enciphered messages
Endnotes
1. Petr Tesař, “A New Method for Generating High Non-linearity S-Boxes,” (p. 1), 2010, www.radioeng.cz/fulltexts/2010/10_01_023_026.pdf.
2. A. Grocholewska-Czurylo, “Cryptographic Properties of Modified AES-Like S-Boxes,” Annales UMCS Informatica, AI XI(2), (2011): 37–48.
3. Ibid.
4. For more about the avalanche effect, see “Differential Cryptanalysis of DES-like Cryptosystems” by E. Biham and A. Shamir, at http://zoo.cs.yale.edu/classes/cs426/2012/bib/biham91differential.pdf.
5. One article that provides information about balancing S-box cryptographic functions is “Improving the Strict Avalanche Characteristics of Cryptographic Functions,” by J. Seberry, X. Zhang, and Y. Zheng, at www.uow.edu.au/~jennie/WEBPDF/1994_09.pdf.
6. For more information about BIC, see “Good S-Boxes Are Easy to Find,” by Carlisle Adams and Stafford Taveres, published in the Journal of Cryptology, vol. 3, no. 1 (1990), pp. 27–41.
7. Bruce Schneier, Applied Cryptography (Wiley, 1996), p. 280.
8. Biham and Shamir, http://zoo.cs.yale.edu/classes/cs426/2012/bib/biham91differential.pdf.
9. J. Daemen and V. Rijmen, “AES Proposal: Rijndael,” 1999, http://csrc.nist.gov/archive/aes/rijndael/Rijndael-ammended.pdf.
10. I. Das, R. Sanjoy, N. Subhrapratim, and M. Subhash, “Random S-Box Generation in AES by Changing Irreducible Polynomial,” 2012. You can purchase and download the document from the IEEE Xplore Digital Library (http://ieeexplore.ieee.org/Xplore/home.jsp).
11. S. Sinha and C. Arya, “Algebraic Construction and Cryptographic Properties of Rijndael Substitution Box,” 2012, http://publications.drdo.gov.in/ojs/index.php/dsj/article/viewFile/1439/605.
12. J. Cui, L. Huang, H. Zhong, C. Chang, and W. Yang, “An Improved AES S-Box and Its Performance Analysis,” 2011, www.ijicic.org/ijicic-10-01041.pdf.
All materials on the site are licensed Creative Commons Attribution-Sharealike 3.0 Unported CC BY-SA 3.0 & GNU Free Documentation License (GFDL)
If you are the copyright holder of any material contained on our site and intend to remove it, please contact our site administrator for approval.
© 2016-2026 All site design rights belong to S.Y.A.