Introduction To Network Security: Theory And Practice (2015)

Chapter 2. Data Encryption Algorithms

2.4 Advanced Encryption Standard

Researchers have never stopped searching for better encryption algorithms that are more efficient, more secure, and more flexible. New encryption algorithms should be able to use longer keys and handle larger blocks. In some applications, people may also want to specify their own key length and block size. Thus, it would be desirable to have key length and block size as parameters.

A number of encryption algorithms have since been devised. Some of the early ones include Blowfish, CAST, GOST (the former Soviet Encryption Standard), International Data Encryption Algorithm (IDEA), LOKI, RC4, RC5, REDOC-II, REDOC-III, SAFER, and Skipjack. Most of these encryption algorithms are Feistel ciphers.

Realizing the urgent need to establish a new encryption standard, NIST launched in 1997 the advanced encryption standard competition for selecting a successor to DES. The following encryption algorithms were submitted for consideration: CAST-256, CRYPTON, DEAL, DFC, E2, FROG, HPC, LOKI97, MAGENTA, MARS, RC6, Rijndael, SAFER, Serpent, and Twofish, where MARS, RC6, Rijndael, Serpent, and Twofish were selected semifinalists. In November 2001, NIST officially chose Rijndael to be the new AES. Rijndael was devised by Belgian cryptographers Joan Daemen and Vincent Rijmen.

2.4.1 AES Basic Structures

AES is a block cipher, but it is not a Feistel cipher. Its encryption and decryption, although similar, are not symmetrical. The basic computation unit in AES is a byte, rather than a bit as in DES. A byte is an 8-bit binary string. AES divides the plaintext string into 128-bit blocks. AES can use encryption keys of three different key lengths. An AES-encryption key can be 16-byte long, 24-byte long, or 32-byte long. Regardless of what key length is used, AES will generate and use 16-byte subkeys, also called round keys. AES can also run a different number of operation rounds. To generate a sufficient number of round keys, AES expands encryption keys depending on the number of rounds and the length of the encryption key specified by the users. Table 2.2 depicts the relations between key lengths, the number of rounds, and the length of expanded encryption keys, where a word is a binary string of length equal to four bytes.

Table 2.2 AES key lengths, the number of rounds, and the length of expanded encryption keys

AES treats a 128-bit block as a sequence of 16 bytes and represents it as a square matrix, where each element is a byte in the block. In particular, let be a plaintext block, where each is a byte. Then AES rewrites as Matrix 2.11:

2.11

We refer to a matrix of bytes as a state matrix. AES encryption executes in each round (except the last round) the same sequence of simple operations on state matrices that transforms the plaintext block into a ciphertext block. These operations are substitute-bytes, shift-rows, mix-columns, and add-round-key.

1. The operation of substitute-bytes is a nonlinear operation based on a specially designed substitution box. The purpose of this operation is to resist differential cryptanalysis, linear cryptanalysis, and other mathematical attacks.

2. The operation of shift-rows is an elementary operation on state matrices. It is a linear operation. The purpose of this operation is to produce diffusion.

3. The operation of mix-columns is also an elementary operation on state matrices. Its purpose is the same as shift-rows.

4. The operation of add-round-key is a simple set of exclusive-OR operations on state matrices. It is a linear operation. The purpose of this operation is to produce confusion.

It is customary to use AES-128, AES-192, and AES-256 to denote, respectively, AES under 128-bit keys, 192-bit keys, and 256-bit keys. These three variants of AES all have the same encryption and decryption structures. They differ only on the number of rounds, where each round uses a different round key.

We describe AES using AES-128. AES-128 first expands the 128-bit key into an array of words. It then rewrites as a sequence of eleven 128-bit round keys . In other words,

where .

For convenience, we use sub to denote the operation of substitute-bytes, shr the operation of shift-rows, mic the operation of mix-columns, and ark the operation of add-round-key. Denote by inv_sub (or ) the inverse operation of sub, inv_shr (or ) the inverse operation of shr, and inv_mic (or ) the inverse operation of mic. Figure 2.2 depicts the AES-128 encryption and decryption block diagram.

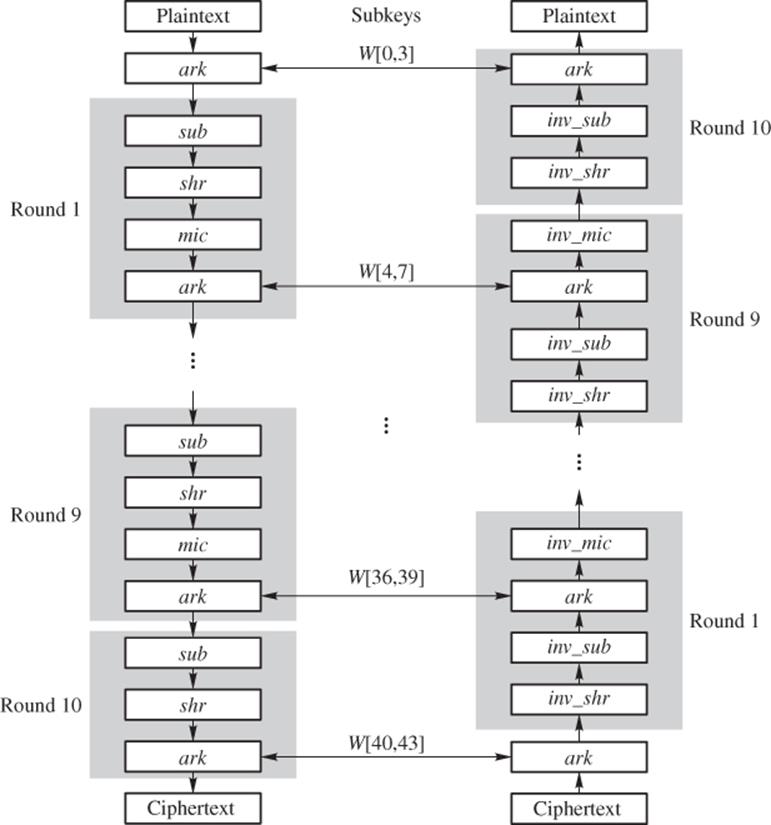
Figure 2.2 AES-128 encryption and decryption diagram

In the following several subsections, we describe AES S-Boxes, the subkey generation algorithm, the operations of ark, sub, shr, mic, and their inverse operations. We then introduce the Galois field and show how S-Boxes are constructed. Skipping the last two topics will not affect the understanding of AES encryption and decryption operations.

2.4.2 AES S-Boxes

AES uses only one S-Box. It is used to generate subkeys and define the operation of substitute bytes. The AES S-Box is a matrix of bytes, which is defined on the basis of the multiplication operation of the Galois field . Unlike the S-Boxes used in DES, the AES S-Box is a permutation of all 256 bytes. Its reverse permutation is called the reverse S-Box.

We only present the S-Box and the reverse S-Box in this subsection, where each element and index is represented by two hexadecimal digits. We describe how they are constructed in Section 2.4.11. We use

to denote the AES S-Box and

to denote its reverse. The S-Box is given in Table 2.3, and the reverse S-Box is given in Table 2.4.

Table 2.3 The S-Box of AES

Table 2.4 The reverse S-Box of AES

Let be a byte, where each is a bit. Define a byte-substitution function as follows: let denote the binary representation of the row index and denote the binary representation of a column index of in the S-Box. Then

2.12

2.13

That is, () is the element on the intersection of the th row and the th column in the S-Box . Likewise, is the element on the intersection of the th row and the th column in the inverse S-Box .

For example, let , then , and .

It is straightforward to see from the S-Box and its reverse that, for any 8-bit string , we have

2.4.3 AES-128 Round Keys

Let be a 4-word encryption key, where each is a 32-bit binary string, . AES expands into a 44-word array . We first define a byte transformation function as follows:

2.14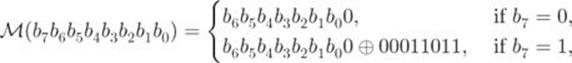

where each is a bit. We see in Section 2.4.10 that represents a multiplication operation of 00000010 and over Galois field .

For example,

Let be a non-negative number. Define () as follows:

2.15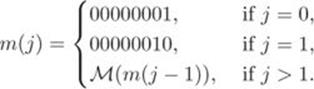

We see in Section 2.4.10 that function () represents the result of multiplying the element 00000010 by itself for times.

We now define a word-substitution function that transforms a 32-bit string to a 32-bit string on the basis of parameter and the AES S-Box. Let , where each is a byte. Let be a positive integer. Let

where is the byte-substitution function defined by Equality 2.12.

We now expand to obtain as follows:

2.4.4 Add Round Keys

Let be an AES-128 round key, where . Rewrite as a matrix of bytes:

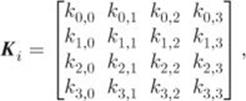
where each element is a byte and .

In what follows we use

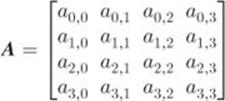
to represent the current state matrix. Initially, (see Matrix 2.11). The add-round-key operation ark is defined as follows:

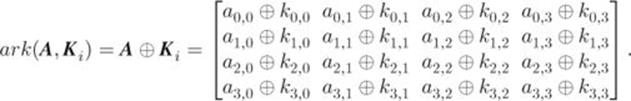
The inverse operation is the same as ark. That is, . It is straightforward to verify that

2.4.5 Substitute-Bytes

The substitute-bytes operation sub is defined as follows:

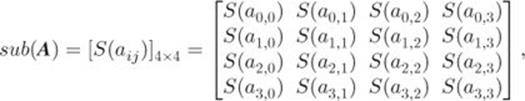
where is the byte-substitution function defined in Section 2.4.2 (see formula 2.12).

It is straightforward to verify that the inverse operation is given by

where is defined in Section 2.4.2 (see formula 2.13). This is because for any byte , we have , which implies that

2.4.6 Shift-Rows

The shift-row operation shr performs a left-circular-shift times on the th row in the state matrix , where . Its inverse performs a right-circular-shift times on the th row. That is,

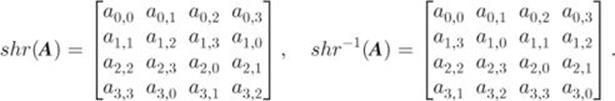
It is straightforward to verify that

2.4.7 Mix-Columns

The mix-columns operation mic is defined as follows:

where each element in is determined by the following operations

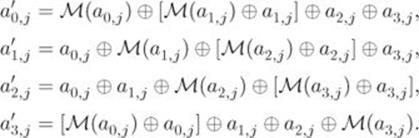
For example, let

2.16

We verify as follows:

The reader is asked to verify the rest of the elements.

Let be a byte and a positive integer. Define

Let

2.17

2.18

2.19

2.20

The inverse operation of is defined by

where each column in is defined as follows:

2.21

2.22

2.23

2.24

We show in Section 2.4.10 that for any state matrix the following relation holds:

2.25

2.4.8 AES-128 Encryption

Let be a sequence of state matrices, where is the initial state matrix (i.e., Matrix 2.11), represents the input state matrix at round , and is the ciphertext block , which is in the form of state matrix. Given below are the encryption steps of AES-128:

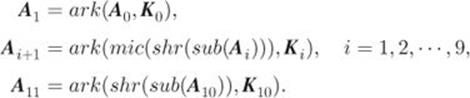
2.4.9 AES-128 Decryption and Correctness Proof

Let be a sequence of state matrices, where is the ciphertext block represents the input state matrix at round , and is the output state matrix at round 10. The following are the decryption steps of AES-128:

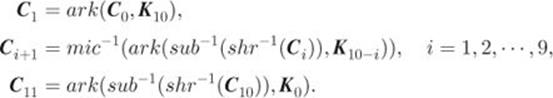
We now show that . We first show the following equality using mathematical induction:

2.26

A proof of Equality 2.26 goes as follows. When , we have

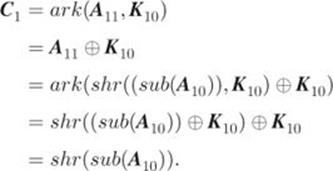
Thus, Equality 2.26 holds. Assume that Equality 2.26 holds for . We have

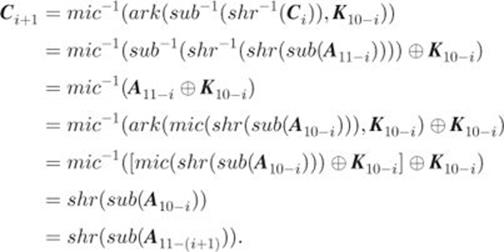
Thus, Equality 2.26 is true.

Finally, we have

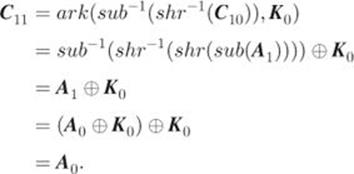
This completes the correctness proof of AES-128 decryption.

2.4.10 Galois Fields

In addition to the shift-rows operation, the basic operations of AES are based on the XOR operation and a special multiplication operation on 8-bit strings. These two operations and the set of all 8-bit strings form a finite field.

A field is an algebraic structure that consists of a set and two operations on elements in . These two operations are addition and multiplication, denoted by and , respectively, which satisfy the following conditions:

1. Closure: .

2. Associativity: :

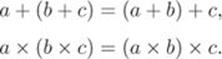
3. Distributivity: :

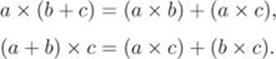
4. Unit element: There are elements , where , such that :

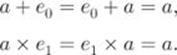
The element is called the unit element of the addition operation and the unit element of the multiplication operation.

5. Inverse:

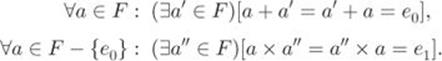
Elements are called, respectively, the additive inverse (denoted by ) and the multiplicative inverse (denoted by .)

6. Commutativity: .

7. Nonzero divisor: If and , then or .

We use to denote a field. It is called a finite field if is a finite set and an infinite field otherwise. The field of real numbers, for example, is the set of all real numbers with the ordinary addition and multiplication operations.

Finite fields have a nice property; namely, any finite field consists of exactly elements for some prime number and integer . A prime number is a positive integer that is divisible only by 1 and by itself. Elements in a finite field of size can be uniquely represented by polynomials of degree with coefficients in the set . A finite field with its elements written in this form is called a Galois field, denoted by . Each element in is represented by the following polynomial

denoted in short by , where each coefficient

The addition operation over is addition modulo of coefficients for terms of the same degree. The multiplication operation first multiplies two polynomials in the normal way. If the degree of the resulting polynomial is greater than , then divide it by a fixedirreducible polynomial of degree , and take the remainder as the result of the multiplication. A polynomial is irreducible if it cannot be expressed as a product of two polynomials whose degrees are at least 1.

Modern electronic computers operate on binary operations using memory with bytes as basic units. Thus, choosing to form the basic operation space for encryption algorithms becomes natural. consists of all 8-bit binary strings as elements, where each element represents the following polynomial:

where the addition operation “” is the exclusive-OR operation , and we use them interchangeably when there is no confusion. Thus, the inverse element of any element is . We use to denote the multiplication operation on . The definition of the multiplication operation depends on the chosen irreducible polynomial. AES chooses the following irreducible polynomial:

This irreducible polynomial makes multiplication simple. We use () mod () to denote the remainder polynomial of dividing () by (). It is straightforward to verify that

Hence, we have

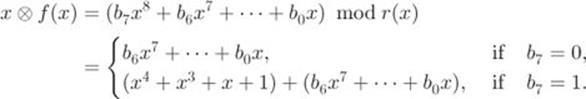
Denoting this formula using binary strings and XOR, we have

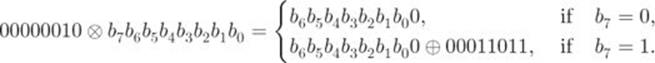
This is the definition of function defined in Section 2.4.3 (see Formula 2.14). That is,

The function () defined in Section 2.4.3 is the result of multiplying 00000010 by itself for times. That is,

where the number of is .

We now verify Equality 2.25. We first note that and are the products of the following matrix multiplications:

2.27

2.28

The matrix multiplication in this case follows the standard rule, with being the addition operation and the multiplication operation. In particular, we can verify Equality 2.27 from Equalities 2.17 –2.20 by noting that

Likewise, we can verify Equality 2.28 from Equalities 2.21 –2.24 by noting that

Hence,

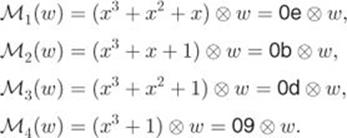
We can therefore show that by verifying the following equalities, where is the identity matrix of size 4:

2.29

2.30

For example, the first element at the right-hand side in Equality 2.29 is

2.4.11 Construction of the AES S-Box and Its Inverse

The S-Box used by AES is constructed as follows:

1. Initially, is a matrix of all 8-bit strings in the lexicographical order. That is, its first row is vector , its second row is vector , and so on, and its last row is vector .

2. Keep the first two elements in (i.e., 00 and 01) unchanged, and replace any other element with its inverse .

For example, as 02's multiplication inverse is 8d, the element 02 is replaced with 8d.

3. Replace each element with , where each bit is determined by

and .

For example, from Step 2 we know that the element at the intersection of the first row and the third column is . Thus,

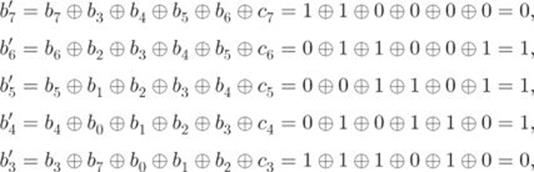
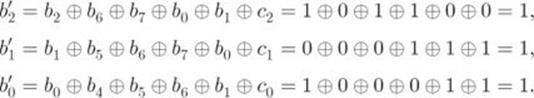
Hence, .

It is required that each element in the inverse S-Box must satisfy the following relations:

Element , where , can be calculated as follows: first find the element ij in . Let . Then let .

For example, as , we have .

2.4.12 AES Security Strength

AES is designed to resist differential cryptanalysis and linear cryptanalysis. It uses 128-bit (or longer) encryption keys to resist brute-force attacks. It modifies each element in the current state matrix in each round, and so it will achieve good diffusion and confusion effects after a few rounds of execution. AES is believed to be superior to DES.

In June 2003, the U.S. government decided that classified government information should be encrypted using AES-128, and for TOP SECRET information, AES-192 or AES-256 must be used. The New European Schemes for Signatures, Integrity, and Encryption (NESSIE) also supported the use of AES. In June 2004, the Institute of Electrical and Electronics Engineers (IEEE) adopted AES in its 802.11i wireless security standard. IEEE 802.11i is also known as Wireless-Fidelity Protected Access 2 (Wi-Fi WPA 2). Today, AES has been used in almost all network security protocols and software products.

No methods have been found that are efficient enough to be considered serious threats to AES, although certain types of side channel attacks have been discovered. Algebraic attacks, however, have attracted attentions. For example, if the attacker knows a pair of AES-128 plaintext and ciphertext blocks, then the attacker may be able to calculate the AES encryption key by solving a system of 1600 quadratic equations of 8000 unknowns. Although solving a system of quadratic equations of this magnitude by today's mathematical theory and computing technology is hopeless, this study opens up a new direction of investigation.