Algorithms Third Edition in C++ Part 5. Graph Algorithms (2006)
CHAPTER TWENTY-TWO
Network Flow
22.1 Flow Networks
To describe network-flow algorithms, we begin with an idealized physical model in which several of the basic concepts are intuitive. Specifically, we imagine a collection of interconnected oil pipes of varying sizes, with switches controlling the direction of flow at junctions, as in the example illustrated in Program 22.5. We suppose further that the network has a single source (say, an oil field) and a single sink (say, a large refinery) to which all the pipes ultimately connect. At each vertex, the flowing oil reaches an equilibrium where the amount of oil flowing in is equal to the amount flowing out. We measure both flow and pipe capacity in the same units (say, gallons per second).
If every switch has the property that the total capacity of the ingoing pipes is equal to the total capacity of the outgoing pipes, then there is no problem to solve: We simply fill all pipes to full capacity. Otherwise, not all pipes are full, but oil flows through the network, controlled by switch settings at the junctions, such that the amount of oil flowing into each junction is equal to the amount of oil flowing out. But this local equilibrium at the junctions implies an equilibrium in the network as a whole: We prove in Property 22.1 that the amount of oil flowing into the sink is equal to the amount flowing out of the source. Moreover, as illustrated in Program 22.6, the switch settings at the junctions of this amount of flow from source to sink have nontrivial effects on the flow through the network. Given these facts, we are interested in the following question: What switch settings will maximize the amount of oil flowing from source to sink?
We can model this situation directly with a network (a weighted digraph, as defined in Chapter 21) that has a single source and a single sink. The edges in the network correspond to the oil pipes, the vertices correspond to the junctions with switches that control how much oil goes into each outgoing edge, and the weights on the edges correspond to the capacity of the pipes. We assume that the edges are directed, specifying that oil can flow in only one direction in each pipe. Each pipe has a certain amount of flow, which is less than or equal to its capacity, and every vertex satisfies the equilibrium condition that the flow in is equal to the flow out.
Figure 22.6 Controlling flow in a network
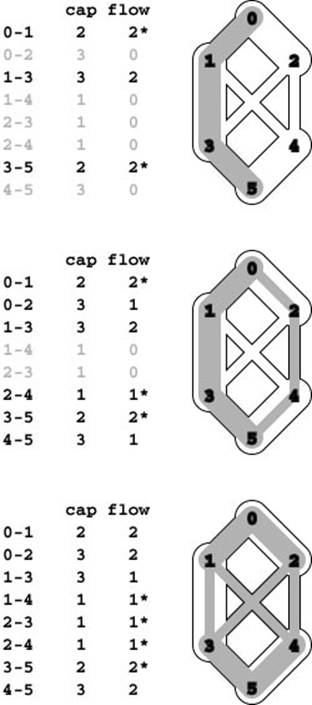
We might initialize the flow in this network by opening the switches along the path 0-1-3-5, which can handle 2 units of flow (top), and by opening switches along the path 0-2-4-5 to get another 1 unit of flow in the network (center). Asterisks indicate full edges.
Since 0-1, 2-4, and 3-5 are full, there is no direct way to get more flow from 0 to 5, but if we change the switch at 1 to redirect enough flow to fill 1-4, we open up enough capacity in 3-5 to allow us to add flow on 0-2-3-5, giving a maxflow for this network (bottom).
This flow-network abstraction is a useful problem-solving model that applies directly to a variety of applications and indirectly to still more. We sometimes appeal to the idea of oil flowing through pipes for intuitive support of basic ideas, but our discussion applies equally well to goods moving through distribution channels and to numerous other situations.
The flow model directly applies to a distribution scenario: We interpret the flow values as rates of flow, so that a flow network describes the flow of goods in a manner precisely analogous to the flow of oil. For example, we can interpret the flow in Program 22.5 as specifying that we should be sending two items per time unit from 0 to 1 and from 0 to 2, one item per time unit from 1 to 3 and from 1 to 4, and so forth.
Another way to interpret the flow model for a distribution scenario is to interpret flow values as amounts of goods so that a flow network describes a one-time transfer of goods. For example, we can interpret the flow in Program 22.5 as describing the transfer of four items from 0 to 5 in the following three-step process: First, send two items from 0 to 1 and two items from 0 to 2, leaving two items at each of those vertices. Second, send one item each from 1 to 3, 1 to 4, 2 to 3, and 2 to 4, leaving two items each at 3 and 4. Third, complete the transfer by sending two items from 3 to 5 and two items from 4 to 5.
As with our use of distance in shortest-paths algorithms, we are free to abandon any physical intuition when convenient because all the definitions, properties, and algorithms that we consider are based entirely on an abstract model that does not necessarily obey physical laws. Indeed, a prime reason for our interest in the network-flow model is that it allows us to solve numerous other problems through reduction, as we see in Sections 22.4 and 22.6. Because of this broad applicability, it is worthwhile to consider precise statements of the terms and concepts that we have just informally introduced.
Definition 22.1 We refer to a network with a designated source s and a designated sink t as an st-network.
We use the modifier “designated” here to mean that s does not necessarily have to be a source (vertex with no incoming edges) and t does not necessarily have to be a sink (vertex with no outgoing edges), but that we nonetheless treat them as such, because our discussion (and our algorithms) will ignore edges directed into s and edges directed out of t. To avoid confusion, we use networks with a single source and a single sink in examples; we consider more general situations in Section 22.4. We refer to s and t as “the source” and “the sink,” respectively, in the st -network because those are the roles that they play in the network. We also refer to the other vertices in the network as the internal vertices.
Definition 22.2 A flow network is an st-network with positive edge weights, which we refer to as capacities. A flow in a flow network is a set of nonnegative edge weights—which we refer to as edge flows —satisfying the conditions that no edge’s flow is greater than that edge’s capacity and that the total flow into each internal vertex is equal to the total flow out of that vertex.
We refer to the total flow into a vertex (the sum of the flows on its incoming edges) as the vertex’s inflow and the total flow out of a vertex (the sum of the flows on its outgoing edges) as the vertex’s outflow. By convention, we set the flow on edges into the source and edges out of the sink to zero, and in Property 22.1 we prove that the source’s outflow is always equal to the sink’s inflow, which we refer to as the network’s value. With these definitions, the formal statement of our basic problem is straightforward.
Maximum flow Given an st -network, find a flow such that no other flow from s to t has larger value. For brevity, we refer to such a flow as a maxflow and the problem of finding one in a network as the maxflow problem. In some applications, we might be content to know just the maxflow value, but we generally want to know a flow (edge flow values) that achieves that value.
Variations on the problem immediately come to mind. Can we allow multiple sources and sinks? Should we be able to handle networks with no sources or sinks? Can we allow flow in either direction in the edges? Can we have capacity restrictions for the vertices instead of or in addition to the restrictions for the edges? As is typical with graph algorithms, separating restrictions that are trivial to handle from those that have profound implications can be a challenge. We investigate this challenge and give examples of reducing to maxflow a variety of problems that seem different in character, after we consider algorithms to solve the basic problem, in Sections 22.2 and 22.3.
Figure 22.7 Flow equilibrium
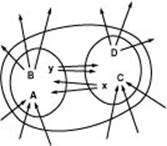
This diagram illustrates the preservation of flow equilibrium when we merge sets of vertices. The two smaller figures represent any two disjoint sets of vertices, and the letters represent flow in sets of edges as indicated: A is the amount of flow into the set on the left from outside the set on the right, x is the amount of flow into the set on the left from the set on the right, and so forth. Now, if we have flow equilibrium in the two sets, then we must have
A + x =B + y
for the set on the left and
C + y =D + x
for the set on the right. Adding these two equations and canceling the x + y terms, we conclude that
A + C =B + D,
or inflow is equal to outflow for the union of the two sets.
The characteristic property of flows is the local equilibrium condition that inflow be equal to outflow at each internal vertex. There is no such constraint on capacities; indeed, the imbalance between total capacity of incoming edges and total capacity of outgoing edges is what characterizes the maxflow problem. The equilibrium constraint has to hold at each and every internal vertex, and it turns out that this local property determines global movement through the network, as well. Although this idea is intuitive, it needs to be proved.
Property 22.1 Any st-flow has the property that outflow from s is equal to the inflow to t.
Proof: (We use the term st-flow to mean “flow in an st -network.”) Augment the network with an edge from a dummy vertex into s, with flow and capacity equal to the outflow from s, and with an edge from t to another dummy vertex, with flow and capacity equal to the inflow to t. Then, we can prove a more general property by induction: Inflow is equal to outflow for any set of vertices (not including the dummy vertices).
This property is true for any single vertex, by local equilibrium. Now, assume that it is true for a given set of vertices S and that we add a single vertex v to make the set S ′=S {v}. To compute inflow and outflow for S ′, note that each edge from v to some vertex in S reduces outflow (from v ) by the same amount as it reduces inflow (to S); each edge to v from some vertex in S reduces inflow (to v ) by the same amount as it reduces outflow (from S ); and all other edges provide inflow or outflow for S ′ if and only if they do so for S or v. Thus, inflow and outflow are equal for S ′, and the value of the flow is equal to the sum of the values of the flows of v and S minus sum of the flows on the edges connecting v to a vertex in S (in either direction).
Applying this property to the set of all the network’s vertices, we find that the source’s inflow from its associated dummy vertex (which
is equal to the source’s outflow) is equal to the sink’s outflow to its associated dummy vertex (which is equal to the sink’s inflow).
Figure 22.8 Cycle flow representation

This figure demonstrates that the circulation at left decomposes into the four cycles 1-3-5-4-1, 0-1-3-5-4-2-0, 1-3-5-4-2-1, 3-5-4-3, with weights 2, 1, 1, and 3, respectively. Each cycle’s edges appear in its respective column, and summing each edge’s weight from each cycle in which it appears (across its respective row) gives its weight in the circulation.
Corollary The value of the flow for the union of two sets of vertices is equal to the sum of the values of the flows for the two sets minus the sum of the weights of the edges that connect a vertex in one to a vertex in the other.
Proof: The proof just given for a set S and a vertex v still works if we replace v by a set T (which is disjoint from S ) in the proof. An example of this property is illustrated in Program 22.7.
We can dispense with the dummy vertices in the proof of Property 22.1, augment any flow network with an edge from t to s with flow and capacity equal to the network’s value, and know that inflow is equal to outflow for any set of nodes in the augmented network. Such a flow is called acirculation, and this construction demonstrates that the maxflow problem reduces to the problem of finding a circulation that maximizes the flow along a given edge. This formulation simplifies our discussion in some situations. For example, it leads to an interesting alternate representation of flows as a set of cycles, as illustrated in Program 22.8.
Given a set of cycles and a flow value for each cycle, it is easy to compute the corresponding circulation by following through each cycle and adding the indicated flow value to each edge. The converse property is more surprising: We can find a set of cycles (with a flow value for each) that is equivalent to any given circulation.
Property 22.2 (Flow decomposition theorem) Any circulation can be represented as flow along a set of at most E directed cycles.
Proof: A simple algorithm establishes this result. Iterate the following process as long as there is any edge that has flow: Starting with any
edge that has flow, follow any edge leaving that edge’s destination vertex that has flow and continue until encountering a vertex that has already been visited (a cycle has been detected). Go back around the cycle to find an edge with minimal flow; then reduce the flow on every edge in the cycle by that amount. Each iteration of this process reduces the flow on at least one edge to 0, so there are at most E cycles.
Figure 22.9 Cycle flow decomposition process
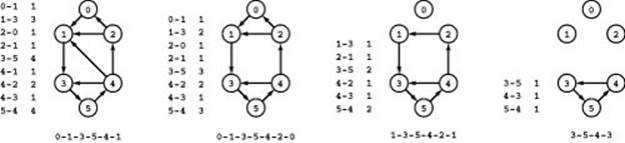
To decompose any circulation into a set of cycles, we iterate the following process: Follow any path until encountering a node for the second time, then find the minimum weight on the indicated cycle, then subtract that weight from each edge on the cycle and remove any edge whose weight becomes 0. For example, the first iteration is to follow the path 0-1-3-5-4-1 to find the cycle 1-3-5-4-1, then subtract 1 from the weights of each of the edges on the cycle, which causes us to remove 4-1 because its weight becomes 0. In the second iteration, we remove 0-1 and 2-0; in the third iteration, we remove 1-3, 4-2, and 2-1; and in the fourth iteration, we remove 3-5, 5-4, and 4-3.
Figure 22.9 illustrates the process described in the proof. For st-flows, applying this property to the circulation created by the addition of an edge from t to s gives the result that any st -flow can be represented as flow along a set of at most E directed paths, each of which is either a path from sto t or a cycle.
Corollary Any st-network has a maxflow such that the subgraph induced by nonzero flow values is acyclic.
Proof: Cycles that do not contain t-s do not contribute to the value of the flow, so we can change the flow to 0 along any such cycle without changing the value of the flow.
Corollary Any st-network has a maxflow that can be represented as flow along a set of at most E directed paths from s to t.
Proof: Immediate.
This representation provides a useful insight into the nature of flows that is helpful in the design and analysis of maxflow algorithms.
On the one hand, we might consider a more general formulation of the maxflow problem where we allow for multiple sources and sinks. Doing so would allow our algorithms to be used for a broader range of applications. On the other hand, we might consider special cases, such as restricting attention to acyclic networks. Doing so might make the problem easier to solve. In fact, as we see in Section 22.4, these variants are equivalent in difficulty to the version that we are considering. Therefore, in the first case, we can adapt our algorithms and implementations to the broader range of applications; in the second case, we cannot expect an easier solution. In our figures, we use acyclic networks because the examples are easier to understand when they have an implicit flow direction (down the page), but our implementations allow networks with cycles.
To implement maxflow algorithms, we use the GRAPH class of Chapter 20, but with pointers to a more sophisticated EDGE class. Instead of the single weight that we used in Chapters 20 and 21, we use pcap and pflow private data members (with cap() and flow() public member functions that return their values) for capacity and flow, respectively. Even though networks are directed graphs, our algorithms need to traverse edges in both directions, so we use the undirected graph representation from Chapter 20 and the member function from to distinguish u-v from v-u.
This approach allows us to separate the abstraction needed by our algorithms (edges going in both directions) from the client’s concrete data structure and leaves a simple goal for our algorithms: Assign values to the flow data members in the client’s edges that maximize flow through the network. Indeed, a critical component of our implementations involves a changing network abstraction that is dependent on flow values and implemented with EDGE member functions. We will consider an EDGE implementation (Program 22.2) in Section 22.2.
Since flow networks are typically sparse, we use an adjacency-lists-based GRAPH representation like the SparseMultiGRAPH implementation of Program 20.5. More important, typical flow networks may have multiple edges (of varying capacities) connecting two given vertices. This situation requires no special treatment with SparseMultiGRAPH, but with an adjacency-matrix–based representation, clients have to collapse such edges into a single edge.
In the network representations of Chapters 20 and 21, we used the convention that weights are real numbers between 0 and 1. In this chapter, we assume that the weights (capacities and flows) are all m-bit integers (between 0 and 2m − 1). We do so for two primary reasons. First, we frequently need to test for equality among linear combinations of weights, and doing so can be inconvenient in floating-point representations. Second, the running times of our algorithms
Program 22.1 Flow check and value computation
A call to flow(G, v) computes the difference between v’s ingoing and outgoing flows in G. A call to flow(G, s, t) checks the network flow values from the source (s) to the sink (t), returning 0 if ingoing flow is not equal to outgoing flow at some internal node or if some flow value is negative; the flow value otherwise.

can depend on the relative values of the weights, and the parameter M = 2m gives us a convenient way to bound weight values. For example, the ratio of the largest weight to the smallest nonzero weight is less than M. The use of integer weights is but one of many possible alternatives (see, for example, Exercise 20.8) that we could choose to address these problems.
We sometimes refer to edges as having infinite capacity, or, equivalently, as being uncapacitated. That might mean that we do not compare flow against capacity for such edges, or we might use a sentinel value that is guaranteed to be larger than any flow value.
Figure 22.10 Flow network for exercises
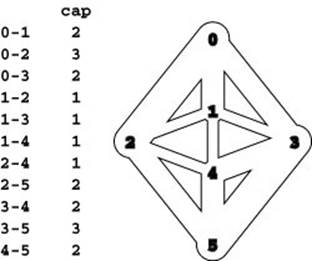
This flow network is the subject of several exercises throughout the chapter.
Program 22.1 is an client function that checks whether a flow satisfies the equilibrium condition at every node and returns that flow’s value if the flow does. Typically, we might include a call to this function as the final action of a maxflow algorithm. Despite our confidence as mathematicians in Property 22.1, our paranoia as programmers dictates that we also check that the flow out of the source is equal to the flow into the sink. It might also be prudent to check that no edge’s flow exceeds that edge’s capacity and that the data structures are internally consistent (see Exercise 22.12).
Exercises
• 22.1 Find two different maxflows in the flow network shown in Program 22.10.
22.2 Under our assumption that capacities are positive integers less than M, what is the maximum possible flow value for any st-network with V vertices and E edges? Give two answers, depending on whether or not parallel edges are allowed.
• 22.3 Give an algorithm to solve the maxflow problem for the case that the network forms a tree if the sink is removed.
• 22.4 Give a family of networks with E edges having circulations where the process described in the proof of Property 22.2 produces E cycles.
22.5 Write an EDGE class that represents capacities and flows as real numbers between 0 and 1 that are expressed with d digits to the right of the decimal point, where d is a fixed constant.
• 22.6 Write a program that builds a flow network by reading edges (pairs of integers between 0 and V − 1) with integer capacities from standard input. Assume that the capacity upper bound M is less than 220.
22.7 Extend your solution to Exercise 22.6 to use symbolic names instead of integers to refer to vertices (see Program 17.10).
• 22.8 Find a large network online that you can use as a vehicle for testing flow algorithms on realistic data. Possibilities include transportation networks (road, rail, or air), communications networks (telephone or computer connections), or distribution networks. If capacities are not available, devise a reasonable model to add them. Write a program that uses the interface of Program 22.2 to implement flow networks from your data, perhaps using your solution to Exercise 22.7. If warranted, develop additional private functions to clean up the data, as described in Exercises 17.33–35.
22.9 Write a random-network generator for sparse networks with capacities between 0 and 220, based on Program 17.7. Use a separate class for capacities and develop two implementations: one that generates uniformly distributed capacities and another that generates capacities according to a Gaussian distribution. Implement client programs that generate random networks for both weight distributions with a well-chosen set values of V and E, so that you can use them to run empirical tests on graphs drawn from various distributions of edge weights.
22.10 Write a random-network generator for dense networks with capacities between 0 and 220, based on Program 17.8 and edge-capacity generators as described in Exercise 22.9. Write client programs to generate random networks for both weight distributions with a well-chosen set values of V and E, so that you can use them to run empirical tests on graphs drawn from these models.
• 22.11 Write a program that generates V random points in the plane, then builds a flow network with edges (in both directions) connecting all pairs of points within a given distance d of each other (see Program 3.20), setting each edge’s capacity using one of the random models described inExercise 22.9. Determine how to set d so that the expected number of edges is E.
• 22.12 Modify Program 22.1 to also check that flow is less than capacity for all edges.
• 22.13 Find all the maxflows in the network depicted in Program 22.11. Give cycle representations for each of them.
22.14 Write a function that reads values and cycles (one per line, in the format illustrated in Program 22.8) and builds a network having the corresponding flow.
22.15 Write a client function that finds the cycle representation of a network’s flow using the method described in the proof of Property 22.2 and prints values and cycles (one per line, in the format illustrated in Program 22.8).
• 22.16 Write a function that removes cycles from a network’s st-flow.
• 22.17 Write a program that assigns integer flows to each edge in any given digraph that contains no sinks and no sources such that the digraph is a flow network that is a circulation.
• 22.18 Suppose that a flow represents goods to be transferred by trucks between cities, with the flow on edge u-v representing the amount to be taken from city u to v in a given day. Write a client function that prints out daily orders for truckers, telling them how much and where to pick up and how much and where to drop off. Assume that there are no limits on the supply of truckers and that nothing leaves a given distribution point until everything has arrived.
Figure 22.11 Flow network with cycle
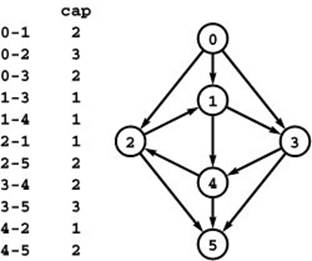
This flow network is like the one depicted in Program 22.10, but with the direction of two of the edges reversed, so there are two cycles. It is also the subject of several exercises throughout the chapter.