The C++ Programming Language (2013)

Part II: Basic Facilities

10. Expressions

Programming is like sex: It may give some concrete results, but that is not why we do it.

– apologies to Richard Feynman

• Introduction

• A Desk Calculator

The Parser; Input; Low-Level Input; Error Handling; The Driver; Headers; Command-Line Arguments; A Note on Style

• Operator Summary

Results; Order of Evaluation; Operator Precedence; Temporary Objects

• Constant Expressions

Symbolic Constants; consts in Constant Expressions; Literal Types; Reference Arguments; Address Constant Expressions

• Implicit Type Conversion

Promotions; Conversions; Usual Arithmetic Conversions

• Advice

10.1. Introduction

This chapter discusses expressions in some detail. In C++, an assignment is an expression, a function call is an expression, the construction of an object is an expression, and so are many other operations that go beyond conventional arithmetic expression evaluation. To give an impression of how expressions are used and to show them in context, I first present a small complete program, a simple “desk calculator.” Next, the complete set of operators is listed and their meaning for builtin types is briefly outlined. The operators that require more extensive explanation are discussed in Chapter 11.

10.2. A Desk Calculator

Consider a simple desk calculator program that provides the four standard arithmetic operations as infix operators on floating-point numbers. The user can also define variables. For example, given the input

r = 2.5
area = pi * r * r

(pi is predefined) the calculator program will write

2.5
19.635

where 2.5 is the result of the first line of input and 19.635 is the result of the second.

The calculator consists of four main parts: a parser, an input function, a symbol table, and a driver. Actually, it is a miniature compiler in which the parser does the syntactic analysis, the input function handles input and lexical analysis, the symbol table holds permanent information, and the driver handles initialization, output, and errors. We could add many features to this calculator to make it more useful, but the code is long enough as it is, and most features would just add code without providing additional insight into the use of C++.

10.2.1. The Parser

Here is a grammar for the language accepted by the calculator:

program:
end // end is end-of-input
expr_list end

expr_list:
expression print // print is newline or semicolon
expression print expr_list

expression:
expression + term
expression – term
term

term:
term / primary
term * primary
primary

primary:
number // number is a floating-point literal
name // name is an identifier
name = expression
– primary
( expression )

In other words, a program is a sequence of expressions separated by semicolons. The basic units of an expression are numbers, names, and the operators *, /, +, – (both unary and binary), and = (assignment). Names need not be declared before use.

I use a style of syntax analysis called recursive descent; it is a popular and straightforward top-down technique. In a language such as C++, in which function calls are relatively cheap, it is also efficient. For each production in the grammar, there is a function that calls other functions. Terminal symbols (for example, end, number, +, and –) are recognized by a lexical analyzer and nonterminal symbols are recognized by the syntax analyzer functions, expr(), term(), and prim(). As soon as both operands of a (sub)expression are known, the expression is evaluated; in a real compiler, code could be generated at this point.

For input, the parser uses a Token_stream that encapsulates the reading of characters and their composition into Tokens. That is, a Token_stream “tokenizes”: it turns streams of characters, such as 123.45, into Tokens. A Token is a {kind-of-token,value} pair, such as {number,123.45}, where the 123.45 has been turned into a floating point value. The main parts of the parser need only to know the name of the Token_stream, ts, and how to get Tokens from it. To read the next Token, it calls ts.get(). To get the most recently read Token (the “current token”), it callsts.current(). In addition to providing tokenizing, the Token_stream hides the actual source of the characters. We’ll see that they can come directly from a user typing to cin, from a program command line, or from any other input stream (§10.2.7).

The definition of Token looks like this:

enum class Kind : char {
name, number, end,
plus='+', minus='–', mul='*', div='/', print=';', assign='=', lp='(', rp=')'
};

struct Token {
Kind kind;
string string_value;
double number_value;
};

Representing each token by the integer value of its character is convenient and efficient and can be a help to people using debuggers. This works as long as no character used as input has a value used as an enumerator – and no current character set I know of has a printing character with a single-digit integer value.

The interface to Token_stream looks like this:

class Token_stream {
public:
Token get(); // read and return next token
const Token& current(); // most recently read token
// ...
};

The implementation is presented in §10.2.2.

Each parser function takes a bool (§6.2.2) argument, called get, indicating whether the function needs to call Token_stream::get() to get the next token. Each parser function evaluates “its” expression and returns the value. The function expr() handles addition and subtraction. It consists of a single loop that looks for terms to add or subtract:

double expr(bool get) // add and subtract
{
double left = term(get);

for (;;) { // "forever"
switch (ts.current().kind) {
case Kind::plus:
left += term(true);
break;
case Kind::minus:
left –= term(true);
break;
default:
return left;
}
}
}

This function really does not do much itself. In a manner typical of higher-level functions in a large program, it calls other functions to do the work.

The switch-statement (§2.2.4, §9.4.2) tests the value of its condition, which is supplied in parentheses after the switch keyword, against a set of constants. The break-statements are used to exit the switch-statement. If the value tested does not match any case label, the default is chosen. The programmer need not provide a default.

Note that an expression such as 2–3+4 is evaluated as (2–3)+4, as specified in the grammar.

The curious notation for(;;) is a way to specify an infinite loop; you could pronounce it “forever” (§9.5); while(true) is an alternative. The switch-statement is executed repeatedly until something different from + and – is found, and then the return-statement in the default case is executed.

The operators += and –= are used to handle the addition and subtraction; left=left+term(true) and left=left–term(true) could have been used without changing the meaning of the program. However, left+=term(true) and left–=term(true) are not only shorter but also express the intended operation directly. Each assignment operator is a separate lexical token, so a + = 1; is a syntax error because of the space between the + and the =.

C++ provides assignment operators for the binary operators:

+ – * / % & | ^ << >>

so that the following assignment operators are possible:

= += –= *= /= %= &= |= ^= <<= >>=

The % is the modulo, or remainder, operator; &, |, and ^ are the bitwise logical operators and, or, and exclusive or; << and >> are the left shift and right shift operators; §10.3 summarizes the operators and their meanings. For a binary operator @ applied to operands of built-in types, an expression x@=y means x=x@y, except that x is evaluated once only.

The function term() handles multiplication and division in the same way expr() handles addition and subtraction:

double term(bool get) // multiply and divide
{
double left = prim(get);

for (;;) {
switch (ts.current().kind) {
case Kind::mul:
left *= prim(true);
break;
case Kind::div:
if (auto d = prim(true)) {
left /= d;
break;
}
return error("divide by 0");
default:
return left;
}
}
}

The result of dividing by zero is undefined and usually disastrous. We therefore test for 0 before dividing and call error() if we detect a zero divisor. The function error() is described in §10.2.4.

The variable d is introduced into the program exactly where it is needed and initialized immediately. The scope of a name introduced in a condition is the statement controlled by that condition, and the resulting value is the value of the condition (§9.4.3). Consequently, the division and assignment left/=d are done if and only if d is nonzero.

The function prim() handling a primary is much like expr() and term(), except that because we are getting lower in the call hierarchy a bit of real work is being done and no loop is necessary:

double prim(bool get) // handle primaries
{
if (get) ts.get(); // read next token

switch (ts.current().kind) {
case Kind::number: // floating-point constant
{ double v = ts.current().number_value;
ts.get();
return v;
}
case Kind::name:
{ double& v = table[ts.current().string_value]; // find the corresponding
if (ts.get().kind == Kind::assign) v = expr(true); // '=' seen: assignment
return v;
}
case Kind::minus: // unary minus
return –prim(true);
case Kind::lp:
{ auto e = expr(true);
if (ts.current().kind != Kind::rp) return error("')' expected");
ts.get(); // eat ')'
return e;
}
default:
return error("primary expected");
}
}

When a Token that is a number (that is, an integer or floating-point literal) is seen, its value is placed in its number_value. Similarly, when a Token that is a name (however defined; see §10.2.2 and §10.2.3) is seen, its value is placed in its string_value.

Note that prim() always reads one more Token than it uses to analyze its primary expression. The reason is that it must do that in some cases (e.g., to see if a name is assigned to), so for consistency it must do it in all cases. In the cases where a parser function simply wants to move ahead to the next Token, it doesn’t use the return value from ts.get(). That’s fine because we can get the result from ts.current(). Had ignoring the return value of get() bothered me, I’d have either added a read() function that just updated current() without returning a value or explicitly “thrown away” the result: void(ts.get()).

Before doing anything to a name, the calculator must first look ahead to see if it is being assigned to or simply read. In both cases, the symbol table is consulted. The symbol table is a map (§4.4.3, §31.4.3):

map<string,double> table;

That is, when table is indexed by a string, the resulting value is the double corresponding to the string. For example, if the user enters

radius = 6378.388;

the calculator will reach case Kind::name and execute

double& v = table["radius"];
// ... expr() calculates the value to be assigned ...
v = 6378.388;

The reference v is used to hold on to the double associated with radius while expr() calculates the value 6378.388 from the input characters.

Chapter 14 and Chapter 15 discuss how to organize a program as a set of modules. However, with one exception, the declarations for this calculator example can be ordered so that everything is declared exactly once and before it is used. The exception is expr(), which calls term(), which calls prim(), which in turn calls expr(). This loop of calls must be broken somehow. A declaration

double expr(bool);

before the definition of prim() will do nicely.

10.2.2. Input

Reading input is often the messiest part of a program. To communicate with a person, the program must cope with that person’s whims, conventions, and seemingly random errors. Trying to force the person to behave in a manner more suitable for the machine is often (rightly) considered offensive. The task of a low-level input routine is to read characters and compose higher-level tokens from them. These tokens are then the units of input for higher-level routines. Here, low-level input is done by ts.get(). Writing a low-level input routine need not be an everyday task. Many systems provide standard functions for this.

First we need to see the complete definition of Token_stream:

class Token_stream {
public:
Token_stream(istream& s) : ip{&s}, owns{false} { }
Token_stream(istream* p) : ip{p}, owns{true} { }

^∼Token_stream() { close(); }

Token get(); // read and return next token
Token& current(); // most recently read token

void set_input(istream& s) { close(); ip = &s; owns=false; }
void set_input(istream* p) { close(); ip = p; owns = true; }

private:
void close() { if (owns) delete ip; }

istream* ip; // pointer to an input stream
bool owns; // does the Token_stream own the istream?
Token ct {Kind::end} ; // current token
};

We initialize a Token_stream with an input stream (§4.3.2, Chapter 38) from which it gets its characters. The Token_stream implements the convention that it owns (and eventually deletes; §3.2.1.2, §11.2) an istream passed as a pointer, but not an istream passed as a reference. This may be a bit elaborate for this simple program, but it is a useful and general technique for classes that hold a pointer to a resource requiring destruction.

A Token_stream holds three values: a pointer to its input stream (ip), a Boolean (owns), indicating ownership of the input stream, and the current token (ct).

I gave ct a default value because it seemed sloppy not to. People should not call current() before get(), but if they do, they get a well-defined Token. I chose Kind::end as the initial value for ct so that a program that misuses current() will not get a value that wasn’t on the input stream.

I present Token_stream::get() in two stages. First, I provide a deceptively simple version that imposes a burden on the user. Next, I modify it into a slightly less elegant, but much easier to use, version. The idea for get() is to read a character, use that character to decide what kind of token needs to be composed, read more characters when needed, and then return a Token representing the characters read.

The initial statements read the first non-whitespace character from *ip (the stream pointed to by ip) into ch and check that the read operation succeeded:

Token Token_stream::get()
{

char ch = 0;
*ip>>ch;

switch (ch) {
case 0:
return ct={Kind::end}; // assign and return

By default, operator >> skips whitespace (that is, spaces, tabs, newlines, etc.) and leaves the value of ch unchanged if the input operation failed. Consequently, ch==0 indicates end-of-input.

Assignment is an operator, and the result of the assignment is the value of the variable assigned to. This allows me to assign the value Kind::end to curr_tok and return it in the same statement. Having a single statement rather than two is useful in maintenance. If the assignment and thereturn became separated in the code, a programmer might update the one and forget to update the other.

Note also how the {}-list notation (§3.2.1.3, §11.3) is used on the right-hand side of an assignment. That is, it is an expression. I could have written that return-statement as:

ct.kind = Kind::end; // assign
return ct; // return

However, I think that assigning a complete object {Kind::end} is clearer than dealing with individual members of ct. The {Kind::end} is equivalent to {Kind::end,0,0}. That’s good if we care about the last two members of the Token and not so good if we are worried about performance. Neither is the case here, but in general dealing with complete objects is clearer and less error-prone than manipulating data members individually. The cases below give examples of the other strategy.

Consider some of the cases separately before considering the complete function. The expression terminator, ';', the parentheses, and the operators are handled simply by returning their values:

case ';': // end of expression; print
case '*':
case '/':
case '+':
case '–':
case '(':
case ')':
case '=':
return ct={static_cast<Kind>(ch)};

The static_cast (§11.5.2) is needed because there is no implicit conversion from char to Kind (§8.4.1); only some characters correspond to Kind values, so we have to “certify” that in this case ch does.

Numbers are handled like this:

case '0': case '1': case '2': case '3': case '4': case '5': case '6': case '7': case '8': case '9':
case '.':

ip–>putback(ch); // put the first digit (or .) back into the input stream
*ip >> ct.number_value; // read the number into ct
ct.kind=Kind::number;
return ct;

Stacking case labels horizontally rather than vertically is generally not a good idea because this arrangement is harder to read. However, having one line for each digit is tedious. Because operator >> is already defined for reading floating-point values into a double, the code is trivial. First the initial character (a digit or a dot) is put back into cin. Then, the floating-point value can be read into ct.number_value.

If the token is not the end of input, an operator, a punctuation character, or a number, it must be a name. A name is handled similarly to a number:

default: // name, name =, or error
if (isalpha(ch)) {
ip–>putback(ch); // put the first character back into the input stream
*ip>>ct.string_value; // read the string into ct
ct.kind=Kind::name;
return ct;
}

Finally, we may simply have an error. The simple-minded, but reasonably effective way to deal with an error is the write call an error() function and then return a print token if error() returns:

error("bad token");
return ct={Kind::print};

The standard-library function isalpha() (§36.2.1) is used to avoid listing every character as a separate case label. Operator >> applied to a string (in this case, string_value) reads until it hits whitespace. Consequently, a user must terminate a name by a space before an operator using the name as an operand. This is less than ideal, so we will return to this problem in §10.2.3.

Here, finally, is the complete input function:

Token Token_stream::get()
{
char ch = 0;
*ip>>ch;

switch (ch) {
case 0:
return ct={Kind::end}; // assign and return
case ';': // end of expression; print
case '*':
case '/':
case '+':
case '–':
case '(':
case ')':
case '=':
return ct=={static_cast<Kind>(ch)};
case '0': case '1': case '2': case '3': case '4': case '5': case '6': case '7': case '8': case '9':
case '.':
ip–>putback(ch); // put the first digit (or .) back into the input stream
*ip >> ct.number_value; // read number into ct
ct.kind=Kind::number;
return ct;
default: // name, name =, or error
if (isalpha(ch)) {
ip–>putback(ch); // put the first character back into the input stream
*ip>>ct.string_value; // read string into ct
ct.kind=Kind::name;
return ct;
}

error("bad token");
return ct={Kind::print};
}
}

The conversion of an operator to its Token value is trivial because the kind of an operator was defined as the integer value of the operator (§10.2.1).

10.2.3. Low-Level Input

Using the calculator as defined so far reveals a few inconveniences. It is tedious to remember to add a semicolon after an expression in order to get its value printed, and having a name terminated by whitespace only is a real nuisance. For example, x=7 is an identifier – rather than the identifier x followed by the operator = and the number 7. To get what we (usually) want, we would have to add whitespace after x: x =7. Both problems are solved by replacing the type-oriented default input operations in get() with code that reads individual characters.

First, we’ll make a newline equivalent to the semicolon used to mark the end-of-expression:

Token Token_stream::get()
{

char ch;

do { // skip whitespace except '\n'
if (!ip–>get(ch)) return ct={Kind::end};
} while (ch!='\n' && isspace(ch));

switch (ch) {
case ';':
case '\n':
return ct={Kind::print};

Here, I use a do-statement; it is equivalent to a while-statement except that the controlled statement is always executed at least once. The call ip–>get(ch) reads a single character from the input stream *ip into ch. By default, get() does not skip whitespace the way >> does. The test if (!ip–>get(ch)) succeeds if no character can be read from cin; in this case, Kind::end is returned to terminate the calculator session. The operator ! (not) is used because get() returns true in case of success.

The standard-library function isspace() provides the standard test for whitespace (§36.2.1); isspace(c) returns a nonzero value if c is a whitespace character and zero otherwise. The test is implemented as a table lookup, so using isspace() is much faster than testing for the individual whitespace characters. Similar functions test if a character is a digit (isdigit()), a letter (isalpha()), or a digit or letter (isalnum()).

After whitespace has been skipped, the next character is used to determine what kind of lexical token is coming.

The problem caused by >> reading into a string until whitespace is encountered is solved by reading one character at a time until a character that is not a letter or a digit is found:

default: // NAME, NAME=, or error
if (isalpha(ch)) {
string_value = ch;
while (ip–>get(ch) && isalnum(ch))
string_value += ch; // append ch to end of string_value
ip–>putback(ch);
return ct={Kind::name};
}

Fortunately, these two improvements could both be implemented by modifying a single local section of code. Constructing programs so that improvements can be implemented through local modifications only is an important design aim.

You might worry that adding characters to the end of a string one by one would be inefficient. It would be for very long strings, but all modern string implementations provide the “small string optimization” (§19.3.3). That means that handling the kind of strings we are likely to use as names in a calculator (or even in a compiler) doesn’t involve any inefficient operations. In particular, using a short string doesn’t require any use of free store. The maximum number of characters for a short string is implementation-dependent, but 14 would be a good guess.

10.2.4. Error Handling

It is always important to detect and report errors. However, for this program, a simple error handling strategy suffices. The error() function simply counts the errors, writes out an error message, and returns:

int no_of_errors;

double error(const string& s)
{
no_of_errors++;
cerr << "error: " << s << '\n';
return 1;
}

The stream cerr is an unbuffered output stream usually used to report errors (§38.1).

The reason for returning a value is that errors typically occur in the middle of the evaluation of an expression, so we should either abort that evaluation entirely or return a value that is unlikely to cause subsequent errors. The latter is adequate for this simple calculator. HadToken_stream::get() kept track of the line numbers, error() could have informed the user approximately where the error occurred. This would be useful when the calculator is used noninteractively.

A more stylized and general error-handling strategy would separate error detection from error recovery. This can be implemented using exceptions (see §2.4.3.1, Chapter 13), but what we have here is quite suitable for a 180-line calculator.

10.2.5. The Driver

With all the pieces of the program in place, we need only a driver to start things. I decided on two functions: main() to do setup and error reporting and calculate() to handle the actual calculation:

Token_stream ts {cin}; // use input from cin

void calculate()
{
for (;;) {
ts.get();
if (ts.current().kind == Kind::end) break;
if (ts.current().kind == Kind::print) continue;
cout << expr(false) << '\n';
}
}

int main()
{
table["pi"] = 3.1415926535897932385; // insert predefined names
table["e"] = 2.7182818284590452354;

calculate();

return no_of_errors;
}

Conventionally, main() returns zero if the program terminates normally and nonzero otherwise (§2.2.1). Returning the number of errors accomplishes this nicely. As it happens, the only initialization needed is to insert the predefined names into the symbol table.

The primary task of the main loop (in calculate()) is to read expressions and write out the answer. This is achieved by the line:

cout << expr(false) << '\n';

The argument false tells expr() that it does not need to call ts.get() to read a token on which to work.

Testing for Kind::end ensures that the loop is correctly exited when ts.get() encounters an input error or an end-of-file. A break-statement exits its nearest enclosing switch-statement or loop (§9.5). Testing for Kind::print (that is, for '\n' and ';') relieves expr() of the responsibility for handling empty expressions. A continue-statement is equivalent to going to the very end of a loop.

10.2.6. Headers

The calculator uses standard-library facilities. Therefore, appropriate headers must be #included to complete the program:

#include<iostream> // I/O
#include<string> // strings
#include<map> // map
#include<cctype> // isalpha(), etc.

All of these headers provide facilities in the std namespace, so to use the names they provide we must either use explicit qualification with std:: or bring the names into the global namespace by

using namespace std;

To avoid confusing the discussion of expressions with modularity issues, I did the latter. Chapter 14 and Chapter 15 discuss ways of organizing this calculator into modules using namespaces and how to organize it into source files.

10.2.7. Command-Line Arguments

After the program was written and tested, I found it a bother to first start the program, then type the expressions, and finally quit. My most common use was to evaluate a single expression. If that expression could be presented as a command-line argument, a few keystrokes could be avoided.

A program starts by calling main() (§2.2.1, §15.4). When this is done, main() is given two arguments specifying the number of arguments, conventionally called argc, and an array of arguments, conventionally called argv. The arguments are C-style character strings (§2.2.5, §7.3), so the type of argv is char*[argc+1]. The name of the program (as it occurs on the command line) is passed as argv[0], so argc is always at least 1. The list of arguments is zero-terminated; that is, argv[argc]==0. For example, for the command

dc 150/1.1934

the arguments have these values:

Because the conventions for calling main() are shared with C, C-style arrays and strings are used.

The idea is to read from the command string in the same way that we read from the input stream. A stream that reads from a string is unsurprisingly called an istringstream (§38.2.2). So to calculate expressions presented on the command line, we simply have to get our Token_stream to read from an appropriate istringstream:

Token_stream ts {cin};

int main(int argc, char* argv[])
{
switch (argc) {
case 1: // read from standard input
break;
case 2: // read from argument string
ts.set_input(new istringstream{argv[1]});
break;
default:
error("too many arguments");
return 1;
}

table["pi"] = 3.1415926535897932385; // insert predefined names
table["e"] = 2.7182818284590452354;

calculate();

return no_of_errors;
}

To use an istringstream, include <sstream>.

It would be easy to modify main() to accept several command-line arguments, but this does not appear to be necessary, especially as several expressions can be passed as a single argument:

dc "rate=1.1934;150/rate;19.75/rate;217/rate"

I use quotes because ; is the command separator on my UNIX systems. Other systems have different conventions for supplying arguments to a program on startup.

Simple as they are, argc and argv are still a source of minor, yet annoying, bugs. To avoid those and especially to make it easier to pass around the program arguments, I tend to use a simple function to create a vector<string>:

vector<string> arguments(int argc, char* argv[])
{
vector<string> res;
for (int i = 0; i!=argc; ++i)
res.push_back(argv[i]);
return res;
}

More elaborate argument parsing functions are not uncommon.

10.2.8. A Note on Style

To programmers unacquainted with associative arrays, the use of the standard-library map as the symbol table seems almost like cheating. It is not. The standard library and other libraries are meant to be used. Often, a library has received more care in its design and implementation than aprogrammer could afford for a handcrafted piece of code to be used in just one program.

Looking at the code for the calculator, especially at the first version, we can see that there isn’t much traditional C-style, low-level code presented. Many of the traditional tricky details have been replaced by uses of standard-library classes such as ostream, string, and map (§4.3.1, §4.2, §4.4.3, §31.4, Chapter 36, Chapter 38).

Note the relative scarcity of loops, arithmetic, and assignments. This is the way things ought to be in code that doesn’t manipulate hardware directly or implement low-level abstractions.

10.3. Operator Summary

This section presents a summary of expressions and some examples. Each operator is followed by one or more names commonly used for it and an example of its use. In these tables:

• A name is an identifier (e.g., sum and map), an operator name (e.g., operator int, operator+, and operator"" km), or the name of a template specialization (e.g., sort<Record> and array<int,10>), possibly qualified using :: (e.g., std::vector and vector<T>::operator[]).

• A class-name is the name of a class (including decltype(expr) where expr denotes a class).

• A member is a member name (including the name of a destructor or a member template).

• An object is an expression yielding a class object.

• A pointer is an expression yielding a pointer (including this and an object of that type that supports the pointer operation).

• An expr is an expression, including a literal (e.g., 17, "mouse", and true)

• An expr-list is a (possibly empty) list of expressions.

• An lvalue is an expression denoting a modifiable object (§6.4.1).

• A type can be a fully general type name (with *, (), etc.) only when it appears in parentheses; elsewhere, there are restrictions (§iso.A).

• A lambda-declarator is a (possibly empty, comma-separated) list of parameters optionally followed by the mutable specifier, optionally followed by a noexcept specifier, optionally followed by a return type (§11.4).

• A capture-list is a (possibly empty) list specifying context dependencies (§11.4).

• A stmt-list is a (possibly empty) list of statements (§2.2.4, Chapter 9).

The syntax of expressions is independent of operand types. The meanings presented here apply when the operands are of built-in types (§6.2.1). In addition, you can define meanings for operators applied to operands of user-defined types (§2.3, Chapter 18).

A table can only approximate the rules of the grammar. For details, see §iso.5 and §iso.A.

Each box holds operators with the same precedence. Operators in higher boxes have higher precedence. For example, N::x.m means (N::m).m rather than the illegal N::(x.m).

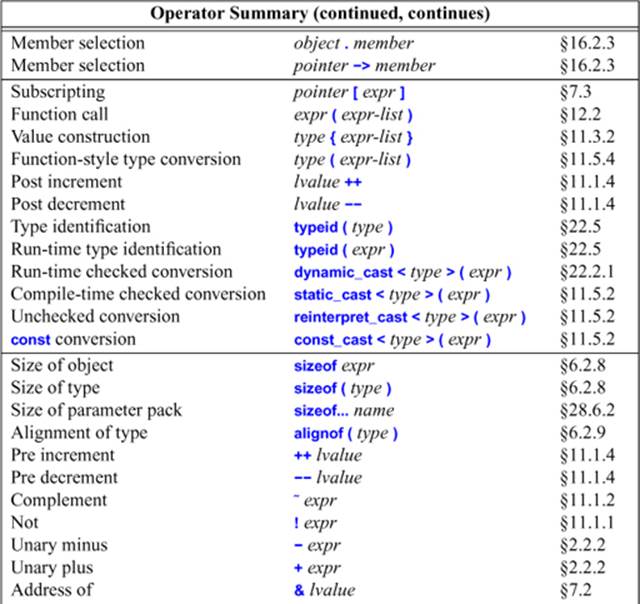
For example, postfix ++ has higher precedence than unary *, so *p++ means *(p++), not (*p)++.

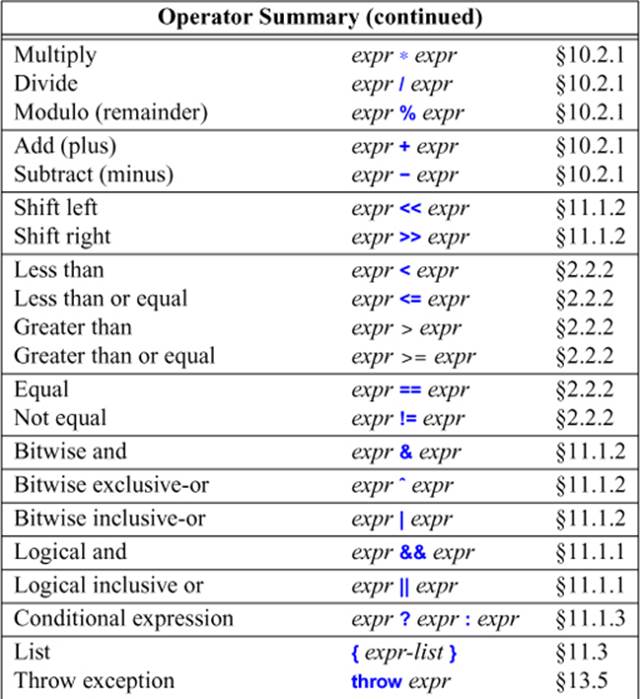
For example: a+b*c means a+(b*c) rather than (a+b)*c because * has higher precedence than +.

Unary operators and assignment operators are right-associative; all others are left-associative. For example, a=b=c means a=(b=c) whereas a+b+c means (a+b)+c.

A few grammar rules cannot be expressed in terms of precedence (also known as binding strength) and associativity. For example, a=b<c?d=e:f=g means a=((b<c)?(d=e):(f=g)), but you need to look at the grammar (§iso.A) to determine that.

Before applying the grammar rules, lexical tokens are composed from characters. The longest possible sequence of characters is chosen to make a token. For example, && is a single operator, rather than two & operators, and a+++1 means (a ++) + 1. This is sometimes called the Max Munch rule.

Whitespace characters (e.g., space, tab, and newline) can be token separators (e.g., int count is a keyword followed by an identifier, rather than intcount) but are otherwise ignored.

Some characters from the basic source character set (§6.1.2), such as |, are not convenient to type on some keywords. Also, some programmers find it odd to use of symbols, such as && and ~, for basic logical operations. Consequently, a set of alternative representation are provided as keywords:

For example

bool b = not (x or y) and z;
int x4 = ~ (x1 bitor x2) bitand x3;

is equivalent to

bool b = !(x || y) && z;
int x4 = ~ (x1 | x2) & x3;

Note that and= is not equivalent to &=; if you prefer keywords, you must write and_eq.

10.3.1. Results

The result types of arithmetic operators are determined by a set of rules known as “the usual arithmetic conversions” (§10.5.3). The overall aim is to produce a result of the “largest” operand type. For example, if a binary operator has a floating-point operand, the computation is done using floating-point arithmetic and the result is a floating-point value. Similarly, if it has a long operand, the computation is done using long integer arithmetic, and the result is a long. Operands that are smaller than an int (such as bool and char) are converted to int before the operator is applied.

The relational operators, ==, <=, etc., produce Boolean results. The meaning and result type of user-defined operators are determined by their declarations (§18.2).

Where logically feasible, the result of an operator that takes an lvalue operand is an lvalue denoting that lvalue operand. For example:

void f(int x, int y)
{
int j = x = y; // the value of x=y is the value of x after the assignment
int* p = &++x; // p points to x
int* q = &(x++); // error: x++ is not an lvalue (it is not the value stored in x)
int* p2 = &(x>y?x:y); // address of the int with the larger value
int& r = (x<y)?x:1; // error: 1 is not an lvalue
}

If both the second and third operands of ?: are lvalues and have the same type, the result is of that type and is an lvalue. Preserving lvalues in this way allows greater flexibility in using operators. This is particularly useful when writing code that needs to work uniformly and efficiently with both built-in and user-defined types (e.g., when writing templates or programs that generate C++ code).

The result of sizeof is of an unsigned integral type called size_t defined in <cstddef>. The result of pointer subtraction is of a signed integral type called ptrdiff_t defined in <cstddef>.

Implementations do not have to check for arithmetic overflow and hardly any do. For example:

void f()
{
int i = 1;
while (0 < i) ++i;
cout << "i has become negative!" << i << '\n';
}

This will (eventually) try to increase i past the largest integer. What happens then is undefined, but typically the value “wraps around” to a negative number (on my machine –2147483648). Similarly, the effect of dividing by zero is undefined, but doing so usually causes abrupt termination of the program. In particular, underflow, overflow, and division by zero do not throw standard exceptions (§30.4.1.1).

10.3.2. Order of Evaluation

The order of evaluation of subexpressions within an expression is undefined. In particular, you cannot assume that the expression is evaluated left-to-right. For example:

int x = f(2)+g(3); // undefined whether f() or g() is called first

Better code can be generated in the absence of restrictions on expression evaluation order. However, the absence of restrictions on evaluation order can lead to undefined results. For example:

int i = 1;
v[i] = i++; // undefined result

The assignment may be evaluated as either v[1]=1 or v[2]=1 or may cause some even stranger behavior. Compilers can warn about such ambiguities. Unfortunately, most do not, so be careful not to write an expression that reads or writes an object more than once, unless it does so using a single operator that makes it well defined, such as ++ and +=, or explicitly express sequencing using , (comma), &&, or ||.

The operators , (comma), && (logical and), and || (logical or) guarantee that their left-hand operand is evaluated before their right-hand operand. For example, b=(a=2,a+1) assigns 3 to b. Examples of the use of || and && can be found in §10.3.3. For built-in types, the second operand of&& is evaluated only if its first operand is true, and the second operand of || is evaluated only if its first operand is false; this is sometimes called short-circuit evaluation. Note that the sequencing operator , (comma) is logically different from the comma used to separate arguments in a function call. For example:

f1(v[i],i++); // two arguments
f2( (v[i],i++) ); // one argument

The call of f1 has two arguments, v[i] and i++, and the order of evaluation of the argument expressions is undefined. So it should be avoided. Order dependence of argument expressions is very poor style and has undefined behavior. The call of f2 has only one argument, the comma expression (v[i],i++), which is equivalent to i++. That is confusing, so that too should be avoided.

Parentheses can be used to force grouping. For example, a*b/c means (a*b)/c, so parentheses must be used to get a*(b/c); a*(b/c) may be evaluated as (a*b)/c only if the user cannot tell the difference. In particular, for many floating-point computations a*(b/c) and (a*b)/c are significantly different, so a compiler will evaluate such expressions exactly as written.

10.3.3. Operator Precedence

Precedence levels and associativity rules reflect the most common usage. For example:

if (i<=0 || max<i) // ...

means “if i is less than or equal to 0 or if max is less than i.” That is, it is equivalent to

if ( (i<=0) || (max<i) ) // ...

and not the legal but nonsensical

if (i <= (0||max) < i) // ...

However, parentheses should be used whenever a programmer is in doubt about those rules. Use of parentheses becomes more common as the subexpressions become more complicated, but complicated subexpressions are a source of errors. Therefore, if you start feeling the need for parentheses, you might consider breaking up the expression by using an extra variable.

There are cases when the operator precedence does not result in the “obvious” interpretation. For example:

if (i&mask == 0) // oops! == expression as operand for &

This does not apply a mask to i and then test if the result is zero. Because == has higher precedence than &, the expression is interpreted as i&(mask==0). Fortunately, it is easy enough for a compiler to warn about most such mistakes. In this case, parentheses are important:

if ((i&mask) == 0) // ...

It is worth noting that the following does not work the way a mathematician might expect:

if (0 <= x <= 99) // ...

This is legal, but it is interpreted as (0<=x)<=99, where the result of the first comparison is either true or false. This Boolean value is then implicitly converted to 1 or 0, which is then compared to 99, yielding true. To test whether x is in the range 0..99, we might use

if (0<=x && x<=99) // ...

A common mistake for novices is to use = (assignment) instead of == (equals) in a condition:

if (a = 7) // oops! constant assignment in condition

This is natural because = means “equals” in many languages. Again, it is easy for a compiler to warn about most such mistakes – and many do. I do not recommend warping your style to compensate for compilers with weak warnings. In particular, I don’t consider this style worthwhile:

if (7 == a) // try to protect against misuse of =; not recommended

10.3.4. Temporary Objects

Often, the compiler must introduce an object to hold an intermediate result of an expression. For example, for v=x+y*z the result of y*z has to be put somewhere before it is added to x. For built-in types, this is all handled so that a temporary object (often referred to as just a temporary) is invisible to the user. However, for a user-defined type that holds a resource knowing the lifetime of a temporary can be important. Unless bound to a reference or used to initialize a named object, a temporary object is destroyed at the end of the full expression in which it was created. A full expression is an expression that is not a subexpression of some other expression.

The standard-library string has a member c_str() (§36.3) that returns a C-style pointer to a zero-terminated array of characters (§2.2.5, §43.4). Also, the operator + is defined to mean string concatenation. These are useful facilities for strings. However, in combination they can cause obscure problems. For example:

void f(string& s1, string& s2, string& s3)
{
const char* cs = (s1+s2).c_str();
cout << cs;
if (strlen(cs=(s2+s3).c_str())<8 && cs[0]=='a') {
// cs used here
}
}

Probably, your first reaction is “But don’t do that!” and I agree. However, such code does get written, so it is worth knowing how it is interpreted.

A temporary string object is created to hold s1+s2. Next, a pointer to a C-style string is extracted from that object. Then – at the end of the expression – the temporary object is deleted. However, the C-style string returned by c_str() was allocated as part of the temporary object holdings1+s2, and that storage is not guaranteed to exist after that temporary is destroyed. Consequently, cs points to deallocated storage. The output operation cout<<cs might work as expected, but that would be sheer luck. A compiler can detect and warn against many variants of this problem.

The problem with the if-statement is a bit more subtle. The condition will work as expected because the full expression in which the temporary holding s2+s3 is created is the condition itself. However, that temporary is destroyed before the controlled statement is entered, so any use of csthere is not guaranteed to work.

Please note that in this case, as in many others, the problems with temporaries arose from using a high-level data type in a low-level way. A cleaner programming style yields a more understandable program fragment and avoids the problems with temporaries completely. For example:

void f(string& s1, string& s2, string& s3)
{
cout << s1+s2;
string s = s2+s3;
if (s.length()<8 && s[0]=='a') {
// use s here
}
}

A temporary can be used as an initializer for a const reference or a named object. For example:

void g(const string&, const string&);

void h(string& s1, string& s2)
{
const string& s = s1+s2;
string ss = s1+s2;

g(s,ss); // we can use s and ss here
}

This is fine. The temporary is destroyed when “its” reference or named object goes out of scope. Remember that returning a reference to a local variable is an error (§12.1.4) and that a temporary object cannot be bound to a non-const lvalue reference (§7.7).

A temporary object can also be created explicitly in an expression by invoking a constructor (§11.5.1). For example:

void f(Shape& s, int n, char ch)
{
s.move(string{n,ch}); // construct a string with n copies of ch to pass to Shape::move()
// ...
}

Such temporaries are destroyed in exactly the same way as the implicitly generated temporaries.

10.4. Constant Expressions

C++ offers two related meanings of “constant”:

• constexpr: Evaluate at compile time (§2.2.3).

• const: Do not modify in this scope (§2.2.3, §7.5).

Basically, constexpr’s role is to enable and ensure compile-time evaluation, whereas const’s primary role is to specify immutability in interfaces. This section is primarily concerned with the first role: compile-time evaluation.

A constant expression is an expression that a compiler can evaluate. It cannot use values that are not known at compile time and it cannot have side effects. Ultimately, a constant expression must start out with an integral value (§6.2.1), a floating-point value (§6.2.5), or an enumerator (§8.4), and we can combine those using operators and constexpr functions that in turn produce values. In addition, some addresses can be used in some forms of constant expressions. For simplicity, I discuss those separately in §10.4.5.

There are a variety of reasons why someone might want a named constant rather than a literal or a value stored in a variable:

[1] Named constants make the code easier to understand and maintain.

[2] A variable might be changed (so we have to be more careful in our reasoning than for a constant).

[3] The language requires constant expressions for array sizes, case labels, and template value arguments.

[4] Embedded systems programmers like to put immutable data into read-only memory because read-only memory is cheaper than dynamic memory (in terms of cost and energy consumption), and often more plentiful. Also, data in read-only memory is immune to most system crashes.

[5] If initialization is done at compile time, there can be no data races on that object in a multi-threaded system.

[6] Sometimes, evaluating something once (at compile time) gives significantly better performance than doing so a million times at run time.

Note that reasons [1], [2], [5], and (partly) [4] are logical. We don’t just use constant expressions because of an obsession with performance. Often, the reason is that a constant expression is a more direct representation of our system requirements.

As part of the definition of a data item (here, I deliberately avoid the word “variable”), constexpr expresses the need for compile-time evaluation. If the initializer for a constexpr can’t be evaluated at compile time, the compiler will give an error. For example:

int x1 = 7;
constexpr int x2 = 7;

constexpr int x3 = x1; // error: initializer is not a constant expression
constexpr int x4 = x2; // OK

void f()
{
constexpr int y3 = x1; // error: initializer is not a constant expression
constexpr int y4 = x2; // OK
// ...
}

A clever compiler could deduce that the value of x1 in the initializer for x3 was 7. However, we prefer not to rely on degrees of cleverness in compilers. In a large program, determining the values of variables at compile time is typically either very difficult or impossible.

The expressive power of constant expressions is great. We can use integer, floating-point, and enumeration values. We can use any operator that doesn’t modify state (e.g., +, ?:, and [], but not = or ++). We can use constexpr functions (§12.1.6) and literal types (§10.4.3) to provide a significant level of type safety and expressive power. It is almost unfair to compare this to what is commonly done with macros (§12.6).

The conditional-expression operator ?: is the means of selection in a constant expression. For example, we can compute an integer square root at compile time:

constexpr int isqrt_helper(int sq, int d, int a)
{
return sq <= a ? isqrt_helper(sq+d,d+2,a) : d;
}

constexpr int isqrt(int x)
{
return isqrt_helper(1,3,x)/2 – 1;
}

constexpr int s1 = isqrt(9); // s1 becomes 3
constexpr int s2 = isqrt(1234);

The condition of a ?: is evaluated and then the selected alternative is evaluated. The alternative not selected is not evaluated and might even not be a constant expression. Similarly, operands of && and || that are not evaluated need not be constant expressions. This feature is primarily useful in constexpr functions that are sometimes used as constant expressions and sometimes not.

10.4.1. Symbolic Constants

The most important single use of constants (constexpr or const values) is simply to provide symbolic names for values. Symbolic names should be used systematically to avoid “magic numbers” in code. Literal values scattered freely around in code is one of the nastiest maintenance hazards. If a numeric constant, such as an array bound, is repeated in code, it becomes hard to revise that code because every occurrence of that constant must be changed to update the code correctly. Using a symbolic name instead localizes information. Usually, a numeric constant represents an assumption about the program. For example, 4 may represent the number of bytes in an integer, 128 the number of characters needed to buffer input, and 6.24 the exchange factor between Danish kroner and U.S. dollars. Left as numeric constants in the code, these values are hard for a maintainer to spot and understand. Also, many such values need to change over time. Often, such numeric values go unnoticed and become errors when a program is ported or when some other change violates the assumptions they represent. Representing assumptions as well-commented named (symbolic) constants minimizes such maintenance problems.

10.4.2. consts in Constant Expressions

A const is primarily used to express interfaces (§7.5). However, const can also be used to express constant values. For example:

const int x = 7;
const string s = "asdf";
const int y = sqrt(x);

A const initialized with a constant expression can be used in a constant expression. A const differs from a constexpr in that it can be initialized by something that is not a constant expression; in that case, the const cannot be used as a constant expression. For example:

constexpr int xx = x; // OK
constexpr string ss = s; // error: s is not a constant expression
constexpr int yy = y; // error: sqrt(x) is not a constant expression

The reasons for the errors are that string is not a literal type (§10.4.3) and sqrt() is not a constexpr function (§12.1.6).

Usually, constexpr is a better choice than const for defining simple constants, but constexpr is new in C++11, so older code tends to use const. In many cases, enumerators (§8.4) are another alternative to consts.

10.4.3. Literal Types

A sufficiently simple user-defined type can be used in a constant expression. For example:

struct Point {
int x,y,z;
constexpr Point up(int d) { return {x,y,z+d}; }
constexpr Point move(int dx, int dy) { return {x+dx,y+dy}; }
// ...
};

A class with a constexpr constructor is called a literal type. To be simple enough to be constexpr, a constructor must have an empty body and all members must be initialized by potentially constant expressions. For example:

constexpr Point origo {0,0};
constexpr int z = origo.x;

constexpr Point a[] = {
origo, Point{1,1}, Point{2,2}, origo.move(3,3)
};
constexpr int x = a[1].x; // x becomes 1

constexpr Point xy{0,sqrt(2)}; // error: sqrt(2) is not a constant expression

Note that we can have constexpr arrays and also access array elements and object members.

Naturally, we can define constexpr functions to take arguments of literal types. For example:

constexpr int square(int x)
{
return x*x;
}

constexpr int radial_distance(Point p)
{
return isqrt(square(p.x)+square(p.y)+square(p.z));
}

constexpr Point p1 {10,20,30}; // the default constructor is constexpr
constexpr p2 {p1.up(20)}; // Point::up() is constexpr
constexpr int dist = radial_distance(p2);

I used int rather than double just because I didn’t have a constexpr floating-point square root function handy.

For a member function constexpr implies const, so I did not have to write:

constexpr Point move(int dx, int dy) const { return {x+dx,y+dy}; }

10.4.4. Reference Arguments

When working with constexpr, the key thing to remember is that constexpr is all about values. There are no objects that can change values or side effects here: constexpr provides a miniature compile-time functional programming language. That said, you might guess that constexpr cannot deal with references, but that’s only partially true because const references refer to values and can therefore be used. Consider the specialization of the general complex<T> to a complex<double> from the standard library:

template<> class complex<double> {
public:
constexpr complex(double re = 0.0, double im = 0.0);
constexpr complex(const complex<float>&);
explicit constexpr complex(const complex<long double>&);

constexpr double real(); // read the real part
void real(double); // set the real part
constexpr double imag(); // read the imaginary part
void imag(double); // set the imaginary part

complex<double>& operator= (double);
complex<double>& operator+=(double);
// ...
};

Obviously, operations, such as = and +=, that modify an object cannot be constexpr. Conversely, operations that simply read an object, such as real() and imag(), can be constexpr and be evaluated at compile time given a constant expression. The interesting member is the template constructor from another complex type. Consider:

constexpr complex<float> z1 {1,2}; // note: <float> not <double>
constexpr double re = z1.real();
constexpr double im = z1.imag();
constexpr complex<double> z2 {re,im}; // z2 becomes a copy of z1
constexpr complex<double> z3 {z1}; // z3 becomes a copy of z1

The copy constructor works because the compiler recognizes that the reference (the const complex<float>&) refers to a constant value and we just use that value (rather than trying anything advanced or silly with references or pointers).

Literal types allow for type-rich compile-time programming. Traditionally, C++ compile-time evaluation has been restricted to using integer values (and without functions). This has resulted in code that was unnecessarily complicated and error-prone, as people encoded every kind of information as integers. Some uses of template metaprogramming (Chapter 28) are examples of that. Other programmers have simply preferred run-time evaluation to avoid the difficulties of writing in an impoverished language.

10.4.5. Address Constant Expressions

The address of a statically allocated object (§6.4.2), such as a global variable, is a constant. However, its value is assigned by the linker, rather than the compiler, so the compiler cannot know the value of such an address constant. That limits the range of constant expressions of pointer and reference type. For example:

constexpr const char* p1 = "asdf";
constexpr const char* p2 = p1; // OK
constexpr const char* p2 = p1+2; // error: the compiler does not know the value of p1
constexpr char c = p1[2]; // OK, c=='d'; the compiler knows the value pointed to by p1

10.5. Implicit Type Conversion

Integral and floating-point types (§6.2.1) can be mixed freely in assignments and expressions. Wherever possible, values are converted so as not to lose information. Unfortunately, some value-destroying (“narrowing”) conversions are also performed implicitly. A conversion is value-preserving if you can convert a value and then convert the result back to its original type and get the original value. If a conversion cannot do that, it is a narrowing conversion (§10.5.2.6). This section provides a description of conversion rules, conversion problems, and their resolution.

10.5.1. Promotions

The implicit conversions that preserve values are commonly referred to as promotions. Before an arithmetic operation is performed, integral promotion is used to create ints out of shorter integer types. Similarly, floating-point promotion is used to create doubles out of floats. Note that these promotions will not promote to long (unless the operand is a char16_t, char32_t, wchar_t, or a plain enumeration that is already larger than an int) or long double. This reflects the original purpose of these promotions in C: to bring operands to the “natural” size for arithmetic operations.

The integral promotions are:

• A char, signed char, unsigned char, short int, or unsigned short int is converted to an int if int can represent all the values of the source type; otherwise, it is converted to an unsigned int.

• A char16_t, char32_t, wchar_t (§6.2.3), or a plain enumeration type (§8.4.2) is converted to the first of the following types that can represent all the values of its underlying type: int, unsigned int, long, unsigned long, or unsigned long long.

• A bit-field (§8.2.7) is converted to an int if int can represent all the values of the bit-field; otherwise, it is converted to unsigned int if unsigned int can represent all the values of the bit-field. Otherwise, no integral promotion applies to it.

• A bool is converted to an int; false becomes 0 and true becomes 1.

Promotions are used as part of the usual arithmetic conversions (§10.5.3).

10.5.2. Conversions

The fundamental types can be implicitly converted into each other in a bewildering number of ways (§iso.4). In my opinion, too many conversions are allowed. For example:

void f(double d)
{
char c = d; // beware: double-precision floating-point to char conversion
}

When writing code, you should always aim to avoid undefined behavior and conversions that quietly throw away information (“narrowing conversions”).

A compiler can warn about many questionable conversions. Fortunately, many compilers do.

The {}-initializer syntax prevents narrowing (§6.3.5). For example:

void f(double d)
{
char c {d}; // error: double-precision floating-point to char conversion
}

If potentially narrowing conversions are unavoidable, consider using some form of run-time checked conversion function, such as narrow_cast<>() (§11.5).

10.5.2.1. Integral Conversions

An integer can be converted to another integer type. A plain enumeration value can be converted to an integer type (§8.4.2) .

If the destination type is unsigned, the resulting value is simply as many bits from the source as will fit in the destination (high-order bits are thrown away if necessary). More precisely, the result is the least unsigned integer congruent to the source integer modulo 2 to the nth, where n is the number of bits used to represent the unsigned type. For example:

unsigned char uc = 1023;// binary 1111111111: uc becomes binary 11111111, that is, 255

If the destination type is signed, the value is unchanged if it can be represented in the destination type; otherwise, the value is implementation-defined:

signed char sc = 1023; // implementation-defined

Plausible results are 127 and –1 (§6.2.3).

A Boolean or plain enumeration value can be implicitly converted to its integer equivalent (§6.2.2, §8.4).

10.5.2.2. Floating-Point Conversions

A floating-point value can be converted to another floating-point type. If the source value can be exactly represented in the destination type, the result is the original numeric value. If the source value is between two adjacent destination values, the result is one of those values. Otherwise, the behavior is undefined. For example:

float f = FLT_MAX; // largest float value
double d = f; // OK: d == f

double d2 = DBL_MAX; // largest double value
float f2 = d2; // undefined if FLT_MAX<DBL_MAX

long double ld = d2; // OK: ld = d3
long double ld2 = numeric_limits<long double>::max();
double d3 = ld2; // undefined if sizeof(long double)>sizeof(double)

DBL_MAX and FLT_MAX are defined in <climits>; numeric_limits is defined in <limits> (§40.2).

10.5.2.3. Pointer and Reference Conversions

Any pointer to an object type can be implicitly converted to a void* (§7.2.1). A pointer (reference) to a derived class can be implicitly converted to a pointer (reference) to an accessible and unambiguous base (§20.2). Note that a pointer to function or a pointer to member cannot be implicitly converted to a void*.

A constant expression (§10.4) that evaluates to 0 can be implicitly converted to a null pointer of any pointer type. Similarly, a constant expression that evaluates to 0 can be implicitly converted to a pointer-to-member type (§20.6). For example:

int* p = (1+2)*(2*(1–1)); // OK, but weird

Prefer nullptr (§7.2.2).

A T* can be implicitly converted to a const T* (§7.5). Similarly, a T& can be implicitly converted to a const T&.

10.5.2.4. Pointer-to-Member Conversions

Pointers and references to members can be implicitly converted as described in §20.6.3.

10.5.2.5. Boolean Conversions

Pointer, integral, and floating-point values can be implicitly converted to bool (§6.2.2). A nonzero value converts to true; a zero value converts to false. For example:

void f(int* p, int i)
{
bool is_not_zero = p; // true if p!=0
bool b2 = i; // true if i!=0
// ...
}

The pointer-to-bool conversion is useful in conditions, but confusing elsewhere:

void fi(int);
void fb(bool);

void ff(int* p, int* q)
{
if (p) do_something(*p); // OK
if (q!=nullptr) do_something(*q); // OK, but verbose
// ...
fi(p); // error: no pointer to int conversion
fb(p); // OK: pointer to bool conversion (surprise!?)
}

Hope for a compiler warning for fb(p).

10.5.2.6. Floating-Integral Conversions

When a floating-point value is converted to an integer value, the fractional part is discarded. In other words, conversion from a floating-point type to an integer type truncates. For example, the value of int(1.6) is 1. The behavior is undefined if the truncated value cannot be represented in the destination type. For example:

int i = 2.7; // i becomes 2
char b = 2000.7; // undefined for 8-bit chars: 2000 cannot be represented as an 8-bit char

Conversions from integer to floating types are as mathematically correct as the hardware allows. Loss of precision occurs if an integral value cannot be represented exactly as a value of the floating type. For example:

int i = float(1234567890);

On a machine where both ints and floats are represented using 32 bits, the value of i is 1234567936.

Clearly, it is best to avoid potentially value-destroying implicit conversions. In fact, compilers can detect and warn against some obviously dangerous conversions, such as floating to integral and long int to char. However, general compile-time detection is impractical, so the programmer must be careful. When “being careful” isn’t enough, the programmer can insert explicit checks. For example:

char checked_cast(int i)
{
char c = i; // warning: not portable (§10.5.2.1)
if (i != c) throw std::runtime_error{"int–to–char check failed"};
return c;
}

void my_code(int i)
{
char c = checked_cast(i);
// ...
}

A more general technique for expressing checked conversions is presented in §25.2.5.1.

To truncate in a way that is guaranteed to be portable requires the use of numeric_limits (§40.2). In initializations, truncation can be avoided by using the {}-initializer notation (§6.3.5).

10.5.3. Usual Arithmetic Conversions

These conversions are performed on the operands of a binary operator to bring them to a common type, which is then used as the type of the result:

[1] If either operand is of type long double, the other is converted to long double.

• Otherwise, if either operand is double, the other is converted to double.

• Otherwise, if either operand is float, the other is converted to float.

• Otherwise, integral promotions (§10.5.1) are performed on both operands.

[2] Otherwise, if either operand is unsigned long long, the other is converted to unsigned long long.

• Otherwise, if one operand is a long long int and the other is an unsigned long int, then if a long long int can represent all the values of an unsigned long int, the unsigned long int is converted to a long long int; otherwise, both operands are converted to unsigned long long int. Otherwise, if either operand is unsigned long long, the other is converted to unsigned long long.

• Otherwise, if one operand is a long int and the other is an unsigned int, then if a long int can represent all the values of an unsigned int, the unsigned int is converted to a long int; otherwise, both operands are converted to unsigned long int.

• Otherwise, if either operand is long, the other is converted to long.

• Otherwise, if either operand is unsigned, the other is converted to unsigned.

• Otherwise, both operands are int.

These rules make the result of converting an unsigned integer to a signed one of possibly larger size implementation-defined. That is yet another reason to avoid mixing unsigned and signed integers.

10.6. Advice

[1] Prefer the standard library to other libraries and to “handcrafted code”; §10.2.8.

[2] Use character-level input only when you have to; §10.2.3.

[3] When reading, always consider ill-formed input; §10.2.3.

[4] Prefer suitable abstractions (classes, algorithms, etc.) to direct use of language features (e.g., ints, statements); §10.2.8.

[5] Avoid complicated expressions; §10.3.3.

[6] If in doubt about operator precedence, parenthesize; §10.3.3.

[7] Avoid expressions with undefined order of evaluation; §10.3.2.

[8] Avoid narrowing conversions; §10.5.2.

[9] Define symbolic constants to avoid “magic constants”; §10.4.1.

[10] Avoid narrowing conversions; §10.5.2.