Java 8 in Action: Lambdas, streams, and functional-style programming (2015)

Part 2. Functional-style data processing

Chapter 5. Working with streams

This chapter covers

· Filtering, slicing, and matching

· Finding, matching, and reducing

· Using numeric streams such as ranges of numbers

· Creating streams from multiple sources

· Infinite streams

In the previous chapter, you saw that streams let you move from external iteration to internal iteration. Instead of writing code as follows where you explicitly manage the iteration over a collection of data (external iteration),

List<Dish> vegetarianDishes = new ArrayList<>();

for(Dish d: menu){

if(d.isVegetarian()){

vegetarianDishes.add(d);

}

}

you can use the Streams API (internal iteration), which supports the filter and collect operations, to manage the iteration over the collection of data for you. All you need to do is pass the filtering behavior as argument to the filter method:

import static java.util.stream.Collectors.toList;

List<Dish> vegetarianDishes =

menu.stream()

.filter(Dish::isVegetarian)

.collect(toList());

This different way of working with data is useful because you let the Streams API manage how to process the data. As a consequence, the Streams API can work out several optimizations behind the scenes. In addition, using internal iteration, the Streams API can decide to run your code in parallel. Using external iteration, this isn’t possible because you’re committed to a single-threaded step-by-step sequential iteration.

In this chapter, you’ll have an extensive look at the various operations supported by the Streams API. These operations will let you express complex data processing queries such as filtering, slicing, mapping, finding, matching, and reducing. Next, we’ll explore special cases of streams: numeric streams, streams built from multiple sources such as files and arrays, and finally infinite streams.

5.1. Filtering and slicing

In this section, we look at how to select elements of a stream: filtering with a predicate, filtering only unique elements, ignoring the first few elements of a stream, or truncating a stream to a given size.

5.1.1. Filtering with a predicate

The Streams interface supports a filter method (which you should be familiar with by now). This operation takes as argument a predicate (a function returning a boolean) and returns a stream including all elements that match the predicate. For example, you can create a vegetarian menu by filtering all vegetarian dishes as follows and as illustrated in figure 5.1:

Figure 5.1. Filtering a stream with a predicate

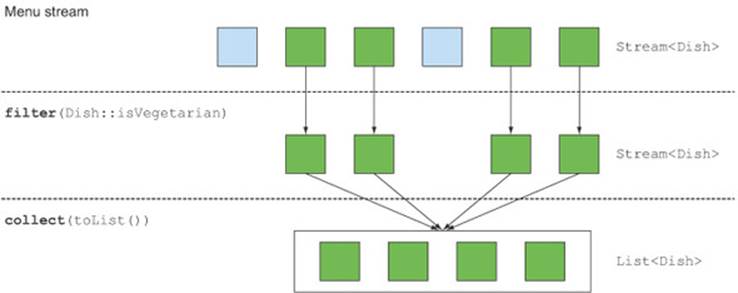
5.1.2. Filtering unique elements

Streams also support a method called distinct that returns a stream with unique elements (according to the implementation of the hashCode and equals methods of the objects produced by the stream). For example, the following code filters all even numbers from a list and makes sure that there are no duplicates. Figure 5.2 shows this visually:

Figure 5.2. Filtering unique elements in a stream

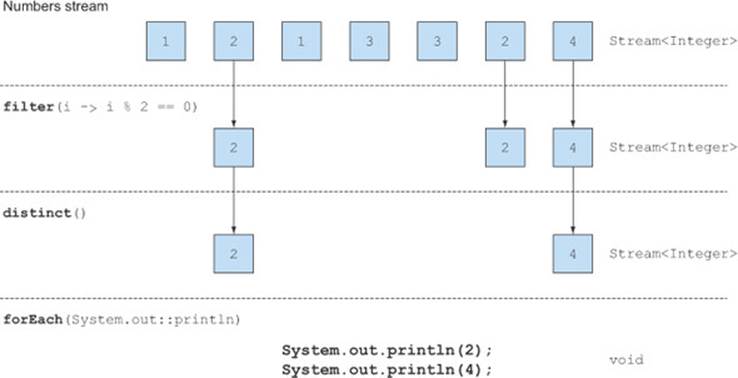
List<Integer> numbers = Arrays.asList(1, 2, 1, 3, 3, 2, 4);

numbers.stream()

.filter(i -> i % 2 == 0)

.distinct()

.forEach(System.out::println);

5.1.3. Truncating a stream

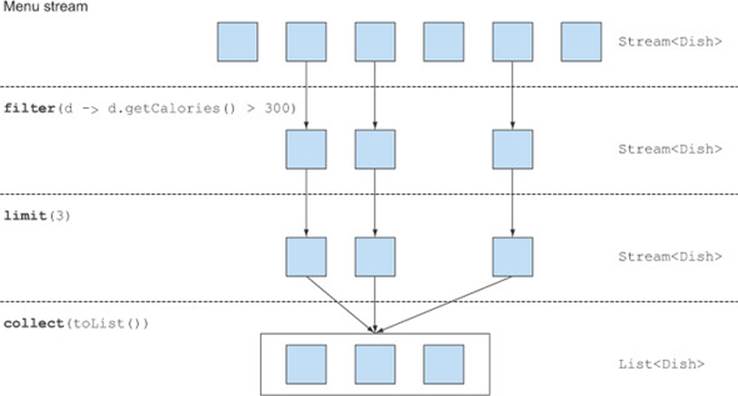
Streams support the limit(n) method, which returns another stream that’s no longer than a given size. The requested size is passed as argument to limit. If the stream is ordered, the first elements are returned up to a maximum of n. For example, you can create a List by selecting the first three dishes that have more than 300 calories as follows:

List<Dish> dishes = menu.stream()

.filter(d -> d.getCalories() > 300)

.limit(3)

.collect(toList());

Figure 5.3 illustrates a combination of filter and limit. You can see that only the first three elements that match the predicate are selected and the result is immediately returned.

Figure 5.3. Truncating a stream

Note that limit also works on unordered streams (for example, if the source is a Set). In this case you shouldn’t assume any order on the result produced by limit.

5.1.4. Skipping elements

Streams support the skip(n) method to return a stream that discards the first n elements. If the stream has fewer elements than n, then an empty stream is returned. Note that limit(n) and skip(n) are complementary! For example, the following code skips the first two dishes that have more than 300 calories and returns the rest. Figure 5.4 illustrates this query:

Figure 5.4. Skipping elements in a stream

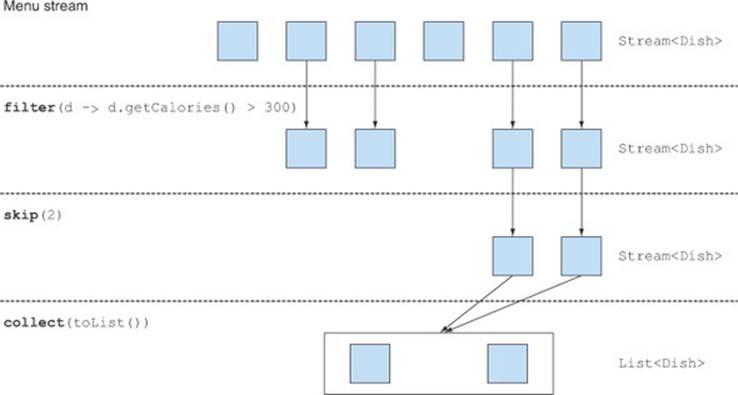
List<Dish> dishes = menu.stream()

.filter(d -> d.getCalories() > 300)

.skip(2)

.collect(toList());

Put what you’ve learned in this section into practice with Quiz 5.1 before we move to mapping operations.

Quiz 5.1: Filtering

How would you use streams to filter the first two meat dishes?

Answer:

You can solve this problem by composing the methods filter and limit together and using collect(toList()) to convert the stream into a list as follows:

List<Dish> dishes =

menu.stream()

.filter(d -> d.getType() == Dish.Type.MEAT)

.limit(2)

.collect(toList());

5.2. Mapping

A very common data processing idiom is to select information from certain objects. For example, in SQL you can select a particular column from a table. The Streams API provides similar facilities through the map and flatMap methods.

5.2.1. Applying a function to each element of a stream

Streams support the method map, which takes a function as argument. The function is applied to each element, mapping it into a new element (the word mapping is used because it has a meaning similar to transforming but with the nuance of “creating a new version of” rather than “modifying”). For example, in the following code you pass a method reference Dish::getName to the map method to extract the names of the dishes in the stream:

List<String> dishNames = menu.stream()

.map(Dish::getName)

.collect(toList());

Because the method getName returns a String, the stream outputted by the map method is of type Stream<String>.

Let’s take a slightly different example to solidify your understanding of map. Given a list of words, you’d like to return a list of the number of characters for each word. How would you do it? You’d need to apply a function to each element of the list. This sounds like a job for the map method! The function to apply should take a word and return its length. You can solve this problem as follows by passing a method reference String::length to map:

List<String> words = Arrays.asList("Java8", "Lambdas", "In", "Action");

List<Integer> wordLengths = words.stream()

.map(String::length)

.collect(toList());

Let’s now return to the example where you extracted the name of each dish. What if you wanted to find out the length of the name of each dish? You could do this by chaining another map as follows:

List<Integer> dishNameLengths = menu.stream()

.map(Dish::getName)

.map(String::length)

.collect(toList());

5.2.2. Flattening streams

You saw how to return the length for each word in a list using the method map. Let’s extend this idea a bit further: how could you return a list of all the unique characters for a list of words? For example, given the list of words ["Hello", "World"] you’d like to return the list ["H", "e","l", "o", "W", "r", "d"].

You might think that this is easy, that you can just map each word into a list of characters and then call distinct to filter duplicate characters. A first go could be like this:

words.stream()

.map(word -> word.split(""))

.distinct()

.collect(toList());

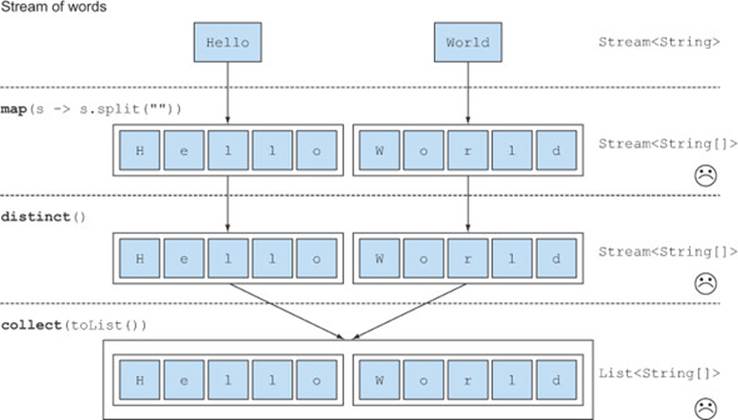
The problem with this approach is that the lambda passed to the map method returns a String[] (an array of String) for each word. So the stream returned by the map method is actually of type Stream<String[]>. What you really want is Stream<String> to represent a stream of characters. Figure 5.5 illustrates the problem.

Figure 5.5. Incorrect use of map to find unique characters from a list of words

Luckily there’s a solution to this problem using the method flatMap! Let’s see step by step how to solve it.

Attempt using map and Arrays.stream

First, you need a stream of characters instead of a stream of arrays. There’s a method called Arrays.stream()that takes an array and produces a stream, for example:

String[] arrayOfWords = {"Goodbye", "World"};

Stream<String> streamOfwords = Arrays.stream(arrayOfWords);

Use it in the previous pipeline to see what happens:

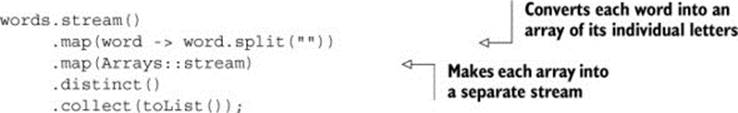
The current solution still doesn’t work! This is because you now end up with a list of streams (more precisely, Stream<Stream<String>>)! Indeed, you first convert each word into an array of its individual letters and then make each array into a separate stream.

Using flatMap

You can fix this problem by using flatMap as follows:

Using the flatMap method has the effect of mapping each array not with a stream but with the contents of that stream. All the separate streams that were generated when using map(Arrays::stream) get amalgamated—flattened into a single stream. Figure 5.6 illustrates the effect of using the flatMap method. Compare it with what map does in figure 5.5.

Figure 5.6. Using flatMap to find the unique characters from a list of words

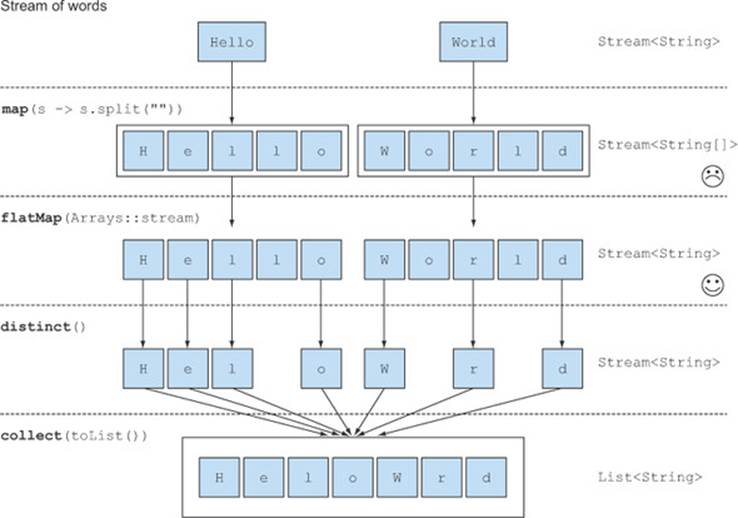
In a nutshell, the flatMap method lets you replace each value of a stream with another stream and then concatenates all the generated streams into a single stream.

We come back to flatMap in chapter 10 when we discuss more advanced Java 8 patterns such as using the new library class Optional for null checking. To solidify your understanding of map and flatMap, try out Quiz 5.2.

Quiz 5.2: Mapping

1. Given a list of numbers, how would you return a list of the square of each number? For example, given [1, 2, 3, 4, 5] you should return [1, 4, 9, 16, 25].

Answer:

You can solve this problem by using map with a lambda that takes a number and returns the square of the number:

List<Integer> numbers = Arrays.asList(1, 2, 3, 4, 5);

List<Integer> squares =

numbers.stream()

.map(n -> n * n)

.collect(toList());

2. Given two lists of numbers, how would you return all pairs of numbers? For example, given a list [1, 2, 3] and a list [3, 4] you should return [(1, 3), (1, 4), (2, 3), (2, 4), (3, 3), (3, 4)]. For simplicity, you can represent a pair as an array with two elements.

Answer:

You could use two maps to iterate on the two lists and generate the pairs. But this would return a Stream<Stream<Integer[]>>. What you need to do is flatten the generated streams to result in a Stream<Integer[]>. This is what flatMap is for:

List<Integer> numbers1 = Arrays.asList(1, 2, 3);

List<Integer> numbers2 = Arrays.asList(3, 4);

List<int[]> pairs =

numbers1.stream()

.flatMap(i -> numbers2.stream()

.map(j -> new int[]{i, j})

)

.collect(toList());

3. How would you extend the previous example to return only pairs whose sum is divisible by 3? For example, (2, 4) and (3, 3) are valid.

Answer:

You saw earlier that filter can be used with a predicate to filter elements from a stream. Because after the flatMap operation you have a stream of int[] that represent a pair, you just need a predicate to check to see if the sum is divisible by 3:

List<Integer> numbers1 = Arrays.asList(1, 2, 3);

List<Integer> numbers2 = Arrays.asList(3, 4);

List<int[]> pairs =

numbers1.stream()

.flatMap(i ->

numbers2.stream()

.filter(j -> (i + j) % 3 == 0)

.map(j -> new int[]{i, j})

)

.collect(toList());

The result is [(2, 4), (3, 3)].

5.3. Finding and matching

Another common data processing idiom is finding whether some elements in a set of data match a given property. The Streams API provides such facilities through the allMatch, anyMatch, noneMatch, findFirst, and findAny methods of a stream.

5.3.1. Checking to see if a predicate matches at least one element

The anyMatch method can be used to answer the question “Is there an element in the stream matching the given predicate?” For example, you can use it to find out whether the menu has a vegetarian option:

if(menu.stream().anyMatch(Dish::isVegetarian)){

System.out.println("The menu is (somewhat) vegetarian friendly!!");

}

The anyMatch method returns a boolean and is therefore a terminal operation.

5.3.2. Checking to see if a predicate matches all elements

The allMatch method works similarly to anyMatch but will check to see if all the elements of the stream match the given predicate. For example, you can use it to find out whether the menu is healthy (that is, all dishes are below 1000 calories):

boolean isHealthy = menu.stream()

.allMatch(d -> d.getCalories() < 1000);

noneMatch

The opposite of allMatch is noneMatch. It ensures that no elements in the stream match the given predicate. For example, you could rewrite the previous example as follows using noneMatch:

boolean isHealthy = menu.stream()

.noneMatch(d -> d.getCalories() >= 1000);

These three operations, anyMatch, allMatch, and noneMatch, make use of what we call short-circuiting, a stream version of the familiar Java short-circuiting && and || operators.

Short-circuiting evaluation

Some operations don’t need to process the whole stream to produce a result. For example, say you need to evaluate a large boolean expression chained with and operators. You need only find out that one expression is false to deduce that the whole expression will return false, no matter how long the expression is; there’s no need to evaluate the entire expression. This is what short-circuiting refers to.

In relation to streams, certain operations such as allMatch, noneMatch, findFirst, and findAny don’t need to process the whole stream to produce a result. As soon as an element is found, a result can be produced. Similarly, limit is also a short-circuiting operation: the operation only needs to create a stream of a given size without processing all the elements in the stream. Such operations are useful, for example, when you need to deal with streams of infinite size, because they can turn an infinite stream into a stream of finite size. We show examples of infinite streams insection 5.7.

5.3.3. Finding an element

The findAny method returns an arbitrary element of the current stream. It can be used in conjunction with other stream operations. For example, you may wish to find a dish that’s vegetarian. You can combine the filter method and findAny to express this query:

Optional<Dish> dish =

menu.stream()

.filter(Dish::isVegetarian)

.findAny();

The stream pipeline will be optimized behind the scenes to perform a single pass and finish as soon as a result is found by using short-circuiting. But wait a minute; what’s this Optional thing in the code?

Optional in a nutshell

The Optional<T> class (java.util.Optional) is a container class to represent the existence or absence of a value. In the previous code, it’s possible that findAny doesn’t find any element. Instead of returning null, which is well known for being error prone, the Java 8 library designers introduced Optional<T>. We won’t go into the details of Optional here, because we show in detail in chapter 10 how your code can benefit from using Optional to avoid bugs related to null checking. But for now, it’s good to know that there are a few methods available inOptional that force you to explicitly check for the presence of a value or deal with the absence of a value:

· isPresent() returns true if Optional contains a value, false otherwise.

· ifPresent(Consumer<T> block) executes the given block if a value is present. We introduced the Consumer functional interface in chapter 3; it lets you pass a lambda that takes an argument of type T and returns void.

· T get() returns the value if present; otherwise it throws a NoSuchElement-Exception.

· T orElse(T other) returns the value if present; otherwise it returns a default value.

For example, in the previous code you’d need to explicitly check for the presence of a dish in the Optional object to access its name:

5.3.4. Finding the first element

Some streams have an encounter order that specifies the order in which items logically appear in the stream (for example, a stream generated from a List or from a sorted sequence of data). For such streams you may wish to find the first element. There’s the findFirst method for this, which works similarly to findAny. For example, the code that follows, given a list of numbers, finds the first square that’s divisible by 3:

List<Integer> someNumbers = Arrays.asList(1, 2, 3, 4, 5);

Optional<Integer> firstSquareDivisibleByThree =

someNumbers.stream()

.map(x -> x * x)

.filter(x -> x % 3 == 0)

.findFirst(); // 9

When to use findFirst and findAny

You may wonder why we have both findFirst and findAny. The answer is parallelism. Finding the first element is more constraining in parallel. If you don’t care about which element is returned, use findAny because it’s less constraining when using parallel streams.

5.4. Reducing

So far, the terminal operations you’ve seen return a boolean (allMatch and so on), void (forEach), or an Optional object (findAny and so on). You’ve also been using collect to combine all elements in a stream into a List.

In this section, you’ll see how you can combine elements of a stream to express more complicated queries such as “Calculate the sum of all calories in the menu,” or “What is the highest calorie dish in the menu?” using the reduce operation. Such queries combine all the elements in the stream repeatedly to produce a single value such as an Integer. These queries can be classified as reduction operations (a stream is reduced to a value). In functional programming-language jargon, this is referred to as a fold because you can view this operation as repeatedly folding a long piece of paper (your stream) until it forms a small square, which is the result of the fold operation.

5.4.1. Summing the elements

Before we investigate how to use the reduce method, it helps to first see how you’d sum the elements of a list of numbers using a for-each loop:

int sum = 0;

for (int x : numbers) {

sum += x;

}

Each element of numbers is combined iteratively with the addition operator to form a result. You reduce the list of numbers into one number by repeatedly using addition. There are two parameters in this code:

· The initial value of the sum variable, in this case 0

· The operation to combine all the elements of the list, in this case +

Wouldn’t it be great if you could also multiply all the numbers without having to repeatedly copy and paste this code? This is where the reduce operation, which abstracts over this pattern of repeated application, can help. You can sum all the elements of a stream as follows:

int sum = numbers.stream().reduce(0, (a, b) -> a + b);

reduce takes two arguments:

· An initial value, here 0.

· A BinaryOperator<T> to combine two elements and produce a new value; here you use the lambda (a, b) -> a + b.

You could just as easily multiply all the elements by passing a different lambda, (a, b) -> a * b, to the reduce operation:

int product = numbers.stream().reduce(1, (a, b) -> a * b);

Figure 5.7 illustrates how the reduce operation works on a stream: the lambda combines each element repeatedly until the stream is reduced to a single value.

Figure 5.7. Using reduce to sum the numbers in a stream

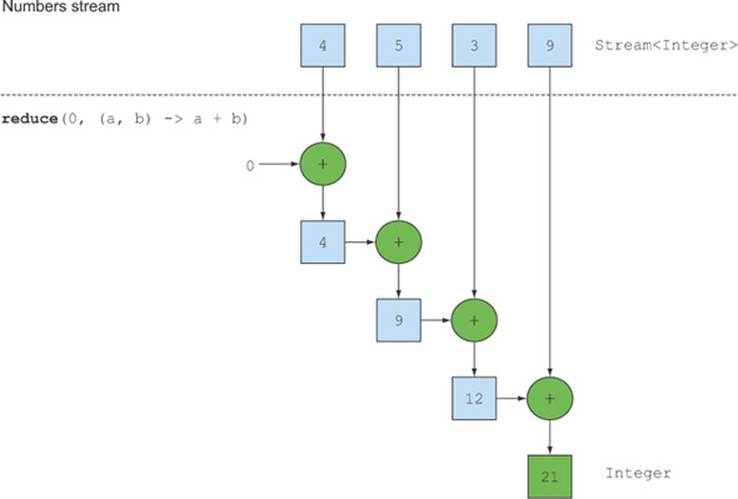
Let’s take an in-depth look into how the reduce operation happens to sum a stream of numbers. First, 0 is used as the first parameter of the lambda (a), and 4 is consumed from the stream and used as the second parameter (b). 0 + 4 produces 4, and it becomes the new accumulated value. Then the lambda is called again with the accumulated value and the next element of the stream, 5, which produces the new accumulated value, 9. Moving forward, the lambda is called again with the accumulated value and the next element, 3, which produces 12. Finally, the lambda is called with 12 and the last element of the stream, 9, which produces the final value, 21.

You can make this code more concise by using a method reference. In Java 8 the Integer class now comes with a static sum method to add two numbers, which is just what you want instead of repeatedly writing out the same code as lambda:

int sum = numbers.stream().reduce(0, Integer::sum);

No initial value

There’s also an overloaded variant of reduce that doesn’t take an initial value, but it returns an Optional object:

Optional<Integer> sum = numbers.stream().reduce((a, b) -> (a + b));

Why does it return an Optional<Integer>? Consider the case when the stream contains no elements. The reduce operation can’t return a sum because it doesn’t have an initial value. This is why the result is wrapped in an Optional object to indicate that the sum may be absent. Now see what else you can do with reduce.

5.4.2. Maximum and minimum

It turns out that reduction is all you need to compute maxima and minima as well! Let’s see how you can apply what you just learned about reduce to calculate the maximum or minimum element in a stream. As you saw, reduce takes two parameters:

· An initial value

· A lambda to combine two stream elements and produce a new value

The lambda is applied step by step to each element of the stream with the addition operator, as shown in figure 5.7. So you need a lambda that, given two elements, returns the maximum of them. The reduce operation will use the new value with the next element of the stream to produce a new maximum until the whole stream is consumed! You can use reduce as follows to calculate the maximum in a stream; this is illustrated in figure 5.8:

Figure 5.8. A reduce operation—calculating the maximum

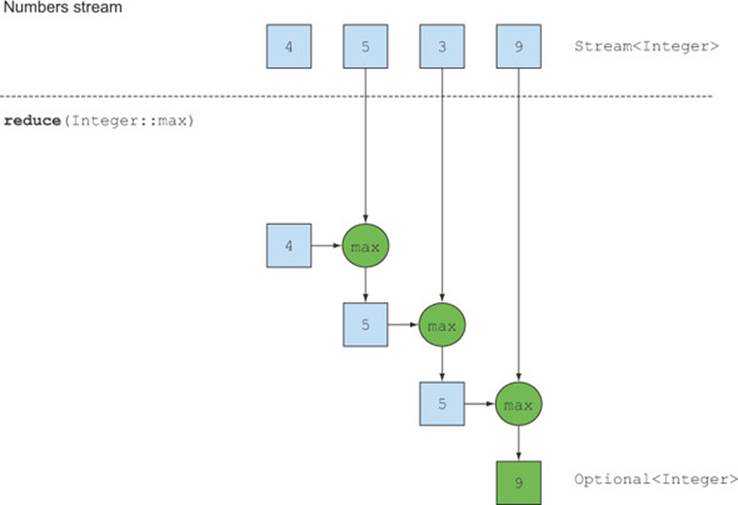
Optional<Integer> max = numbers.stream().reduce(Integer::max);

To calculate the minimum, you need to pass Integer.min to the reduce operation instead of Integer.max:

Optional<Integer> min = numbers.stream().reduce(Integer::min);

You could have equally well used the lambda (x,y)->x<y?x:y instead of Integer::min, but the latter is easier to read.

To test your understanding of the reduce operation, have a go at Quiz 5.3.

Quiz 5.3: Reducing

How would you count the number of dishes in a stream using the map and reduce methods?

Answer:

You can solve this problem by mapping each element of a stream into the number 1 and then summing them using reduce! This is equivalent to counting in order the number of elements in the stream.

int count = menu.stream()

.map(d -> 1)

.reduce(0, (a, b) -> a + b);

A chain of map and reduce is commonly known as the map-reduce pattern, made famous by Google’s use of it for web searching because it can be easily parallelized. Note that in chapter 4 you saw the built-in method count to count the number of elements in the stream:

long count = menu.stream().count();

Benefit of the reduce method and parallelism

The benefit of using reduce compared to the step-by-step iteration summation that you wrote earlier is that the iteration is abstracted using internal iteration, which enables the internal implementation to choose to perform the reduce operation in parallel. The iterative summation example involves shared updates to a sum variable, which doesn’t parallelize gracefully. If you add in the needed synchronization, you’ll likely discover that thread contention robs you of all the performance that parallelism was supposed to give you! Parallelizing this computation requires a different approach: partition the input, sum the partitions, and combine the sums. But now the code is starting to look really different. You’ll see what this looks like in chapter 7 using the fork/join framework. But for now it’s important to realize that the mutable accumulator pattern is a dead end for parallelization. You need a new pattern, and this is what reduce provides you. You’ll also see in chapter 7 that to sum all the elements in parallel using streams, there’s almost no modification to your code: stream() becomes parallelStream():

int sum = numbers.parallelStream().reduce(0, Integer::sum);

But there’s a price to pay to execute this code in parallel, as we explain later: the lambda passed to reduce can’t change state (for example, instance variables), and the operation needs to be associative so it can be executed in any order.

So far you saw reduction examples that produced an Integer: the sum of a stream, the maximum of a stream, or the number of elements in a stream. You’ll see in section 5.6 that built-in methods such as sum and max are available as well to help you write slightly more concise code for common reduction patterns. We investigate a more complex form of reductions using the collect method in the next chapter. For example, instead of reducing a stream into an Integer, you can also reduce it into a Map if you want to group dishes by types.

Stream operations: stateless vs. stateful

You’ve seen a lot of stream operations. An initial presentation can make them seem a panacea; everything just works, and you get parallelism for free when you use parallelStream instead of stream to get a stream from a collection.

Certainly for many applications this is the case, as you’ve seen in the previous examples. You can turn a list of dishes into a stream, filter to select various dishes of a certain type, then map down the resulting stream to add on the number of calories, and then reduce to produce the total number of calories of the menu. You can even do such stream calculations in parallel. But these operations have different characteristics. There are issues about what internal state they need to operate.

Operations like map and filter take each element from the input stream and produce zero or one result in the output stream. These operations are thus in general stateless: they don’t have an internal state (assuming the user-supplied lambda or method reference has no internal mutable state).

But operations like reduce, sum, and max need to have internal state to accumulate the result. In this case the internal state is small. In our example it consisted of an int or double. The internal state is of bounded size no matter how many elements are in the stream being processed.

By contrast, some operations such as sorted or distinct seem at first to behave like filter or map—all take a stream and produce another stream (an intermediate operation), but there’s a crucial difference. Both sorting and removing duplicates from a stream require knowing the previous history to do their job. For example, sorting requires all the elements to be buffered before a single item can be added to the output stream; the storage requirement of the operation is unbounded. This can be problematic if the data stream is large or infinite. (What should reversing the stream of all prime numbers do? It should return the largest prime number, which mathematics tells us doesn’t exist.) We call these operations stateful operations.

You’ve now seen a lot of stream operations that you can use to express sophisticated data processing queries! Table 5.1 summarizes the operations seen so far. You get to practice them in the next section through an exercise.

Table 5.1. Intermediate and terminal operations

5.5. Putting it all into practice

In this section, you get to practice what you’ve learned about streams so far. We give a different domain: traders executing transactions. You’re asked by your manager to find answers to eight queries. Can you do it? We give the solutions in section 5.5.2, but you should try them yourself first to get some practice.

1. Find all transactions in the year 2011 and sort them by value (small to high).

2. What are all the unique cities where the traders work?

3. Find all traders from Cambridge and sort them by name.

4. Return a string of all traders’ names sorted alphabetically.

5. Are any traders based in Milan?

6. Print all transactions’ values from the traders living in Cambridge.

7. What’s the highest value of all the transactions?

8. Find the transaction with the smallest value.

5.5.1. The domain: Traders and Transactions

Here’s the domain you’ll be working with, a list of Traders and Transactions:

Trader raoul = new Trader("Raoul", "Cambridge");

Trader mario = new Trader("Mario","Milan");

Trader alan = new Trader("Alan","Cambridge");

Trader brian = new Trader("Brian","Cambridge");

List<Transaction> transactions = Arrays.asList(

new Transaction(brian, 2011, 300),

new Transaction(raoul, 2012, 1000),

new Transaction(raoul, 2011, 400),

new Transaction(mario, 2012, 710),

new Transaction(mario, 2012, 700),

new Transaction(alan, 2012, 950)

);

Trader and Transaction are classes defined as follows:

public class Trader{

private final String name;

private final String city;

public Trader(String n, String c){

this.name = n;

this.city = c;

}

public String getName(){

return this.name;

}

public String getCity(){

return this.city;

}

public String toString(){

return "Trader:"+this.name + " in " + this.city;

}

}

public class Transaction{

private final Trader trader;

private final int year;

private final int value;

public Transaction(Trader trader, int year, int value){

this.trader = trader;

this.year = year;

this.value = value;

}

public Trader getTrader(){

return this.trader;

}

public int getYear(){

return this.year;

}

public int getValue(){

return this.value;

}

public String toString(){

return "{" + this.trader + ", " +

"year: "+this.year+", " +

"value:" + this.value +"}";

}

}

5.5.2. Solutions

We now provide the solutions in the following code listings, so you can verify your understanding of what you’ve learned so far. Well done!

Listing 5.1. Find all transactions in 2011 and sort by value (small to high)

Listing 5.2. What are all the unique cities where the traders work?

You haven’t seen this yet, but you could also drop distinct() and use toSet() instead, which would convert the stream into a set. You’ll learn more about it in chapter 6.

Set<String> cities =

transactions.stream()

.map(transaction -> transaction.getTrader().getCity())

.collect(toSet());

Listing 5.3. Find all traders from Cambridge and sort them by name

Listing 5.4. Return a string of all traders’ names sorted alphabetically

Note that this solution isn’t very efficient (all Strings are repeatedly concatenated, which creates a new String object at each iteration). In the next chapter, you’ll see a more efficient solution that uses joining() as follows (which internally makes use of a StringBuilder):

String traderStr =

transactions.stream()

.map(transaction -> transaction.getTrader().getName())

.distinct()

.sorted()

.collect(joining());

Listing 5.5. Are any traders based in Milan?

Listing 5.6. Print all transactions’ values from the traders living in Cambridge

Listing 5.7. What’s the highest value of all the transactions?

Listing 5.8. Find the transaction with the smallest value

You can do better. A stream supports the methods min and max that take a Comparator as argument to specify which key to compare with when calculating the minimum or maximum:

Optional<Transaction> smallestTransaction =

transactions.stream()

.min(comparing(Transaction::getValue));

5.6. Numeric streams

You saw earlier that you could use the reduce method to calculate the sum of the elements of a stream. For example, you can calculate the number of calories in the menu as follows:

int calories = menu.stream()

.map(Dish::getCalories)

.reduce(0, Integer::sum);

The problem with this code is that there’s an insidious boxing cost. Behind the scenes each Integer needs to be unboxed to a primitive before performing the summation. In addition, wouldn’t it be nicer if you could call a sum method directly as follows?

int calories = menu.stream()

.map(Dish::getCalories)

.sum();

But this isn’t possible. The problem is that the method map generates a Stream<T>. Even though the elements of the stream are of type Integer, the Streams interface doesn’t define a sum method. Why not? Say you had only a Stream<Dish> like the menu; it wouldn’t make any sense to be able to sum dishes. But don’t worry; the Streams API also supplies primitive stream specializations that support specialized methods to work with streams of numbers.

5.6.1. Primitive stream specializations

Java 8 introduces three primitive specialized stream interfaces to tackle this issue, IntStream, DoubleStream, and LongStream, that respectively specialize the elements of a stream to be int, long, and double—and thereby avoid hidden boxing costs. Each of these interfaces brings new methods to perform common numeric reductions such as sum to calculate the sum of a numeric stream and max to find the maximum element. In addition, they have methods to convert back to a stream of objects when necessary. The thing to remember is that these specializations aren’t more complexity about streams but instead more complexity caused by boxing—the (efficiency-based) difference between int and Integer and so on.

Mapping to a numeric stream

The most common methods you’ll use to convert a stream to a specialized version are mapToInt, mapToDouble, and mapToLong. These methods work exactly like the method map that you saw earlier but return a specialized stream instead of a Stream<T>. For example, you can usemapToInt as follows to calculate the sum of calories in the menu:

Here, the method mapToInt extracts all the calories from each dish (represented as an Integer) and returns an IntStream as the result (rather than a Stream<Integer>). You can then call the sum method defined on the IntStream interface to calculate the sum of calories! Note that if the stream were empty, sum would return 0 by default. IntStream also supports other convenience methods such as max, min, and average.

Converting back to a stream of objects

Similarly, once you have a numeric stream, you may be interested in converting it back to a nonspecialized stream. For example, the operations of an IntStream are restricted to produce primitive integers: the map operation of an IntStream takes a lambda that takes an int and produces an int (an IntUnaryOperator). But you may want to produce a different value such as a Dish. For this you need to access the operations defined in the Streams interface that are more general. To convert from a primitive stream to a general stream (each int will be boxed to anInteger) you can use the method boxed as follows:

You’ll learn in the next section that boxed is particularly useful when you deal with numeric ranges that need to be boxed into a general stream.

Default values: OptionalInt

The sum example was convenient because it has a default value: 0. But if you want to calculate the maximum element in an IntStream, you need something different because 0 is a wrong result. How can you differentiate that the stream has no element and that the real maximum is 0? Earlier we introduced the Optional class, which is a container that indicates the presence or absence of a value. Optional can be parameterized with reference types such as Integer, String, and so on. There’s a primitive specialized version of Optional as well for the three primitive stream specializations: OptionalInt, OptionalDouble, and OptionalLong.

For example, you can find the maximal element of an IntStream by calling the max method, which returns an OptionalInt:

OptionalInt maxCalories = menu.stream()

.mapToInt(Dish::getCalories)

.max();

You can now process the OptionalInt explicitly to define a default value if there’s no maximum:

5.6.2. Numeric ranges

A common use case when dealing with numbers is working with ranges of numeric values. For example, suppose you’d like to generate all numbers between 1 and 100. Java 8 introduces two static methods available on IntStream and LongStream to help generate such ranges: range andrangeClosed. Both methods take the starting value of the range as the first parameter and the end value of the range as the second parameter. But range is exclusive, whereas rangeClosed is inclusive. Let’s look at an example:

Here you use the rangeClosed method to generate a range of all numbers from 1 to 100. It produces a stream so you can chain the filter method to select only even numbers. At this stage no computation has been done. Finally, you call count on the resulting stream. Because count is a terminal operation, it will process the stream and return the result 50, which is the number of even numbers from 1 to 100, inclusive. Note that by comparison, if you were using IntStream.range(1, 100) instead, the result would be 49 even numbers because range is exclusive.

5.6.3. Putting numerical streams into practice: Pythagorean triples

We now look at a more difficult example so you can solidify what you’ve learned about numeric streams and all the stream operations you’ve learned so far. Your mission, if you choose to accept it, is to create a stream of Pythagorean triples.

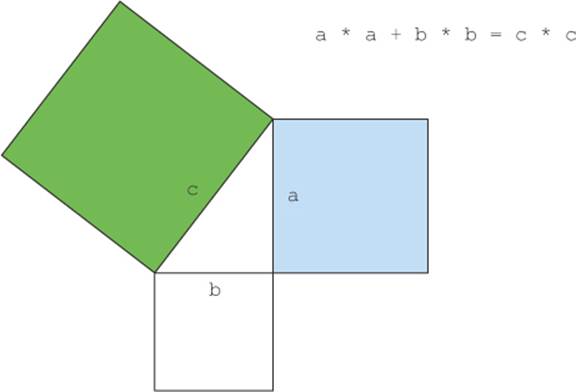
Pythagorean triple

So what’s a Pythagorean triple? We have to go back a few years in the past. In one of your exciting math classes, you learned that the famous Greek mathematician Pythagoras discovered that certain triples of numbers (a, b, c) satisfy the formula a * a + b * b = c * c where a, b, and c are integers. For example, (3, 4, 5) is a valid Pythagorean triple because 3 * 3 + 4 * 4 = 5 * 5 or 9 + 16 = 25. There are an infinite number of such triples. For example, (5, 12, 13), (6, 8, 10), and (7, 24, 25) are all valid Pythagorean triples. Such triples are useful because they describe the three side lengths of a right-angled triangle, as illustrated in figure 5.9.

Figure 5.9. The Pythagorean theorem

Representing a triple

So where do you start? The first step is to define a triple. Instead of (more properly) defining a new class to represent a triple, you can use an array of int with three elements, for example, new int[]{3, 4, 5} to represent the tuple (3, 4, 5). You can now access each individual component of the tuple using array indexing.

Filtering good combinations

Let’s assume someone provides you with the first two numbers of the triple: a and b. How do you know whether that will form a good combination? You need to test whether the square root of a * a + b * b is an integer number; that is, it has no fractional part, which in Java can be expressed using expr % 1.0. If it’s not an integer, that means c is not an integer. You can express this requirement as a filter operation (you’ll see how to connect it later to form valid code):

filter(b -> Math.sqrt(a*a + b*b) % 1 == 0)

Assuming that surrounding code has given a value for a and assuming stream provides possible values for b, filter will select only those values for b that can form a Pythagorean triple with a. You may be wondering what the line Math.sqrt(a*a + b*b) % 1 == 0 is about. It’s basically a way to test whether Math.sqrt(a*a + b*b) returns an integer result. The condition will fail if the result of the square root produces a number with a decimal such as 9.1 (9.0 is valid).

Generating tuples

Following the filter, you know that both a and b can form a correct combination. You now need to create a triple. You can use the map operation to transform each element into a Pythagorean triple as follows:

stream.filter(b -> Math.sqrt(a*a + b*b) % 1 == 0)

.map(b -> new int[]{a, b, (int) Math.sqrt(a * a + b * b)});

Generating b values

You’re getting closer! You now need to generate values for b. You saw that Stream .rangeClosed allows you to generate a stream of numbers in a given interval. You can use it to provide numeric values for b, here 1 to 100:

IntStream.rangeClosed(1, 100)

.filter(b -> Math.sqrt(a*a + b*b) % 1 == 0)

.boxed()

.map(b -> new int[]{a, b, (int) Math.sqrt(a * a + b * b)});

Note that you call boxed after the filter to generate a Stream<Integer> from the IntStream returned by rangeClosed. This is because your map returns an array of int for each element of the stream. The map method from an IntStream expects only another int to be returned for each element of the stream, which isn’t what you want! You can rewrite this using the method mapToObj of an IntStream, which returns an object-valued stream:

IntStream.rangeClosed(1, 100)

.filter(b -> Math.sqrt(a*a + b*b) % 1 == 0)

.mapToObj(b -> new int[]{a, b, (int) Math.sqrt(a * a + b * b)});

Generating a values

There’s one crucial piece that we assumed was given: the value for a. You now have a stream that produces Pythagorean triples provided the value a is known. How can you fix this? Just like with b, you need to generate numeric values for a! The final solution is as follows:

Stream<int[]> pythagoreanTriples =

IntStream.rangeClosed(1, 100).boxed()

.flatMap(a ->

IntStream.rangeClosed(a, 100)

.filter(b -> Math.sqrt(a*a + b*b) % 1 == 0)

.mapToObj(b ->

new int[]{a, b, (int)Math.sqrt(a * a + b * b)})

);

Okay, what’s the flatMap about? First, you create a numeric range from 1 to 100 to generate values for a. For each given value of a you’re creating a stream of triples. Mapping a value of a to a stream of triples would result in a stream of streams! The flatMap method does the mapping and also flattens all the generated streams of triples into a single stream. As a result you produce a stream of triples. Note also that you change the range of b to be a to 100. There’s no need to start the range at the value 1 because this would create duplicate triples (for example, (3, 4, 5) and (4, 3, 5)).

Running the code

You can now run your solution and select explicitly how many triples you’d like to return from the generated stream using the limit operation that you saw earlier:

pythagoreanTriples.limit(5)

.forEach(t ->

System.out.println(t[0] + ", " + t[1] + ", " + t[2]));

This will print

3, 4, 5

5, 12, 13

6, 8, 10

7, 24, 25

8, 15, 17

Can you do better?

The current solution isn’t optimal because you calculate the square root twice. One possible way to make your code more compact is to generate all triples of the form (a*a, b*b, a*a+b*b) and then filter the ones that match your criteria:

5.7. Building streams

Hopefully by now you’re convinced that streams are very powerful and useful to express data processing queries. So far, you were able to get a stream from a collection using the stream method. In addition, we showed you how to create numerical streams from a range of numbers. But you can create streams in many more ways! This section shows how you can create a stream from a sequence of values, from an array, from a file, and even from a generative function to create infinite streams!

5.7.1. Streams from values

You can create a stream with explicit values by using the static method Stream.of, which can take any number of parameters. For example, in the following code you create a stream of strings directly using Stream.of. You then convert the strings to uppercase before printing them one by one:

Stream<String> stream = Stream.of("Java 8 ", "Lambdas ", "In ", "Action");

stream.map(String::toUpperCase).forEach(System.out::println);

You can get an empty stream using the empty method as follows:

Stream<String> emptyStream = Stream.empty();

5.7.2. Streams from arrays

You can create a stream from an array using the static method Arrays.stream, which takes an array as parameter. For example, you can convert an array of primitive ints into an IntStream as follows:

5.7.3. Streams from files

Java’s NIO API (non-blocking I/O), which is used for I/O operations such as processing a file, has been updated to take advantage of the Streams API. Many static methods in java.nio.file.Files return a stream. For example, a useful method is Files.lines, which returns a stream of lines as strings from a given file. Using what you’ve learned so far, you could use this method to find out the number of unique words in a file as follows:

You use Files.lines to return a stream where each element is a line in the given file. You then split each line into words by calling the split method on line. Notice how you use flatMap to produce one flattened stream of words instead of multiple streams of words for each line. Finally, you count each distinct word in the stream by chaining the methods distinct and count.

5.7.4. Streams from functions: creating infinite streams!

The Streams API provides two static methods to generate a stream from a function: Stream.iterate and Stream.generate. These two operations let you create what we call an infinite stream: a stream that doesn’t have a fixed size like when you create a stream from a fixed collection. Streams produced by iterate and generate create values on demand given a function and can therefore calculate values forever! It’s generally sensible to use limit(n) on such streams to avoid printing an infinite number of values.

Iterate

Let’s look at a simple example of how to use iterate before we explain it:

Stream.iterate(0, n -> n + 2)

.limit(10)

.forEach(System.out::println);

The iterate method takes an initial value, here 0, and a lambda (of type Unary-Operator<T>) to apply successively on each new value produced. Here you return the previous element added with 2 using the lambda n -> n + 2. As a result, the iterate method produces a stream of all even numbers: the first element of the stream is the initial value 0. Then it adds 2 to produce the new value 2; it adds 2 again to produce the new value 4 and so on. This iterate operation is fundamentally sequential because the result depends on the previous application. Note that this operation produces an infinite stream—the stream doesn’t have an end because values are computed on demand and can be computed forever. We say the stream is unbounded. As we discussed earlier, this is a key difference between a stream and a collection. You’re using the limit method to explicitly limit the size of the stream. Here you select only the first 10 even numbers. You then call the forEach terminal operation to consume the stream and print each element individually.

In general, you should use iterate when you need to produce a sequence of successive values, for example, a date followed by its next date: January 31, February 1, and so on. To see a more difficult example of how you can apply iterate, try out Quiz 5.4.

Quiz 5.4: Fibonacci tuples series

The Fibonacci series is famous as a classic programming exercise. The numbers in the following sequence are part of the Fibonacci series: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55.... The first two numbers of the series are 0 and 1, and each subsequent number is the sum of the previous two.

The series of Fibonacci tuples is similar; you have a sequence of a number and its successor in the series: (0, 1), (1, 1), (1, 2), (2, 3), (3, 5), (5, 8), (8, 13), (13, 21)....

Your task is to generate the first 20 elements of the series of Fibonacci tuples using the iterate method!

Let us help you get started. The first problem is that the iterate method takes a UnaryOperator<T> as argument and you need a stream of tuples such as (0, 1). You can, again rather sloppily, use an array of two elements to represent a tuple. For example, new int[]{0, 1} represents the first element of the Fibonacci series (0, 1). This will be the initial value of the iterate method:

Stream.iterate(new int[]{0, 1}, ???)

.limit(20)

.forEach(t -> System.out.println("(" + t[0] + "," + t[1] +")"));

In this quiz, you need to figure out the highlighted code with the ???. Remember that iterate will apply the given lambda successively.

Answer:

Stream.iterate(new int[]{0, 1},

t -> new int[]{t[1], t[0]+t[1]})

.limit(20)

.forEach(t -> System.out.println("(" + t[0] + "," + t[1] +")"));

How does it work? iterate needs a lambda to specify the successor element. In the case of the tuple (3, 5) the successor is (5, 3+5) = (5, 8). The next one is (8, 5+8). Can you see the pattern? Given a tuple, the successor is (t[1], t[0] + t[1]). This is what the following lambda specifies: t ->new int[]{t[1],t[0] + t[1]}. By running this code you’ll get the series (0, 1), (1, 1), (1, 2), (2, 3), (3, 5), (5, 8), (8, 13), (13, 21).... Note that if you just wanted to print the normal Fibonacci series, you could use a map to extract only the first element of each tuple:

Stream.iterate(new int[]{0, 1},

t -> new int[]{t[1],t[0] + t[1]})

.limit(10)

.map(t -> t[0])

.forEach(System.out::println);

This code will produce the Fibonacci series: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34....

Generate

Similarly to the method iterate, the method generate lets you produce an infinite stream of values computed on demand. But generate doesn’t apply successively a function on each new produced value. It takes a lambda of type Supplier<T> to provide new values. Let’s look at an example of how to use it:

Stream.generate(Math::random)

.limit(5)

.forEach(System.out::println);

This code will generate a stream of five random double numbers from 0 to 1. For example, one run gives the following:

0.9410810294106129

0.6586270755634592

0.9592859117266873

0.13743396659487006

0.3942776037651241

The static method Math.random is used as a generator for new values. Again you limit the size of the stream explicitly using the limit method; otherwise the stream would be unbounded!

You may be wondering if there’s anything else useful you can do using the method generate. The supplier we used (a method reference to Math.random) was stateless: it wasn’t recording any values somewhere that can be used in later computations. But a supplier doesn’t have to be stateless. You can create a supplier that stores state that it can modify and use when generating the next value of the stream. As an example, we show how you can also create the Fibonacci series from Quiz 5.4 using generate so you can compare it with the approach using the iteratemethod! But it’s important to note that a supplier that’s stateful isn’t safe to use in parallel code. So what follows is shown just for completeness but should be avoided! We discuss the problem of operations with side effects and parallel streams further in chapter 7.

We’ll use an IntStream in our example to illustrate code that’s designed to avoid boxing operations. The generate method on IntStream takes an IntSupplier instead of a Supplier<T>. For example, here’s how to generate an infinite stream of ones:

IntStream ones = IntStream.generate(() -> 1);

You saw in the chapter 3 that lambdas let you create an instance of a functional interface by providing the implementation of the method directly inline. You can also pass an explicit object as follows by implementing the getAsInt method defined in the IntSupplier interface (although this seems gratuitously long-winded, please bear with us):

IntStream twos = IntStream.generate(new IntSupplier(){

public int getAsInt(){

return 2;

}

});

The generate method will use the given supplier and repeatedly call the getAsInt method, which always returns 2. But the difference between the anonymous class used here and a lambda is that the anonymous class can define state via fields, which the getAsInt method can modify. This is an example of a side effect. All lambdas you’ve seen so far were side-effect free; they didn’t change any state.

To come back to our Fibonacci tasks, what you need to do now is create an IntSupplier that maintains in its state the previous value in the series, so getAsInt can use it to calculate the next element. In addition, it can update the state of the IntSupplier for the next time it’s called. The following code shows how to create an IntSupplier that will return the next Fibonacci element when it’s called:

IntSupplier fib = new IntSupplier(){

private int previous = 0;

private int current = 1;

public int getAsInt(){

int oldPrevious = this.previous;

int nextValue = this.previous + this.current;

this.previous = this.current;

this.current = nextValue;

return oldPrevious;

}

};

IntStream.generate(fib).limit(10).forEach(System.out::println);

In the preceding code you create an instance of IntSupplier. This object has mutable state: it tracks the previous Fibonacci element and the current Fibonacci element in two instance variables. The getAsInt method changes the state of the object when it’s called so that it produces new values on each call. In comparison, our approach using iterate was purely immutable: you didn’t modify existing state but were creating new tuples at each iteration. You’ll learn in chapter 7 that you should always prefer an immutable approach in order to process a stream in parallel and expect a correct result.

Note that because you’re dealing with a stream of infinite size, you have to limit its size explicitly using the operation limit; otherwise, the terminal operation (in this case forEach) will compute forever. Similarly, you can’t sort or reduce an infinite stream because all elements need to be processed, but this would take forever because the stream is infinite!

5.8. Summary

It’s been a long but rewarding chapter! You can now process collections more effectively. Indeed, streams let you express sophisticated data processing queries concisely. In addition, streams can be parallelized transparently. Here are some key concepts to take away from this chapter:

· The Streams API lets you express complex data processing queries. Common stream operations are summarized in table 5.1.

· You can filter and slice a stream using the filter, distinct, skip, and limit methods.

· You can extract or transform elements of a stream using the map and flatMap methods.

· You can find elements in a stream using the findFirst and findAny methods. You can match a given predicate in a stream using the allMatch, noneMatch, and anyMatch methods.

· These methods make use of short-circuiting: a computation stops as soon as a result is found; there’s no need to process the whole stream.

· You can combine all elements of a stream iteratively to produce a result using the reduce method, for example, to calculate the sum or find the maximum of a stream.

· Some operations such as filter and map are stateless; they don’t store any state. Some operations such as reduce store state to calculate a value. Some operations such as sorted and distinct also store state because they need to buffer all the elements of a stream before returning a new stream. Such operations are called stateful operations.

· There are three primitive specializations of streams: IntStream, DoubleStream, and LongStream. Their operations are also specialized accordingly.

· Streams can be created not only from a collection but also from values, arrays, files, and specific methods such as iterate and generate.

· An infinite stream is a stream that has no fixed size.