D3.js in Action (2015)

Part 2. The pillars of information visualization

Chapter 6. Network visualization

This chapter covers

· Creating adjacency matrices and arc diagrams

· Using the force-directed layout

· Representing directionality

· Adding and removing network nodes and edges

Network analysis and network visualization are more common now with the growth of online social networks like Twitter and Facebook, as well as social media and linked data in what was known as Web 2.0. Network visualizations like the kind you’ll see in this chapter, some of which are shown in figure 6.1, are particularly interesting because they focus on how things are related. They represent systems more accurately than the traditional flat data seen in more common data visualizations.

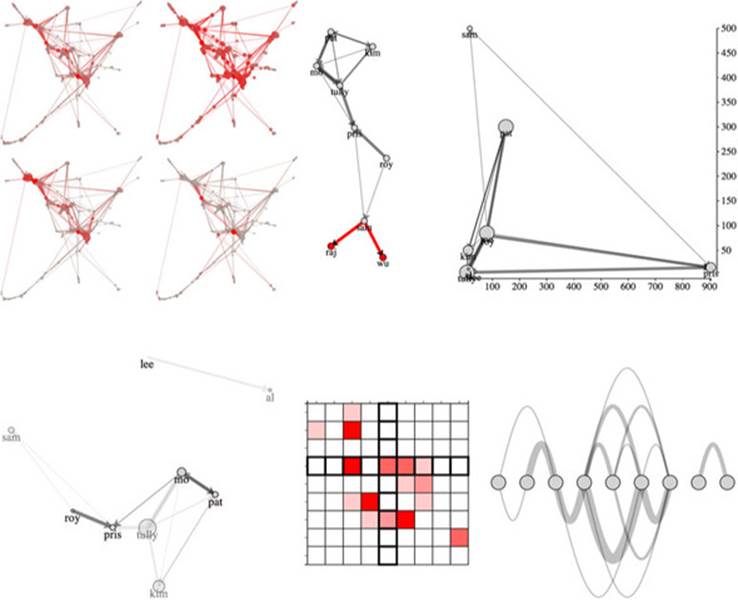
Figure 6.1. Along with explaining the basics of network analysis (section 6.2.3), this chapter includes laying out networks using xy positioning (section 6.2.5), force-directed algorithms (section 6.2), adjacency matrices (section 6.1.2), and arc diagrams (section 6.1.3).

This chapter focuses on representing networks, so it’s important that you understand network terminology. In general, when dealing with networks you refer to the things being connected (like people) as nodes and the connections between them (such as being a friend on Facebook) as edgesor links. You may hear nodes referred to as vertices, because that’s where the edges join. Although it may seem useful to have a figure with nodes and edges labeled, one of the lessons from this chapter is that there is no one way to represent a network. Networks may also be referred to asgraphs, because that’s what they’re called in mathematics. Finally, the importance of a node in a network is typically referred to as centrality. There’s more, but that should be enough to get you started.

Networks aren’t just a data format; they’re a perspective on data. When you work with network data, you typically try to discover and display patterns of the network or of parts of the network, and not of individual nodes in the network. Although you may use a network visualization because it makes a cool graphical index, like a mind map or a network map of a website, in general you’ll find that the typical information visualization techniques are designed to showcase network structure, and not individual nodes.

6.1. Static network diagrams

Network data is different from hierarchical data. Networks present the possibility of many-to-many connections, like the Sankey layout from chapter 5, whereas in hierarchical data a node can have many children but only one parent, like the tree and pack layouts from chapter 5. A network doesn’t have to be a social network. This format can represent many different structures, such as transportation networks and linked open data. In this chapter we’ll look at four common forms for representing networks: as data, as adjacency matrices, as arc diagrams, and using force-directed network diagrams.

In each case, the graphical representation will be quite different. For instance, in the case of a force-directed layout, we’ll represent the nodes as circles and the edges as lines. But in the case of the adjacency matrix, nodes will be positioned on x- and y-axes and the edges will be filled squares. Networks don’t have a default representation, but the examples you’ll see in this chapter are the most common.

6.1.1. Network data

Although you can store networks in several data formats, the most straightforward is known as the edge list. An edge list is typically represented as a CSV like that shown in listing 6.1, with a source column and a target column, and a string or number to indicate which nodes are connected. Each edge may also have other attributes, indicating the type of connection or its strength, the time period when the connection is valid, its color, or any other information you want to store about a connection. The important thing is that only the source and target columns are necessary.

In the case of directed networks, the source and target columns indicate the direction of connection between nodes. A directed network means that nodes may be connected in one direction but not in the other. For instance, you could follow a user on Twitter, but that doesn’t necessarily mean that the user follows you. Undirected networks still typically have the columns listed as “source” and “target,” but the connection is the same in both directions. Take the example of a network made up of connections indicating people have shared classes. Then if I’m in a class with you, you’re likewise in a class with me. You’ll see directed and weighted networks represented throughout this chapter.

Listing 6.1. edgelist.csv

source,target,weight

sam,pris,1

roy,pris,5

roy,sam,1

tully,pris,5

tully,kim,3

tully,pat,1

tully,mo,3

kim,pat,2

kim,mo,1

mo,tully,7

mo,pat,1

mo,pris,1

pat,tully,1

pat,kim,2

pat,mo,5

lee,al,3

Our network also has a weight value for the connections, which indicates the strength of connections. In our case, our edge list represents how many times the source favorited the tweets of the target. Sam favorited one tweet made by Pris, and Roy favorited 5 tweets made by Pris, and so on. This is a weighted network because the edges have a value. It’s a directed network because the edges have direction. Therefore, we have a weighted directed network, and we need to account for both weight and direction in our network visualizations.

Technically, you only need an edge list to create a network, because you can derive a list of nodes from the unique values in the edge list. This is done by traditional network analysis software packages like Gephi. Although you can derive a node list with JavaScript, it’s more common to have a corresponding node list that provides more information about the nodes in your network, like we have in the following listing.

Listing 6.2. nodelist.csv

id,followers,following

sam,17,500

roy,83,80

pris,904,15

tully,7,5

kim,11,50

mo,80,85

pat,150,300

lee,38,7

al,12,12

Because these are Twitter users, we have more information about them based on their Twitter stats, in this case, the number of followers and the number of people they follow. As with the edge list, it’s not necessary to have more than an ID. But having access to more data gives you the chance to modify your network visualization to reflect the node attributes.

How you represent a network depends on its size and the nature of the network. If a network doesn’t represent discrete connections between similar things, but rather the flow of goods or information or traffic, then you could use a Sankey diagram like we did in chapter 5. Recall that the data format for the Sankey is exactly the same as what we have here: a table of nodes and a table of edges. The Sankey diagram is only suitable for specific kinds of network data. Other chart types, such as an adjacency matrix, are more generically useful for network data.

Before we get started with code to create a network visualizations, let’s put together a CSS page so that we can set color based on class and use inline styles as little as possible. Listing 6.3 gives the CSS necessary for all the examples in this chapter. Keep in mind that we’ll still need to set some inline styles when we want the numerical value of an attribute to relate to the data bound to that graphical element, for example, when we base the stroke-width of a line on the strength of that line.

Listing 6.3. networks.css

.grid {

stroke: black;

stroke-width: 1px;

fill: red;

}

.arc {

stroke: black;

fill: none;

}

.node {

fill: lightgray;

stroke: black;

stroke-width: 1px;

}

circle.active {

fill: red;

}

path.active {

stroke: red;

}

6.1.2. Adjacency matrix

As you see more and more networks represented graphically, it seems like the only way to represent a network is with a circle or square that represents the node and a line (whether straight or curvy) that represents the edge. It may surprise you that one of the most effective network visualizations has no connecting lines at all. Instead, the adjacency matrix uses a grid to represent connections between nodes.

The principle of an adjacency matrix is simple: you place the nodes along the x-axis and then place the same nodes along the y-axis. If two nodes are connected, then the corresponding grid square is filled; otherwise, it’s left blank. In our case, because it’s a directed network, the nodes along the y-axis are considered the source and the nodes along the x-axis are considered the target, as you’ll see in a few pages. Because our network is also weighted, we’ll use saturation to indicate weight, with lighter colors indicating a weaker connection and darker colors indicating a stronger connection.

The only problem with building an adjacency matrix in D3 is that it doesn’t have an existing layout, which means you have to build it by hand like we did with the bar chart, scatterplot, and boxplot. Mike Bostock has an impressive example at http://bost.ocks.org/mike/miserables/, but you can make something that’s functional without too much code, which we’ll do with the function in listing 6.4. In doing so, though, we need to process the two JSON arrays that are created from our CSVs and format the data so that it’s easy to work with. This is close to writing our own layout, something we’ll do in chapter 10, and a good idea generally.

Listing 6.4. The adjacency matrix function

A few new things are going on here. For one, we’re using a new scale: d3.scale.ordinal, which takes an array of distinct values and allows us to place them on an axis like we do with the names of our nodes in this example. We need to use a scale function that you haven’t seen before,rangePoints, which creates a set of bins for each of our values for display on an axis or otherwise. It does this by associating each of those unique values with a numerical position within the range given. Each point can also have an offset declared in the second, optional variable. The other new piece of code uses queue.js, which we need because we’re loading two CSV files and we don’t want to run our function until those two CSVs are loaded. We’re building this matrix array of objects that may seem obscure. But if you examine it in your console, you’ll see, as in figure 6.2, it’s just a list of every possible connection and the strength of that connection, if it exists.

Figure 6.2. The array of connections we’re building. Notice that every possible connection is stored in the array. Only those connections that exist in our dataset have a weight value other than 0. Notice, also, that our CSV import creates the weight value as a string.

Figure 6.3 shows the resulting adjacency matrix based on the node list and edge list.

Figure 6.3. A weighted, directed adjacency matrix where lighter red indicates weaker connections and darker red indicates stronger connections. The source is on the y-axis, and the target is on the x-axis. The matrix shows that Roy favorited tweets by Sam but Sam didn’t favorite any tweets by Roy.

You’ll notice in many adjacency matrices that the square indicating the connection from a node to itself is always filled. In network parlance this is a self-loop, and it occurs when a node is connected to itself. In our case, it would mean that someone favorited their own tweet, and fortunately no one in our dataset is a big enough loser to do that.

If we want, we can add interactivity to help make the matrix more readable. Grids can be hard to read without something to highlight the row and column of a square. It’s simple to add highlighting to our matrix. All we have to do is add a mouseover event listener that fires a gridOverfunction to highlight all rectangles that have the same x or y value:

d3.selectAll("rect.grid").on("mouseover", gridOver);

function gridOver(d,i) {

d3.selectAll("rect").style("stroke-width", function (p) {

return p.x == d.x || p.y == d.y ? "3px" : "1px"});

};

Now you can see in figure 6.4 how moving your cursor over a grid square highlights the row and column of that grid square.

Figure 6.4. Adjacency highlighting column and row of the grid square. In this instance, the mouse is over the Tully-to-Kim edge. You can see that Tully favorited tweets by four people, one of whom was Kim, and that Kim only had tweets favorited by one other person, Pat.

6.1.3. Arc diagram

Another way to graphically represent networks is by using an arc diagram. An arc diagram arranges the nodes along a line and draws the links as arcs above and/or below that line. Again, there isn’t a layout available for arc diagrams, and there are even fewer examples, but the principle is rather simple after you see the code. We build another pseudo-layout like we did with the adjacency matrix, but this time we need to process the nodes as well as the links.

Listing 6.5. Arc diagram code

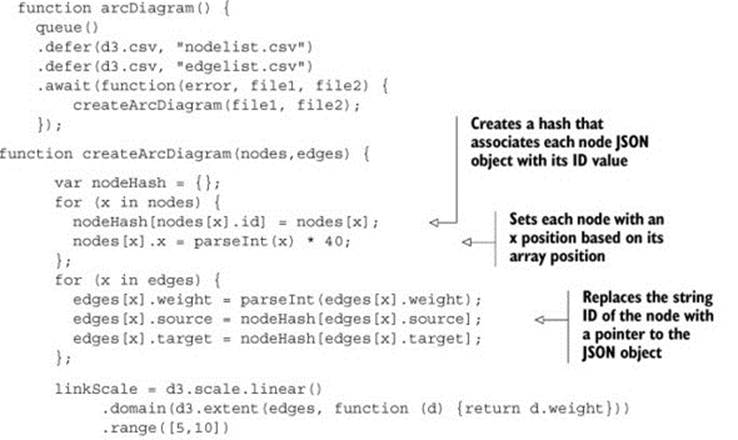
Notice that the edges array that we build uses a hash with the ID value of our edges to create object references. By building objects that have references to the source and target nodes, we can easily calculate the graphical attributes of the <line> or <path> element we’re using to represent the connection. This is the same method used in the force layout that we’ll look at later in the chapter. The result of the code is your first arc diagram, shown in figure 6.5.

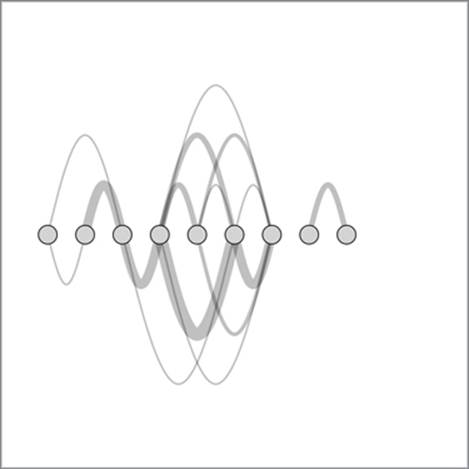
Figure 6.5. An arc diagram, with connections between nodes represented as arcs above and below the nodes. Arcs above the nodes indicate the connection is from left to right, while arcs below the nodes indicate the source is on the right and the target is on the left.

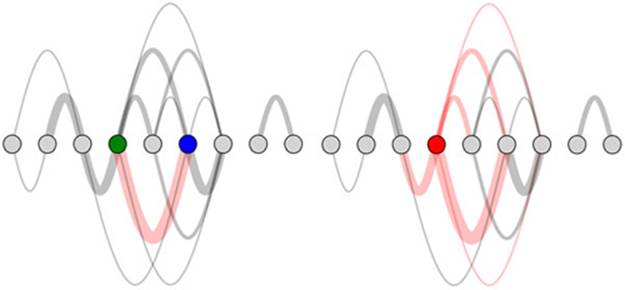
With abstract charts like these, you’re getting to the point where interactivity is no longer optional. Even though the links follow rules, and you’re not dealing with too many nodes or edges, it can be hard to make out what is connected to what and how. You can add useful interactivity by having the edges highlight the connecting nodes on mouseover. You can also have the nodes highlight connected edges on mouseover by adding two new functions as shown in the following listing, with the results in figure 6.6.

Figure 6.6. Mouseover behavior on edges (left), with the edge being moused over in pink, the source node in blue, and the target node in green. Mouseover behavior on nodes (right), with the node being moused over in red and the connected edges in pink.

Listing 6.6. Arc diagram interactivity

If you’re interested in exploring arc diagrams further and want to use them for larger datasets, you’ll also want to look into hive plots, which are arc diagrams arranged on spokes. We won’t deal with hive plots in this book, but there’s a plugin layout for hive plots that you can see athttps://github.com/d3/d3-plugins/tree/master/hive. Both the adjacency matrix and arc diagram benefit from the control you have over sorting and placing the nodes, as well as the linear manner in which they’re laid out. The next method for network visualization, which is our focus for the rest of the chapter, uses entirely different principles for determining how and where to place nodes and edges.

6.2. Force-directed layout

The force layout gets its name from the method by which it determines the most optimal graphical representation of a network. Like the word cloud and the Sankey diagram from chapter 5, the force() layout dynamically updates the positions of its elements to find the best fit. Unlike those layouts, it does it continuously in real time rather than as a preprocessing step before rendering. The principle behind a force layout is the interplay between three forces, shown in figure 6.7. These forces push nodes away from each other, attract connected nodes to each other, and keep nodes from flying out of sight.

Figure 6.7. The forces in a force-directed algorithm: repulsion, gravity, and attraction. Other factors, such as hierarchical packing and community detection, can also be factored into force-directed algorithms, but these features are the most common. Forces are approximated for larger networks to improve performance.

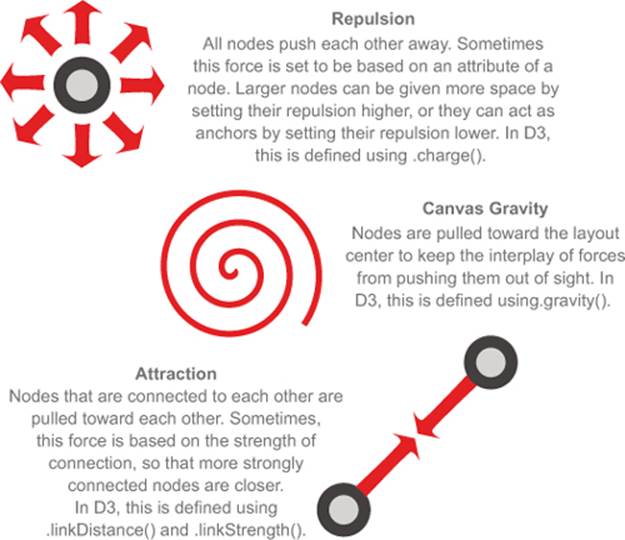
In this section, you’ll learn how force-directed layouts work, how to make them, and some general principles from network analysis that will help you better understand them. You’ll also learn how to add and remove nodes and edges, as well as adjust the settings of the layout on the fly.

6.2.1. Creating a force-directed network diagram

The force() layout you see initialized in listing 6.7 has some settings you’ve already seen before. The most obvious is size(), which uses an array containing the width and height of our layout region to calculate the necessary force settings. The nodes() and links() settings are the same as for the Sankey layout in chapter 5. They take, as you’d expect, arrays of data that correspond to the nodes and links. We’re creating our own source and target references in our links array, just like we did with the arc diagram, and that’s the formatting that force() expects. It also accepts integer values where the integer values correspond to the array position of a node in the nodes array, like the formatting of data for the Sankey diagram links array from chapter 5. As you can see in the following listing, the one setting that’s new is charge(), which determines how much each node pushes away other nodes. There’s also a new event listener, "tick", that needs to get associated with a tick function that updates the position of your nodes and edges.

Listing 6.7. Force layout function

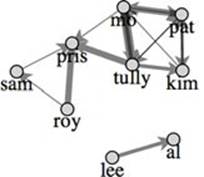
The animated nature of the force layout is lost on the page, but you can see in figure 6.8 general network structure that’s less prominent in an adjacency matrix or arc diagram. It’s readily apparent that four nodes (Mo, Tully, Kim, and Pat) are all connected to each other (forming what in network terms is called a clique), and three nodes (Roy, Pris, and Sam) are more peripheral. Over on the right, two nodes (Lee and Al) are connected only to each other. The only reason those nodes are still onscreen is because the layout’s gravity pulls unconnected pieces toward the center.

Figure 6.8. A force-directed layout based on our dataset and organized graphically using default settings in the force layout

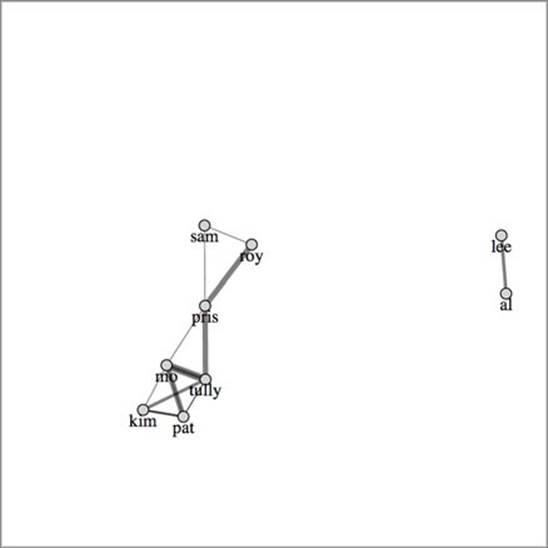
The thickness of the lines corresponds to the strength of connection. But although we have edge strength, we’ve lost the direction of the edges in this layout. You can tell that the network is directed only because the links are drawn as semitransparent, so you can see when two links of different weights overlap each other. We need to use some method to show if these links are to or from a node. One way to do this is to turn our lines into arrows using SVG markers.

6.2.2. SVG markers

Sometimes you want to place a symbol, such as an arrowhead, on a line or path that you’ve drawn. In that case, you have to define a marker in your svg:defs and then associate that marker with the element on which you want it to draw. You can define your marker statically in HTML, or you can create it dynamically like any SVG element, as we’ll do next. The marker we define can be any sort of SVG shape, but we’ll use a path because it lets us draw an arrowhead. A marker can be drawn at the start, end, or middle of a line, and has settings to determine its direction relative to its parent element.

Listing 6.8. Marker definition and application

With the markers defined in listing 6.9, you can now read the network (as shown in figure 6.9) more effectively. You see how the nodes are connected to each other, and you can spot which nodes have reciprocal ties with each other (where nodes are connected in both directions). Reciprocation is important to identify, because there’s a big difference between people who favorite Katy Perry’s tweets and people whose tweets are favorited by Katy Perry (the current Twitter user with the most followers). Direction of edges is important, but you can represent direction in other ways, such as using curved edges or edges that grow fatter on one end than the other. To do something like that, you’d need to use a <path> rather than a <line> for the edges like we did with the Sankey layout or the arc diagram.

Figure 6.9. Edges now display markers (arrowheads) indicating the direction of connection. Notice that all the arrowheads are the same size.

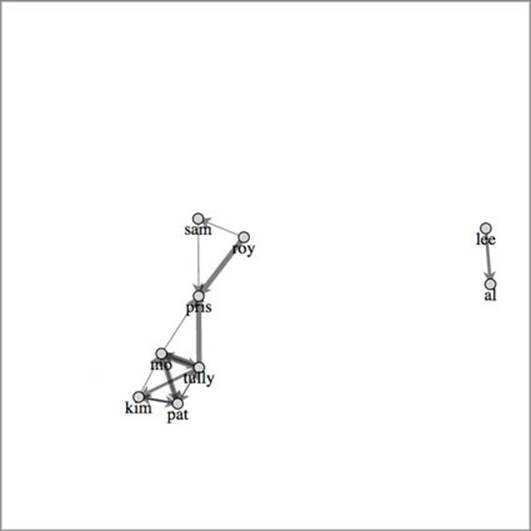
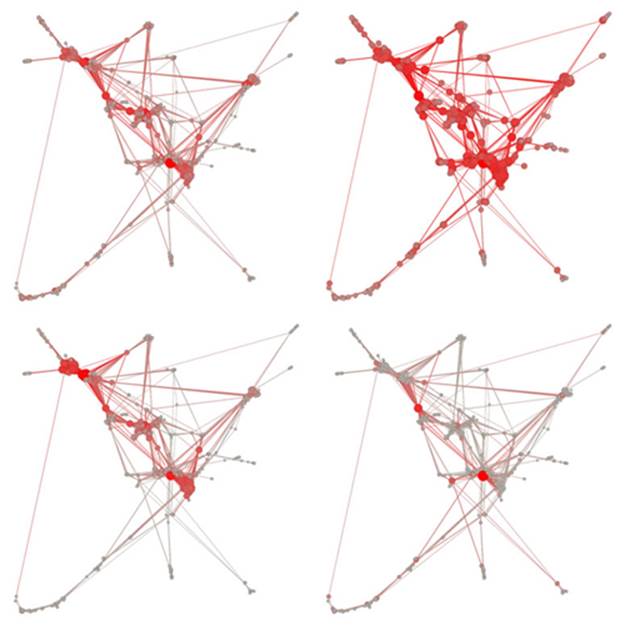
If you’ve run this code on your own, your network probably looks a little different than what’s shown in figure 6.9. That’s because network visualizations created with force-directed layouts are the result of the interplay of forces, and, even with a small network like this, that interplay can result in different positions for nodes. This can confuse users, who think that these variations indicate different networks. One way around this is to generate a network using a force-directed layout and then fix it in place to create a network basemap. You can then apply any later graphical changes to that fixed network. The concept of a basemap comes from geography, and in network visualization refers to the use of the same layout with differently sized and/or colored nodes and edges. It allows readers to identify regions of the network that are significantly different according to different measures. You can see this concept of a basemap in use in figure 6.10, which shows how one network can be measured in multiple ways.

Figure 6.10. The same network measured using degree centrality (top left), closeness centrality (top right), eigenvector centrality (bottom left), and betweenness centrality (bottom right). More-central nodes are larger and bright red, whereas less-central nodes are smaller and gray. Notice that although some nodes are central according to all measures, their relative centrality varies, as does the overall centrality of other nodes.

Infoviz term: hairball

Network visualizations are impressive, but they can also be so complex that they’re unreadable. For this reason, you’ll encounter critiques of networks that are too dense to be readable. These network visualizations are often referred to as hairballs due to extensive overlap of edges that make them resemble a mass of unruly hair.

If you think a force-directed layout is hard to read, you can pair it with another network visualization, such as an adjacency matrix, and highlight both as the user navigates either visualization. You’ll see techniques for pairing visualizations like this in chapter 11.

The force-directed layout provides the added benefit of seeing larger structures. Depending on the size and complexity of your network, they may be enough. But you may need to represent other network measurements when working with network data.

6.2.3. Network measures

Networks have been studied for a long time—at least decades and, if you consider graph theory in mathematics, centuries. As a result, you may encounter a few terms and measures when working with networks. This is only meant to be a brief overview. If you want to learn more about networks, I would suggest reading the excellent introduction to networks and network analysis by S. Weingart, I. Milligan, and S. Graham at http://www.themacroscope.org/?page_id=337.

Edge weight

You’ll notice that our dataset contains a “weight” value for each link. This represents the strength of the connection between two nodes. In our case, we assume that the more favorites, the stronger a connection that one Twitter user has. We drew thicker lines for a higher weight, but we can also adjust the way the force layout works based on that weight, as you’ll see next.

Centrality

Networks are representations of systems, and one of the things you want to know about the nodes in a system is which ones are more important than the others, referred to as centrality. Central nodes are considered to have more power or influence in a network. There are many different measurements of centrality, a few of which are shown in figure 6.10, and different measures more accurately assess centrality in different network types. One measure of centrality is computed by D3’s force() layout: degree centrality.

Degree

Degree, also known as degree centrality, is the total number of links that are connected to a node. In our example data, Mo has a degree of 6, because he’s the source or target of 6 links. Degree is a rough measure of the importance of a node in a network, because you assume that people or things with more connections have more power or influence in a network. Weighted degree is used to refer to the total value of the connections to a node, which would give Mo a value of 18. Further, you can differentiate degree into in degree and out degree, which are used to distinguish between incoming and outgoing links, and which for Mo’s case would be 4 and 2, respectively.

Every time you start the force() layout, D3 computes the total number of links per node, and updates that node’s weight attribute to reflect that. We’ll use that to affect the way the force layout runs. For now, let’s add a button that resizes the nodes based on their weight attribute:

d3.select("#controls").append("button")

.on("click", sizeByDegree).html("Degree Size");

function sizeByDegree() {

force.stop();

d3.selectAll("circle")

.attr("r", function(d) {return d.weight * 2;});

};

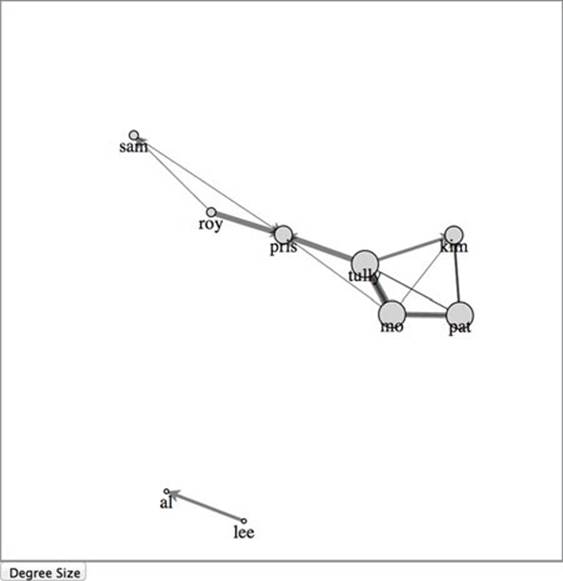
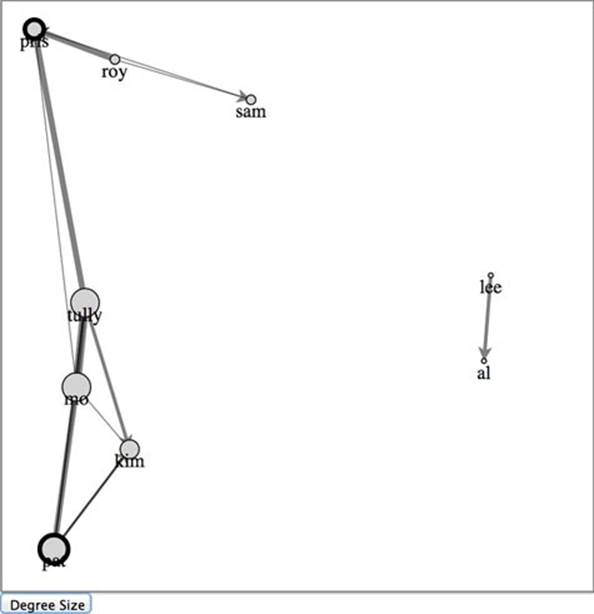
Figure 6.11 shows the value of the degree centrality measure. Although you can see and easily count the connections and nodes in this small network, being able to spot at a glance the most and least connected nodes is extremely valuable. Notice that we’re counting links in both directions, so that even though Tully is connected to more people, he’s the same size as Mo and Pat, who are connected as many times but to fewer people.

Figure 6.11. Sizing nodes by weight indicates the number of total connections for each node by setting the radius of the circle equal to the weight times 2.

Clustering and modularity

One of the most important things to find out about a network is whether any communities exist in that network and what they look like. This is done by looking at whether some nodes are more connected to each other than to the rest of the network, known as modularity. You can also look at whether nodes are interconnected, known as clustering. Cliques, mentioned earlier, are part of the same measurement, and clique is a term for a group of nodes that are fully connected to each other.

Notice that this interconnectedness and community structure is supposed to arise visually out of a force-directed layout. You see the four highly connected users in a cluster and the other users farther away. If you’d prefer to measure your networks to try to reveal these structures, you can see an implementation of a community detection algorithm implemented by David Mimno with D3 at http://mimno.infosci.cornell.edu/community/. This algorithm runs in the browser and can be integrated with your network quite easily to color your network based on community membership.

6.2.4. Force layout settings

When we initialized our force layout, we started out with a charge setting of -1000. Charge and a few other settings give you more control over the way the force layout runs.

Charge

Charge sets the rate at which nodes push each other away. If you don’t set charge, then it has a default setting of -30. The reason we set charge to -1000 was because the default settings for charge with our network would have resulted in a tiny network onscreen (see figure 6.12).

Figure 6.12. The layout of our network with the default charge, which displays the nodes too closely together to be easily read

Along with setting fixed values for charge, you can use an accessor function to base the charge values on an attribute of the node. For instance, you could base the charge on the weight (the degree centrality) of the node so that nodes with many connections push nodes away more, giving them more space on the chart.

Negative charge values represent repulsion in a force-directed layout, but you could set them to positive if you wanted your nodes to exert an attractive force. This would likely cause problems with a traditional network visualization but may come in handy for a more complicated visualization.

Gravity

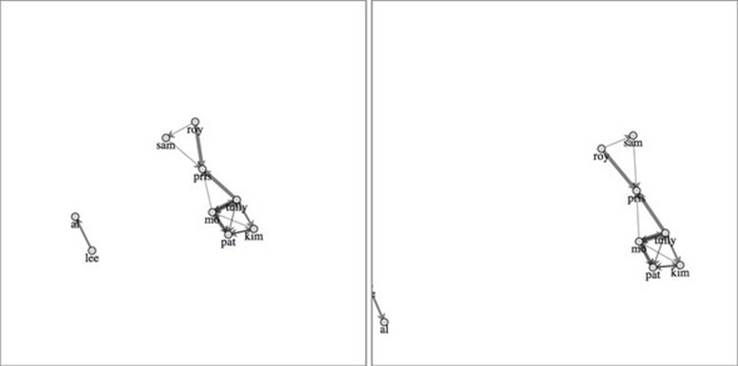
With nodes pushing each other, the only thing to stop them from flying off the edge of your chart is what’s known as canvas gravity, which pulls all nodes toward the center of the layout. When gravity isn’t specifically set, it defaults to .1. Figure 6.13 shows the results of increasing or decreasing the gravity (from our original charge(-1000) setting).

Figure 6.13. Increasing the gravity to .2 (left) pulls the two components closer to the center of the layout area. Decreasing the gravity to .05 (right) allows the small component to drift offscreen.

Gravity, unlike charge, doesn’t accept an accessor function and only accepts a fixed setting.

linkDistance

Attraction between nodes is determined by setting the link-Distance property, which is the optimal distance between connected nodes. One of the reasons we needed to set our charge so high was because the linkDistance defaults to 20. If we set it to 50, then we can reduce the charge to -100 and produce the results in figure 6.14.

Figure 6.14. With linkDistance adjusted, our network becomes much more readable.

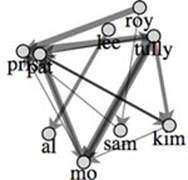
Setting your linkDistance parameter too high causes your network to fold back in on itself, which you can identify by the presence of prominent triangles in the network visualization. Figure 6.15 shows this folding occur with linkDistance set to 200.

Figure 6.15. Distortion based on high linkDistance makes it look like Pris is connected to Pat and otherwise clusters nodes together despite their being unrelated.

You can set linkDistance to be a function and associate it with edge weight so that edges with higher or lower weight values have lower or higher distance settings. A better way to achieve that effect is to use linkStrength.

linkStrength

A force layout is a physical simulation, meaning it uses physical metaphors to arrange the network to its optimal graphical shape. If your network has stronger and weaker links, like our example does, then it makes sense to have those edges exert stronger and weaker effects on the controlling nodes. You can achieve this by using link-Strength, which can accept a fixed setting but can also take an accessor function to base the strength of an edge on an attribute of that edge:

force.linkStrength(function (d) {return weightScale(d.weight);});

Figure 6.16 dramatically demonstrates the results, which reflect the weak nature of some of the connections.

Figure 6.16. By basing the strength of the attraction between nodes on the strength of the connections between nodes, you see a dramatic change in the structure of the network. The weaker connections between x and y allow that part of the network to drift away.

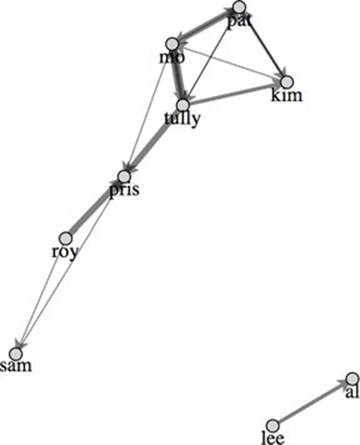
6.2.5. Updating the network

When you create a network, you want to provide your users with the ability to add or remove nodes to the network, or drag them around. You may also want to adjust the various settings dynamically rather than changing them when you first create the force layout.

Stopping and restarting the layout

The force layout is designed to “cool off” and eventually stop after the network is laid out well enough that the nodes no longer move to new positions. When the layout has stopped like this, you’ll need to restart it if you want it to animate again. Also, if you’ve made any changes to the force settings or want to add or remove parts of the network, then you’ll need to stop it and restart it.

force.stop()

You can turn off the force interaction by using force.stop(), which stops running the simulation. It’s good to stop the network when there’s an interaction with a component elsewhere on your web page or some change in the styling of the network.

force.start()

To begin or restart the animation of the layout, use force.start(). You’ve already seen .start(), because we used it in our initial example to get the force layout going.

force.resume()

If you haven’t made any changes to the nodes or links in your network and you want the network to start moving again, you can use force.resume(). It resets a cooling parameter, which causes the force layout to start moving again.

force.tick()

Finally, if you want to move the layout forward one step, you can use force.tick(). Force layouts can be resource-intensive, and you may want to use one for just a few seconds rather than let it run continuously.

force.drag()

With traditional network analysis programs, the user can drag nodes to new positions. This is implemented using the behavior force.drag(). A behavior is like a component in that it’s called by an element using .call(), but instead of creating SVG elements, it creates a set of event listeners.

In the case of force.drag(), those event listeners correspond to dragging events that give you the ability to click and drag your nodes around while the force layout runs. You can enable dragging on all your nodes by selecting them and calling force.drag() on that selection:

d3.selectAll("g.node").call(force.drag());

fixed

When a force layout is associated with nodes, each node has a boolean attribute called fixed that determines whether the node is affected by the force during ticks. One effective interaction technique is to set a node as fixed when the user interacts with it. This allows users to drag nodes to a position on the canvas so they can visually sort the important nodes. To differentiate fixed nodes from unfixed nodes, we’ll also have the function give fixed nodes a thicker "stroke-width". The effect of dragging some of our nodes is shown in figure 6.17.

Figure 6.17. The node representing Pat has been dragged to the bottom-left corner and fixed in position, while the node representing Pris has been dragged to the top-left corner and fixed in position. The remaining unfixed nodes have taken their positions based on the force-directed layout.

d3.selectAll("g.site").on("click", fixNode);

function fixNode(d) {

d3.select(this).select("circle").style("stroke-width", 4);

d.fixed = true;

};

6.2.6. Removing and adding nodes and links

When dealing with networks, you may want to filter the networks or give the user the ability to add or remove nodes. To filter a network, you need to stop() it, remove any nodes and links that are no longer part of the network, rebind those arrays to the force layout, and then start() the layout.

This can be done as a filter on the array that makes up your nodes. For instance, we may want to only see the network of people with more than 20 followers, because we want to see how the most influential people are connected.

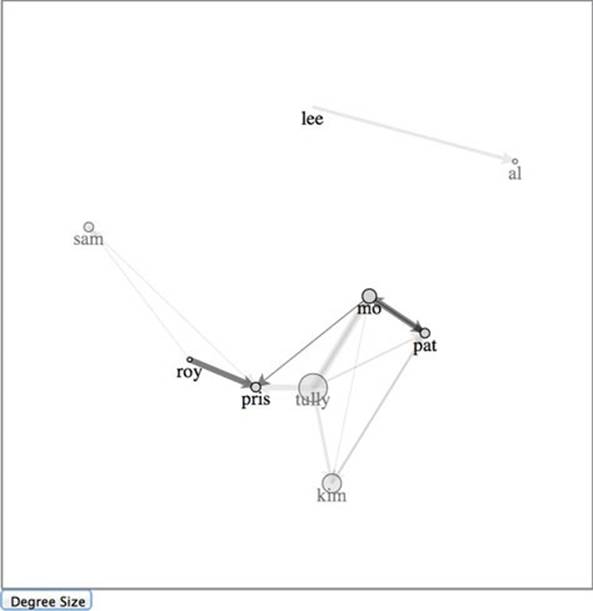
But that’s not enough, because we would still have links in our layout that reference nodes that no longer exist. We’ll need a more involved filter for our links array. By using the .indexOf function of an array, though, we can easily create our filtered links by checking to see if the source and target are both in our filtered nodes array. Because we used key values when we first bound our arrays to our selection in listing 6.8, we can use the selection.exit() behavior to easily update our network. You can see how to do this in the following listing and the effects in figure 6.18.

Figure 6.18. The network has been filtered to only show nodes with more than 20 followers, after clicking the Degree Size button. Notice that Lee, with no connections, has a degree of 0 and so the associated circle has a radius of 0, rendering it invisible. This catches two processes in midstream, the transition of nodes from full to 0 opacity and the removal of edges.

Listing 6.9. Filtering a network

Because the force algorithm is restarted after the filtering, you can see how the shape of the network changes with the removal of so many nodes. That animation is important because it reveals structural changes in the network.

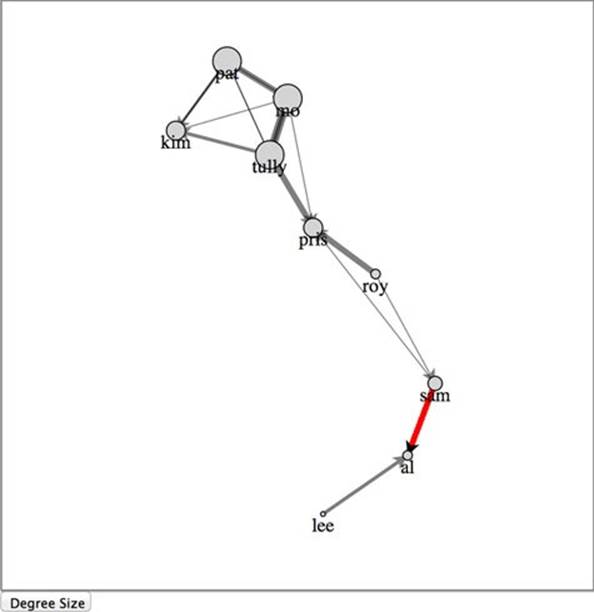
Putting more nodes and edges into the network is easy, as long as you properly format your data. You stop the force layout, add the properly formatted nodes or edges to the respective arrays, and rebind the data as you’ve done in the past. If, for instance, we want to add an edge between Sam and Al as shown in figure 6.19, we need to stop the force layout like we did earlier, create a new datapoint for that edge, and add it to the array we’re using for the links. Then we rebind the data and append a new line element for that edge before we restart the force layout.

Figure 6.19. Network with a new edge added. Notice that because we re-initialized the force layout, it correctly recalculated the weight for Al.

Listing 6.10. A function for adding edges

function addEdge() {

force.stop();

var oldEdges = force.links();

var nodes = force.nodes();

newEdge = {source: nodes[0], target: nodes[8], weight: 5};

oldEdges.push(newEdge);

force.links(oldEdges);

d3.select("svg").selectAll("line.link")

.data(oldEdges, function(d) {

return d.source.id + "-" + d.target.id;

})

.enter()

.insert("line", "g.node")

.attr("class", "link")

.style("stroke", "red")

.style("stroke-width", 5)

.attr("marker-end", "url(#Triangle)");

force.start();

};

If we want to add new nodes as shown in figure 6.20, we’ll also want to add edges at the same time, not because we have to, but because otherwise they’ll float around in space and won’t be connected to our current network. The code and process, which you can see in the following listing, should look familiar to you by now.

Figure 6.20. Network with two new nodes added (Raj and Wu), both with links to Sam

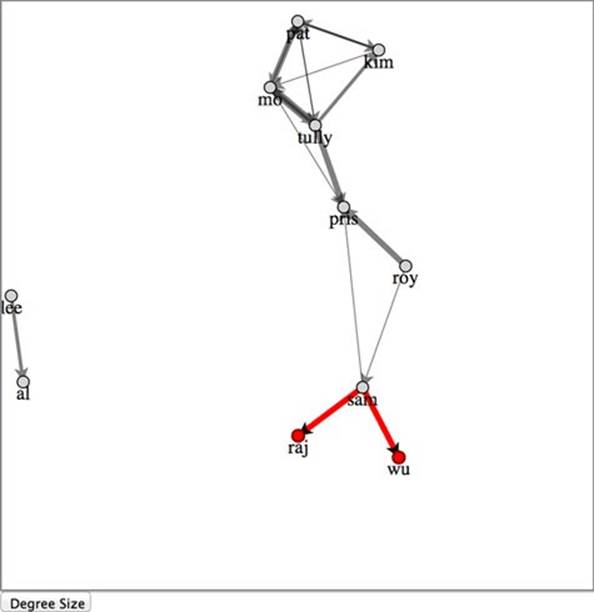
Listing 6.11. Function for adding nodes and edges

function addNodesAndEdges() {

force.stop();

var oldEdges = force.links();

var oldNodes = force.nodes();

var newNode1 = {id: "raj", followers: 100, following: 67};

var newNode2 = {id: "wu", followers: 50, following: 33};

var newEdge1 = {source: oldNodes[0], target: newNode1, weight: 5};

var newEdge2 = {source: oldNodes[0], target: newNode2, weight: 5};

oldEdges.push(newEdge1,newEdge2);

oldNodes.push(newNode1,newNode2);

force.links(oldEdges).nodes(oldNodes);

d3.select("svg").selectAll("line.link")

.data(oldEdges, function(d) {

return d.source.id + "-" + d.target.id

})

.enter()

.insert("line", "g.node")

.attr("class", "link")

.style("stroke", "red")

.style("stroke-width", 5)

.attr("marker-end", "url(#Triangle)");

var nodeEnter = d3.select("svg").selectAll("g.node")

.data(oldNodes, function (d) {

return d.id

}).enter()

.append("g")

.attr("class", "node")

.call(force.drag());

nodeEnter.append("circle")

.attr("r", 5)

.style("fill", "red")

.style("stroke", "darkred")

.style("stroke-width", "2px");

nodeEnter.append("text")

.style("text-anchor", "middle")

.attr("y", 15)

.text(function(d) {return d.id;});

force.start();

};

6.2.7. Manually positioning nodes

The force-directed layout doesn’t move your elements. Instead, it calculates the position of elements based on the x and y attributes of those elements in relation to each other. During each tick, it updates those x and y attributes. The tick function selects the <line> and <g> elements and moves them to these updated x and y values.

When you want to move your elements manually, you can do so like you normally would. But first you need to stop the force so that you prevent that tick function from overwriting your elements’ positions. Let’s lay out our nodes like a scatterplot, looking at the number of followers by the number that each node is following. We’ll also add axes to make it readable. You can see the code in the following listing and the results in figure 6.21.

Figure 6.21. When the network is represented as a scatterplot, the links increase the visual clutter. It provides a useful contrast to the force-directed layout, but can be hard to read on its own.

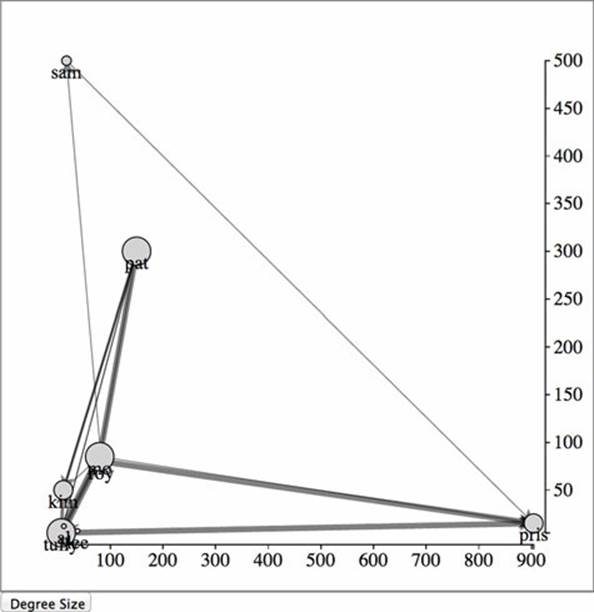
Listing 6.12. Moving our nodes manually

function manuallyPositionNodes() {

var xExtent = d3.extent(force.nodes(), function(d) {

return parseInt(d.followers)

});

var yExtent = d3.extent(force.nodes(), function(d) {

return parseInt(d.following)

});

var xScale = d3.scale.linear().domain(xExtent).range([50,450]);

var yScale = d3.scale.linear().domain(yExtent).range([450,50]);

force.stop();

d3.selectAll("g.node")

.transition()

.duration(1000)

.attr("transform", function(d) {

return "translate("+ xScale(d.followers)

+","+yScale(d.following) +")";

});

d3.selectAll("line.link")

.transition()

.duration(1000)

.attr("x1", function(d) {return xScale(d.source.followers);})

.attr("y1", function(d) {return yScale(d.source.following);})

.attr("x2", function(d) {return xScale(d.target.followers);})

.attr("y2", function(d) {return yScale(d.target.following);});

var xAxis = d3.svg.axis().scale(xScale).orient("bottom").tickSize(4);

var yAxis = d3.svg.axis().scale(yScale).orient("right").tickSize(4);

d3.select("svg").append("g").attr("transform",

"translate(0,460)").call(xAxis);

d3.select("svg").append("g").attr("transform",

"translate(460,0)").call(yAxis);

d3.selectAll("g.node").each(function(d){

d.x = xScale(d.followers);

d.px = xScale(d.followers);

d.y = yScale(d.following);

d.py = yScale(d.following);

});

};

Notice that you need to update the x and y attributes of each node, but you also need to update the px and py attributes of each node. The px and py attributes are the previous x and y coordinates of the node before the last tick. If you don’t update them, then the force layout thinks that the nodes have high velocity, and will violently move them from their new position.

If you didn’t update the x, y, px, and py attributes, then the next time you started the force layout, the nodes would immediately return to their positions before you moved them. This way, when you restart the force layout with force.start(), the nodes and edges animate from their current position.

6.2.8. Optimization

The force layout is extremely resource-intensive. That’s why it cools off and stops running by design. And if you have a large network running with the force layout, you can tax a user’s computer until it becomes practically unusable. The first tip to optimization, then, is to limit the number of nodes in your network, as well as the number of edges. A general rule is no more than 100 nodes, unless you know your audience is going to be using the browsers that perform best with SVG, like Safari and Chrome.

But if you have to present more nodes and want to reduce the performance press, you can use force.chargeDistance() to set a maximum distance when computing the repulsive charge for each node. The lower this setting, the less structured the force layout will be, but the faster it will run. Because networks vary so much, you’ll have to experiment with different values for chargeDistance to find the best one for your network.

6.3. Summary

In this chapter you learned several methods for displaying network data, and looked in-depth at the force layouts available for network data in D3. There’s no one way to visually represent a network. Now you have multiple methods, and static, dynamic, and interactive variations, with which to work. Specifically, we covered

· Formatting a node and edge list in the manner D3 typically uses

· Building a weighted, directed adjacency matrix and adding interaction to explore it

· Building an interactive weighted, directed arc diagram

· Applying simple techniques to find links to a node

· Building and customizing force-directed layouts

· The basics of network terminology and statistics, such as edge, node, degree, and centrality

· Using accessors to create dynamic forces

· Adding interactivity to update node size based on degree centrality

We focused on network information visualization because our world is awash in network data. In the next chapter, we’ll look at another broadly applicable but specific domain: geographic information visualization. Just as you’ve seen several different ways to represent networks in this chapter, in chapter 7 you’ll learn different ways of making maps, including tiled maps, globes, and traditional data-driven polygon maps.