Bitcoin for the Befuddled (2015)

Chapter 6. THE CRYPTOGRAPHY BEHIND BITCOIN

Bitcoin relies on cryptography to function, which is why it is sometimes called a cryptocurrency.¹ But what role does cryptography play in Bitcoin, and why is it needed? We’ll begin with a short introduction to some necessary cryptography concepts (if they are familiar to you, you can just skip to “The Reasons Bitcoin Needs Cryptography” on page 137), and then we’ll explore the specific cryptographic methods used in Bitcoin.

If you flipped to this chapter only because you wanted to know whether the cryptography used by Bitcoin is safe, you can rest easy knowing that Bitcoin uses only tried-and-tested cryptographic techniques: All of the cryptographic methods used by Bitcoin have been widely used in the past by governments and major corporations to secure financial, medical, and other sensitive information, as well as personal identification data.

In fact, the cryptography in Bitcoin could be described as boring, simply because it relies on very conservative cryptographic algorithms. But in some fields of study, such as accounting and dentistry, boring is good; in the case of Bitcoin, conservative and well-established cryptography helps make it more secure. The interesting part is what Bitcoin does with cryptography.

Fortunately, as you’ll see, although Bitcoin cryptography may be old hat to the experts, it is still immensely fascinating to a novice!

A Brief Cryptography Overview

Historically, cryptography was used to send secret messages when necessary to protect information. Messages were systematically scrambled, or encrypted, in a way that hopefully only the recipient of the message knew how to decrypt. A well-encrypted message might be intelligible as battle plans to the intended recipient, but to anyone else it would just be a well-tossed word salad with a side order of alphabet soup. Historically, encryption and decryption were laborious tasks and were reserved only for secure clandestine communication (usually of a military or illicit romantic nature). With the advent of computers, which could do in milliseconds what used to take hours manually, cryptography is now used routinely by the masses to encrypt/decrypt very important (e.g., financial) and not-so-important (e.g., pay-per-view TV) communication. Perhaps surprisingly, the convenience and speed of computers has led to the adoption of cryptographic methods for more than just encrypting secret messages. Common examples include logging in to websites with a username and password combination and using a registration key to install software. Both use cryptographic methods, but no message encryption is involved in either case.

In addition to encrypting messages, modern cryptography is used to verify the validity of information (through cryptographic hash functions) and to prove one’s identity (through digital signatures). For example, without modern cryptography, you wouldn’t be able to distinguish between two identical websites that both claimed to belong to your bank. One might be phony and run by thieves to steal your money. But only your bank’s website can provide the correct digital signature. Before we explain how digital signatures and cryptographic hash functions work, let’s explore one-way functions, a feature that both rely on.

One-Way Functions

One-way functions are mathematical functions that make it easy to calculate an output based on the input but difficult to do the reverse. A precise mathematical definition of what is easy or difficult doesn’t exist but depends on the complexity of the calculation and the effort required to solve it.

A typical example is called integer factorization, which asks you to write an integer² as the product of only prime numbers—for example, the factors of 6 are 2 and 3, which are both prime. Given the prime factors as input, it is easy to multiply them to produce an output integer, but the reverse is not true (at least for larger numbers). Given a large integer, finding its prime factors is very difficult. The only known methods involve systematically guessing different combinations of prime factors, but the amount of time required to find the right answer increases exponentially with the number of digits. Imagine trying to multiply 2 × 7 × 7 in your head. It is not that difficult to calculate the answer of 98; however, if you were given the number 98 and were required to find its prime factors, generating 2, 2, and 7 would be more difficult. A typical laptop can factor a 60–80 digit number in less than a second, but the required time grows exponentially: To factor a 300-digit number or greater would take a modern supercomputer decades.

Prime factors (2,7,7,13) → 2x7x7x13 → Output integer 1274 (easy)
Output integer 1274 → ??????????? → Prime factors (2,7,7,13) (hard)

Another one-way function, which is a bit more complicated but is commonly used in cryptography, involves the discrete logarithm. Consider a set of integers {0, 1, 2, 3, ..., n − 1} where n is a prime number and where we only use modular arithmetic with modulo n:³

Example: n = 7 3 + 6 (mod 7) = 2 3 x 6 (mod 7) = 4

It is easy (as in, you can do it with a pocket calculator) to raise an integer, a, to the kth power to calculate the integer b:

Example: a^k (mod n) = b 3^2 (mod 5) = 4

However, the discrete logarithm, which is finding k given only a, b, and n, is difficult to calculate. The only known methods to find k are variations on trying to guess every value between 0 and n that satisfy the preceding equation. The larger the value of n, the harder it is (and the more time it will take) to calculate k.

Example:
a = 4; k = 4781; n = 17627 → 4^(4781) (mod 17627) = 2685 → b = 2685 (easy)
a = 4; b = 2685; n = 17627 → ????? → k = 4781 (hard)

In the early days of computers, people started applying the asymmetry in these one-way functions to build various classes of cryptographic algorithms, which is what we’ll discuss next.

Cryptographic Hash Functions Verify Information

Cryptographic hash functions are one-way functions designed to take arbitrary data as input (e.g., a number, a short message, an image, or the collected works of Shakespeare) and generate fixed-length output (e.g., a 128-bit or 256-bit number). The output is called a hash or hash value. Hash values can act like a fingerprint—a unique identifier—for files or texts. They’re designed in a way that makes it extremely unlikely that any two non-identical inputs would output the same hash value (when this does happen, it is called a collision). In particular, even a small change to the input data, such as changing one letter in the entire collected works of Shakespeare, would result in a new hash value that is completely unrelated to the original hash.

A commonly used cryptographic hash function is MD5 (message digest algorithm, iteration five), which takes any data as input and outputs a 128-bit hash value, like this:

MD5("hello world") = 5eb63bbbe01eeed093cb22bb8f5acdc3

As you can see, changing just one character in mysecretpasswordisCATS results in a completely different hash output:

MD5("mysecretpasswordisCATS") = 399257907fd42e2ee3fcb39b04192b04
MD5("mysecretpasswordisBATS") = b12d76c8b8c063616dbf7b8b7349aed0

This property enables hash functions to be used to verify that certain information is correct or to match what someone else claims is correct, without needing to scrutinize the actual information. For example, MD5 is used to check whether a downloaded file is safe to use and is free of errors that might have occurred during data transmission. If the MD5 hash value of the downloaded data matches the hash value provided by a reputable source, you can be certain that data does not contain any hidden viruses and was not corrupted during the file transfer. The slightest alteration to the file would cause a noticeable change to the hash output. A hash is like a tamperproof seal: If it’s broken, don’t buy the product.

Another, more exciting, use of cryptographic hash functions is proving that you know a secret password without giving it away. Imagine you are a spy behind enemy lines. After many days of traveling under the cloak of darkness, you finally reach a guarded warehouse to meet with fellow agents. A guard at the front door asks you for the secret code, but you aren’t sure whether the guard is on your side. You need to prove that you know the code without risking the mission by letting your secret code fall into the wrong hands! What do you do? You give him a hash of the secret code. If he knows the code, he can calculate the hash and verify that you also know it. If he doesn’t and isn’t supposed to know the code, you haven’t revealed it.

This dramatic example describes current standard procedure whenever you create a new account with a username and password for a website. The password is never stored on the website’s servers; instead, the hash of the password is stored, and the server checks whether the hash of what you typed matches what is on record. As a result, if the server is ever stolen or hacked into, no passwords will be revealed.

Public Key Cryptography

The invention of public key cryptography in the 1970s was a significant breakthrough, allowing for much of the technology we take for granted today. Until then, all methods of encryption required the sender and receiver to know the same secret encryption key to encrypt and decrypt the message (also known as symmetric key cryptography). However, this method presented a problem because it assumed that, at some earlier time, the sender and receiver had a safe way of communicating to decide on an encryption key without the fear of anyone eavesdropping.

In public key cryptography (also known as asymmetric key cryptography), two different keys are created: a public key that is shared to encrypt the message and a private key that is confidential to decrypt the message (yes, the same private key that is used to spend bitcoins). With asymmetric key cryptography, communicating securely with anyone using an unsafe channel, like the radio or Internet, is easy: You share your public key with others who want to communicate with you, and then anyone can send you encrypted messages that only you can read using your private key. Because the public key cannot be used to decrypt messages, no danger occurs if it falls into the wrong hands. If others want you to send them encrypted messages, they give you their public key, and so on.

How does asymmetric key cryptography work? The original method, called RSA encryption after its developers—Ron Rivest, Adi Shamir, and Leonard Adleman, is based on integer factorization.⁴ Let’s imagine that Crowley wants to communicate with others using the RSA method. Crowley first needs to create a public and a private key (see Table 7-1). He can do this at any time before he starts his communications.

Table 7-1: Sending an Encrypted Message Using the RSA Method

Once the public and private keys are generated, Crowley can distribute the public key widely (along with the prime product, n). Then anyone can use this key to encrypt a message meant only for Crowley.

Of course, to encrypt and decrypt messages, you need some way of converting text into a mathematical form, which is called encoding. Converting a number back to text is called decoding. Encoding and decoding should not be confused with encrypting or decrypting because you are not scrambling the information. Many different encoding schemes exist, and it doesn’t matter which one you use, but all parties involved need to use the same one.

Let’s assume that the letter a becomes a 0, the letter b becomes a 1, the letter c becomes a 2, and so on through the alphabet. In Table 7-2 we’ve encoded the message “fade” using this technique.

Table 7-2: Encoding the Word “Fade” Using a Simple Scheme

Now that we have an encoded message we want to send to Crowley, as well as Crowley’s public key, we can encrypt his message so that only Crowley can decrypt it, as shown in Table 7-3.

Table 7-3: Encrypting the Word “Fade” Using Crowley’s Public Key

Almost an identical scheme can be used to prove one’s identity, using what is referred to as a digital signature.

Digital Signatures

In the public key encryption scheme described earlier, anyone can send you encrypted messages without you knowing who they are. Consider Crowley on his island trying to arrange a transfer of pineapples with Satoshi on another island. If Crowley receives two messages with contradictory information both claiming to come from Satoshi (for example, “Send pineapples to the north island. —Your friend, Satoshi” and “Send pineapples to the south island. —Your friend, Satoshi”), how does Crowley know which message really came from Satoshi?

Fortunately, Satoshi can use a trick to prove his identity and the authenticity of his messages: He can encrypt messages not only with his public key but also with his private key. This backward encryption method reverses the mathematics of encryption, just as you’d expect: Although it’s very difficult to encrypt a message (only the person with access to the private key can accomplish this), it’s very easy to decrypt a message (anyone with the public key can do so).

Therefore, if Satoshi uses this backward method to encrypt the message: “My name is Satoshi, I live on the south island, and I double-pinky-swear to pay you for some pineapples,” anyone, including Crowley, can decrypt this message using Satoshi’s public key (which, let’s assume, was previously established to be 100 percent authentic). Crowley can then say, “I know Satoshi is the only person on Earth who has access to his private key, and this message was written by someone who must have access to this private key; therefore, these words are Satoshi’s words.”

When you use this method to prove your identity, the functions of the public and private key are reversed. Satoshi can use his private key to encrypt a message, and everyone else can decrypt it using his public key. Because others have Satoshi’s public key, the contents of the message wouldn’t be secret, but the fact that it was encrypted using Satoshi’s private key proves that it could not have been sent by anyone else.

Whis Is It Called a Digital Signature?

The term digital signature is used because the most convenient way to send a reverse encryption is to send two separate bits of information: a message and a message signature.

Think about it: Satoshi has nothing to hide in the message he is sending (in fact, he explicitly wants everyone to be able to read his message); therefore, it is arguably more convenient for Satoshi to send the message in an unencrypted form and then a duplicate it in encrypted form. Crowley can easily read the message and only bother using Satoshi’s public key to decrypt the duplicate if he is suspicious of whether Satoshi actually wrote it.

However, it seems inefficient to send a message twice. Clearly, Satoshi must send the entire unencrypted message to get the message out to the world. But could the encrypted message be shortened? In fact it can, by using cryptographic hash functions. Remember that if anyone tries to tamper with a message, the hash of that message will be different as a result. Satoshi can therefore simply calculate the hash output of his message and then encrypt only that hash using his private key. Then anyone who reads the message can decrypt Satoshi’s hash output (using his public key) and also calculate the hash of the unencrypted message, checking whether the two agree.

Keep in mind that a hash of a message, no matter how long the original message, is a short piece of data. Therefore, by only encrypting the hash of the original message, you can create a short digital signature of a much longer message. More important, even the slightest alteration to the unencrypted message would cause the cryptographic hash to be completely different, thus preventing any interceptor from modifying the signed message. As a result, not only does a digital signature prove that the real Satoshi signed the message, but it also proves that he signed a very specific message. In this regard, digital signatures are even better than analog handwritten signatures.

Using Digital Signatures

Using the RSA encryption scheme, implementing digital signatures is straightforward. Let’s assume that we are using the same encoding scheme as in Table 7-2 and we want to send the message “fade” unencrypted but signed. Table 7-4 shows how to use a digital signature to prove authorship of the message.

Now we can send the message “fade” and sign it with ifda. The recipient doesn’t need any additional information to read the message, because it can be read plainly. But to verify the identity of the sender, the recipient needs to know the hash function used (in this case MD5), the prime product n, and the public key of the sender, e. The recipient then decrypts the signature with the public key to obtain the hash value, in this case 8808, and checks to see whether it matches the MD5 hash of the message “fade.” If a match is made, the recipient knows who the message came from and that the message was not altered in transit.

Table 7-4: Signing the Message “Fade” Using RSA Encryption

* If you are following along, keep in mind that the input format for a hash function is important. The MD5 hash of the integer 5034 is not the same as the MD5 hash of the word 5034, which is in text format. For numbers, the base of the number needs to be specified as well.

This is how digital signatures work. Of course, in this example, the prime product chosen was a low number so the examples were easy to follow. In practice, RSA cryptography uses 512-bit or 1024-bit prime products (or even higher for military communications), which looks something like this:

Example RSA-1024 key:
570854064335125300374580392844230066956632116097468377067570536794795107733730 255544946767158528487632613554731246509184251330806267264906570307315620158833 679440939508928340421956875991672660426563565615307186600294486104820050904319 1065262154874848937338866257399506142323572694928592907380693479819082939185

Other small details differ in practice to further increase the security of the procedure.

Why Bitcoin Needs Cryptography

So why is cryptography necessary to make Bitcoin work, even though Bitcoin does not involve sending secret messages? In Bitcoin, hash functions and digital signatures are used for the following important purposes:

• Authorizing transactions with digital signatures

• Verifying the validity of the transaction history

• Proof-of-work in Bitcoin mining

• Extra protection for Bitcoin private keys

Let’s explore the functions of Bitcoin that require cryptography and then delve into the specific methods that Bitcoin uses.

Authorizing Transactions with Digital Signatures

Bitcoin uses digital signatures to authorize transactions so that you, and only you, can spend the bitcoins you own. With credit card payments and bank transfers, you authorize a transaction by providing proof of your personal identity (and these days, the amount of proof you have to show is getting quite burdensome). With Bitcoin, no personal information is tied to any Bitcoin address; instead, you must prove that you own the private key. Showing people your private key would certainly be valid as proof, but by knowing the private key, the people you’ve shown could then claim they owned the bitcoins at that address. Therefore, you need to prove that you have the private key without actually sharing it. But there’s more to it than that.

A Bitcoin transaction contains a fair amount of information: the number of bitcoins transferred, the address they are being transferred to, the transaction fee, and so on. You don’t want any of that information to be altered without your permission, so in addition to proving you own the bitcoins you are sending, you also need to ensure that the transaction details are followed exactly as you wrote them. A Bitcoin transaction is a message with instructions, and by signing it with a digital signature, you simultaneously prove that you have the private key and ensure that the transaction details are what you intended. If the signature is missing or doesn’t match the public key, nodes on the Bitcoin network will consider the transaction invalid and will not add it to the blockchain.

Verifying the Validity of the Transaction History

Bitcoin depends on the blockchain being widely distributed among the nodes in the network. But how can you be sure that any individual node in the network with a copy of the blockchain has not been surreptitiously altered? A malicious attacker could try to distribute a fraudulent blockchain where just a single transaction has been modified in the attacker’s favor. However, such an attack could never work for several reasons. One reason is that the slightest change in the transaction history would completely change the block hash of all the blocks after it in the chain.

Each block in the blockchain contains a list of transactions and a hash of the transactions in the previous block in the chain. Hence, it’s impossible to alter just one transaction in a block in the middle without causing a mismatch between the expected block hash and the hash recorded in the next block.

This verification provides an efficient way for a single node to check whether transactions in its copy of the blockchain have been tampered with. Rather than checking every transaction in the entire transaction history, a node can simply check whether the hash of each block matches the recorded hash of subsequent blocks.

Proof-of-Work in Bitcoin Mining

Bitcoin mining is based on a lottery system that you can win only by guessing numbers repeatedly, but that makes it is easy for others to check when you’re right. If this sounds similar to a one-way function, that’s because it is. The one-way function used in Bitcoin mining is a cryptographic hash function. Miners are given the output criteria (the output can be any number less than some threshold), but by design, cryptographic hash functions make it difficult to reverse calculate what the corresponding input needs to be. Therefore, Bitcoin miners can only randomly choose different inputs, hoping that the output will be a number below the threshold. Once a miner determines the correct input value, it is easy to prove his or her work to others by sharing that value with others who can easily recalculate the hash.

Extra Protection for Bitcoin Private Keys

Authorizing transactions with digital signatures requires sharing your public key with others. Although it is thought to be computationally infeasible to calculate a private key from a public key, it is similarly difficult to calculate the input of a hash function given just the output, and it is doubly difficult to do both. Instead of sharing a public key, users share a Bitcoin address, which is a cryptographic hash of a public key. In fact, the public key is hashed twice using two different cryptographic hash functions to create a Bitcoin address. This extra protection ensures that no amount of analysis of a Bitcoin address can reveal the underlying private key.

Bitcoin uses cryptographic hash functions to accomplish a variety of other important tasks as well. Next, you’ll explore the specific cryptographic methods Bitcoin uses.

Cryptographic Methods Used in Bitcoin

Public key cryptography is a high-level framework that can be implemented many different ways. You learned how the RSA method, using integers factored into large prime numbers, could be used to implement digital signatures. But how are digital signatures implemented in Bitcoin? Many different cryptographic hash functions exist, and although the MD5 method mentioned earlier is widely used, it is not sufficiently secure for a cryptocurrency (collisions have been detected in MD5, resulting in two different inputs leading to the same output).

SHA256 and RIPEMD160 are the two cryptographic hash functions used in the Bitcoin protocol.

Cryptographic Hash Functions: SHA256 and RIPEMD160

Secure Hash Algorithm (SHA) was developed by the US National Security Agency (NSA). Race Integrity Primitives Evaluation Message Digest (RIPEMD) was designed in the academic community by Hans Dobbertin, Antoon Bosselaers, and Bart Preneel at the Katholieke Universiteit Leuven.⁵

The prefixes SHA and RIPEMD refer to the underlying algorithms, and the numerical suffixes 256 and 160 refer to the bit-length of the output. A spectrum of other SHA functions, like SHA224 and SHA512, output other bit-length hashes as well.

Both SHA256 and RIPEMD160 are widely used, but the SHA methods are more popular and have undergone a higher degree of scrutiny from cryptographers. At the time of this writing, nobody has detected a collision in either SHA256 or RIPEMD160, which is an important measure of the security of a cryptographic hash function.

In the Bitcoin protocol, SHA256 and RIPEMD160 are used together to protect the public key used in digital signatures. The SHA256 method is also used for the proof-of-work function in Bitcoin mining and as part of the digital signature algorithm. Here are some examples of encrypting a sentence with a slight variation in both SHA256 and RIPEMD160 (all of the following outputs are in base 16 format):

SHA256("Crowley is trapped on an island")
= 1e8f7e62b42f07766c3c4367e670a328d73b7eb596602198f126324f013f30a5

A completely different result is produced with a single character change:

SHA256("Crowley is trapped on an Island")
= 91a382b6584261e0e7690da2c43cec9f7ce251b47396b543bddb3ed6ada8c9cc

The same happens using RIPEMD160:

RIPEMD160("Crowley is trapped on an island")
= 64d50d0853d09d97c4567117a616954ca648e46c

This hash is completely different:

RIPEMD160("Crowley is trapped on an Island")
= b84aec162a0aa5786541b5e4f3286f8734e3bc3c

As you’d expect and appreciate in an effective hash function, a minor change to the text (capitalizing the word Island) completely changes the resulting hash value in both methods.

Now that you understand the hash functions Bitcoin uses, let’s discuss the algorithm Bitcoin digital signatures use.

Crowley and the Unfortunate Jelly-Filled Donut Incident

For the remainder of this chapter, we’ll discuss the details of elliptical curve cryptography (ECC). But before we delve into the details of this algorithm, and to help you understand the basic concept behind it, let us tell you a story.

One day Crowley was driving through Cryptoville in his car, minding his own business, when suddenly, BAM! His car was thrown into the air!

He had been driving by a donut shop that was trying to beat the world record for the largest jelly-filled donut. Unfortunately, the bakers miscalculated the correct pressure of jelly to inject into the donut, causing the explosion.

After tumbling through the air, Crowley landed safely and was relieved to realize he wasn’t hurt. However, he was a bit shaken from this frightful incident, and his car was covered in jelly. Because he had tumbled through the air, he was lost and no longer knew where he was in Cryptoville. What was he going to do now?

Suddenly, Satoshi stepped out of a nearby house. Quite by accident, Crowley had found out where the secretive Satoshi lived!

Crowley proceeded to explain to Satoshi what had happened to him and his car. Satoshi was concerned to hear that Crowley was lost but also a bit relieved because it meant that his home address was still a secret.

Crowley asked Satoshi to give him a ride home or call a tow truck. But Satoshi refused, saying, “If I do either of those things, you’ll be able to figure out where you are in Cryptoville, and then you’ll be able to figure out my secret home address. Luckily I have another idea: Why don’t you come into my home as a guest and enjoy a cup of coffee as you regain your wits from your harrowing experience today. I’ll be back in a couple of hours and will then share my plan to get you and your car home again.”

Sure enough, Satoshi returned to the house after a while carrying an iPod, of all things. “OK, Crowley, here’s what I did. I just drove to your house with my own car. While doing so, I recorded my drive on this iPod and recorded every action as I drove along. When I turned the steering wheel 10 degrees to the left, I said this on the recording. If I accelerated from 20 mph to 40 mph, I recorded this as well. Everything I did I recorded at the exact time I did it.”

Crowley then understood the plan: Even though his car was covered in jelly and it was impossible for him to see through the windows, he could still follow the simple instructions on the tape. After all, his car motor still ran fine, and he could see the speedometer on his car’s dashboard. Satoshi added, “It’ll be very hard for you to reverse engineer the exact physics of how the car was driving based solely on the instructions I recorded on the iPod. Therefore, the location of my home will remain unknown to you. However, to make it extra hard, I also took a very circuitous route, driving through almost all of Cryptoville along the way to your house!”

But sure enough, using Satoshi’s iPod, Crowley was able to drive his car back home without being able to see a thing through his car windows. He simply followed the instructions, and when the recording finished, he was back home. He still didn’t have the slightest clue where Satoshi lived, and he miraculously avoided hitting any pedestrians or other cars in the process!

To thank Satoshi for helping him, Crowley sent Satoshi an email inviting him to lasagna at Crowley’s house on Saturday night and asking him to suggest a time for dinner. Here is the email Satoshi wrote back:

Thanks Crowley—Dinner sounds great, and I love lasagna! Let’s meet at 9:25 P.M.

Oh, and to prove that this email is legit, I can tell you that I was on the 300 block of Main Street driving north at exactly 38.7 mph when the iPod displayed 9 minutes and 25 seconds.

Being a stickler for verifying identities, Crowley tested this fact: He first had his car (still covered in jelly) towed to the location mentioned in the email and then started the iPod at the 9 minute and 25 second mark. Following the instructions on the iPod explicitly until they completed, he once again stepped out of the car and found he was back at home!

This silly parable is meant to give you a rough outline of one way you could create a digital signature: Imagine that Satoshi’s home address is Satoshi’s private key, and Crowley’s home address is the public key. The instructions on an iPod are a one-way function that’s difficult to reverse. Using this information, you could sign an arbitrary message (in this case the number 925, which corresponds to the meeting time). Only the person who knows the private key (Satoshi’s home address) could generate this signature.

As you’ll see, with ECC, we’ll instead “drive around town” by jumping between points on a special two-dimensional curve, which makes it even harder to reverse engineer the directions. However, the overall process will remain roughly analogous to that in the story.

Moving Around on a Line

Before we start thinking about what’s involved in driving around on a curve, let’s use an easier scenario and imagine driving around on a line (see Figure 7-1).

If we have a straight line that passes through the origin (i.e., the point at x = 0, y = 0), we can create a new point on the line by using two points A and B to create a point C by simply adding A and B. Here is the obvious formula for adding two points:

A(x₁, y₁) + B(x₂, y₂) = C(x₃, y₃) x₃ = x₁ + x₂ y₃ = y₁ + y₂

We need to add the two x-coordinates to get a new x (simply 1 + 3 = 4) and add the two y-coordinates (also 1 + 3 = 4). Note that we can also use a simple geometric trick to generate point C without using arithmetic: Simply start at point B and then move at the same angle and amount as point A is from the origin.

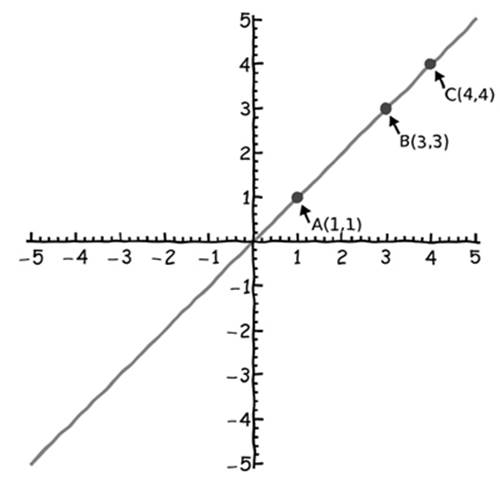
Figure 7-1: Adding two points (A and B) on a line to get point C

For a line, this addition process is very simple but is not useful for cryptography (and equally not useful for creating driving instructions for our “car” that are hard to reverse engineer). But as you’ll see, the process for adding points is very different with elliptical curves.

Elliptic Curve Digital Signature Algorithm (ECDSA)

Instead of integer factorization-based schemes, digital signatures in Bitcoin are based on ECC. Although integer factorization works well in principle, faster computers and better algorithms to factor integers have over time increasingly required the use of ever larger prime factors to ensure reasonable security. The recommended size of encryption keys used for RSA encryption is between 1024 and 4096 bits. In contrast, elliptic curves offer the same functionality but are not affected by advances in factoring integers; therefore, shorter keys can be used (a 256-bit key in ECC is believed to offer comparable security to a 1024-bit key in an RSA-type scheme). In short, ECC is thought to be stronger than methods based on factoring integers for the same key length.

Bitcoin uses elliptic curves to create digital signatures, specifically by using a protocol called the Elliptic Curve Digital Signature Algorithm (ECDSA). An elliptic curve is any two-dimensional curve that satisfies the equation:

y² = x³ + ax + b

A few sample curves that satisfy this equation are shown in Figure 7-2. Public/private key pairs are generated by choosing points on these elliptic curves that are mathematically related to each other.

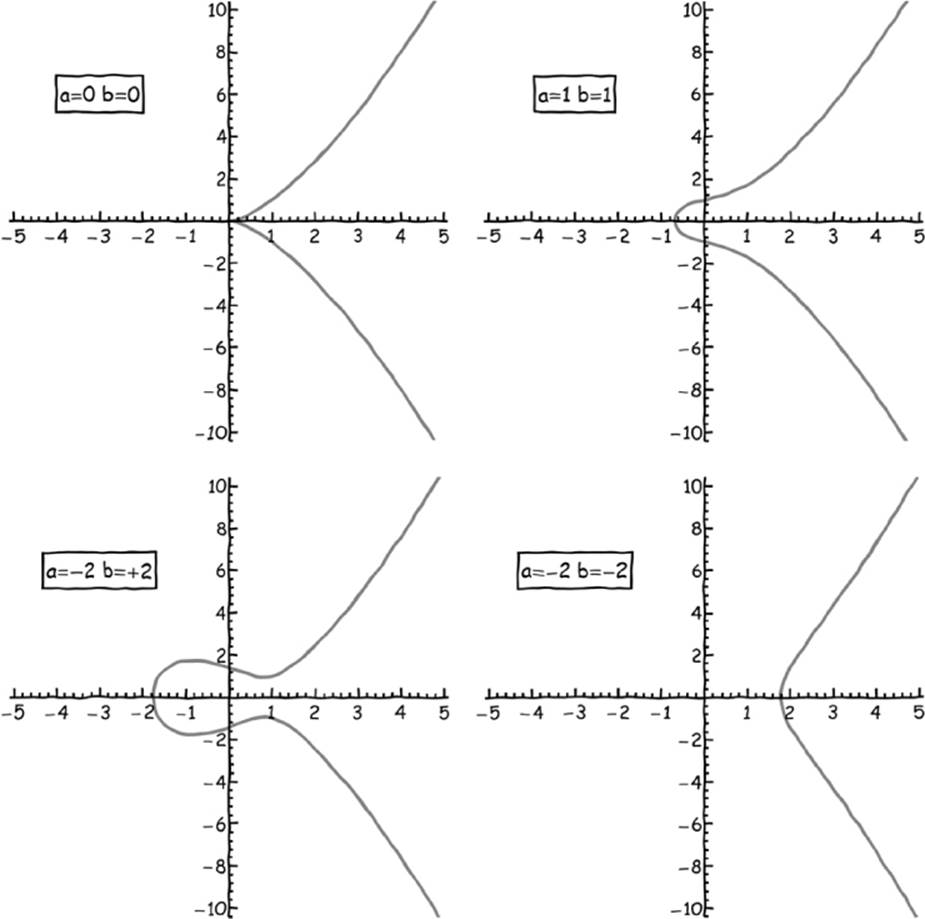
Figure 7-2: Different elliptic curves can be generated using different parameters in our starting equation.

As with the property of a straight line, when you add the coordinates of any two points on the curve, the result is another point on the curve.

However, with elliptic curves addition has a special meaning and is defined as follows:

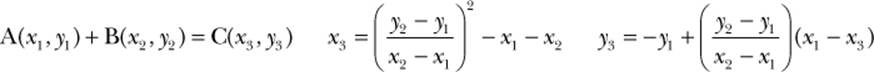
Clearly, this formula for adding two points is much more complex than the addition formula we used for straight lines. Figure 7-3 shows an example elliptic curve with two points A and B and the resulting point C created by following these addition rules.

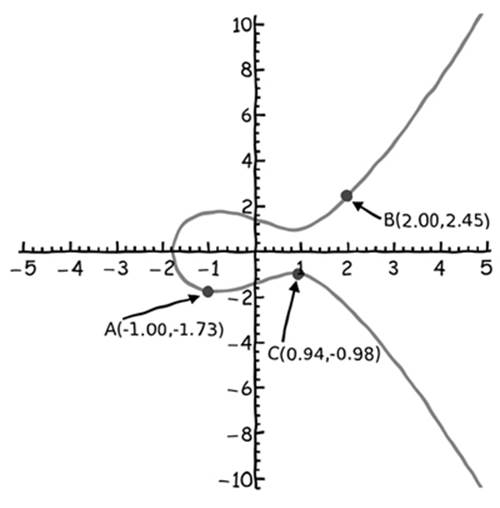
Figure 7-3: Two points (A and B) on an elliptic curve are added to create point C, using our special method of addition.

In the example in Figure 7-3, points A and B are not special in any way. Choosing different A and B points would lead to a different point C (Figure 7-4), which is the whole point of using this type of addition for cryptography: In the earlier jelly donut incident, Crowley had to drive a long, circuitous route back to his house so Satoshi’s home address would remain obscured. Repeatedly jumping between points on the elliptic curve using this method of addition can help you obscure your private key in a digital signature system in the same way, as you’ll soon see.

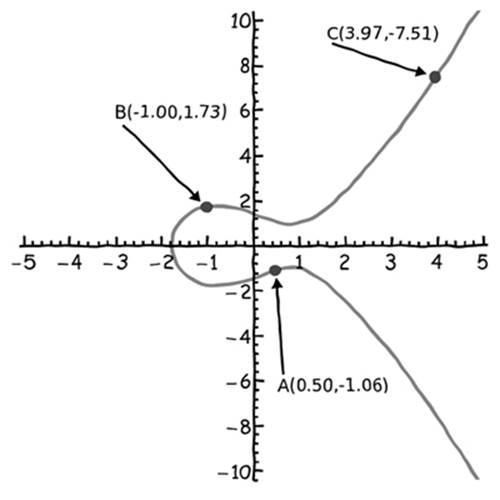
Figure 7-4: When different points A and B are chosen, a different point C is created.

Similar to lines, you can use a geometric trick to calculate the sum of adding two points on elliptic curves (i.e., without needing to do the tedious arithmetic). Simply draw a line through points A and B, and find another location where the line intersects the curve. Then draw a vertical line starting at this point of intersection and see where else it crosses the elliptic curve. This second crossing is point C (Figure 7-5).

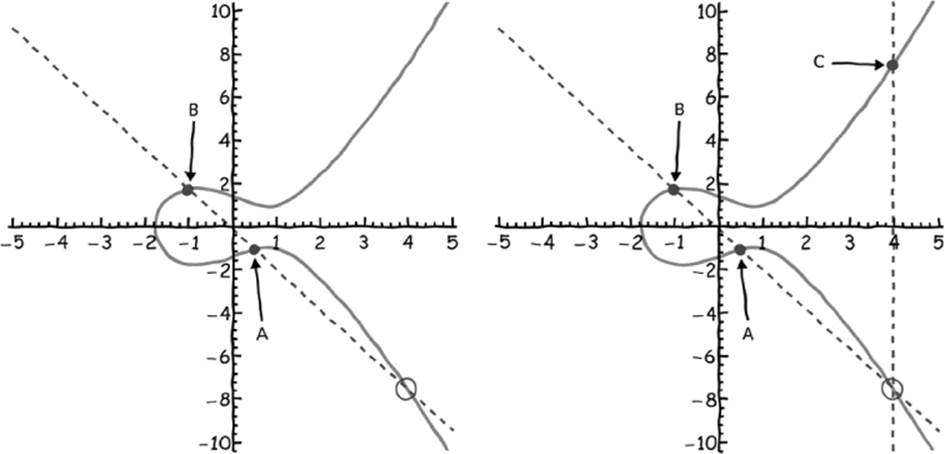
Figure 7-5: Using simple geometry, you can find point C by just drawing a line through points A and B and then moving vertically to find point C.

A fundamental property of elliptic curves is that any line that intersects at least two points must also intersect a third (except for vertical lines and lines that are tangent to a point on the curve⁶).

Of course, if we want to “drive around” our elliptic curve, as in our conceptual example involving a car, it’s somewhat awkward that we need two points to generate every new point: As with a car, it would be ideal to go from a single point to another single point so our “car” only has to be in one place at a time. Fortunately, this is possible with elliptic curves as well by using a form of multiplication to multiply a point on the curve by an integer, which is the same as adding a point to itself multiple times. It might seem like the geometric trick does not work in this case. How do you draw a straight line through two points if they are in the same place? You can probably guess by imagining what happens when you consider adding two points, A and B, that are very close together: The line that passes through A and B will resemble the tangent to the curve near those points. So when we add A + A (or equivalently, multiply A by 2), we draw a tangent to the curve at point A and find where else it intersects. Then we draw a vertical line, as before, to find the resulting point, 2A (Figure 7-6).

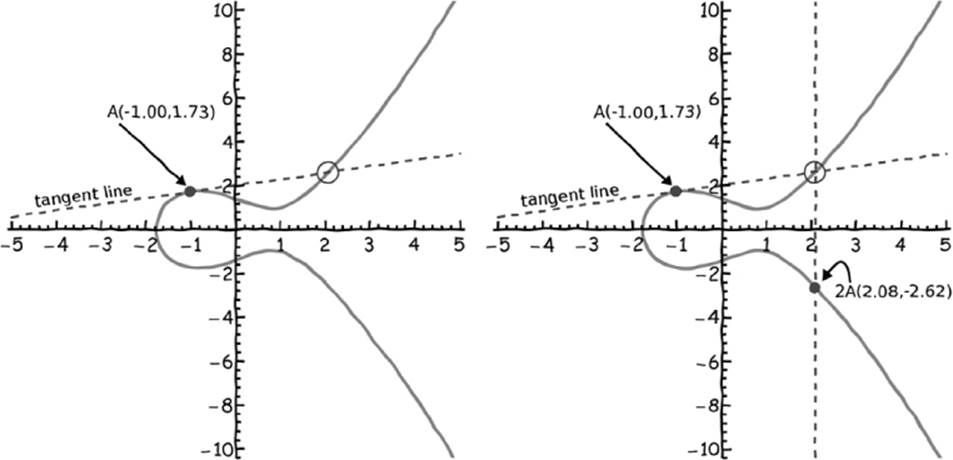
Figure 7-6: With only one starting point, we can point multiply by 2 by using the tangent line through point A.

To calculate 3A, you first calculate 2A, as we just did, and then adding an additional A is just like adding any two nonoverlapping points. In elliptic curve terminology, calculating kA, where k is an arbitrary integer, is called point multiplication. Calculating kA for large values of k is computationally expensive without efficient implementations.

So as with our conceptual example, we’ll now use point multiplication to “drive” from one point on the curve to another. In ECC, point multiplication is used to generate the public key from the private key. However, there will be one important difference between our jelly-filled donut story and how ECC really works. In our story, Satoshi’s house represented a private key and Crowley’s house a public key, but in ECC the starting point and destination point are both publicly known—it is only the path between them that is secret. So it is in fact the path that is the private key; the destination point is the public key (as it was before), and the starting point is simply a standard location that everyone agrees to use. In ECC it’s as if Satoshi’s home address were widely known to be in the center of a very complex labyrinth—everyone knows where he lives, but no one knows how to get there. Given a previously agreed-upon point on the curve, G, and a private key, d, the public key, Q, is calculated by point multiplication such that Q = dG. Note that the public key is a point on the curve but the private key is just an integer.

So far we’ve been depicting elliptic curves as smooth, continuous functions that extend into infinity. However, computers have limited memory, and it isn’t possible to use real-valued numbers as coordinates for points on the curve without introducing rounding errors (which are unacceptable in cryptography). For practical implementations, only integer-valued points on elliptic curves are allowed, and modular arithmetic is used to keep all of the points within certain bounds (from 0 to 512, for example). This technique of using only integer-valued points is best illustrated with an example. Let’s first choose the same elliptic curve that Bitcoin uses, which is called a Koblitz curve (Figure 7-7), using the parameters a = 0 and b = 7.

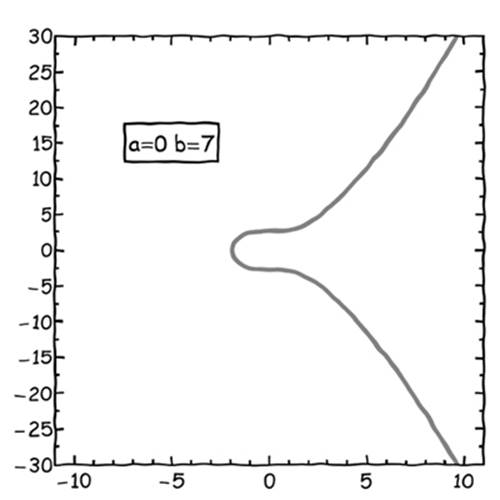
Figure 7-7: A Koblitz curve

We then choose a prime modulo p so that the elliptic curve satisfies this equation:

y² = x² + ax + b(modp)

NOTE
In this type of math notation, the modulo operation is performed after the additions so first you calculate x² + ax + b and then you perform mod p on the result.

Bitcoin uses a very large p value (specifically p = 2²⁵⁶ − 2³² − 2⁹ − 2⁸ − 2⁷ − 2⁶ − 2⁴ − 1), which is important for cryptographic strength, but we can use a smaller number to illustrate how “driving around on integer-valued points on a Koblitz curve” works. Let’s choose p = 67. In fact, many curves satisfy the modular equation (namely, every curve where p is added to or subtracted from the b parameter any number of times; see the left-hand chart in Figure 7-8), and from those curves we can use all of the points that have integer-valued coordinates (shown in Figure 7-8 as dots).

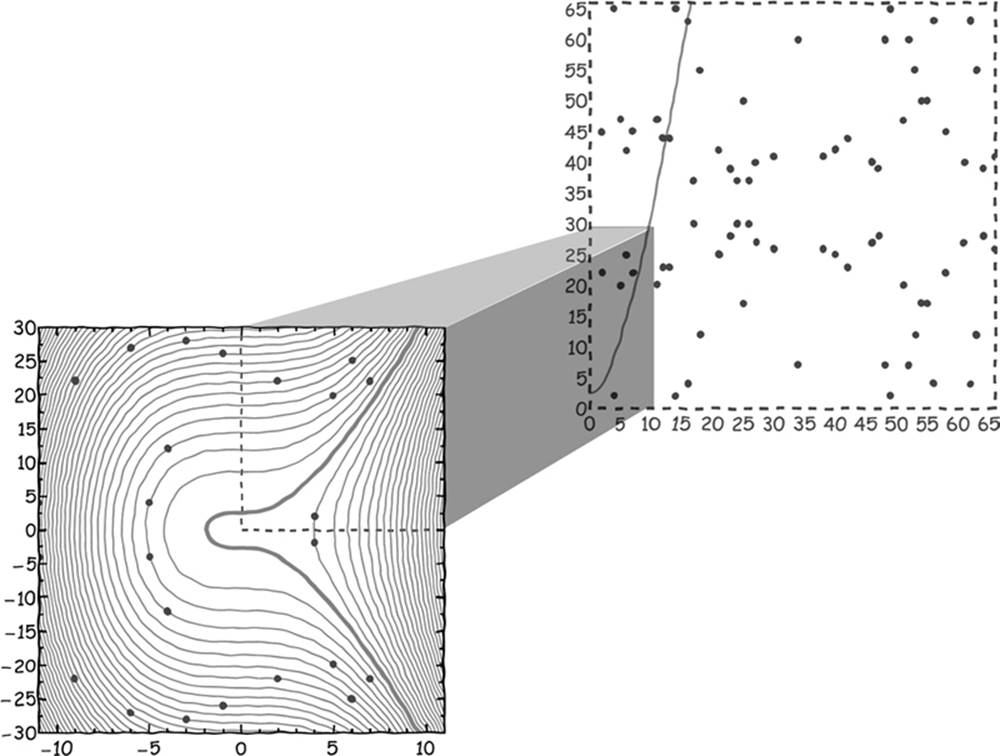
Figure 7-8: On the left is a standard picture of the elliptic curve in the form we’re familiar with (the bold curve) with additional curves that are drawn by using other multiples of p (the thin curves.) On the right, we’ve taken a larger section of the coordinate plane that is an expansion of the upper-right quadrant. This is the section of the curve that is most convenient when using the integer-based variant of ECC.

Given the choice of p = 67, only 79 unique points with integer-valued coordinates exist, and 78 of them can be found in the upper-right quadrant from 0 < x < 66 and 0 < y < 66 (shown in the chart on the right in Figure 7-8; note that the left chart shows the entire range). The number of unique points, n, is called the order of the curve. The 79th point is the zero point, which is not at (0,0) as you might expect but rather is the point at y = infinity. The zero point is important because it is valid output from an addition or point multiplication operation and therefore needs to be carefully accounted for (see the sample code in “Pseudocode for Elliptic Point Summation and Point Multiplication” on page 158).

As a last step before we can generate public/private key pairs, we need to choose one of the 79 points to be a generator point, G. The generator needs to have the property that one can calculate every one of the other 78 points by multiplying G by some integer, k (i.e., so you can generateevery point by calculating G, 2G, 3G, ..., 79G). If we choose the point (5,47) as our generator point, we can check whether by successively incrementing k we can travel to every point in the set (see Figure 7-9).

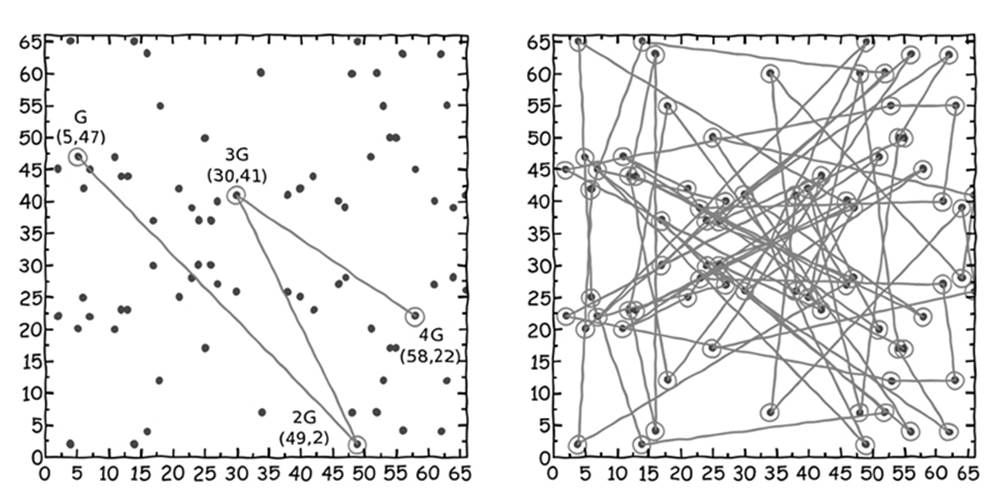
Figure 7-9: On the left, starting with point G, we multiply G successively to create new points at 2G, 3G, and 4G. On the right, you see what happens when this multiplication is repeated even further.

If the order of the curve is prime (i.e., there is a prime number of points), any point except the zero point works equally well as a generator. If the order is not prime, regardless of the k value, some points will travel only to a subset of points (which can lead to a reduction in cryptographic strength). In our case, we can safely use the point (5,47) because it generates all the other 78 points (as depicted in the chart in Figure 7-9).

To return to our conceptual car example, point G in this figure could be Satoshi’s house and point 4G, for example, could be Crowley’s house. The points between represent the complicated drive through Cryptoville. Until you carry out the point multiplication operation, it certainly isn’t obvious what the path from G to 4G is. The 4 in 4G gives away the answer, namely that the path connecting those points can be found by taking three steps from G. However, if G and 4G were instead labeled A and B, it would take a long time to guess how to get from one to the other. In other words, if you know only the start and end points (i.e., the public key), it would take a long time to guess the path (i.e., the private key). But if you know the starting point and the path, then calculating the end point is easy. In terms of Bitcoin, it means that if someone knows the Bitcoin address that contains your money (which is based on the public key), it is still impossible for that person to figure out your private key to spend the bitcoins at that address.

Signing a Bitcoin Transaction Using ECDSA

Now that we’ve chosen p, a, b, and G and determined the order, n, we have all the information we need to create a public/private key pair following the steps in Table 7-5.⁷

Table 7-5: Creating a Public/Private Key Pair with ECDSA, Assuming p = 67, a = 0, b = 7, G = (5,47), n = 79

* A clever way to generate a seemingly random but memorable private key is by coming up with a passphrase (i.e., Crowley and Satoshi sitting in a tree) and feeding it into a cryptographic hash function, which outputs an integer. This is called using a brainwallet. Because there are just slightly fewer than 2²⁵⁶ points on the curve Bitcoin uses (because the p value is much higher than the one we are using), brainwallets can use the SHA256 hash function (due to its 256-bit output).

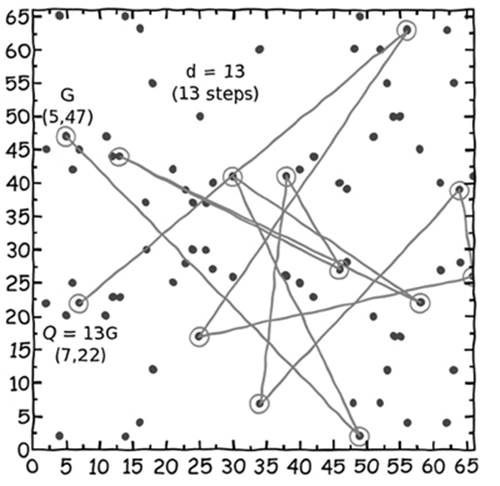
Figure 7-10: Here are the 13 points we “drive through” as we point multiply to create a digital signature.

Now let’s look at how we sign messages with our private and public keys (or Bitcoin transactions): The receiver of our message will need all the values we have calculated so far except the private key, namely p, a, b, G, n, and Q, in order to verify that the signature is valid. Let’s assume that our message is this: Please update the blockchain so that 5 bitcoins from Crowley are given to Satoshi. The steps to sign the message are listed in Table 7-6.

Table 7-6: Signing a Message with ECDSA, Assuming p = 67, a = 0, b = 7, G = (5,47), n = 79, d = 13

When the message is signed, the receiver will need p, a, b, n, G, Q, and the signature pair (r,s) (and the message, of course). However, the parameters p, a, b, n, and G are standard to the Bitcoin protocol and therefore don’t need to be shared with every transaction. The only information specific to your message that needs to be shared is Q, (r,s), and the message. The message recipient can verify that you signed the message with your private key by using the steps in Table 7-7.

Table 7-7: Verifying a Signature with ECDSA, Assuming the Receiver Gets Q = (7,22), (r = 46, s = 2), and the message

In our car example, we were able to sign messages in a similar way by relating a message to a point that the car passed as it traveled toward its destination. However, this is where this analogy reaches its limits: In the car example, providing information about where the car traveled conveys some clues as to the path the car took, compromising the secret of Satoshi’s address a bit. Using the math in Table 7-7 shows that signing a document does not provide any useful information that compromises the private key. We can sign as many documents as we want, and the private key will continue to remain fully obscured.

So this is how bitcoins are spent. When you sign a Bitcoin transaction with your private key, other nodes in the Bitcoin network can check that your signature is valid (by matching your public key and the contents of the transaction) and safely know you authorized it. Of course, if your private key falls into the wrong hands, someone else can sign transactions and steal your bitcoins.

Note that until you actually need to spend bitcoins, there is no need to share the public key. Although in principle sharing your public key far in advance of signing a transaction should be no problem, it’s possible that a weakness in ECC will be discovered that could allow an attacker with enough time and computing power to figure out your private key from your public key (i.e., figure out d, given G and Q in the equation Q = dG). So why give an attacker the extra time if it isn’t necessary? If an attacker doesn’t know your public key, the ability to determine your private key is drastically reduced. For this reason, Bitcoin users share addresses instead of public keys.

The Bitcoin address described at length earlier in this book is actually a hash of the public key, using the SHA256 and RIPEMD160 hash functions. The public key is first input into the SHA256 hash function, and then the output is fed as input into the RIPEMD160 hash function. The resulting double hash is used to generate the Bitcoin address in a standard way.⁸ When you spend bitcoins from a Bitcoin address, you must provide your public key, and others can check that the public key corresponds to the Bitcoin address by repeating the same double hash calculation (and of course, the signature proves that you have the private key).

In cryptography, the double hash scheme results in extremely strong security. Given only a Bitcoin address, it would require a simultaneously discovered weakness in three different cryptographic methods—SHA256, RIPEMD160, and ECDSA—for an attacker to guess a private key. If a weakness was discovered in one method but not the others, there would be time to update the cryptographic methods used in Bitcoin before anyone’s bitcoins were at risk.

The Security of Bitcoin’s Cryptography

A common anxiety among those new to Bitcoin is to wonder whether the cryptography used in Bitcoin is secure enough to protect against threats. Could a big, powerful government with huge computing resources break Bitcoin’s cryptography? What about a very clever hacker who might bring down the entire system? What about super powerful computers of the future, like quantum computers?

These are healthy concerns to have when a person is deciding whether Bitcoin is a sound protocol and worth investing in. Every Bitcoin private key is some number between 1 and 2²⁵⁶, and in principle a computer could continue generating numbers billions or trillions of times per second until it found one that could access your bitcoins. However, 2²⁵⁶ is a very big number; in fact, it’s approximately 10⁷⁷ or a 1 with 77 zeroes behind it. Putting that in perspective, approximately 10⁵⁰ atoms make up the earth. If you chose a single atom in the earth at random, and then chose a second atom, also at random, the odds that you picked the same atom twice would be significantly greater than randomly guessing someone’s private key.

Could an extremely powerful computer, based on futuristic technology that is yet to be invented, guess a private key? Theoretical physicists have estimated that the smallest amount of energy to perform the simplest computation (changing a 0 to a 1 or vice versa) requires at least 3 × 10⁻²¹joules (this is known as the Landauer limit⁹). A computer that used this amount of energy per computation would theoretically be the most efficient computer allowed by the laws of thermodynamics. If you then could harness 100 percent of the energy of the sun (not just the tiny fraction that falls on the earth, but the entire amount, by building a sphere of perfect solar panels surrounding the entire star), with no losses, you could theoretically capture 10³⁴ joules per year. If you harvested that energy for 100 years and fed all of it into your maximally efficient computer designed for the single purpose of guessing someone’s Bitcoin private key, it would be able to perform only 10⁵⁵ computations. Of course, calculating a private key is more complicated than flipping a 0 into a 1, but even if we assume that this computer could calculate 10⁵⁵ private keys, it would run out of energy before it would even have onetrillionth of a chance of correctly guessing yours.

In summary, it is physically impossible, independent of future technological developments, to create a computer that could steal bitcoins by randomly guessing private keys. However, that does not eliminate the concern that a weakness exists in the cryptographic methods that Bitcoin uses. Perhaps it is easier than we think to work backward from a Bitcoin address to calculate the underlying private key. Here, it is important to note that the cryptographic methods used by Bitcoin are standard methods used by governments and major corporations to ensure security incommunications, financial transactions, and network security. If a weakness exists in the methods that Bitcoin uses, a weakness exists in the methods the entire world uses.

Also, if weaknesses are discovered in the cryptographic standards, such that new methods need to be used, it is possible to update the methods that Bitcoin uses without affecting how Bitcoin functions. A new version of the SHA256 algorithm may be used in the future, or ECDSA might be replaced with a different digital signature algorithm. However, Bitcoin’s reliance on cryptography in general will not change.

The bottom line is that Bitcoin’s cryptography has a solid technical foundation. If a hacker ever does steal your bitcoins, it is far more likely the hacker would do so by finding a bug in a specific implementation of this cryptography that is flawed or by using the many other ways we’ve discussed, such as simply stealing your private key through a computer virus. It is far less likely that a hacker would be able to steal your money by finding a flaw in the mathematics of the cryptography.

Pseudocode for Elliptic Point Summation and Point Multiplication

To follow along with the elliptic curve digital signature examples earlier in the chapter, you’ll need to be able to correctly calculate elliptic point summations and point multiplication operations using modular arithmetic. Pseudocode for the implementation of these operations follows:

Assumptions: p, a, b, G, and n are defined elsewhere
Elliptic curve point summation (ECPS): A + B = C
ECPS(A,B) returns a point on the elliptic curve, C
Begin
If A is the zero point then return C = B➊
If B is the zero point then return C = A
If Ax != Bx then➋
find inv such that inv*(Bx – Ax) (mod p) == 1
lambda = (By – Ay)*inv (mod p)
Cx = lambda^2 – Ax – Bx
Cy = -Ay + lambda*(Ax – Cx)
return C = (Cx (mod p), Cy (mod p))
If Ax == Bx and Ay != By then return C = the zero point➌
If Ax == Bx and Ay == By then➍
find inv such that inv*2Ay (mod p) == 1
lambda = (3*Ax^2 + a)*inv (mod p)
Cx = lambda^2 – 2Ax
Cy = -Ay + lambda*(Ax – Cx)
return C = (Cx (mod p), Cy (mod p))
End

In this elliptic curve point summation (ECPS) pseudocode, which allows you to add two points on the elliptic curve to generate a third point, we first check whether A or B is the zero point ➊ (recall that this is the single weird point that’s part of an elliptic curve that is essentially at infinity). Next, we handle the typical case where two points have different x locations, and we don’t need to worry about the slope between the points being divided by zero ➋. Then, we handle the case where the slope is indeed zero, which forces C to be at the zero point ➌. Finally, we handle the case where A and B are the same, in which case we need to calculate the answer differently using a mathematical derivative to calculate C using the point’s tangent line ➍.

Elliptic curve point multiplication (ECPM): kA = C
ECPM(k,A) returns a point on the elliptic curve, C
Begin
C = A
Do the following k times:
C = ECPS(C,A)➊
return C
End

For elliptic curve multiplication, we simply run the ECPS function repeatedly ➊. This is really inefficient! In fact, this method of point multiplication is so inefficient that it ceases to be a “one-way” function. It is just as computationally difficult to calculate the public key (knowing the private key) as it is to guess the private key (knowing the public key). For the small number of points we were using in this chapter, it’s fine to use our bruteforce approach, but for practical applications, more efficient schemes for point multiplication need to be used. We leave this as an exercise for the reader.