Functional PHP (2017)

Chapter 7. Functional Techniques and Topics

We've covered the foundational techniques relative to functional programming. But, as you can probably imagine, there are a lot more topics to cover. In this chapter, you will learn about some of those patterns and ideas.

Some topics will be covered in depth and others will be mentioned with pointers to external resources if you want to learn more. As this is an introductory book to functional programming in PHP, the most advanced ideas are out of scope. If you encounter an article about such a topic somewhere, you should, however, have enough understanding to grasp at least the gist of it.

The sections of this chapter are not necessarily linked with one another. Some content might be novel to you and some is linked to excerpts presented earlier.

In this chapter, we will cover the following topics:

· Type systems, type signature, and their uses

· Point-free style

· Using the const keyword to facilitate anonymous function usage

· Recursion, stack overflows, and trampolines

· Pattern matching

· Type classes

· Algebraic structures and category theory

· Monad transformers

· Lenses

Type systems

Disclaimer: I have no intention to launch quarrels between static and dynamic typing aficionados. Discussing which one is better and why is not at all the objective of this book and I'll let each and every one of you decide what you prefer. If the subject interests you, I can recommend reading http://pchiusano.github.io/2016-09-15/static-vs-dynamic.html, which is a good summary, even if a bit biased in favor of static typing.

That is said, types and typing systems are an important topic in functional programming, even if said types aren't enforced by the language. The types of a function signature are a meta language enabling succinct and effective communication about the purpose of a function.

As we will see, clearly declaring the expected types of the input and output of a function is an important part of its documentation. Not only does it reduce the cognitive burden by allowing you to skip reading the function code, it also allows you to deduce important facts about what is happening and derive free theorems.

The Hindley-Milner type system

Hindley-Milner, also known as Damas-Milner or Damas-Hindley-Milner, from the name of the people whom first theorized it, is a type system. A type system is a set of rules that define what type a variable or parameter can have and how different types interact with each other.

One of the main features of Hindley-Milner is that it allows type inference. This means that you often don't have to explicitly define the type; it can be inferred from other sources such as the context or the types of surrounding elements. To be exact, the type inference is done by an algorithm called Algorithm W and is related to, but not the same as, the Hindley-Milner type system.

It also allows polymorphism; this means that if you have a function returning the length of a list, the type of the elements of the list doesn't need to be known as it doesn't matter for the computation. It is an idea akin to the Generics that you can find in C++ or Java, but not quite the same as it is more powerful.

Most statically typed functional languages, such as Haskell, OCaml, and F#, use Hindley-Milner as their type system, often with extensions to manage some edge cases. Scala is notable for using its own type system.

Besides the theory about type systems, there is a commonly accepted way to describe the input and output parameters of a function and this is what we are interested in here. It is quite different from the type hints you can use with PHP and it is often put in a comment at the top of a function when the language does not use this particular syntax. As of now we will refer to such type annotation as the type signature of a function.

Type signatures

As a first and simple example, we will start with the type signatures of the strtoupper and strlen PHP functions:

// strtoupper :: string -> string

// strlen :: string -> int

It's pretty simple to understand: we start with the function name, followed by the type of the parameter, an arrow, and the type of the return value.

What about functions with multiple arguments? Consider the following:

// implode :: string -> [string] -> string

Why are there multiple arrows? If you think of currying this might help you to get the answer. If we write the same function signature using parentheses, this will probably help you further:

// implode :: string -> ([string] -> string)

Basically, we have a function that takes a string type and returns a new function taking an array of strings and returning a string. The right most type is always the type of the return value. All other types are the various parameters in order. Parentheses are used to denote a function. Let's see how it looks with more parameters:

// number_format :: float -> (int -> (string -> (string -> string)))

Or without parentheses:

// number_format :: float -> int -> string -> string -> string

I don't know what your opinion is, but I personally prefer the latter as it is less noisy and once you get used to it, the parentheses don't bring much information.

If you are familiar with the number_format function, you might have noted that the type signature I proposed contains all parameters, even the optional ones. This is because there is no canonical way to convey this information, because functional languages usually do not allow such parameters. However, Haskell has an Optional data type that is used to emulate this. With this information in mind, arguments with a default value are sometimes displayed like this:

// number_format :: float -> Optional int -> Optional string -> Optional string -> string

This works fairly well and is self-explanatory, until you have a type called the Optional data type. There is also no common way to express what the default value is.

As far as I know, there is no way to convey the information that a function takes a variable number of arguments. Since PHP 7.0 introduced a new syntax for this, I propose we use that for the remainder of this book:

// printf :: string -> ...string -> int

We saw earlier that parentheses are used to express the idea of functions, but that they were usually not used for readability reasons. However, this is not true when using functions as parameters. In this case, we need to retain the information that the function expects or returns another function:

// array_reduce :: [a] -> (b -> a -> b) -> Optional a -> b

// array_map :: (a -> b) -> ...[a] -> [b]

You might be asking yourself, What are those a and b variables? This is the polymorphism feature we were talking about earlier. The array_reduce and array_map functions do not care about what the real types of the elements contained in the array are, they don't need to know that information to perform their job. We could have used mixed function like we did earlier with the printf method, but then we would have lost some useful data.

The a variable is a certain type, and the b variable is another, or it could also be the same. Variables like a and b are sometimes called type variables. What those type signatures are saying is that we have an array of values having a certain type (the type a), a function that takes such a value and returns one having another type (the type b); obviously, the final value is the same as the one of the callback.

The names a and b are a convention, but you are free to use anything you want. In some occasions, using a longer name or some particular letter might help convey more information.

Note

If you have trouble understanding the signature for the array_reduce function, this is perfectly normal. You are not familiar with the syntax yet. Let's try to take the arguments one by one:

· An array containing elements of type a type

· A function, taking a type b (the accumulator), a type a (the current value), and returning a type b (the new accumulator content)

· An optional initial value of the same type as the array elements

· The return value is of type b, the same type as the accumulator

What this signature does not tell us is the exact types of a and b. For all we care, b could be an array itself, a class, a Boolean, really anything. The types a and b can also be of the same type.

You can also have a unique type variable, as is the case for the array_filter function:

// array_filter :: (a -> bool) -> [a] -> [a]

Since the type signature only uses the a type, this means that the elements in the input array and the returned array will have exactly the same type. Since the a type is not a specific type, this type signature also informs us that the array_filter function works for all types, meaning it cannot transform the values. The elements inside of the list can only be rearranged or filtered.

One final feature of type signatures is that you can narrow down the possible types for a given type variable. For example, you can specify that a certain type m should be a child of a given class:

// filterM :: Monad m => (a -> m Bool) -> [a] -> m [a]

We just introduced a new double arrow symbol. You will always find it at the beginning of the type signature, never in the middle of one. It means that what comes before defines some kind of specificity.

In our case, we constraint the m type variable to be a descendant of the Monad class. This allows us to declare that the filterM method first takes a function returning a Boolean value enclosed in a monad as a first argument and that its return value will be enclosed in the same monad.

You can specify multiple constraints if you'd like. If we imagine having two types, the TypeA and the Typeb types, we could have the following type signature:

// some_function :: TypeA a TypeB b => a -> b -> string

What this function does is not clear just by looking at the type signature, but we know that it expects one instance of the TypeA type and one instance of the TypeB type. The return value will be a string, obviously the result of a computation based on the parameters.

In this case, we cannot make the same assumption as for the array_filter method, namely that no transformation will happen, because we have a constraint on the type variables. Our functions may very well know how to operate on our data since they are an instance of a certain type or its children.

I know there are a lot of things to take in, but as the preceding the array_reduce function example proves, type signatures allow us to encode a lot of information in a concise way. They are also more precise than PHP type hints as they, for example, allow us to say that the array_map method can transform from one type to another, whereas the array_filter method will maintain the types in the array.

If you've perused the code of the php-functional library, you might have noticed that the author used such type signatures in the doc blocks of most of the functions. You will also find that some other functional libraries do the same and the habit is also spreading in the JavaScript world for example.

Free theorems

Not only do type signatures give us insight in to what the function does, they also allow us to deduce useful theorems and rules based on the type information. These are called free theorems because they come for free with the type signature. The idea was developed by Philip Walder in the paper Theorems for free! published in 1989.

By using a free theorem, we can affirm the following:

// head :: [a] -> a

// map :: (a -> b) -> [a] -> [b]

head(map(f, $x)) == f(head($x)

This might seem obvious to you using a bit of common sense and knowing what the functions do, but a computer lacks common sense. So, in order to optimize the left hand of our equality to the right hand, our compiler or interpreter must rely on the free theorem to do so.

How can the type signatures prove this theorem? Remember when we said that the type a is a generic type that our functions know nothing about? The corollary is that they cannot modify the values inside the array because such a generic function does not exist. The only function that knows how to transform something is f because it needs to conform to the (a -> b) type signature enforced by map.

Since nor head nor map functions modify the elements, we can deduce that first applying the function and then taking the first element is exactly the same as taking the first element and applying the function. Only the second way is much faster:

// filter :: (a -> Bool) -> [a] -> [a]

map(f, filter(compose(p, f), $x)) === filter(p, map(f, $x))

A bit more complicated, this free theorem says that if your predicate needs a value transformed using the function f and then you apply the f function on the result it is exactly the same as first applying f to all elements and filtering afterward. Again the idea is to optimize for performances by applying f only one time instead of two.

When composing functions together or calling them after one another, try to look at the type signatures to see if you cannot improve your code by deducing some free theorems.

Haskell users even have a free theorem generator at their disposition at http://www-ps.iai.uni-bonn.de/cgi-bin/free-theorems-webui.cgi.

Closing words

Type signatures bring so much to the table that you can find function search engines based on them. Sites such as https://www.haskell.org/hoogle/ and http://scala-search.org/ lets you search for functions based solely on their type signature.

When working with functional techniques, it also often happens that you have a certain structure for your data and you need to transform that to something else. Since most functions are totally generic, it is often complicated coming up for the right keyword to search for what you are looking for. This is also where type signatures and search engines like Hoogle come in handy. Just enter the type structure of your input, the wanted type of the output, and peruse the function list returned by the search engine.

PHP being a dynamically typed language and only having recently introduced scalar typing, useful tools around type signatures obviously don't yet exist. But maybe it is only a matter of time before people will come up with something.

Point-free style

Point-free style, also called tacit programming is a way of writing functions where you don't explicitly define the parameters or points, hence the name. Depending on the language, it is possible to apply this particular style on different levels. How can you have functions without identified arguments? By using function composition or currying.

In fact, we already did some point-free style programming before in this book. Let's use an example from Chapter 4, Composing Function, to illustrate what it is about:

<?php

// traditional

function safe_title(string $s)

{

return strtoupper(htmlspecialchars($s));

}

// point-free

$safe_title = compose('htmlspecialchars', 'strtoupper');

The first part is a traditional function where you declare an input parameter. In the second case, however, you can see no explicit parameter declarations; you rely on the definitions of the composed functions. The second function is said to be in point-free style.

PHP syntax forces us to assign our composed or curryied function to a variable, but there is no such clear separation in some other languages. Here are three examples in Haskell:

-- traditional

sum (x:xs) = x + sum xs

sum [] = 0

-- using foldr

sum xs = foldr (+) 0 xs

-- point-free

sum = foldr (+) 0

As we can see, the structure of the function definition is the same in the three cases. The first one is how you would define the sum method without using folding. The second example acknowledges that we can simply fold on the data, but still keeps the argument explicitly declared. Finally, the last example is point-free as there is no trace at all of the arguments.

Another language where the difference between functions and variables is more tenuous than in PHP is JavaScript. In fact, all functions are variables and since there is no special syntax for variables, there is no distinction between a traditional function and an anonymous one assigned to a variable:

// traditional

function snakeCase(word) {

return word.toLowerCase().replace(/\s+/ig, '_');

};

// point-free

var snakeCase = compose(replace(/\s+/ig, '_'), toLowerCase);

Obviously, this is not valid JavaScript because there is no native compose function and both functions working on strings cannot be called like that so simply. There are, however, multiple libraries allowing you to write such code with ease, such as Ramda, which I highly recommend. The point of the example is just to demonstrate that you cannot distinguish a traditional function and an anonymous function in JavaScript, as is the case in PHP.

There are some benefits to using such a style:

· You usually have a more concise code, which some consider cleaner and easier to read.

· It helps thinking in terms of abstraction. The parameter name word in the JavaScript examples hints that the function works on single words only whereas it can work on any string. This is especially true for more generic functions such as those working on lists, for example.

· It helps developers think in terms of function composition instead of data structures, which often results in better code.

There are, however, also some possible drawbacks:

· Removing explicit arguments from the definition might make things harder to understand; having no parameter name, for example, sometimes removes useful information.

· Long chains of composed functions can lead to losing sight of the data structure and types.

· Code can be more difficult to maintain. When you have an explicit function you can easily add new lines, debugging, and so on. This is made nearly impossible when functions are composed together.

Some opponents to the paradigm sometimes use the term pointless style to describe this technique as a result of those issues.

Reading and using point-free code definitely takes some time getting used to. I have personally no strong opinion about it. I advise you to use the style that suits you best and also, even if you prefer one, there are situations where the other is arguably better so don't hesitate to mix the two.

As a closing word, I would like to remind you that "Parameter order matters, a lot!" as we discussed in Chapter 4, Composing functions. And it is especially true if you want to use a point-free style. If the data you need to work on isn't the last parameter, you won't be able to.

Using const for functions

This technique is not related to functional programming, but rather it is a neat trick in PHP itself. It will, however, probably help you a lot, so here we go.

If you've had a look at the code of the functional-php library, you might have noticed that there are definitions of constants at the top of nearly all functions. Here is a small example:

<?php

const push = 'Widmogrod\Functional\push';

function push(array $array, array $values)

{

// [...]

}

The idea behind this is to allow a simpler usage of functions as parameters. We've seen earlier that the way you pass a function or method as an argument is to use something called a callable, which usually is either a string or an array for methods composed of an object instance and a string for the method to call.

Using a const keyword allows us to have something much more akin to what you can find in languages where functions are not a separate construct from variables:

<?php const increment = 'increment';

function increment(int $i) { return $i + 1; }

// using a 'callable'

array_map('increment' [1, 2, 3, 4]);

// using our const

array_map(increment, [1, 2, 3, 4]);

Exit the awkward quotes around our function name. It really looks like you are passing the function itself, as would be the case in other languages such as Python or JavaScript.

If you are using an IDE it gets even better. You can use the Go to declaration or equivalent function and the file where you defined the const will open on the line where it is defined. If you declared it either just on top or at the bottom of the real function, you will have quick access to its definition.

Some IDE, I am not aware of, might offer the same feature for callable in the form of strings, but it is at least not the case for the one that I am using. Whereas if I press Ctrl + click on the increment function in the second example, it focuses on the const declaration, which is a real time-saver.

When declaring constants like that, you are not limited to shadow functions; it also works with static object methods. You can also use DocBlock annotations to declare that your constant represents a callabletype:

<?php

class A {

public static function static_test() {}

public function test() {}

}

/** @var callable */

const A_static = ['A', 'static_test'];

Sadly, this trick will not work for anonymous functions stored inside a variable or calling methods on object instances. If you try to do so, PHP will gratify you with a resounding Warning: Constants may only evaluate to scalar values or arrays warning.

Although not a silver bullet and accompanied by limitations, this little technique will help you write code that is a bit cleaner and easier to navigate in if you are using an IDE.

Recursion, stack overflows, and trampolines

We first presented recursion as a possible solution to programming problems in Chapter 3, Functional basis in PHP. Some memory complications were hinted at; it is time to investigate those further.

Tail-calls

A call to a function that is the last statement done before returning a value is called a tail-call. Let's have a look at some examples to get a grasp of what it means:

<?php

function simple() {

return strtoupper('Hello!');

}

This is without any doubt a tail-call. The last statement of the function returns the result of the strtoupper function:

<?php

function multiple_branches($name) {

if($name == 'Gilles') {

return strtoupper('Hi friend!');

}

return strtoupper('Greetings');

}

Here, both calls to the strtoupper function are tail-calls. The position inside the function does not matter; what does matter is if there are any kinds of operations made after the call to the function is made. In our case, if the argument value is Gilles the last thing the function will do is call the strtoupper function, making it a tail-call:

<?php

function not_a_tail_call($name) {

return strtoupper('Hello') + ' ' + $name;

}

function also_not_a_tail_call($a) {

return 2 * max($a, 10);

}

None of those two functions have a tail-call. In both cases, the return value of the call is used to compute a final value before the function returns. The order of operation does not matter, the interpreter needs to first get the value of the strtoupper and the max functions in order to compute the result.

As we just saw, spotting a tail-call is not always easy. You can have one in the first few lines of a very long function, and being on the last line is not a sufficient criterion.

If the tail-call is made to the function itself, or in other words it is a recursive call, the term of tail recursion is often used.

Tail-call elimination

Why bother you are maybe asking yourself? Because compilers and parsers can perform something called tail-call elimination or sometimes Tail-Call Optimization (TCO) in short.

Instead of performing a new function call and suffering from all the related overhead, the program simply jumps to the next function without adding more information to the stack and wasting precious time passing parameters around.

This particularly matters in cases of tail recursion as it allows the stack to stay flat, not using any more memory than the first function call.

It sounds great, but as with most advanced compilation techniques, the PHP engine does not implement tail-call elimination. However, other languages do:

· Any ECMAScript 6 compliant JavaScript engine

· Python after installing the tco module

· Scala, you even have an annotation (@tailrec) to trigger a compiler error if your method is not tail recursive

· Elixir

· Lua

· Perl

· Haskell

There is also ongoing proposition and work to perform tail-call elimination at the Java Virtual Machine (JVM) level, but no concrete implementation so far has landed in Java 8, as this is not considered a priority feature.

Tail recursive functions are usually simpler to work with especially with regards to folding; as we saw in this section, techniques exist to alleviate the growing stack issue at the cost of some processing power.

From recursion to tail recursion

Now that we have a clearer understanding of what we are talking about, let's learn how we can transform a recursive function in to a tail recursive one if that is not already the case.

We declined to use the computation of a factorial as a good recursion example in Chapter 3, Functional Basis in PHP, but as it is probably the simplest recursive function that could be written, we will start with that example:

<?php

function fact($n)

{

return $n <= 1 ? 1 : $n * fact($n - 1);

}

Is this function tail-recursive? No, we multiply a value with the result of our recursive call to fact method. Let's see the various steps in more detail:

fact(4)

4 * fact(3)

4 * 3 * fact(2)

4 * 3 * 2 * fact(1)

4 * 3 * 2 * 1

-> 24

Any idea how we can transform this to a tail-recursive function? Take some time to play around with some ideas before reading further. If you need a hint, think about how functions used for folding operate.

The usual answer when it comes to tail recursion revolves around using accumulators:

<?php

function fact2($n)

{

$fact = function($n, $acc) use (&$fact) {

return $n <= 1 ? $acc : $fact($n - 1, $n * $acc);

};

return $fact($n, 1);

}

Here we wrote it using an inner helper to hide the implementation detail of the accumulator, but we could just have written it using a unique function:

<?php

function fact3($n, $acc = 1)

{

return $n <= 1 ? $acc : fact3($n - 1, $n * $acc);

}

Let's have a look at the steps once again:

fact(4)

fact(3, 4 * 1)

fact(2, 3 * 4)

fact(1, 2 * 12) -> 24

Great, no more pending operation after each recursive call; we truly have a tail recursive function. Our fact function was pretty simple. What about the Tower of Hanoi solver we wrote earlier? Here it is so you don't have to search for it:

<?php

function hanoi(int $disc, string $source, string $destination, string $via)

{

if ($disc === 1) {

echo("Move a disc from the $source rod to the $destination rod\n");

} else {

// step 1 : move all discs but the first to the "via" rod

hanoi($disc - 1, $source, $via, $destination);

// step 2 : move the last disc to the destination

hanoi(1, $source, $destination, $via);

// step 3 : move the discs from the "via" rod to the destination

hanoi($disc - 1, $via, $destination, $source);

}

}

Like for our factorial computation, take some time to try transforming the function into a tail recursive one yourself:

<?php

use Functional as f;

class Position

{

public $disc;

public $src;

public $dst;

public $via;

public function __construct($n, $s, $d, $v)

{

$this->disc = $n;

$this->src = $s;

$this->dst = $d;

$this->via = $v;

}

}

function hanoi(Position $pos, array $moves = [])

{

if ($pos->disc === 1) {

echo("Move a disc from the {$pos->src} rod to the {$pos- >dst} rod\n");

if(count($moves) > 0) {

hanoi(f\head($moves), f\tail($moves));

}

} else {

$pos1 = new Position($pos->disc - 1, $pos->src, $pos->via, $pos->dst);

$pos2 = new Position(1, $pos->src, $pos->dst, $pos->via);

$pos3 = new Position($pos->disc - 1, $pos->via, $pos->dst, $pos->src);

hanoi($pos1, array_merge([$pos2, $pos3], $moves));

}

}

hanoi(new Position(3, 'left', 'right', 'middle'));

As you can see, the solution is pretty similar, even when there are multiple recursive calls inside the function, we can still use an accumulator. The trick is to use an array instead of storing only the current value. In most cases, the accumulator will be a stack, meaning you can only add elements at the beginning and remove them from the beginning. A stack is said to be a Last In, First Out (LIFO) structure.

If you don't quite get why this refactoring works, I encourage you to write down the steps for both variants as we did for the fact method so that you can get a better feel for the involved mechanics.

In fact, taking the time to write down the steps of a recursive algorithm is often a great way to clearly understand what is happening and how it can be refactored to be tail recursive or fix a bug if there is one.

Stack overflows

The fact we used a stack-like data structure for our tail recursive Hanoi solver is no coincidence. When you call functions, all needed information is also stored in a stack-like structure in memory. In the case of recursion, it will look something like this:

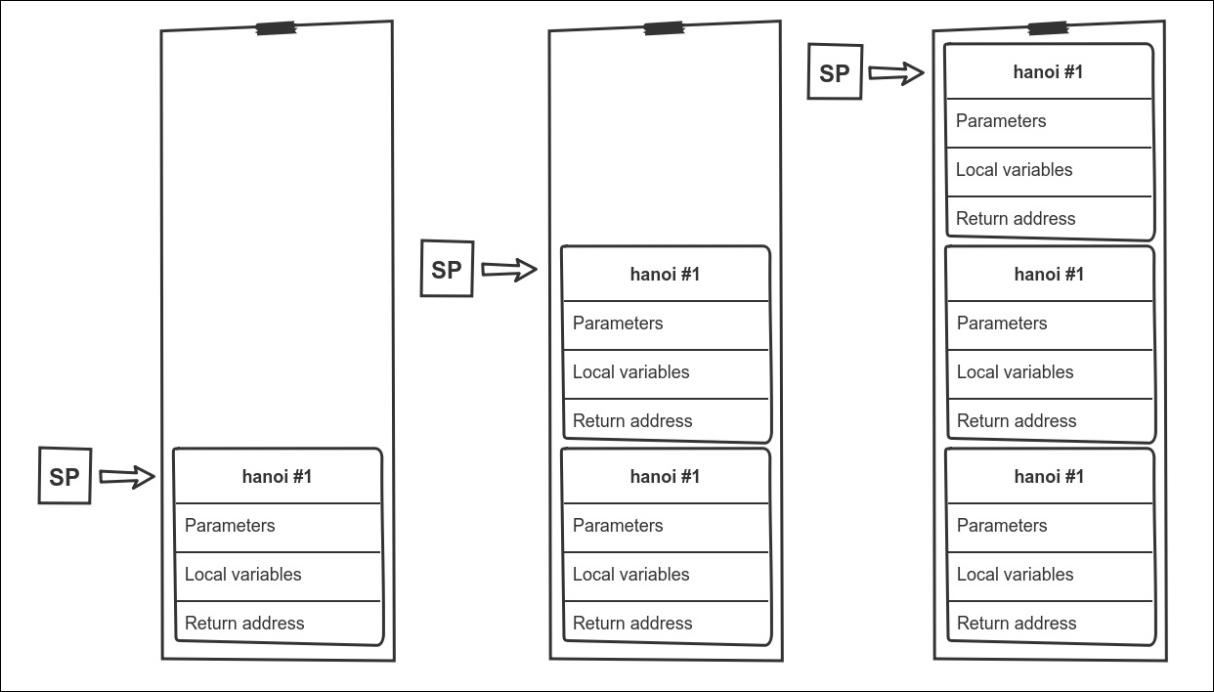
This stack has a limited size. It is bound through the memory_limit configuration option and even if you remove the limit you won't be able to go beyond the available memory in the system. Also, extensions such as Xdebug introduce specific mechanisms to avoid having too many nested recursive calls. For example, you have a configuration option named xdebug.max_nesting_level, which defaults to 256, meaning that if you call a function recursively more than that, an error will be raised.

If PHP performed tail-call optimization, instead of stacking the pieces of function information on top of one another, the call would replace the current information in the stack. It is safe to do so because the final result of a tail-call does not depend on any variable local to the function.

Since PHP does not perform this kind of optimization, we need to find another solution to avoid blowing up the stack. If you encounter this issue and you are willing to sacrifice some processing power to limit the memory usage, you can use trampolines.

Trampolines

The only way we can avoid stack growth is to return a value instead of calling a new function. This value can hold information needed to perform a new function call, which will continue the computation. This also means we need some cooperation from the caller of the function.

This helpful caller is the trampoline and here is how it works:

· The trampoline calls our function f

· Instead of making a recursive call, the f function returns the next call encapsulated inside a data structure with all the arguments

· The trampoline extracts the information and performs a new call to the f function

· Repeat the two last steps until the f function returns a real value

· The trampoline receives a value and it returns to the real caller

These steps should also explain where the name of the technique comes from, each time the function returns to the trampoline, it bounced back with the next arguments.

To perform these steps, we need a data structure holding both the function to call in the form of a callable and the arguments. We also need a helper function that will continue calling whatever is stored inside the data structure until it gets a real value:

<?php

class Bounce

{

private $f;

private $args;

public function __construct(callable $f, ...$args)

{

$this->f = $f;

$this->args = $args;

}

public function __invoke()

{

return call_user_func_array($this->f, $this->args);

}

}

function trampoline(callable $f, ...$args) {

$return = call_user_func_array($f, $args);

while($return instanceof Bounce) {

$return = $return();

}

return $return;

}

Simple enough, let's try it:

<?php

function fact4($n, $acc = 1)

{

return $n <= 1 ? $acc : new Bounce('fact4', $n - 1, $n * $acc);

}

echo trampoline('fact4', 5)

// 120

Works fine, and the code isn't that much harder to read. There is, however, a performance hit when using trampolines. In the case of computing a factorial, the trampoline version is roughly five times slower on my laptop. This is explained by the fact that the interpreter has to do to a lot more work than simply calling the next function.

Knowing this, if your recursive algorithm has a bound depth and you are certain that you are at no risk of a stack overflow, I recommend you to just perform a traditional recursion instead of using a trampoline. In the case of doubt, however, don't hesitate, as a stack overflow error can be critical on a production system.

Multi-step recursion

Trampolines even have their usefulness for languages performing incomplete tail-call elimination. For example, Scala is unable to perform such an optimization when there are two functions involved. Instead of trying to explain what I am talking about, let's see some code:

<?php

function even($n) {

return $n == 0 ? 'yes' : odd($n - 1);

}

function odd($n) {

return $n == 0 ? 'no' : even($n - 1);

}

echo even(10);

// yes

echo odd(10);

// no

This might not be the best and most efficient way to determine if a number is odd or even, but it has the merits to simply illustrate what I am talking about. Both functions are calling themselves until the number reaches 0, at which time we can decide if it is odd or even.

Depending on whom you ask, this might or might not be recursion. It respects the academic definition we gave in Chapter 3, Functional basis in PHP:

Recursion is the idea to divide a problem into smaller instance of the same problem.

However, the function does not call itself, so this is why some people will try to define what is happening here with other terms. In the end, what we call that does not matter; we will have a stack overflow on a big number.

As I was saying, Scala performs an incomplete tail-call elimination as it will only do so if the function calls itself as its last instruction, leading to a stack overflow error as PHP will do. This is why trampolines are used even in some functional languages.

As a real simple exercise, I invite you to rewrite both odd and even functions using trampolines.

The trampoline library

If you want to use trampolines in your own project, I invite you to install the following library using the composer command, as it offers some helpers compared to our crude implementation:

composer require functional-php/trampoline

The data structure and features have been conflated inside the same class called Trampoline. Helpers are available in the form of functions:

· The bounce helper is used to create a new function wrapper. It takes a callable and the arguments.

· The trampoline helper runs a callable until completion. It takes a callable and its arguments. The method also accepts a Trampoline class instance as parameter, but in this case, the arguments will be ignored as they are already wrapped inside the instance.

The class also defines __callStatic, which allows us to call any function from the global namespace on the class directly.

Here are some examples taken from the documentation:

<?php

use FunctionalPHP\Trampoline as t;

use FunctionalPHP\Trampoline\Trampoline;

function factorial($n, $acc = 1) {

return $n <= 1 ? $acc : t\bounce('factorial', $n - 1, $n * $acc);

};

echo t\trampoline('factorial', 5);

// 120

echo Trampoline::factorial(5);

// 120

echo Trampoline::strtoupper('Hello!');

// HELLO!

Another helper returning a callable with all the trampoline capabilities turned on also exists, and it is called the trampoline_wrapper helper:

<?php

$fact = t\trampoline_wrapper('factorial');

echo $fact(5);

// 120

As an exercise, you can try to transform our Tower of Hanoi solver to use the trampoline library and see if you get the same results.

Alternative method

Instead of using trampolines to solve stack overflow issues, it is also possible to use a queue to store all the arguments of the successive recursive calls to our function.

The original function needs to be wrapped inside a helper that will hold the queue and call the original function with all the arguments in a chain. In order for this to work, the recursive call needs to be made to the wrapper instead:

· Create the wrapper function

· First call to the wrapper with the first arguments

· The wrapper enters a loop that calls the original function while there are arguments in the queue

· Each subsequent call to the wrapper adds arguments to the queue instead of calling the original function

· Once the loop is finished (that is, all recursive calls have been made), the wrapper returns the final value

For it to work, it is really important that the original function calls the wrapper when making a recursive call. This can be done either by using an anonymous function that you use inside of your wrapped function or using the bindTo method on the Closure class, as we discussed in Chapter 1, Functions as First Class Citizen in PHP.

The trampoline library has an implementation of this method using the later technique. Here is how you can use it instead of a trampoline:

<?php

use FunctionalPHP\Trampoline as t;

$fact = T\pool(function($n, $acc = 1) {

return $n <= 1 ? $acc : $this($n - 1, $n * $acc);

});

echo $fact(5);

// 120

The wrapper created by the pool function binds an instance of the Pool class to $this. This class has an __invoke method, which is callable inside our original function. Doing so will call the wrapper again, but this time it will add the arguments to the queue instead of calling the original function.

From a performance standpoint there is no difference between this method and the trampoline, both should perform roughly the same way. However, you cannot do multi-step recursion using a pool function as the wrapper is only aware of one function.

Also, until PHP 7.1 is released, this method is also limited to anonymous functions due to some difficulties transforming a callable in the form of a string to an instance of Closure class in order to bind the class to it. PHP 7.1 will introduce a new fromCallable method on Closure, which allows lifting this limitation.

Closing words

As a final note, both the trampoline and queue techniques we've seen to solve the stack overflow problem will only work if the recursive function is tail recursive. This is a mandatory condition as the function needs to fully return in order for the helper to continue the computation.

Also, as the trampoline method has fewer drawbacks, I would recommend this instead of the pool function implementation.

Pattern matching

Pattern matching is a really powerful feature of most functional languages. It is embedded inside the language at various levels. In Scala, for example, you can use it as a beefed up switch statement, and in Haskell it is an integral part of function definition.

Pattern matching is the process of checking a series of tokens against a pattern. It is different from pattern recognition as the match needs to be exact. The process does not only match as a switch statement does, it also assigns the value as with the list construct in PHP, a process called destructuring assignment.

It is not to be confused with regular expressions. Regular expressions can only operate on the content of strings, where as pattern matching can also operate on the structure of the data. For example, you can match on the number of elements of an array.

Let's see some examples in Haskell so we get a feel for it. The simplest form of pattern matching is to match to a specific value:

fact :: (Integral a) => a -> a

fact 0 = 1

fact n = n * fact (n-1)

This is how you could define fact function in Haskell:

· The first line is the type signature, which should remind you something we saw earlier in this chapter; Integral is a type that is a bit less restrictive than the Integer type without entering in the details.

· The second line is the function body if the argument has the value 0.

· The last line is executed in all other cases. The value is assigned to the n variable.

If you are not interested in some values, you can ignore them using the _ (underscore) wildcard pattern. For example, you can easily define functions to get the first, second, and third value from a tuple:

first :: (a, b, c) -> a

first (x, _, _) = x

second :: (a, b, c) -> b

second (_, y, _) = y

third :: (a, b, c) -> c

third (_, _, z) = z

Note

A tuple is a data structure with a fixed number of elements, as opposed to an array, which can change size. The (1, 2) and ('a', 'b') tuples are both of size two. The advantage of using tuples over arrays when there is a known number of elements lies in enforcing the correct size and performance.

Languages such as Haskell, Scala, Python, C#, and Ruby have a tuple type inside their core or standard library.

You can destruct the values into more than just one variable. In order to understand the following examples, you need to know that ":" (colon) is the operator to prepend an element to a list. This means that the 1:[2, 3] tuple will return the list [1, 2, 3]:

head :: [a] -> a

head [] = error "empty list"

head (x:_) = x

tail :: [a] -> [a]

tail [] = error "empty list"

tail (_:xs) = xs

sum :: (Num a) => [a] -> a

sum [] = 0

sum (x:xs) = x + sum xs

The head and tail variable have the same structure, if the list is empty, they return an error. Otherwise either return x, which is the element at the beginning of the list, or xs, which is the rest of the list. The sumvariable is also similar, but instead it uses both x and xs. By the way, Haskell would disallow defining those two functions as they already exist:

firstThree :: [a] -> (a, a, a)

firstThree (x:y:z:_) = (x, y, z)

firstThree _ = error "need at least 3 elements"

The firstThree variable is a bit different. It first tries to match a list with at least three elements, x, y, and z. In this case the _ pattern can be the empty list or not, the pattern will match. If it doesn't succeed, we know that the list has fewer than three elements and we display an error.

You can also use pattern matching as a beefed up switch statement. For example, this would also be a valid implementation of head:

head :: [a] -> a

head xs = case xs of [] -> error "empty lists"

(x:_) -> x

If you want to use both the destructuring data and the whole value, you can use as patterns:

firstLetter :: String -> String

firstLetter "" = error "empty string"

firstLetter all@(x:_) = "The first letter of " ++ all ++ " is " ++ [x]

Finally, you can also use constructors when doing pattern matching. Here is a small example using the Maybe type:

increment :: Maybe Int -> Int

increment Nothing = 0

increment (Just x) = x + 1

Yes, you can get the value inside a monad just like that, using destructuring.

You can have overlapping patterns; Haskell will use the first one that matches. And if it isn't able to find a matching one, it will raise an error saying Non-exhaustive patterns in function XXX.

We could demonstrate roughly the same kind of features for Scala, Clojure, or other functional languages, but as this was just an example to understand what pattern matching is about, I would rather advise you to read tutorials on the subject if the topic is of interest to you. Instead, we will try to emulate part of this powerful feature in PHP.

Pattern matching in PHP

Obviously, we will never be able to declare functions the same way we just saw in Haskell as this needs to be implemented at the heart of the language. However, a library tries to emulate pattern matching as best as possible to create a more powerful version of the switch statement with automatic destructuring.

You can install the library using composer command in Composer:

composer require functional-php/pattern-matching

In order to be as expressive as possible to what is available in Haskell, it uses a string to hold the patterns. Here is a table defining the various possible syntaxes:

At the time of writing, there is no support for automatic destructuring of values inside a Monad, or other types, nor the possibility to constrain the type of a particular item we match upon. There are, however, opened issues concerning those two features https://github.com/functional-php/pattern-matching/issues.

As there is no possibility to use named parameters in PHP, the parameters will be passed in the order they are defined in the pattern and there will be no matching done based on their names. This makes using the library a bit tedious at times.

Better switch statements

The library can be used to perform more advanced switch statements by also using the structure and extracting data instead of just equating on the value. Since the functions are curryied, you can also map them over arrays contrary to a switch statement:

<?php

use FunctionalPHP\PatternMatching as m;

$users = [

[ 'name' => 'Gilles', 'status' => 10 ],

[ 'name' => 'John', 'status' => 5 ],

[ 'name' => 'Ben', 'status' => 0],

[],

'some random string'

];

$statuses = array_map(m\match([

'[_, 10]' => function() { return 'admin'; },

'[_, 5]' => 'moderator',

'[_, _]' => 'normal user',

'_' => 'n/a',

]), $users);

print_r($statuses);

// Array (

// [0] => Gilles - admin

// [1] => John - moderator

// [2] => Ben - normal user

// [3] => incomplete array

// [4] => n/a

// )

The first pattern in the list that matches is used. As you can see, the callback can either be a function as for the first pattern or a constant that will be returned. Obviously in this case all of them could have been constants, but this was for the sake of the example.

One of the benefits over a traditional switch statement as you can see is that you are not constrained by the structure of the data to perform your match. In our case, we created a catch-all pattern at the end for erroneous data. Using a switch statement you would have needed to either filter out the data or perform some kind of other data normalization.

This example could also use the destructuring to avoid having three patterns with constants (and while we are at it, we will also use the name from the array):

<?php

$group_names = [ 10 => 'admin', 5 => 'moderator' ];

$statuses = array_map(m\match([

'[name, s]' => function($name, $s) use($group_names) {

return $name.

' - '.

(isset($group_names[$s]) ? $group_names[$s] : 'normal user');

},

'[]' => 'incomplete array',

'_' => 'n/a',]), $users);

print_r($statuses);

// Array (

// [0] => admin

// [1] => moderator

// [2] => normal user

// [3] => incomplete array

// [4] => n/a

// )

You could also write patterns that match a wide variety of different structures and use that to determine what to do based on it. It could also be used to perform some kind of basic routing inside a web application:

$url = 'user/10';

function homepage() { return "Hello!"; }

function user($id) { return "user $id"; }

function add_user_to_group($group, $user) { return "done."; }

$result = m\match([

'["user", id]' => 'user',

'["group", group, "add", user]' => 'add_user_to_group',

'_' => 'homepage',

], explode('/', $url));

echo $result;

// user 10

Obviously a more specialized library would do a better job at routing with a better performances, but keeping the possibility in mind can come in handy and it demonstrates the versatility of pattern matching.

Other usages

If you are just interested in destructuring your data, the extract function has you covered:

<?php

$data = [

'Gilles',

['Some street', '12345', 'Some City'],

'xxx xx-xx-xx',

['admin', 'staff'],

['username' => 'gilles', 'password' => '******'],

[12, 34, 53, 65, 78, 95, 102]

];

print_r(m\extract('[name, _, phone, groups, [username, _], posts@(first:_)]', $data));

// Array (

// [name] => Gilles

// [phone] => xxx xx-xx-xx

// [groups] => Array ( [0] => admin [1] => staff )

// [username] => gilles

// [posts] => Array ( ... )

// [first] => 12

//)

Once you've extracted your data, you can use the extract function from PHP to import the variables into the current scope.

If you want to create functions a bit like we saw in the Haskell examples, there is the func helper method. Obviously the syntax is not as good, but it can come in handy:

<?php

$fact = m\func([

'0' => 1,

'n' => function($n) use(&$fact) {

return $n * $fact($n - 1);

}

]);

Beware that function creation is still in the beta stage at the time of writing. There are some issues, so the API might change in the future. If you encounter any issues, consult the documentation.

Type classes

Another idea you will encounter often when reading papers, posts, or tutorials about functional programming is the type class, especially if the content is about Haskell.

The concept of a type class was first introduced in Haskell as a way of implementing operators that could be easily overloaded for various types. Since then a lot of other uses have been discovered for them. For example, in Haskell, functors, applicatives, and monads are all type classes.

Haskell needed type classes mostly because it is not an object-oriented language. The overloading of operators was, for example, solved differently in Scala. You can write equivalents to type classes in Scala, but it is more of a pattern than a language feature. In other languages, there are various ways to emulate some features of Haskell type classes using traits and interfaces.

In Haskell, a type class is a set of functions that need to be implemented on a given type. One of the simplest examples is the Eq type class:

class Eq a where

(==) :: a -> a -> Bool

(/=) :: a -> a -> Bool

Any type implementing, the dedicated term is derives, the Eq class must also have corresponding implementation for the == and /= operators, otherwise you will have a compilation error. This is exactly like an interface for a class, but for a type instead. This means you can enforce the creation of operators, like in our case, not just methods.

You can create instances for your type class pretty easily; here is one for the Maybe instance:

instance (Eq m) => Eq (Maybe m) where

Just x == Just y = x == y

Nothing == Nothing = True

_ == _ = False

It should be fairly easy to understand. The two Just values on the left are equal if their inner content is, the Nothing value is equal to itself, anything else is different. Defining these Eq instances allows you to check for the equality of two monads anywhere in your Haskell code. The instance definition in itself just enforces that the type m variable stored inside the monad also implements the Eq type class.

As you can see, the functions from the type class are not implemented inside the type. It is done as a separate instance. This allows you to declare this instance anywhere in your code.

You can even have multiple instances for the same type class for any given type and import the one you need. Imagine, for example, having two monoid instances for integers, one for the product and the other for the sum. This is, however, discouraged as it causes conflicts when both instances are imported:

Prelude> Just 2 == Just 2

True

Prelude> Just 2 == Just 3

False

Prelude> Just 2 == Nothing

False

Note

Prelude> is the prompt in the Haskell REPL on which you can simply run Haskell code like you do when running PHP on the CLI with the -a parameter.

We might think that type classes are just interfaces, or rather traits as they can also contain implementation. But if we take a closer look at both our type class and its implementation for monads, there are at least three shortcomings that anything we could do in PHP, at least while being reasonable, will have.

To demonstrate this, let's imagine we created a PHP interface called Comparable:

<?php

interface Comparable

{

/**

* @param Comparable $a the object to compare with

* @return int

* 0 if both object are equal

* 1 is $a is smaller

* -1 otherwise

*/

public function compare(Comparable $a): int;

}

Setting aside the fact that PHP does not allow for operator overloading like we demonstrated with the == symbol in Haskell, try thinking of the three features that a Haskell type class allows that are near to impossible to emulate in PHP.

Two of them are about enforcing the correct type. Haskell will do checks for us automatically, but in PHP we will have to write code to check if our values are of the right type. The third issue is related to extensibility. Think, for example, of classes declared in an external library that you want to compare.

The first issue is related to the fact that the compare function expects a value of the same type as the interface, meaning if you have two unrelated classes, A and B, both implementing the Comparable interface, you could compare an instance of the class A with an instance of the B class without any error from PHP. Obviously this is wrong and this forces you to first check if both values are of the same type before comparing them.

Things get even trickier when you have a class hierarchy as you don't really know what type to test for. Haskell, however, will automatically get the first common type both values share and use the related comparator.

The second issue is a bit more complicated to find out. If we implement the Comparable interface on any kind of container, we will need to check when the comparison is run that the contained values are also comparable. In Haskell, the type signature (Eq m) => Eq (Maybe m) already takes care of that for us and an error will be raised automatically if you try to compare two monads that hold non-comparable values.

The Haskell type system also enforces that the values inside the monad are of the same type, which is an issue related to the first problem we spotted previously.

Finally, the third and probably biggest issue is about the possibility to implement the Comparable interface on a class from an external library or the core of PHP. Since Haskell type class instances are outside of the class itself, you can add one for anything at anytime, be it for an existing type class or a new one you just created.

You can create adapters or wrapping classes around those objects, but then you will have to perform some kind of boxing/unboxing dance to pass the right type to the various methods using your objects, which is far from a pleasant experience.

Scala being an object-oriented language without core support for type classes, the extensibility issue is solved cleverly by using a feature of the language called implicit conversion. Broadly, the idea is that you define a conversion from type A to type B and when the compiler finds a method expecting an instance of the B class, but you passed an instance of the A class, it will look for this conversion and apply it if available.

This way, you can create the adapters or wrappers we proposed using before, but instead of having to perform the transformation manually, the Scala compilers take care of it for you, making the process completely transparent.

As a closing note, since we spoke about comparing objects and redefining operators, there are currently two RFCs proposed for PHP about these two topics:

· https://wiki.php.net/rfc/operator-overloading

· https://wiki.php.net/rfc/comparable

There is, however, no RFC in sight concerning type classes or implicit type casting like we saw exists in Scala.

Algebraic structures and category theory

Until now we have avoided talking too much about mathematics. This section will try to do so in a light way as most functional concepts have roots in mathematics and a lot of abstractions we already discussed are ideas taken from the field of category theory. The content in this section will probably help you to gain a better understanding of the content of this book, but there is no need to understand them perfectly to use functional programming.

Throughout this section, mathematical terms will be defined when encountered. It is not that important that you get all the nuances, it is just to give you a broad idea of what we are talking about.

The root of functional programming is the lambda calculus, or λ-calculus. It is a Turing complete formal system in mathematical logic to express computation. The term lambda to refer to closure and anonymous functions comes from this. Any code you write can be transformed to lambda calculus.

Note

A language or system is said to be Turing-complete when it can be used to simulate a Turing machine. A synonym is computationally universal. All major programming languages are Turing-complete, meaning that anything you can write in C, Java, PHP, Haskell, JavaScript, and so on, can be also written in any of the others. A formal system is composed of the following elements:

· A finite set of symbols or keywords

· A grammar defining a valid syntax

· A set of axioms, or founding rules

· A set of inference rules to derive other rules from the axioms

An algebraic structure is a set with one or more operations defined on it and a list of axioms, or laws. All abstractions we studied in the previous chapters are algebraic structures: monoids, functors, applicatives, and monads. This is important, because, when a new problem is shown to follow the same rules as an existing set, anything that was previously theorized can be reused.

Note

A set is a fundamental concept in mathematics. It is a collection of distinct objects. You can decide to group anything together and call it a set, for example, the numbers 5, 23, and 42 can form a set {5, 23, 42}. Sets can be defined explicitly as we just did, or using a rule, for example, all positive integers.

Category theory is the field that studies the relationship between two or more mathematical structures. It formalizes them in terms of a collection of objects and arrows, or morphisms. A morphism transforms one object or one category to another. A category has two properties:

· The ability to compose morphisms associatively

· An identity morphism going from one object or category to itself

Sets are one of the multiple possible categories that respect these two properties. The idea of category, objects, and morphisms can be highly abstract. For example, you can consider types, functions, functors, or monoids as categories. They can be finite or infinite and hold a variety objects as long as the two properties are respected.

If you are interested in this subject and want to learn more about the mathematical aspect of it, I can recommend the book Cakes, Custard and Category Theory: Easy Recipes for Understanding Complex Mathswritten by Eugenia Cheng. It is really accessible, no prior mathematical knowledge is required, and actually fun to read.

The whole idea of pure functions and referential transparency comes from the lambda calculus. Type systems, and especially Hindley-Milner, are deeply ingrained in formal logic and category theory. The concept of morphism is so close to the one of function and the fact that composition is at the center of category theory results in the fact that most advances made in the last couple of years on functional languages being in one way or another linked to this mathematical field.

From mathematics to computer science

As we just saw, category theory is an important cornerstone in the functional world. You don't have to know about it to code functionally, but it definitely helps you understand the underlying concepts and reason about the most abstract stuff. Also, a lot of the terms used in papers about functional programming or even libraries are taken directly from category theory. So, if you develop a good instinct about it, it will usually be a lot easier to understand what you are reading.

A category is in fact a pretty simple concept. It is only some objects with arrows that go between them. If you are able to represent something graphically using those ideas, it will most probably be correct and it will greatly help you to understand what is happening. For example, if we decide to represent function composition we will end up with something like this:

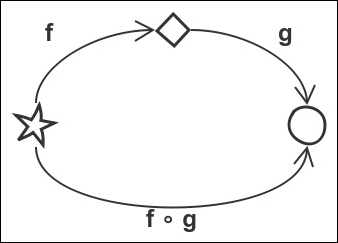
In the diagram, it doesn't really matter if our three shapes are whole categories or objects in a given category. What is, however, immediately clear is that if we have two morphisms, f and g, the result is the same if we apply them sequentially or if we apply the composed version. The function can work on the same types, for example, we transform from one shape to another, or the triangle represents the strings, the diamond represents chars, and the circles represent integers. It makes no difference.

Another example would be the homomorphism law for applicative; pure(f)->apply($x) == pure(f($x)). If we consider the pure function to be a morphism from one category to the category that represents the possible objects for the applicative, we can visualize the law as follows:

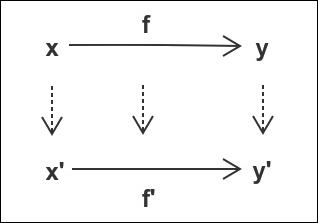
The dotted arrow is the pure function, which is used to move x, f, and y over the applicative category. It becomes fairly self-evident that the law is sound when we see it like that. What do you think? By the way, both those diagrams are called commutative diagrams. In a commutative diagram, each path with the same start and endpoints are equivalent when using composition between the arrows.

Also, you could consider that each type is a category and that a morphism is a function. You can imagine functions as morphisms going from an object in a category to an object in the same category or a different one. You can represent the type and class hierarchy by smaller categories inside bigger ones. For example, integers and floats would be two categories inside the numeric category and they would overlap on some numbers.

This might not be the most academically sound way to describe both types and functions and category theory, but it's an easy one to grasp. It makes it easier to conceptualize abstract concepts such as functors or monads in parallel with what we are accustomed to.

You can visualize more traditional functions operating on values themselves. For example, the strtoupper function is a morphism from an object in the string category to another object in the same category, whereas the count method is a morphism from an object in the array category to an object in the integer category. So these are arrows from an object to another object.

If we step back from our basic types as we did in the second diagram, we can imagine functions working on types themselves. For example, the pure function of a monad takes a certain category, be it a type or a function, and lifts it to a new category in which all objects are now wrapped inside the context of the monad.

The idea is interesting, because any arrows that you had before can also be lifted and will continue to have the same results inside their new context, as proved by the homomorphism law we just visualized.

This means that, if you have trouble understanding what is happening when you use a monad, or any abstraction really, just draw the operations on a sheet of paper using categories, objects, and arrows and you can then boil everything down to its essence either by removing or adding context.

Important mathematical terms

There are some mathematical terms that you might encounter when reading about functional programming. They are used because they allow us to quickly convey what the topic is about and what properties can be expected from the structure currently described.

One such term we already learned about is the monoid. One mathematical definition you can find about it is A monoid is a set that is closed under an associative binary operation and possess an identity element. At this point you should be able to understand this definition; however, here is a quick rundown for the string concatenation monoid:

· The set is all possible string values

· The binary operation is the string concatenation operator, .

· The identity element is the empty string, ''

The idea of a set being closed under an operation indicates that the given operation result is also part of the set. For example, performing an addition of two integers will always result in an integer.

Here is a quick glossary of various mathematical terms that you might encounter in your readings.

· Associative: An operation is associative if the order of operation does not matter; examples are addition, and product is a + (b + c) === (a + b) + c.

· Commutative: An operation is commutative if you can change the order of the operands. Most associative operations are also commutative as a + b === b + a`. An example of an associative operation that isn't commutative is function composition as f (g h) === (f g) h but f g != g f.

· Distributive: Two operations are distributive if a * (b + c) == (a * b) + (a * c). In this case, multiplication is "distributive over" addition. In the example, * and + can be replaced by any binary operation.

· Semigroup: A set closed under an associative operation.

· Monoid: A semigroup with an identity element.

· Group: A monoid with inverse elements. The inverse is a value you can add to another element to get the identity. For example, 10 + -10 = 0, -10 is the inverse of 10 in the integer addition group.

· Abelian group: A group where the operation is commutative.

· Ring: An abelian group with a second monoidal operation, which is distributive over the first one. For example, integers are a ring where addition is the first operation and multiplication is the second.

· Semiring: A ring where the abelian group is replaced by a commutative monoid (that is, the inverse element does not exist).

· Comonad, cofunctor, coXXX: The dual category to monad, functor, or anything. Another word for dual would be opposite. If a monad is a way to put something in a context, its comonad would be the way to get it out from it. This is a really vague definition without explaining the use, which would require a chapter in itself.

Fantasy Land

Now that we've got the theory out of the way, I want to present you the JavaScript project that describes interfaces for common algebraic structures named Fantasy Landat https://github.com/fantasyland/fantasy-land.

It has been widely adopted by the community and more and more projects each day implement the proposed interface for a better interoperability between various implementations of those algebraic structures. Under the Fantasy Land namespace itself you can find implementations of the various monads we already discovered before and many other more advanced functional constructs. Notably, there is also the Bilby library (http://bilby.brianmckenna.org/), which tries to be as close as possible to the Haskell philosophy.

Why am I talking about a JavaScript library? Because the php-functional library has kind of ported the Fantasy Land specification to PHP https://github.com/widmogrod/php-functional/tree/master/src/FantasyLand.

I would like nothing better than other projects using those as a base for their own implementation of functional code as it would bolster functional programming in PHP by providing developers with a bigger set of possible features they can use.

At the time of writing, there are discussions to separate the Fantasy Land port from the rest of the library so that it can be used without also depending on everything else. I hope by the time you read this, undertaking has been completed and I urge you to use this set of common interfaces.

Monad transformers

We saw that monads are already a pretty powerful idea if you take each of them separately. What if I told that you can compose monads together to benefit from the features of multiples of them at the same time? For example, a Maybe interface and a Writer monad that could inform you why the operation returned no result.

This is exactly what monad transformers are about. A monad transformer is in every respect similar to the monad that it exemplifies, except that it is not a standalone entity, instead it modifies the behavior of another monad. In a way, we can imagine this as adding a new monadic layer in top of some other monad. Of course, you can stack multiple layers on top of one another.

In Haskell, most existing monads have a corresponding transformer. Usually, they have the same name with a T suffixed: StateT, ReaderT, WriterT. If you were to apply a transformer to the identity monad, the result will have the exact same feature as the equivalent monad as the identity monad is just a simple container.

In order for this to work correctly, the State, Reader, Writer, and other Haskell monads are in fact type classes with two instances; one is the transformer and the other is the traditional monad.

We will end our foray here as there are no implementations of this concept I am aware of in PHP; it would be sufficiently difficult to try doing it ourselves and it would require at least one full chapter.

At least you've heard about the idea and who knows, maybe someone will create a library adding monad transformers to PHP in the future.

Lenses

Modifying data when everything is immutable can become cumbersome pretty quickly if you have some complicated data structure. Say, for example, you have a list of users, each user has a list of post associated to them and you need to change something on one of the posts. You will need to copy or recreate everything just to modify your value, since you cannot change anything in place.

Like I said, cumbersome. But as with mostly everything, there is a nice and clean solution in the form of lenses. Imagine your lens as if it was a part of a binocular; it lets you focus on one part of your data structure easily. You then have the tools to modify this as easily and get a whole new shiny data structure with your data changed to whatever you want it to be.

A lens is a lookup function that lets you get a particular field at the current depth of your data structure. You can read from a lens, it will return the pointed value. And you can write to a lens, it will return you the whole data structure with your modification.

What is really great about lenses is that since they are functions you can compose them, so if you want to go deeper than the first level, compose your second lookup function with the first one. And you can add a third, fourth, and so on lookups on top of that. At each step you could get or set the value if you want.

And since they are functions, you can use them as any other function, you can map them, put them in applicatives, bind them to a monad. Suddenly, an operation that was very cumbersome can leverage all the power of your language.

Sadly, as immutable data structures are not really common in PHP, no one took the time to write a lens library for it. Also, the details of how this is possible are a bit messy and would need quite some time to explain. This is why we'll leave it here for now.

If you are interested, the Haskell lens library has a webpage with lots of information and a great introduction, although a truly challenging video, at http://lens.github.io/.

Summary

In this chapter, we covered a lot of different topics. Some were concepts you will be able to use when developing in PHP such as avoiding stack overflows when doing recursion, pattern matching, the point-free style, and the usage of the const keyword to make your code a bit easier to read.

Others were purely theoretical with no current usage in PHP, ideas that were only presented so that you will be able to understand a bit better other writings about functional programming, such as monad transformers, the link between functional programming and category theory, and lenses.

Finally, some topics were somewhat in the middle, useful in your day-to-day coding, but a bit harder to put in to practice as the support in PHP is lacking. Even if it is not perfect, you are now aware of type classes, type signatures, and algebraic structures.

I have faith that you were not too much put off by the never-ending change of topics in this chapter and that you learned some valuable and interesting stuff. I also hope that this content sparked some interest in you to learn more about those topics and maybe try a functional language to see what all that hinted goodness was about.

In the next chapter, we'll get back to a more practical topic as we will discuss testing functional code first, and second we will learn about a methodology called property-based testing, which is not strictly speaking about functional programming, but was first theorized in Haskell.