Foundations of Coding: Compression, Encryption, Error Correction (2015)

Introduction

This work is aimed at providing a textbook for master students in applied mathematics or computer science. It can be used as a reference book by teachers, researchers, or companies involved in telecommunication or information security. The book is, to a certain extent, self-contained, that is, all used concepts are introduced. However, some training in algebra, algorithmics, and probability theory will be helpful. Indeed, the originality of this book is to present fundamental structures and applications, covering all coding operations, in a single framework.

The subject is the automatic transmission of numerical information. We will focus on the structure of information, without regarding the type of transmission support. Information can be of any kind as long as we can give a numerical representation of it: for example texts, images, sounds, and videos. Transmission of this type of data is ubiquitous in technology, especially in telecommunications. Hence, it is necessary to rely on solid bases for that transmission to be reliable, the term “reliable” having several different meanings depending on the objectives that will guide us throughout this book.

Transmission channels can also be of any kind (wirenets or wavenets), possibly through data storage. We will not consider the physical issues coming with transmission, which are the subjects of the theory known as “ signal” theory. “ Coding” deals with information itself when it is meant to be transmitted or stored.

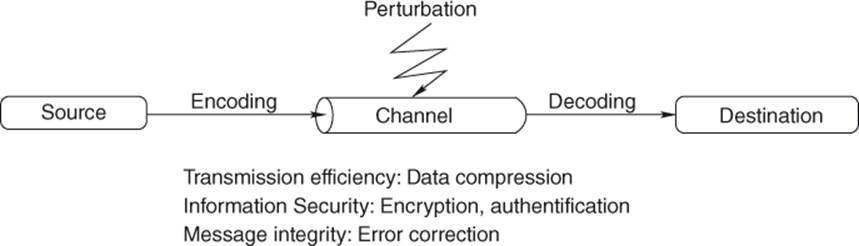
Figure I.1 Fundamental coding scheme

Communication of a piece of information begins with a sender writing it, goes on with its transmission through a channel and ends with the reconstruction of the message by the recipient. Sometimes, the sender is also the recipient: it is the case of a processor or a person saving data in a register, a memory, or a disk and reading it later on. Information has to be fully, safely, and quickly transmitted to its recipient. However, whatever the channel may be, with variations depending on the support, it can never be considered “ safe” in several ways: errors can appear during transmissions, and the message is likely to be read, and even modified, by a potentially malicious third party.

It is up to the sender to compose his messages in a form that allows the recipient to reconstruct them—considering potential alterations during the transfer or confidentiality of some information—while minimizing the size of data.

These constraints are the starting points of several fields in mathematics and computing that are often developed separately although they deal with the same subject. The purpose of this book is to gather them into one volume and to present a single theory whose subject is the form given to information during its transmission, namely a general coding theory.

In 1948, Claude Shannon layed the foundation stone of what he called a “ mathematical theory of communication.” It is said that his theory began with his comments on natural languages: Shannon used to hide some parts of the text he was reading and to recover them from the visible part. When removing a few words, he was able to determine the meaning of a sentence with absolute certainty. Actually, the hidden words were redundant, they did not add anything to the meaning of the message. If he removed too many words, he was unable to guess the message with certainty. Then Shannon developed a theory that would allow one to calculate the “ amount of information” of any kind of message, hence the determination of a redundancy rate.

Nowadays, the operation of reducing redundancy is called compression or “ information theory.” Here, we are not only looking for efficiency in terms of optimization of the storage space but mainly in terms of transmission speed: we are interested in having the shortest message by keeping only what is necessary, or even better, reformulating it without redundancy.

Another and older concern in the transmission of a piece of information is confidentiality. Assuming that roads (as well as numerical channels) are not safe—and that a message can be intercepted during the transmission—the text has to be transformed, uncorrelated from its signification, while guaranteeing that only its recipients are given the decryption keys. The history of societies and nations is full of secret code stories and battles between code inventors and code breakers (who wanted to recover the meaning of the message without knowing the key). Shannon also contributed in this field by giving the first theoretical proof of confidentiality in 1949.

Today, a scientific discipline is dedicated to secret codes—cryptology. Not only do current techniques guarantee the secrecy of a message, but they also allow one tosign documents and identify a sender.

In addition to ill-intentioned third parties, all channels that are used in transmission of numerical information can suffer from perturbations that are likely to alter some parts of the messages, hence to modify their meaning. If the information is sent without redundancy, the least significant modification can lead to misunderstandings once at destination. As for natural languages, most of the errors will not alter the perception of the reader because redundancy will allow him to recover the initial message. Once again, Shannon presented a revolutionary result in 1948: even on channels with high error rate, it is still possible to add enough redundancy so that the message will be entirely received. But the proof is not constructive and this theorem keeps motivating the development of methods including ordered and optimized redundancy for the recipient to be able to detect modifications of the message (detection codes) and to correct potential errors himself (correction codes). All these methods are customizable—flexible—depending on the kind of support considered and its error rate.

Efficiency, security, and integrity are the three concerns for developers of information transmission methods. This book tackles those issues in one single volume through their common object—the code—which is used to structure the information on all current technological support.

The general theory of codes is based on a background coming from linear algebra, arithmetic, probability theory, algorithmic, and combinatorial analysis. In the first chapter of this book, we will present the mathematical models and the first algorithmic developments that structure the notion of code. The presentation of these models includes some introduction to useful mathematical concepts for the manipulation of codes, as well as general notions on the efficiency of calculation methods, which will be frequently used throughout the present work. Reading this chapter will require a basic theoretical knowledge of linear algebra (a first course in this field should be sufficient). Some elements go beyond the standard knowledge of nonmathematician students and are presented in detail here. The reader will soon be aware of their real practical importance, most of the time during their very introduction. Figure I.2 clarifies the usefulness of these notions and the dependencies between them.

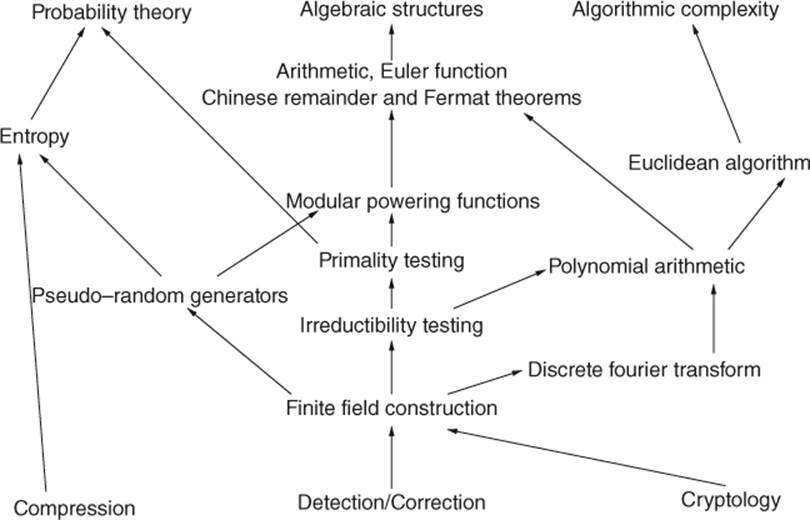
Figure I.2 Notions introduced in Chapter 1

As linear reading is not necessary, this scheme will also allow a reader in a hurry – or only interested in a specific part of this book—to quickly find his way. Although the first chapter is meant to introduce the foundations of coding, it can also be used as a reference toolbox during the reading of the following chapters. Those chapters deal with the notions of compression, cryptography, detection, and correction codes separately. They present the fundamental theoretical results and the algorithms that follow from them. Each chapter is illustrated with concrete examples and training exercises in the field of telecommunications. We have striven to present both classical coding theories and the most recent developments dealing with them as far as such an introductory book allow us to.

Not only does this book gathers mathematical theories sharing the same subject, but its creed is also algorithmic. Here, the mathematical properties of the functions are used in order to make their calculation efficient. Computation methods are always detailed and can be immediately implemented in any programming language. Efficiency of the methods is always stated and debated. Existing implementations are compared.

These sciences are derived from both Greek mathematics—whose quality was based on their aesthetic nature—and oriental mathematics—which focused on usefulness and calculation. This is what can also bring together the foundations of coding, and one of their greatest merit is to call upon rigorous mathematics—which are appreciated by aesthetes—in order to build efficient methods applied to common communications. Hence, this book is at the confluence of these rivers and will attract technology and number theory enthusiasts, as well as all those whose imagination is still fired by stories of decryption of arcane languages, machines that correct their own errors and secret codes.