Computer Science Programming Basics in Ruby (2013)

Chapter 1. Introduction to Computer Science

IN THIS CHAPTER

§ Defining computer science

§ Programming techniques

§ Algorithms and algorithm efficiency

1.1 Introduction

Introductory students often confuse programming with computer science, but programming is merely a strategy to implement computer science concepts. We introduce the basics of computer science using the Ruby programming language. Given our goal, we intentionally forgo many of the intricacies of the language.

Computer science is never tied to a programming language; it is tied to the task of solving problems efficiently using a computer. A computer comes with some resources, which will be discussed in Chapter 2, such as internal memory for short-term storage, processing capability, and long-term storage devices. A complete program is a set of instructions that use the computer to solve a real problem. The tool for producing these instructions is called a programming language. The goal is to develop solutions that use these resources efficiently to solve real problems.

Programming languages come and go, but the essence of computer science stays the same. If we need to sort a sequence of numbers, for example, it is immaterial if we sort them using programming language A or B. The steps the program will follow, commonly referred to as the algorithm, will remain the same. Hence, the core goal of computer science is to study algorithms that solve real problems. Computer scientists strive to create a correct sequence of steps that minimize resource demands, operate in a timely fashion, and yield correct results.

Algorithms are typically specified using pseudocode. Pseudocode, which may itself be simply written in plain language, specifies the logical, conceptual steps that must occur without specifying the necessary details needed to actually execute each step. However, we think that a properly selected subset of Ruby is sufficiently simple to introduce the algorithms. So, instead of creating an algorithm by writing it in plain language, generating equivalent pseudocode, and transforming it into a programming language, we go straight from the plain-language definition of an algorithm to Ruby code.

1.2 Application Development

When writing a program, it is important to keep in mind that the computer will do exactly what you tell it to do. It cannot think as a human would, so you must provide clear instructions for every step.

When giving instructions to others, people will often fill in blanks in logic without even realizing it. For example, if you instruct someone to “go to the bank,” you may not say what mode of transportation should be used. A computer, however, does not have the ability to “fill in the blanks.” A computer will only do exactly what you tell it to do.

Imagine, for example, explaining to a person and to a computer how to make a peanut butter and jelly sandwich. To the person, all you might need to say is, “Spread the peanut butter on one slice of bread, the jelly on the other slice of bread, and then put the pieces of bread together.” If these instructions were given to a computer, however, the computer would not know where to start. Implied in these instructions are many logical steps that a human can automatically infer and the computer cannot. For example, the human would know that the jar must first be opened to scoop peanut butter out before you can spread it onto a slice of bread. The computer might try to spread the actual jar across the bread, without taking the peanut butter or jelly out—assuming it could even find them!

Computer science is ultimately about problem solving. The following is a basic approach to solving problems:

Step 1: Understand the Problem

During this step, you try to answer all questions about the problem at hand. For example, you may be asked to create a program that stores a list of names, like a directory. Instead of just creating this program with little forethought, it is important to know all the details of the problem. Here are some examples:

§ How many names will be stored?

§ Do first and last names need to be stored separately?

§ Are middle names needed?

§ What is the maximum length that a name can be?

Step 2: Write Out the Solution in Plain Language

Once the problem is understood, the next step is to write an outline of how you will solve it. An example of the process of storing a name might look like a sequence of sentences:

Step 3: Translate the Language into Code

Once the plain-language version is written, it is time to translate it into actual code. The Ruby code for the preceding example is shown in Example 1-1, but you are certainly not expected to understand it yet.

Note the pound sign (#) on the righthand side. This sign means that the remainder of the line is a comment. A comment is not part of the instructions given to the computer. That is, a comment is a nonexecutable segment of code. Typically, comments are used to explain what the code does. Not only is it critical to comment code for the sake of readability and understanding, but using comments is considered good programming style, and the liberal use of comments is essential. Always remember that you (or someone else) may have to fix errors—colloquially referred to as bugs—years after you write a program; comments will help you understand what your code does years after you initially wrote it.

Example 1-1. Plain language → Ruby code

1 puts "Enter first name: " # Ask for the first name

2 first_name = gets # Store the first name

3 puts "Enter last name: " # Ask for the last name

4 last_name = gets # Store the last name

5 puts "Enter middle initial: " # Ask for the middle initial

6 middle_initial = gets # Store the middle initial

Step 4: Test the Code in the Computer

This step entails running the program you created and seeing that it runs properly. It is best to test portions of your code as you write them, instead of writing an entire program only to find out that none of it works.

1.3 Algorithms

Algorithms are step-by-step methods of solving problems. The process of reading in names previously described is an example of an algorithm, though a very simple one. Some are extremely complicated, and many vary their execution depending on input. Often algorithms take input and generate output, but not always. However, all algorithms have something in common: they all do something.

GEM OF WISDOM

Algorithms are the core of computer science. Correct and efficient algorithms guarantee that the computer works smart rather than only hard. Thus, think about the problem, come up with a good algorithm, and then determine how many steps the computer needs to complete the task.

Imagine a website like Google Maps, which has an algorithm to get directions from one point to another in either North America or Europe. It typically requires two inputs: a source and a destination. It also gives two outputs: the narrative directions to get from the source to the destination, and a map of the route.

The directions produced are also an algorithm; they accomplish the task of getting from the source to the destination. Imagine getting the directions to your friend’s house shown on the map in Figure 1-1.

1. Start going south on River Road.

2. Turn left (east) on Main Street.

3. Take a right (south) on Ruby Lane.

4. Turn left (east) toward Algorithm Circle.

5. Continue until you come to 345 Algorithm Circle (your friend’s house).

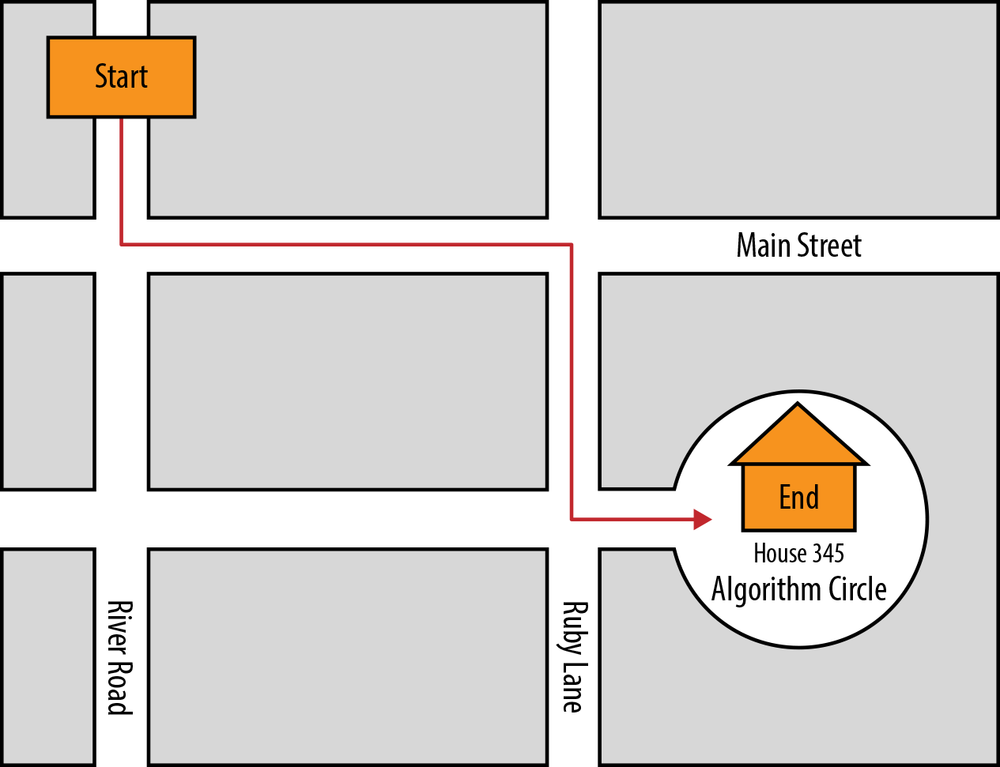
Figure 1-1. Directions “algorithm”

First notice that the directions are numbered; each step happens in sequential order. Additionally, it describes general steps like, “Turn left (east) on Main Street.” It does not say, “Turn on your left turn signal and wait for the light to turn green, and then turn left on Main Street.” That is not the point of an algorithm. An algorithm does not need to write out every single detail, but it needs to have all the important parts.

1.3.1 Algorithm Efficiency

Different algorithms may accomplish the same task, but some will do it much faster than others. Consider the algorithm just described for going to your friend’s house, which certainly is not the only route to her or his home. Instead of getting on Ruby Lane, you could have hopped on the expressway, gone to the airport, and then taken a cab from the airport to your friend’s house—but that would be extremely inefficient. Likewise, there may be a more efficient route to your friend’s house than the one described. Just because you have created an algorithm does not make it efficient, and being able to create efficient algorithms is one of the factors that distinguishes a good computer scientist. For example, imagine receiving the following set of directions to your friend’s house instead of the ones shown in the previous section, illustrated on the map in Figure 1-2:

1. Start going south on River Road.

2. Turn left (east) one block south of Main Street onto Algorithm Circle.

3. Continue until you come to 345 Algorithm Circle (your friend’s house).

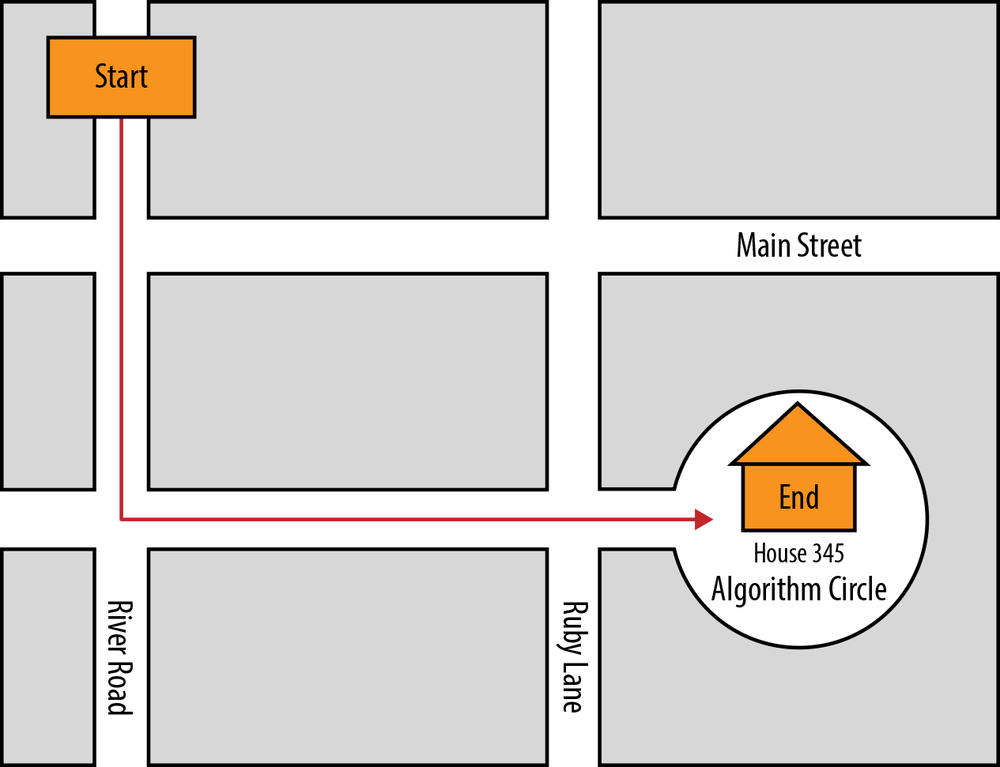
Figure 1-2. Directions “efficient algorithm”

Here we use a different algorithm that accomplishes the same task, and it does so slightly more efficiently. That is, fewer turns are involved.

1.4 Summary

You now understand the core foundations of computer science, namely the use of algorithms to solve real-world problems. Ruby, as used throughout the remainder of the book, is a powerful, yet relatively easy to understand, programming language that can be used to implement these algorithms. It is, however, critical to remember that independent of the programming language used, without a good algorithm, your solution will be ineffective.

1.4.1 Key Concepts

§ The essence of computer science is problem solving. Computer science involves using the computer as a tool to model or solve various problems, from storing names in a database to finding efficient directions to a friend’s house.

§ When programming, it is important to understand that the computer is never wrong. It is merely following the directions you have given it.

§ The following are basic steps for solving a computer science problem:

§ Algorithms are step-by-step methods for solving problems. When writing an algorithm, it is important to keep in mind the algorithm’s efficiency.

GEM OF WISDOM

Once we have an algorithm, we can compare it to other algorithms and pick the best one for the job. Once the algorithm is done, we can write a program to implement it.

1.4.2 Key Definitions

§ Algorithm: A step-by-step method for solving problems.

§ Algorithm efficiency: A measurement that determines how efficient one algorithm is compared with another.

1.5 Exercises

1. Imagine that you are creating a pocket calculator. You have created the functionality for all the buttons except x², the button that squares a number, and exp, which allows you to calculate base^exponent, where exponent is an integer. You may use any other functionality a calculator would normally have: for example, (+, -, *, /, =).

a. Create the functionality for the x² button.

b. Create the functionality for the exp button.

2. In the third-grade math class of French mathematician Carl Gauss, the teacher needed to give the students some busywork. She asked the class to compute the sum of the first 100 numbers (1 to 100). Long before the rest of the class had finished. Carl raised his hand and told his teacher that he had the answer: 5,050.

a. Craft an algorithm that will sum the first n numbers (assuming n ≥ 1). How many steps does your algorithm take to complete when n = 100? How many steps does it take when n = 1,000?

b. Can you create an algorithm like Gauss’s where the number of steps does not depend on n?

3. A palindrome is a word or phrase that reads the same way forward and backward, like “racecar.” Describe a sequence of steps that determines if a word or phrase is a palindrome.

4. Consider the three mazes shown in Figure 1-3. Describe two different algorithms for solving a maze. Discuss advantages and disadvantages of each algorithm. Then look at the maze and predict which algorithm will complete first. See if your predictions were correct by applying your algorithms to the mazes.

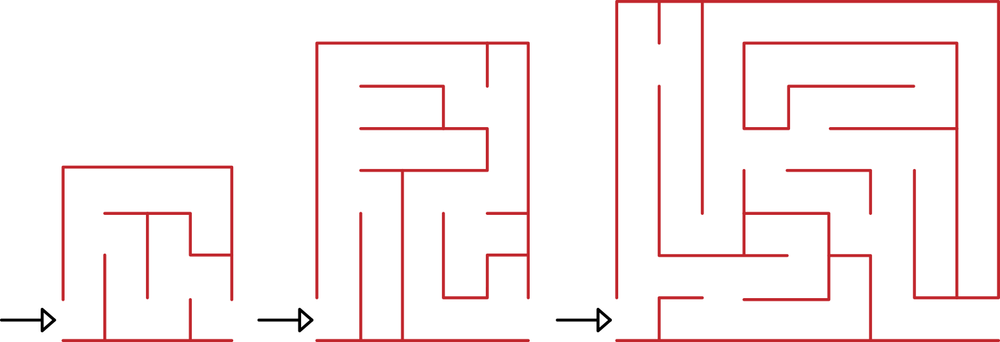
Figure 1-3. Three mazes for Exercise 4

5. Figure 1-4 shows an alternative way to represent an algorithm. (Note: we introduce this construct in detail later on. If it looks too intimidating, skip it until after you’ve read Chapter 4.)

a. Starting at the circle labeled “Start” work your way through the figure. What is the purpose of this algorithm?

b. Translate the figure into simple language. Note that a diamond in the figure represents a condition that may be true or false.

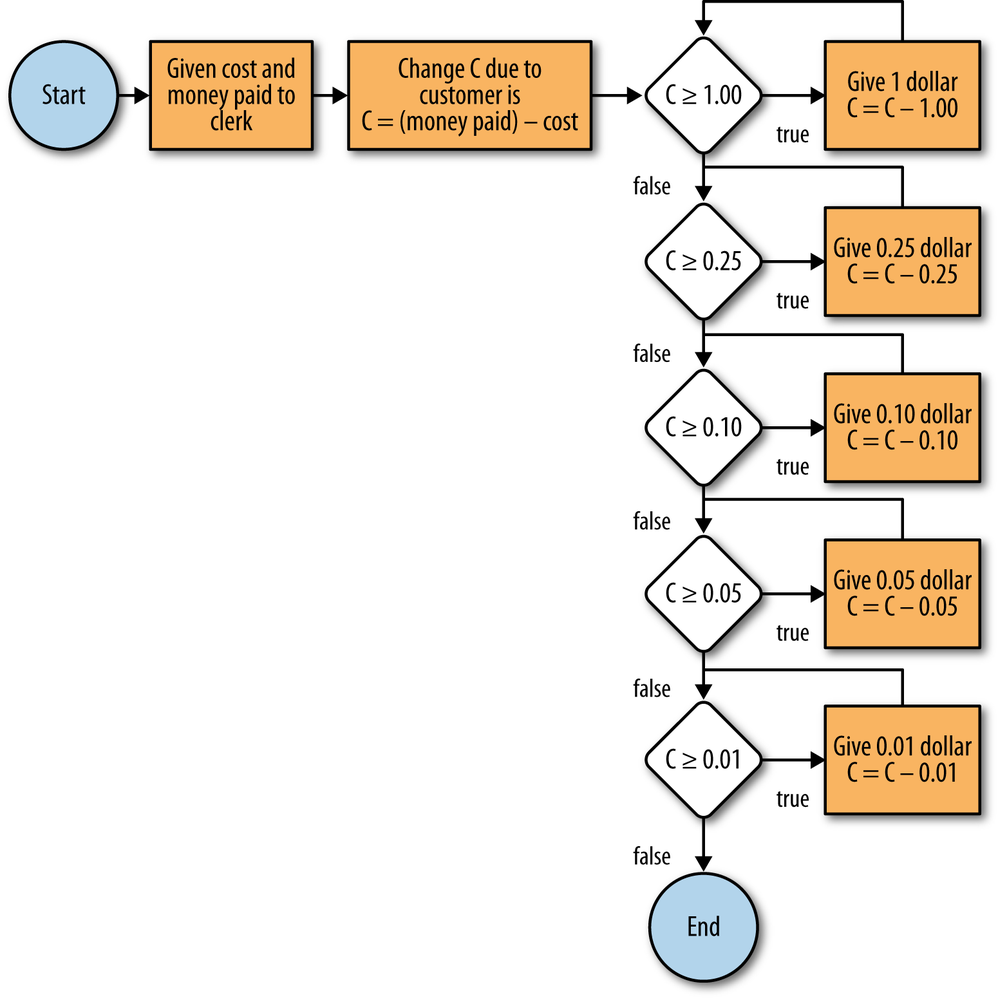
Figure 1-4. Alternative representation of an algorithm for Exercise 5

6. A cable company must use cables to connect 15 homes together so that every home is reachable by every other home. The company has estimated the costs of different cable routes (Figure 1-5 shows the numbers associated with each link). One engineer provides an algorithm, shown in Figure 1-5, that will find the cheapest set of routes to pick. Does the engineer’s algorithm work for this case? Why or why not?

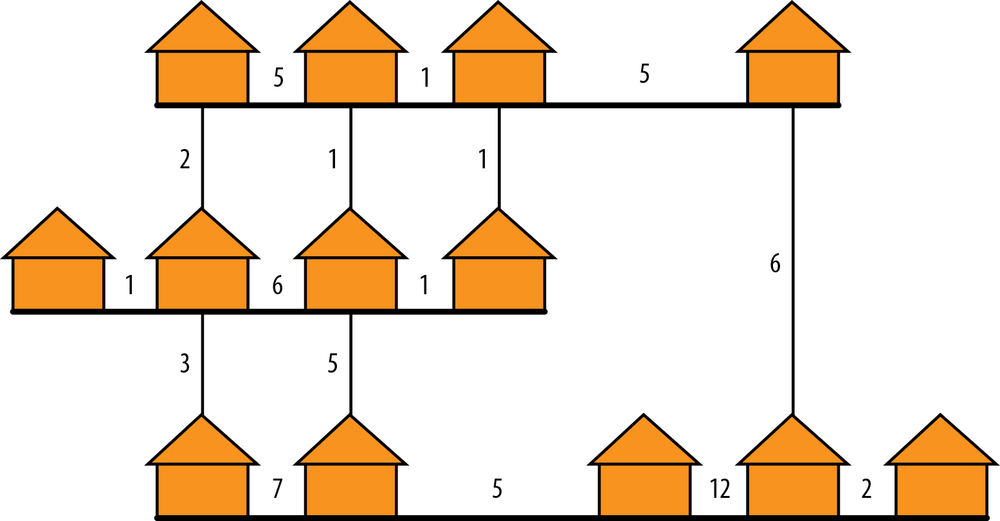
Figure 1-5. Cable company dilemma for Exercise 6

Engineer’s Algorithm:

a. Pick one cable route with the lowest cost not already picked. Add this route to the set of cheapest routes.

b. Check if every house is connected to every other house through any series of cables. If it isn’t, go back to step 1. If every house is connected, then the cheapest set of routes has been found.