Python Programming Made Easy (2016)
Chapter 10: Datastructures
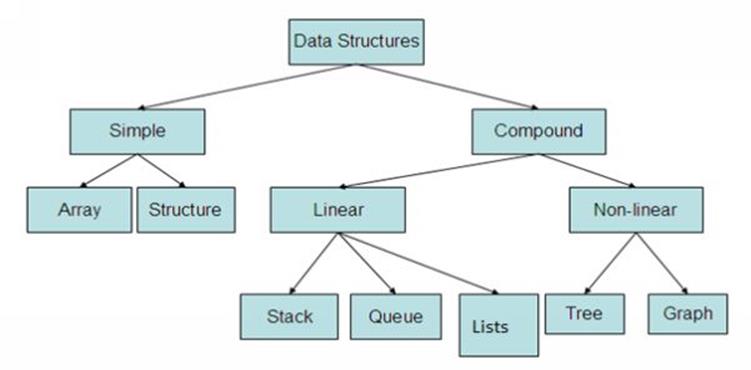
Fig 10.1: Datastructures
Linear data structure
A linear data structure traverses the data elements sequentially, in which only one data element can directly be reached. Ex: Arrays, Linked Lists
Arrays
Arrays refer to a named list of similar data elements. Each of the elements can be referenced by indexes.
|
int a[10]; è Refers to an array of 10 integers |
Structures
Structure refers to collection of variables of different data types.
|
struct student { int rollno; char name [20]; } s; |
Stacks
Stack data structures refer to the lists stored and accessed in last in first out (LIFO). Insertions and deletions take place at only at one end called the top.
Queues
Queues are first in first out lists, where insertions take place at the rear end of the queues and deletions take place at the front end.
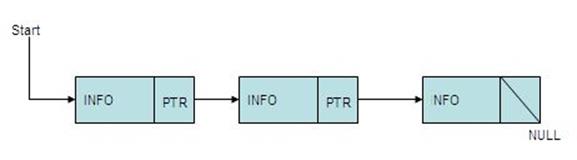
Linked Lists
Each element is called a node and is linked to another element (node). Each node has 2 parts INFO and PTR. INFO contains information and PTR is a pointer to the next node.
Non-Linear data structure
Every data item is attached to several other data items in a way that is specific for reflecting relationships. The data items are not arranged in a sequential structure. Ex: Trees, Graphs.
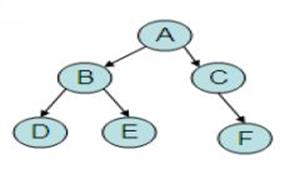
Trees
Trees are multilevel data structures having a hierarchical relationship among its elements called nodes. Topmost node is called root of the tree and bottommost nodes are called leaves of the tree.
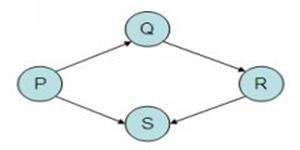
Graphs
A tree only allows a node to have children, and there cannot be any loops in the tree, with a more general graph we can represent many different situations.
Implementation of lists in memory
Python lists are arrays of variable length. A list in Python is an array of pointers of a specific size. It occupies 4 bytes in 32-bit machine and 8 bytes in 64-bit machine.
Algorithms on List Operations
Traversal
a) The for-in statement makes it easy to loop over the items in a list:
for item in L:
print item
b) If we need both the index and the item, we use the enumerate function:
for index, item in enumerate(L):
print index, item
c) If we need only the index, use range and len:
for index in range(len(L)):
print index
Insertion
Ø append method adds a single item to the end of the list
Ø extend method adds items from another list (or any sequence) to the end
Ø insert inserts an item at a given index, and move the remaining items to the right.
L.append(item)
L.extend(sequence)
L.insert(index, item)
Deletion
Ø The del statement can be used to remove an individual item, or to remove all items identified by a slice.
Ø The pop method removes an individual item and returns it
del L[i]
del L[i:j]
item = L.pop() # last item
item = L.pop(0) # first item
item = L.pop(index)
L.remove(item)
Array Searching
A linear search looks down a list, one item at a time, without jumping.
Program:
The in operator can be used to check if an item is present in the list:
if value in L:
print "list contains", value
To get the index of the first matching item, use index:
i = L.index(value)
The index method does a linear search, and stops at the first matching item. If no matching item is found, it raises a ValueError exception.
try:
i = L.index(value)
except ValueError:
i = -1 # no match
To get the index for all matching items, you can use a loop, and pass in a start index:
i = -1
try:
while 1:
i = L.index(value, i+1)
print "match at", i
except ValueError:
pass
A binary search is when we start with the middle of a sorted list, and see whether that's greater than or less than the value we’re looking for, which determines whether the value is in the first or second half of the list. Jump to the half way through the sublist, and compare again etc. This is similarto humans typically look up a word in a dictionary.
complexity - O (log n)
Program:
|
def binary_search(nums, x): high = len(nums) low=0 while low < high: mid = (low+high)//2 midval = nums[mid] if midval < x: low = mid+1 elif midval > x: high = mid else: return mid else: return -1 # Get the sorted list nums = [] print "Enter the numbers to sort press -1 to quit" while True: number =int(raw_input("Enter number?")) if number <> -1: nums.append(number) else: break nums.sort() print nums # Call Bin search function x=int(raw_input("Enter number to be searched")) pos =binary_search(nums,x) if pos <> -1: print x,"found at position",pos else: print x,"not found" |
Array Sorting
Bubble Sort
Bubble sort is a simple sorting algorithm that works by repeatedly stepping through the list to be sorted, comparing each pair of adjacent items and swapping them if they are in the wrong order. The pass through the list is repeated until no swaps are needed, which indicates that the list is sorted. The algorithm gets its name from the way smaller elements "bubble" to the top of the list. Because it only uses comparisons to operate on elements, it is a comparison sort. Although the algorithm is simple, most other algorithms are more efficient for sorting large lists.
Program:
|
#Bubble Sort def bubble_Sort(numbers): i = 0 j = 0 l = len(numbers) for i in range(l): for j in range(i,l): if numbers[i] > numbers[j]: numbers[i],numbers[j] = numbers[j],numbers[i] print "LIST AFTER SORTING",numbers numbers = [90,78,20,46,54,1] print "LIST BEFORE SORTING",numbers bubble_Sort(numbers) names = ['Neena','Meeta','Geeta','Reeta','Seeta'] print "LIST BEFORE SORTING",names bubble_Sort(names) |
Selection Sort
Selection sort performs the following steps:
1) Starting at index 0, search the entire array to find the smallest value
2) Swap the smallest value found with the value at index 0
3) Repeat steps 1 & 2 starting from the next index
In other words, we’re going to find the smallest element in the array, and put it in the first position. Then we’re going to find the next smallest element, and put it in the second position. This process will be repeated until we run out of elements. Here is an example of this algorithm working on 5 elements. Let’s start with a sample array:
{30, 50, 20, 10, 40}
First, we find the smallest element, starting from index 0:
{30, 50, 20, 10, 40}
We then swap this with the element at index 0:
{10, 50, 20, 30, 40}
Now that the first element is sorted, we can ignore it. Consequently, we find the smallest element, starting from index 1:
{10, 50, 20, 30, 40}
And swap it with the element in index 1:
{10, 20, 50, 30, 40}
Find the smallest element starting at index 2:
{10, 20, 50, 30, 40}
And swap it with the element in index 2:
{10, 20, 30, 50, 40}
Find the smallest element starting at index 3:
{10, 20, 30, 50, 40}
And swap it with the element in index 3:
{10, 20, 30, 40, 50}
Finally, find the smallest element starting at index 4:
{10, 20, 30, 40, 50}
And swap it with the element in index 4 (no change)
{10, 20, 30, 40, 50}
Program:
|
def SelSort(nums): n =len(nums) # Find the smallest item in nums[0]...nums[n-1] for i in range(n-1): pointer = i for j in range(i+1, n): if(nums[j] < nums[pointer]): pointer = j # swap nums[i],nums[pointer] = nums[pointer],nums[i] print "List after sorting" print nums nums = [] sortedlist = [] print "Enter the numbers to sort press -1 to quit" while True: number =int(raw_input("Enter number?")) if number <> -1: nums.append(number) else: break print "List before sorting" print nums # Call selection sort method SelSort(nums) |
Insertion Sort
Every repetition of insertion sort removes an element from the input data, inserting it into the correct position in the already-sorted list, until no input elements remain. The choice of which element to remove from the input is arbitrary and can be made using almost any choice algorithm. It's the same strategy that we use for sorting our bridge hand. We pick up a card, start at the beginning of our hand and find the place to insert the new card, insert it and move all the others up one place.
Program:
|
def insertion_sort(numbers): for K in range (1, len(numbers)): temp=numbers[K] ptr=K-1 while(ptr>=0) and numbers[ptr]>temp: numbers[ptr+1]=numbers[ptr] ptr=ptr-1 numbers[ptr+1]=temp print numbers numbers = [15,-5,20,-10,10] print "LIST BEFORE SORTING",numbers insertion_sort(numbers) |
Stacks
A stack is a data structure that allows adding and removing elements according to the Last-In First-Out (LIFO) principle. Every time an element is added, it goes on the top of the stack; the only element that can be removed is the element that was at the top of the stack.
The operations performed on the stack are:
à Push: Adding (inserting) new element on to the stack.
à Pop: Removing (deleting) an element from the stack
à Traversal: Printing elements of the stack
Adding new element to the stack list is called push operation. When the stack is empty, the value of top is -1. Basically, an empty stack is initialized with an invalid subscript. Whenever a Push operation is performed, the top is incremented by one and then the new value is inserted on the top of the list till the time the value of top is less than or equal to the size of the stack.
Removing existing elements from the stack list is called pop operation. Here we have to check if the stack is empty by checking the value of top. If the value of top is -1, then the stack is empty and such a situation is called Underflow. Otherwise Pop operation can be performed in the stack. The top is decremented by one if an element is deleted from the list.
Traversal is moving through the elements of the stack. If you want to display all the elements of the stack, the algorithm will be as follows:
In Python, pop() and append() functions are there so there is no need to write the code to add and remove elements in the stack. Consider the following programs that perform the Push and Pop operation on the stack through append() and pop().
Program
|
stack = [] choice =3 while choice <> 5: choice = int(raw_input("1- CREATE 2-PUSH 3-POP 4-VIEW 5-EXIT")) if choice==1: print "Creating Stack" while True: print "Enter the elements of Stack enter -1 when done" n = int(raw_input("Enter element?")) if n<> -1: stack.append(n) else: break elif choice==2: ch='y' print "Performing PUSH" while ch == 'y': n = int (raw_input("Enter number to be inserted?")) stack.append(n) ch = raw_input("Are there more numbers? y-yes n-no") elif choice==3: ch='y' print "Performing POP" while ch == 'y': stack.pop() ch = raw_input("Continue Popping? y-yes n-no") elif choice==4: print "STACK CONTENTS ARE" print stack else: break |
Application of stacks
1. Expression evaluation
2. Backtracking (game playing, finding paths, exhaustive searching)
3. Memory management, run-time environment for nested language features.
Expression evaluation
We are accustomed to write arithmetic expressions with the operation between the two operands: a+b or c/d. If we write a+b*c, however, we have to apply precedence rules to avoid the ambiguous evaluation (add first or multiply first?). Postfix expressions are easily evaluated with the aid of a stack.
Postfix Evaluation Algorithm
Assume we have a string of operands and operators, an informal, by hand process is
1. Scan the expression left to right
2. Skip values or variables (operands)
3. When an operator is found, apply the operation to the preceding two operands
4. Replace the two operands and operator with the calculated value (three symbols are replaced with one operand)
5. Continue scanning until only a value remains--the result of the expression
Let us see how the above algorithm will be implemented using an example.
|
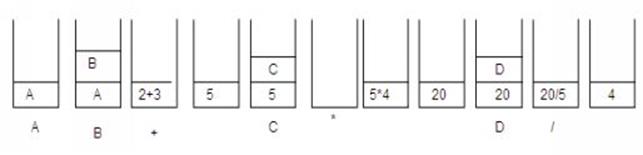
Example: AB + C* D/ If A=2, B=3, C=4, D=5
|
Infix transformation to Postfix
This process uses a stack. We have to hold information that's expressed inside parentheses while scanning to find the closing ')'. We also have to hold information on operations that are of lower precedence on the stack.
The algorithm is:
1. Create an empty stack and an empty postfix output string/stream
2. Scan the infix input string/stream left to right
3. If the current input token is an operand, simply append it to the output string (note the examples above that the operands remain in the same order)
4. If the current input token is an operator, pop off all operators that have equal or higher precedence and append them to the output string; push the operator onto the stack. The order of popping is the order in the output.
5. If the current input token is '(', push it onto the stack
6. If the current input token is ')', pop off all operators and append them to the output string until a '(' is popped; discard the '('.
7. If the end of the input string is found, pop all operators and append them to the output string.
This algorithm doesn't handle errors in the input, although careful analysis of parenthesis or lack of parenthesis could point to such error determination.
Example: Convert A+ (B*C – (D / E ^ F) * G) * H into postfix form showing stack status after every step in tabular form
|
S.No |
Element |
Stack |
Expression |
|
1 |
A |
( |
A |
|
2 |
+ |
(+ |
A |
|
3 |
( |
( + ( |
A |
|
4 |
B |
( + ( |
AB |
|
5 |
* |
( + ( * |
AB |
|
6 |
C |
( + ( * |
ABC |
|
7 |
- |
( + ( - |
ABC* |
|
8 |
( |
( + ( - ( |
ABC* |
|
9 |
D |
( + ( - ( |
ABC*D |
|
10 |
/ |
( + ( - ( \ |
ABC*D |
|
11 |
E |
( + ( - ( \ |
ABC*DE |
|
12 |
^ |
( + ( - ( \ ^ |
ABC*DE |
|
13 |
F |
( + ( - ( \ ^ |
ABC*DEF |
|
14 |
) |
( + ( - |
ABC*DEF^/ |
|
15 |
* |
( + ( - * |
ABC*DEF^/ |
|
16 |
G |
( + ( - * |
ABC*DEF^/ G |
|
17 |
) |
( + |
ABC*DEF^/ G *- |
|
18 |
* |
( + * |
ABC*DEF^/ G *- |
|
19 |
H |
( + * |
ABC*DEF^/ G *- H |
|
20 |
) |
ABC*DEF^/ G *- H * + |
Queue
Queue is a first-in, first-out (FIFO) data structure. i.e. the element added first to the queue will be the one to be removed first. Elements are always added to the rear of the queue and removed from the front of the queue.
· If front=0, then queue is empty
· The no. of elements in the queue is given by
|
N = front – rear + 1 |
Program:
|
queue = [] choice =3 while choice <> 5: choice = int(raw_input("1- CREATE 2-INSERT 3-DELETE 4-VIEW 5-EXIT")) if choice==1: print "Creating Queue" while True: print "Enter the elements of Queue enter -1 when done" n = int(raw_input("Enter element?")) if n<> -1: queue.append(n) else: break elif choice==2: ch='y' print "Performing INSERT" while ch == 'y': n = int (raw_input("Enter number to be inserted?")) queue.append(n) ch = raw_input("Are there more numbers? y-yes n-no") elif choice==3: ch='y' print "Performing DELETE" while ch == 'y': queue.pop(0) ch = raw_input("Continue delete? y-yes n-no") elif choice==4: print "QUEUE CONTENTS ARE" print queue else: break |
Deque (Double-ended queues)
Deques are the refined queues which allows insertions and deletions at both ends of the list. They are of 2 types
è Input restricted deques – allows insertions at one end only
è Output restricted deques – allows deletions at one end only
Circular Queues
Circular Queues are the queues implemented in circular form rather than a straight line. The circular queue considers itself contiguous at opposite ends. That is why if space is there in the beginning, the rear shifts back to beginning after reaching the max size.
Solved Examples
1. Define a data structure.
Ans. A data structure is a group of data which can be processed as a single unit. This group of data may be of similar or dissimilar data types. Data Structures are very useful while programming because they allow processing of the entire group of data as a single unit.
2. Give one point of difference between an array and a list in Python.
Ans. An array is defined as a set of contiguous data of similar data type. Python lists are actually arrays of variable length. The elements of a list are of heterogeneous types which means they are of different data types
3. How is memory allocated to a list in Python?
Ans. A list in Python is an array that contains elements (pointers to objects) of a specific size only and this is a common feature of all dynamically typed languages. For implementation of a list, a contiguous array of references to other objects is used. Python keeps a pointer to this array and the array's length is stored in a list head structure. This makes indexing of a list independent of the size of the list or the value of the index. When items are appended or inserted, the array of references is resized.
4. How is linear search different from binary search?
Ans.
· Binary search requires the input data to be sorted; linear search doesn't
· Binary search requires an ordering comparison; linear search only requires equality comparisons
· Binary search has complexity O(log n); linear search has complexity O(n) as discussed earlier
· Binary search requires random access to the data; linear search only requires sequential access (this can be very important - it means a linear search can stream data of arbitrary size)
5. Write a program to get a list of numbers and a number to be searched and print its position in the list.
Ans.
maxrange = input("Enter Count of numbers: ")
marks = []
flag=False
for i in range(0, maxrange):
marks.append(input("?"))
number = input("Enter number to be searched")
for i in range(0, maxrange):
if marks[i]==number:
print number,"found at position",i
flag=True
if flag==False:
print number,"not found in list"
6. Write a function that takes a list that is sorted in ascending order and a number as arguments. The function should do the following:
a. Insert the number passed as argument in a sorted list.
b. Delete the number from the list.
Ans.
from bisect import bisect
def listfunc(sortedlist,number):
insert_point = bisect (sortedlist, number)
sortedlist.insert(insert_point,number)
print "List after Insertion"
print sortedlist
sortedlist.remove(number)
print "List after Deletion"
print sortedlist
maxrange = input("Enter Count of numbers: ")
numlist = []
flag=False
for i in range(0, maxrange):
numlist.append(input("?"))
numlist.sort()
number = input("Enter the number")
listfunc(numlist,number)
7. Write a function for binary search.
Ans.
def binary_search(SORTEDLIST, number):
low=0
high=len(SORTEDLIST)
found=False
while(low<high) and found==False:
mid=(int)(low+high/2)
if SORTEDLIST[mid]==number:
print "Number found at",mid
found=True
break
elif SORTEDLIST[mid]<number:
low=mid+1
else:
high=mid-1
if low >= high:
print "Number not found"
maxrange = input("Enter Count of numbers: ")
numlist = []
for i in range(0, maxrange):
numlist.append(input("?"))
numlist.sort()
print "Sorted list",numlist
number = input("Enter the number")
binary_search(numlist,number)
8. In the following list containing integers, sort the list using Insertion sort algorithm. Also show the status of the list after each iteration.
10,-2,6,-1,5
Ans.
def insertion_sort(NUMLIST):
for K in range (1, len(NUMLIST)):
temp= NUMLIST[K]
ptr=K-1
while(ptr>=0) and NUMLIST[ptr]>temp:
NUMLIST[ptr+1]= NUMLIST[ptr]
ptr=ptr-1
NUMLIST [ptr+1]=temp
print NUMLIST
NUMLIST = [10,-2,6,-1,5]
print "LIST BEFOR SORTING", NUMLIST
insertion_sort(NUMLIST)
LIST BEFOR SORTING [10, -2, 6, -1, 5]
[-2, 10, 6, -1, 5]
[-2, 6, 10, -1, 5]
[-2, -1, 6, 10, 5]
[-2, -1, 5, 6, 10]
9. Write a program to sort a list containing names of students in ascending order using selection sort.
Ans.
def selection_sort(NUMLIST):
for i in range(0, len (NUMLIST)):
min = i
for j in range(i + 1, len(NUMLIST)):
if DATA_LIST[j] < NUMLIST [min]:
min = j
# swapping
temp= NUMLIST [min]
NUMLIST [min] = NUMLIST [i]
NUMLIST [i]=temp
print NUMLIST
NAME_LIST = ['Neena','Beeta','Reeta','Geeta','Seeta']
print "LIST BEFORE SORTING",NAME_LIST
selection_sort(NAME_LIST)
LIST BEFORE SORTING ['Neena', 'Beeta', 'Reeta', 'Geeta', 'Seeta']
['Beeta', 'Neena', 'Reeta', 'Geeta', 'Seeta']
['Beeta', 'Geeta', 'Reeta', 'Neena', 'Seeta']
['Beeta', 'Geeta', 'Neena', 'Reeta', 'Seeta']
['Beeta', 'Geeta', 'Neena', 'Reeta', 'Seeta']
['Beeta', 'Geeta', 'Neena', 'Reeta', 'Seeta']
10. Consider the following unsorted list
90 78 20 46 54 1
Write the list after:
a. 3rd iteration of selection sort
b. 4th iteration of bubble ort
c. 5th iteration of insertion sort
Ans.
Working
|
Bubble sort |
Selection Sort |
Insertion sort |
|
[1, 90, 78, 46, 54, 20] [1, 20, 90, 78, 54, 46] [1, 20, 46, 90, 78, 54] [1, 20, 46, 54, 90, 78] [1, 20, 46, 54, 78, 90] [1, 20, 46, 54, 78, 90] |
[1, 78, 20, 46, 54, 90] [1, 20, 78, 46, 54, 90] [1, 20, 46, 78, 54, 90] [1, 20, 46, 54, 78, 90] [1, 20, 46, 54, 78, 90] [1, 20, 46, 54, 78, 90] |
[78, 90, 20, 46, 54, 1] [20, 78, 90, 46, 54, 1] [20, 46, 78, 90, 54, 1] [20, 46, 54, 78, 90, 1] [1, 20, 46, 54, 78, 90] |
a. 3rd iteration of selection sort: [1, 20, 46, 78, 54, 90]
b. 4th iteration of bubble sort: [1, 20, 46, 54, 90, 78]
c. 5th iteration of insertion sort: [1, 20, 46, 54, 78, 90]
11. Expand the following:
(i) LIFO (ii) FIFO
Ans.
LIFO: Last-In First-Out
FIFO: First-In First-Out
12. What is stack?
Ans. A stack is a data structure that allows adding and removing elements in a particular order. Every time an element is added, it goes on the top of the stack; the only element that can be removed is the element that was at the top of the stack.
13. What is Queue?
Ans. Queue is a first-in, first-out (FIFO) data structure. i.e. the element added first to the queue will be the one to be removed first. Elements are always added to the rear of the queue and removed from the front of the queue.
14. Give one example each of infix, postfix and prefix expression.
Ans.
Infix: A + B *C / D
Postfix: ABC*D/+
Prefix: +/*BCDA
15. What is the advantage of postfix expressions?
Ans: An infix expression is difficult for the machine to know and keep track of precedence of operators. A postfix expression itself determines the precedence of operators so it is easier for the machine to carry out a postfix expression than an infix expression.
16. What are the advantages of circular queues?
Ans: In circular queues memory is utilized efficiently. In queue when we delete any element only front increments by 1but that position is not used later. When we perform more add and delete operation memory wastage increases. But in circular queue memory is utilized if we delete any element that position is used later because it is circular.
17. Consider the following circular queue with a capacity of 6 elements:Front= 2 rear = 4;
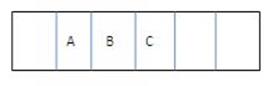
Describe the queue as the following operations take place.
a) Add D , E
b) Delete 2 letters
c) Add X,Y,Z
Ans:
|
a) Front =2 Rear = 6 |
|
|
|
b) Front = 4 Rear = 6 |
|
|
|
c) Front = 4 Rear = (6+3) mod 6 = 3 |
|
|
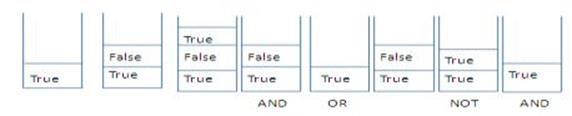
18. Evaluate the following Boolean postfix expression showing stack status after every step: True, False, True, AND, OR, False, NOT, AND
Ans:
|
|
19. Evaluate using stack 10, 3,*, 30, 2,*,-
Ans.
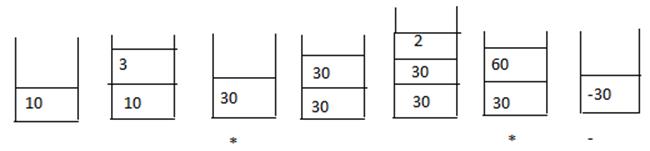
20. Convert A+ (B*C – (D / E ^ F) * G) * H into postfix form showing stack status after every step.
|
S.No |
Element |
Stack |
Expression |
|
1 |
A |
( |
A |
|
2 |
+ |
(+ |
A |
|
3 |
( |
( + ( |
A |
|
4 |
B |
( + ( |
AB |
|
5 |
* |
( + ( * |
AB |
|
6 |
C |
( + ( * |
ABC |
|
7 |
- |
( + ( - |
ABC* |
|
8 |
( |
( + ( - ( |
ABC* |
|
9 |
D |
( + ( - ( |
ABC*D |
|
10 |
/ |
( + ( - ( \ |
ABC*D |
|
11 |
E |
( + ( - ( \ |
ABC*DE |
|
12 |
^ |
( + ( - ( \ ^ |
ABC*DE |
|
13 |
F |
( + ( - ( \ ^ |
ABC*DEF |
|
14 |
) |
( + ( - |
ABC*DEF^/ |
|
15 |
* |
( + ( - * |
ABC*DEF^/ |
|
16 |
G |
( + ( - * |
ABC*DEF^/ G |
|
17 |
) |
( + |
ABC*DEF^/ G *- |
|
18 |
* |
( + * |
ABC*DEF^/ G *- |
|
19 |
H |
( + * |
ABC*DEF^/ G *- H |
|
20 |
) |
ABC*DEF^/ G *- H * + |
21. What are the applications of queue in computer?
Ans.
1. In a single processor multi tasking computer, job(s) waiting to be processed form a queue. Same happens when we share a printer with many computers.
2. Compiling a HLL code
3. Using down load manager, for multiple files also uses queue for ordering the files.
4. In multiuser OS - job scheduling is done through queue.
22. Write a function to push any student's information to stack.
Ans.
def push(stack):
s = []
print "STACK BEFORE PUSH"
display(stack)
s.append(input("Enter student rollno?"))
s.append(raw_input("Enter student name"))
s.append(raw_input("Enter student grade"))
stack.append(s)
def display(stack):
l=len(stack)
print "STACK CONTENTS"
for i in range(l-1,-1,-1):
print stack[i]
stack = []
print "Creating Stack"
n = input("Enter the number of students")
for i in range(n):
student = []
student.append(input("Enter student rollno?"))
student.append(raw_input("Enter student name"))
student.append(raw_input("Enter student grade"))
stack.append(student)
push(stack)
display(stack)
23. Write the push operation of stack containing names using class.
Ans.
class stack:
s=[]
def push(self):
a=raw_input("Enter any name :")
stack.s.append(a)
def display(self):
l=len(stack.s)
for i in range(l-1,-1,-1):
print stack.s[i]
a=stack()
n= input("Enter no. of names")
for i in range(n):
a.push()
a.display()
24. Write the pop operation of stack containing names using class.
Ans.
class stack:
s=[]
def push(self):
a=raw_input("Enter any name :")
stack.s.append(a)
def pop(self):
if (a.s==[]):
print "Stack Empty"
else:
print "Deleted element is : ",a.s.pop()
def display(self):
l=len(stack.s)
print "STACK CONTENTS"
for i in range(l-1,-1,-1):
print stack.s[i]
a=stack()
n= input("Enter no. of names")
for i in range(n):
a.push()
a.pop()
a.display()
25. Write a function to add any customer's information to queue.
Ans.
def insert(queue):
customer = []
print "QUEUE BEFORE INSERT"
display(queue)
customer.append(input("Enter customer number?"))
customer.append(raw_input("Enter customer name"))
customer.append(input("Enter customer phone number"))
queue.append(customer)
def display(queue):
l=len(queue)
for i in range(0,l):
print queue[i]
queue = []
print "Creating Queue"
n = input("Enter the number of customers")
for i in range(n):
customer = []
customer.append(input("Enter customer number?"))
customer.append(raw_input("Enter customer name"))
customer.append(input("Enter customer phone number"))
queue.append(customer)
insert(queue)
display(queue)
26. Write the deletion operation of queue containing numbers using class.
Ans.
class queue:
s=[]
def insert(self):
a=input("Enter the number:")
queue.s.append(a)
def delete(self):
if (a.s==[]):
print "Queue Empty"
else:
print "Deleted element is: ",queue.s[0]
del queue.s[0]
def display(self):
l=len(queue.s)
print "QUEUE CONTENTS"
for i in range(0,l):
print queue.s[i]
a=queue()
n= input("Enter no. of numbers")
for i in range(n):
a.insert()
a.delete()
a.display()
Practice Questions
1. Write a program to sort a list of items using bubble sort. Use classes to store item details.
2. Write a python program to sort a list of numbers using insertion sort algorithm.
3. Convert the following infix expression to its equivalent postfix expression showing stack contents for the conversion:
a) A + B *(C – D) / E ^ F
b) (A+B)*(C^ (D-E) +F)-G
4 . Evaluate the following postfix notation of expression: (Show status of stack after execution of each operation):
a) 20, 30, +, 50, 40, - ,*
b) 5, 20, 15,-,*, 25, 2,*, +
5. Write a complete program in Python to implement a dynamically allocated queue containing names of cities.
6. Write the pop operation of stack containing numbers using class.
7. Write a program to maintain a stack of books.
8. Write a program to simulate a reservation queue using classes.
All materials on the site are licensed Creative Commons Attribution-Sharealike 3.0 Unported CC BY-SA 3.0 & GNU Free Documentation License (GFDL)
If you are the copyright holder of any material contained on our site and intend to remove it, please contact our site administrator for approval.
© 2016-2026 All site design rights belong to S.Y.A.