Algorithms Third Edition in C++ Part 5. Graph Algorithms (2006)
CHAPTER TWENTY
Minimum Spanning Trees
20.2 Underlying Principles of MST Algorithms
The MST problem is one of the most heavily studied problems that we encounter in this book. Basic approaches to solving it were invented long before the development of modern data structures and modern techniques for analyzing the performance of algorithms, at a time when finding the MST of a graph that contained, say, thousands of edges was a daunting task. As we shall see, several new MST algorithms differ from old ones essentially in their use and implementation of modern algorithms and data structures for basic tasks, which (coupled with modern computing power) makes it possible for us to compute MSTs with millions or even billions of edges.
One of the defining properties of a tree (see Section 5.4) is that adding an edge to a tree creates a unique cycle. This property is the basis for proving two fundamental properties of MSTs, which we now consider. All the algorithms that we encounter are based on one or both of these two properties.
The first property, which we refer to as the cut property, has to do with identifying edges that must be in an MST of a given graph. The few basic terms from graph theory that we define next make possible a concise statement of this property, which follows.
Definition 20.2 A cut in a graph is a partition of the vertices into two disjoint sets. A crossing edge is one that connects a vertex in one set with a vertex in the other.
We sometimes specify a cut by specifying a set of vertices, leaving implicit the assumption that the cut comprises that set and its complement. Generally, we use cuts where both sets are nonempty—otherwise there are no crossing edges.
Property 20.1 (Cut property) Given any cut in a graph, every minimal crossing edge belongs to some MST of the graph, and every MST contains a minimal crossing edge.
Proof: The proof is by contradiction. Suppose that e is a minimal crossing edge that is not in any MST, and let T be any MST; or suppose that T is an MST that contains no minimal crossing edge, and let e be any minimal crossing edge. In either case, T is an MST that does not contain the minimal crossing edge e. Now consider the graph formed by adding e to T. This graph has a cycle that contains e, and that cycle must contain at least one other crossing edge—say, f, which is equal or higher weight than e (since e is minimal). We can get a spanning tree of equal or lower weight by deleting f and adding e, contradicting either the minimality of T or the assumption that e is not in T.
If a graph’s edge weights are distinct, it has a unique MST; and the cut property says that the shortest crossing edge for every cut must be in the MST. When equal weights are present, we may have multiple minimal crossing edges. At least one of them will be in any given MST and the others may be present or absent.
Figure 20.5 illustrates several examples of this cut property. Note that there is no requirement that the minimal edge be the only MST edge connecting the two sets; indeed, for typical cuts there are several MST edges that connect a vertex in one set with a vertex in the other. If we could be sure that there were only one such edge, we might be able to develop divide-and-conquer algorithms based on judicious selection of the sets; but that is not the case.
We use the cut property as the basis for algorithms to find MSTs, and it also can serve as an optimality condition that characterizes MSTs. Specifically, the cut property implies that every edge in an MST is a minimal crossing edge for the cut defined by the vertices in the two subtrees connected by the edge.
Figure 20.5 Cut property

These four examples illustrate Property 20.1. If we color one set of vertices gray and another set white, then the shortest edge connecting a gray vertex with a white one belongs to an MST.
The second property, which we refer to as the cycle property, has to do with identifying edges that do not have to be in a graph’s MST. That is, if we ignore these edges, we can still find an MST.
Property 20.2 (Cycle property) Given a graph G, consider the graph G[prime] defined by adding an edge e to G. Adding e to an MST of G and deleting a maximal edge on the resulting cycle gives an MST of G[prime].
Proof: If e is longer than all the other edges on the cycle, it cannot be on an MST of G [prime], because of Property 20.1: Removing e from any such MST would split the latter into two pieces, and e would not be the shortest edge connecting vertices in each of those two pieces, because some other edge on the cycle must do so. Otherwise, let t be a maximal edge on the cycle created by adding e to the MST of G. Removing t would split the original MST into two pieces, and edges of G connecting those pieces are no shorter than t;so e is a minimal edge in G [prime] connecting vertices in those two pieces. The subgraphs induced by the two subsets of vertices are identical for G and G [prime], so an MST for G [prime] consists of e and the MSTs of those two subsets.
In particular, note that if e is maximal on the cycle, then we have shown that there exists an MST of G [prime] that does not contain e (the MST of G ).
Figure 20.6 illustrates this cycle property. Note that the process of taking any spanning tree, adding an edge that creates a cycle, and then deleting a maximal edge on that cycle gives a spanning tree of weight less than or equal to the original. The new tree weight will be less than the original if and only if the added edge is shorter than some edge on the cycle.
The cycle property also serves as the basis for an optimality condition that characterizes MSTs: It implies that every edge in a graph that is not in a given MST is a maximal edge on the cycle that it forms with MST edges.
The cut property and the cycle property are the basis for the classical algorithms that we consider for the MST problem. We consider edges one at a time, using the cut property to accept them as MST edges or the cycle property to reject them as not needed. The algorithms differ in their approaches to efficiently identifying cuts and cycles.
Figure 20.6 Cycle property
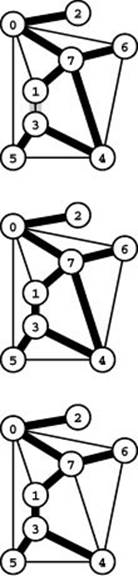
Adding the edge 1-3 to the graph in Figure 20.1 invalidates the MST (top). To find the MST of the new graph, we add the new edge to the MST of the old graph, which creates a cycle (center). Deleting the longest edge on the cycle (4-7) yields the MST of the new graph (bottom). One way to verify that a spanning tree is minimal is to check that each edge not on the MST has the largest weight on the cycle that it forms with tree edges. For example, in the bottom graph, 4-6 has the largest weight on the cycle 4-6-7-1-3-4.
The first approach to finding the MST that we consider in detail is to build the MST one edge at a time: Start with any vertex as a single-vertex MST, then add V − 1 edges to it, always taking next a minimal edge that connects a vertex on the MST to a vertex not yet on the MST. This method is known as Prim’s algorithm; it is the subject of Section 20.3.
Property 20.3 Prim’s algorithm computes an MST of any connected graph.
Proof: As described in detail in Section 20.2, the method is a generalized graph-search method. Implicit in the proof of Property 18.12 is the fact that the edges chosen are a spanning tree. To show that they are an MST, apply the cut property, using vertices on the MST as the first set and vertices not on the MST as the second set.
Another approach to computing the MST is to apply the cycle property repeatedly: We add edges one at a time to a putative MST, deleting a maximal edge on the cycle if one is formed (see Exercises 20.33 and 20.71). This method has received less attention than the others that we consider because of the comparative difficulty of maintaining a data structure that supports efficient implementation of the “delete the longest edge on the cycle” operation.
The second approach to finding the MST that we consider in detail is to process the edges in order of their length (shortest first), adding to the MST each edge that does not form a cycle with edges previously added, stopping after V − 1 edges have been added. This method is known asKruskal’s algorithm; it is the subject of Section 20.4.
Property 20.4 Kruskal’s algorithm computes an MST of any connected graph.
Proof: We prove by induction that the method maintains a forest of MST subtrees. If the next edge to be considered would create a cycle, it is a maximal edge on the cycle (since all others appeared before it in the sorted order), so ignoring it still leaves an MST, by the cycle property. If the next edge to be considered does not form a cycle, apply the cut property, using the cut defined by the set of vertices connected to one of the edge’s vertex by MST edges (and its complement). Since the edge does not create a cycle, it is the only crossing edge, and since we consider the edges in sorted order, it is a minimal edge and therefore in an MST. The basis for the induction is the V individual vertices; once we have chosen V − 1 edges, we have one tree (the MST). No unexamined edge is shorter than an MST edge, and all would create a cycle, so ignoring all of the rest of the edges leaves an MST, by the cycle property.
The third approach to building an MST that we consider in detail is known as Boruvka’s algorithm; it is the subject of Section 20.4. The first step is to add to the MST the edges that connect each vertex to its closest neighbor. If edge weights are distinct, this step creates a forest of MST subtrees (we prove this fact and consider a refinement that does so even when equal-weight edges are present in a moment). Then, we add to the MST the edges that connect each tree to a closest neighbor (a minimal edge connecting a vertex in one tree with a vertex in any other), and iterate the process until we are left with just one tree.
Property 20.5 Boruvka’s algorithm computes the MST of any connected graph.
First, suppose that the edge weights are distinct. In this case, each vertex has a unique closest neighbor, the MST is unique, and we know that each edge added is an MST edge by applying the cut property (it is the shortest edge crossing the cut from a vertex to all the other vertices). Since every edge chosen is from the unique MST, there can be no cycles, each edge added merges two trees from the forest into a bigger tree, and the process continues until a single tree, the MST, remains.
If edge weights are not distinct, there may be more than one closest neighbor, and a cycle could form when we add the edges to closest neighbors (see Figure 20.7). Put another way, we might include two edges from the set of minimal crossing edges for some vertex, when only one belongs on the MST. To avoid this problem, we need an appropriate tie-breaking rule. One choice is to choose, among the minimal neighbors, the one with the lowest vertex number. Then any cycle would present a contradiction: If v is the highest-numbered vertex in the cycle, then neither neighbor of v would have led to its choice as the closest, and v would have led to the choice of only one of its lower-numbered neighbors, not both.
Figure 20.7 Cycles in Boruvka’s algorithm
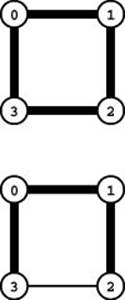
In the graph of four vertices and four edges shown here, the edges are all the same length. When we connect each vertex to a nearest neighbor, we have to make a choice between minimal edges. In the example at the top, we choose 1 from 0, 2 from 1, 3 from 2, and 0 from 3, which leads to a cycle in the putative MST. Each of the edges are in some MST, but not all are in every MST. To avoid this problem, we adopt a tie-breaking rule, as shown in the bottom: Choose the minimal edge to the vertex with the lowest index. Thus, we choose 1 from 0, 0 from 1, 1 from 2, and 0 from 3, which yields an MST. The cycle is broken because highest-numbered vertex 3 is not chosen from either of its neighbors 2 or 1, and it can choose only one of them (0).
These algorithms are all special cases of a general paradigm that is still being used by researchers seeking new MST algorithms. Specifically, we can apply in arbitrary order the cut property to accept an edge as an MST edge or the cycle property to reject an edge, continuing until neither can increase the number of accepted or rejected edges. At that point, any division of the graph’s vertices into two sets has an MST edge connecting them (so applying the cut property cannot increase the number of MST edges), and all graph cycles have at least one non-MST edge (so applying the cycle property cannot increase the number of non-MST edges). Together, these properties imply that a complete MST has been computed.
More specifically, the three algorithms that we consider in detail can be unified with a generalized algorithm where we begin with a forest of single-vertex MST subtrees (each with no edges) and perform the step of adding to the MST a minimal edge connecting any two subtrees in the forest, continuing until V − 1 edges have been added and a single MST remains. By the cut property, no edge that causes a cycle need be considered for the MST, since some other edge was previously a minimal edge crossing a cut between MST subtrees containing each of its vertices. With Prim’s algorithm, we grow a single tree an edge at a time; with Kruskal’s and Boruvka’s algorithms, we coalesce trees in a forest.
As described in this section and in the classical literature, the algorithms involve certain high-level abstract operations, such as the following:
• Find a minimal edge connecting two subtrees.
• Determine whether adding an edge would create a cycle.
• Delete the longest edge on a cycle.
Our challenge is to develop algorithms and data structures that implement these operations efficiently. Fortunately, this challenge presents us with an opportunity to put to good use basic algorithms and data structures that we developed earlier in this book.
MST algorithms have a long and colorful history that is still evolving; we discuss that history as we consider them in detail. Our evolving understanding of different methods of implementing the basic abstract operations has created some confusion surrounding the origins of the algorithms over the years. Indeed, the methods were first described in the 1920s, pre-dating the development of computers as we know them, as well as pre-dating our basic knowledge about sorting and other algorithms. As we now know, the choices of underlying algorithm and data structure can have substantial influences on performance, even when we are implementing the most basic schemes. In recent years, research on the MST problem has concentrated on such implementation issues, still using the classical schemes. For consistency and clarity, we refer to the basic approaches by the names listed here, although abstract versions of the algorithms were considered earlier, and modern implementations use algorithms and data structures invented long after these methods were first contemplated.
As yet unsolved in the design and analysis of algorithms is the quest for a linear-time MST algorithm. As we shall see, many of our implementations are linear-time in a broad variety of practical situations, but they are subject to a nonlinear worst case. The development of an algorithm that is guaranteed to be linear-time for sparse graphs is still a research goal.
Beyond our normal quest in search of the best algorithm for this fundamental problem, the study of MST algorithms underscores the importance of understanding the basic performance characteristics of fundamental algorithms. As programmers continue to use algorithms and data structures at increasingly higher levels of abstraction, situations of this sort become increasingly common. Our ADT implementations have varying performance characteristics—as we use higher-level ADTs as components when solving more yet higher-level problems, the possibilities multiply. Indeed, we often use algorithms that are based on using MSTs and similar abstractions (enabled by the efficient implementations that we consider in this chapter) to help us solve other problems at a yet higher level of abstraction.
Exercises
• 20.26 Label the following points in the plane 0 through 5, respectively:
(1, 3) (2, 1) (6, 5) (3, 4) (3, 7) (5, 3).
Taking edge lengths to be weights, give an MST of the graph defined by the edges
1-0 3-5 5-2 3-4 5-1 0-3 0-4 4-2 2-3.
20.27 Suppose that a graph has distinct edge weights. Does its shortest edge have to belong to the MST? Prove that it does or give a counterexample.
20.28 Answer Exercise 20.27 for the graph’s longest edge.
20.29 Give a counterexample that shows why the following strategy does not necessarily find the MST:
“Start with any vertex as a single-vertex MST, then add V − 1 edges to it, always taking next a minimal edge incident upon the vertex most recently added to the MST.”
20.30 Suppose that a graph has distinct edge weights. Does a minimal edge on every cycle have to belong to the MST? Prove that it does or give a counterexample.
20.31 Given an MST for a graph G, suppose that an edge in G is deleted. Describe how to find an MST of the new graph in time proportional to the number of edges in G.
20.32 Show the MST that results when you repeatedly apply the cycle property to the graph in Figure 20.1, taking the edges in the order given.
20.33 Prove that repeated application of the cycle property gives an MST.
20.34 Describe how each of the algorithms described in this section can be adapted (if necessary) to the problem of finding a minimal spanning forest of a weighted graph (the union of the MSTs of its connected components).