The C++ Programming Language (2013)
Part III: Abstraction Mechanisms
29. A Matrix Design
Never express yourself more clearly than you are able to think.
– Niels Bohr
• Introduction
Basic Matrix Uses; Matrix Requirements
• A Matrix Template
Construction and Assignment; Subscripting and Slicing
• Matrix Arithmetic Operations
Scalar Operations; Addition; Multiplication
• Matrix Implementation
slice; Matrix Slices; Matrix_ref; Matrix List Initialization; Matrix Access; Zero-Dimensional Matrix
• Solving Linear Equations
Classical Gaussian Elimination; Pivoting; Testing; Advice
29.1. Introduction
A language feature in isolation is boring and useless. This chapter demonstrates how features can be used in combination to address a challenging design task: a general N-dimensional matrix.
I have never seen a perfect matrix class. In fact, given the wide variety of uses of matrices, it is doubtful whether one could exist. Here, I present the programming and design techniques needed to write a simple N-dimensional dense matrix. If nothing else, this Matrix is far easier to use, and just as compact and fast, as anything a programmer would have time to write using vectors or builtin arrays directly. The design and programming techniques used for Matrix are widely applicable.
29.1.1. Basic Matrix Uses
Matrix<T,N> is an N-dimensional matrix of some value type T. It can be used like this:
Matrix<double,0> m0{1}; // zero dimensions: a scalar
Matrix<double,1> m1{1,2,3,4}; // one dimension: a vector (4 elements)
Matrix<double,2> m2{ // two dimensions (4*3 elements)
{00,01,02,03}, //row 0
{10,11,12,13}, //row 1
{20,21,22,23} //row 2
};
Matrix<double,3> m3(4,7,9); // three dimensions (4*7*9 elements), all 0-initialized
Matrix<complex<double>,17> m17;// 17 dimensions (no elements so far)
The element type must be something we can store. We do not require every property that we have for a floating-point number from every element type. For example:
Matrix<double,2> md; // OK
Matrix<string,2> ms; // OK: just don't try arithmetic operations
Matrix<Matrix<int,2>,2> mm { // 3-by-2 matrix of 2-by-2 matrices
// a matrix is a plausible "number"
{ // row 0
{{1, 2}, {3, 4}}, // col 0
{{4, 5}, {6, 7}}, // col 1
},
{ // row 1
{{8, 9}, {0, 1}}, // col 0
{{2, 3}, {4, 5}}, // col 1
},
{ // row 2
{{1, 2}, {3, 4}}, // col 0
{{4, 5}, {6, 7}}, // col 1
}
};
Matrix arithmetic doesn’t have exactly the same mathematical properties as integer or floating-point arithmetic (e.g., matrix multiplication is not commutative), so we must be careful how we use such a matrix.
As for vector, we use () to specify sizes and {} to specify element values (§17.3.2.1, §17.3.4.1). The number rows must match the specified number of dimensions and the number of elements in each dimension (each column) must match. For example:
Matrix<char,2> mc1(2,3,4); // error: too many dimension sizes
Matrix<char,2> mc2 {
{'1','2','3'} // error: initializer missing for second dimension
};
Matrix<char,2> mc2 {
{'1','2','3'},
{'4','5'} // error: element missing for third column
};
Matrix<T,N> has its number of dimensions (its order()) specified as a template argument (here, N). Each dimension has a number of elements (its extent()) deduced from the initializer list or specified as a Matrix constructor argument using the () notation. The total number of elements is referred to as its size(). For example:
Matrix<double,1> m1(100); // one dimension: a vector (100 elements)
Matrix<double,2> m2(50,6000); // two dimensions: 50*6000 elements
auto d1 = m1.order(); // 1
auto d2 = m2.order(); // 2
auto e1 = m1.extent(0); // 100
auto e1 = m1.extent(1); // error: m1 is one-dimensional
auto e2 = m2.extent(0); // 50
auto e2 = m2.extent(1); // 6000
auto s1 = m1.size(); // 100
auto s2 = m2.size(); // 50*6000
We can access Matrix elements by several forms of subscripting. For example:
Matrix<double,2> m { // two dimensions (4*3 elements)
{00,01,02,03}, // row 0
{10,11,12,13}, // row 1
{20,21,22,23} // row 2
};
double d1 = m(1,2); // d==12
double d2 = m[1][2]; // d==12
Matrix<double,1> m1 = m[1]; // row 1: {10,11,12,13}
double d3 = m1[2]; // d==12
We can define an output function for use in debugging like this:
template<typename M>
Enable_if<Matrix_type<M>(),ostream&>
operator<<(ostream& os, const M& m)
{
os << '{';
for (size_t i = 0; i!=rows(m); ++i){
os << m[i];
if (i+1!=rows(m)) os << ',';
}
return os << '}';
}
Here, Matrix_type is a concept (§24.3). Enable_if is an alias for enable_if’s type (§28.4), so this operator<<() returns an ostream&.
Given that, cout<<m prints: {{0,1,2,3},{10,11,12,13},{20,21,22,23}}.
29.1.2. Matrix Requirements
Before proceeding with an implementation, consider what properties we might like to have:
• N dimensions, where N is a parameter that can vary from 0 to many, without specialized code for every dimension.
• N-dimensional storage is useful in general, so the element type can be anything we can store (like a vector element).
• The mathematical operations should apply to any type that can reasonably be described as a number, including a Matrix.
• Fortran-style subscripting using one index per dimension, for example, m(1,2,3) for a 3-D Matrix, yielding an element.
• C-style subscripting, for example, m[7], yielding a row (a row is an N–1-D sub-Matrix of an N-D Matrix).
• Subscripting should be potentially fast and potentially range checked.
• Move assignment and move constructor to ensure efficient passing of Matrix results and to eliminate expensive temporaries.
• Some mathematical matrix operations, such as + and *=.
• A way to read, write, and pass around references to submatrices, Matrix_refs, for use for both reading and writing elements.
• The absence of resource leaks in the form of the basic guarantee (§13.2).
• Fused critical operations, for example, m*v+v2 as a single function call.
This is a relatively long and ambitious list, but it does not add up to “everything for everybody.” For example, I did not list:
• Many more mathematical matrix operations
• Specialized matrices (e.g., diagonal and triangular matrices)
• Sparse Matrix support
• Support for parallel execution of Matrix operations
However valuable those properties are, they go beyond what is needed to present basic programming techniques.
To provide this, I use a combination of several language features and programming techniques:
• Classes (of course)
• Parameterization with numbers and types
• Move constructors and assignments (to minimize copying)
• RAII (relying on constructors and destructors)
• Variadic templates (for specifying extents and for indexing)
• Initializer lists
• Operator overloading (to get conventional notation)
• Function objects (to carry information about subscripting)
• Some simple template metaprogramming (e.g., for checking initializer lists and for distinguishing reading and writing for Matrix_refs)
• Implementation inheritance for minimizing code replication.
Obviously, a Matrix like this could be a built-in type (as it is in many languages), but the point here is exactly that in C++ it is not built in. Instead, facilities are provided for users to make their own.
29.2. A Matrix Template
To give an overview, here is the declaration of Matrix with its most interesting operations:
template<typename T, size_t N>
class Matrix {
public:
static constexpr size_t order = N;
using value_type = T;
using iterator = typename std::vector<T>::iterator;
using const_iterator = typename std::vector<T>::const_iterator;
Matrix() = default;
Matrix(Matrix&&) = default; // move
Matrix& operator=(Matrix&&) = default;
Matrix(Matrix const&) = default; // copy
Matrix& operator=(Matrix const&) = default;
~Matrix() = default;
template<typename U>
Matrix(const Matrix_ref<U,N>&); // construct from Matrix_ref
template<typename U>
Matrix& operator=(const Matrix_ref<U,N>&); // assign from Matrix_ref
template<typename...Exts> // specify the extents
explicit Matrix(Exts... exts);
Matrix(Matrix_initializer<T,N>); // initialize from list
Matrix& operator=(Matrix_initializer<T,N>); // assign from list
template<typename U>
Matrix(initializer_list<U>) =delete; // don't use {} except for elements
template<typename U>
Matrix& operator=(initializer_list<U>) = delete;
static constexpr size_t order() { return N; } // number of dimensions
size_t extent(size_t n) const { return desc.extents[n]; } // #elements in the nth dimension
size_t size() const { return elems.size(); } // total number of elements
const Matrix_slice<N>& descriptor() const { return desc; } // the slice defining subscripting
T* data() { return elems.data(); } // "flat" element access
const T* data() const { return elems.data(); }
// ...
private:
Matrix_slice<N> desc; // slice defining extents in the N dimensions
vector<T> elems; // the elements
};
Using a vector<T> to hold the elements relieves us from concerns of memory management and exception safety. A Matrix_slice holds the sizes necessary to access the elements as an N-dimensional matrix (§29.4.2). Think of it as a gslice (§40.5.6) specialized for our Matrix.
A Matrix_ref (§29.4.3) behaves just like a Matrix except that it refers to a Matrix, typically a sub-Matrix such as a row or a column, rather than owning its own elements. Think of it as a reference to a sub-Matrix.
A Matrix_initializer<T,N> is a suitably nested initializer list for a Matrix<T,N> (§29.4.4).
29.2.1. Construction and Assignment
The default copy and move operations have just the right semantics: memberwise copy or move of the desc (slice descriptor defining subscripting) and the elements. Note that for management of the storage for elements, Matrix gets all the benefits from vector. Similarly, the default constructor and destructor have just the right semantics.
The constructor that takes extents (numbers of elements in dimensions) is a fairly trivial example of a variadic template (§28.6):
template<typename T, size_t N>
template<typename ... Exts>
Matrix<T,N>::Matrix(Exts... exts)
:desc{exts...}, // copy extents
elems(desc.size) // allocate desc.size elements and default initialize them
{}
The constructor that takes an initializer list requires a bit of work:
template<typename T, size_t N>
Matrix<T, N>::Matrix(Matrix_initializer<T,N> init)
{
Matrix_impl::derive_extents(init,desc.extents); // deduce extents from initializer list (§29.4.4)
elems.reserve(desc.size); // make room for slices
Matrix_impl::insert_flat(init,elems); // initialize from initializer list (§29.4.4)
assert(elems.size() == desc.size);
}
The Matrix_initializer is a suitably nested initializer_list (§29.4.4). The extents are deduced by the Matrix_slice constructor, checked, and stored in desc. Then, the elements are stored in elems by insert_flat() from the Matrix_impl namespace.
To ensure that {} initialization is only used for lists of elements, I =deleted the simple initializer_list constructor. This is to enforce the use of () initialization for extents. For example:
enum class Piece { none, cross, naught };
Matrix<Piece,2> board1 {
{Piece::none, Piece::none, Piece::none},
{Piece::none, Piece::none, Piece::none},
{Piece::none, Piece::none, Piece::cross}
};
Matrix<Piece,2> board2(3,3); // OK
Matrix<Piece,2> board3 {3,3}; // error: constructor from initializer_list<int> deleted
Without that =delete, that last definition would have been accepted.
Finally, we have to be able to construct from a Matrix_ref, that is, from a reference to a Matrix or a part of a Matrix (a submatrix):
template<typename T, size_t N>
template<typename U>
Matrix<T,N>::Matrix(const Matrix_ref<U,N>& x)
:desc{x.desc}, elems{x.begin(),x.end()} // copy desc and elements
{
static_assert(Convertible<U,T>(),"Matrix constructor: incompatible element types");
}
The use of a template allows us to construct from a Matrix with a compatible element type.
As usual, the assignments resemble the constructors. For example:
template<typename T, size_t N>
template<typename U>
Matrix<T,N>& Matrix<T,N>::operator=(const Matrix_ref<U,N>& x)
{
static_assert(Convertible<U,T>(),"Matrix =: incompatible element types");
desc = x.desc;
elems.assign(x.begin(),x.end());
return *this;
}
That is, we copy the members of Matrix.
29.2.2. Subscripting and Slicing
A Matrix can be accessed through subscripting (to elements or rows), through rows and columns, or through slices (parts of rows or columns).

These are all member functions:
template<typename T, size_t N>
class Matrix {
public:
// ...
template<typename ... Args> // m(i,j,k) subscripting with integers
Enable_if<Matrix_impl::Requesting_element<Args...>(), T&>
operator()(Args... args);
template<typename ... Args>
Enable_if<Matrix_impl::Requesting_element<Args...>(), const T&>
operator()(Args... args) const;
template<typename ... Args> // m(s1,s2,s3) subscripting with slices
Enable_if<Matrix_impl::Requesting_slice<Args...>(), Matrix_ref<T, N>>
operator()(const Args&... args);
template<typename ... Args>
Enable_if<Matrix_impl::Requesting_slice<Args...>(), Matrix_ref<const T,N>>
operator()(const Args&... args) const;
Matrix_ref<T,N–1> operator[](size_t i) { return row(i); } // m[i] row access
Matrix_ref<const T,N–1> operator[](size_t i) const { return row(i); }
Matrix_ref<T,N–1> row(size_t n); // row access
Matrix_ref<const T,N–1> row(size_t n) const;
Matrix_ref<T,N–1> col(size_t n); // column access
Matrix_ref<const T,N–1> col(size_t n) const;
// ...
};
C-style subscripting is done by m[i] selecting and returning the ith row:
template<typename T, size_t N>
Matrix_ref<T,N–1> Matrix<T,N>::operator[](size_t n)
{
return row(n); // §29.4.5
}
Think of a Matrix_ref (§29.4.3) as a reference to a sub-Matrix.
Matrix_ref<T,0> is specialized so that it refers to a single element (§29.4.6).
Fortran-style subscripting is done by listing an index for each dimension, for example, m(i,j,k), yielding a scalar:
Matrix<int,2> m2 {
{01,02,03},
{11,12,13}
};
m(1,2) = 99; // overwrite the element in row 1 column 2; that is 13
auto d1 = m(1); // error: too few subscripts
auto d2 = m(1,2,3); // error: too many subscripts
In addition to subscripting with integers, we can subscript with slices. A slice describes a subset of the elements of a dimension (§40.5.4). In particular, slice{i,n} refers to elements [i:i+n) of the dimension to which it applies. For example:
Matrix<int> m2 {
{01,02,03},
{11,12,13},
{21,22,23}
};
auto m22 = m(slice{1,2},slice{0,3});
Now m22 is a Matrix<int,2> with the value
{
{11,12,13},
{21,22,23}
}
The first (row) subscript slice{1,2} selects the last two rows, and the second (column) subscript slice{0,3} selects all elements in the columns.
The return type for a () with slice subscripts is a Matrix_ref, so we can use it as the target of an assignment. For example:
m(slice{1,2},slice{0,3}) = {
{111,112,113},
{121,122,123}
}
Now m has the value
{
{01,02,03},
{111,112,113},
{121,122,123}
}
Selecting all elements from a point onward is so common that there is a shorthand: slice{i} means slice{i,max} where max is larger than the largest subscript in the dimension. So, we can simplify m(slice{1,2},slice{0,3}) to the equivalent m(slice{1,2},slice{0}).
The other simple common case is to select all elements of a single row or column, so a plain integer subscript i among a set of slice subscripts is interpreted as slice{i,1}. For example:
Matrix<int> m3 {
{01,02,03},
{11,12,13},
{21,22,23}
};
auto m31 = m(slice{1,2},1); // m31 becomes {{12},{22}}
auto m32 = m(slice{1,2},0); // m33 becomes {{11},{21}}
auto x = m(1,2); // x == 13
The notion of slicing subscripts is supported in essentially all languages used for numeric programming, so hopefully it is not too unfamiliar.
The implementations of row(), column(), and operator()() are presented in §29.4.5. The implementations of const versions of these functions are basically the same as those of their non-const versions. The key difference is that const versions return results with const elements.
29.3. Matrix Arithmetic Operations
So, we can create Matrixes, copy them, access their elements and rows. However, what we often want is to have mathematical operations that save us from expressing our algorithms in terms of accesses to individual elements (scalars). For example:
Matrix<int,2> mi {{1,2,3}, {4,5,6 }}; // 2-by-3
Matrix<int,2> m2 {mi}; // copy
mi*=2; // scale: {{2,4,6},{8,10,12}}
Matrix<int,2> m3 = mi+m2; // add: {{3,6,9},{12,15,18}}
Matrix<int,2> m4 {{1,2}, {3,4}, {5,6}}; // 3-by-2
Matrix<int,1> v = mi*m4; // multiply: {{18,24,30},{38,52,66},{58,80,102}}
The mathematical operations are defined like this:
template<typename T, size_t N>
class Matrix {
// ...
template<typename F>
Matrix& apply(F f); // f(x) for every element x
template<typename M, typename F>
Matrix& apply(const M& m, F f); // f(x,mx) for corresponding elements
Matrix& operator=(const T& value); // assignment with scalar
Matrix& operator+=(const T& value); // scalar addition
Matrix& operator-=(const T& value); // scalar subtraction
Matrix& operator*=(const T& value); // scalar multiplication
Matrix& operator/=(const T& value); // scalar division
Matrix& operator%=(const T& value); // scalar modulo
template<typename M> // matrix addition
Matrix& operator+=(const M& x);
template<typename M> // matrix subtraction
Matrix& operator-=(const M& x);
// ...
};
// Binary +, -, * are provided as nonmember functions
29.3.1. Scalar Operations
A scalar arithmetic operation simply applies its operation and right-hand operand to each element. For example:
template<typename T, size_t N>
Matrix<T,N>& Matrix<T,N>::operator+=(const T& val)
{
return apply([&](T& a) { a+=val; } ); // using a lambda (§11.4)
}
This apply() applies a function (or a function object) to each element of its Matrix:
template<typename T, size_t N>
template<typename F>
Matrix<T,N>& Matrix<T,N>::apply(F f)
{
for (auto& x : elems) f(x); // this loop uses stride iterators
return *this;
}
As usual, returning *this enables chaining. For example:
m.apply(abs).apply(sqrt); // m[i] = sqrt(abs(m[i])) for all i
As usual (§3.2.1.1, §18.3), we can define the “plain operators,” such as +, outside the class using the assignment operators, such as +=. For example:
template<typename T, size_t N>
Matrix<T,N> operator+(const Matrix<T,N>& m, const T& val)
{
Matrix<T,N> res = m;
res+=val;
return res;
}
Without the move constructor, this return type would be a bad performance bug.
29.3.2. Addition
Addition of two Matrixes is very similar to the scalar versions:
template<typename T, size_t N>
template<typename M>
Enable_if<Matrix_type<M>(),Matrix<T,N>&> Matrix<T,N>::operator+=(const M& m)
{
static_assert(m.order()==N,"+=: mismatched Matrix dimensions");
assert(same_extents(desc,m.descriptor())); // make sure sizes match
return apply(m, [](T& a,Value_type<M>&b) { a+=b; });
}
Matrix::apply(m,f) is the two-argument version of Matrix::apply(f). It applies its f to its two Matrixes (m and *this):
template<typename T, size_t N>
template<typename M, typename F>
Enable_if<Matrix_type<M>(),Matrix<T,N>&> Matrix<T,N>::apply(M& m, F f)
{
assert(same_extents(desc,m.descriptor())); // make sure sizes match
for (auto i = begin(), j = m.begin(); i!=end();++i,++j)
f(*i,*j);
return *this;
}
Now operator+() is easily defined:
template<typename T, size_t N>
Matrix<T,N> operator+(const Matrix<T,N>& a, const Matrix<T,N>& b)
{
Matrix<T,N> res = a;
res+=b;
return res;
}
This defines + for two Matrixes of the same type yielding a result of that type. We could generalize:
template<typename T, typename T2, size_t N,
typename RT = Matrix<Common_type<Value_type<T>,Value_type<T2>>,N>
Matrix<RT,N> operator+(const Matrix<T,N>& a, const Matrix<T2,N>& b)
{
Matrix<RT,N> res = a;
res+=b;
return res;
}
If, as is common, T and T2 are the same type, Common_type is that type. The Common_type type function is derived from std::common_type (§35.4.2). For built-in types it, like ?:, gives a type that best preserves values of arithmetic operations. If Common_type is not defined for a pair of types we want to use in combination, we can define it. For example:
template<>
struct common_type<Quad,long double> {
using type = Quad;
};
Now Common_type<Quad,long double> is Quad.
We also need operations involving Matrix_refs (§29.4.3). For example:
template<typename T, size_t N>
Matrix<T,N> operator+(const Matrix_ref<T,N>& x, const T& n)
{
Matrix<T,N>
res = x; res+=n;
return res;
}
Such operations look exactly like their Matrix equivalents. There is no difference between Matrix and Matrix_ref element access: the difference between Matrix and Matrix_ref is in the initialization and ownership of elements.
Subtraction, multiplication, etc., by scalars and the handling of Matrix_refs are just repetition of the techniques used for addition.
29.3.3. Multiplication
Matrix multiplication is not as simple as addition: the product of an N-by-M matrix and a M-by-P matrix is an N-by-P matrix. For M==1 we get that the product of two vectors is a matrix, and from P==1 we get that the product of a matrix and a vector is a vector. We can generalize matrix multiplication into higher dimensions, but to do that we have to introduce tensors [Kolecki,2002], and I don’t want to divert this discussion of programming techniques and how to use language features into a physics and engineering math lesson. So, I’ll stick to one and two dimensions.
Treating one Matrix<T,1> as an N-by-1 matrix and another as a 1-by-M matrix, we get:
template<typename T>
Matrix<T,2> operator*(const Matrix<T,1>& u, const Matrix<T,1>& v)
{
const size_t n = u.extent(0);
const size_t m = v.extent(0);
Matrix<T,2> res(n,m); // an n-by-m matrix
for (size_t i = 0; i!=n; ++i)
for (size_t j = 0; j!=m; ++j)
res(i,j) = u[i]*v[j];
return res;
}
This is the simplest case: matrix element res(i,j) is u[i]*v[j]. I have not tried to generalize to handle the cases where the element types of the vectors are different. If necessary, the techniques discussed for addition can be used.
Note that I’m writing to each element of res twice: once to initialize to T{} and once to assign u[i]*v[j]. This roughly doubles the cost of the multiplication. If that bothers you, write a multiplication without that overhead and see if the difference matters in your program.
Next, we can multiply an N-by-M matrix with a vector seen as an M-by-1 matrix. The result is an N-by-1 matrix:
template<typename T>
Matrix<T,1> operator*(const Matrix<T,2>& m, const Matrix<T,1>& v)
{
assert(m.extent(1)==v.extent(0));
const size_t n = m.extent(0);
Matrix<T,1> res(n);
for (size_t i = 0; i!=n; ++i)
for (size_t j = 0; j!=n; ++j)
res(i) += m(i,j)*v(j);
return res;
}
Note that the declaration of res initializes its elements to T{}, which is zero for numeric types, so that the += starts out from zero.
The N-by-M matrix times M-by-P matrix is handled similarly:
template<typename T>
Matrix<T,2> operator*(const Matrix<T,2>& m1, const Matrix<T,2>& m2)
{
const size_t n = m1.extent(0);
const size_t m = m1.extent(1);
assert(m==m2.extent(0)); // columns must match rows
const size_t p = m2.extent(1);
Matrix<T,2> res(n,p);
for (size_t i = 0; i!=n; ++i)
for (size_t j = 0; j!=m; ++j)
for (size_t k = 0; k!=p; ++k)
res(i,j) = m1(i,k)*m2(k,j);
return res;
}
There are numerous ways of optimizing this important operation.
That innermost loop could be more elegantly expressed as:
res(i,j) = dot_product(m1[i],m2.column(j))
Here, dot_product() is simply an interface to the standard-library inner_product() (§40.6.2):
template<typename T>
T dot_product(const Matrix_ref<T,1>& a, const Matrix_ref<T,1>& b)
{
return inner_product(a.begin(),a.end(),b.begin(),0.0);
}
29.4. Matrix Implementation
So far, I have delayed the presentation of the most complicated (and for some programmers the most interesting) “mechanical” parts of the Matrix implementation. For example: What is a Matrix_ref? What is a Matrix_slice? How do you initialize a Matrix from a nest of initializer_lists and make sure the dimensions are reasonable? How do we ensure that we don’t instantiate a Matrix with an unsuitable element type?
The easiest way to present this code is to place all of Matrix in a header file. In that case, add inline the definition of every nonmember function.
The definitions of functions that are not members of Matrix, Matrix_ref, Matrix_slice, or part of the general interface are placed in namespace Matrix_impl.
29.4.1. slice()
A simple slice as used for slice subscripting describes a mapping from an integer (subscript) to an element location (index) in terms of three values:
struct slice {
slice() :start(-1), length(-1), stride(1) { }
explicit slice(size_t s) :start(s), length(-1), stride(1) { }
slice(size_t s, size_t l, size_t n = 1) :start(s), length(l), stride(n) { }
size_t operator()(size_t i) const { return start+i*stride; }
static slice all;
size_t start; // first index
size_t length; // number of indices included (can be used for range checking)
size_t stride; // distance between elements in sequence
};
There is a standard-library version of slice; see §40.5.4 for a more thorough discussion. This version provides notational convenience (e.g., the default values provided by the constructors).
29.4.2. Matrix Slices
A Matrix_slice is the part of the Matrix implementation that maps a set of subscripts to the location of an element. It uses the idea of generalized slices (§40.5.6):
template<size_t N>
struct Matrix_slice {
Matrix_slice() = default; // an empty matrix: no elements
Matrix_slice(size_t s, initializer_list<size_t> exts); // extents
Matrix_slice(size_t s, initializer_list<size_t> exts, initializer_list<size_t> strs);// extents and strides
template<typename...Dims> // N extents
Matrix_slice(Dims... dims);
template<typename... Dims,
typename = Enable_if<All(Convertible<Dims,size_t>()...)>>
size_t operator()(Dims... dims) const; // calculate index from a set of subscripts
size_t size; // total number of elements
size_t start; // starting offset
array<size_t,N> extents; // number of elements in each dimension
array<size_t,N> strides; // offsets between elements in each dimension
};
In other words, a Matrix_slice describes what is considered rows and columns in a region of memory. In the usual C/C++ row-major layout of a matrix, the elements of rows are contiguous, and the elements of a column are separated by a fixed number of elements (a stride). A Matrix_sliceis a function object, and its operator()() does a stride calculation (§40.5.6):
template<size_t N>
template<typename... Dims>
size_t Matrix_slice<N>::operator()(Dims... dims) const
{
static_assert(sizeof...(Dims) == N, "");
size_t args[N] { size_t(dims)... }; // Copy arguments into an array
return inner_product(args,args+N,strides.begin(),size_t(0));
}
Subscripting must be efficient. This is a simplified algorithm that needs to be optimized. If nothing else, specialization can be used to eliminate the simplifying copy of subscripts out of the variadic template’s parameter pack. For example:
template<>
struct Matrix_slice<1> {
// ...
size_t operator()(size_t i) const
{
return i;
}
}
template<>
struct Matrix_slice<2> {
// ...
size_t operator()(size_t i, size_t j) const
{
return i*stides[0]+j;
}
}
The Matrix_slice is fundamental for defining the shape of a Matrix (its extents) and for implementing N-dimensional subscripting. However, it is also useful for defining submatrices.
29.4.3. Matrix_ref
A Matrix_ref is basically a clone of the Matrix class used to represent sub-Matrixes. However, a Matrix_ref does not own its elements. It is constructed from a Matrix_slice and a pointer to elements:
template<typename T, size_t N>
class Matrix_ref {
public:
Matrix_ref(const Matrix_slice<N>& s, T* p) :desc{s}, ptr{p} {}
// ... mostly like Matrix ...
private:
Matrix_slice<N> desc; // the shape of the matrix
T* ptr; // the first element in the matrix
};
A Matrix_ref simply points to the elements of “its” Matrix. Obviously, a Matrix_ref should not outlive its Matrix. For example:
Matrix_ref<double,1> user()
{
Matrix<double,2> m = {{1,2}, {3,4}, {5,6}};
return m.row(1);
}
auto mr = user(); // trouble
The great similarity between Matrix and Matrix_ref leads to duplication. If that becomes a bother, we can derive both from a common base:
template<typename T, size_t N>
class Matrix_base {
// ... common stuff ...
};
template<typename T, size_t N>
class Matrix : public Matrix_base<T,N> {
// ... special to Matrix ...
private:
Matrix_slice<N> desc; // the shape of the matrix
vector<T> elements;
};
template<typename T, size_t N>
class Matrix_ref : public Matrix_base<T,N> {
// ... special to Matrix_ref ...
private:
Matrix_slice<N> desc; // the shape of the matrix
T* ptr;
};
29.4.4. Matrix List Initialization
The Matrix constructor that constructs from an initializer_list takes as its argument type the alias Matrix_initializer:
template<typename T, size_t N>
using Matrix_initializer = typename Matrix_impl::Matrix_init<T, N>::type;
Matrix_init describes the structure of a nested initializer_list.
Matrix_init<T,N> simply has Matrix_init<T,N–1> as its member type:
template<typename T, size_t N>
struct Matrix_init {
using type = initializer_list<typename Matrix_init<T,N–1>::type>;
};
The N==1 is special. That is where we get to the (most deeply nested) initializer_list<T>:
template<typename T>
struct Matrix_init<T,1> {
using type = initializer_list<T>;
};
To avoid surprises, we define N=0 to be an error:
template<typename T>
struct Matrix_init<T,0>; // undefined on purpose
We can now complete the Matrix constructor that takes a Matrix_initializer:
template<typename T, size_t N>
Matrix<T, N>::Matrix(Matrix_initializer<T,N> init)
{
Matrix_impl::derive_extents(init,desc.extents); // deduce extents from initializer list (§29.4.4)
elems.reserve(desc.size); // make room for slices
Matrix_impl::insert_flat(init,elems); // initialize from initializer list (§29.4.4)
assert(elems.size() == desc.size);
}
To do so, we need two operations that recurse down a tree of initializer_lists for a Matrix<T,N>:
• derive_extents() determines the shape of the Matrix:
• Checks that the tree really is N deep
• Checks that each row (sub-initialize_list) has the same number of elements
• Sets the extent of each row
• insert_flat() copies the elements of the tree of initializer_list<T>s into the elems of a Matrix.
The derived_extents() called from a Matrix constructor to initialize its desc looks like this:
template<size_t N, typename List>
array<size_t, N> derive_extents(const List& list)
{
array<size_t,N> a;
auto f = a.begin();
add_extents<N>(f,list); // put extents from list into f[]
return a;
}
You give it an initializer_list and it returns an array of extents.
The recursion is done from N to the final 1 where the initializer_list is an initializer_list<T>.
template<size_t N, typename I, typename List>
Enable_if<(N>1),void> add_extents(I& first, const List& list)
{
assert(check_non_jagged(list));
*first = list.size();
add_extents<N-1>(++first,*list.begin());
}
template<size_t N, typename I, typename List>
Enable_if<(N==1),void> add_extents(I& first, const List& list)
{
*first++ = list.size(); // we reached the deepest nesting
}
The check_non_jagged() function checks that all rows have the same number of elements:
template<typename List>
bool check_non_jagged(const List& list)
{
auto i = list.begin();
for (auto j = i+1; j!=list.end(); ++j)
if (i->size()!=j->size())
return false;
return true;
}
We need insert_flat() to take a possibly nested initializer list and present its elements to Matrix<T> as a vector<T>. It takes the initializer_list given to a Matrix as the Matrix_initializer and provides the elements as the target:
template<typename T, typename Vec>
void insert_flat(initializer_list<T> list, Vec& vec)
{
add_list(list.begin(),list.end(),vec);
}
Unfortunately, we can’t rely on the elements being allocated contiguously in memory, so we need to build the vector through a set of recursive calls. If we have a list of initializer_lists, we recurse through each:
template<typename T, typename Vec> // nested initializer_lists
void add_list(const initializer_list<T>* first, const initializer_list<T>* last, Vec& vec)
{
for (;first!=last;++first)
add_list(first->begin(),first->end(),vec);
}
When we reach a list with non-initializer_list elements, we insert those elements into our vector:
template<typename T, typename Vec>
void add_list(const T *first, const T *last, Vec& vec)
{
vec.insert(vec.end(),first,last);
}
I use vec.insert(vec.end(),first,last) because there is no push_back() that takes a sequence argument.
29.4.5. Matrix Access
A Matrix provides access by row, column, slice (§29.4.1), and element (§29.4.3). A row() or column() operation returns a Matrix_ref<T,N–1>, the () subscript operation with integers returns a T&, and the () subscript operation with slices returns a Matrix<T,N>.
The row of a Matrix<T,N> is a Matrix_ref<T,N–1> as long as 1<N:
template<typename T, size_t N>
Matrix_ref<T,N-1> Matrix<T,N>::row(size_t n)
{
assert(n<rows());
Matrix_slice<N-1> row;
Matrix_impl::slice_dim<0>(n,desc,row);
return {row,data()};
}
We need specializations for N==1 and N==0:
template<typename T>
T& Matrix<T,1>::row(size_t i)
{
return &elems[i];
}
template<typename T>
T& Matrix<T,0>::row(size_t n) = delete;
Selecting a column() is essentially the same as selecting a row(). The difference is simply in the construction of the Matrix_slice:
template<typename T, size_t N>
Matrix_ref<T,N-1> Matrix<T,N>::column(size_t n)
{
assert(n<cols());
Matrix_slice<N-1> col;
Matrix_impl::slice_dim<1>(n,desc,col);
return {col,data()};
}
The const versions are equivalent.
Requesting_element() and Requesting_slice() are concepts for a set of integers used for subscripting with a set of integers and subscripting by a slice, respectively (§29.4.5). They check that a sequence of access-function arguments are of suitable types for use as subscripts.
Subscripting with integers is defined like this:
template<typename T, size_t N> // subscripting with integers
template<typename... Args>
Enable_if<Matrix_impl::Requesting_element<Args...>(),T&>
Matrix<T,N>::operator()(Args... args)
{
assert(Matrix_impl::check_bounds(desc, args...));
return *(data() + desc(args...));
}
The check_bounds() predicate checks that the number of subscripts equals the number of dimensions and that the subscripts are within bounds:
template<size_t N, typename... Dims>
bool check_bounds(const Matrix_slice<N>& slice, Dims... dims)
{
size_t indexes[N] {size_t(dims)...};
return equal(indexes, indexes+N, slice.extents, less<size_t> {});
}
The actual location of the element in the Matrix is calculated by invoking the Matrix’s Matrix_slice’s generalized slice calculation presented as a function object: desc(args...). Add that to the start of the data (data()) and we have our location:
return *(data() + desc(args...));
This leaves the most mysterious part of the declaration for last. The specification of operator()()’s return type looks like this:
Enable_if<Matrix_impl::Requesting_element<Args...>(),T&>
So the return type is T& provided that
Matrix_impl::Requesting_element<Args...>()
is true (§28.4). This predicate simply checks that every subscript can be converted to the required size_t by using a concept version of the standard-library predicate is_convertible (§35.4.1):
template<typename ... Args>
constexpr bool Requesting_element()
{
return All(Convertible<Args,size_t>()...);
}
All() simply applies its predicate to every element of a variadic template:
constexpr bool All() { return true; }
template<typename ... Args>
constexpr bool All(bool b, Args... args)
{
return b && All(args...);
}
The reason for using a predicate (Requesting_element) and the Enable_if() “hidden” within Request is to choose between the element and the slice subscript operators. The predicate used by the slice subscript operator looks like this:
template<typename... Args>
constexpr bool Requesting_slice()
{
return All((Convertible<Argssize_t>() || Same<Args,slice>())...)
&& Some(Same<Args,slice>()...);
}
That is, if there is at least one slice argument and if all arguments are either convertible to slice or size_t, we have something that can be used to describe a Matrix<T,N>:
template<typename T, size_t N> // subscripting with slices
template<typename... Args>
Enable_if<Matrix_impl::Requesting_slice<Args...>(), Matrix_ref<T,N>>
Matrix<T,N>::operator()(const Args&... args)
{
matrix_slice<N> d;
d.start = matrix_impl::do_slice(desc,d,args...);
return {d,data()};
}
The slices represented as extents and strides in a Matrix_slice and used for slice subscripting are computed like this:
template<size_t N, typename T, typename... Args>
size_t do_slice(const Matrix_slice<N>& os, Matrix_slice<N>& ns, const T& s, const Args&... args)
{
size_t m = do_slice_dim<sizeof...(Args)+1>(os,ns,s);
size_t n = do_slice(os,ns,args...);
return m+n;
}
As usual, the recursion is terminated by a simple function:
template<size_t N>
size_t do_slice(const Matrix_slice<N>& os, Matrix_slice<N>& ns)
{
return 0;
}
The do_slice_dim() is a tricky bit of computation (to get the slice values right) but illustrates no new programming techniques.
29.4.6. Zero-Dimensional Matrix
The Matrix code contains a lot of occurrences of N–1 where N is the number of dimensions. Thus, N==0 could easily become a nasty special case (for the programming as well as for the mathematics). Here, we solve the problem by defining a specialization:
template<typename T>
class Matrix<T,0> {
public:
static constexpr size_t order = 0;
using value_type = T;
Matrix(const T& x) : elem(x) { }
Matrix& operator=(const T& value) { elem = value; return *this; }
T& operator()() { return elem; }
const T& operator()() const { return elem; }
operator T&() { return elem; }
operator const T&() { return elem; }
private:
T elem;
};
Matrix<T,0> is not really a matrix. It stores a single element of type T and can only be converted to a reference to that type.
29.5. Solving Linear Equations
The code for a numerical computation makes sense if you understand the problem being solved and the math used to express the solution and tends to appear to be utter nonsense if you don’t. The example used here should be rather trivial if you have learned basic linear algebra; if not, just see it as an example of transcribing a textbook solution into code with minimal rewording.
The example here is chosen to demonstrate a reasonably realistic and important use of Matrixes. We will solve a set (any set) of linear equations of this form:
a1,1 x1 + ... + a1,n xn = b1
...
an,1 x1 + ... + an,n xn = bn
Here, the xs designate the n unknowns; as and bs are given constants. For simplicity, we assume that the unknowns and the constants are floating-point values. The goal is to find values for the unknowns that simultaneously satisfy the n equations. These equations can compactly be expressed in terms of a matrix and two vectors:
Ax =b
Here, A is the square n-by-n matrix defined by the coefficients:
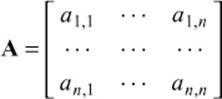
The vectors x and b are the vectors of unknowns and constants, respectively:
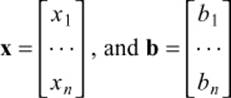
This system may have zero, one, or an infinite number of solutions, depending on the coefficients of the matrix A and the vector b. There are various methods for solving linear systems. We use a classic scheme, called Gaussian elimination [Freeman,1992], [Stewart,1998], [Wood,1999]. First, we transform A and b so that A is an upper-triangular matrix. By “upper-triangular,” we mean all the coefficients below the diagonal of A are zero. In other words, the system looks like this:
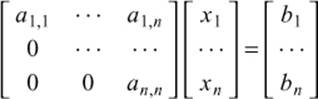
This is easily done. A zero for position a(i,j) is obtained by multiplying the equation for row i by a constant so that a(i,j) equals another element in column j, say a(k,j). That done, we just subtract the two equations, and a(i,j)==0 and the other values in row i change appropriately.
If we can get all the diagonal coefficients to be nonzero, then the system has a unique solution, which can be found by “back substitution.” The last equation is easily solved:
an,n xn = bn
Obviously, x[n] is b[n]/a(n,n). That done, eliminate row n from the system and proceed to find the value of x[n–1], and so on, until the value for x[1] is computed. For each n, we divide by a(n,n) so the diagonal values must be nonzero. If that does not hold, the back substitution method fails, meaning that the system has zero or an infinite number of solutions.
29.5.1. Classical Gaussian Elimination
Now let us look at the C++ code to express this. First, we’ll simplify our notation by conventionally naming the two Matrix types that we are going to use:
using Mat2d = Matrix<double,2>;
using Vec = Matrix<double,1>;
Next, we will express our desired computation:
Vec classical_gaussian_elimination(Mat2d A, Vec b)
{
classical_elimination(A, b);
return back_substitution(A, b);
}
That is, we make copies of our inputs A and b (using call-by-value), call a function to solve the system, and then calculate the result to return by back substitution. The point is that our breakdown of the problem and our notation for the solution are right out of the textbook. To complete our solution, we have to implement classical_elimination() and back_substitution(). Again, the solution is in the textbook:
void classical_elimination(Mat2d& A, Vec& b)
{
const size_t n = A.dim1();
// traverse from 1st column to the next-to-last, filling zeros into all elements under the diagonal:
for (size_t j = 0; j!=n-1; ++j) {
const double pivot = A(j, j);
if (pivot==0) throw Elim_failure(j);
// fill zeros into each element under the diagonal of the ith row:
for (size_t i = j+1; i!=n; ++i) {
const double mult = A(i,j) / pivot;
A[i](slice(j)) = scale_and_add(A[j](slice(j)), -mult,A[i](slice(j)));
b(i) -= mult*b(j); // make the corresponding change to b
}
}
}
The pivot is the element that lies on the diagonal of the row we are currently dealing with. It must be nonzero because we need to divide by it; if it is zero, we give up by throwing an exception:
Vec back_substitution(const Mat2d& A, const Vec& b)
{
const size_t n = A.dim1();
Vec x(n);
for (size_t i = n-1; i>=0; --i) {
double s = b(i)-dot_product(A[i](slice(i+1)),x(slice(i+1)));
if (double m = A(i,i))
x(i) = s/m;
else
throw Back_subst_failure(i);
}
return x;
}
29.5.2. Pivoting
We can avoid the divide-by-zero problem and also achieve a more robust solution by sorting the rows to get zeros and small values away from the diagonal. By “more robust” we mean less sensitive to rounding errors. However, the values change as we go along placing zeros under the diagonal, so we have to also reorder to get small values away from the diagonal (that is, we can’t just reorder the matrix and then use the classical algorithm):
void elim_with_partial_pivot(Mat2d& A, Vec& b)
{
const size_t n = A.dim1();
for (size_t j = 0; j!=n; ++j) {
size_t pivot_row = j;
// look for a suitable pivot:
for (size_t k = j+1; k!=n; ++k)
if (abs(A(k,j)) > abs(A(pivot_row,j)))
pivot_row = k;
// swap the rows if we found a better pivot:
if (pivot_row!=j) {
A.swap_rows(j,pivot_row);
std::swap(b(j),b(pivot_row));
}
// elimination:
for (size_t i = j+1; i!=n; ++i) {
const double pivot = A(j,j);
if (pivot==0) error("can't solve: pivot==0");
const double mult = A(i,j)/pivot;
A[i].slice(j) = scale_and_add(A[j].slice(j), –mult, A[i].slice(j));
b(i) –= mult*b(j);
}
}
}
We use swap_rows() and scale_and_multiply() to make the code more conventional and to save us from writing an explicit loop.
29.5.3. Testing
Obviously, we have to test our code. Fortunately, there is a simple way to do that:
void solve_random_system(size_t n)
{
Mat2d A = random_matrix(n); // generate random Mat2d
Vec b = random_vector(n); // generate random Vec
cout << "A = " << A << endl;
cout << "b = " << b << endl;
try {
Vec x = classical_gaussian_elimination(A, b);
cout << "classical elim solution is x = " << x << endl;
Vec v = A * x;
cout << " A * x = "<<v<< endl;
}
catch(const exception& e) {
cerr << e.what() << endl;
}
}
We can get to the catch-clause in three ways:
• A bug in the code (but, being optimists, we don’t think there are any)
• An input that trips up classical_elimination() (using elim_with_partial_pivot() would minimize the chances of that)
• Rounding errors
However, our test is not as realistic as we’d like because genuinely random matrices are unlikely to cause problems for classical_elimination().
To verify our solution, we print out A*x, which had better equal b (or close enough for our purpose, given rounding errors). The likelihood of rounding errors is the reason we didn’t just do:
if (A*x!=b) error("substitution failed");
Because floating-point numbers are just approximations to real numbers, we have to accept approximately correct answers. In general, using == and != on the result of a floating-point computation is best avoided: floating-point is inherently an approximation. Had I felt the need for a machine check, I would have defined an equal() function with a notion of which error ranges to consider acceptable and then written:
if (equal(A*x,b)) error("substitution failed");
The random_matrix() and random_vector() are simple uses of random numbers and are left as simple exercises for the reader.
29.5.4. Fused Operations
In addition to providing efficient primitive operations, a general matrix class must handle three related problems to satisfy performance-conscious users:
[1] The number of temporaries must be minimized.
[2] Copying of matrices must be minimized.
[3] Multiple loops over the same data in composite operations must be minimized.
Consider U=M*V+W, where U, V, and W are vectors (Matrix<T,1>) and M is a Matrix<T,2>. A naive implementation introduces temporary vectors for M*V and M*V+W and copies the results of M*V and M*V+W. A smart implementation calls a functionmul_add_and_assign(&U,&M,&V,&W) that introduces no temporaries, copies no vectors, and touches each element of the matrices the minimum number of times.
The move constructor helps: the temporary used for M*V is used for (M*V)+W. If we had written
Matrix<double,1> U=M*V+W;
we would have eliminated all element copies: the elements allocated in the local variable in M*V are the ones ending up in U.
That leaves the problem of merging the loops: loop fusion. This degree of optimization is rarely necessary for more than a few kinds of expressions, so a simple solution to efficiency problems is to provide functions such as mul_add_and_assign() and let the user call those where it matters. However, it is possible to design a Matrix so that such optimizations are applied automatically for expressions of the right form. That is, we can treat U=M*V+W as a use of a single operator with four operands. The basic technique was demonstrated for ostream manipulators (§38.4.5.2). In general, it can be used to make a combination of n binary operators act like an (n+1)-ary operator. Handling U=M*V+W requires the introduction of two auxiliary classes. However, the technique can result in impressive speedups (say, 30 times) on some systems by enabling more powerful optimization techniques. First, for simplicity, let us restrict ourselves to two-dimensional matrices of double-precision floating-point numbers:
using Mat2d = Matrix<double,2>;
using Vec = Matrix<double,1>;
We define the result of multiplying a Mat2d by a Vec:
struct MVmul {
const Mat2d& m;
const Vec& v;
MVmul(const Mat2d& mm, const Vec &vv) :m{mm}, v{vv} { }
operator Vec();// evaluate and return result
};
inline MVmul operator*(const Mat2d& mm, const Vec& vv)
{
return MVmul(mm,vv);
}
This “multiplication” should replace the one from §29.3 and does nothing except store references to its operands; the evaluation of M*V is deferred. The object produced by * is closely related to what is called a closure in many technical communities. Similarly, we can deal with what happens if we add a Vec:
struct MVmulVadd {
const Mat2d& m;
const Vec& v;
const Vec& v2;
MVmulVadd(const MVmul& mv, const Vec& vv) :m(mv.m), v(mv.v), v2(vv) { }
operator Vec();// evaluate and return result
};
inline MVmulVadd operator+(const MVmul& mv, const Vec& vv)
{
return MVmulVadd(mv,vv);
}
This defers the evaluation of M*V+W. We now have to ensure that it all gets evaluated using a good algorithm when it is assigned to a Vec:
template<>
class Matrix<double,1> { // specialization (just for this example)
// ...
public:
Matrix(const MVmulVadd& m) // initialize by result of m
{
// allocate elements, etc.
mul_add_and_assign(this,&m.m,&m.v,&m.v2);
}
Matrix& operator=(const MVmulVadd& m) // assign the result of m to *this
{
mul_add_and_assign(this,&m.m,&m.v,&m.v2);
return *this;
}
// ...
};
Now U=M*V+W is automatically expanded to
U.operator=(MVmulVadd(MVmul(M,V),W))
which because of inlining resolves to the desired simple call
mul_add_and_assign(&U,&M,&V,&W)
Clearly, this eliminates the copying and the temporaries. In addition, we might write mul_add_and_assign() in an optimized fashion. However, if we just wrote it in a fairly simple and unoptimized fashion, it would still be in a form that offered great opportunities to an optimizer.
The importance of this technique is that most really time-critical vector and matrix computations are done using a few relatively simple syntactic forms. Typically, there is no real gain in optimizing expressions of half a dozen operators. For that we typically want to write a function anyway.
This technique is based on the idea of using compile-time analysis and closure objects to transfer evaluation of a subexpression into an object representing a composite operation. It can be applied to a variety of problems with the common attribute that several pieces of information need to be gathered into one function before evaluation can take place. I refer to the objects generated to defer evaluation as composition closure objects, or simply compositors.
If this composition technique is used to delay execution of all operations, it is referred to as expression templates [Vandevoorde,2002] [Veldhuizen,1995]. Expression templates systematically use function objects to represent expressions as abstract syntax trees (ASTs).
29.6. Advice
[1] List basic use cases; §29.1.1.
[2] Always provide input and output operations to simplify simple testing (e.g., unit testing); §29.1.1.
[3] Carefully list the properties a program, class, or library ideally should have; §29.1.2.
[4] List the properties of a program, class, or library that are considered beyond the scope of the project; §29.1.2.
[5] When designing a container template, carefully consider the requirements on the element type; §29.1.2.
[6] Consider how the design might accommodate run-time checking (e.g., for debugging); §29.1.2.
[7] If possible, design a class to mimic existing professional notation and semantics; §29.1.2.
[8] Make sure that the design does not leak resources (e.g., have a unique owner for each resource and use RAII); §29.2.
[9] Consider how a class can be constructed and copied; §29.1.1.
[10] Provide complete, flexible, efficient, and semantically meaningful access to elements; §29.2.2, §29.3.
[11] Place implementation details in their own _impl namespace; §29.4.
[12] Provide common operations that do not require direct access to the representation as helper functions; §29.3.2, §29.3.3.
[13] For fast access, keep data compact and use accessor objects to provide necessary nontrivial access operations; §29.4.1,§29.4.2, §29.4.3.
[14] The structure of data can often be expressed as nested initializer lists; §29.4.4.
[15] When dealing with numbers, aways consider “end cases,” such as zero and “many”; §29.4.6.
[16] In addition to unit testing and testing that the code meets its requirements, test the design through examples of real use; §29.5.
[17] Consider how the design might accommodate unusually stringent performance requirements; §29.5.4