The C++ Programming Language (2013)
Part IV: The Standard Library
31. STL Containers
It was new. It was singular. It was simple. It must succeed!
– H. Nelson
• Introduction
• Container Overview
Container Representation; Element Requirements
• Operations Overview
Member Types; Constructors, Destructor, and Assignments; Size and Capacity; Iterators; Element Access; Stack Operations; List Operations; Other Operations
• Containers
vector; Lists; Associative Containers
• Container Adaptors
stack; queue; priority_queue
• Advice
31.1. Introduction
The STL consists of the iterator, container, algorithm, and function object parts of the standard library. The rest of the STL is presented in Chapter 32 and Chapter 33.
31.2. Container Overview
A container holds a sequence of objects. This section summarizes the types of containers and briefly outlines their properties. Operations on containers are summarized in §31.3.
Containers can be categorized like this:
• Sequence containers provide access to (half-open) sequences of elements.
• Associative containers provide associative lookup based on a key.
In addition, the standard library provides types of objects that hold elements while not offering all of the facilities of sequence containers or associative containers:
• Container adaptors provide specialized access to underlying containers.
• Almost containers are sequences of elements that provide most, but not all, of the facilities of a container.
The STL containers (the sequence and associative containers) are all resource handles with copy and move operations (§3.3.1). All operations on containers provide the basic guarantee (§13.2) to ensure that they interact properly with exception-based error handling.

The A template argument is the allocator that the container uses to acquire and release memory (§13.6.1, §34.4). For example:
template<typename T, typename A = allocator<T>>
class vector {
// ...
};
A is defaulted to std::allocator<T> (§34.4.1) which uses operator new() and operator delete() when it needs to acquire or release memory for its elements.
These containers are defined in <vector>, <list>, and <deque>. The sequence containers are contiguously allocated (e.g., vector) or linked lists (e.g., forward_list) of elements of their value_type (T in the notation used above). A deque (pronounced “deck”) is a mixture of linked-list and contiguous allocation.
Unless you have a solid reason not to, use a vector. Note that vector provides operations for inserting and erasing (removing) elements, allowing a vector to grow and shrink as needed. For sequences of small elements, a vector can be an excellent representation for a data structure requiring list operations.
When inserting and erasing elements of a vector, elements may be moved. In contrast, elements of a list or an associative container do not move when new elements are inserted or other elements are erased.
A forward_list (a singly-linked list) is basically a list optimized for empty and very short lists. An empty forward_list takes up only one word. There are surprisingly many uses for lists where most are empty (and the rest are very short).
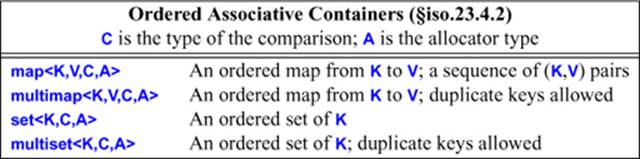
These containers are usually implemented as balanced binary trees (usually red-black trees).
The default ordering criterion for a key, K, is std::less<K> (§33.4).
As for sequence containers, the A template argument is the allocator that the container uses to acquire and release memory (§13.6.1, §34.4). The A template argument is defaulted to std::allocator<std::pair<const K,T>> (§31.4.3) for maps and std::allocator<K> for sets.
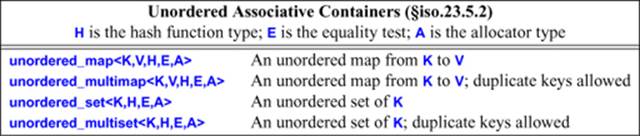
These containers are implemented as hash tables with linked overflow. The default hash function type, H, for a type K is std::hash<K> (§31.4.3.2). The default for the equality function type, E, for a type K is std::equal_to<K> (§33.4); the equality function is used to decide whether two objects with the same hash code are equal.
The associative containers are linked structures (trees) with nodes of their value_type (in the notation used above, pair<const K,V> for maps and K for sets). The sequence of a set, map, or multimap is ordered by its key value (K). An unordered container need not have an ordering relation for its elements (e.g., <) and uses a hash function instead (§31.2.2.1). The sequence of an unordered container does not have a guaranteed order. A multimap differs from a map in that a key value may occur many times.
Container adaptors are containers providing specialized interfaces to other containers:

The default for a priority_queue’s priority function, Cmp, is std::less<T>. The default for the container type, C,is std::deque<T> for queue and std::vector<T> for stack and priority_queue. See §31.5.
Some data types provide much of what is required of a standard container, but not all. We sometimes refer to those as “almost containers.” The most interesting of those are:

For basic_string, A is the allocator (§34.4) and Tr is the character traits (§36.2.2).
Prefer a container, such as vector, string, or array, over an array when you have a choice. The implicit array-to-pointer conversion and the need to remember the size for a built-in array are major sources of errors (e.g., see §27.2.1).
Prefer the standard strings to other strings and to C-style strings. The pointer semantics of C-style strings imply an awkward notation and extra work for the programmer, and they are a major source of errors (such as memory leaks) (§36.3.1).
31.2.1. Container Representation
The standard doesn’t prescribe a particular representation for a standard container. Instead, the standard specifies the container interfaces and some complexity requirements. Implementers will choose appropriate and often cleverly optimized implementations to meet the general requirements and common uses. In addition to what is needed to manipulate elements, such a “handle” will hold an allocator (§34.4).
For a vector, the element data structure is most likely an array:

The vector will hold a pointer to an array of elements, the number of elements, and the capacity (the number of allocated, currently unused slots) or equivalent (§13.6).
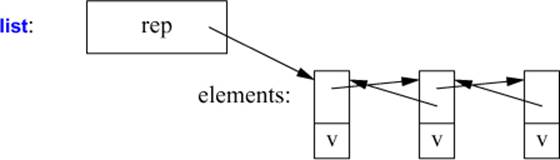
A list is most likely represented by a sequence of links pointing to the elements and the number of elements:
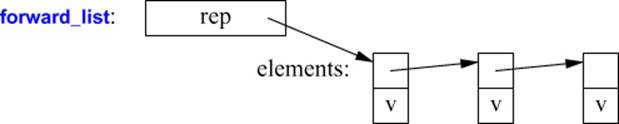
A forward_list is most likely represented by a sequence of links pointing to the elements:
A map is most likely implemented as a (balanced) tree of nodes pointing to (key,value) pairs:
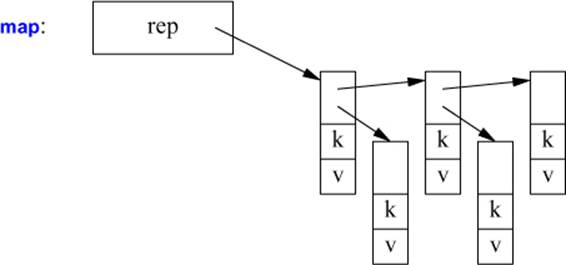
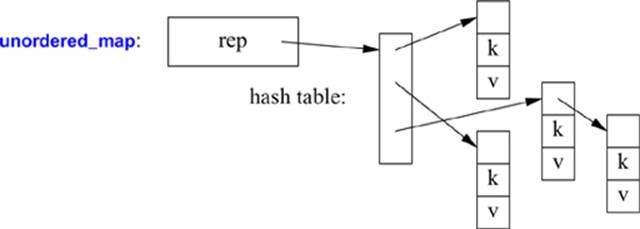
An unordered_map is most likely implemented as a hash table:
A string might be implemented as outlined in §19.3 and §23.2; that is, for short strings the characters are stored in the string handle itself, and for longer strings the elements are stored contiguously on the free-store (like vector elements). Like vector, a string can grow into “free space” allocated to avoid repeated reallocations:

Like a built-in array (§7.3), an array is simply a sequence of elements, with no handle:
![]()
This implies that a local array does not use any free store (unless it is allocated there) and that an array member of a class does not imply any free store operations.
31.2.2. Element Requirements
To be an element of a container, an object must be of a type that allows the container implementation to copy or move it, and to swap elements. If a container copies an element using a copy constructor or copy assignment, the result of the copy must be an equivalent object. This roughly means that any test for equality that you can devise on the value of the objects must deem the copy equal to the original. In other words, copying an element must work much like an ordinary copy of an int. Similarly, a move constructor and a move assignment must have the conventional definitions and move semantics (§17.5.1). In addition, it must be possible to swap() elements with the usual semantics. If a type has copy or move, the standard-library swap() will work.
The details of the element requirements are scattered over the standard and quite hard to read (§iso.23.2.3, §iso.23.2.1, §iso.17.6.3.2), but basically a container can hold elements of a type that has conventional copy or move operations. Many basic algorithms, such as copy(), find(), andsort() will work as long as the requirements for being a container element are met as well as the algorithm’s specific requirements (such as elements being ordered; §31.2.2.1).
Some violations of the rules for standard containers can be detected by a compiler, but others cannot and might then cause unexpected behavior. For example, an assignment operation that throws an exception might leave a partially copied element behind. That would be bad design (§13.6.1) and would violate the rules of the standard by not providing the basic guarantee (§13.2). An element in an invalid state could cause serious trouble later.
When copying objects is not reasonable, an alternative is to put pointers to objects into containers instead of the objects themselves. The most obvious example is polymorphic types (§3.2.2, §20.3.2). For example, we use vector<unique_ptr<Shape>> or vector<Shape*> rather thanvector<Shape> to preserve polymorphic behavior.
31.2.2.1. Comparisons
Associative containers require that their elements can be ordered. So do many operations that can be applied to containers (e.g., sort() and merge()). By default, the < operator is used to define the order. If < is not suitable, the programmer must provide an alternative (§31.4.3, §33.4). The ordering criterion must define a strict weak ordering. Informally, this means that both less-than and equality (if defined) must be transitive. That is, for an ordering criterion cmp (think of it as “less than”) we require:
[1] Irreflexivity: cmp(x,x) is false.
[2] Antisymmetry: cmp(x,y) implies !cmp(y,x).
[3] Transitivity: If cmp(x,y) and cmp(y,z), then cmp(x,z).
[4] Transitivity of equivalence: Define equiv(x,y) to be !(cmp(x,y)||cmp(y,x)). If equiv(x,y) and equiv(y,z), then equiv(x,z).
The last rule is the one that allows us to define equality (x==y) as !(cmp(x,y)||cmp(y,x)) if we need ==.
Standard-library operations that require a comparison come in two versions. For example:
template<typename Ran>
void sort(Ran first, Ran last); // use < for comparison
template<typename Ran, typename Cmp>
void sort(Ran first, Ran last, Cmp cmp); // use cmp
The first version uses < and the second uses a user-supplied comparison cmp. For example, we might decide to sort fruit using a comparison that isn’t case sensitive. We do that by defining a function object (§3.4.3, §19.2.2) that does the comparison when invoked for a pair of strings:
class Nocase { // case-insensitive string compare
public:
bool operator()(const string&, const string&) const;
};
bool Nocase::operator()(const string& x, const string& y) const
// return true if x is lexicographically less than y, not taking case into account
{
auto p = x.begin();
auto q = y.begin();
while (p!=x.end() && q!=y.end() && toupper(*p)==toupper(*q)) {
++p;
++q;
}
if (p == x.end()) return q != y.end();
if (q == y.end()) return false;
return toupper(*p) < toupper(*q);
}
We can call sort() using that comparison criterion. Consider:
fruit:
apple pear Apple Pear lemon
Sorting using sort(fruit.begin(),fruit.end(),Nocase()) would yield something like
fruit:
Apple apple lemon Pear pear
Assuming a character set in which uppercase letters precede lowercase letters, plain sort(fruit.begin(),fruit.end()) would give:
fruit:
Apple Pear apple lemon pear
Beware that < on C-style strings (i.e., const char*s) compares pointer values (§7.4). Thus, associative containers will not work as most people would expect them to if C-style strings are used as keys. To make them work properly, a less-than operation that compares based on lexicographical order must be used. For example:
struct Cstring_less {
bool operator()(const char* p, const char* q) const { return strcmp(p,q)<0; }
};
map<char*,int,Cstring_less> m; // map that uses strcmp() to compare const char* keys
31.2.2.2. Other Relational Operators
By default, containers and algorithms use < when they need to do a less-than comparison. When the default isn’t right, a programmer can supply a comparison criterion. However, no mechanism is provided for also passing an equality test. Instead, when a programmer supplies a comparisoncmp, equality is tested using two comparisons. For example:
if (x == y) // not done where the user supplied a comparison
if (!cmp(x,y) && !cmp(y,x)) // done where the user supplied a comparison cmp
This saves the user from having to provide an equality operation for every type used as the value type for an associative container or by an algorithm using a comparison. It may look expensive, but the library doesn’t check for equality very often, in about 50% of the cases only a single call of cmp() is needed, and often the compiler can optimize away the double check.
Using an equivalence relationship defined by less-than (by default <) rather than equality (by default ==) also has practical uses. For example, associative containers (§31.4.3) compare keys using an equivalence test !(cmp(x,y)||cmp(y,x)). This implies that equivalent keys need not be equal. For example, a multimap (§31.4.3) that uses case-insensitive comparison as its comparison criterion will consider the strings Last, last, lAst, laSt, and lasT equivalent, even though == for strings deems them different. This allows us to ignore differences we consider insignificant when sorting.
If equals (by default ==) always gives the same result as the equivalence test !(cmp(x,y)||cmp(y,x)) (by default cmp() is <), we say that we have a total order.
Given < and ==, we can easily construct the rest of the usual comparisons. The standard library defines them in the namespace std::rel_ops and presents them in <utility> (§35.5.3).
31.3. Operations Overview
The operations and types provided by the standard containers can be summarized like this:
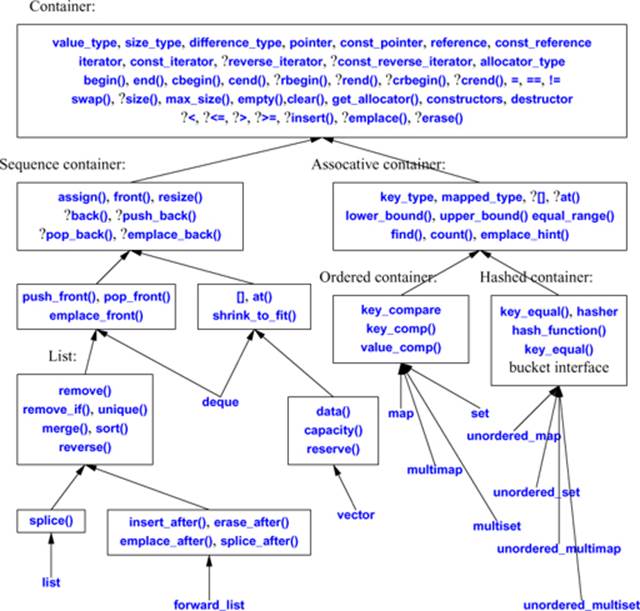
An arrow indicates that a set of operations is provided for a container; it is not an inheritance operation. A question mark (?) indicates a simplification: I have included operations that are provided for only some of the containers. In particular:
• A multi* associative container or a set does not provide [] or at().
• A forward_list does not provide insert(), erase(), or emplace(); instead, it provides the *_after operations.
• A forward_list does not provide back(), push_back(), pop_back(), or emplace_back().
• A forward_list does not provide reverse_iterator, const_reverse_iterator, rbegin(), rend(), crbegin(), crend(), or size().
• A unordered_* associative container does not provide <, <=, >, or >=.
The [] and at() operations are replicated simply to reduce the number of arrows.
The bucket interface is described in §31.4.3.2.
Where meaningful, an access operation exists in two versions: one for const and one for non-const objects.
The standard-library operations have complexity guarantees:
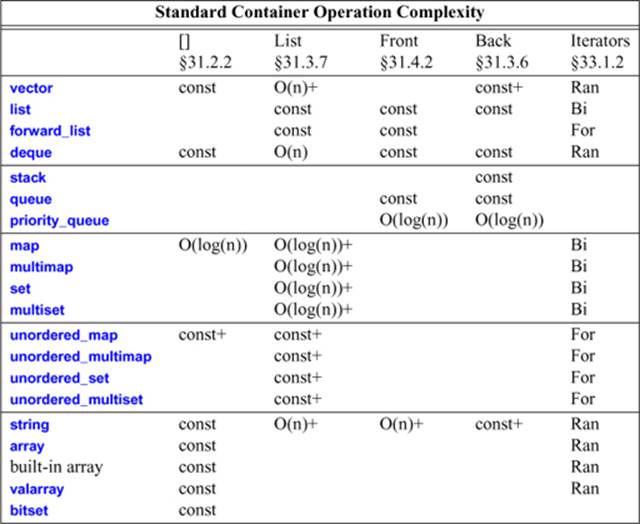
“Front” operations refer to insertion and deletion before the first element. Similarly, “Back” operations refer to insertion and deletion after the last element, and “List” operations refer to insertion and deletion not necessarily at the ends of a container.
In the Iterators column, “Ran” means “random-access iterator,” “For” means “forward iterator,” and “Bi” means “bidirectional iterator” (§33.1.4).
Other entries are measures of the efficiency of the operations. A const entry means the operation takes an amount of time that does not depend on the number of elements in the container; another conventional notation for constant time is O(1). O(n) means the operation takes time proportional to the number of elements involved. A + suffix indicates that occasionally a significant extra cost is incurred. For example, inserting an element into a list has a fixed cost (so it is listed as const), whereas the same operation on a vector involves moving the elements following the insertion point (so it is listed as O(n)). Occasionally, all elements of a vector must be relocated (so I added a +). The “big O” notation is conventional. I added the + for the benefit of programmers who care about predictability in addition to average performance. A conventional term forO(n)+ is amortized linear time.
Naturally, if a constant is large, it can dwarf a small cost proportional to the number of elements. However, for large data structures const tends to mean “cheap,” O(n) to mean “expensive,” and O(log(n)) to mean “fairly cheap.” For even moderately large values of n, O(log(n)), where logis the binary logarithm, is far closer to constant time than to O(n). For example:

People who care about cost must take a closer look. In particular, they must understand what elements are counted to get the n. However, the message is clear: don’t mess with quadratic algorithms for larger values of n.
The measures of complexity and cost are upper bounds. The measures exist to give users some guidance as to what they can expect from implementations. Naturally, implementers will try to do better in important cases.
Note that the “Big O” complexity measures are asymptotic; that is, it could require a lot of elements before complexity differences matter. Other factors, such as the cost of an individual operation on an element, may dominate. For example, traversing a vector and a list both have complexity O(n). However, given modern machine architectures, getting to the next element through a link (in a list) can be very much more expensive than getting to the next element of a vector (where the elements are contiguous). Similarly, a linear algorithm may take significantly more or significantly less than ten times as long for ten times as many elements because of the details of memory and processor architecture. Don’t just trust your intuition about cost and your complexity measures; measure. Fortunately, the container interfaces are so similar that comparisons are easy to code.
The size() operation is constant time for all operations. Note that forward_list does not have size(), so if you want to know the number of elements, you must count them yourself (at the cost of O(n)). A forward_list is optimized for space and does not store its size or a pointer to its last element.
The string estimates are for longer strings. The “short string optimization” (§19.3.3) makes all operations of short strings (e.g., less than 14 characters) constant time.
The entries for stack and queue reflect the cost for the default implementation using a deque as the underlying container (§31.5.1, §31.5.2).
31.3.1. Member Types
A container defines a set of member types:
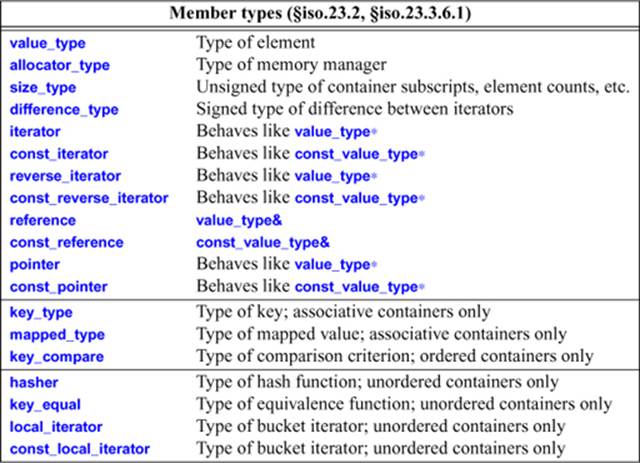
Every container and “almost container” provides most of these member types. However, they don’t provide types that are not meaningful. For example, array does not have an allocator_type and vector does not have a key_type.
31.3.2. Constructors, Destructor, and Assignments
Containers provide a variety of constructors and assignment operations. For a container called C (e.g., vector<double> or map<string,int>) we have:


Additional constructors for associative containers are described in §31.4.3.
Note that an assignment does not copy or move allocators. A target container gets a new set of elements but retains its old container, which it uses to allocate space for the new elements (if any). Allocators are described in §34.4.
Remember that a constructor or an element copy may throw an exception to indicate that it cannot perform its tasks.
The potential ambiguities for initializers are discussed in §11.3.3 and §17.3.4.1. For example:
void use()
{
vector<int> vi {1,3,5,7,9}; // vector initialized by five ints
vector<string> vs(7); // vector initialized by seven empty strings
vector<int> vi2;
vi2 = {2,4,6,8}; // assign sequence of four ints to vi2
vi2.assign(&vi[1],&vi[4]); // assign the sequence 3,5,7 to vi2
vector<string> vs2;
vs2 = {"The Eagle", "The Bird and Baby"}; // assign two strings to vs2
vs2.assign("The Bear", "The Bull and Vet"); // run-time error
}
The error in the assignment to vs2 is that a pair of pointers are passed (not an initializer_list) and the two pointers do not point into the same array. Use () for size initializers and {} for every other kind of iterator.
Containers are often large, so we almost always pass them by reference. However, because they are resource handles (§31.2.1), we can return them (implicitly using move) efficiently. Similarly, we can move them as arguments when we don’t want aliasing. For example:
void task(vector<int>&& v);
vector<int> user(vector<int>& large)
{
vector<int> res;
// ...
task(move(large)); // transfer ownership of data to task()
// ...
return res;
}
31.3.3. Size and Capacity
The size is the number of elements in the container; the capacity is the number of elements that a container can hold before allocating more memory:

When changing the size or the capacity, the elements may be moved to new storage locations. That implies that iterators (and pointers and references) to elements may become invalid (i.e., point to the old element locations). For an example, see §31.4.1.1.
An iterator to an element of an associative container (e.g., a map) is only invalidated if the element to which it points is removed from the container (erase()d; §31.3.7). To contrast, an iterator to an element of a sequence container (e.g., a vector) is invalidated if the elements are relocated (e.g., by a resize(), reserve(), or push_back()) or if the element to which it points is moved within the container (e.g., by an erase() or insert() of an element with a lower index).
It is tempting to assume that reserve() improves performance, but the standard growth strategies for vector (§31.4.1.1) are so effective that performance is rarely a good reason to use reserve(). Instead, see reserve() as a way of increasing the predictability of performance and for avoiding invalidation of iterators.
31.3.4. Iterators
A container can be viewed as a sequence either in the order defined by the containers iterator or in the reverse order. For an associative container, the order is based on the containers comparison criterion (by default <):

The most common form of iteration over elements is to traverse a container from its beginning to its end. The simplest way of doing that is by a range-for (§9.5.1) which implicitly uses begin() and end(). For example:
for (auto& x : v) // implicit use of v.begin() and v.end()
cout << x << '\n';
When we need to know the position of an element in a container or if we need to refer to more than one element at a time, we use iterators directly. In such cases, auto is useful to minimize source code size and eliminate opportunities for typos. For example, assuming a random-access iterator:
for (auto p = v.begin(); p!=end(); ++p) {
if (p!=v.begin() && *(p–1)==*p)
cout << "duplicate " << *p << '\n';
}
When we don’t need to modify elements, cbegin() and cend() are appropriate. That is, I should have written:
for (auto p = v.cbegin(); p!=cend(); ++p) { // use const iterators
if (p!=v.cbegin() && *(p–1)==*p)
cout << "duplicate " << *p << '\n';
}
For most containers and most implementations, using begin() and end() repeatedly is not a performance problem, so I did not bother to complicate the code like this:
auto beg = v.cbegin();
auto end = v.cend();
for (auto p = beg; p!=end; ++p) {
if (p!=beg && *(p–1)==*p)
cout << "duplicate " << *p << '\n';
}
31.3.5. Element Access
Some elements can be accessed directly:

Some implementations – especially debug versions – always do range checking, but you cannot portably rely on that for correctness or on the absence of checking for performance. Where such issues are important, examine your implementations.
The associative containers map and unordered_map have [] and at() that take arguments of the key type, rather than positions (§31.4.3).
31.3.6. Stack Operations
The standard vector, deque, and list (but not forward_list or the associative containers) provide efficient operations at the end (back) of their sequence of elements:

A c.push_back(x) moves or copies x into c, increasing c’s size by one. If we run out of memory or x’s copy constructor throws an exception, c.push_back(x) fails. A failed push_back() has no effect on the container: the strong guarantee is offered (§13.2).
Note that pop_back() does not return a value. Had it done so, a copy constructor throwing an exception could seriously complicate the implementation.
In addition, list and deque provide the equivalent operations on the start (front) of their sequences (§31.4.2). So does forward_list.
The push_back() is a perennial favorite for growing a container without preallocation or chance of overflow, but emplace_back() can be used similarly. For example:
vector<complex<double>> vc;
for (double re,im; cin>>re>>im; ) // read two doubles
vc.emplace_back(re,im); // add complex<double>{re,im} at the end
31.3.7. List Operations
Containers provide list operations:

For insert() functions, the result, q, points to the last element inserted. For erase() functions, q points to the element that followed the last element erased.
For containers with contiguous allocation, such as vector and deque, inserting and erasing an element can cause elements to be moved. An iterator pointing to a moved element becomes invalid. An element is moved if its position is after the insertion/deletion point or if all elements are moved because the new size exceeds the previous capacity. For example:
vector<int> v {4,3,5,1};
auto p = v.begin()+2; // points to v[2], that is, the 5
v.push_back(6); // p becomes invalid; v == {4,3,5,1,6}
p = v.begin()+2; // points to v[2], that is, the 5
auto p2 = v.begin()+4; // p2 points to v[4], that is, the 6
v.erase(v.begin()+3); // v == {4,3,5,6}; p is still valid; p2 is invalid
Any operation that adds an element to a vector may cause every element to be reallocated (§13.6.4).
The emplace() operation is used when it is notationally awkward or potentially inefficient to first create an object and then copy (or move) it into a container. For example:
void user(list<pair<string,double>>& lst)
{
auto p = lst.begin();
while (p!=lst.end()&& p–>first!="Denmark") // find an insertion point
/* do nothing */ ;
p=lst.emplace(p,"England",7.5); // nice and terse
p=lst.insert(p,make_pair("France",9.8)); // helper function
p=lst.insert(p,pair<string,double>>{"Greece",3.14}); // verbose
}
The forward_list does not provide operations, such as insert(), that operate before an element identified by an iterator. Such an operation could not be implemented because there is no general way of finding the previous element in a forward_list given only an iterator. Instead,forward_iterator provides operations, such as insert_after(), that operate after an element identified by an iterator. Similarly, unordered containers use emplace_hint() to provide a hint rather than “plain” emplace().
31.3.8. Other Operations
Containers can be compared and swapped:

When comparing containers with an operator (e.g., <=), the elements are compared using the equivalent element operator generated from == or < (e.g., a>b is done using !(b<a)).
The swap() operations exchange both elements and allocators.
31.4. Containers
This section goes into more detail about:
• vector, the default container (§31.4.1)
• The linked lists: list and forward_list (§31.4.2)
• The associative containers, such as map and unordered_map (§31.4.3)
31.4.1. vector
The STL vector is the default container. Use it unless you have a good reason not to. If your suggested alternative is a list or a built-in array, think twice.
§31.3 describes the operations on vector and implicitly contrasts them with what is provided for other containers. However, given the importance of vector, this section takes a second look with more emphasis on how the operations are provided.
The vector’s template argument and member types are defined like this:
template<typename T, typename Allocator = allocator<T>>
class vector {
public:
using reference = value_type&;
using const_reference = const value_type&;
using iterator = /* implementation-defined */;
using const_iterator = /* implementation-defined */;
using size_type = /* implementation-defined */;
using difference_type = /* implementation-defined */;
using value_type = T;
using allocator_type = Allocator;
using pointer = typename allocator_traits<Allocator>::pointer;
using const_pointer = typename allocator_traits<Allocator>::const_pointer;
using reverse_iterator = std::reverse_iterator<iterator>;
using const_reverse_iterator = std::reverse_iterator<const_iterator>;
// ...
};
31.4.1.1. vector and Growth
Consider the layout of a vector object (as described in §13.6):
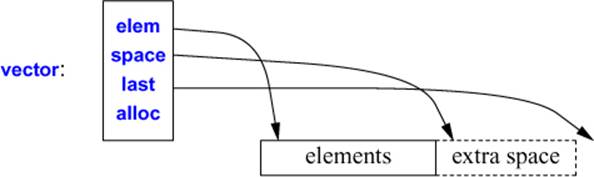
The use of both a size (number of elements) and a capacity (the number of available slots for elements without reallocation) makes growth through push_back() reasonably efficient: there is not an allocation operation each time we add an element, but only every time we exceed capacity (§13.6). The standard does not specify by how much capacity is increased when it is exceeded, but adding half the size is common. I used to be careful about using reserve() when I was reading into a vector. I was surprised to find that for essentially all of my uses, calling reserve() did not measurably affect performance. The default growth strategy worked just as well as my estimates, so I stopped trying to improve performance using reserve(). Instead, I use it to increase predictability of reallocation delays and to prevent invalidation of pointers and iterators.
The notion of capacity allows for iterators into a vector to be valid unless a reallocation actually happens. Consider reading letters into a buffer and keeping track of word boundaries:
vector<char> chars; // input "buffer" for characters
constexpr int max = 20000;
chars.reserve(max);
vector<char*> words; // pointers to start of words
bool in_word = false;
for (char c; cin.get(c)) {
if (isalpha(c)) {
if (!in_word) { // found beginning of word
in_word = true;
chars.push_back(0); // end of previous word
chars.push_back(c);
words.push_back(&chars.back());
}
else
chars.push_back(c);
}
else
in_word = false;
}
if (in_word)
chars.push_back(0); // terminate last word
if (max<chars.size()) { // oops: chars grew beyond capacity; the words are invalid
// ...
}
chars.shrink_to_fit(); // release any surplus capacity
Had I not used reserve() here, the pointers in words would have been invalidated if chars.push_back() caused a relocation. By “invalidated,” I mean that any use of those pointers would be undefined behavior. They may – or may not – point to an element, but almost certainly not to the elements they pointed to before the relocation.
The ability to grow a vector using push_back() and related operations implies that low-level C-style use of malloc() and realloc() (§43.5) is as unnecessary as it is tedious and error-prone.
31.4.1.2. vector and Nesting
A vector (and similar contiguously allocated data structures) has three major advantages compared to other data structures:
• The elements of a vector are compactly stored: there is no per-element memory overhead. The amount of memory consumed by a vec of type vector<X> is roughly size of (vector<X>)+vec.size()*size of (X). The size of (vector<X>) is about 12 bytes, which is insignificant for larger vectors.
• Traversal of a vector is very fast. To get to the next element, the code does not have to indirect through a pointer, and modern machines are optimized for consecutive access through a vector-like structure. This makes linear scans of vector elements, as in find() and copy(), close to optimal.
• vector supports simple and efficient random access. This is what makes many algorithms on vectors, such as sort() and binary_search(), efficient.
It is easy to underestimate these benefits. For example, a doubly-linked list, such as list, usually incurs a four-words-per-element memory overhead (two links plus a free-store allocation header), and traversing it can easily be an order of magnitude more expensive than traversing a vectorcontaining equivalent data. The effect can be so spectacular and surprising that I suggest you test it yourself [Stroustrup,2012a].
The benefits of compactness and efficiency of access can be unintentionally compromised. Consider how to represent a two-dimensional matrix. There are two obvious alternatives:
• A vector of vectors: vector<vector<double>> accessed by C-style double subscripting: m[i][j]
• A specific matrix type, Matrix<2,double> (Chapter 29), that stores elements contiguously (e.g., in a vector<double>) and computes locations in that vector from a pair of indices: m(i,j)
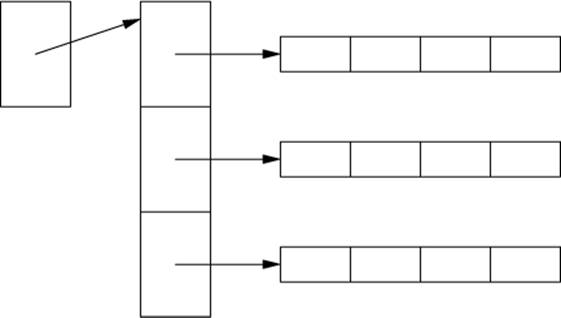
The memory layout for a 3-by-4 vector<vector<double>> looks like this:
The memory layout for Matrix<2,double> looks like this:
![]()
To construct the vector<vector<double>>, we need four constructor calls with four free-store allocation operations. To access an element, we need to do a double indirection.
To construct the Matrix<2,double>, we need one constructor call with one free-store allocation. To access an element, we need a single indirection.
Once we reach an element of a row, we don’t need a further indirection to access its successor, so access to the vector<vector<double>> is not always twice as costly as access to Matrix<2,double>. However, for algorithms that require high performance, the allocation, deallocation, and access costs implied by the linked structure of vector<vector<double>> could be a problem.
The vector<vector<double>> solution implies the possiblity of the row having different sizes. There are cases where that is an advantage, but more often it is simply an opportunity for errors and a burden for testing.
The problems and overhead get worse when we need higher dimensions: compare the number of added indirections and allocations for a vector<vector<vector<double>>> and a Matrix<3,double>.
In summary, I note that the importance of compactness of data structures is often underestimated or compromised. The advantages are logical as well as performance related. Combine this with a tendency to overuse pointers and new and we have a widespread problem. For example, consider the development complexities, run-time costs, memory costs, and opportunities for errors in an implementation of a two-dimensional structure when the rows are implemented as independent objects on the free store: vector<vector<double>*>.
31.4.1.3. vector and Arrays
A vector is a resource handle. This is what allows it to be resized and enables efficient move semantics. However, that occasionally puts it at a disadvantage compared to data structures (such as built-in arrays and array) that do not rely on storing elements separately from a handle. Keeping a sequence of elements on the stack or in another object can give a performance advantage, just as it can be a disadvantage.
A vector deals with properly initialized objects. This is what allows us to use them simply and rely on proper destruction of elements. However, that occasionally puts it at a disadvantage compared to data structures (such as built-in arrays and array) that allow uninitialized elements.
As an example, we need not initialize array elements before reading into them:
void read()
{
array<int,MAX]> a;
for (auto& x : a)
cin.get(&x);
}
For vector, we might use emplace_back() to achieve a similar effect (without having to specify a MAX).
31.4.1.4. vector and string
A vector<char> is a resizable, contiguous sequence of chars, and so is a string. So how do we choose between the two?
A vector is a general mechanism for storing values. It makes no assumptions about the relationships among the values stored in it. To a vector<char>, the string Hello, World! is just a sequence of 13 elements of type char. Sorting them into !,HWdellloor (preceded by a space) makes sense. To contrast, a string is intended to hold character sequences. The relationships among the characters are assumed to be important. So, for example, we rarely sort the characters in a string because that destroys meaning. Some string operations reflect that (e.g., c_str(), >>, and find()“know” that C-style strings are zero-terminated). The implementations of string reflect assumptions about the way we use strings. For example, the short-string optimization (§19.3.3) would be a pure pessimization if it wasn’t for the fact that we use many short strings, so that minimizing free-store use becomes worthwhile.
Should there be a “short-vector optimization”? I suspect not, but it would require a massive empirical study to be sure.
31.4.2. Lists
The STL provides two linked-list types:
• list: a doubly-linked list
• forward_list: a singly-linked list
A list is a sequence optimized for insertion and deletion of elements. When you insert into a list or delete an element from a list, the locations of other elements of the list are not affected. In particular, iterators referring to other elements are not affected.
Compared to vector, subscripting could be painfully slow, so subscripting is not provided for lists. If necessary, use advance() and similar operations to navigate lists (§33.1.4). A list can be traversed using iterators: list provides bidirectional iterators (§33.1.2) and forward_list provides forward iterators (hence the name of that type of list).
By default, list elements are individually allocated in memory and include predecessor and successor pointers (§11.2.2). Compared to a vector, a list uses more memory per element (usually at least four words more per element), and traversals (iteration) are significantly slower because they involve indirection through pointers rather than simple consecutive access.
A forward_list is a singly-linked list. Think of it as a data structure optimized for empty or very short lists that you typically traverse starting from the beginning. For compactness, forward_list doesn’t even provide a size(); an empty forward_list takes up just one word of memory. If you need to know the number of elements of a forward_list, just count them. If there are enough elements to make counting them expensive, maybe you should use a different container.
With the exception of subscripting, capacity management, and size() for forward_list, the STL lists provide the member types and operations offered by vector (§31.4). In addition, list and forward_list provide specific list member functions:

As opposed to the general remove() and unique() algorithms (§32.5), the member algorithms really do affect the size of a list. For example:
void use()
{
list<int> lst {2,3,2,3,5};
lst.remove(3); // lst is now {2,2,5}
lst.unique(); // lst is now {2,5}
cout << lst.size() << '\n'; // writes 2
}
The merge() algorithm is stable; that is, equivalent elements keep their relative order.

A splice() operation does not copy element values and does not invalidate iterators to elements. For example:
list<int> lst1 {1,2,3};
list<int> lst2 {5,6,7};
auto p = lst1.begin();
++p; // p points to 2
auto q = lst2.begin();
++q; // q points to 6
lst1.splice(p,lst2); // lst1 is now {1,5,6,7,2,3}; lst2 is now {}
// p still points to 2 and q still points to 6
A forward_list cannot access the element before one pointed to by an iterator (it does not have a predecessor link), so its emplace(), insert(), erase(), and splice() operations operate on the position after an iterator:

These list operations are all stable; that is, they preserve the relative order of elements that have equivalent values.
31.4.3. Associative Containers
Associative containers provide lookup based on keys. They come in two variants:
• Ordered associative containers do lookup based on an ordering criterion, by default < (less than). They are implemented as balanced binary trees, usually red-black trees.
• Unordered associative containers do lookup based on a hash function. They are implemented as hash tables with linked overflow.
Both come as
• maps: sequences of {key,value} pairs
• sets: maps without values (or you could say that the key is also the value)
Finally, maps and sets, whether ordered or unordered, come in two variants:
• “Plain” sets or maps with a unique entry for each key
• “Multi” sets or maps for which multiple entries can exist for each key
The name of an associate container indicates its place in this 3-dimensional space: {set|map, plain|unordered, plain|multi}. “Plain” is never spelled out, so the associative containers are:

Their template arguments are described in §31.4.
Internally, a map and an unordered_map are very different. See §31.2.1 for graphical representations. In particular, map uses its comparison criterion (typically <) on a key to search through a balanced tree (an O(log(n)) operation), whereas unordered_map applies a hash function on a key to find a slot in a hash table (an O(1) operation for a good hash function).
31.4.3.1. Ordered Associative Containers
Here are the template arguments and member types for map:
template<typename Key,
typename T,
typename Compare = less<Key>,
typename Allocator = allocator<pair<const Key, T>>>
class map {
public:
using key_type = Key;
using mapped_type = T;
using value_type = pair<const Key, T>;
using key_compare = Compare;
using allocator_type = Allocator;
using reference = value_type&;
using const_reference = const value_type&;
using iterator = /* implementation-defined */ ;
using const_iterator = /* implementation-defined */ ;
using size_type = /* implementation-defined */ ;
using difference_type = /* implementation-defined */ ;
using pointer = typename allocator_traits<Allocator>::pointer;
using const_pointer = typename allocator_traits<Allocator>::const_pointer;
using reverse_iterator = std::reverse_iterator<iterator>;
using const_reverse_iterator = std::reverse_iterator<const_iterator>;
class value_compare { /* operator()(k1,k2) does a key_compare()(k1,k2) */ };
// ...
};
In addition to the constructors mentioned in §31.3.2, the associative containers have constructors allowing a programmer to supply a comparator:

For example:
map<string,pair<Coordinate,Coordinate>> locations
{
{"Copenhagen",{"55:40N","12:34E"}},
{"Rome",{"41:54N","12:30E"}},
{"New York",{"40:40N","73:56W"}
};
The associative containers offer a variety of insertion and lookup operations:


Operations specific to unordered containers are presented in §31.4.3.5.
If a key, k, is not found by a subscript operation, m[k], a default value is inserted. For example:
map<string,string> dictionary;
dictionary["sea"]="large body of water"; // insert or assign to element
cout << dictionary["seal"]; // read value
If seal is not in the dictionary, nothing is printed: the empty string was entered as the value for seal and returned as the result of the lookup.
If that is not the desired behavior, we can use find() and insert() directly:
auto q = dictionary.find("seal"); // lookup; don't insert
if (q==dictionary.end()) {
cout << "entry not found";
dictionary.insert(make_pair("seal","eats fish"));
}
else
cout q–>second;
In fact, [] is little more than a convenient notation for insert(). The result of m[k] is equivalent to the result of (*(m.insert(make_pair(k,V{})).first)).second, where V is the mapped type.
The insert(make_pair()) notation is rather verbose. Instead, we could use emplace():
dictionary.emplace("sea cow","extinct");
Depending on the quality of the optimizer, this may also be more efficient.
If you try to insert a value into a map and there already is an element with its key, the map is unchanged. If you want to have more than one value for a single key, use a multimap.
The first iterator of the pair (§34.2.4.1) returned by equal_range() is lower_bound() and the second upper_bound(). You can print the value of all elements with the key "apple" in a multimap<string,int> like this:
multimap<string,int> mm {{"apple",2}, { "pear",2}, {"apple",7}, {"orange",2}, {"apple",9}};
const string k {"apple"};
auto pp = mm.equal_range(k);
if (pp.first==pp.second)
cout << "no element with value '" << k << "'\n";
else {
cout << "elements with value '" << k << "':\n";
for (auto p=pp.first; p!=pp.second; ++p)
cout << p–>second << ' ';
}
This prints 2 7 9.
I could equivalently have written:
auto pp = make_pair(m.lower_bound(),m.upper_bound());
// ...
However, that would imply an extra traversal of the map. The equal_range(), lower_bound(), and upper_bound() are also provided for sorted sequences (§32.6).
I tend to think of a set as a map with no separate value_type. For a set, the value_type is also the key_type. Consider:
struct Record {
string label;
int value;
};
To have a set<Record>, we need to provide a comparison function. For example:
bool operator<(const Record& a, const Record& b)
{
return a.label<b.label;
}
Given that, we can write:
set<Record> mr {{"duck",10}, {"pork",12}};
void read_test()
{
for (auto& r : mr) {
cout << '{' << r.label << ':' << r.value << '}';
}
cout << endl;
}
The key of an element in an associative container is immutable (§iso.23.2.4). Therefore, we cannot change the values of a set. We cannot even change a member of an element that takes no part in the comparison. For example:
void modify_test()
{
for (auto& r : mr)
++r.value; // error: set elements are immutable
}
If you need to modify an element, use a map. Don’t try to modify a key: if you were to succeed, the underlying mechanism for finding elements would break.
31.4.3.2. Unordered Associative Containers
The unordered associative containers (unordered_map, unordered_set, unordered_multimap, unordered_multiset) are hash tables. For simple uses, there are few differences from (ordered) containers because the associative containers share most operations (§31.4.3.1). For example:
unordered_map<string,int> score1 {
{"andy", 7}, {"al",9}, {"bill",–3}, {"barbara",12}
};
map<string,int> score2 {
{"andy", 7}, {"al",9}, {"bill",–3}, {"barbara",12}
};
template<typename X, typename Y>
ostream& operator<<(ostream& os, pair<X,Y>& p)
{
return os << '{' << p.first << ',' << p.second << '}';
}
void user()
{
cout <<"unordered: ";
for (const auto& x : score1)
cout << x << ", ";
cout << "\nordered: ";
for (const auto& x : score2)
cout << x << ", ";
}
The visible difference is that iteration through a map is ordered and for an unordered_map it is not:
unordered: {andy,7}, {al,9}, {bill,–3}, {barbara,12},
ordered: {al,9}, {andy, 7}, {barbara,12}, {bill,–3},
Iteration over an unordered_map depends on the order of insertion, the hash function, and the load factor. In particular, there is no guarantee that elements are printed in the order of their insertion.
31.4.3.3. Constructing unordered_maps
The unordered_map has a lot of template arguments and member type aliases to match:
template<typename Key,
typename T,
typename Hash = hash<Key>,
typename Pred = std::equal_to<Key>,
typename Allocator = std::allocator<std::pair<const Key, T>>>
class unordered_map {
public:
using key_type = Key;
using value_type = std::pair<const Key, T>;
using mapped_type = T;
using hasher = Hash;
using key_equal = Pred;
using allocator_type = Allocator;
using pointer = typename allocator_traits<Allocator>::pointer;
using const_pointer= typename allocator_traits<Allocator>::const_pointer;
using reference = value_type&;
using const_reference = const value_type&
using size_type = /* implementation-defined */;
using difference_type = /* implementation-defined */;
using iterator = /* implementation-defined */;
using const_iterator = /* implementation-defined */;
using local_iterator = /* implementation-defined */;
using const_local_iterator = /* implementation-defined */;
// ...
};
By default, an unordered_map<X> uses hash<X> for hashing and equal_to<X> to compare keys.
The default equal_to<X> (§33.4) simply compares X values using ==.
The general (primary) template hash doesn’t have a definition. It is up to users of a type X to define hash<X> if needed. For common types, such as string, standard hash specializations are provided, so the user need not provide them:

A hash function (e.g., a specialization of hash for a type T or a pointer to function) must be callable with an argument of type T and return a size_t (§iso.17.6.3.4). Two calls of a hash function for the same value must give the same result, and ideally such results are uniformly distributed over the set of size_t values so as to minimize the chances that h(x)==h(y) if x!=y.
There is a potentially bewildering set of combinations of template argument types, constructors, and defaults for an unordered container. Fortunately, there is a pattern:

Here, n is an element count for an otherwise empty unordered_map.

Here, we get the initial elements from a sequence [b:e). The number of elements will be then number of elements in [b:e), distance(b,e).

Here, we get the initial elements from a sequence from a {}-delimited initializer list of elements. The number of elements in the unordered_map will be the number of elements in the initializer list.
Finally, unordered_map has copy and move constructors, and also equivalent constructors that supply allocators:

Be careful when constructing an unordered_map with one or two arguments. There are many possible combinations of types, and mistakes can lead to strange error messages. For example:
map<string,int> m {My_comparator}; // OK
unordered_map<string,int> um {My_hasher}; // error
A single constructor argument must be another unordered_map (for a copy or move constructor), a bucket count, or an allocator. Try something like:
unordered_map<string,int> um {100,My_hasher}; // OK
31.4.3.4. Hash and Equality Functions
Naturally, a user can define a hash function. In fact, there are several ways to do that. Different techniques serve different needs. Here, I present several versions, starting with the most explicit and ending with the simplest. Consider a simple Record type:
struct Record {
string name;
int val;
};
I can define Record hash and equality operations like this:
struct Nocase_hash {
int d = 1; // shift code d number of bits in each iteration
size_t operator()(const Record& r) const
{
size_t h = 0;
for (auto x : r.name) {
h <<= d;
h ^= toupper(x);
}
return h;
}
};
struct Nocase_equal {
bool operator()(const Record& r,const Record& r2) const
{
if (r.name.size()!=r2.name.size()) return false;
for (int i = 0; i<r.name.size(); ++i)
if (toupper(r.name[i])!=toupper(r2.name[i]))
return false;
return true;
}
};
Given that, I can define and use an unordered_set of Records:
unordered_set<Record,Nocase_hash,Nocase_equal> m {
{ {"andy", 7}, {"al",9}, {"bill",–3}, {"barbara",12} },
Nocase_hash{2},
Nocase_equal{}
};
for (auto r : m)
cout << "{" << r.name << ',' << r.val << "}\n";
If, as is most common, I wanted to use the default values for my hash and equality functions, I could do that by simply not mentioning them as constructor arguments. By default, the unordered_set uses the default versions:
unordered_set<Record,Nocase_hash,Nocase_equal> m {
{"andy", 7}, {"al",9}, {"bill",–3}, {"barbara",12}
// use Nocase_hash{} and Nocase_equal{}
};
Often, the easiest way of writing a hash function is to use the standard-library hash functions provided as specializations of hash (§31.4.3.2). For example:
size_t hf(const Record& r) { return hash<string>()(r.name)^hash<int>()(r.val); };
bool eq (const Record& r, const Record& r2) { return r.name==r2.name && r.val==r2.val; };
Combining hash values using exclusive OR (^) preserves their distributions over the set of values of type size_t (§3.4.5, §10.3.1).
Given this hash function and equality function, we can define an unordered_set:
unordered_set<Record,decltype(&hf),decltype(&eq)> m {
{ {"andy", 7}, {"al",9}, {"bill",–3}, {"barbara",12} },
hf,
eq
};
for (auto r : m)
cout << "{" << r.name << ',' << r.val << "}\n";
}
I used decltype to avoid having to explicitly repeat the types of hf and eq.
If we don’t have an initializer list handy, we can give an initial size instead:
unordered_set<Record,decltype(&hf),decltype(&eq)> m {10,hf,eq};
That also makes it a bit easier to focus on the hash and equality operations.
If we wanted to avoid separating the definitions of hf and eq from their point of use, we could try lambdas:
unordered_set<Record, // value type
function<size_t(const Record&)>, // hash type
function<bool(const Record&,const Record&)> // equal type
> m { 10,
[](const Record& r) { return hash<string>{}(r.name)^hash<int>{}(r.val); },
[](const Record& r, const Record& r2) { return r.name==r2.name && r.val==r2.val; }
};
The point about using (named or unnamed) lambdas instead of functions is that they can be defined locally in a function, next to their use.
However, here, function may incur overhead that I would prefer to avoid if the unordered_set was heavily used. Also, I consider that version messy and prefer to name the lambdas:
auto hf = [](const Record& r) { return hash<string>()(r.name)^hash<int>()(r.val); };
auto eq = [](const Record& r, const Record& r2) { return r.name==r2.name && r.val==r2.val; };
unordered_set<Record,decltype(hf),decltype(eq)> m {10,hf,eq};
Finally, we may prefer to define the meaning of hash and equality once for all unordered containers of Record by specializing the standard-library hash and equal_to templates used by unordered_map:
namespace std {
template<>
struct hash<Record>{
size_t operator()(const Record &r) const
{
return hash<string>{}(r.name)^hash<int>{}(r.val);
}
};
template<>
struct equal_to<Record> {
bool operator()(const Record& r, const Record& r2) const
{
return r.name==r2.name && r.val==r2.val;
}
};
}
unordered_set<Record> m1;
unordered_set<Record> m2;
The default hash and hashes obtained from it by using exclusive-or are often pretty good. Don’t rush to use homemade hash functions without experimentation.
31.4.3.5. Load and Buckets
Significant parts of the implementation of an unordered container are made visible to the programmer. Keys with the same hash value are said to be “in the same bucket” (see §31.2.1). A programmer can examine and set the size of the hash table (known as “the number of buckets”):

The load factor of an unordered associative container is simply the fraction of the capacity that has been used. For example, if the capacity() is 100 elements and the size() is 30, the load_factor() is 0.3.
Note that setting the max_load_factor, calling rehash(), or calling reserve() can be very expensive operations (worst case O(n*n)) because they can – and in realistic scenarios typically do – cause rehashing of all elements. These functions are used to ensure that rehashing takes place at relatively convenient times in a program’s execution. For example:
unordered_set<Record,[](const Record& r) { return hash(r.name); }> people;
// ...
constexpr int expected = 1000000; // expected maximum number of elements
people.max_load_factor(0.7); // at most 70% full
people.reserve(expected); // about 1,430,000 buckets
You need to experiment to find a suitable load factor for a given set of elements and a particular hash function, but 70% (0.7) is often a good choice.

Use of an n for which c.max_bucket_count()<=n as an index into a bucket is undefined (and probably disastrous).
One use for the bucket interface is to allow experimentation with hash functions: a poor hash function will lead to large bucket_count()s for some key values. That is, it will lead to many keys being mapped to the same hash value.
31.5. Container Adaptors
A container adaptor provides a different (typically restricted) interface to a container. Container adaptors are intended to be used only through their specialized interfaces. In particular, the STL container adaptors do not offer direct access to their underlying container. They do not offer iterators or subscripting.
The techniques used to create a container adaptor from a container are generally useful for nonintrusively adapting the interface of a class to the needs of its users.
31.5.1. stack
The stack container adaptor is defined in <stack>. It can be described by a partial implementation:
template<typename T, typename C = deque<T>>
class stack { // §iso.23.6.5.2
public:
using value_type = typename C::value_type;
using reference = typename C::reference;
using const_reference = typename C::const_reference;
using size_type = typename C::size_type;
using container_type = C;
public:
explicit stack(const C&); // copy from container
explicit stack(C&& = C{}); // move from container
// default copy, move, assignment, destructor
template<typename A>
explicit stack(const A& a); // default container, allocator a
template<typename A>
stack(const C& c, const A& a); // elements from c, allocator a
template<typename A>
stack(C&&, const A&);
template<typename A>
stack(const stack&, const A&);
template<typename A>
stack(stack&&, const A&);
bool empty() const { return c.empty(); }
size_type size() const { return c.size(); }
reference top() { return c.back(); }
const_reference top() const { return c.back(); }
void push(const value_type& x) { c.push_back(x); }
void push(value_type&& x) { c.push_back(std::move(x)); }
void pop() { c.pop_back(); } // pop the last element
template<typename ... Args>
void emplace(Args&&... args)
{
c.emplace_back(std::forward<Args>(args)...);
}
void swap(stack& s) noexcept(noexcept(swap(c, s.c)))
{
using std::swap; // be sure to use the standard swap()
swap(c,s.c);
}
protected:
C c;
};
That is, a stack is an interface to a container of the type passed to it as a template argument. A stack eliminates the non-stack operations on its container from the interface, and provides the conventional names: top(), push(), and pop().
In addition, stack provides the usual comparison operators (==, <, etc.) and a nonmember swap().
By default, a stack makes a deque to hold its elements, but any sequence that provides back(), push_back(), and pop_back() can be used. For example:
stack<char> s1; // uses a deque<char> to store elements
stack<int,vector<int>> s2; // uses a vector<int> to store elements
Often, vector is faster than deque and uses less memory.
Elements are added to a stack using push_back() on the underlying container. Consequently, a stack cannot “overflow” as long as there is memory available on the machine for the container to acquire. On the other hand, a stack can underflow:
void f()
{
stack<int> s;
s.push(2);
if (s.empty()) { // underflow is preventable
// don't pop
}
else { // but not impossible
s.pop(); // fine: s.size() becomes 0
s.pop(); // undefined effect, probably bad
}
}
We do not pop() an element to use it. Instead, the top() is accessed and then pop()ed when it is no longer needed. This is not too inconvenient, can be more efficient when a pop() is not necessary, and greatly simplifies the implementation of exception guarantees. For example:
void f(stack<char>& s)
{
if (s.top()=='c') s.pop(); // optionally remove optional initial 'c'
// ...
}
By default, a stack relies on the allocator from its underlying container. If that’s not enough, there are a handful of constructors for supplying another.
31.5.2. queue
Defined in <queue>, a queue is an interface to a container that allows the insertion of elements at the back() and the extraction of elements at the front():
template<typename T, typename C = deque<T> >
class queue { //§iso.23.6.3.1
// ... like stack ...
void pop() { c.pop_front(); } // pop the first element
};
Queues seem to pop up somewhere in every system. One might define a server for a simple message-based system like this:
void server(queue<Message>& q, mutex& m)
{
while (!q.empty()) {
Message mess;
{ lock_guard<mutex> lck(m); // lock while extracting message
if (q.empty()) return; // somebody else got the message
mess = q.front();
q.pop();
}
// serve request
}
}
31.5.3. priority_queue
A priority_queue is a queue in which each element is given a priority that controls the order in which the elements get to be the top(). The declaration of priority_queue is much like the declaration of queue with additions to deal with a comparison object and a couple of constructors initializing from a sequence:
template<typename T, typename C = vector<T>, typename Cmp = less<typename C::value_type>>
class priority_queue { // §iso.23.6.4
protected:
C c;
Cmp comp;
public:
priority_queue(const Cmp& x, const C&);
explicit priority_queue(const Cmp& x = Cmp{}, C&& = C{});
template<typename In>
priority_queue(In b, In e, const Cmp& x, const C& c); // insert [b:e) into c
// ...
};
The declaration of priority_queue is found in <queue>.
By default, the priority_queue simply compares elements using the < operator, and top() returns the largest element:
struct Message {
int priority;
bool operator<(const Message& x) const { return priority < x.priority; }
// ...
};
void server(priority_queue<Message>& q, mutex& m)
{
while (!q.empty()) {
Message mess;
{ lock_guard<mutex> lck(m); // hold lock while extracting message
if (q.empty()) return; // somebody else got the message
mess = q.top();
q.pop();
}
// serve highest priority request
}
}
This differs from the queue version (§31.5.2) in that Messages with higher priority will get served first. The order in which elements with equal priority come to the head of the queue is not defined. Two elements are considered of equal priority if neither has higher priority than the other (§31.2.2.1).
Keeping elements in order isn’t free, but it needn’t be expensive either. One useful way of implementing a priority_queue is to use a tree structure to keep track of the relative positions of elements. This gives an O(log(n)) cost of both push() and pop(). A priority_queue is almost certainly implemented using a heap (§32.6.4).
31.6. Advice
[1] An STL container defines a sequence; §31.2.
[2] Use vector as your default container; §31.2, §31.4.
[3] Insertion operators, such as insert() and push_back() are often more efficient on a vector than on a list; §31.2, §31.4.1.1.
[4] Use forward_list for sequences that are usually empty; §31.2, §31.4.2.
[5] When it comes to performance, don’t trust your intuition: measure; §31.3.
[6] Don’t blindly trust asymptotic complexity measures; some sequences are short and the cost of individual operations can vary dramatically; §31.3.
[7] STL containers are resource handles; §31.2.1.
[8] A map is usually implemented as a red-black tree; §31.2.1, §31.4.3.
[9] An unordered_map is a hash table; §31.2.1, §31.4.3.2.
[10] To be an element type for a STL container, a type must provide copy or move operations; §31.2.2.
[11] Use containers of pointers or smart pointers when you need to preserve polymorphic behavior; §31.2.2.
[12] Comparison operations should implement a strict weak order; §31.2.2.1.
[13] Pass a container by reference and return a container by value; §31.3.2.
[14] For a container, use the ()-initializer syntax for sizes and the {}-initializer syntax for lists of elements; §31.3.2.
[15] For simple traversals of a container, use a range-for loop or a begin/end pair of iterators; §31.3.4.
[16] Use const iterators where you don’t need to modify the elements of a container; §31.3.4.
[17] Use auto to avoid verbosity and typos when you use iterators; §31.3.4.
[18] Use reserve() to avoid invalidating pointers and iterators to elements; §31.3.3, §31.4.1.
[19] Don’t assume performance benefits from reserve() without measurement; §31.3.3.
[20] Use push_back() or resize() on a container rather than realloc() on an array; §31.3.3, §31.4.1.1.
[21] Don’t use iterators into a resized vector or deque; §31.3.3.
[22] When necessary, use reserve() to make performance predictable; §31.3.3.
[23] Do not assume that [] range checks; §31.2.2.
[24] Use at() when you need guaranteed range checks; §31.2.2.
[25] Use emplace() for notational convenience; §31.3.7.
[26] Prefer compact and contiguous data structures; §31.4.1.2.
[27] Use emplace() to avoid having to pre-initialize elements; §31.4.1.3.
[28] A list is relatively expensive to traverse; §31.4.2.
[29] A list usually has a four-word-per-element memory overhead; §31.4.2.
[30] The sequence of an ordered container is defined by its comparison object (by default <); §31.4.3.1.
[31] The sequence of an unordered container (a hashed container) is not predictably ordered; §31.4.3.2.
[32] Use unordered containers if you need fast lookup for large amounts of data; §31.3.
[33] Use unordered containers for element types with no natural order (e.g., no reasonable <); §31.4.3.
[34] Use ordered associative containers (e.g., map and set) if you need to iterate over their elements in order; §31.4.3.2.
[35] Experiment to check that you have an acceptable hash function; §31.4.3.4.
[36] Hash function obtained by combining standard hash functions for elements using exclusive or are often good; §31.4.3.4.
[37] 0.7 is often a reasonable load factor; §31.4.3.5.
[38] You can provide alternative interfaces for containers; §31.5.
[39] The STL adaptors do not offer direct access to their underlying containers; §31.5.
All materials on the site are licensed Creative Commons Attribution-Sharealike 3.0 Unported CC BY-SA 3.0 & GNU Free Documentation License (GFDL)
If you are the copyright holder of any material contained on our site and intend to remove it, please contact our site administrator for approval.
© 2016-2025 All site design rights belong to S.Y.A.