Emerging Trends in Image Processing, Computer Vision, and Pattern Recognition, 1st Edition (2015)

Part II. Computer Vision and Recognition Systems

Chapter 29. Effective finger vein-based authentication

Kernel principal component analysis

S. Damavandinejadmonfared; V. Varadharajan Department of Computing, Advanced Cyber Security Research Centre, Macquarie University, Sydney, New South Wales, Australia

Abstract

Kernel functions have been very useful in data classification for the purpose of identification and verification so far. Applying such mappings first and using some methods on the mapped data such as principal component analysis (PCA) has been proven novel in many different areas. A lot of improvements have been proposed on PCA, such as kernel PCA, and kernel entropy component analysis, which are known as very novel and reliable methods in face recognition and data classification. In this paper, we implemented four different kernel mapping functions on finger database to determine the most appropriate one in terms of analyzing finger vein data using one-dimensional PCA. Extensive experiments have been conducted for this purpose using polynomial, Gaussian, exponential, and Laplacian PCA in four different examinations to determine the most significant one.

Keywords

Biometrics

Finger vein recognition

Principal component analysis (PCA)

Kernel principal component analysis (KPCA)

1 Introduction

The importance of reliability in verification and identification has gained lots of attention recently [1]. Finger vein is a newly proposed method of biometrics that has been able to gain many researchers' attention due to the fact that it is something internal and reliable to be used for this purpose. Furthermore, it has been proven by the medical studies that finger vein pattern is unique and stable [2]. As the data in finger vein recognition [3–5] is “image,” some face recognition algorithms [6–10] have been proposed to be used in this case. Principal component analysis (PCA) [11,7,6] is one of the common and known methods of pattern recognition and face recognition [12,13] that has been used a lot in biometrics. PCA, however, is a linear method which makes it unable to properly deal with nonlinear patterns which might be in data. To overcome the mentioned drawback of PCA, kernel principal component analysis (KPCA) [14,8] was proposed, which is known to be more appropriate than PCA in many cases, such as pattern recognition and face recognition. It is because of the fact that using kernel function in the system makes it nonlinear. Kernel entropy component analysis (KECA) is also an extension on KPCA that has been introduced in finger vein area [15,16] as well as some extensions of two-dimensional PCA [17]. The mentioned reasons motivated us to conduct a comparative analysis between two known and mostly used methods called PCA and KPCA [9,18–20] in finger vein recognition. The main difference between PCA and KPCA is the fact that PCA is a linear method, whereas KPCA is the nonlinear version of PCA in which kernel transforming is used. In PCA, it is ensured that the transferred data are uncorrelated, and only preserve maximally the second-order statistics of the original data, which is why PCA is known as insensitive to the dependencies of multiple features of the pattern. In KPCA, the mentioned problem has been overcome as it is not a linear method. In KPCA, however, it is essential that which kernel mapping function is chosen to be used. It could be considered very important due to the fact that each kernel mapping has particular characteristics and the data after being mapped will be in a totally different and high-dimensional space where it could be too complicated to extract the valuable features. As PCA is a well-known method of dimensionality reduction, the combination of PCA and kernel mapping will lead to a more reliable system. This work is an extension of the work of Damavandinejadmonfared and Varadharajan [21] presented in IPCV 2014 conference. There are several different types of kernel mapping which have been proven to be novel in different machine learning algorithms. In this research, we use four famous kernel mappings such as polynomial, Gaussian, exponential, and Laplacian as they have an extensive use within image processing related algorithms. Comparison in this paper is between different types of KPCA using the mentioned four kernel functions to map the data to achieve a twofold contribution; first, KPCA is appropriate enough to be used in finger vein area, and second, which kernel mapping function is the most superior one.

The remainder of this paper is organized as follows:

In Section 2, image acquisition is explained. In Section 3, PCA is explained. In Section 4, KPCA is introduced. In Section 5, experimental results on the finger vein database are given. Finally, Section 6 concludes the paper.

2 Image Acquisition

Based on the proven scientific fact that the light rays can be absorbed by deoxygenated hemoglobin in the vein, absorption coefficient of the vein is higher than other parts of finger. In order to provide the finger vein images, four low-cost prototype devices are needed such as an infrared (IR) LED and its control circuit with wavelength 830 nm, a camera to capture the images, a microcomputer unit to control the LED array, and a computer to process the images. The webcam has an IR blocking filter; hence, it is not sensitive to the IR rays. To solve this problem, an IR blocking filter is used to prevent the infrared rays from being blocked (Figure 1).

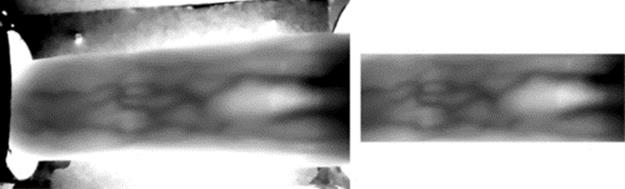
FIGURE 1 Original and cropped image.

3 Principal component analysis

PCA is known as a very powerful method for feature extraction. The usage of extracting eigenvectors and their corresponding eigenvalues to project the input data onto has been very common in image analysis, such as face recognition and image classification. PCA, actually, extracts the features from the data and reduces the dimension of it. When the features are extracted, a classifier can be applied to classify them and the final decision can be made. Euclidian distance is used in our algorithm which is very fast and sufficient to our purpose. In the rest of this section, PCA is explained briefly:First, the mean canter of the images is computed. m represents the mean image.

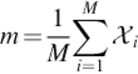(1)

The mean cantered image is calculated by Equation (2)

(2)

First covariance matrix is calculated by:

(3)

where W is a matrix composed of the column vectors w_i placed side by side.

Assuming that λ is eigenvector and v is eigenvalue, by solving λv = Cv eigenvectors and eigenvalues could be obtained.

By multiplying both side by W and substitution of C, we can get the following equation.

(4)

which means the first M − 1 eigenvectors λ and eigenvalues v can be obtained by calculatingWW^T.

When we have M eigenvectors and eigenvalues, the images could be projected onto L M dimensions by computing

(5)

where Ω is the projected value. Finally, to determine which face provides the best description of an input image, the Euclidean distance is calculated using Equation (6).

(6)

And finally, the minimum ∈ _kwill decide the unknown data into k class.

4 Kernel principal component analysis

4.1 KPCA Algorithm

Unlike PCA, KPCA extracts the features of the data nonlinearly. It obtains the principal components in F which is a high-dimensional feature space that is related to the feature spaces nonlinearly. The main idea of KPCA is to map the input data to the feature spaceF first using a nonlinear mapping Φ when input data have nonlinearly been mapped, the PCA will be performed on the mapped data [3]. Assuming that F is centered, where M is the number of input data. The covariance matrix of F can be defined as

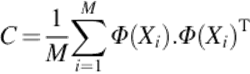(7)

To do this, this equation λv = Cv which is the eigenvalue equation should be solved for eigenvalues λ ≥ 0and eigenvactors v ∈ F.

As Cv = (1/M) ∑ _{i = 1}^M(Φ(X_i) · v)Φ(X_i), solutions for v with λ ≠ 0 lie within the span of Φ(X₁), … Φ (X_M), these coefficients α_i(i = 1, …, M) are obtained such that

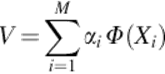(8)

The equations can be considered as follows

(9)

Having M × M matrix K by K_ij = k(X_i, X_j) = Φ(X_i) · Φ(X_j), causes an eigenvalue problem.

The solution to this is

(10)

By selecting the kernels properly, various mappings can be achieved. One of these mappings can be achieved by taking the d-order correlations, which is known as ARG, between the entries, X_i, of the input vector X. The required computation is prohibitive whend > 2.

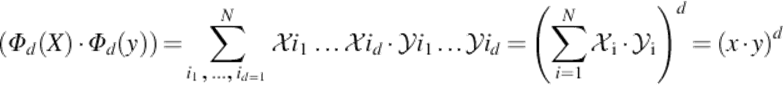(11)

To map the input data into the feature space F, there are four common methods such as linear (polynomial degree 1), polynomial, Gaussian, and sigmoid, which all are examined in this work in addition to PCA.

4.2 Kernel Feature Space versus PCA Feature Space

In PCA, covariance matrix of the input data is given after some processing stapes such as centring the data and calculating the mean. Then, the feature space is given by extracting the eigenvectors from this matrix. Indeed, each eigenvector has its corresponding eigenvalue whose greatness determines the value of its principal axis. Projection of the data onto a spanned subspace of the mention feature space is the actual data transformation and depending on how many principal axes to project the data onto, the dimension of the transferred data is determined. It means that the dimension of the input data can be reduced to even “one” when using just the first principal ax for projection. On the other hand, the maximum dimension data can have after transformation is equal to its original dimension when using all principal axes to project the data onto. Note that, in PCA the dimension of the feature space, where the spanned subspace is selected, is equal to the dimension of the input data. For example, let X = [x₁, …, x_N], where x_t ∈ R^dmeaning that we have N input data having the dimension of d. In this case, no matter how large N is, the feature space has the fixed dimension of d, which can be considered an advantage for PCA as the dimension of feature space is limited to that of input data and it does not get too high in terms of analyzing potentially large number of data.

In KPCA, however, it is different. The kernel feature space has a higher dimension than that of input data. Indeed, in KPCA, the whole input data space is mapped into kernel feature space by a specific kernel function which is nonlinear, and uses inner products. It is given by considering kernel matrix as input data space for PCA. It means that, unlike PCA, the dimension of kernel feature space is not dependent to the dimension of the input data. Indeed, it is equal to the number of input data. Let X be [x₁, …, x_N], for instance, and x_t ∈ R^d meaning that we have N input data with the dimension of d. In KPCA, no matter how high the dimension of the input data d is, the kernel feature space is N dimensional as the kernel matrix (Gram matrix) is [N × N]. Kernel matrix and its feature space is defined in Shawe-Taylor and Cristianini [22] as follows:

Given a set of vectors X = [x₁, …, x_N], the gram matrix is defined as the [N × N] matrix G whose entries are G_ij = ⟨x_i, x_j⟩. If we are using a kernel function k to evaluate the inner products in a feature space with feature map φ, the associated Gram matrix has entries

(12)

In this case, the matrix is often referred to as kernel matrix displaying as follows:

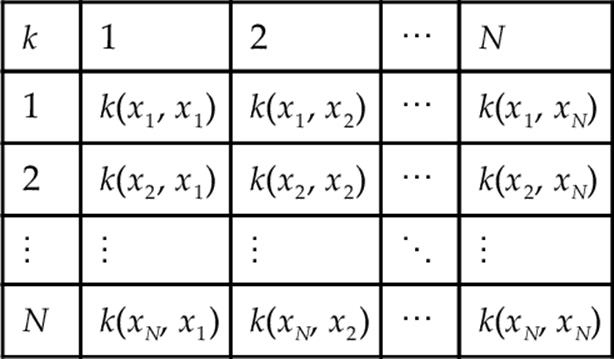
Mapping the data into another space nonlinearly makes this method (KPCA) nonlinear, which has been stated more superior than the linear PCA in many applications and literature. However, it can lead to the problem of complexity as the dimension of feature space is as high as the number of input data specially when analyzing a huge amount of data. It can also make it too complex to find the optimized subspace of the feature space for projection.

5 Experimental results

In this section, the experiments are conducted to corroborate the performance of Gaussian KPCA over other kinds of KPCA such as polynomial, exponential, and Laplacian PCA in terms of finger vein recognition. Finger vein database used in the experiments consists of 500 images from 50 individuals; 10 samples from each subject were taken. In this experiment, 4, 5, 6, and 7 images are used to train and the remaining 6, 5, 4, and 3 images are used to test, respectively. In each experiment, the accuracy is calculated using the first 100 components of the extracted features meaning that each experiment is repeated 100 times using the first 100 features to project the data onto, and also the dimension is reduced from 60% to 85% in different experiments. The results are shown in Figures 2–5. As it was expected, use of kernel functions to map the data first and then applying PCA on the mapped data (KPCA) results in acceptable accuracies varying from over 70% up to near 100% in different experiments. Polynomial KPCA, however, seems to be the worst among all types of KPCA and there is a great discrepancy between polynomial and other kinds of kernel KPCA in terms of final outputs of the system. The results show that polynomial kernel reaches its optimized point when using even less than ten components and it remains the same no matter how many more components to be used. It could be considered an advantage as using this kernel can be faster than others as it gets to its peak in the point 10 or less than that. The accuracy in polynomial KPCA, however, is not satisfying at all and is less than the others in almost all experiments. From another point of view, when four images are used to train, the highest accuracy obtained is around 95%, while the accuracy rate almost reaches 99% when using seven images to train which means, the more the number of training images is, the higher accuracy gets.

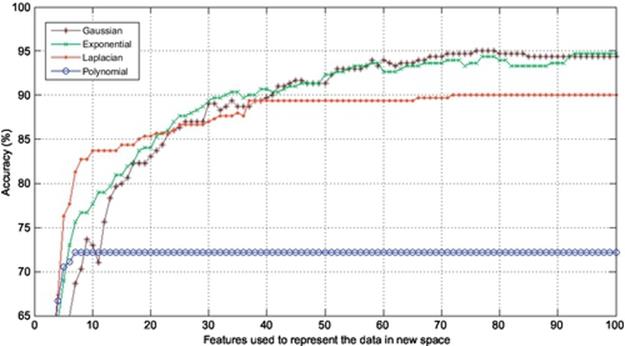
FIGURE 2 Comparison of accuracies obtained using four images to train and six to test.

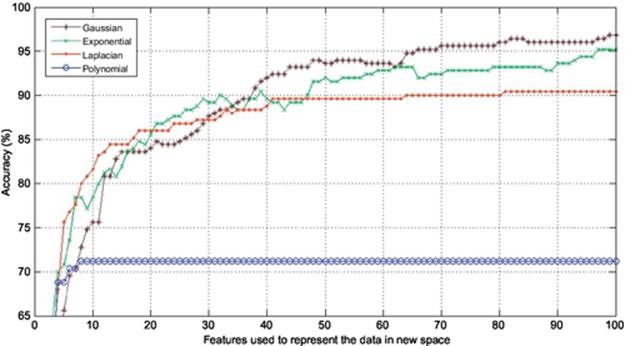
FIGURE 3 Comparison of accuracies obtained using five images to train and five to test.

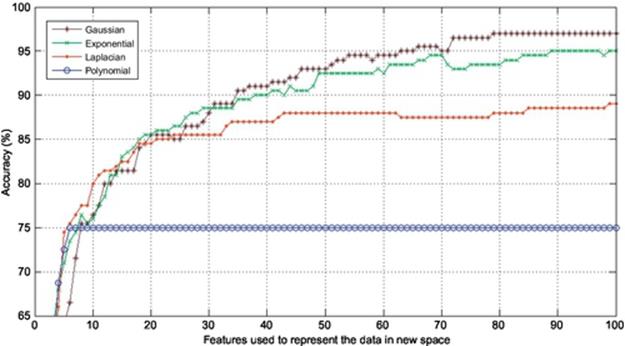
FIGURE 4 Comparison of accuracies obtained using six images to train and four to test.

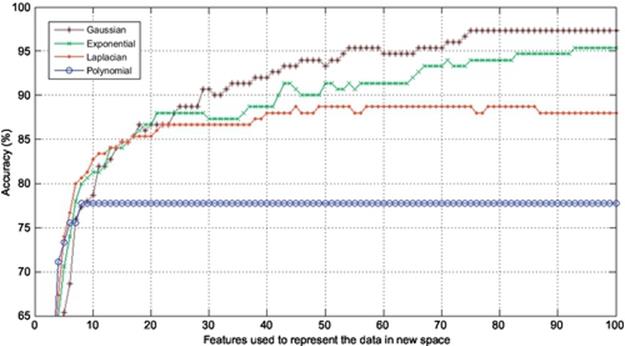
FIGURE 5 Comparison of accuracies obtained using seven images to train and three to test.

It is observed from the results that the accuracies achieved using Laplacian KPCA are not very close to those of the exponential and Gaussian methods; it is also understood that although the accuracies of Gaussian KPCA are close to those of exponential KPCA, the exponential method in a majority of implementations results in less accuracy compared to Gaussian.

Results indicate that in the first experiment, where four images were used to train and the remaining six images to test, the difference between the accuracies obtained using Gaussian, exponential, and Laplacian were not that significant as Laplacian, exponential, and Gaussian reached 90%, 94%, and 95%, respectively. However, the more the number of training images get, the higher accuracy Gaussian KPCA obtains and its discrepancy in accuracy becomes larger to the point that leads to the conclusion that Gaussian KPCA is the most superior kernel mapping in finger vein recognition systems.

6 Conclusion

The performance of four different types of KPCA on finger vein recognition has been validated in this paper. The first contribution is that KPCA might not be efficient enough in image classification and recognition as it might be sometimes too time consuming and computationally expensive; however, KPCA can be very reliable and accurate as it is able to deal with nonlinear patterns in the data. Among the examined kernel mapping in this work, it is shown that not only is the Gaussian KPCA the most appropriate one in comparison with the other types of KPCA (polynomial, exponential, and Laplacian), but also this method is efficient enough to be used in finger vein recognition as for such a big data base the accuracy is very high and promising.

References

[1] Jain AK, Ross A, Prabhakar S. An introduction to biometric recognition. IEEE Trans Circuits Syst. 2004;14(1):4–20.

[2] Kumar A, Zhou Y. Human identification using finger images. IEEE T Image Process. 2012;21(4):2228–2244.

[3] Beng TS, Rosdi BA. Finger-vein identification using pattern map and principal component analysis. In: 2011 IEEE international conference on signal image processing and applications; 2011:530–534.

[4] Song W, Kim T, Kim HC, Choi JH, Kong H-J, Lee S-R. A finger-vein verification system using mean curvature. Pattern Recogn Lett. 2011;32(11):1541–1547.

[5] Wu J-D, Liu C-T. Finger-vein pattern identification using principal component analysis and the neural network technique. Expert Syst Appl. 2011;38(5):5423–5427.

[6] Wen C, Zhang J. Palmprint recognition based on Gabor wavelets and 2-dimensional PCA&PCA. In: International conference on wavelet analysis and pattern recognition; 2007:2–4.

[7] Zhao W, et al. Face recognition: a literature survey. ACM Comput Surv (CSUR). 2003;35(4):399–458.

[8] Ebied RM. Feature extraction using PCA and kernel-PCA for face recognition. International conference on informatics and systems. 2012;8:72–77.

[9] Nhat VDM, Lee S. Kernel-based 2DPCA for face recognition. In: 2007 IEEE international symposium on signal processing and information technology; 2007:35–39.

[10] Yu C, Qing H, Zhang L. K2DPCA plus 2DPCA: an efficient approach for appearance based object recognition. In: 2009 3rd international conference on bioinformatics and biomedical engineering; 2009:1–4.

[11] Lin S, Ph D. An introduction to face recognition technology. Pattern Recogn. 1997;1995:1–7.

[12] Zuo W, Zhang D, Wang K. Bidirectional PCA with assembled matrix distance metric for image recognition. IEEE T Syst Man Cybern B Cybern. 2006;36(4):863–872.

[13] Zhang D, Zhou Z-H. Two-directional two-dimensional PCA for efficient face representation and recognition. Neurocomputing. 2005;69(1–3):224–231.

[14] Kim KI, Jung K, Kim HJ. Face recognition using kernel principal component analysis. Signal Process. 2002;9(2):40–42.

[15] Damavandinejadmonfared S. Kernel entropy component analysis using local mean-based k-nearest centroid neighbour (LMKNCN) as a classifier for face recognition in video surveillance camera systems. In: IEEE international conference on intelligent computer communication and processing (ICCP); 2012:253–256.

[16] Damavandinejadmonfared S. Finger vein recognition using linear kernel entropy component analysis. In: IEEE international conference on intelligent computer communication and processing (ICCP); 2012:249–252.

[17] Damavandinejadmonfared S, Varadharajan V. Finger vein recognition in row and column directions using two dimensional kernel principal component analysis. In: The 2014 international conference on image processing, computer vision, and pattern recognition; 2014.

[18] Peng H, Yang A.-P. Indefinite kernel entropy component analysis. In: 2010 International Conference on Multimedia Technology (ICMT). 29–31 Oct. 2010. p. 1, 4.

[19] Jenssen R. Kernel entropy component analysis. IEEE T Pattern Anal Mach Intell. 2010;32(5):847–860.

[20] Shekar BH, Sharmila Kumari M, Mestetskiy LM, Dyshkant NF. Face recognition using kernel entropy component analysis. Neurocomputing. 2011;74(6):1053–1057.

[21] Damavandinejadmonfared S, Varadharajan V. Effective kernel mapping for one-dimensional principal component analysis in finger vein recognition. In: The 2014 international conference on image processing, computer vision, and pattern recognition; 2014.

[22] Shawe-Taylor J, Cristianini N. Kernel methods for pattern analysis. New York, NY: Cambridge University Press; 2004 p. 462.