JUMP START HTML5 (2014)
Chapter 19 Canvas & SVG: SVG Bézier Curves
Bézier curves are used extensively in graphics software and are sometimes described as a polynomial expression, which is basically used to describe a curve. Sometimes, Bézier curves are referred to simply as curves, which can be slightly confusing if you're not familiar with all of the common (or less common) terms when it comes to design.
A Bézier curve is constructed by control points, as shown in Figure 19.1. A quadratic Bézier curve has one control point, whilst a cubic has two.
Quadratic Bézier Curves
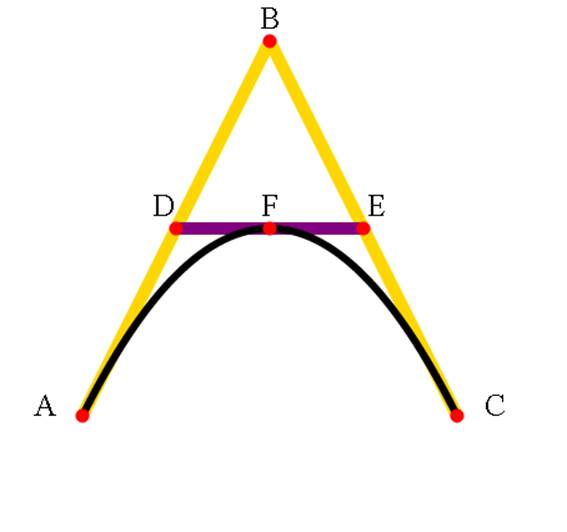
Figure 19.1. A quadratic Bézier curve
Now let's look at creating this whole image in SVG. Save the following code using your text editor and then open it up in your browser and you should see an A shape with a curved line reaching to the line that crosses the shape:
<!DOCTYPE html>
<html>
<body>
<svg width="500" height="500"
↵xmlns="http://www.w3.org/2000/svg" version="1.1">
<!-- lines -->
<path id="lineAB" d="M 100 350 l 150 -300" stroke="gold"
↵stroke-width="10" fill="none" />
<path id="lineBC" d="M 250 50 l 150 300" stroke="gold"
↵stroke-width="10" fill="none" />
<path id="lineDE" d="M 175 200 l 150 0" stroke="purple"
↵stroke-width="10" fill="none" />
<!-- quadratic bezier curve -->
<path d="M 100 350 q 150 -300 300 0" stroke="black"
↵stroke-width="6" fill="none" />
<!-- mark points with a red dot -->
<g stroke="red" stroke-width="5" fill="red">
<circle id="pointA" cx="100" cy="350" r="3" />
<circle id="pointB" cx="250" cy="50" r="3" />
<circle id="pointC" cx="400" cy="350" r="3" />
</g>
<!-- Add labels to each point -->
<g font-size="25" font="sans-serif" fill="black" stroke="none"
↵text-anchor="middle">
<text x="100" y="350" dx="-30">A</text>
<text x="250" y="50" dy="-10">B</text>
<text x="400" y="350" dx="30">C</text>
</g>
</svg>
</body>
</html>
The quadratic Bézier curve is defined by the path tag:
<path d="M 100 350 q 150 -300 300 0" stroke="black"
↵stroke-width="6" fill="none" />
The d attribute instructs the parser to move to coordinate (100,350). The 'q' defines two further coordinates which are relative to (100,350). The first is the control point (150,-300)—which equates to the absolute position (450,50). The second is the ending point of the curve at (300,0)—which equates to the absolute position (400,350).
Alternatively, we could have used an uppercase 'Q' to use absolute, rather than relative, coordinate references.
Cubic Bézier Curves
While quadratic Bézier curves have one control point, cubic Bézier curves have two. This allows more complex shapes which can reverse direction or wrap back on to themselves.
The following code provides three cubic Bézier examples:
<!DOCTYPE html>
<html>
<body>
<svg width="1200" height="500"
↵xmlns="http://www.w3.org/2000/svg" version="1.1">
<!-- cubic bezier curves -->
<path id="cubic1" d="M 100 350 c 150 -300 150 -300 300 0"
↵stroke="red" stroke-width="5" fill="none"/>
<path id="cubic2" d="M 450 350 c 200 -300 100 -300 300 0"
↵stroke="red" stroke-width="5" fill="none"/>
<path id="cubic3" d="M 800 350 c 100 -300 200 -300 300 0"
↵stroke="red" stroke-width="5" fill="none"/>
<!-- show control points -->
<g stroke="blue" stroke-width="3" fill="blue">
<!-- left curve -->
<circle cx="250" cy="50" r="3"/>
<!-- middle curve control points -->
<circle cx="650" cy="50" r="3"/>
<circle cx="550" cy="50" r="3"/>
<!-- right curve control points -->
<circle cx="900" cy="50" r="3"/>
<circle cx="1000" cy="50" r="3"/>
</g>
<!-- text -->
<g font-size="30" font="sans-serif"
↵fill="red" stroke="none" text-anchor="middle">
<text x="250" y="50" dy="-10">
Both control points
</text>
<text x="650" y="50" dy="-10">
CP1
</text>
<text x="550" y="50" dy="-10">
CP2
</text>
<text x="900" y="50" dy="-10">
CP2
</text>
<text x="1000" y="50" dy="-10">
CP1
</text>
</g>
</svg>
</body>
</html>
This will produce the output shown in Figure 19.2.
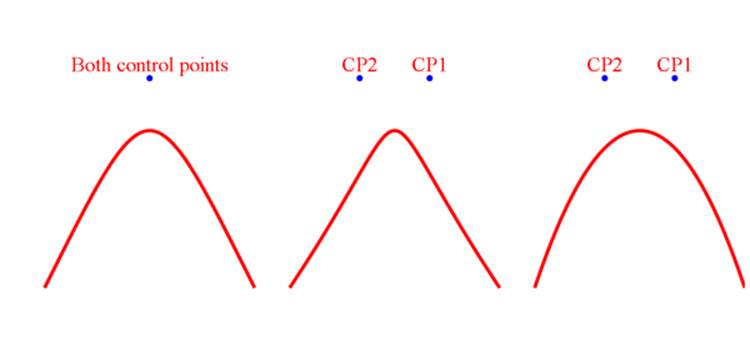
Figure 19.2. A cubic Bézier curve
Let's examine the third curve:
<path id="cubic3" d="M 800 350 c 100 -300 200 -300 300 0"
↵stroke="red" stroke-width="5" fill="none"/>
The d attribute instructs the parser to move to coordinate (800,350). The 'c' defines three further coordinates which are relative to (800,350). The first is the start control point (100,-300)—which equates to the absolute position (900,50). The second is the end control point (200,-300)—which equates to the absolute position (1000,50). The third is the ending point of the curve at (300,0)—which equates to the absolute position (1100,350).
Alternatively, we could have used an uppercase 'C' directive to use absolute, rather than relative, coordinate references.
There are also shorthand 'S' (absolute) and 's' (relative) directives. These accept two coordinates; the end control point and the end point itself. The start control point is assumed to be the same as the end control point.
These commands can be used to change the shape of cubic Bézier curves depending on the position of the control points. Have a play about and don't just view your results in the same browser window either, resize them, look at them on your tablet or smartphone and marvel at how well SVG copes with resizing.
Fortunately, there are tools to help you define curve directives. SitePoint's Craig Buckler has created Quadratic Bézier Curve and Cubic Bézier Curve tools, which allow you to move the control points and copy/paste the resulting SVG code.
In the next chapter, we'll take a look at filters.