Pragmatic Unit Testing in Java 8 with JUnit (2015)

Part 2. Mastering Manic Mnemonics!

Chapter 7. Boundary Conditions: The CORRECT Way

Your unit tests can help you prevent shipping some of the defects that often involve boundary conditions—the edges around the happy-path cases where things often go wrong.

In the previous chapter, you got a whiff of the CORRECT acronym, which can help you think about the boundary conditions to consider for your unit tests:

· Conformance—Does the value conform to an expected format?

· Ordering—Is the set of values ordered or unordered as appropriate?

· Range—Is the value within reasonable minimum and maximum values?

· Reference—Does the code reference anything external that isn’t under direct control of the code itself?

· Existence—Does the value exist (is it non-null, nonzero, present in a set, and so on)?

· Cardinality—Are there exactly enough values?

· Time (absolute and relative)—Is everything happening in order? At the right time? In time?

For each of the CORRECT criteria, consider the impact of data from all possible origins—including arguments passed in, fields, and locally managed variables. Then seek to fully answer the question:

What else can go wrong?

Any time you think of something that could go wrong, jot down a test name. If you have time, flesh out the test. Thinking about one possible errant scenario can often trigger your brain to think of other, possibly related scenarios. As long as you’re able to dream up tests, keep at it!

[C]ORRECT: [C]onformance

Many data elements must conform to a specific format. For example, an email address generally follows the form:

name@somedomain

(Where somedomain might be pragprog.com.) The name and domain portions of the address each follow a different set of fairly detailed rules. You can find many of them laid out at Wikipedia.^[28] Imagine that you want to validate the conformance of an email address to the many rules. (You really don’t want to, however. This is a case where you’re much better off leaning on the efforts of others. See the complete spec.^[29])

Perhaps your code parses an email address, attempting to extract its name portion—the part leading up to the @ sign. But you want to worry about what to do if there is no @, or if the name portion is empty. How to design the code is up to you. You might choose to return a null value or an empty string, or even throw an exception. Regardless, you need to write tests that demonstrate what happens when each of these boundary conditions occurs.

Validating formatted string data such as email addresses, phone numbers, account numbers, and filenames might involve a lot of rules, but it’s usually straightforward. More-complex structured data can create a combinatorial explosion of cases to test.

Suppose you’re reading report data composed of a header record, some number of data records, and a trailer record. Here are some of the boundary conditions you need to test:

· No header, just data and a trailer

· No data, just a header and trailer

· No trailer, just a header and data

· Just a trailer

· Just a header

· Just data

You’ll get better at brainstorming the ways in which data doesn’t conform to the expected structure the more you do it. You’ll find more defects in the process, because they often live around the interesting boundaries of your system. But when should you stop writing tests?

A field like account number might get passed to countless methods in your system. However, if you’ve validated the field at the point where it’s introduced in the system (perhaps through a UI, as an argument to a publicly exposed API, or read from a file), you need not validate it for every method that takes the field on as an argument. Understanding the flow of data through your system will help you minimize the number of unnecessary tests.

C[O]RRECT: [O]rdering

The order of data, or the position of one piece of data within a larger collection, represents a CORRECTness criterion where it’s easy for code to go wrong.

Let’s look at a need for ordering in the iloveyouboss application. One of the application’s core features is to score a list of companies based on how well they match criteria. Naturally, we always want to see the best match first, followed by the losers, biggest loser last.

The answersResultsInScoredOrder test represents the ordering need:

The paraphrased test is:

· Add a negative answer to the question for Smelt Inc.

· Add a positive answer to the question for Langrsoft.

· Add each question to the profile pool.

· Create a “sole need” criteria object that says it’s important that they reimburse tuition.

· Pass the criteria object to the score() method of the pool.

· Assert that the ranked profiles have Langrsoft first (because they answered true to the question and Smelt Inc. answered false).

The smeltInc, langrsoft, pool, and doTheyReimburseTuition fields are named to minimize our need to look at how they are declared or initialized. The also-interestingly-named soleNeed() method collapses the effort to create a Criteria object with a single Criterion to a single line:

The implementation shows that the core aspect to ranking the profiles is a sort that compares the scores of each profile:

Oh crud—it fails! It’s easy to get these things wrong! The order is backward. To make the test pass, swap the compareTo around:

CO[R]RECT: [R]ange

When you use Java’s built-in types for variables, you often get far more capacity than you need. If you represent a person’s age using an int, you’d be safe for at least a couple million more centuries. Inevitably, things will go wrong, and you’ll end up with a person a few times older than Methuselah, or a backward time traveler—someone with a negative age.

Excessive use of primitive datatypes is a code smell known as primitive obsession. A benefit of an object-oriented language like Java is that it lets you define your own custom abstractions in the form of classes.

A circle has only 360 degrees. Rather than store the direction of travel as a native type, create a class named Bearing that encapsulates the direction along with logic to constrain its range. Tests show how it works.

The constraint is implemented in the constructor of the Bearing class:

Note that angleBetween() returns an int. We’re not placing any range restrictions (such as that it must not be negative) on the result.

The Bearing abstraction makes it impossible for client code to create out-of-range bearings. As long as the rest of the system accepts and works with Bearing objects, the gate on range-related defects is shut.

Other constraints might not be as straightforward. Suppose we have a class that maintains two points, each an x, y integer tuple. The constraint on the range is that the two points must describe a rectangle with no side greater than 100 units. That is, the allowed range of values for both x, ypairs is interdependent.

We want a range assertion for any behavior that can affect a coordinate, to ensure that the resulting range of the x, y pairs remains legitimate—that the invariant on the Rectangle holds true.

More formally: an invariant is a condition that holds true throughout the execution of some chunk of code. In this case, we want the invariant to hold true for the lifetime of the Rectangle object—that is, any time its state changes.

We can add invariants, in the form of assertions, to the @After method so that they run upon completion of any test. Here’s what an implementation for the invariant for our constrained Rectangle class looks like:

For all the tests that manipulate a rectangle instance, we can sleep safely, knowing that JUnit will always check the invariant. The last test, allowsDynamicallyChangingSize, violates the invariant and thus fails.

Creating a Custom Matcher to Verify an Invariant

The assertion in the @After method uses a custom Hamcrest matcher named constrainsSidesTo. The matcher provides an assertion phrasing that reads well left-to-right: assert that (the) rectangle constrains (its) sides to 100.

To implement our custom Hamcrest matcher, we extend a class from org.hamcrest.TypeSafeMatcher bound to the type that we’re matching on—Rectangle in our case. By convention, we name the class ConstrainsSidesTo to correspond with the matcher phrasing constrainsSidesTo.

The class must override the matchesSafely() method to be useful. matchesSafely() contains the behavior we’re trying to enforce. It returns true as long as both rectangle sides remain in range. A false return fails the constraint. The custom matcher class should override the describeTo() method to provide a meaningful message when the assertion fails.

The custom matcher class should also supply a static factory method that returns the matcher instance. You use this factory method when phrasing an assertion. The constrainsSidesTo() factory method passes the length constraint (100 in the test) to the constructor of the matcher, to be subsequently used by matchesSafely():

Testing Ranges by Embedding Invariant Methods

The most common ranges you’ll test will likely depend on data-structure concerns, not application-domain constraints.

Let’s look at a questionable implementation of a sparse array—a data structure designed to save space. The sweet spot for a sparse array is a broad range of indexes where most of the corresponding values are null. It accomplishes this goal by storing only non-null values, using a pair of arrays that work in concert: an array of indexes corresponds to an array of values.

Here’s the bulk of the source for the SparseArray class:

One of the tests we want to write involves ensuring that we can add a couple of entries, then retrieve them both:

The sparse-array code has some intricacies around tracking and altering the pair of arrays. One way to help prevent errors is to determine what invariants exist for the implementation specifics. In the case of our sparse-array implementation, which accepts only non-null values, the tracked size of the array must match the count of non-null values.

We might consider writing tests that probe at the values stored in the private arrays, but that would require exposing true private implementation details unnecessarily. Instead, we devise a checkInvariants() method that can do the skullduggery for us, throwing an exception if any invariants (well, we have only one so far) fail to hold true.

(We could also implement invariant failures using the Java assert keyword.)

Now we can scatter checkInvariants() calls in our tests any time we do something to the sparse-array object:

The test errors out with an InvariantException:

Our code indeed has a problem with tracking the internal size. Challenge: where’s the defect?

Even though the later parts of the test would fail anyway given the defect, the checkInvariants calls allow us to pinpoint more easily where the code is failing.

Indexing needs present a variety of potential errors. As a parting note on the [R]ange part of the CORRECT mnemonic, here are a few test scenarios to consider when dealing with indexes:

· Start and end index have the same value

· First is greater than last

· Index is negative

· Index is greater than allowed

· Count doesn’t match actual number of items

COR[R]ECT: [R]eference

When testing a method, consider:

· What it references outside its scope

· What external dependencies it has

· Whether it depends on the object being in a certain state

· Any other conditions that must exist

A web app that displays a customer’s account history might require the customer to be logged on. The pop() method for a stack requires a nonempty stack. Shifting your car’s transmission from Drive to Park requires you to first stop—if your transmission allowed the shift while the car was moving, it’d likely deliver some hefty damage to your fine Geo Metro.

When you make assumptions about any state, you should verify that your code is reasonably well-behaved when those assumptions are not met. Imagine you’re developing the code for your car’s microprocessor-controlled transmission. You want tests that demonstrate how the transmission behaves when the car is moving versus when it is not. Our tests for the Transmission code cover three critical scenarios: that it remains in Drive after accelerating, that it ignores the damaging shift to Park while in Drive, and that it does allow the shift to Park once the car isn’t moving:

The preconditions for a method represent the state things must be in for it to run. The precondition for putting a transmission in Park is that the car must be at a standstill. We want to ensure that the method behaves gracefully when its precondition isn’t met (in our case, we ignore the Park request).

Postconditions state the conditions that you expect the code to make true— essentially, the assert portion of your test. Sometimes this is simply the return value of a called method. You might also need to verify other side effects—changes to state that occur as a result of invoking behavior. In the allowsShiftToParkWhenNotMoving test case, calling brakeToStop() on the car instance has the side effect of setting the car’s speed to 0.

CORR[E]CT: [E]xistence

You can uncover a good number of potential defects by asking yourself, “Does some given thing exist?” For a given method that accepts an argument or maintains a field, think through what will happen if the value is null, zero, or otherwise empty.

Java libraries tend to choke and throw an exception when faced with nonexistent or uninitialized data. Unfortunately, by the time a null value reaches the point where something chokes on it, it can be hard to understand the original source of the problem. An exception that reports a specific message, such as “profile name not set,” greatly simplifies tracking down the problem.

As programmers, we usually focus first and most on building the happy path. We give only afterthought to the unhappy paths that can surface when expected data isn’t available. You want to add tests that probe at these potential highways to hell. Write tests that see what happens when a called lookup method returns null. Or when an expected file doesn’t exist. Or when the network is down.

Ah, yes: things in the environment can wink out of existence as you sneeze— networks, license keys, users, printers, files’ URLs—you name it. Test with plenty of nulls, zeros, empty strings, and other nihilist trappings.

CORRE[C]T: [C]ardinality

Many programmers aren’t so hot at counting, especially past ten when our fingers can no longer assist us. Answer the following question quickly and off the top of your head, without benefit of fingers, paper, or Google:

You have to erect a number of fence sections to cover a straight line 12 meters long. Each section of fencing covers 3 meters, and each end of a section must be held up with a fence post:

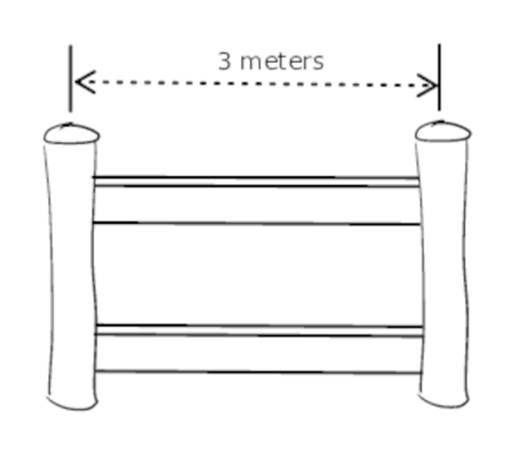
How many fence posts do you need?

If you’re like most of us, you probably offered an answer in short order, and it’s probably incorrect. Think again. Then take a look at the following figure for the answer. The errors that arise from not thinking hard enough about the problem occur so often that they have a name: fencepost errors.

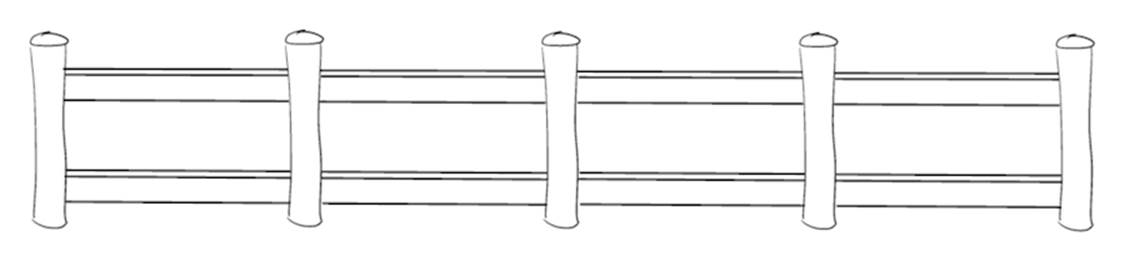
Fencepost errors represent one of many ways you can be off by one, an often fatal condition that we all succumb to at one point or another. Think about ways to test how well your code counts, and check to see just how many of a thing you might have.

Existence (see CORR[E]CT: [E]xistence) is technically a special case of cardinality. With cardinality, you’re looking at more-specific answers than “some” or “none.” Still, the count of some set of values is only interesting in these three cases:

· Zero

· One

· Many (more than one)

Some folks refer to this as the 0-1-n rule. Zero matters, as you just learned in the discussion of existence. Having one and only one of something is often important. As far as collections of things are concerned, usually your code is the same whether you’re dealing with ten, a hundred, or a thousand things. (Of course there are cases where the exact count makes a difference…and that count is always 42.)

(The 0-10-n rule has broader applicability than just code-cardinality concerns. Tim Ottinger and Jeff Langr discuss the notion of ZOM in a blog entry entitled “Simplify Design With Zero, One, Many.”^[30])

Suppose you maintain a list of the top ten food items ordered in JJ’s Pancake House. Every time an order is taken, you adjust the top-ten list, which the Pancake Boss iPhone app expects to see updated in real time. The notion of cardinality can help you derive a list of things to test out:

· Producing a report when there are no items in the list

· Producing a report when there’s only one item in the list

· Producing a report when there aren’t yet ten items in the list

· Adding an item when there are no items in the list

· Adding an item when there’s only one item in the list

· Adding an item when there aren’t yet ten items in the list

· Adding an item when there are already ten items in the list

Now that you’ve written all those tests (great!), the big boss at JJ’s Pancake House insists on a top-twenty list instead. Think about how many lines of code you must change and hope the answer is one, something like:

When the boss demands a top-five report instead, you make the change in one place without breaking a sweat. Your tests don’t change either, because they use the same constant.

Your tests should concentrate on boundary conditions of 0, 1, and n, where n can and will change as the business demands.

CORREC[T]: [T]ime

The last boundary condition in the CORRECT acronym is time. You need to keep several aspects of time in mind:

· Relative time (ordering in time)

· Absolute time (elapsed and wall clock)

· Concurrency issues

Some interfaces are inherently stateful. You expect login() to be called before logout(), open() before read(), read() before close(), and so on.

Consider what happens if methods are called out of order. Try various alternate sequences. Try skipping the first, last, and middle of a sequence. Just as order of data matters (see the examples in C[O]RRECT: [O]rdering), the order of the calling sequence of methods matters.

Relative time might also include issues of timeouts. You must decide how long your code will wait for an ephemeral resource to become available. You want to emulate possible conditions in your code, including things such as timeouts. Seek conditions that aren’t guarded by timeouts, which can cause your code to wait forever for something that might not happen.

Something you’re waiting on might take “too much” time. You need to determine whether or not the elapsed time for your method is too much for an impatient caller.

Actual wall-clock time might represent another consideration. Every rare once in a while, time of day matters, perhaps in subtle ways. A quick quiz:

True or false? Every day of the year is 24 hours long (not counting leap seconds).

The answer: it depends. In UTC (Universal Coordinated Time, the modern version of Greenwich Mean Time, or GMT), the answer is yes. In areas of the world that do not observe Daylight Saving Time (DST), the answer is yes. In most of the United States (which observes DST), the answer is no. One day in March will have 23 hours (spring forward) and one in November will have 25 (fall back).

The result of our complicated time-world is that arithmetic doesn’t always work as you expect. (It’s even worse than we thought. The original version of this book indicated April and October for DST-switchover dates. An astute reviewer caught the errors. Let’s strive to write tests that do the same!) Thirty minutes later than 1:45 a.m. is not 2:15 a.m. on two days out of the year. Make sure that you test any time-sensitive code on those boundary days—for locations that honor DST and for those that do not.

Don’t assume that any underlying library handles these issues correctly on your behalf. When it comes to time, there’s a lot of broken code out there. (One of your modest authors once became a reluctant expert at iCalendar, a file format for communicating calendar events, and quickly realized that no two implementations realized the specification the same or correctly.)

Another recipe for failure is to write tests that depend on the system clock. You want to instead change your application so that it requests the time from another source—one under control of your tests. See FI[R]ST: Good Tests Should Be [R]epeatable for an example of how to do this.

Finally, one of the most insidious problems brought about by time occurs in the context of concurrency and synchronized access issues. Entire books have been written on the topic of designing, implementing, and debugging multithreaded, concurrent programs (such as Brian Goetz’s Java Concurrency in Practice),^[31] and we’re striving to keep this humble tome thin and focused, so we’ll only touch on the topic. (That’s all doublespeak, mind you, for sheer laziness on our part.)

As a starter set of questions, ask yourself: what will happen if multiple threads access the same object at the same time? Do you need to synchronize any global or instance-level data or methods? How about external access to files or hardware? If your client might have concurrency needs, you need to write tests that demonstrate the use of multiple client threads.

After

We all need to know our boundaries! In tests, even more so: boundary conditions are where we often create nasty little defects. The CORRECT mnemonic will help you remember the boundaries you want to consider when writing unit tests.

Now that you’ve learned to test the right thing and how to build high-quality tests, you can start to reap the benefits of lower maintenance costs and fewer defects. However, most code leaves something to be desired when the characters first hit the screen. You need to pay some attention to cleaning it up. You’ll see how in Chapter 8, Refactoring to Cleaner Code, the leadoff chapter in a section on unit testing and design.

Footnotes