Coding for Beginners in Easy Steps: Basic Programming for All Ages (2015)

7. Sorting algorithms

This chapter demonstrates how to code a variety of sorting algorithm instruction sequences.

Copying sorts

Selecting sorts

Inserting sorts

Bubbling sorts

Merging sorts

Partitioning sorts

Summary

Copying sorts

An “algorithm” is a well-defined sequence of instructions to perform a specific task. Each algorithm takes one or more values as input and produces one or more resulting values as output.

An algorithm may be created in code as a function whose statements define a sequence of instructions to perform the task. Input values can be passed as arguments in the function call and resulting values can be returned as output from the function. Algorithms can be coded, using data structures and control structures in a variety of ways, to perform tasks such as sorting lists into order.

Python provides the sort() method for lists (described here) but examples in this chapter demonstrate how to code various sorting algorithms that are found in many programming languages.

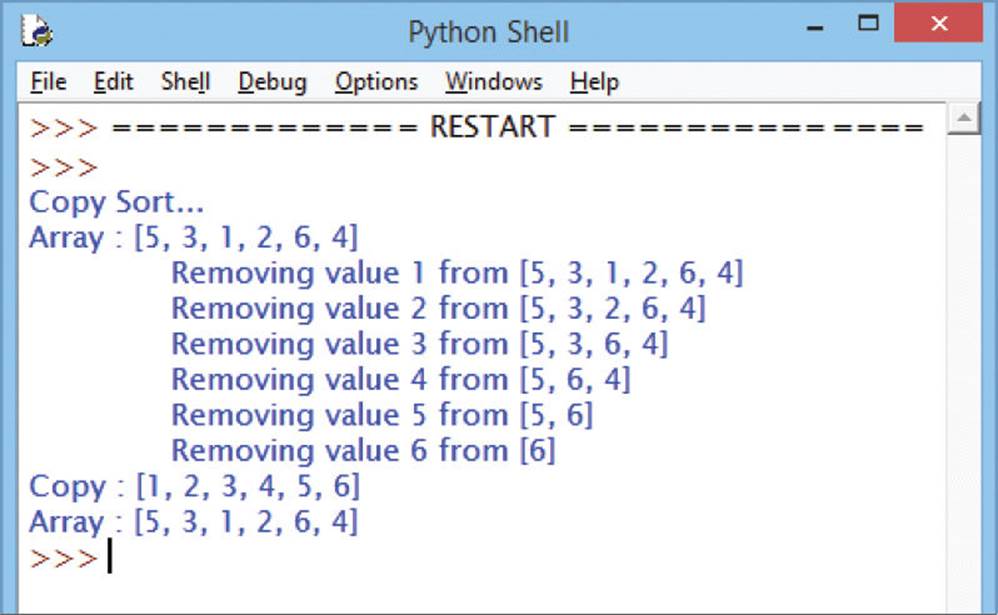
Sorting efficiency may depend upon the nature of the list to be sorted so different algorithms may be best-suited to particular tasks. Where the task requires a list to be sorted, while the original unsorted list remains intact, an algorithm function can be passed a reference to the list in an argument as input. The function can then make a copy of the original list, sort elements of that copy into order, then return the sorted copy list as output. This algorithm simply copies element values from the original list into a new list array then arranges them in ascending value order.

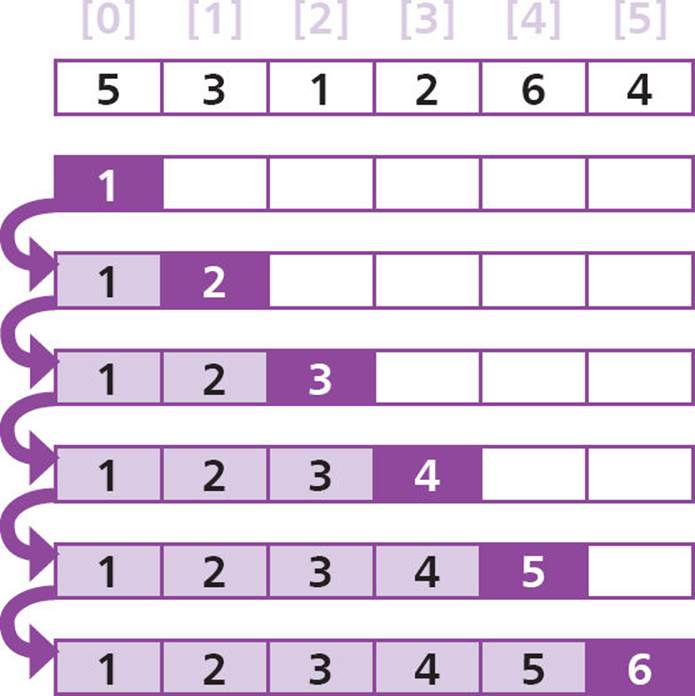
Array list elements are numbered from zero. So here, element [0] contains 5, element [1] contains 3, and so on.

copy.py

Start a new program by declaring a function to receive a list reference as input and return a sorted copy as output

def copy_sort( array ) :

copy = array[ : ]

sorted_copy = [ ]

# Algorithm sequence to be added here.

return sorted_copy

Next, add the indented algorithm sequence to insert the copied element values into the empty list in order

while len( copy ) > 0 :

minimum = 0

for element in range( 0 , len( copy ) ) :

if copy[ element ] < copy[ minimum ] :

minimum = element

print( ‘\tRemoving value’ , copy[ minimum ] , \

‘from’ , copy )

sorted_copy.append( copy.pop( minimum ) )

Now, add statements to create and display an unsorted list

array = [ 5 , 3 , 1 , 2 , 6 , 4 ]

print( ‘Copy Sort...\nArray :’ , array )

Finally, add statements to display the unsorted list and its sorted copy then save and run the program – to see the original list remains intact in unsorted order

print( ‘Copy :’ , copy_sort( array ) )

print( ‘Array :’ , array )

Each value is popped off the list copy in sequence – to build the sorted version by appending each to the empty array.

Selecting sorts

Often you will want to sort the elements of an unsorted list array “in place” rather than sort a copy of the original list, as demonstrated in the previous example. There are several popular algorithms you can employ to sort arrays in place, each using a different technique with their own strengths and weaknesses.

A “selection sort” algorithm examines each element in the unsorted part of an array list and selects the element containing the lowest value. It then swaps the selected element value with that contained in the element at the beginning of the unsorted part of the array list – thereby increasing the size of the sorted part of the array and decreasing its unsorted part. This process is repeated until all element values are sorted into ascending order.

Selection sort is a simple swap-based algorithm that is relatively easy to understand and code as a function algorithm. It is one of the two most efficient algorithms for sorting small arrays of 20 or so elements.

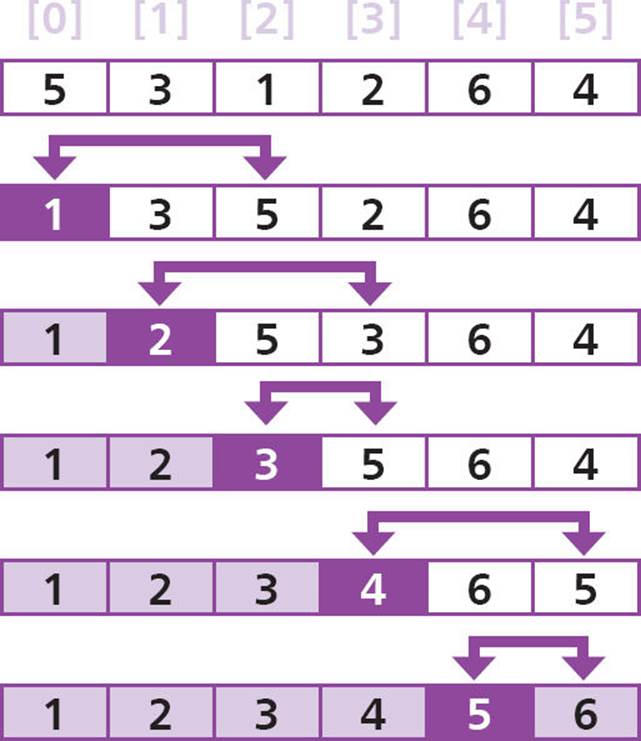
In this example, the final element will already contain the highest value when the penultimate element has been sorted.

selection.py

Start a new program by declaring a function to receive a list reference as input and begin a loop to store each element’s value and current index number

def selection_sort( array ) :

for index in range( 0 , len( array ) -1 ) :

value = array[ index ]

current = index

# Algorithm sequence to be added here.

Next, add the algorithm sequence to repeatedly swap the smallest unsorted value with the first unsorted value

for element in range( index+1 , len( array ) ) :

if array[ element ] < array[ current ] :

current = element

array[ index ] = array[ current ]

array[ current ]= value

print( ‘\tResolving element[‘ , index , ‘] to ‘ , array )

Now, add statements to create and display an unsorted list

array = [ 5 , 3 , 1 , 2 , 6 , 4 ]

print( ‘Selection Sort...\nArray :’ , array )

Finally, add statements to call the algorithm function and display the list once more – to see the list sorted in place

selection_sort( array )

print( ‘Array :’ , array )

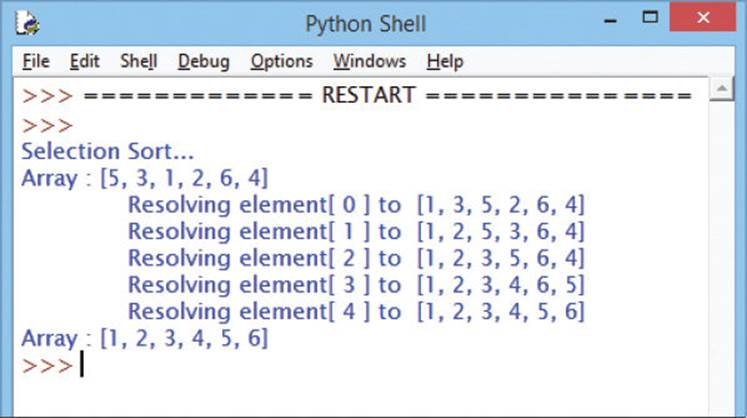
Sorting in place swaps the element values contained in the original referenced array list.

Inserting sorts

The technique of swapping elements with a selection sort algorithm, demonstrated in the previous example, works well but an alternative technique can be employed to simply insert elements into an array list at the correct ascending order position.

An “insertion sort” algorithm examines the next element in the unsorted part of an array list and, if required, inserts the element at the correct ascending order position in the array list. To accommodate the inserted element, all other elements in the unsorted part of the list shift to the right – increasing the size of the sorted part of the array and decreasing its unsorted part. This process is repeated for each element in turn until all element values are sorted into ascending order.

Insertion sort is a simple algorithm that is relatively easy to understand and code as a function algorithm. Along with the selection sort algorithm it is one of the two most efficient algorithms for sorting small arrays of 20 or so elements. Typically, insertion sort will require fewer comparisons than a selection sort so is often seen as the best method for sorting small arrays.

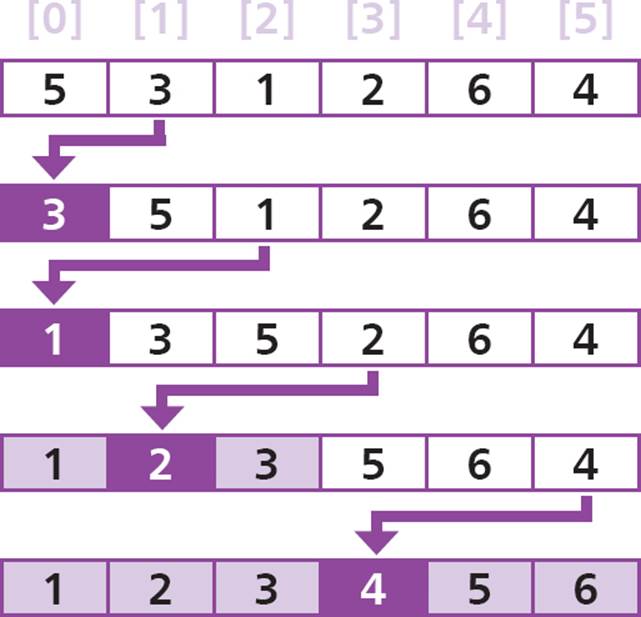
In this example, two steps are needed to get the lowest value into the very first element – as 3 is less than 5, then 1 is less than 3.

insertion.py

Start a new program by declaring a function to receive a list reference as input and begin a loop to store the current element’s value

def insertion_sort( array ) :

for index in range( 1 , len( array ) ) :

value = array[ index ]

# Algorithm sequence to be added here.

print( ‘\tResolving element[‘ , index , ‘] to ‘ , array )

Next, add the algorithm sequence to repeatedly insert the current value if smaller than that in the current element

while array[ index-1 ] > value and index >= 1 :

array[ index ] = array[ index-1 ]

index -=1

array[ index ] = value

Now, add statements to create and display an unsorted list

array = [ 5 , 3 , 1 , 2 , 6 , 4 ]

print( ‘Insertion Sort...\nArray :’ , array )

Finally, add statements to call the algorithm function and display the list once more – to see the list sorted in place

insertion_sort( array )

print( ‘Array :’ , array )

On some iterations this algorithm recognizes that elements in the “unsorted” part are already sorted following earlier insertions.

Bubbling sorts

A “bubble sort” algorithm is a further simple alternative to the selection and insertion sort techniques. This algorithm repeatedly examines each adjacent pair of elements in an array list and, if required, swaps them around to place a lower value before a higher value – until all elements are sorted into ascending order.

Bubble sort is a simple algorithm that is very easy to understand and code as a function algorithm. Although the bubble sort technique is generally less efficient than insertion sort or selection sort, it is one of the quickest algorithms for nearly-sorted arrays.

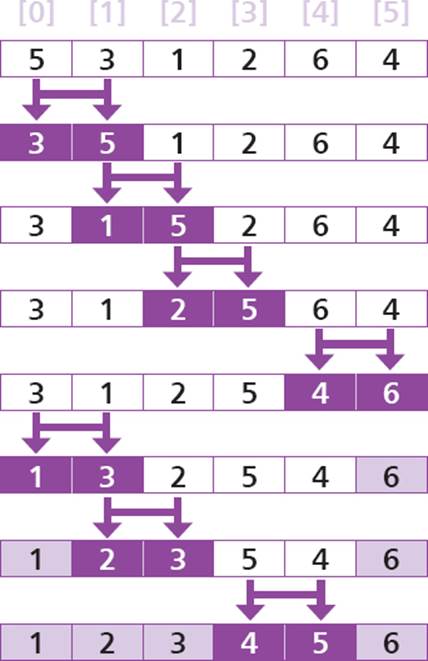
In this example, no swap is needed on the first pass for element [3] and [4] as their values 5 and 6 are in correct order.

bubble.py

Start a new program by declaring a function to receive a list reference as input and begin an outer loop to repeatedly iterate through the array list

def bubble_sort( array ) :

for index in range( len( array ) ) :

# Algorithm sequence to be added here.

Next, add the algorithm sequence to iterate through the array list elements, up to the penultimate element, and swap values if the next is greater than the current value

for element in range( len( array -1 ) - index ) :

if array[ element ] > array[ element+1 ] :

array[ element ] , array[ element+1 ] = \

array[ element+1 ] , array[ element ]

print( ‘\tResolving element[‘ , element , \

‘] to ‘ , array )

Now, add statements to create and display an unsorted list

array = [ 5 , 3 , 1 , 2 , 6 , 4 ]

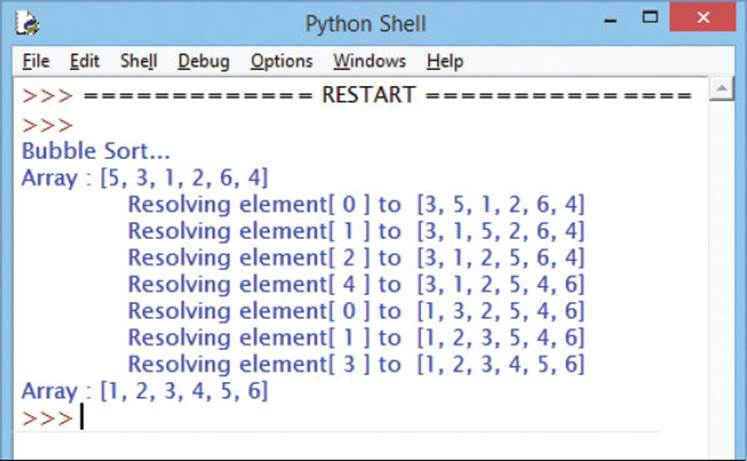
print( ‘Bubble Sort...\nArray :’ , array )

Finally, add statements to call the algorithm function and display the list once more – to see the list sorted in place

bubble_sort( array )

print( ‘Array :’ , array )

In average simple cases, insertion sort outperforms selection sort, and selection sort outperforms bubble sort.

Merging sorts

While the simple selection sort, insertion sort, and bubble sort techniques work well on small array lists, more efficient complex sorting algorithms generally work better on larger array lists. Typically, these complex sorting algorithms employ a “divide and conquer” strategy to first repeatedly divide the list into sub-sections, then re-assemble those sub-sections in sorted order.

A “merge sort” algorithm is a complex sorting algorithm that first repeatedly divides an array into left and right sub-sections from the array’s mid-point until it is empty or has just one element. Once the division is complete, all sub-sections are individual elements. The algorithm then merges all the individual elements into a single sorted list.

Merge sort is a complex algorithm that can be coded as a function algorithm, which makes “recursive” calls to repeatedly divide an array. Merge sort is a fast algorithm that only compares element values when merging the elements back into a sorted array list.

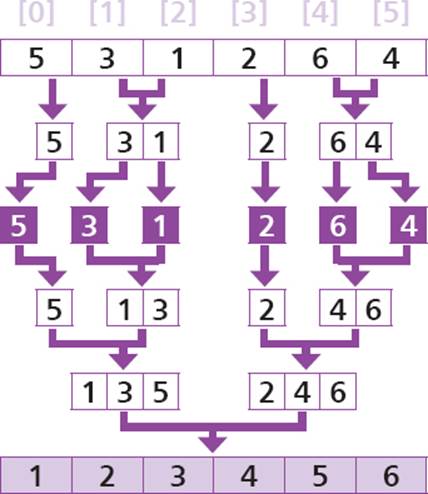
In this example, the array is only small but the merge sort algorithm efficiently divides then re-assembles large arrays in exactly the same way.

Start a new program by declaring a function to receive a list reference and repeatedly iterate through an array list

def merge_sort( array ) :

if len( array ) > 1 :

middle = int( len( array ) / 2 )

left = array[ 0 : middle ] ; right = array[ middle : ]

print( ‘\tSplit to’ , left , right )

merge_sort( left ) ; merge_sort( right )

# Algorithm sequence to be added here.

merge.py

Next, add the algorithm sequence to divide the array list elements into sub-sections then merge them together

i = j = 0

for element in range( len( array ) ) :

L = left[ i ] if i < len( left ) else None

R = right[ j ] if j < len( right ) else None

if( ( L and R ) and ( L < R ) ) or R is None :

array[ element ] = L ; i += 1

elif( ( L and R ) and ( L >= R ) ) or L is None :

array[ element ] = R ; j += 1

print( ‘\t\tMerging’ , left , right )

Now, add statements to create and display the array list

array = [ 5 , 3 , 1 , 2 , 6 , 4 ]

print( ‘Merge Sort...\nArray :’ , array )

merge_sort( array )

print( ‘Array :’ , array )

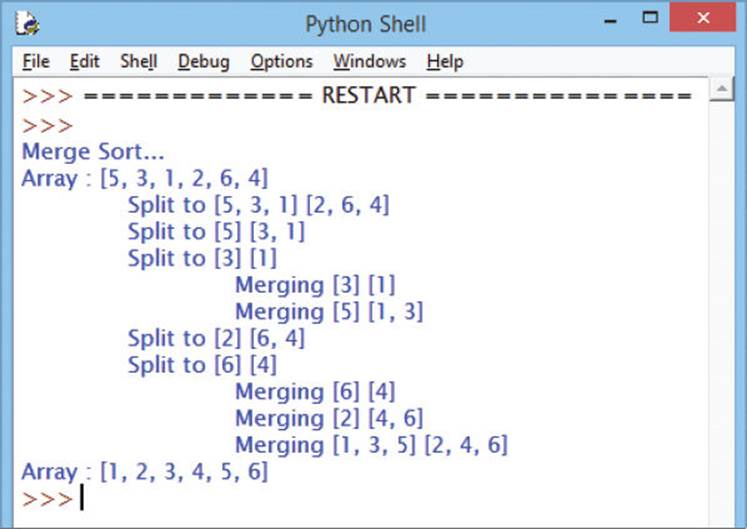
The code listed here uses a semi-colon ; separator to write two statements on some lines – due only to page limitations.

Partitioning sorts

The technique of dividing an array list into sub-sections around the array’s mid-point with a merge sort algorithm, demonstrated in the previous example, works well but an alternative technique can be employed to partition an array list around a “pivot” point.

A “quick sort” algorithm is a complex sorting algorithm that also employs the “divide and conquer” strategy. This first specifies a particular array element whose value will act as the pivot. The algorithm then repeatedly divides the array into two “partitions” – one partition containing values less than the pivot and the other partition containing values more than the pivot. Once the partition operation is complete, the final pivot is in its correct position so the algorithm then merges the lesser partition with the pivot and the greater partition into a single sorted list.

Quick sort is a complex algorithm that can be coded as a function algorithm, which makes “recursive” calls to repeatedly divide an array. Quick sort is a fast algorithm that compares element values when dividing the elements into partitions.

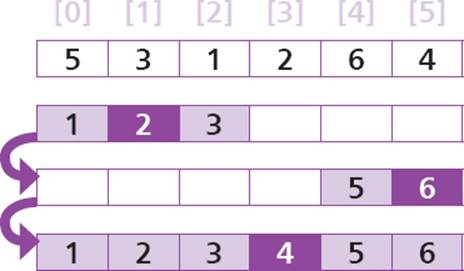
In this example the array is only small but the quick sort algorithm efficiently partitions then re-assembles large arrays in exactly the same way.

Opinions vary as to which element is best to choose as the pivot in the quick sort algorithm. Some coders like to choose a middle element, as in the merge sort algorithm in the previous example. Others prefer to choose the first or last element, or an element at some arbitrary position in between – like the example opposite.

Start a new program by declaring a function to receive a list reference and repeatedly iterate through an array list

def quick_sort( array ) :

if len( array ) > 1 :

pivot = int( len( array ) -1 )

less = [ ] ; more = [ ]

# Algorithm sequence to be added here.

quick_sort( less ) ; quick_sort( more )

print( ‘\tLess:’ , less , ‘\tPivot:’ , array[ pivot ] , \

‘\tMore:’ , more )

array[ : ] = less + [ array[ pivot ] ] + more
print( ‘\t\t...Merged:’ , array )

quick.py

Next, add the algorithm sequence to divide the array list elements into partitions then merge them together

for element in range( len( array ) ) :

value = array[ element ]

if element != pivot :

if value < array[ pivot ] :

less.append( value )

else :

more.append( value )

Now, add statements to create and display the array list

array = [ 5 , 3 , 1 , 2 , 6 , 4 ]

print( ‘Quick Sort...\nArray :’ , array )

quick_sort( array )

print( ‘Array :’ , array )

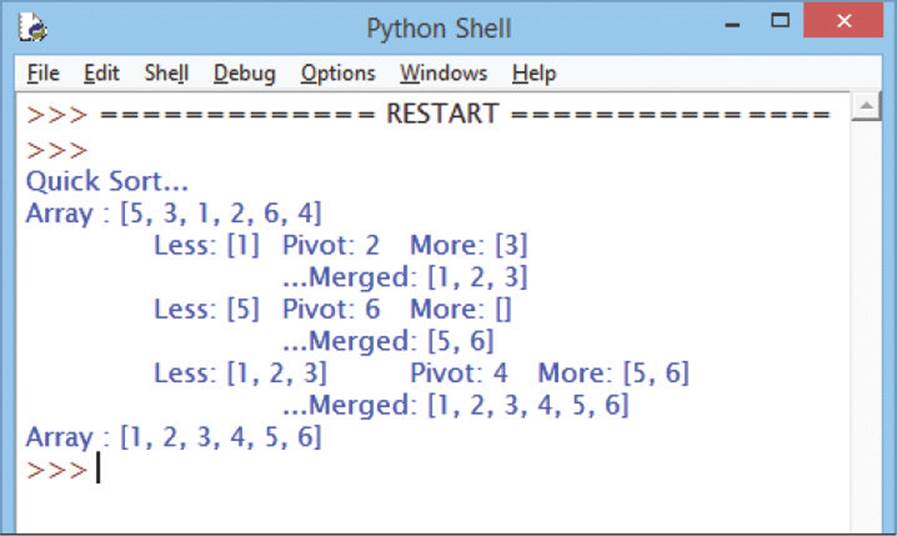
The quick sort algorithm uses less memory than merge sort and is often considered to be the best sorting algorithm.

Summary

•An algorithm is a well-defined sequence of instructions to perform a specific task

•Each algorithm takes one or more values as input and produces one or more resulting values as output

•An algorithm may be created in code as a function whose statements define a sequence of instructions to perform a task

•The efficiency of sorting algorithms may depend upon the nature of the list to be sorted

•A sorting algorithm function can make a copy of a list passed as input and return a sorted copy of that list as output

•There are several popular algorithms to sort array lists in place but each have their own strengths and weaknesses

•Selection Sort algorithms repeatedly select the lowest element in the unsorted section of an array list and move it to the end of the sorted section of that array

•Insertion Sort algorithms repeatedly take the next element in the unsorted section of an array list and insert it into the sorted section of that array at the correct position

•Bubble Sort algorithms repeatedly compare adjacent elements in an unsorted array list and swap them into the correct order

•Selection Sort, Insertion Sort, and Bubble Sort are simple comparison algorithms but are relatively slow

•Merge Sort algorithms repeatedly divide an unsorted array list into left and right sub-sections from the array’s mid-point then merge the sub-sections into a single sorted list

•Quick Sort algorithms repeatedly divide an unsorted array list into partitions containing values greater or less than a pivot value then merge the partitions into a single sorted list

•Merge Sort and Quick Sort algorithms are fast complex algorithms that each employ a divide-and-conquer strategy