Functional Thinking (2014)
Chapter 5. Evolve
Functional programming languages approach code reuse differently from object-oriented languages. Object-oriented languages tend to have many data structures with many operations, whereas functional languages exhibit few data structures with many operations. Object-oriented languages encourage you to create class-specific methods, and you can capture recurring patterns for later reuse. Functional languages help you achieve reuse by encouraging the application of common transformations to data structures, with higher-order functions to customize the operation for specific instances.
In this chapter, I cover various ways that languages have evolved solutions to particular recurring problems in software. I discuss the attitudinal change in functional programming with respect to custom data structures; talk about the malleability of languages and solutions; and cover dispatch options, operator overloading, and functional data structures.
Few Data Structures, Many Operations
It is better to have 100 functions operate on one data structure than 10 functions on 10 data structures.
— Alan Perlis
In object-oriented imperative programming languages, the units of reuse are classes and the messages they communicate with, typically captured in a class diagram. The seminal work in that space, Design Patterns: Elements of Reusable Object-Oriented Software (Addison-Wesley, 1994), includes at least one class diagram with each pattern. In the OOP world, developers are encouraged to create unique data structures, with specific operations attached in the form of methods. Functional programming languages don’t try to achieve reuse in the same way. They prefer a few key data structures (such as list, set, and map) with highly optimized operations on those data structures. You pass data structures plus higher-order functions to “plug into” this machinery, customizing it for a particular use. For example, the filter() function I’ve shown in several languages accepts a code block as the “plug-in” higher-order function that determines the filter criteria, and the machinery applies the filter criteria in an efficient way, returning the filtered list.
Encapsulation at the function level enables reuse at a more granular, fundamental level than building custom class structures. One advantage of this approach is already appearing in Clojure. For example, consider the case of parsing XML. A huge number of frameworks exist for this task in Java, each with custom data structures and method semantics (for example, SAX versus DOM). Clojure parses XML into a standard Map structure, rather than encouraging you to use a custom data structure. Because Clojure includes lots of tools for working with maps, performing XPath-style queries is simple using the built-in list-comprehension function, for, as shown in Example 5-1.
Example 5-1. Parsing XML in Clojure
(use 'clojure.xml)
(def WEATHER-URI "http://weather.yahooapis.com/forecastrss?w=%d&u=f")
(defn get-location [city-code]
(for [x (xml-seq (parse (format WEATHER-URI city-code)))
:when (= :yweather:location (:tag x))]
(str (:city (:attrs x)) "," (:region (:attrs x)))))
(defn get-temp [city-code]
(for [x (xml-seq (parse (format WEATHER-URI city-code)))
:when (= :yweather:condition (:tag x))]
(:temp (:attrs x))))
(println "weather for " (get-location 12770744) "is " (get-temp 12770744))
In Example 5-1, I access Yahoo!’s weather service to fetch a given city’s weather forecast. Because Clojure is a Lisp variant, it’s easiest to read inside out. The actual call to the service endpoint occurs at (parse (format WEATHER-URI city-code)), which uses String’s format()function to embed the city-code into the string. The list comprehension function, for, places the parsed XML, cast using xml-seq into a queryable map named x. The :when predicate determines the match criteria; in this case, I’m searching for a tag (translated into a Clojure keyword):yweather:condition.
To understand the syntax used to pull values from the data structure, it’s useful to see what’s in it. When parsed, the pertinent call to the weather service returns the data structure shown in this excerpt:
({:tag :yweather:condition, :attrs {:text Fair, :code 34, :temp 62, :date Tue,
04 Dec 2012 9:51 am EST}, :content nil})
Because Clojure is optimized to work with maps, keywords become functions on the maps that contain them. The call in Example 5-1 to (:tag x) is shorthand for “retrieve the value corresponding to the :tag key from the map stored in x.” Thus, :yweather:condition yields the maps values associated with that key, which includes the attrs map that I fetch the :temp value from using the same syntax.
One of the initially daunting details in Clojure is the seemingly endless ways to interact with maps and other core data structures. However, it’s a reflection of the fact that most things in Clojure try to resolve to these core, optimized data structures. Rather than trap parsed XML in a unique framework, it tries instead to convert it to an existing structure that already has tools in place.
An advantage of the reliance on fundamental data structures appears in the XML libraries in Clojure. For traversing tree-shaped structures (such as XML documents), a useful data structure called a zipper was created in 1997. A zipper allows you to navigate trees structurally by providing coordinate directions. For example, starting from the root of the tree, you can issue commands such as (→ z/down z/down z/left) to navigate to the second-level left element. Functions already exist in Clojure to convert parsed XML into a zipper, enabling consistent navigation across all tree-shaped structures.
Bending the Language Toward the Problem
Most developers labor under the misconception that their job is to take a complex business problem and translate it into a language such as Java. They do that because Java isn’t particularly flexible as a language, forcing you to mold your ideas into the rigid structure already there. But as developers use malleable languages, they see the opportunity to bend the language more toward their problem rather than the problem toward their language. Languages like Ruby—with its friendlier-than-mainstream support for domain-specific languages (DSLs)—demonstrated that potential. Modern functional languages go even further. Scala was designed to accommodate hosting internal DSLs, and all Lisps (including Clojure) have unparalleled flexibility in enabling the developer to mold the language to the problem. For instance, Example 5-2 uses the XML primitives in Scala to implement Example 5-1’s weather example.
Example 5-2. Scala’s syntactic sugar for XML
importscala.xml._
importjava.net._
importscala.io.Source
val theUrl = "http://weather.yahooapis.com/forecastrss?w=12770744&u=f"
val xmlString =Source.fromURL(newURL(theUrl)).mkString
val xml =XML.loadString(xmlString)
val city = xml \\ "location" \\ "@city"
val state = xml \\ "location" \\ "@region"
val temperature = xml \\ "condition" \\ "@temp"
println(city + ", " + state + " " + temperature)
Scala was designed for malleability, allowing extensions such as operator overloading (covered ) and implicit types. In Example 5-2, Scala is extended to allow XPath-like queries using the \\ operator.
While not specifically a functional language feature, the ability to gracefully mold your language closer to your problem domain is common in modern languages and facilitates a functional, declarative style of coding.
NOTE
Evolve your program toward the problem, not the other way around.
Rethinking Dispatch
Chapter 3 introduced the concept of Scala pattern matching, one example of an alternative dispatch mechanism, which I’m using as a broad term to describe ways languages dynamically choose behavior. This section extends the discussion to show how dispatch mechanisms in various functional JVM languages enable more conciseness and flexibility than their Java counterparts.
Improving Dispatch with Groovy
In Java, conditional execution ends up using the if statement except in very limited cases where the switch statement applies. Because long series of if statements become difficult to read, Java developers often rely on the Gang of Four (GoF) Factory (or Abstract Factory) pattern. If you use a language that includes a more flexible decision expression, you can simplify a lot of your code without resorting to the extra structure of patterns.
Groovy has a powerful switch statement that mimics the syntax—but not the behavior—of Java’s switch statement, as shown in Example 5-3.
Example 5-3. Groovy’s vastly improved switch statement
package com.nealford.ft.polydispatch
classLetterGrade {
def gradeFromScore(score) {
switch (score) {
case 90..100 : return "A"
case 80..<90 : return "B"
case 70..<80 : return "C"
case 60..<70 : return "D"
case 0..<60 : return "F"
case ~"[ABCDFabcdf]" : return score.toUpperCase()
default: thrownew IllegalArgumentException("Invalid score: ${score}")
}
}
}
The code in Example 5-3 accepts a score and returns the corresponding letter grade. Unlike Java, Groovy’s switch statement accepts a wide variety of dynamic types. In Example 5-3, the score parameter should be either a number between 0 and 100 or a letter grade. As in Java, you must terminate each case with either a return or break, following the same fall-through semantics. But in Groovy, unlike Java, I can specify ranges (90..100, noninclusive ranges (80..<90), regular expressions (~"[ABCDFabcdf]"), and a default condition.
Groovy’s dynamic typing enables me to send different types of parameters and react appropriately, as shown in the unit tests in Example 5-4.
Example 5-4. Testing Groovy letter grades
importorg.junit.Test
importcom.nealford.ft.polydispatch.LetterGrade
importstatic org.junit.Assert.assertEquals
classLetterGradeTest {
@Test
publicvoid test_letter_grades() {
def lg = new LetterGrade()
assertEquals("A", lg.gradeFromScore(92))
assertEquals("B", lg.gradeFromScore(85))
assertEquals("D", lg.gradeFromScore(65))
assertEquals("F", lg.gradeFromScore("f"))
}
}
A more powerful switch gives you a useful middle ground between serial ifs and the Factory design pattern. Groovy’s switch lets you match ranges and other complex types, which is similar in intent to pattern matching in Scala.
Clojure’s “Bendable” Language
Java and languages like it include keywords—the syntactic scaffolding of the language. Developers can’t create new keywords in the language (although some Java-like languages allow extension via metaprogramming), and keywords have semantics unavailable to developers. For example, the Java if statement “understands” things like short-circuit Boolean evaluation. Although you can create functions and classes in Java, you can’t create fundamental building blocks, so you need to translate problems into the syntax of the programming language. (In fact, many developers think their job is to perform this translation.) In Lisp variants such as Clojure, the developer can modify the language toward the problem, blurring the distinction between what the language designer and developers using the language can create.
In Clojure, developers use the language to create readable (Lisp) code. For instance, Example 5-5 shows the letter-grade example in Clojure.
Example 5-5. Letter grades in Clojure
(ns lettergrades)
(defn in [score low high]
(and (number? score) (<= low score high)))
(defn letter-grade [score]
(cond
(in score 90 100) "A"
(in score 80 90) "B"
(in score 70 80) "C"
(in score 60 70) "D"
(in score 0 60) "F"
(re-find #"[ABCDFabcdf]" score) (.toUpperCase score)))
In Example 5-5, I wrote the letter-grade function to read nicely, then implemented the in function to make it work. In this code, the cond function enables me to evaluate a sequence of tests, handled by my in function. As in the previous examples, I handle both numeric and existing letter-grade strings. Ultimately, the return value should be an uppercase character, so if the input is in lowercase, I call the toUpperCase function on the returned string. In Clojure, functions are first-class citizens rather than classes, making function invocations “inside-out”: the call toscore.toUpperCase() in Java is equivalent to Clojure’s (.toUpperCase score).
I test Clojure’s letter-grade implementation in Example 5-6.
Example 5-6. Testing Clojure letter grades
(ns nealford-test
(:use clojure.test)
(:use lettergrades))
(deftest numeric-letter-grades
(dorun (map #(is (= "A" (letter-grade %))) (range 90 100)))
(dorun (map #(is (= "B" (letter-grade %))) (range 80 89)))
(dorun (map #(is (= "C" (letter-grade %))) (range 70 79)))
(dorun (map #(is (= "D" (letter-grade %))) (range 60 69)))
(dorun (map #(is (= "F" (letter-grade %))) (range 0 59))))
(deftest string-letter-grades
(dorun (map #(is (= (.toUpperCase %)
(letter-grade %))) ["A" "B" "C" "D" "F" "a" "b" "c" "d" "f"])))
(run-all-tests)
In this case, the test code is more complex than the implementation! However, it shows how concise Clojure code can be.
In the numeric-letter-grades test, I want to check every value in the appropriate ranges. Reading inside out, the code #(is (= "A" (letter-grade %))) creates a new anonymous function that takes a single parameter and returns true if the correct letter grade returns. The mapfunction maps this anonymous function across the collection in the second parameter, which is the list of numbers within the appropriate range.
The (dorun ) function allows side effects to occur, which the testing framework relies on. Calling map across each range in Example 5-6 returns a list of all true values. The (is ) function from the clojure.test namespace verifies the value as a side effect. Calling the mapping function within (dorun ) allows the side effect to occur correctly and execute the tests.
Clojure Multimethods and a la carte Polymorphism
A long series of if statements is hard to read and debug, yet Java doesn’t have any particularly good alternatives at the language level. This problem is typically solved by using either the Factory or Abstract Factory design patterns from the GoF. The Factory Pattern works in Java because of class-based polymorphism, allowing me to define a general method signature in a parent class or interface, then choose the implementation that executes dynamically.
Many developers dismiss Clojure because it isn’t an object-oriented language, believing that object-oriented languages are the pinnacle of power. That’s a mistake: Clojure has all the features of an object-oriented language, implemented independently of other features. For example, Clojure supports polymorphism but isn’t restricted to evaluating the class to determine dispatch. Clojure supports polymorphic multimethods whereby dispatch is triggered by whatever characteristic (or combination) the developer wants.
In Clojure, data typically resides in structs, which mimic the data part of classes. Consider the Clojure code in Example 5-7.
Example 5-7. Defining a color structure in Clojure
(defstruct color :red :green :blue)
(defn red [v]
(struct color v 0 0))
(defn green [v]
(struct color 0 v 0))
(defn blue [v]
(struct color 0 0 v))
In Example 5-7, I define a structure that holds three values, corresponding to color values. I also create three methods that return a structure saturated with a single color.
A multimethod in Clojure is a method definition that accepts a dispatch function, which returns the decision criteria. Subsequent definitions allow you to flesh out different versions of the method. Example 5-8 shows a multimethod definition.
Example 5-8. Defining a multimethod
(defn basic-colors-in [color]
(for [[k v] color :when (not= v 0)] k))
(defmulti color-string basic-colors-in)
(defmethod color-string [:red] [color]
(str "Red: " (:red color)))
(defmethod color-string [:green] [color]
(str "Green: " (:green color)))
(defmethod color-string [:blue] [color]
(str "Blue: " (:blue color)))
(defmethod color-string :default [color]
(str "Red:" (:red color) ", Green: " (:green color) ", Blue: " (:blue color)))
In Example 5-8, I define a dispatch function called basic-colors-in, which returns a vector of all nonzero color values. For the variations on the method, I specify what should happen if the dispatch function returns a single color; in this case, it returns a string with its color. The last case includes the optional :default keyword, which handles remaining cases. For this one, I cannot assume that I received a single color, so the return lists the values of all the colors.
Tests to exercise these multimethods appear in Example 5-9.
Example 5-9. Testing colors in Clojure
(ns color-dispatch.core-test
(:require [clojure.test :refer :all]
[color-dispatch.core :refer :all]))
(deftest pure-colors
(is (= "Red: 5" (color-string (struct color 5 0 0))))
(is (= "Green: 12" (color-string (struct color 0 12 0))))
(is (= "Blue: 40" (color-string (struct color 0 0 40)))))
(deftest varied-colors
(is (= "Red:5, Green: 40, Blue: 6" (color-string (struct color 5 40 6)))))
(run-all-tests)
In Example 5-9, when I call the method with a single color, it executes the singular color version of the multimethod. If I call it with a complex color profile, the default method returns all colors.
Decoupling polymorphism from inheritance provides a powerful, contextualized dispatch mechanism. For example, consider the problem of image file formats, each one having a different set of characteristics to define the type. By using a dispatch function, Clojure enables you to build powerful dispatch as contextualized as Java polymorphism but with fewer limitations.
Operator Overloading
A common feature of functional languages is operator overloading—the ability to redefine operators (such as +, -, or *) to work with new types and exhibit new behaviors. Omission of operator overloading was a conscious decision during Java’s formative period, but virtually every modern language now features it, including the natural successors to Java.
Groovy
Groovy tries to update Java’s syntax while preserving its natural semantics. Thus, Groovy allows operator overloading by automatically mapping operators to method names. For example, if you want to overload the + operator on the Integer class, you override its plus() method. The entire list of mappings is available online; Table 5-1 shows a partial list.
Table 5-1. Partial list of Groovy operator/method mappings
|
Operator |
Method |
|
x + y |
x.plus(y) |
|
x * y |
x.multiply(y) |
|
x / y |
x.div(y) |
|
x ** y |
x.power(y) |
As an example of operator overloading, I’ll create a ComplexNumber class in both Groovy and Scala. Complex numbers are a mathematical concept with both a real and imaginary part, typically written as, for example, 3 + 4i. Complex numbers are common in many scientific fields, including engineering, physics, electromagnetism, and chaos theory. Developers writing applications in those fields greatly benefit from the ability to create operators that mirror their problem domain.
A Groovy ComplexNumber class appears in Example 5-10.
Example 5-10. ComplexNumber in Groovy
package complexnums
classComplexNumber {
def real, imaginary
public ComplexNumber(real, imaginary) {
this.real = real
this.imaginary = imaginary
}
def plus(rhs) {
new ComplexNumber(this.real + rhs.real, this.imaginary + rhs.imaginary)
}
// formula: (x + yi)(u + vi) = (xu – yv) + (xv + yu)i.
def multiply(rhs) {
new ComplexNumber(
real * rhs.real - imaginary * rhs.imaginary,
real * rhs.imaginary + imaginary * rhs.real)
}
def String toString() {
real.toString() + ((imaginary < 0 ? "" : "+") + imaginary + "i").toString()
}
}
In Example 5-10, I create a class that holds both real and imaginary parts, and I create the overloaded plus() and multiply() operators. Adding two complex numbers is straightforward: the plus() operator adds the two numbers’ respective real and imaginary parts to each other to produce the result. Multiplying two complex numbers requires this formula:
(x + yi)(u + vi) = (xu - yv) + (xv + yu)i
The multiply() operator in Example 5-10 replicates the formula. It multiplies the numbers’ real parts, then subtracts the product of the imaginary parts, which is added to the product of the real and imaginary parts both multiplied by each other.
Example 5-11 exercises the new complex-number operators.
Example 5-11. Testing complex-number operators
package complexnums
importorg.junit.Test
importstatic org.junit.Assert.assertTrue
importorg.junit.Before
classComplexNumberTest {
def x, y
@Before void setup() {
x = new ComplexNumber(3, 2)
y = new ComplexNumber(1, 4)
}
@Test void plus() {
def z = x + y;
assertTrue 3 + 1 == z.real
assertTrue 2 + 4 == z.imaginary
}
@Test void multiply() {
def z = x * y
assertTrue(-5 == z.real)
assertTrue 14 == z.imaginary
}
@Test void to_string() {
assertTrue "3+2i" == x.toString()
assertTrue "4+6i" == (x + y).toString()
assertTrue "3+0i" == new ComplexNumber(3, 0).toString()
assertTrue "4-2i" == new ComplexNumber(4, -2).toString()
}
}
In Example 5-11, the plus() and multiply() test methods’ use of the overloaded operators—both of which are represented by the same symbols that the domain experts use—is indistinguishable from similar use of built-in types.
Scala
Scala allows operator overloading by discarding the distinction between operators and methods: operators are merely methods with special names. Thus, to override the multiplication operator in Scala, you override the * method. I create complex numbers in Scala in Example 5-12.
Example 5-12. Complex numbers in Scala
finalclassComplex(val real:Int, val imaginary:Int) extendsOrdered[Complex] {
def +(operand:Complex) =
newComplex(real + operand.real, imaginary + operand.imaginary)
def +(operand:Int) =
newComplex(real + operand, imaginary)
def -(operand:Complex) =
newComplex(real - operand.real, imaginary - operand.imaginary)
def -(operand:Int) =
newComplex(real - operand, imaginary)
def *(operand:Complex) =
newComplex(real * operand.real - imaginary * operand.imaginary,
real * operand.imaginary + imaginary * operand.real)
overridedef toString() =
real + (if (imaginary < 0) "" else "+") + imaginary + "i"
overridedef equals(that:Any) = that match {
case other :Complex => (real == other.real) && (imaginary == other.imaginary)
case other :Int => (real == other) && (imaginary == 0)
case_=>false
}
overridedef hashCode():Int =
41 * ((41 + real) + imaginary)
def compare(that:Complex) :Int = {
def myMagnitude =Math.sqrt(real ^ 2 + imaginary ^ 2)
def thatMagnitude =Math.sqrt(that.real ^ 2 + that.imaginary ^ 2)
(myMagnitude - thatMagnitude).round.toInt
}
}
The class in Example 5-12 includes real and imaginary members, as well as the plus and multiply operators/functions. In Scala, constructor parameters appear as class parameters; my class accepts real and imaginary parts. Because Scala automatically provides fields, the remainder of the class contains method definitions. For plus, minus, and multiply, I declare eponymous methods that accept Complex numbers as parameters.
The toString() method in Example 5-12 exemplifies another bit of common ground among many functional languages: use of expressions rather than statements. In the toString() method, I must supply the + sign if the imaginary part is positive, but the real part’s sign will suffice otherwise. In Scala, if is an expression rather than a statement, eliminating the need for Java’s ternary operator (?:).
I can use ComplexNumbers naturally, as shown in Example 5-13.
Example 5-13. Using complex numbers in Scala
importorg.scalatest.FunSuite
classComplexTestextendsFunSuite {
def fixture =
new {
val a =newComplex(1, 2)
val b =newComplex(30, 40)
}
test("plus") {
val f = fixture
val z = f.a + f.b
assert(1 + 30 == z.real)
}
test("comparison") {
val f = fixture
assert(f.a < f.b)
assert(newComplex(1, 2) >= newComplex(3, 4))
assert(newComplex(1, 1) < newComplex(2,2))
assert(newComplex(-10, -10) > newComplex(1, 1))
assert(newComplex(1, 2) >= newComplex(1, 2))
assert(newComplex(1, 2) <= newComplex(1, 2))
}
}
Java’s designers explicitly decided against operator overloading, feeling from their experience with C++ that it added too much complexity. Most modern languages have removed much of the definitional complexity, but the warning against abuse still resonates.
NOTE
Overload operators to bend your language toward an existing problem domain, not to create a brand new language.
Functional Data Structures
In Java, errors are traditionally handled by exceptions and the language’s support for creating and propagating them. But what if structured exception handling didn’t exist? Many functional languages don’t support the exception paradigm, so they must find alternate ways of expressing error conditions.
Exceptions violate a couple of premises that most functional languages adhere to. First, they prefer pure functions, which have no side effects. However, throwing an exception is a side effect that causes unusual (exceptional) program flow. Functional languages tend to deal with values, prefering to react to return values that indicate an error rather than interrupt program flow.
The other feature that functional programs tend toward is referential transparency: the calling routine shouldn’t care whether it accesses a value or a function that returns a value. If a function can also throw an exception, it isn’t a safe substitute for a value.
In this section, I show type-safe, error-handling mechanisms in Java that bypass the normal exception-propagation mechanism (with assistance in some examples from the Functional Java framework).
Functional Error Handling
If you want to handle errors in Java without using exceptions, the fundamental obstacle is the language limitation of a single return value from methods. But methods can, of course, return a single Object (or subclass) reference, which can hold multiple values. So I could enable multiple return values by using a Map. Consider the divide() method in Example 5-14.
Example 5-14. Using Map to handle multiple returns
publicstatic Map<String, Object> divide(int x, int y) {
Map<String, Object> result = new HashMap<String, Object>();
if (y == 0)
result.put("exception", new Exception("div by zero"));
else
result.put("answer", (double) x / y);
return result;
}
In Example 5-14, I create a Map with String as the key and Object as the value. In the divide() method, I put either exception to indicate failure or answer to indicate success. Both modes are tested in Example 5-15.
Example 5-15. Testing success and failure with Maps
@Test
publicvoid maps_success() {
Map<String, Object> result = RomanNumeralParser.divide(4, 2);
assertEquals(2.0, (Double) result.get("answer"), 0.1);
}
@Test
publicvoid maps_failure() {
Map<String, Object> result = RomanNumeralParser.divide(4, 0);
assertEquals("div by zero", ((Exception) result.get("exception")).getMessage());
}
In Example 5-15, the maps_success test verifies that the correct entry exists in the returned Map. The maps_failure test checks for the exception case.
This approach has some obvious problems. First, whatever ends up in the Map isn’t type-safe, which disables the compiler’s ability to catch certain errors. Enumerations for the keys would improve this situation slightly, but not much. Second, the method invoker doesn’t know if the method call was a success, placing the burden on the caller to check the dictionary of possible results. Third, nothing prevents both keys from having values, which makes the result ambiguous.
What I need is a mechanism that allows me to return two (or more) values in a type-safe way.
The Either Class
The need to return two distinct values occurs frequently in functional languages, and a common data structure used to model this behavior is the Either class. Either is designed to hold either a left or right value (but never both). This data structure is referred to as a disjoint union. Some C-based languages contain the union data type, which can hold one instance of several different types. A disjoint union has slots for two types but holds an instance for only one of them.
Scala includes an instance of Either, as shown in Example 5-16.
Example 5-16. Scala’s predefined Either class
typeError = String
typeSuccess = String
def call(url:String):Either[Error,Success]={
val response =WS.url(url).get.value.get
if (valid(response))
Right(response.body)
elseLeft("Invalid response")
}
As Example 5-16 shows, a common use for Either is for error handling. Either integrates nicely into the overall Scala ecosystem; a popular case includes pattern matching on an instance of Either, as shown in Example 5-17.
Example 5-17. Scala Either and pattern matching
getContent(newURL("http://nealford.com")) match {
caseLeft(msg) => println(msg)
caseRight(source) => source.getLines.foreach(println)
}
Even though it isn’t built into the Java language, I can create a substitute using generics; I create a simple Either class, as shown in Example 5-18.
Example 5-18. Returning two (type-safe) values via the Either class
package com.nealford.ft.errorhandling;
publicclassEither<A,B> {
private A left = null;
private B right = null;
private Either(A a,B b) {
left = a;
right = b;
}
publicstatic <A,B> Either<A,B> left(A a) {
returnnew Either<A,B>(a,null);
}
public A left() {
return left;
}
publicboolean isLeft() {
return left != null;
}
publicboolean isRight() {
return right != null;
}
public B right() {
return right;
}
publicstatic <A,B> Either<A,B> right(B b) {
returnnew Either<A,B>(null,b);
}
publicvoid fold(F<A> leftOption, F<B> rightOption) {
if(right == null)
leftOption.f(left);
else
rightOption.f(right);
}
}
In Example 5-18, the Either class has a private constructor, making construction the responsibility of either of the two static methods left(A a) or right(B b). The remaining methods in the class are helpers that retrieve and investigate the class members.
Armed with Either, I can write code that returns either an exception or a legitimate result (but never both) while retaining type safety. The common functional convention is that the left of an Either class contains an exception (if any), and the right contains the result.
Parsing Roman numerals
To illustrate the use of Either, I have a class named RomanNumeral that appears in Example 5-19.
Example 5-19. Naive implementation of Roman numerals in Java
package com.nealford.ft.errorhandling;
publicclassRomanNumeral {
privatestaticfinal String NUMERAL_MUST_BE_POSITIVE =
"Value of RomanNumeral must be positive.";
privatestaticfinal String NUMERAL_MUST_BE_3999_OR_LESS =
"Value of RomanNumeral must be 3999 or less.";
privatestaticfinal String DOES_NOT_DEFINE_A_ROMAN_NUMERAL =
"An empty string does not define a Roman numeral.";
privatestaticfinal String NO_NEGATIVE_ROMAN_NUMERALS =
"Negative numbers not allowed";
privatestaticfinal String NUMBER_FORMAT_EXCEPTION =
"Illegal character in Roman numeral.";
privatefinalint num;
privatestaticint[] numbers = {1000, 900, 500, 400, 100, 90,
50, 40, 10, 9, 5, 4, 1};
privatestatic String[] letters = {"M", "CM", "D", "CD", "C", "XC",
"L", "XL", "X", "IX", "V", "IV", "I"};
public RomanNumeral(int arabic) {
if (arabic < 1)
thrownew NumberFormatException(NUMERAL_MUST_BE_POSITIVE);
if (arabic > 3999)
thrownew NumberFormatException(NUMERAL_MUST_BE_3999_OR_LESS);
num = arabic;
}
public RomanNumeral(String roman) {
if (roman.length() == 0)
thrownew NumberFormatException(DOES_NOT_DEFINE_A_ROMAN_NUMERAL);
if (roman.charAt(0) == '-')
thrownew NumberFormatException(NO_NEGATIVE_ROMAN_NUMERALS);
roman = roman.toUpperCase();
int positionInString = 0;
int arabicEquivalent = 0;
while (positionInString < roman.length()) {
char letter = roman.charAt(positionInString);
int number = letterToNumber(letter);
if (number < 0)
thrownew NumberFormatException(NUMBER_FORMAT_EXCEPTION);
positionInString++;
if (positionInString == roman.length())
arabicEquivalent += number;
else {
int nextNumber = letterToNumber(roman.charAt(positionInString));
if (nextNumber > number) {
arabicEquivalent += (nextNumber - number);
positionInString++;
} else
arabicEquivalent += number;
}
}
if (arabicEquivalent > 3999)
thrownew NumberFormatException(NUMERAL_MUST_BE_3999_OR_LESS);
num = arabicEquivalent;
}
privateint letterToNumber(char letter) {
switch (letter) {
case 'I':
return 1;
case 'V':
return 5;
case 'X':
return 10;
case 'L':
return 50;
case 'C':
return 100;
case 'D':
return 500;
case 'M':
return 1000;
default:
return -1;
}
}
public String toString() {
String romanNumeral = "";
int remainingPartToConvert = num;
for (int i = 0; i < numbers.length; i++) {
while (remainingPartToConvert >= numbers[i]) {
romanNumeral += letters[i];
remainingPartToConvert -= numbers[i];
}
}
return romanNumeral;
}
publicint toInt() {
return num;
}
}
I also have a class named RomanNumeralParser that calls the RomanNumeral class. The parseNumber() method and illustrative tests appear in Example 5-20.
Example 5-20. Parsing Roman numerals
publicstatic Either<Exception, Integer> parseNumber(String s) {
if (! s.matches("[IVXLXCDM]+"))
return Either.left(new Exception("Invalid Roman numeral"));
else
return Either.right(new RomanNumeral(s).toInt());
}
I can verify the results via tests, as shown in Example 5-21.
Example 5-21. Testing parse of Roman numerals
@Test
publicvoid parsing_success() {
Either<Exception, Integer> result = RomanNumeralParser.parseNumber("XLII");
assertEquals(Integer.valueOf(42), result.right());
}
@Test
publicvoid parsing_failure() {
Either<Exception, Integer> result = RomanNumeralParser.parseNumber("FOO");
assertEquals(INVALID_ROMAN_NUMERAL, result.left().getMessage());
}
In Example 5-21, the parseNumber() method performs an astoundingly naive validation (for the purpose of showing an error), placing the error condition in the Either’s left or the result in its right. Both cases are shown in the unit tests.
This is a big improvement over passing Map data structures around. I retain type safety (note that I can make the exception as specific as I like); the errors are obvious in the method declaration via the generics; and my results come back with one extra level of indirection, unpacking the result (whether exception or answer) from Either. And the extra level of indirection enables laziness.
Lazy parsing and Functional Java
The Either class appears in many functional algorithms and is so common in the functional world that the Functional Java framework contains an implementation of Either that would work in Examples 5-18 and 5-20. But it was made to work with other Functional Java constructs. Accordingly, I can use a combination of Either and Functional Java’s P1 class to create lazy error evaluation.
In Functional Java, a P1 class is a simple wrapper around a single method named _1() that takes no parameters. (Other variants—P2, P3, etc.—hold multiple methods.) A P1 is used in Functional Java to pass a code block around without executing it, enabling you to execute the code in a context of your choosing, substituting for a higher-order function.
In Java, exceptions are instantiated as soon as you throw an exception. By returning a lazily evaluated method, I can defer the creation of the exception until a later time. Consider the example and associated tests in Example 5-22.
Example 5-22. Using Functional Java to create a lazy parser
publicstatic P1<Either<Exception, Integer>> parseNumberLazy(final String s) {
if (! s.matches("[IVXLXCDM]+"))
returnnew P1<Either<Exception, Integer>>() {
public Either<Exception, Integer> _1() {
return Either.left(new Exception("Invalid Roman numeral"));
}
};
else
returnnew P1<Either<Exception, Integer>>() {
public Either<Exception, Integer> _1() {
return Either.right(new RomanNumeral(s).toInt());
}
};
}
The test appears in Example 5-23.
Example 5-23. Testing Functional Java–based lazy parser
@Test
publicvoid parse_lazy() {
P1<Either<Exception, Integer>> result =
RomanNumeralParser.parseNumberLazy("XLII");
assertEquals(42, result._1().right().intValue());
}
@Test
publicvoid parse_lazy_exception() {
P1<Either<Exception, Integer>> result =
RomanNumeralParser.parseNumberLazy("FOO");
assertTrue(result._1().isLeft());
assertEquals(INVALID_ROMAN_NUMERAL, result._1().left().getMessage());
}
The code in Example 5-22 is similar to Example 5-20, with an extra P1 wrapper. In the parse_lazy test, I must unpack the result via the call to _1() on the result, which returns Either’s right, from which I can retrieve the value. In the parse_lazy_exception test, I can check for the presence of a left, and I can unpack the exception to discern its message.
The exception (along with its expensive-to-generate stack trace) isn’t created until you unpack Either’s left with the _1() call. Thus, the exception is lazy, letting you defer execution of the exception’s constructor.
Providing defaults
Laziness isn’t the only benefit of using Either for error handling. Another is that you can provide default values. Consider the code in Example 5-24.
Example 5-24. Providing reasonable default return values
privatestaticfinalint MIN = 0;
privatestaticfinalint MAX = 1000;
publicstatic Either<Exception, Integer> parseNumberDefaults(final String s) {
if (! s.matches("[IVXLXCDM]+"))
return Either.left(new Exception("Invalid Roman numeral"));
else {
int number = new RomanNumeral(s).toInt();
return Either.right(new RomanNumeral(number >= MAX ? MAX : number).toInt());
}
}
The corresponding tests that illustrate default values appear in Example 5-25.
Example 5-25. Testing defaults
@Test
publicvoid parse_defaults_normal() {
Either<Exception, Integer> result =
RomanNumeralParser.parseNumberDefaults("XLII");
assertEquals(42, result.right().intValue());
}
@Test
publicvoid parse_defaults_triggered() {
Either<Exception, Integer> result =
RomanNumeralParser.parseNumberDefaults("MM");
assertEquals(1000, result.right().intValue());
}
In Example 5-25, let’s assume that I never allow any Roman numerals greater than MAX, and any attempt to set one greater will default to MAX. parseNumberDefaults() ensures that the default is placed in Either’s right.
Wrapping exceptions
I can also use Either to wrap exceptions, converting structured exception handling to functional, as shown in Example 5-26.
Example 5-26. Catching other people’s exceptions
publicstatic Either<Exception, Integer> divide(int x, int y) {
try {
return Either.right(x / y);
} catch (Exception e) {
return Either.left(e);
}
}
Tests that illustrate wrapping exceptions appear in Example 5-27.
Example 5-27. Testing wrapping exceptions
@Test
publicvoid catching_other_people_exceptions() {
Either<Exception, Integer> result = FjRomanNumeralParser.divide(4, 2);
assertEquals((long) 2, (long) result.right().value());
Either<Exception, Integer> failure = FjRomanNumeralParser.divide(4, 0);
assertEquals("/ by zero", failure.left().value().getMessage());
}
In Example 5-26, I attempt division, potentially raising an ArithmeticException. If an exception occurs, I wrap it in Either’s left; otherwise I return the result in right. Using Either enables you to convert traditional exceptions (including checked ones) into a more functional style.
Of course, you can also lazily wrap exceptions thrown from called methods, as shown in Example 5-28.
Example 5-28. Lazily catching exceptions
publicstatic P1<Either<Exception, Integer>> divideLazily(finalint x, finalint y) {
returnnew P1<Either<Exception, Integer>>() {
public Either<Exception, Integer> _1() {
try {
return Either.right(x / y);
} catch (Exception e) {
return Either.left(e);
}
}
};
}
Example 5-29 shows tests around lazily catching exceptions.
Example 5-29. Example of handling thrown exceptions
@Test
publicvoid lazily_catching_other_peoples_exceptions() {
P1<Either<Exception, Integer>> result = FjRomanNumeralParser.divideLazily(4, 2);
assertEquals((long) 2, (long) result._1().right().value());
P1<Either<Exception, Integer>> failure = FjRomanNumeralParser.divideLazily(4, 0);
assertEquals("/ by zero", failure._1().left().value().getMessage());
}
Modeling Either in Java is cumbersome because it doesn’t natively include the concept, so I must resort to generics and classes to model it by hand. Languages like Scala have Either and similar constructs built in. Languages like Clojure and Groovy don’t include something like Eithernatively because it’s easy to generate values in a dynamically typed language. For example, in Clojure, rather than create a specific two-part data structure, you’d likely return a keyword, a Clojure constant string used to symbolically identify things.
The Option Class
Either is a handy generic two-part return concept, useful for building generic structures (such as tree-shaped data structures, shown later in this chapter). For the specific case of returning results from a function, a similar class to Either exists in several languages and frameworks calledOption, which provides a simpler exception case: either none, indicating no legitimate value, or some, indicating successful return. Option from Functional Java is demonstrated in Example 5-30.
Example 5-30. Using Option
publicstatic Option<Double> divide(double x, double y) {
if (y == 0)
return Option.none();
return Option.some(x / y);
}
Example 5-31 shows an Option class appearing in tests.
Example 5-31. Testing Option behavior
@Test
publicvoid option_test_success() {
Option result = FjRomanNumeralParser.divide(4.0, 2);
assertEquals(2.0, (Double) result.some(), 0.1);
}
@Test
publicvoid option_test_failure() {
Option result = FjRomanNumeralParser.divide(4.0, 0);
assertEquals(Option.none(), result);
}
As illustrated in Example 5-30, an Option contains either none() or some(), similar to left and right in Either but specific to methods that might not have a legitimate return value. The Option class is considered a simpler subset of Either; Option typically holds success or failure, whereas Either can hold anything.
Either Trees and Pattern Matching
In this section, I continue my exploration of Either, using it to build tree-shaped structures—which in turn enables me to mimic Scala’s pattern matching for building traversal methods.
Using generics in Java, an Either becomes a single data structure that accepts either of two types, which it stores in left and right parts.
In the previous section’s Roman numeral parser example, Either holds either an Exception (left) or an Integer (right), as illustrated in Figure 5-1.
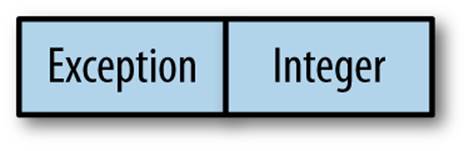
Figure 5-1. The Either abstraction holding either of two types
In that example, this assignment populates the Either:
Either<Exception, Integer> result = RomanNumeralParser.parseNumber("XLII");
I will use this data structure to create a tree-shaped structure, but first I need to cover pattern matching to illustrate the benefit of a data structure like Either.
Scala pattern matching
One of the nice features of Scala is the ability to use pattern matching for dispatch. It’s easier to show than to describe, so consider the function in Example 5-32 , which converts numerical scores to letter grades.
Example 5-32. Using Scala pattern matching to assign letter grades based on score
valVALID_GRADES=Set("A", "B", "C", "D", "F")
def letterGrade(value:Any) :String = value match {
case x:Intif (90 to 100).contains(x) => "A"
case x:Intif (80 to 90).contains(x) => "B"
case x:Intif (70 to 80).contains(x) => "C"
case x:Intif (60 to 70).contains(x) => "D"
case x:Intif (0 to 60).contains(x) => "F"
case x:StringifVALID_GRADES(x.toUpperCase) => x.toUpperCase
}
Statements that illustrate letter grade evaluation at work appear in Example 5-33.
Example 5-33. Testing letter grades
printf("Amy scores %d and receives %s\n", 91, letterGrade(91))
printf("Bob scores %d and receives %s\n", 72, letterGrade(72))
printf("Sam never attened class, scored %d, and received %s\n",
44, letterGrade(44))
printf("Roy transfered and already had %s, which translated as %s\n",
"B", letterGrade("B"))
In Example 5-32, the entire body of the function consists of match applied to a value. For each of the options, a pattern guard enables me to filter the matches based on criteria in addition to the argument’s type. The advantage of this syntax is a clean partitioning of the options instead of a cumbersome series of if statements.
Pattern matching works in conjunction with Scala’s case classes, which are classes with specialized properties—including the ability to perform pattern matching—to eliminate decision sequences. Consider matching color combinations, as shown in Example 5-34.
Example 5-34. Matching case classes in Scala
classColor(val red:Int, val green:Int, val blue:Int)
caseclassRed(r:Int) extendsColor(r, 0, 0)
caseclassGreen(g:Int) extendsColor(0, g, 0)
caseclassBlue(b:Int) extendsColor(0, 0, b)
def printColor(c:Color) = c match {
caseRed(v) => println("Red: " + v)
caseGreen(v) => println("Green: " + v)
caseBlue(v) => println("Blue: " + v)
case col:Color => {
print("R: " + col.red + ", ")
print("G: " + col.green + ", ")
println("B: " + col.blue)
}
casenull=> println("invalid color")
}
In Example 5-34, I create a base Color class, then create specialized single color versions as case classes. When determining which color was passed to the function, I use match to pattern match against all the possible options, including the last case, which handles null.
CASE CLASSES IN SCALA
Simple classes that act as data holders are common in object-oriented systems, particularly ones that must communicate with dissimilar systems. The prevalence of this type of class encouraged Scala to go even further and create case classes. Case classes automatically provide several syntactic conveniences:
§ You can create a factory method based on the name of the class. For example, you can construct a new instance without bothering with the new keyword: val bob = Person("Bob", 42).
§ All arguments in the parameter list of the class are automatically vals, meaning that they are maintained as immutable internal fields.
§ The compiler generates reasonable default equals(), hashCode(), and toString() methods for your class.
§ The compiler adds a copy() method to your class to allow you to make mutating changes by returning a new copy.
Case classes are a good example of how Java successors don’t merely fix syntactic warts but also manifest a better understanding of how modern software works, molding their facilities toward it, a good example of how languages have evolved over time.
Java doesn’t have pattern matching, so it can’t replicate Scala’s ability to create cleanly readable dispatch code. But marrying generics and well-known data structures brings it close, which brings me back to Either.
Either trees
It is possible to model a tree data structure with three abstractions, as shown in Table 5-2.
Table 5-2. Building a tree with three abstractions
|
Tree abstraction |
Description |
|
empty |
Cell has no value |
|
leaf |
Cell has a value of a particular data type |
|
node |
Points to other leafs or nodes |
For convenience, I use the Either class from the Functional Java framework. Conceptually, the Either abstraction expands into as many slots as needed. For example, consider the declaration Either<Empty, Either<Leaf, Node>>, which creates a three-part data structure like the one shown in Figure 5-2.

Figure 5-2. Either<Empty, Either<Leaf, Node>> data structure
Armed with an Either implementation of the three tree abstractions, I define a tree as shown in Example 5-35.
Example 5-35. Tree based on Either
package com.nealford.ft.structuralpatternmatching;
importfj.data.Either;
importstatic fj.data.Either.left;
importstatic fj.data.Either.right;
publicabstractclassTree {
private Tree() {}
publicabstract Either<Empty, Either<Leaf, Node>> toEither();
publicstaticfinalclassEmptyextends Tree {
public Either<Empty, Either<Leaf, Node>> toEither() {
return left(this);
}
public Empty() {}
}
publicstaticfinalclassLeafextends Tree {
publicfinalint n;
@Override
public Either<Empty, Either<Leaf, Node>> toEither() {
return right(Either.<Leaf, Node>left(this));
}
public Leaf(int n) { this.n = n; }
}
publicstaticfinalclassNodeextends Tree {
publicfinal Tree left;
publicfinal Tree right;
public Either<Empty, Either<Leaf, Node>> toEither() {
return right(Either.<Leaf, Node>right(this));
}
public Node(Tree left, Tree right) {
this.left = left;
this.right = right;
}
}
}
The abstract Tree class in Example 5-35 defines within it three final concrete classes: Empty, Leaf, and Node. Internally, the Tree class uses the three-slotted Either shown in Figure 5-2, enforcing the convention that the leftmost slot always holds Empty, the middle slot holds a Leaf, and the rightmost slot holds a Node. It does this by requiring each class to implement the toEither() method, returning the appropriate “slot” for that type. Each “cell” in the data structure is a union in the traditional computer science sense, designed to hold only one of the three possible types at any given time.
Given this tree structure and the fact that I know that its internal structure is based on <Either, <Left, Node>>, I can mimic pattern matching for visiting each element in the tree.
Pattern matching for tree traversal
Scala’s pattern matching encourages you to think about discrete cases. The left() and right() methods of Functional Java’s Either implementation both implement the Iterable interface; this enables me to write pattern-matching-inspired code, as shown in Example 5-36, to determine the tree’s depth.
Example 5-36. Checking a tree’s depth using pattern-matching-like syntax
staticpublicint depth(Tree t) {
for (Empty e : t.toEither().left())
return 0;
for (Either<Leaf, Node> ln: t.toEither().right()) {
for (Leaf leaf : ln.left())
return 1;
for (Node node : ln.right())
return 1 + max(depth(node.left), depth(node.right));
}
thrownew RuntimeException("Inexhaustible pattern match on tree");
}
The depth() method in Example 5-36 is a recursive depth-finding function. Because my tree is based on a specific data structure (<Either, <Left, Node>>), I can treat each “slot” as a specific case. If the cell is empty, this branch has no depth. If the cell is a leaf, I count it as a tree level. If the cell is a node, I know that I should recursively search both left and right sides, adding a 1 for another level of recursion.
I can also use the same pattern-matching syntax to perform a recursive search of the tree, as shown in Example 5-37.
Example 5-37. Determining presence in a tree
staticpublicboolean inTree(Tree t, int value) {
for (Empty e : t.toEither().left())
returnfalse;
for (Either<Leaf, Node> ln: t.toEither().right()) {
for (Leaf leaf : ln.left())
return value == leaf.n;
for (Node node : ln.right())
return inTree(node.left, value) | inTree(node.right, value);
}
returnfalse;
}
As before, I specify the return value for each possible “slot” in the data structure. If I encounter an empty cell, I return false; my search has failed. For a leaf, I check the passed value, returning true if they match. Otherwise, when encountering a node, I recurse through the tree, using the| (non-short-circuited or operator) to combine the returned Boolean values.
To see tree creation and searching in action, consider the unit test in Example 5-38.
Example 5-38. Testing tree searchability
@Test
publicvoid more_elaborate_searchp_test() {
Tree t = new Node(new Node(new Node(new Node(
new Node(new Leaf(4),new Empty()),
new Leaf(12)), new Leaf(55)),
new Empty()), new Leaf(4));
assertTrue(inTree(t, 55));
assertTrue(inTree(t, 4));
assertTrue(inTree(t, 12));
assertFalse(inTree(t, 42));
}
In Example 5-38, I build a tree, then investigate whether elements are present. The inTree() method returns true if one of the leaves equals the search value, and the true propagates up the recursive call stack because of the | operator, as shown in Example 5-37.
The code in Example 5-37 determines if an element appears in the tree. A more sophisticated version also checks for the number of occurrences, as shown in Example 5-39.
Example 5-39. Finding number of occurrences in a tree
staticpublicint occurrencesIn(Tree t, int value) {
for (Empty e: t.toEither().left())
return 0;
for (Either<Leaf, Node> ln: t.toEither().right()) {
for (Leaf leaf : ln.left())
if (value == leaf.n) return 1;
for (Node node : ln.right())
return occurrencesIn(node.left, value)
+ occurrencesIn(node.right, value);
}
return 0;
}
In Example 5-39, I return 1 for every matching leaf, allowing me to count the number of occurrences of each number in the tree.
The code in Example 5-40 illustrates tests for depth(), inTree(), and occurrencesIn() for a complex tree.
Example 5-40. Testing depth, presence, and occurrences in complex trees
@Test
publicvoid multi_branch_tree_test() {
Tree t = new Node(new Node(new Node(new Leaf(4),
new Node(new Leaf(1), new Node(
new Node(new Node(new Node(
new Node(new Node(new Leaf(10), new Leaf(0)),
new Leaf(22)), new Node(new Node(
new Node(new Leaf(4), new Empty()),
new Leaf(101)), new Leaf(555))),
new Leaf(201)), new Leaf(1000)),
new Leaf(4)))),
new Leaf(12)), new Leaf(27));
assertEquals(12, depth(t));
assertTrue(inTree(t, 555));
assertEquals(3, occurrencesIn(t, 4));
}
Because I’ve imposed regularity on the tree’s internal structure, I can analyze the tree during traversal by thinking individually about each case, reflected in the type of element. Although not as expressive as full-blown Scala pattern matching, the syntax comes surprisingly close to the Scala ideal.