Functional Programming in Scala (2015)
Part 4. Effects and I/O
Chapter 15. Stream processing and incremental I/O
We said in the introduction to part 4 that functional programming is a complete paradigm. Every imaginable program can be expressed functionally, including programs that interact with the external world. But it would be disappointing if the IO type were the only way to construct such programs. IO and ST work by simply embedding an imperative programming language into the purely functional subset of Scala. While programming within the IO monad, we have to reason about our programs much like we would in ordinary imperative programming.
We can do better. In this chapter, we’ll show how to recover the high-level compositional style developed in parts 1–3 of this book, even for programs that interact with the outside world. The design space in this area is enormous, and our goal here is not to explore it completely, but just to convey ideas and give a sense of what’s possible.
15.1. Problems with imperative I/O: an example
We’ll start by considering a simple concrete usage scenario that we’ll use to highlight some of the problems with imperative I/O embedded in the IO monad. Our first easy challenge in this chapter is to write a program that checks whether the number of lines in a file is greater than 40,000.
This is a deliberately simple task that illustrates the essence of the problem that our library is intended to solve. We could certainly accomplish this task with ordinary imperative code, inside the IO monad. Let’s look at that first.
Listing 15.1. Counting line numbers in imperative style

We can then run this IO action with unsafePerformIO(linesGt40k("lines.txt")), where unsafePerformIO is a side-effecting method that takes IO[A], returning A and actually performing the desired effects (see section 13.6.1).
Although this code uses low-level primitives like a while loop, a mutable Iterator, and a var, there are some good things about it. First, it’s incremental—the entire file isn’t loaded into memory up front. Instead, lines are fetched from the file only when needed. If we didn’t buffer the input, we could keep as little as a single line of the file in memory at a time. It also terminates early, as soon as the answer is known.
There are some bad things about this code, too. For one, we have to remember to close the file when we’re done. This might seem obvious, but if we forget to do this, or (more commonly) if we close the file outside of a finally block and an exception occurs first, the file will remain open.[1] This is called a resource leak. A file handle is an example of a scarce resource—the operating system can only have a limited number of files open at any given time. If this task were part of a larger program—say we were scanning an entire directory recursively, building up a list of all files with more than 40,000 lines—our larger program could easily fail because too many files were left open.
1 The JVM will actually close an InputStream (which is what backs a scala.io.Source) when it’s garbage collected, but there’s no way to guarantee this will occur in a timely manner, or at all! This is especially true in generational garbage collectors that perform “full” collections infrequently.
We want to write programs that are resource-safe—they should close file handles as soon as they’re no longer needed (whether because of normal termination or an exception), and they shouldn’t attempt to read from a closed file. Likewise for other resources like network sockets, database connections, and so on. Using IO directly can be problematic because it means our programs are entirely responsible for ensuring their own resource safety, and we get no help from the compiler in making sure that they do this. It would be nice if our library would ensure that programs are resource-safe by construction.
But even aside from the problems with resource safety, there’s something unsatisfying about this code. It entangles the high-level algorithm with low-level concerns about iteration and file access. Of course we have to obtain the elements from some resource, handle any errors that occur, and close the resource when we’re done, but our program isn’t about any of those things. It’s about counting elements and returning a value as soon as we hit 40,000. And that happens between all of those I/O actions. Intertwining the algorithm and the I/O concerns is not just ugly—it’s a barrier to composition, and our code will be difficult to extend later. To see this, consider a few variations of the original scenario:
· Check whether the number of nonempty lines in the file exceeds 40,000.
· Find a line index before 40,000 where the first letters of consecutive lines spell out "abracadabra".
For the first case, we could imagine passing a String => Boolean into our linesGt40k function. But for the second case, we’d need to modify our loop to keep track of some further state. Besides being uglier, the resulting code will likely be tricky to get right. In general, writing efficient code in the IO monad generally means writing monolithic loops, and monolithic loops are not composable.
Let’s compare this to the case where we have a Stream[String] for the lines being analyzed:
lines.zipWithIndex.exists(_._2 + 1 >= 40000)
Much nicer! With a Stream, we get to assemble our program from preexisting combinators, zipWithIndex and exists. If we want to consider only nonempty lines, we can easily use filter:
lines.filter(!_.trim.isEmpty).zipWithIndex.exists(_._2 + 1 >= 40000)
And for the second scenario, we can use the indexOfSlice function defined on Stream,[2] in conjunction with take (to terminate the search after 40,000 lines) and map (to pull out the first character of each line):
2 If the argument to indexOfSlice doesn’t exist as a subsequence of the input, it returns -1. See the API docs for details, or experiment with this function in the REPL.
lines.filter(!_.trim.isEmpty).
take(40000).
map(_.head).
indexOfSlice("abracadabra".toList)
We want to write something like the preceding when reading from an actual file. The problem is that we don’t have a Stream[String]; we have a file from which we can read. We could cheat by writing a function lines that returns an IO[Stream[String]]:
def lines(filename: String): IO[Stream[String]] = IO {
val src = io.Source.fromFile(filename)
src.getLines.toStream append { src.close; Stream.empty }
}
This is called lazy I/O. We’re cheating because the Stream[String] inside the IO monad isn’t actually a pure value. As elements of the stream are forced, it’ll execute side effects of reading from the file, and only if we examine the entire stream and reach its end will we close the file. Although lazy I/O is appealing in that it lets us recover the compositional style to some extent, it’s problematic for several reasons:
· It isn’t resource-safe. The resource (in this case, a file) will be released only if we traverse to the end of the stream. But we’ll frequently want to terminate traversal early (here, exists will stop traversing the Stream as soon as it finds a match) and we certainly don’t want to leak resources every time we do this.
· Nothing stops us from traversing that same Stream again, after the file has been closed. This will result in one of two things, depending on whether the Stream memoizes (caches) its elements once they’re forced. If they’re memoized, we’ll see excessive memory usage since all of the elements will be retained in memory. If they’re not memoized, traversing the stream again will cause a read from a closed file handle.
· Since forcing elements of the stream has I/O side effects, two threads traversing a Stream at the same time can result in unpredictable behavior.
· In more realistic scenarios, we won’t necessarily have full knowledge of what’s happening with the Stream[String]. It could be passed to some function we don’t control, which might store it in a data structure for a long period of time before ever examining it. Proper usage now requires some out-of-band knowledge: we can’t just manipulate this Stream[String] like a typical pure value—we have to know something about its origin. This is bad for composition, where we shouldn’t have to know anything about a value other than its type.
15.2. Simple stream transducers
Our first step toward recovering the high-level style we’re accustomed to from Stream and List while doing I/O is to introduce the notion of stream transducers or stream processors. A stream transducer specifies a transformation from one stream to another. We’re using the term streamquite generally here to refer to a sequence, possibly lazily generated or supplied by an external source. This could be a stream of lines from a file, a stream of HTTP requests, a stream of mouse click positions, or anything else. Let’s consider a simple data type, Process, that lets us express stream transformations.[3]
3 We’ve chosen to omit variance annotations in this chapter for simplicity, but it’s possible to write this as Process[-I,+O]. We’re also omitting some trampolining that would prevent stack overflows in certain circumstances. See the chapter notes for discussion of more robust representations.
Listing 15.2. The Process data type

A Process[I,O] can be used to transform a stream containing I values to a stream of O values. But Process[I,O] isn’t a typical function Stream[I] => Stream[O], which could consume the input stream and construct the output stream. Instead, we have a state machine that must be driven forward with a driver, a function that simultaneously consumes both our Process and the input stream. A Process can be in one of three states, each of which signals something to the driver:
· Emit(head,tail) indicates to the driver that the head value should be emitted to the output stream, and the machine should then be transitioned to the tail state.
· Await(recv) requests a value from the input stream. The driver should pass the next available value to the recv function, or None if the input has no more elements.
· Halt indicates to the driver that no more elements should be read from the input or emitted to the output.
Let’s look at a sample driver that will actually interpret these requests. Here’s one that transforms a Stream. We can implement this as a method on Process:

Thus, given p: Process[I,O] and in: Stream[I], the expression p(in) produces a Stream[O]. What’s interesting is that Process is agnostic to how it’s fed input. We’ve written a driver that feeds a Process from a Stream, but we could also write a driver that feeds a Processfrom a file. We’ll get to writing such a driver a bit later, but first let’s look at how we can construct a Process, and try things out in the REPL.
15.2.1. Creating processes
We can convert any function f: I => O to a Process[I,O]. We just Await and then Emit the value received, transformed by f:
def liftOne[I,O](f: I => O): Process[I,O] =
Await {
case Some(i) => Emit(f(i))
case None => Halt()
}
Let’s try this out in the REPL:
scala> val p = liftOne((x: Int) => x * 2)
p: Process[Int,Int] = Await(<function1>)
scala> val xs = p(Stream(1,2,3)).toList
xs: List[Int] = List(2)
As we can see, this Process just waits for one element, emits it, and then stops. To transform a whole stream with a function, we do this repeatedly in a loop, alternating between awaiting and emitting. We can write a combinator for this, repeat, as a method on Process:

This combinator replaces the Halt constructor of the Process with a recursive step, repeating the same process forever.
We can now lift any function to a Process that maps over a Stream:
def lift[I,O](f: I => O): Process[I,O] = liftOne(f).repeat
Since the repeat combinator recurses forever and Emit is strict in its arguments, we have to be careful not to use it with a Process that never waits! For example, we can’t just say Emit(1).repeat to get an infinite stream that keeps emitting 1. Remember, Process is a streamtransducer, so if we want to do something like that, we need to transduce one infinite stream to another:
scala> val units = Stream.continually(())
units: scala.collection.immutable.Stream[Unit] = Stream((), ?)
scala> val ones = lift((_:Unit) => 1)(units)
ones: Stream[Int] = Stream(1, ?)
We can do more than map the elements of a stream from one type to another—we can also insert or remove elements. Here’s a Process that filters out elements that don’t match the predicate p:
def filter[I](p: I => Boolean): Process[I,I] =
Await[I,I] {
case Some(i) if p(i) => emit(i)
case _ => Halt()
}.repeat
We simply await some input and, if it matches the predicate, emit it to the output. The call to repeat makes sure that the Process keeps going until the input stream is exhausted. Let’s see how this plays out in the REPL:
scala> val even = filter((x: Int) => x % 2 == 0)
even: Process[Int,Int] = Await(<function1>)
scala> val evens = even(Stream(1,2,3,4)).toList
evens: List[Int] = List(2, 4)
Let’s look at another example of a Process, sum, which keeps emitting a running total of the values seen so far:
def sum: Process[Double,Double] = {
def go(acc: Double): Process[Double,Double] =
Await {
case Some(d) => Emit(d+acc, go(d+acc))
case None => Halt()
}
go(0.0)
}
This kind of definition follows a common pattern in defining a Process—we use an inner function that tracks the current state, which in this case is the total so far.
Here’s an example of using sum in the REPL:
scala> val s = sum(Stream(1.0, 2.0, 3.0, 4.0)).toList
s: List[Double] = List(1.0, 3.0, 6.0, 10.0)
Let’s write some more Process combinators to help you get accustomed to this style of programming. Try to work through implementations of at least some of these exercises until you get the hang of it.
Exercise 15.1
![]()
Implement take, which halts the Process after it encounters the given number of elements, and drop, which ignores the given number of arguments and then emits the rest. Also implement takeWhile and dropWhile, that take and drop elements as long as the given predicate remains true.
def take[I](n: Int): Process[I,I]
def drop[I](n: Int): Process[I,I]
def takeWhile[I](f: I => Boolean): Process[I,I]
def dropWhile[I](f: I => Boolean): Process[I,I]
Exercise 15.2
![]()
Implement count. It should emit the number of elements seen so far. For instance, count(Stream("a", "b", "c")) should yield Stream(1, 2, 3) (or Stream(0, 1, 2, 3), your choice).
def count[I]: Process[I,Int]
Exercise 15.3
![]()
Implement mean. It should emit a running average of the values seen so far.
def mean: Process[Double,Double]
Just as we’ve seen many times throughout this book, when we notice common patterns when defining a series of functions, we can factor these patterns out into generic combinators. The functions sum, count and mean all share a common pattern. Each has a single piece of state, has a state transition function that updates this state in response to input, and produces a single output. We can generalize this to a combinator, loop:
def loop[S,I,O](z: S)(f: (I,S) => (O,S)): Process[I,O] =
Await((i: I) => f(i,z) match {
case (o,s2) => emit(o, loop(s2)(f))
})
Exercise 15.4
![]()
Write sum and count in terms of loop.
15.2.2. Composing and appending processes
We can build up more complex stream transformations by composing Process values. Given two Process values f and g, we can feed the output of f to the input of g. We’ll name this operation |> (pronounced pipe or compose) and implement it as a function on Process.[4] It has the nice property that f |> g fuses the transformations done by f and g. As soon as values are emitted by f, they’re transformed by g.
4 This operation might remind you of function composition, which feeds the (single) output of a function as the (single) input to another function. Both Process and Function1 are instances of a wider abstraction called a category. See the chapter notes for details.
Exercise 15.5
![]()
Hard: Implement |> as a method on Process. Let the types guide your implementation.
def |>[O2](p2: Process[O,O2]): Process[I,O2]
We can now write expressions like filter(_ % 2 == 0) |> lift(_ + 1) to filter and map in a single transformation. We’ll sometimes call a sequence of transformations like this a pipeline.
Since we have Process composition, and we can lift any function into a Process, we can easily implement map to transform the output of a Process with a function:
def map[O2](f: O => O2): Process[I,O2] = this |> lift(f)
This means that the type constructor Process[I,_] is a functor. If we ignore the input side I for a moment, we can just think of a Process[I,O] as a sequence of O values. This implementation of map is then analogous to mapping over a Stream or a List.
In fact, most of the operations defined for ordinary sequences are defined for Process as well. We can, for example, append one process to another. Given two processes x and y, the expression x ++ y is a process that will run x to completion and then run y on whatever input remains afterx has halted. For the implementation, we simply replace the Halt of x with y (much like how ++ on List replaces the Nil terminating the first list with the second list):
def ++(p: => Process[I,O]): Process[I,O] = this match {
case Halt() => p
case Emit(h, t) => Emit(h, t ++ p)
case Await(recv) => Await(recv andThen (_ ++ p))
}
With the help of ++ on Process, we can define flatMap:
def flatMap[O2](f: O => Process[I,O2]): Process[I,O2] = this match {
case Halt() => Halt()
case Emit(h, t) => f(h) ++ t.flatMap(f)
case Await(recv) => Await(recv andThen (_ flatMap f))
}
The obvious question is then whether Process[I,_] forms a monad. It turns out that it does! To write the Monad instance, we have to partially apply the I parameter of Process—a trick we’ve used before:
def monad[I]: Monad[({ type f[x] = Process[I,x]})#f] =
new Monad[({ type f[x] = Process[I,x]})#f] {
def unit[O](o: => O): Process[I,O] = Emit(o)
def flatMap[O,O2](p: Process[I,O])(
f: O => Process[I,O2]): Process[I,O2] =
p flatMap f
}
The unit function just emits the argument and then halts, similar to unit for the List monad.
This Monad instance is the same idea as the Monad for List. What makes Process more interesting than just List is that it can accept input. And it can transform that input through mapping, filtering, folding, grouping, and so on. It turns out that Process can express almost any stream transformation, all the while remaining agnostic to how exactly it’s obtaining its input or what should happen with its output.
Exercise 15.6
![]()
Implement zipWithIndex. It emits a running count of values emitted along with each value; for example, Process("a","b").zipWithIndex yields Process(("a",0), ("b",1)).
Exercise 15.7
![]()
Hard: Come up with a generic combinator that lets you express mean in terms of sum and count. Define this combinator and implement mean in terms of it.
Exercise 15.8
![]()
Implement exists. There are multiple ways to implement it, given that exists(_ % 2 == 0)(Stream(1,3,5,6,7)) could produce Stream(true) (halting, and only yielding the final result), Stream(false,false,false,true) (halting, and yielding all intermediate results), orStream(false,false,false,true,true) (not halting, and yielding all the intermediate results). Note that because |> fuses, there’s no penalty to implementing the “trimming” of this last form with a separate combinator.
def exists[I](f: I => Boolean): Process[I,Boolean]
We can now express the core stream transducer for our line-counting problem as count |> exists(_ > 40000). Of course, it’s easy to attach filters and other transformations to our pipeline.
15.2.3. Processing files
Our original problem of answering whether a file has more than 40,000 elements is now easy to solve. But so far we’ve just been transforming pure streams. Luckily, we can just as easily use a file to drive a Process. And instead of generating a Stream as the result, we can accumulate what the Process emits similar to what foldLeft does on List.
Listing 15.3. Using Process with files instead of streams
def processFile[A,B](f: java.io.File,
p: Process[String, A],
z: B)(g: (B, A) => B): IO[B] = IO {
@annotation.tailrec
def go(ss: Iterator[String], cur: Process[String, A], acc: B): B =
cur match {
case Halt() => acc
case Await(recv) =>
val next = if (ss.hasNext) recv(Some(ss.next))
else recv(None)
go(ss, next, acc)
case Emit(h, t) => go(ss, t, g(acc, h))
}
val s = io.Source.fromFile(f)
try go(s.getLines, p, z)
finally s.close
}
We can now solve the original problem with the following:
processFile(f, count |> exists(_ > 40000), false)(_ || _)
Exercise 15.9
![]()
Write a program that reads degrees Fahrenheit as Double values from a file, one value per line, sends each value through a process to convert it to degrees Fahrenheit, and writes the result to another file. Your program should ignore blank lines in the input file, as well as lines that start with the # character. You can use the function toCelsius.
def toCelsius(fahrenheit: Double): Double =
(5.0 / 9.0) * (fahrenheit - 32.0)
15.3. An extensible process type
Our existing Process type implicitly assumes an environment or context containing a single stream of values. Furthermore, the protocol for communicating with the driver is also fixed. A Process can only issue three instructions to the driver—Halt, Emit, and Await—and there’s no way to extend this protocol short of defining a completely new type. In order to make Process extensible, we’ll parameterize on the protocol used for issuing requests of the driver. This works in much the same way as the Free type we covered in chapter 13.
Listing 15.4. An extensible Process type

Unlike Free[F,A], a Process[F,O] represents a stream of O values (O for output) produced by (possibly) making external requests using the protocol F via Await. The F parameter serves the same role here in Await as the F parameter used for Suspend in Free from chapter 13.
The important difference between Free and Process is that a Process can request to Emit values multiple times, whereas Free always contains one answer in its final Return. And instead of terminating with Return, the Process terminates with Halt.
To ensure resource safety when writing processes that close over some resource like a file handle or database connection, the recv function of Await takes an Either[Throwable,A]. This lets recv decide what should be done if there’s an error while running the request req.[5] We’ll adopt the convention that the End exception indicates that there’s no more input, and Kill indicates the process is being forcibly terminated and should clean up any resources it’s using.[6]
5 The recv function should be trampolined to avoid stack overflows by returning a TailRec[Process[F,O]], but we’ve omitted this detail here for simplicity.
6 There are some design decisions here—we’re using exceptions, End and Kill, for control flow, but we could certainly choose to indicate normal termination with Option, say with Halt[F[_],O](err: Option [Throwable]).
The Halt constructor picks up a reason for termination in the form of a Throwable. The reason may be End, indicating normal termination due to exhausted input; Kill, indicating forcible termination; or some other error (note that Exception is a subtype of Throwable).
This new Process type is more general than the previous Process, which we’ll refer to from now on as a “single-input Process” or a “Process1”, and we can represent a single-input Process as a special instance of this generalized Process type. We’ll see how this works in section 15.3.3.
First, note that a number of operations are defined for Process regardless of the choice of F. We can still define ++ (append), map, and filter for Process, and the definitions are almost identical to before. Here’s ++ (see chapter code for other functions, including repeat, map, andfilter), which we define in terms of a more general function, onHalt.
Listing 15.5. The onHalt and ++ functions
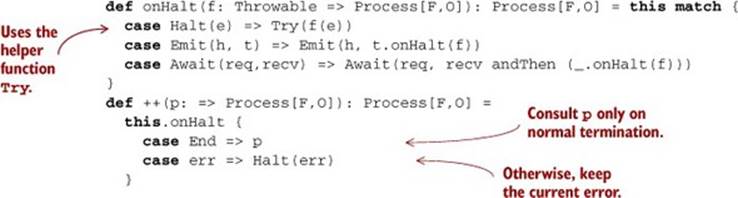
A call to p.onHalt(f) replaces the e inside the Halt(e) at the end of p with f(e), allowing us to extend a process with further logic and giving us access to the reason for termination. The definition uses the helper function Try with a capital T, which safely evaluates a Process, catching any exceptions and converting them to Halt (see the following code). This is important for resource safety. In general, our goal is to catch and deal with all exceptions, rather than placing that burden on users of our library. Luckily, there are just a few key combinators that can generate exceptions. As long as we ensure these combinators are exception-safe, we’ll be able to guarantee the resource safety of all programs that use Process. The ++ function is defined in terms of onHalt—so long as the first Process terminates normally, we continue with the second process; otherwise, we re-raise the error.
Here’s the helper function Try:
def Try[F[_],O](p: => Process[F,O]): Process[F,O] =
try p
catch { case e: Throwable => Halt(e) }
We’ll also introduce the helper function await, which is a curried version of the Await constructor for better type inference:
def await[F[_],A,O](
req: F[A])(
recv: Either[Throwable,A] => Process[F,O]): Process[F,O] =
Await(req, recv)
Again, using ++, we define flatMap. This is another combinator where we must take care to ensure exception safety—we don’t know for sure whether f will throw an exception, so we wrap calls to f in Try once again. Other than that, the definition looks very similar to what we wrote before:
def flatMap[O2](f: O => Process[F,O2]): Process[F,O2] =
this match {
case Halt(err) => Halt(err)
case Emit(o, t) => Try(f(o)) ++ t.flatMap(f)
case Await(req,recv) =>
Await(req, recv andThen (_ flatMap f))
}
Let’s see what else we can express with this new Process type. The F parameter gives us a lot of flexibility.
15.3.1. Sources
Before, we had to write a separate function to drive a process forward while reading from a file. Now, we can represent an effectful source directly using a Process[IO,O].[7]
7 There are some issues with making this representation resource-safe that we’ll discuss shortly.
To see how Process[IO,O] is indeed a source of O values, consider what the Await constructor looks like when we substitute IO for F:
case class Await[A,O](
req: IO[A],
recv: Either[Throwable, A] => Process[IO,O]
) extends Process[IO,O]
Thus, any requests of the “external” world can be satisfied just by running or flatMap-ing into the IO action req. If this action returns an A successfully, we invoke the recv function with this result, or a Throwable if req throws one. Either way, the recv function can fall back to another process or clean up any resources as appropriate. Here’s a simple interpreter of an I/O Process that collects all the values emitted.
Listing 15.6. The runLog function
def runLog[O](src: Process[IO,O]): IO[IndexedSeq[O]] = IO {
val E = java.util.concurrent.Executors.newFixedThreadPool(4)
@annotation.tailrec
def go(cur: Process[IO,O], acc: IndexedSeq[O]): IndexedSeq[O] =
cur match {
case Emit(h,t) => go(t, acc :+ h)
case Halt(End) => acc
case Halt(err) => throw err
case Await(req,recv) =>
val next =
try recv(Right(unsafePerformIO(req)(E)))
catch { case err: Throwable => recv(Left(err)) }
go(next, acc)
}
try go(src, IndexedSeq())
finally E.shutdown
}
An example usage of this is to enumerate all the lines in a file:
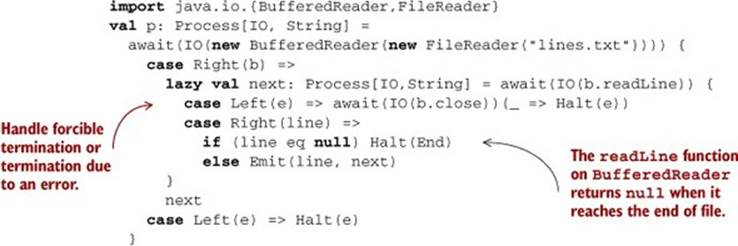
Then we can use runLog(p) to get all the lines in the file lines.txt as an IO[IndexedSeq[String]].
Note that we’re making sure that the file is closed regardless of how the process terminates. In section 15.3.2, we’ll discuss how to ensure that all such processes close the resources they use (they’re resource-safe), and discover a few generic combinators for ensuring resource safety.
Exercise 15.10
![]()
The runLog function can be defined more generally for any Monad in which it’s possible to catch and raise exceptions (for instance, the Task type mentioned in chapter 13, which adds this capability to the IO type). Define this more general version of runLog. Note that this interpreter can’t be tail-recursive, and relies on the underlying monad for stack safety.
trait Process[F[_],O] {
def runLog(implicit F: MonadCatch[F]): F[IndexedSeq[O]]
...
}
trait MonadCatch[F[_]] extends Monad[F] {
def attempt[A](a: F[A]): F[Either[Throwable,A]]
def fail[A](t: Throwable): F[A]
}
15.3.2. Ensuring resource safety
Process[IO,O] can be used for talking to external resources like files and database connections, but we must take care to ensure resource safety—we want all file handles to be closed, database connections released, and so on, even (especially!) if exceptions occur. Let’s look at what we need to make this happen. We already have most of the machinery in place. The Await constructor’s recv argument can handle errors, choosing to clean up if necessary. And we’re catching exceptions in flatMap and other relevant combinators so we can ensure that we gracefully pass them to recv. All we have to do is make sure that the recv function actually calls the necessary cleanup code.
To make the discussion concrete, suppose we have lines: Process[IO,String] representing the lines of some large file. This is a source or producer, and it implicitly references a resource (a file handle) that we want to ensure is closed regardless of how this producer is consumed.
When should we close this file handle? At the very end of our program? No, ideally we’d close the file once we know we’re done reading from lines. We’re certainly done if we reach the last line of the file—at that point there are no more values to produce and it’s safe to close the file. So this gives us our first simple rule to follow: A producer should free any underlying resources as soon as it knows it has no further values to produce, whether due to normal exhaustion or an exception.
This isn’t sufficient though, because the consumer of a process may itself decide to terminate consumption early. Consider runLog { lines("names.txt") |> take(5) }. The take(5) process will halt early after only five elements have been received, possibly before the file has been exhausted. In this case, we want to make sure before halting that any necessary resource freeing is run before the overall process completes. Note that runLog can’t be responsible for this, since runLog has no idea that the Process it’s interpreting is internally composed of two otherProcess values, one of which requires finalization.
Thus, we have our second simple rule to follow: Any process d that consumes values from another process p must ensure that cleanup actions of p are run before d halts.
This sounds rather error prone, but luckily we get to deal with this concern in just a single place, the |> combinator. We’ll show how that works in section 15.3.3, when we show how to encode single-input processes using our general Process type.
So to summarize, a process p may terminate due to the following:
· Producer exhaustion, signaled by End, when the underlying source has no further values to emit
· Forcible termination, signaled by Kill, due to the consumer of p indicating it’s finished consuming, possibly before the producer p is exhausted
· Abnormal termination due to some e: Throwable in either the producer or consumer
And no matter the cause, we want to close the underlying resource(s) in each case.
Now that we have our guidelines, how do we actually implement this? We need to make sure the recv function in the Await constructor always runs the “current” set of cleanup actions when it receives a Left. Let’s introduce a new combinator, onComplete, which lets us append logic to aProcess that will be run regardless of how the first Process terminates. The definition is similar to ++, with one twist:

The p process is always run when this halts, but we take care to re-raise any errors that occur (rather than swallowing them) after running the cleanup action. The asFinalizer method converts a “normal” Process to one that will invoke itself when given Kill. The definition is subtle, but we use this to ensure that in p1.onComplete(p2), p2 is always run, even if the consumer of the stream wishes to terminate early:
def asFinalizer: Process[F,O] = this match {
case Emit(h, t) => Emit(h, t.asFinalizer)
case Halt(e) => Halt(e)
case Await(req,recv) => await(req) {
case Left(Kill) => this.asFinalizer
case x => recv(x)
}
}
Putting all this together, we can use the onComplete combinator to create a resource-safe Process[IO,O] backed by the lines of a file. We define it in terms of the more general combinator, resource:
def resource[R,O](acquire: IO[R])(
use: R => Process[IO,O])(
release: R => Process[IO,O]): Process[IO,O] =
await[IO,R,O](acquire)(r => use(r).onComplete(release(r)))
Exercise 15.11
![]()
This idiom of using await to “evaluate” the result of some IO action isn’t specific to IO. Implement the generic combinator eval to promote some F[A] to a Process that emits only the result of that F[A]. Also implement eval_, which promotes an F[A] to a Process, emitting no values. Note that implementing these functions doesn’t require knowing anything about F.
def eval[F[_],A](a: F[A]): Process[F,A]
def eval_[F[_],A,B](a: F[A]): Process[F,B]
And now here is lines:
def lines(filename: String): Process[IO,String] =
resource
{ IO(io.Source.fromFile(filename)) }
{ src =>
lazy val iter = src.getLines // a stateful iterator
def step = if (iter.hasNext) Some(iter.next) else None
lazy val lines: Process[IO,String] = eval(IO(step)).flatMap {
case None => Halt(End)
case Some(line) => Emit(line, lines)
}
lines
}
{ src => eval_ { IO(src.close) } }
The resource combinator, using onComplete, ensures that our underlying resource is freed regardless of how the process is terminated. The only thing we need to ensure is that |> and other consumers of lines gracefully terminate it when they’re finished consuming. We’ll address this next, when we redefine single-input processes and implement the |> combinator for our generalized Process type.
15.3.3. Single-input processes
We now have nice, resource-safe sources, but we don’t yet have any way to apply transformations to them. Fortunately, our Process type can also represent the single-input processes we introduced earlier in this chapter. To represent Process1[I,O], we craft an appropriate F that only allows the Process to make requests for elements of type I. Let’s look at how this works—the encoding is unusual in Scala, but there’s nothing fundamentally new here:
case class Is[I]() {
sealed trait f[X]
val Get = new f[I] {}
}
It’s strange to define the trait f inside of Is. Let’s unpack what’s going on. Note that f takes one parameter, X, but we have just one instance, Get, which fixes X to be the I in the outer Is[I]. Therefore, the type Is[I]#f[8] can only ever be a request for a value of type I! Given the typeIs[I]#f[A], Scala will complain with a type error unless the type A is the type I. Now that we have all this, we can define Process1 as just a type alias:
8 Note on syntax: recall that if x is a type, x#foo references the type foo defined inside x.
type Process1[I,O] = Process[Is[I]#f, O]
To see what’s going on, it helps to substitute the definition of Is[I]#f into a call to Await:
case class Await[A,O](
req: Is[I]#f[A], recv: Either[Throwable,A] => Process[Is[I]#f,O]
) extends Process[Is[I]#f,R]
From the definition of Is[I]#f, we can see that req can only be Get: f[I], the only value of this type. Therefore, I and A must be the same type, so recv must accept an I as its argument, which means that Await can only be used to request I values. This is important to understand—if this explanation didn’t make sense, try working through these definitions on paper, substituting the type definitions.
Our Process1 alias supports all the same operations as our old single-input Process. Let’s look at a couple. We first introduce a few helper functions to improve type inference when calling the Process constructors.
Listing 15.7. Type inference helper functions
def await1[I,O](
recv: I => Process1[I,O],
fallback: Process1[I,O] = halt1[I,O]): Process1[I, O] =
Await(Get[I], (e: Either[Throwable,I]) => e match {
case Left(End) => fallback
case Left(err) => Halt(err)
case Right(i) => Try(recv(i))
})
def emit1[I,O](h: O, tl: Process1[I,O] = halt1[I,O]): Process1[I,O] =
emit(h, tl)
def halt1[I,O]: Process1[I,O] = Halt[Is[I]#f, O](End)
Using these, our definitions of combinators like lift and filter look almost identical to before, except they return a Process1:
def lift[I,O](f: I => O): Process1[I,O] =
await1[I,O](i => emit(f(i))) repeat
def filter[I](f: I => Boolean): Process1[I,I] =
await1[I,I](i => if (f(i)) emit(i) else halt1) repeat
Let’s look at process composition next. The implementation looks similar to before, but we make sure to run the latest cleanup action of the left process before the right process halts:

We use a helper function, kill—it feeds the Kill exception to the outermost Await of a Process but ignores any of its remaining output.
Listing 15.8. kill helper function

Note that |> is defined for any Process[F,O] type, so this operation works for transforming a Process1 value, an effectful Process[IO,O], and the two-input Process type we’ll discuss next.
With |>, we can add convenience functions on Process for attaching various Process1 transformations to the output. For instance, here’s filter, defined for any Process[F,O]:
def filter(f: O => Boolean): Process[F,O] =
this |> Process.filter(f)
We can add similar convenience functions for take, takeWhile, and so on. See the chapter code for more examples.
15.3.4. Multiple input streams
Imagine if we wanted to “zip” together two files full of temperatures in degrees Fahrenheit, f1.txt and f2.txt, add corresponding temperatures together, convert the result to Celsius, apply a five-element moving average, and output the results one at a time to celsius.txt.
We can address these sorts of scenarios with our general Process type. Much like effectful sources and Process1 were just specific instances of our general Process type, a Tee, which combines two input streams in some way,[9] can also be expressed as a Process. Once again, we simply craft an appropriate choice of F:
9 The name Tee comes from the letter T, which approximates a diagram merging two inputs (the top of the T) into a single output.
case class T[I,I2]() {
sealed trait f[X] { def get: Either[I => X, I2 => X] }
val L = new f[I] { def get = Left(identity) }
val R = new f[I2] { def get = Right(identity) }
}
def L[I,I2] = T[I,I2]().L
def R[I,I2] = T[I,I2]().R
This looks similar to our Is type from earlier, except that we now have two possible values, L and R, and we get an Either[I => X, I2 => X] to distinguish between the two types of requests during pattern matching.[10] With T, we can now define a type alias, Tee, for processes that accept two different types of inputs:
10 The functions I => X and I2 => X inside the Either are a simple form of equality witness, which is just a value that provides evidence that one type is equal to another.
type Tee[I,I2,O] = Process[T[I,I2]#f, O]
Once again, we define a few convenience functions for building these particular types of Process.
Listing 15.9. Convenience functions for each input in a Tee
def haltT[I,I2,O]: Tee[I,I2,O] =
Halt[T[I,I2]#f,O](End)
def awaitL[I,I2,O](
recv: I => Tee[I,I2,O],
fallback: => Tee[I,I2,O] = haltT[I,I2,O]): Tee[I,I2,O] =
await[T[I,I2]#f,I,O](L) {
case Left(End) => fallback
case Left(err) => Halt(err)
case Right(a) => Try(recv(a))
}
def awaitR[I,I2,O](
recv: I2 => Tee[I,I2,O],
fallback: => Tee[I,I2,O] = haltT[I,I2,O]): Tee[I,I2,O] =
await[T[I,I2]#f,I2,O](R) {
case Left(End) => fallback
case Left(err) => Halt(err)
case Right(a) => Try(recv(a))
}
def emitT[I,I2,O](h: O, tl: Tee[I,I2,O] = haltT[I,I2,O]): Tee[I,I2,O] =
emit(h, tl)
Let’s define some Tee combinators. Zipping is a special case of Tee—we read from the left, then the right (or vice versa), and then emit the pair. Note that we get to be explicit about the order we read from the inputs, a capability that can be important when a Tee is talking to streams with external effects:[11]
11 We may also wish to be inexplicit about the order of the effects, allowing the driver to choose nondeterministically and allowing for the possibility that the driver will execute both effects concurrently. See the chapter notes for some additional discussion.
def zipWith[I,I2,O](f: (I,I2) => O): Tee[I,I2,O] =
awaitL[I,I2,O](i =>
awaitR (i2 => emitT(f(i,i2)))) repeat
def zip[I,I2]: Tee[I,I2,(I,I2)] = zipWith((_,_))
This transducer will halt as soon as either input is exhausted, just like the zip function on List. There are lots of other Tee combinators we could write. Nothing requires that we read values from each input in lockstep. We could read from one input until some condition is met and then switch to the other; read 5 values from the left and then 10 values from the right; read a value from the left and then use it to determine how many values to read from the right, and so on.
We’ll typically want to feed a Tee by connecting it to two processes. We can define a function on Process that combines two processes using a Tee. It’s analogous to |> and works similarly. This function works for any Process type.
Listing 15.10. The tee function

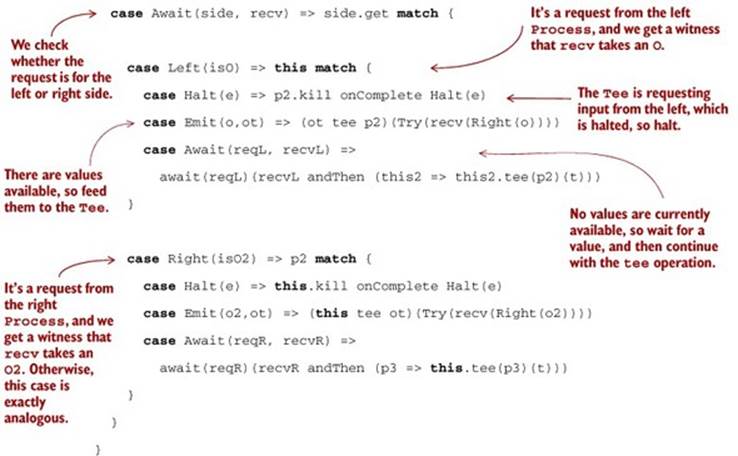
15.3.5. Sinks
How do we perform output using our Process type? We’ll often want to send the output of a Process[IO,O] to some sink (perhaps sending a Process[IO,String] to an output file). Somewhat surprisingly, we can represent a sink as a process that emits functions:
type Sink[F[_],O] = Process[F[_], O => Process[F,Unit]]
This makes a certain kind of sense. A Sink[F[_], O] provides a sequence of functions to call with the input type O. The function returns Process[F,Unit]. Let’s look at a Sink that writes strings to a file:

That was easy. And notice what isn’t included—there’s no exception handling code here—the combinators we’re using guarantee that the FileWriter will be closed if exceptions occur or when whatever is feeding the Sink signals it’s done.
We can use tee to implement a combinator to, a method on Process which pipes its output to a Sink:
def to[O2](sink: Sink[F,O]): Process[F,Unit] =
join { (this zipWith sink)((o,f) => f(o)) }
Exercise 15.12
![]()
The definition of to uses a new combinator, join, defined for any Process, which concatenates a nested Process. Implement join using existing primitives. This combinator should be quite familiar to you from previous chapters.
def join[F[_],O](p: Process[F, Process[F,O]]): Process[F,O]
Using to, we can now write programs like the following:
val converter: Process[IO,Unit] =
lines("fahrenheit.txt").
filter(!_.startsWith("#")).
map(line => fahrenheitToCelsius(line.toDouble).toString).
pipe(intersperse("\n")).
to(fileW("celsius.txt")).
drain
This uses the helper function drain, which just ignores all output of a Process:
final def drain[O2]: Process[F,O2] = this match {
case Halt(e) => Halt(e)
case Emit(h, t) => t.drain
case Await(req,recv) => Await(req, recv andThen (_.drain))
}
When run via runLog, converter will open the input file and the output file and incrementally transform the input stream, ignoring commented lines.
15.3.6. Effectful channels
We can generalize to to allow responses other than Unit. The implementation is identical! It turns out that the operation just has a more general type than we gave it. Let’s call the more general operation through:
def through[O2](p2: Process[F, O => Process[F,O2]]): Process[F,O2] =
join { (this zipWith p2)((o,f) => f(o)) }
Let’s introduce a type alias for this pattern:
type Channel[F[_],I,O] = Process[F, I => Process[F,O]]
Channel is useful when a pure pipeline must execute some I/O action as one of its stages. A typical example might be an application that needs to execute database queries. It would be nice if our database queries could return a Process[IO,Row], where Row is some representation of a database row. This would allow the program to process the result set of a query using all the fancy stream transducers we’ve built up so far.
Here’s a signature for a simple query executor, which uses Map[String,Any] as the (untyped) row representation (see the chapter code for the implementation):
import java.sql.{Connection, PreparedStatement, ResultSet}
def query(conn: IO[Connection]):
Channel[IO, Connection => PreparedStatement, Map[String,Any]]
We could certainly write a Channel[PreparedStatement, Source[Map[String,Any]]], so why don’t we? Because we don’t want code that uses our Channel to have to worry about how to obtain a Connection (which is needed to build a PreparedStatement). That dependency is managed entirely by the Channel itself, which also takes care of closing the connection when it’s finished executing queries.
15.3.7. Dynamic resource allocation
Realistic programs may need to allocate resources dynamically, while transforming some input stream. For example, we may encounter scenarios like the following:
· Dynamic resource allocation —Read a file, fahrenheits.txt, containing a list of filenames. Concatenate these files into a single logical stream, convert this stream to Celsius, and output the joined stream to celsius.txt.
· Multi-sink output —Similar to dynamic resource allocation, but rather than producing a single output file, produce an output file for each input file in fahrenheits.txt. Name the output file by appending .celsius onto the input file name.
Can these capabilities be incorporated into our definition of Process in a way that preserves resource safety? Yes, they can! We actually already have the power to do these things, using the flatMap combinator that we’ve already defined for an arbitrary Process type.
For instance, flatMap plus our existing combinators let us write this first scenario as follows:

This code is completely resource-safe—all file handles will be closed automatically by the runner as soon as they’re finished, even in the presence of exceptions. Any exceptions encountered will be thrown to the runLog function when invoked.
We can write to multiple files just by switching the order of the calls to flatMap:
val convertMultisink: Process[IO,Unit] = (for {
file <- lines("fahrenheits.txt")
_ <- lines(file).
map(line => fahrenheitToCelsius(line.toDouble)).
map(_ toString).
to(fileW(file + ".celsius"))
} yield ()) drain
And of course, we can attach transformations, mapping, filtering, and so on at any point in the process:
val convertMultisink2: Process[IO,Unit] = (for {
file <- lines("fahrenheits.txt")
_ <- lines(file).
filter(!_.startsWith("#")).
map(line => fahrenheitToCelsius(line.toDouble)).
filter(_ > 0). // ignore below zero temperatures
map(_ toString).
to(fileW(file + ".celsius"))
} yield ()) drain
There are additional examples using this library in the chapter code.
15.4. Applications
The ideas presented in this chapter are widely applicable. A surprising number of programs can be cast in terms of stream processing—once you’re aware of the abstraction, you begin seeing it everywhere. Let’s look at some domains where it’s applicable:
· File I/O —We’ve already demonstrated how to use stream processing for file I/O. Although we’ve focused on line-by-line reading and writing for the examples here, we can also use the library for processing binary files.
· Message processing, state machines, and actors —Large systems are often organized as a system of loosely coupled components that communicate via message passing. These systems are often expressed in terms of actors, which communicate via explicit message sends and receives. We can express components in these architectures as stream processors. This lets us describe extremely complex state machines and behaviors using a high-level, compositional API.
· Servers, web applications —A web application can be thought of as converting a stream of HTTP requests to a stream of HTTP responses.
· UI programming —We can view individual UI events such as mouse clicks as streams, and the UI as one large network of stream processors determining how the UI responds to user interaction.
· Big data, distributed systems —Stream-processing libraries can be distributed and parallelized for processing large amounts of data. The key insight here is that the nodes of a stream-processing network need not all live on the same machine.
If you’re curious to learn more about these applications (and others), see the chapter notes for additional discussion and links to further reading. The chapter notes and code also discuss some extensions to the Process type we discussed here, including the introduction of nondeterministic choice, which allows for concurrent evaluation in the execution of a Process.
15.5. Summary
We began this book with a simple premise: that we assemble our programs using only pure functions. From this sole premise and its consequences, we were led to explore a completely new approach to programming that’s both coherent and principled. In this final chapter, we constructed a library for stream processing and incremental I/O, demonstrating that we can retain the compositional style developed throughout this book even for programs that interact with the outside world. Our story, of how to use FP to architect programs both large and small, is now complete.
FP is a deep subject, and we’ve only scratched the surface. By now you should have everything you need to continue the journey on your own, to make functional programming a part of your own work. Though good design is always difficult, expressing your code functionally will become effortless over time. As you apply FP to more problems, you’ll discover new patterns and more powerful abstractions.
Enjoy the journey, keep learning, and good luck!