Functional Programming in Scala (2015)
Part 4. Effects and I/O
Chapter 14. Local effects and mutable state
In the first chapter of this book, we introduced the concept of referential transparency, setting the premise for purely functional programming. We declared that pure functions can’t mutate data in place or interact with the external world. In chapter 13, we learned that this isn’t exactly true. Wecan write purely functional and compositional programs that describe interactions with the outside world. These programs are unaware that they can be interpreted with an evaluator that has an effect on the world.
In this chapter we’ll develop a more mature concept of referential transparency. We’ll consider the idea that effects can occur locally inside an expression, and that we can guarantee that no other part of the larger program can observe these effects occurring.
We’ll also introduce the idea that expressions can be referentially transparent with regard to some programs and not others.
14.1. Purely functional mutable state
Up until this point, you may have had the impression that in purely functional programming, you’re not allowed to use mutable state. But if we look carefully, there’s nothing about the definitions of referential transparency and purity that disallows mutation of local state. Let’s refer to our definitions from chapter 1:
Definition of referential transparency and purity
An expression e is referentially transparent if for all programs p all occurrences of e in p can be replaced by the result of evaluating e without affecting the meaning of p.
A function f is pure if the expression f(x) is referentially transparent for all referentially transparent x.
By that definition, the following function is pure, even though it uses a while loop, an updatable var, and a mutable array.
Listing 14.1. In-place quicksort with a mutable array

The quicksort function sorts a list by turning it into a mutable array, sorting the array in place using the well-known quicksort algorithm, and then turning the array back into a list. It’s not possible for any caller to know that the individual subexpressions inside the body of quicksortaren’t referentially transparent or that the local methods swap, partition, and qs aren’t pure, because at no point does any code outside the quicksort function hold a reference to the mutable array. Since all of the mutation is locally scoped, the overall function is pure. That is, for any referentially transparent expression xs of type List[Int], the expression quicksort(xs) is also referentially transparent.
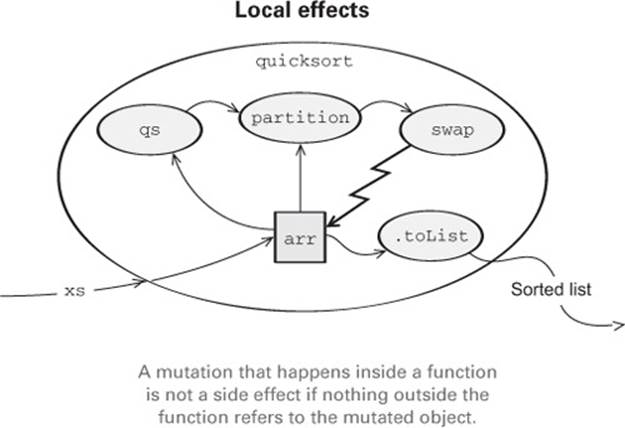
Some algorithms, like quicksort, need to mutate data in place in order to work correctly or efficiently. Fortunately for us, we can always safely mutate data that’s created locally. Any function can use side-effecting components internally and still present a pure external interface to its callers, and we should feel no shame taking advantage of this in our own programs. We may prefer purely functional components in our implementations for other reasons—they’re easier to get right, can be assembled more easily from other pure functions, and so on—but in principle there’s nothing wrong with building a pure function using local side effects in the implementation.
14.2. A data type to enforce scoping of side effects
The preceding section makes it clear that pure functions may have side effects with respect to data that’s locally scoped. The quicksort function may mutate the array because it allocated that array, it’s locally scoped, and it’s not possible for any outside code to observe the mutation. If, on the other hand, quicksort somehow mutated its input list directly (as is common in mutable collection APIs), that side effect would be observable to all callers of quicksort.
There’s nothing wrong with doing this sort of loose reasoning to determine the scoping of side effects, but it’s sometimes desirable to enforce effect scoping using Scala’s type system. The constituent parts of quicksort would have direct side effects if used on their own, and with the types we’re using, we get no help from the compiler in controlling the scope of these side effects. Nor are we alerted if we accidentally leak side effects or mutable state to a broader scope than intended. In this section, we’ll develop a data type that uses Scala’s type system to enforce scoping of mutations.[1]
1 There’s a cost in terms of efficiency and notational convenience, so think of this as another technique you have at your disposal, not something that must be employed every time you make use of local mutation.
Note that we could just work in IO, but that’s really not appropriate for local mutable state. If quicksort returned IO[List[Int]], then it would be an IO action that’s perfectly safe to run and would have no side effects, which isn’t the case in general for arbitrary IO actions. We want to be able to distinguish between effects that are safe to run (like locally mutable state) and external effects like I/O. So a new data type is in order.
14.2.1. A little language for scoped mutation
The most natural approach is to make a little language for talking about mutable state. Writing and reading a state is something we can already do with the State[S,A] monad, which you’ll recall is just a function of type S => (A, S) that takes an input state and produces a result and an output state. But when we’re talking about mutating the state in place, we’re not really passing it from one action to the next. What we’ll pass instead is a kind of token marked with the type S. A function called with the token then has the authority to mutate data that’s tagged with the same type S.
This new data type will employ Scala’s type system to gain two static guarantees. We want our code to not compile if it violates these invariants:
· If we hold a reference to a mutable object, then nothing can observe us mutating it.
· A mutable object can never be observed outside of the scope in which it was created.
We relied on the first invariant for our implementation of quicksort—we mutated an array, but since no one else had a reference to that array, the mutation wasn’t observable outside our function definition. The second invariant is more subtle; it’s saying that we won’t leak references to any mutable state as long as that mutable state remains in scope. This invariant is important for some use cases; see the sidebar.
Another use case for typed scoping of mutation
Imagine writing a file I/O library. At the lowest level, the underlying OS file read operation might fill up a mutable buffer of type Array[Byte], reusing the same array on every read instead of allocating a new buffer each time. In the interest of efficiency, it might be nice if the I/O library could simply return a “read-only” view of type Seq[Byte] that’s backed by this array, rather than defensively copying the bytes to a fresh data structure. But this isn’t quite safe—the caller may keep around this (supposedly) immutable sequence, and when we overwrite the underlying array on the next read, that caller will observe the data changing out from under it! To make the recycling of buffers safe, we need to restrict the scope of the Seq[Byte] view we give to callers and make sure that callers can’t retain references (directly or indirectly) to these mutable buffers when we begin the next read operation that clobbers the underlying Array[Byte]. See the chapter notes for chapter 15 for more discussion of this sort of use case.
We’ll call this new local-effects monad ST, which could stand for state thread, state transition, state token, or state tag. It’s different from the State monad in that its run method is protected, but otherwise its structure is exactly the same.
Listing 14.2. Our new ST data type

The run method is protected because an S represents the ability to mutate state, and we don’t want the mutation to escape. So how do we then run an ST action, giving it an initial state? These are really two questions. We’ll start by answering the question of how we specify the initial state.
It’s not necessary that you understand every detail of the implementation of ST. What matters is the idea that we can use the type system to constrain the scope of mutable state.
14.2.2. An algebra of mutable references
Our first example of an application for the ST monad is a little language for talking about mutable references. This takes the form of a combinator library with some primitives. The language for talking about mutable memory cells should have these primitive commands:
· Allocate a new mutable cell
· Write to a mutable cell
· Read from a mutable cell
The data structure we’ll use for mutable references is just a wrapper around a protected var:
sealed trait STRef[S,A] {
protected var cell: A
def read: ST[S,A] = ST(cell)
def write(a: A): ST[S,Unit] = new ST[S,Unit] {
def run(s: S) = {
cell = a
((), s)
}
}
}
object STRef {
def apply[S,A](a: A): ST[S, STRef[S,A]] = ST(new STRef[S,A] {
var cell = a
})
}
The methods on STRef to read and write the cell are pure, since they just return ST actions. Note that the type S is not the type of the cell that’s being mutated, and we never actually use the value of type S. Nevertheless, in order to call apply and actually run one of these ST actions, we do need to have a value of type S. That value therefore serves as a kind of token—an authorization to mutate or access the cell—but it serves no other purpose.
The STRef trait is sealed, and the only way to construct an instance is by calling the apply method on the STRef companion object. The STRef is constructed with an initial value for the cell, of type A. But what’s returned is not a naked STRef, but an ST[S, STRef[S,A]] action that constructs the STRef when run and given the token of type S. It’s important to note that the ST action and the STRef that it creates are tagged with the same S type.
At this point, let’s try writing a trivial ST program. It’s awkward right now because we have to choose a type S arbitrarily. Here, we arbitrarily choose Nothing:
for {
r1 <- STRef[Nothing,Int](1)
r2 <- STRef[Nothing,Int](1)
x <- r1.read
y <- r2.read
_ <- r1.write(y+1)
_ <- r2.write(x+1)
a <- r1.read
b <- r2.read
} yield (a,b)
This little program allocates two mutable Int cells, swaps their contents, adds one to both, and then reads their new values. But we can’t yet run this program because run is still protected (and we could never actually pass it a value of type Nothing anyway). Let’s work on that.
14.2.3. Running mutable state actions
By now you may have figured out the plot with the ST monad. The plan is to use ST to build up a computation that, when run, allocates some local mutable state, proceeds to mutate it to accomplish some task, and then discards the mutable state. The whole computation is referentially transparent because all the mutable state is private and locally scoped. But we want to be able to guarantee that. For example, an STRef contains a mutable var, and we want Scala’s type system to guarantee that we can never extract an STRef out of an ST action. That would violate the invariant that the mutable reference is local to the ST action, breaking referential transparency in the process.
So how do we safely run ST actions? First we must differentiate between actions that are safe to run and ones that aren’t. Spot the difference between these types:
· ST[S, STRef[S, Int]] (not safe to run)
· ST[S, Int] (completely safe to run)
The former is an ST action that returns a mutable reference. But the latter is different. A value of type ST[S,Int] is literally just an Int, even though computing the Int may involve some local mutable state. There’s an exploitable difference between these two types. The STRef involves the type S, but Int doesn’t.
We want to disallow running an action of type ST[S, STRef[S,A]] because that would expose the STRef. And in general we want to disallow running any ST[S,T] where T involves the type S. On the other hand, it’s easy to see that it should always be safe to run an ST action that doesn’t expose a mutable object. If we have such a pure action of a type like ST[S,Int], it should be safe to pass it an S to get the Int out of it. Furthermore, we don’t care what S actually is in that case because we’re going to throw it away. The action might as well be polymorphic in S.
In order to represent this, we’ll introduce a new trait that represents ST actions that are safe to run—in other words, actions that are polymorphic in S:
trait RunnableST[A] {
def apply[S]: ST[S,A]
}
This is similar to the idea behind the Translate trait from chapter 13. A value of type RunnableST[A] is a function that takes a type S and produces a value of type ST[S,A].
In the previous section, we arbitrarily chose Nothing as our S type. Let’s instead wrap it in RunnableST making it polymorphic in S. Then we don’t have to choose the type S at all. It will be supplied by whatever calls apply:
val p = new RunnableST[(Int, Int)] {
def apply[S] = for {
r1 <- STRef(1)
r2 <- STRef(2)
x <- r1.read
y <- r2.read
_ <- r1.write(y+1)
_ <- r2.write(x+1)
a <- r1.read
b <- r2.read
} yield (a,b)
}
We’re now ready to write the runST function that will call apply on any polymorphic RunnableST by arbitrarily choosing a type for S. Since the RunnableST action is polymorphic in S, it’s guaranteed to not make use of the value that gets passed in. So it’s actually completely safe to pass(), the value of type Unit!
The runST function must go on the ST companion object. Since run is protected on the ST trait, it’s accessible from the companion object but nowhere else:
object ST {
def apply[S,A](a: => A) = {
lazy val memo = a
new ST[S,A] {
def run(s: S) = (memo, s)
}
}
def runST[A](st: RunnableST[A]): A =
st.apply[Unit].run(())._1
}
We can now run our trivial program p from earlier:
scala> val p = new RunnableST[(Int, Int)] {
| def apply[S] = for {
| r1 <- STRef(1)
| r2 <- STRef(2)
| x <- r1.read
| y <- r2.read
| _ <- r1.write(y+1)
| _ <- r2.write(x+1)
| a <- r1.read
| b <- r2.read
| } yield (a,b)
| }
p: RunnableST[(Int, Int)] = $anon$1@e3a7d65
scala> val r = ST.runST(p)
r: (Int, Int) = (3,2)
The expression runST(p) uses mutable state internally, but it doesn’t have any side effects. As far as any other expression is concerned, it’s just a pair of integers like any other. It will always return the same pair of integers and it’ll do nothing else.
But this isn’t the most important part. Most importantly, we cannot run a program that tries to return a mutable reference. It’s not possible to create a RunnableST that returns a naked STRef:
scala> new RunnableST[STRef[Nothing,Int]] {
| def apply[S] = STRef(1)
| }
<console>:17: error: type mismatch;
found : ST[S,STRef[S,Int]]
required: ST[S,STRef[Nothing,Int]]
def apply[S] = STRef(1)
In this example, we arbitrarily chose Nothing just to illustrate the point. The point is that the type S is bound in the apply method, so when we say new RunnableST, that type isn’t accessible.
Because an STRef is always tagged with the type S of the ST action that it lives in, it can never escape. And this is guaranteed by Scala’s type system! As a corollary, the fact that you can’t get an STRef out of an ST action guarantees that if you have an STRef, then you are inside of the STaction that created it, so it’s always safe to mutate the reference.
A note on the wildcard type
It’s possible to bypass the type system in runST by using the wildcard type. If we pass it a RunnableST[STRef[_,Int]], this will allow an STRef to escape:
scala> val ref = ST.runST(new RunnableST[STRef[_, Int]] {
| def apply[S] = for {
| r1 <- STRef(1)
| } yield r1
| })
ref: STRef[_, Int] = STRef$$anonfun$apply$1$$anon$6@20e88a41
The wildcard type is an artifact of Scala’s interoperability with Java’s type system. Fortunately, when you have an STRef[_,Int], using it will cause a type error:
scala> new RunnableST[Int] {
| def apply[R] = for { x <- ref.read } yield x }
error : type mismatch;
found : ST[_$1,Int]
required: ST[R,Int]
def apply[R] = for { x <- ref.read } yield x }
^
This type error is caused by the fact that the wildcard type in ref represents some concrete type that only ref knows about. In this case it’s the S type that was bound in the apply method of the RunnableST where it was created. Scala is unable to prove that this is the same type as R. Therefore, even though it’s possible to abuse the wildcard type to get the naked STRef out, this is still safe since we can’t use it to mutate or access the state.
14.2.4. Mutable arrays
Mutable references on their own aren’t all that useful. Mutable arrays are a much more compelling use case for the ST monad. In this section, we’ll define an algebra for manipulating mutable arrays in the ST monad and then write an in-place quicksort algorithm compositionally. We’ll need primitive combinators to allocate, read, and write mutable arrays.
Listing 14.3. An array class for our ST monad

Note that Scala can’t create arrays for every type A. It requires that a Manifest[A] exists in implicit scope. Scala’s standard library provides manifests for most types that you would in practice want to put in an array.
Just like with STRef, we always return an STArray packaged in an ST action with a corresponding S type, and any manipulation of the array (even reading it) is an ST action tagged with the same type S. It’s therefore impossible to observe a naked STArray outside of the ST monad (except by code in the Scala source file in which the STArray data type itself is declared).
Using these primitives, we can write more complex functions on arrays.
Exercise 14.1
![]()
Add a combinator on STArray to fill the array from a Map where each key in the map represents an index into the array, and the value under that key is written to the array at that index. For example, xs.fill(Map(0->"a", 2->"b")) should write the value "a" at index 0 in the array xsand "b" at index 2. Use the existing combinators to write your implementation.
def fill(xs: Map[Int,A]): ST[S,Unit]
Not everything can be done efficiently using these existing combinators. For example, the Scala library already has an efficient way of turning a list into an array. Let’s make that primitive as well:
def fromList[S,A:Manifest](xs: List[A]): ST[S, STArray[S,A]] =
ST(new STArray[S,A] {
lazy val value = xs.toArray
})
14.2.5. A purely functional in-place quicksort
The components for quicksort are now easy to write in ST—for example, the swap function that swaps two elements of the array:
def swap[S](i: Int, j: Int): ST[S,Unit] = for {
x <- read(i)
y <- read(j)
_ <- write(i, y)
_ <- write(j, x)
} yield ()
Exercise 14.2
![]()
Write the purely functional versions of partition and qs.
def partition[S](arr: STArray[S,Int],
n: Int, r: Int, pivot: Int): ST[S,Int]
def qs[S](a: STArray[S,Int], n: Int, r: Int): ST[S,Unit]
With those components written, quicksort can now be assembled out of them in the ST monad:
def quicksort(xs: List[Int]): List[Int] =
if (xs.isEmpty) xs else ST.runST(new RunnableST[List[Int]] {
def apply[S] = for {
arr <- STArray.fromList(xs)
size <- arr.size
_ <- qs(arr, 0, size - 1)
sorted <- arr.freeze
} yield sorted
})
As you can see, the ST monad allows us to write pure functions that nevertheless mutate the data they receive. Scala’s type system ensures that we don’t combine things in an unsafe way.
Exercise 14.3
![]()
Give the same treatment to scala.collection.mutable.HashMap as we’ve given here to references and arrays. Come up with a minimal set of primitive combinators for creating and manipulating hash maps.
14.3. Purity is contextual
In the preceding section, we talked about effects that aren’t observable because they’re entirely local to some scope. A program can’t observe mutation of data unless it holds a reference to that data.
But there are other effects that may be non-observable, depending on who’s looking. As a simple example, let’s take a kind of side effect that occurs all the time in ordinary Scala programs, even ones that we’d usually consider purely functional:
scala> case class Foo(s: String)
scala> val b = Foo("hello") == Foo("hello")
b: Boolean = true
scala> val c = Foo("hello") eq Foo("hello")
c: Boolean = false
Here Foo("hello") looks pretty innocent. We could be forgiven if we assumed that it was a completely referentially transparent expression. But each time it appears, it produces a different Foo in a certain sense. If we test two appearances of Foo("hello") for equality using the ==function, we get true as we’d expect. But testing for reference equality (a notion inherited from the Java language) with eq, we get false. The two appearances of Foo("hello") aren’t references to the “same object” if we look under the hood.
Note that if we evaluate Foo("hello") and store the result as x, then substitute x to get the expression x eq x, it has a different result:
scala> val x = Foo("hello")
x: Foo = Foo(hello)
scala> val d = x eq x
d: Boolean = true
Therefore, by our original definition of referential transparency, every data constructor in Scala has a side effect. The effect is that a new and unique object is created in memory, and the data constructor returns a reference to that new object.
For most programs, this makes no difference, because most programs don’t check for reference equality. It’s only the eq method that allows our programs to observe this side effect occurring. We could therefore say that it’s not a side effect at all in the context of the vast majority of programs.
Our definition of referential transparency doesn’t take this into account. Referential transparency is with regard to some context and our definition doesn’t establish this context.
A more general definition of referential transparency
An expression e is referentially transparent with regard to a program p if every occurrence of e in p can be replaced by the result of evaluating e without affecting the meaning of p.
This definition is only slightly modified to reflect the fact that not all programs observe the same effects. We say that an effect of e is non-observable by p if it doesn’t affect the referential transparency of e with regard to p. For instance, most programs can’t observe the side effect of calling a constructor, because they don’t make use of eq.
This definition is still somewhat vague. What is meant by “evaluating”? And what’s the standard by which we determine whether the meaning of two programs is the same?
In Scala, there’s a kind of standard answer to this first question. We’ll take evaluation to mean reduction to some normal form. Since Scala is a strictly evaluated language, we can force the evaluation of an expression e to normal form in Scala by assigning it to a val:
val v = e
And referential transparency of e with regard to a program p means that we can rewrite p, replacing every appearance of e with v without changing the meaning of our program.
But what do we mean by “changing the meaning of our program”? Just what is the meaning of a program? This is a somewhat philosophical question, and there are various ways of answering it that we won’t explore in detail here.[2] But the general point is that when we talk about referential transparency, it’s always with regard to some context. The context determines what sort of programs we’re interested in, and also how we assign meaning to our programs. Establishing this context is a choice; we need to decide what aspects of a program participate in that program’s meaning.
2 See the chapter notes for links to further reading.
Let’s explore this subtlety a bit further.
14.3.1. What counts as a side effect?
Earlier, we talked about how the eq method is able to observe the side effect of object creation. Let’s look more closely at this idea of observable behavior and program meaning. It requires that we delimit what we consider observable and what we don’t. Take, for example, this method that has a definite side effect:
def timesTwo(x: Int) = {
if (x < 0) println("Got a negative number")
x * 2
}
If we replace timesTwo(1) with 2 in our program, we don’t have the same program in every respect. It may compute the same result, but we can say that the meaning of the program has changed. But this isn’t true for all programs that call timesTwo, nor for all notions of program equivalence.
We need to decide up front whether changes in standard output are something we care to observe—whether it’s part of the changes in behavior that matter in our context. In this case, it’s exceedingly unlikely that any other part of the program will be able to observe that println side effect occurring inside timesTwo.
Of course, timesTwo has a hidden dependency on the I/O subsystem. It requires access to the standard output stream. But as we’ve seen, most programs that we’d consider purely functional also require access to some of the underlying machinery of Scala’s environment, like being able to construct objects in memory and discard them. At the end of the day, we have to decide for ourselves which effects are important enough to track. We could use the IO monad to track println calls, but maybe we don’t want to bother. If we’re just using the console to do some temporary debug logging, it seems like a waste of time to track that. But if the program’s correct behavior depends in some way on what it prints to the console (like if it’s a UNIX command line utility), then we definitely want to track it.
This brings us to an essential point: tracking effects is a choice we make as programmers. It’s a value judgement, and there are trade-offs associated with how we choose. We can take it as far as we want. But as with the context of referential transparency, in Scala there’s a kind of standard choice. For example, it would be completely valid and possible to track memory allocations in the type system if that really mattered to us. But in Scala we have the benefit of automatic memory management, so the cost of explicit tracking is usually higher than the benefit.
The policy we should adopt is to track those effects that program correctness depends on. If a program is fundamentally about reading and writing files, then file I/O should be tracked in the type system to the extent feasible. If a program relies on object reference equality, it would be nice to know that statically as well. Static type information lets us know what kinds of effects are involved, and thereby lets us make educated decisions about whether they matter to us in a given context.
The ST type in this chapter and the IO monad in the previous chapter should have given you a taste for what it’s like to track effects in the type system. But this isn’t the end of the road. You’re limited only by your imagination and the expressiveness of Scala’s types.
14.4. Summary
In this chapter, we discussed two different implications of referential transparency.
We saw that we can get away with mutating data that never escapes a local scope. At first blush it may seem that mutating state can’t be compatible with pure functions. But as we’ve seen, we can write components that have a pure interface and mutate local state behind the scenes, and we can use Scala’s type system to guarantee purity.
We also discussed that what counts as a side effect is actually a choice made by the programmer or language designer. When we talk about functions being pure, we should have already chosen a context that establishes what it means for two things to be equal, what it means to execute a program, and which effects we care to take into account when assigning meaning to our program.