Functional Programming in Scala (2015)
Part 1. Introduction to functional programming
We begin this book with a radical premise—that we will restrict ourselves to constructing programs using only pure functions with no side effects such as reading from files or mutating memory. This idea, of functional programming, leads to a very different way of writing programs than you may be used to. We therefore start from the very beginning, relearning how to write the simplest of programs in a functional way.
In the first chapter, we’ll explain exactly what functional programming means and give you some idea of its benefits. The rest of the chapters in part 1 introduce the basic techniques for functional programming in Scala. Chapter 2 introduces Scala the language and covers fundamentals like how to write loops functionally and manipulate functions as ordinary values. Chapter 3 deals with in-memory data structures that may change over time. Chapter 4 talks about handling errors in pure functions, and chapter 5 introduces the notion of non-strictness, which can be used to improve the efficiency and modularity of functional code. Finally, chapter 6 introduces modeling stateful programs using pure functions.
The intent of this first part of the book is to get you thinking about programs purely in terms of functions from inputs to outputs, and to teach you the techniques you’ll need in part 2, when we start writing some practical code.
Chapter 1. What is functional programming?
Functional programming (FP) is based on a simple premise with far-reaching implications: we construct our programs using only pure functions—in other words, functions that have no side effects. What are side effects? A function has a side effect if it does something other than simply return a result, for example:
· Modifying a variable
· Modifying a data structure in place
· Setting a field on an object
· Throwing an exception or halting with an error
· Printing to the console or reading user input
· Reading from or writing to a file
· Drawing on the screen
We’ll provide a more precise definition of side effects later in this chapter, but consider what programming would be like without the ability to do these things, or with significant restrictions on when and how these actions can occur. It may be difficult to imagine. How is it even possible to write useful programs at all? If we can’t reassign variables, how do we write simple programs like loops? What about working with data that changes, or handling errors without throwing exceptions? How can we write programs that must perform I/O, like drawing to the screen or reading from a file?
The answer is that functional programming is a restriction on how we write programs, but not on what programs we can express. Over the course of this book, we’ll learn how to express all of our programs without side effects, and that includes programs that perform I/O, handle errors, and modify data. We’ll learn how following the discipline of FP is tremendously beneficial because of the increase in modularity that we gain from programming with pure functions. Because of their modularity, pure functions are easier to test, reuse, parallelize, generalize, and reason about. Furthermore, pure functions are much less prone to bugs.
In this chapter, we’ll look at a simple program with side effects and demonstrate some of the benefits of FP by removing these side effects. We’ll also discuss the benefits of FP more generally and define two important concepts—referential transparency and the substitution model.
1.1. The benefits of FP: a simple example
Let’s look at an example that demonstrates some of the benefits of programming with pure functions. The point here is just to illustrate some basic ideas that we’ll return to throughout this book. This will also be your first exposure to Scala’s syntax. We’ll talk through Scala’s syntax much more in the next chapter, so don’t worry too much about following every detail. As long as you have a basic idea of what the code is doing, that’s what’s important.
1.1.1. A program with side effects
Suppose we’re implementing a program to handle purchases at a coffee shop. We’ll begin with a Scala program that uses side effects in its implementation (also called an impure program).
Listing 1.1. A Scala program with side effects

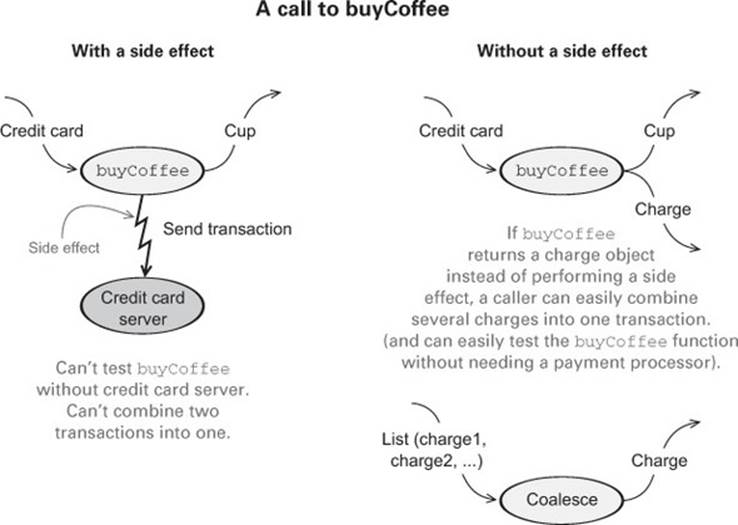
The line cc.charge(cup.price) is an example of a side effect. Charging a credit card involves some interaction with the outside world—suppose it requires contacting the credit card company via some web service, authorizing the transaction, charging the card, and (if successful) persisting some record of the transaction for later reference. But our function merely returns a Coffee and these other actions are happening on the side, hence the term “side effect.” (Again, we’ll define side effects more formally later in this chapter.)
As a result of this side effect, the code is difficult to test. We don’t want our tests to actually contact the credit card company and charge the card! This lack of testability is suggesting a design change: arguably, CreditCard shouldn’t have any knowledge baked into it about how to contact the credit card company to actually execute a charge, nor should it have knowledge of how to persist a record of this charge in our internal systems. We can make the code more modular and testable by letting Credit-Card be ignorant of these concerns and passing a Payments object intobuyCoffee.
Listing 1.2. Adding a payments object
class Cafe {
def buyCoffee(cc: CreditCard, p: Payments): Coffee = {
val cup = new Coffee()
p.charge(cc, cup.price)
cup
}
}
Though side effects still occur when we call p.charge(cc, cup.price), we have at least regained some testability. Payments can be an interface, and we can write a mock implementation of this interface that is suitable for testing. But that isn’t ideal either. We’re forced to makePayments an interface, when a concrete class may have been fine otherwise, and any mock implementation will be awkward to use. For example, it might contain some internal state that we’ll have to inspect after the call to buy-Coffee, and our test will have to make sure this state has been appropriately modified (mutated) by the call to charge. We can use a mock framework or similar to handle this detail for us, but this all feels like overkill if we just want to test that buyCoffee creates a charge equal to the price of a cup of coffee.
Separate from the concern of testing, there’s another problem: it’s difficult to reuse buyCoffee. Suppose a customer, Alice, would like to order 12 cups of coffee. Ideally we could just reuse buyCoffee for this, perhaps calling it 12 times in a loop. But as it is currently implemented, that will involve contacting the payment system 12 times, authorizing 12 separate charges to Alice’s credit card! That adds more processing fees and isn’t good for Alice or the coffee shop.
What can we do about this? As the figure at the top of page 6 illustrates, we could write a whole new function, buyCoffees, with special logic for batching up the charges.[1] Here, that might not be such a big deal, since the logic of buyCoffee is so simple, but in other cases the logic we need to duplicate may be nontrivial, and we should mourn the loss of code reuse and composition!
1 We could also write a specialized BatchingPayments implementation of the Payments interface, that somehow attempts to batch successive charges to the same credit card. This gets complicated though. How many charges should it try to batch up, and how long should it wait? Do we force buyCoffee to indicate that the batch is finished, perhaps by calling closeBatch? And how would it know when it’s appropriate to do that, anyway?
1.1.2. A functional solution: removing the side effects
The functional solution is to eliminate side effects and have buyCoffee return the charge as a value in addition to returning the Coffee. The concerns of processing the charge by sending it off to the credit card company, persisting a record of it, and so on, will be handled elsewhere. Again, we’ll cover Scala’s syntax more in later chapters, but here’s what a functional solution might look like:

Here we’ve separated the concern of creating a charge from the processing or interpretation of that charge. The buyCoffee function now returns a Charge as a value along with the Coffee. We’ll see shortly how this lets us reuse it more easily to purchase multiple coffees with a single transaction. But what is Charge? It’s a data type we just invented containing a CreditCard and an amount, equipped with a handy function, combine, for combining charges with the same CreditCard:

Now let’s look at buyCoffees, to implement the purchase of n cups of coffee. Unlike before, this can now be implemented in terms of buyCoffee, as we had hoped.
Listing 1.3. Buying multiple cups with buyCoffees

Overall, this solution is a marked improvement—we’re now able to reuse buyCoffee directly to define the buyCoffees function, and both functions are trivially testable without having to define complicated mock implementations of some Payments interface! In fact, the Cafe is now completely ignorant of how the Charge values will be processed. We can still have a Payments class for actually processing charges, of course, but Cafe doesn’t need to know about it.
Making Charge into a first-class value has other benefits we might not have anticipated: we can more easily assemble business logic for working with these charges. For instance, Alice may bring her laptop to the coffee shop and work there for a few hours, making occasional purchases. It might be nice if the coffee shop could combine these purchases Alice makes into a single charge, again saving on credit card processing fees. Since Charge is first-class, we can write the following function to coalesce any same-card charges in a List[Charge]:
def coalesce(charges: List[Charge]): List[Charge] =
charges.groupBy(_.cc).values.map(_.reduce(_ combine _)).toList
We’re passing functions as values to the groupBy, map, and reduce methods. You’ll learn to read and write one-liners like this over the next several chapters. The _.cc and _ combine _ are syntax for anonymous functions, which we’ll introduce in the next chapter.
You may find this kind of code difficult to read because the notation is very compact. But as you work through this book, reading and writing Scala code like this will become second nature to you very quickly. This function takes a list of charges, groups them by the credit card used, and then combines them into a single charge per card. It’s perfectly reusable and testable without any additional mock objects or interfaces. Imagine trying to implement the same logic with our first implementation of buyCoffee!
This is just a taste of why functional programming has the benefits claimed, and this example is intentionally simple. If the series of refactorings used here seems natural, obvious, unremarkable, or standard practice, that’s good. FP is merely a discipline that takes what many consider a good idea to its logical endpoint, applying the discipline even in situations where its applicability is less obvious. As you’ll learn over the course of this book, the consequences of consistently following the discipline of FP are profound and the benefits enormous. FP is a truly radical shift in how programs are organized at every level—from the simplest of loops to high-level program architecture. The style that emerges is quite different, but it’s a beautiful and cohesive approach to programming that we hope you come to appreciate.
What about the real world?
We saw in the case of buyCoffee how we could separate the creation of the Charge from the interpretation or processing of that Charge. In general, we’ll learn how this sort of transformation can be applied to any function with side effects to push these effects to the outer layers of the program. Functional programmers often speak of implementing programs with a pure core and a thin layer on the outside that handles effects.
But even so, surely at some point we must actually have an effect on the world and submit the Charge for processing by some external system. And aren’t there other useful programs that necessitate side effects or mutation? How do we write such programs? As we work through this book, we’ll discover how many programs that seem to necessitate side effects have some functional analogue. In other cases we’ll find ways to structure code so that effects occur but aren’t observable. (For example, we can mutate data that’s declared locally in the body of some function if we ensure that it can’t be referenced outside that function, or we can write to a file as long as no enclosing function can observe this occurring.)
1.2. Exactly what is a (pure) function?
We said earlier that FP means programming with pure functions, and a pure function is one that lacks side effects. In our discussion of the coffee shop example, we worked off an informal notion of side effects and purity. Here we’ll formalize this notion, to pinpoint more precisely what it means to program functionally. This will also give us additional insight into one of the benefits of functional programming: pure functions are easier to reason about.
A function f with input type A and output type B (written in Scala as a single type: A => B, pronounced “A to B” or “A arrow B”) is a computation that relates every value a of type A to exactly one value b of type B such that b is determined solely by the value of a. Any changing state of an internal or external process is irrelevant to computing the result f(a). For example, a function intToString having type Int => String will take every integer to a corresponding string. Furthermore, if it really is a function, it will do nothing else.
In other words, a function has no observable effect on the execution of the program other than to compute a result given its inputs; we say that it has no side effects. We sometimes qualify such functions as pure functions to make this more explicit, but this is somewhat redundant. Unless we state otherwise, we’ll often use function to imply no side effects.[2]
2 Procedure is often used to refer to some parameterized chunk of code that may have side effects.
You should be familiar with a lot of pure functions already. Consider the addition (+) function on integers. It takes two integer values and returns an integer value. For any two given integer values, it will always return the same integer value. Another example is the length function of aString in Java, Scala, and many other languages where strings can’t be modified (are immutable). For any given string, the same length is always returned and nothing else occurs.
We can formalize this idea of pure functions using the concept of referential transparency (RT). This is a property of expressions in general and not just functions. For the purposes of our discussion, consider an expression to be any part of a program that can be evaluated to a result—anything that you could type into the Scala interpreter and get an answer. For example, 2 + 3 is an expression that applies the pure function + to the values 2 and 3 (which are also expressions). This has no side effect. The evaluation of this expression results in the same value 5 every time. In fact, if we saw 2 + 3 in a program we could simply replace it with the value 5 and it wouldn’t change a thing about the meaning of our program.
This is all it means for an expression to be referentially transparent—in any program, the expression can be replaced by its result without changing the meaning of the program. And we say that a function is pure if calling it with RT arguments is also RT. We’ll look at some examples next.
Referential transparency and purity
An expression e is referentially transparent if, for all programs p, all occurrences of e in p can be replaced by the result of evaluating e without affecting the meaning of p. A function f is pure if the expression f(x) is referentially transparent for all referentially transparent x.[3]
3 There are some subtleties to this definition, and we’ll refine it later in this book. See the chapter notes at our GitHub site (https://github.com/pchiusano/fpinscala; see the preface) for more discussion.
1.3. Referential transparency, purity, and the substitution model
Let’s see how the definition of RT applies to our original buyCoffee example:
def buyCoffee(cc: CreditCard): Coffee = {
val cup = new Coffee()
cc.charge(cup.price)
cup
}
Whatever the return type of cc.charge(cup.price) (perhaps it’s Unit, Scala’s equivalent of void in other languages), it’s discarded by buyCoffee. Thus, the result of evaluating buyCoffee(aliceCreditCard) will be merely cup, which is equivalent to a new Coffee(). ForbuyCoffee to be pure, by our definition of RT, it must be the case that p(buyCoffee(aliceCreditCard)) behaves the same as p(new Coffee()), for any p. This clearly doesn’t hold—the program new Coffee() doesn’t do anything, whereas buyCoffee(aliceCreditCard)will contact the credit card company and authorize a charge. Already we have an observable difference between the two programs.
Referential transparency forces the invariant that everything a function does is represented by the value that it returns, according to the result type of the function. This constraint enables a simple and natural mode of reasoning about program evaluation called the substitution model. When expressions are referentially transparent, we can imagine that computation proceeds much like we’d solve an algebraic equation. We fully expand every part of an expression, replacing all variables with their referents, and then reduce it to its simplest form. At each step we replace a term with an equivalent one; computation proceeds by substituting equals for equals. In other words, RT enables equational reasoning about programs.
Let’s look at two more examples—one where all expressions are RT and can be reasoned about using the substitution model, and one where some expressions violate RT. There’s nothing complicated here; we’re just formalizing something you likely already understand.
Let’s try the following in the Scala interpreter (also known as the Read-Eval-Print-Loop or REPL, pronounced like “ripple,” but with an e instead of an i). Note that in Java and in Scala, strings are immutable. A “modified” string is really a new string and the old string remains intact:

Suppose we replace all occurrences of the term x with the expression referenced by x (its definition), as follows:

This transformation doesn’t affect the outcome. The values of r1 and r2 are the same as before, so x was referentially transparent. What’s more, r1 and r2 are referentially transparent as well, so if they appeared in some other part of a larger program, they could in turn be replaced with their values throughout and it would have no effect on the program.
Now let’s look at a function that is not referentially transparent. Consider the append function on the java.lang.StringBuilder class. This function operates on the StringBuilder in place. The previous state of the StringBuilder is destroyed after a call to append. Let’s try this out:

So far so good. Now let’s see how this side effect breaks RT. Suppose we substitute the call to append like we did earlier, replacing all occurrences of y with the expression referenced by y:

This transformation of the program results in a different outcome. We therefore conclude that StringBuilder.append is not a pure function. What’s going on here is that although r1 and r2 look like they’re the same expression, they are in fact referencing two different values of the sameStringBuilder. By the time r2 calls x.append, r1 will have already mutated the object referenced by x. If this seems difficult to think about, that’s because it is. Side effects make reasoning about program behavior more difficult.
Conversely, the substitution model is simple to reason about since effects of evaluation are purely local (they affect only the expression being evaluated) and we need not mentally simulate sequences of state updates to understand a block of code. Understanding requires only local reasoning. We need not mentally track all the state changes that may occur before or after our function’s execution to understand what our function will do; we simply look at the function’s definition and substitute the arguments into its body. Even if you haven’t used the name “substitution model,” you have certainly used this mode of reasoning when thinking about your code.[4]
4 In practice, programmers don’t spend time mechanically applying substitution to determine if code is pure—it will usually be obvious.
Formalizing the notion of purity this way gives insight into why functional programs are often more modular. Modular programs consist of components that can be understood and reused independently of the whole, such that the meaning of the whole depends only on the meaning of the components and the rules governing their composition; that is, they are composable. A pure function is modular and composable because it separates the logic of the computation itself from “what to do with the result” and “how to obtain the input”; it’s a black box. Input is obtained in exactly one way: via the argument(s) to the function. And the output is simply computed and returned. By keeping each of these concerns separate, the logic of the computation is more reusable; we may reuse the logic wherever we want without worrying about whether the side effect being done with the result or the side effect requesting the input are appropriate in all contexts. We saw this in the buyCoffee example—by eliminating the side effect of payment processing being done with the output, we were more easily able to reuse the logic of the function, both for purposes of testing and for purposes of further composition (like when we wrote buyCoffees and coalesce).
1.4. Summary
In this chapter, we introduced functional programming and explained exactly what FP is and why you might use it. Though the full benefits of the functional style will become more clear over the course of this book, we illustrated some of the benefits of FP using a simple example. We also discussed referential transparency and the substitution model and talked about how FP enables simpler reasoning about programs and greater modularity.
In this book, you’ll learn the concepts and principles of FP as they apply to every level of programming, starting from the simplest of tasks and building on that foundation. In subsequent chapters, we’ll cover some of the fundamentals—how do we write loops in FP? Or implement data structures? How do we deal with errors and exceptions? We need to learn how to do these things and get comfortable with the low-level idioms of FP. We’ll build on this understanding when we explore functional design techniques in parts 2, 3, and 4.