Functional Programming in Scala (2015)
Part 1. Introduction to functional programming
Chapter 5. Strictness and laziness
In chapter 3 we talked about purely functional data structures, using singly linked lists as an example. We covered a number of bulk operations on lists—map, filter, foldLeft, foldRight, zipWith, and so on. We noted that each of these operations makes its own pass over the input and constructs a fresh list for the output.
Imagine if you had a deck of cards and you were asked to remove the odd-numbered cards and then flip over all the queens. Ideally, you’d make a single pass through the deck, looking for queens and odd-numbered cards at the same time. This is more efficient than removing the odd cards and then looking for queens in the remainder. And yet the latter is what Scala is doing in the following code:[1]
1 We’re now using the Scala standard library’s List type here, where map and filter are methods on List rather than standalone functions like the ones we wrote in chapter 3.
scala> List(1,2,3,4).map(_ + 10).filter(_ % 2 == 0).map(_ * 3)
List(36,42)
In this expression, map(_ + 10) will produce an intermediate list that then gets passed to filter(_ % 2 == 0), which in turn constructs a list that gets passed to map(_ * 3), which then produces the final list. In other words, each transformation will produce a temporary list that only ever gets used as input to the next transformation and is then immediately discarded.
Think about how this program will be evaluated. If we manually produce a trace of its evaluation, the steps would look something like this.
Listing 5.1. Program trace for List
List(1,2,3,4).map(_ + 10).filter(_ % 2 == 0).map(_ * 3)
List(11,12,13,14).filter(_ % 2 == 0).map(_ * 3)
List(12,14).map(_ * 3)
List(36,42)
Here we’re showing the result of each substitution performed to evaluate our expression. For example, to go from the first line to the second, we’ve replaced List(1,2,3,4).map(_ + 10) with List(11,12,13,14), based on the definition of map.[2] This view makes it clear how the calls to map and filter each perform their own traversal of the input and allocate lists for the output. Wouldn’t it be nice if we could somehow fuse sequences of transformations like this into a single pass and avoid creating temporary data structures? We could rewrite the code into a whileloop by hand, but ideally we’d like to have this done automatically while retaining the same high-level compositional style. We want to compose our programs using higher-order functions like map and filter instead of writing monolithic loops.
2 With program traces like these, it’s often more illustrative to not fully trace the evaluation of every subexpression. In this case, we’ve omitted the full expansion of List(1,2,3,4).map(_ + 10). We could “enter” the definition of map and trace its execution, but we chose to omit this level of detail here.
It turns out that we can accomplish this kind of automatic loop fusion through the use of non-strictness (or, less formally, laziness). In this chapter, we’ll explain what exactly this means, and we’ll work through the implementation of a lazy list type that fuses sequences of transformations. Although building a “better” list is the motivation for this chapter, we’ll see that non-strictness is a fundamental technique for improving on the efficiency and modularity of functional programs in general.
5.1. Strict and non-strict functions
Before we get to our example of lazy lists, we need to cover some basics. What are strictness and non-strictness, and how are these concepts expressed in Scala?
Non-strictness is a property of a function. To say a function is non-strict just means that the function may choose not to evaluate one or more of its arguments. In contrast, a strict function always evaluates its arguments. Strict functions are the norm in most programming languages, and indeed most languages only support functions that expect their arguments fully evaluated. Unless we tell it otherwise, any function definition in Scala will be strict (and all the functions we’ve defined so far have been strict). As an example, consider the following function:
def square(x: Double): Double = x * x
When you invoke square(41.0 + 1.0), the function square will receive the evaluated value of 42.0 because it’s strict. If you invoke square(sys.error("failure")), you’ll get an exception before square has a chance to do anything, since the sys.error ("failure")expression will be evaluated before entering the body of square.
Although we haven’t yet learned the syntax for indicating non-strictness in Scala, you’re almost certainly familiar with the concept. For example, the short-circuiting Boolean functions && and ||, found in many programming languages including Scala, are non-strict. You may be used to thinking of && and || as built-in syntax, part of the language, but you can also think of them as functions that may choose not to evaluate their arguments. The function && takes two Boolean arguments, but only evaluates the second argument if the first is true:
scala> false && { println("!!"); true } // does not print anything
res0: Boolean = false
And || only evaluates its second argument if the first is false:
scala> true || { println("!!"); false } // doesn't print anything either
res1: Boolean = true
Another example of non-strictness is the if control construct in Scala:
val result = if (input.isEmpty) sys.error("empty input") else input
Even though if is a built-in language construct in Scala, it can be thought of as a function accepting three parameters: a condition of type Boolean, an expression of some type A to return in the case that the condition is true, and another expression of the same type A to return if the condition is false. This if function would be non-strict, since it won’t evaluate all of its arguments. To be more precise, we’d say that the if function is strict in its condition parameter, since it’ll always evaluate the condition to determine which branch to take, and non-strict in the two branches for the true and false cases, since it’ll only evaluate one or the other based on the condition.
In Scala, we can write non-strict functions by accepting some of our arguments unevaluated. We’ll show how this is done explicitly just to illustrate what’s happening, and then show some nicer syntax for it that’s built into Scala. Here’s a non-strict if function:

The arguments we’d like to pass unevaluated have a () => immediately before their type. A value of type () => A is a function that accepts zero arguments and returns an A.[3] In general, the unevaluated form of an expression is called a thunk, and we can force the thunk to evaluate the expression and get a result. We do so by invoking the function, passing an empty argument list, as in onTrue() or onFalse(). Likewise, callers of if2 have to explicitly create thunks, and the syntax follows the same conventions as the function literal syntax we’ve already seen.
3 In fact, the type () => A is a syntactic alias for the type Function0[A].
Overall, this syntax makes it very clear what’s happening—we’re passing a function of no arguments in place of each non-strict parameter, and then explicitly calling this function to obtain a result in the body. But this is such a common case that Scala provides some nicer syntax:
def if2[A](cond: Boolean, onTrue: => A, onFalse: => A): A =
if (cond) onTrue else onFalse
The arguments we’d like to pass unevaluated have an arrow => immediately before their type. In the body of the function, we don’t need to do anything special to evaluate an argument annotated with =>. We just reference the identifier as usual. Nor do we have to do anything special to call this function. We just use the normal function call syntax, and Scala takes care of wrapping the expression in a thunk for us:
scala> if2(false, sys.error("fail"), 3)
res2: Int = 3
With either syntax, an argument that’s passed unevaluated to a function will be evaluated once for each place it’s referenced in the body of the function. That is, Scala won’t (by default) cache the result of evaluating an argument:
scala> def maybeTwice(b: Boolean, i: => Int) = if (b) i+i else 0
maybeTwice: (b: Boolean, i: => Int)Int
scala> val x = maybeTwice(true, { println("hi"); 1+41 })
hi
hi
x: Int = 84
Here, i is referenced twice in the body of maybeTwice, and we’ve made it particularly obvious that it’s evaluated each time by passing the block {println("hi"); 1+41}, which prints hi as a side effect before returning a result of 42. The expression 1+41 will be computed twice as well. We can cache the value explicitly if we wish to only evaluate the result once, by using the lazy keyword:
scala> def maybeTwice2(b: Boolean, i: => Int) = {
| lazy val j = i
| if (b) j+j else 0
| }
maybeTwice: (b: Boolean, i: => Int)Int
scala> val x = maybeTwice2(true, { println("hi"); 1+41 })
hi
x: Int = 84
Adding the lazy keyword to a val declaration will cause Scala to delay evaluation of the right-hand side of that lazy val declaration until it’s first referenced. It will also cache the result so that subsequent references to it don’t trigger repeated evaluation.
Formal definition of strictness
If the evaluation of an expression runs forever or throws an error instead of returning a definite value, we say that the expression doesn’t terminate, or that it evaluates to bottom. A function f is strict if the expression f(x) evaluates to bottom for all x that evaluate to bottom.
As a final bit of terminology, we say that a non-strict function in Scala takes its arguments by name rather than by value.
5.2. An extended example: lazy lists
Let’s now return to the problem posed at the beginning of this chapter. We’ll explore how laziness can be used to improve the efficiency and modularity of functional programs using lazy lists, or streams, as an example. We’ll see how chains of transformations on streams are fused into a single pass through the use of laziness. Here’s a simple Stream definition. There are a few new things here we’ll discuss next.
Listing 5.2. Simple definition for Stream

This type looks identical to our List type, except that the Cons data constructor takes explicit thunks (() => A and () => Stream[A]) instead of regular strict values. If we wish to examine or traverse the Stream, we need to force these thunks as we did earlier in our definition of if2. For instance, here’s a function to optionally extract the head of a Stream:
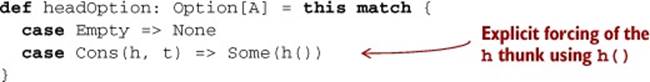
Note that we have to force h explicitly via h(), but other than that, the code works the same way as it would for List. But this ability of Stream to evaluate only the portion actually demanded (we don’t evaluate the tail of the Cons) is useful, as we’ll see.
5.2.1. Memoizing streams and avoiding recomputation
We typically want to cache the values of a Cons node, once they are forced. If we use the Cons data constructor directly, for instance, this code will actually compute expensive(x) twice:
val x = Cons(() => expensive(x), tl)
val h1 = x.headOption
val h2 = x.headOption
We typically avoid this problem by defining smart constructors, which is what we call a function for constructing a data type that ensures some additional invariant or provides a slightly different signature than the “real” constructors used for pattern matching. By convention, smart constructors typically lowercase the first letter of the corresponding data constructor. Here, our cons smart constructor takes care of memoizing the by-name arguments for the head and tail of the Cons. This is a common trick, and it ensures that our thunk will only do its work once, when forced for the first time. Subsequent forces will return the cached lazy val:
def cons[A](hd: => A, tl: => Stream[A]): Stream[A] = {
lazy val head = hd
lazy val tail = tl
Cons(() => head, () => tail)
}
The empty smart constructor just returns Empty, but annotates Empty as a Stream[A], which is better for type inference in some cases.[4] We can see how both smart constructors are used in the Stream.apply function:
4 Recall that Scala uses subtyping to represent data constructors, but we almost always want to infer Stream as the type, not Cons or Empty. Making smart constructors that return the base type is a common trick.
def apply[A](as: A*): Stream[A] =
if (as.isEmpty) empty
else cons(as.head, apply(as.tail: _*))
Again, Scala takes care of wrapping the arguments to cons in thunks, so the as.head and apply(as.tail: _*) expressions won’t be evaluated until we force the Stream.
5.2.2. Helper functions for inspecting streams
Before continuing, let’s write a few helper functions to make inspecting streams easier.
Exercise 5.1
![]()
Write a function to convert a Stream to a List, which will force its evaluation and let you look at it in the REPL. You can convert to the regular List type in the standard library. You can place this and other functions that operate on a Stream inside the Stream trait.
def toList: List[A]
Exercise 5.2
![]()
Write the function take(n) for returning the first n elements of a Stream, and drop(n) for skipping the first n elements of a Stream.
Exercise 5.3
![]()
Write the function takeWhile for returning all starting elements of a Stream that match the given predicate.
def takeWhile(p: A => Boolean): Stream[A]
You can use take and toList together to inspect streams in the REPL. For example, try printing Stream(1,2,3).take(2).toList.
5.3. Separating program description from evaluation
A major theme in functional programming is separation of concerns. We want to separate the description of computations from actually running them. We’ve already touched on this theme in previous chapters in different ways. For example, first-class functions capture some computation in their bodies but only execute it once they receive their arguments. And we used Option to capture the fact that an error occurred, where the decision of what to do about it became a separate concern. With Stream, we’re able to build up a computation that produces a sequence of elements without running the steps of that computation until we actually need those elements.
More generally speaking, laziness lets us separate the description of an expression from the evaluation of that expression. This gives us a powerful ability—we may choose to describe a “larger” expression than we need, and then evaluate only a portion of it. As an example, let’s look at the function exists that checks whether an element matching a Boolean function exists in this Stream:
def exists(p: A => Boolean): Boolean = this match {
case Cons(h, t) => p(h()) || t().exists(p)
case _ => false
}
Note that || is non-strict in its second argument. If p(h()) returns true, then exists terminates the traversal early and returns true as well. Remember also that the tail of the stream is a lazy val. So not only does the traversal terminate early, the tail of the stream is never evaluated at all! So whatever code would have generated the tail is never actually executed.
The exists function here is implemented using explicit recursion. But remember that with List in chapter 3, we could implement a general recursion in the form of foldRight. We can do the same thing for Stream, but lazily:

This looks very similar to the foldRight we wrote for List, but note how our combining function f is non-strict in its second parameter. If f chooses not to evaluate its second parameter, this terminates the traversal early. We can see this by using foldRight to implement exists:[5]
5 This definition of exists, though illustrative, isn’t stack-safe if the stream is large and all elements test false.
def exists(p: A => Boolean): Boolean =
foldRight(false)((a, b) => p(a) || b)
Here b is the unevaluated recursive step that folds the tail of the stream. If p(a) returns true, b will never be evaluated and the computation terminates early.
Since foldRight can terminate the traversal early, we can reuse it to implement exists. We can’t do that with a strict version of foldRight. We’d have to write a specialized recursive exists function to handle early termination. Laziness makes our code more reusable.
Exercise 5.4
![]()
Implement forAll, which checks that all elements in the Stream match a given predicate. Your implementation should terminate the traversal as soon as it encounters a nonmatching value.
def forAll(p: A => Boolean): Boolean
Exercise 5.5
![]()
Use foldRight to implement takeWhile.
Exercise 5.6
![]()
Hard: Implement headOption using foldRight.
Exercise 5.7
![]()
Implement map, filter, append, and flatMap using foldRight. The append method should be non-strict in its argument.
Note that these implementations are incremental—they don’t fully generate their answers. It’s not until some other computation looks at the elements of the resulting Stream that the computation to generate that Stream actually takes place—and then it will do just enough work to generate the requested elements. Because of this incremental nature, we can call these functions one after another without fully instantiating the intermediate results.
Let’s look at a simplified program trace for (a fragment of) the motivating example we started this chapter with, Stream(1,2,3,4).map(_ + 10).filter(_ % 2 == 0). We’ll convert this expression to a List to force evaluation. Take a minute to work through this trace to understand what’s happening. It’s a bit more challenging than the trace we looked at earlier in this chapter. Remember, a trace like this is just the same expression over and over again, evaluated by one more step each time.
Listing 5.3. Program trace for Stream
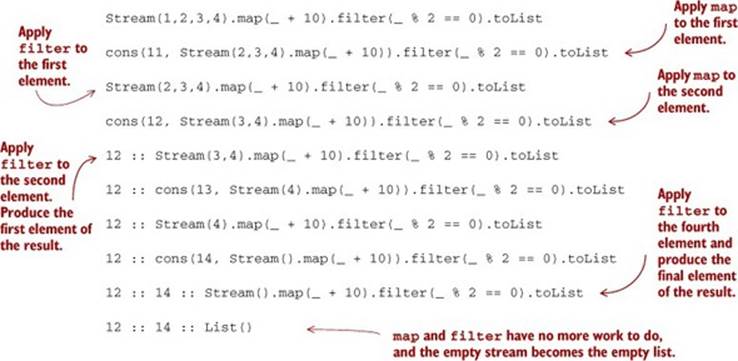
The thing to notice in this trace is how the filter and map transformations are inter-leaved—the computation alternates between generating a single element of the output of map, and testing with filter to see if that element is divisible by 2 (adding it to the output list if it is). Note that we don’t fully instantiate the intermediate stream that results from the map. It’s exactly as if we had interleaved the logic using a special-purpose loop. For this reason, people sometimes describe streams as “first-class loops” whose logic can be combined using higher-order functions like map andfilter.
Since intermediate streams aren’t instantiated, it’s easy to reuse existing combinators in novel ways without having to worry that we’re doing more processing of the stream than necessary. For example, we can reuse filter to define find, a method to return just the first element that matches if it exists. Even though filter transforms the whole stream, that transformation is done lazily, so find terminates as soon as a match is found:
def find(p: A => Boolean): Option[A] =
filter(p).headOption
The incremental nature of stream transformations also has important consequences for memory usage. Because intermediate streams aren’t generated, a transformation of the stream requires only enough working memory to store and transform the current element. For instance, in the transformation Stream(1,2,3,4).map(_ + 10).filter (_ % 2 == 0), the garbage collector can reclaim the space allocated for the values 11 and 13 emitted by map as soon as filter determines they aren’t needed. Of course, this is a simple example; in other situations we might be dealing with larger numbers of elements, and the stream elements themselves could be large objects that retain significant amounts of memory. Being able to reclaim this memory as quickly as possible can cut down on the amount of memory required by your program as a whole.
We’ll have a lot more to say about defining memory-efficient streaming calculations, in particular calculations that require I/O, in part 4 of this book.
5.4. Infinite streams and corecursion
Because they’re incremental, the functions we’ve written also work for infinite streams. Here’s an example of an infinite Stream of 1s:
val ones: Stream[Int] = Stream.cons(1, ones)
Although ones is infinite, the functions we’ve written so far only inspect the portion of the stream needed to generate the demanded output. For example:
scala> ones.take(5).toList
res0: List[Int] = List(1, 1, 1, 1, 1)
scala> ones.exists(_ % 2 != 0)
res1: Boolean = true
Try playing with a few other examples:
· ones.map(_ + 1).exists(_ % 2 == 0)
· ones.takeWhile(_ == 1)
· ones.forAll(_ != 1)
In each case, we get back a result immediately. Be careful though, since it’s easy to write expressions that never terminate or aren’t stack-safe. For example, ones.forAll(_ == 1) will forever need to inspect more of the series since it’ll never encounter an element that allows it to terminate with a definite answer (this will manifest as a stack overflow rather than an infinite loop).[6]
6 It’s possible to define a stack-safe version of forAll using an ordinary recursive loop.
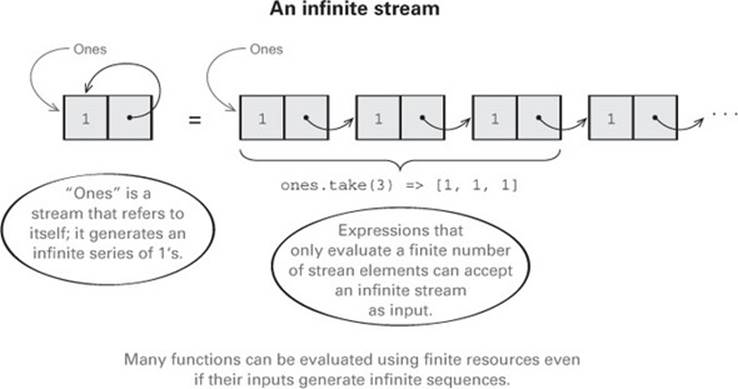
Let’s see what other functions we can discover for generating streams.
Exercise 5.8
![]()
Generalize ones slightly to the function constant, which returns an infinite Stream of a given value.
def constant[A](a: A): Stream[A]
Exercise 5.9
![]()
Write a function that generates an infinite stream of integers, starting from n, then n + 1, n + 2, and so on.[7]
7 In Scala, the Int type is a 32-bit signed integer, so this stream will switch from positive to negative values at some point, and will repeat itself after about four billion elements.
def from(n: Int): Stream[Int]
Exercise 5.10
![]()
Write a function fibs that generates the infinite stream of Fibonacci numbers: 0, 1, 1, 2, 3, 5, 8, and so on.
Exercise 5.11
![]()
Write a more general stream-building function called unfold. It takes an initial state, and a function for producing both the next state and the next value in the generated stream.
def unfold[A, S](z: S)(f: S => Option[(A, S)]): Stream[A]
Option is used to indicate when the Stream should be terminated, if at all. The function unfold is a very general Stream-building function.
The unfold function is an example of what’s sometimes called a corecursive function. Whereas a recursive function consumes data, a corecursive function produces data. And whereas recursive functions terminate by recursing on smaller inputs, corecursive functions need not terminate so long as they remain productive, which just means that we can always evaluate more of the result in a finite amount of time. The unfold function is productive as long as f terminates, since we just need to run the function f one more time to generate the next element of the Stream. Corecursion is also sometimes called guarded recursion, and productivity is also sometimes called cotermination. These terms aren’t that important to our discussion, but you’ll hear them used sometimes in the context of functional programming. If you’re curious to learn where they come from and understand some of the deeper connections, follow the references in the chapter notes.
Exercise 5.12
![]()
Write fibs, from, constant, and ones in terms of unfold.[8]
8 Using unfold to define constant and ones means that we don’t get sharing as in the recursive definition val ones: Stream[Int] = cons(1, ones). The recursive definition consumes constant memory even if we keep a reference to it around while traversing it, while the unfold-based implementation does not. Preserving sharing isn’t something we usually rely on when programming with streams, since it’s extremely delicate and not tracked by the types. For instance, sharing is destroyed when calling even xs.map(x => x).
Exercise 5.13
![]()
Use unfold to implement map, take, takeWhile, zipWith (as in chapter 3), and zipAll. The zipAll function should continue the traversal as long as either stream has more elements—it uses Option to indicate whether each stream has been exhausted.
def zipAll[B](s2: Stream[B]): Stream[(Option[A],Option[B])]
Now that we have some practice writing stream functions, let’s return to the exercise we covered at the end of chapter 3—a function, hasSubsequence, to check whether a list contains a given subsequence. With strict lists and list-processing functions, we were forced to write a rather tricky monolithic loop to implement this function without doing extra work. Using lazy lists, can you see how you could implement hasSubsequence by combining some other functions we’ve already written?[9] Try to think about it on your own before continuing.
9 This small example, of assembling hasSubsequence from simpler functions using laziness, is from Cale Gibbard. See this post: http://lambda-the-ultimate.org/node/1277#comment-14313.
Exercise 5.14
![]()
Hard: Implement startsWith using functions you’ve written. It should check if one Stream is a prefix of another. For instance, Stream(1,2,3) startsWith Stream(1,2) would be true.
def startsWith[A](s: Stream[A]): Boolean
Exercise 5.15
![]()
Implement tails using unfold. For a given Stream, tails returns the Stream of suffixes of the input sequence, starting with the original Stream. For example, given Stream(1,2,3), it would return Stream(Stream(1,2,3), Stream(2,3), Stream(3), Stream()).
def tails: Stream[Stream[A]]
We can now implement hasSubsequence using functions we’ve written:
def hasSubsequence[A](s: Stream[A]): Boolean =
tails exists (_ startsWith s)
This implementation performs the same number of steps as a more monolithic implementation using nested loops with logic for breaking out of each loop early. By using laziness, we can compose this function from simpler components and still retain the efficiency of the more specialized (and verbose) implementation.
Exercise 5.16
![]()
Hard: Generalize tails to the function scanRight, which is like a foldRight that returns a stream of the intermediate results. For example:
scala> Stream(1,2,3).scanRight(0)(_ + _).toList
res0: List[Int] = List(6,5,3,0)
This example should be equivalent to the expression List(1+2+3+0, 2+3+0, 3+0, 0). Your function should reuse intermediate results so that traversing a Stream with n elements always takes time linear in n. Can it be implemented using unfold? How, or why not? Could it be implemented using another function we’ve written?
5.5. Summary
In this chapter, we introduced non-strictness as a fundamental technique for implementing efficient and modular functional programs. Non-strictness can be thought of as a technique for recovering some efficiency when writing functional code, but it’s also a much bigger idea—non-strictness can improve modularity by separating the description of an expression from the how-and-when of its evaluation. Keeping these concerns separate lets us reuse a description in multiple contexts, evaluating different portions of our expression to obtain different results. We weren’t able to do that when description and evaluation were intertwined as they are in strict code. We saw a number of examples of this principle in action over the course of the chapter, and we’ll see many more in the remainder of the book.
We’ll switch gears in the next chapter and talk about purely functional approaches to state. This is the last building block needed before we begin exploring the process of functional design.