Functional Programming in Scala (2015)
Part 1. Introduction to functional programming
Chapter 4. Handling errors without exceptions
We noted briefly in chapter 1 that throwing exceptions is a side effect. If exceptions aren’t used in functional code, what is used instead? In this chapter, we’ll learn the basic principles for raising and handling errors functionally. The big idea is that we can represent failures and exceptions with ordinary values, and we can write higher-order functions that abstract out common patterns of error handling and recovery. The functional solution, of returning errors as values, is safer and retains referential transparency, and through the use of higher-order functions, we can preserve the primary benefit of exceptions—consolidation of error-handling logic. We’ll see how this works over the course of this chapter, after we take a closer look at exceptions and discuss some of their problems.
For the same reason that we created our own List data type in the previous chapter, we’ll re-create in this chapter two Scala standard library types: Option and Either. The purpose is to enhance your understanding of how these types can be used for handling errors. After completing this chapter, you should feel free to use the Scala standard library version of Option and Either (though you’ll notice that the standard library versions of both types are missing some of the useful functions we define in this chapter).
4.1. The good and bad aspects of exceptions
Why do exceptions break referential transparency, and why is that a problem? Let’s look at a simple example. We’ll define a function that throws an exception and call it.
Listing 4.1. Throwing and catching an exception

Calling failingFn from the REPL gives the expected error:
scala> failingFn(12)
java.lang.Exception: fail!
at .failingFn(<console>:8)
...
We can prove that y is not referentially transparent. Recall that any RT expression may be substituted with the value it refers to, and this substitution should preserve program meaning. If we substitute throw new Exception("fail!") for y in x + y, it produces a different result, because the exception will now be raised inside a try block that will catch the exception and return 43:

We can demonstrate this in the REPL:
scala> failingFn2(12)
res1: Int = 43
Another way of understanding RT is that the meaning of RT expressions does not depend on context and may be reasoned about locally, whereas the meaning of non-RT expressions is context-dependent and requires more global reasoning. For instance, the meaning of the RT expression 42 + 5 doesn’t depend on the larger expression it’s embedded in—it’s always and forever equal to 47. But the meaning of the expression throw new Exception("fail") is very context-dependent—as we just demonstrated, it takes on different meanings depending on which try block (if any) it’s nested within.
There are two main problems with exceptions:
· As we just discussed, exceptions break RT and introduce context dependence, moving us away from the simple reasoning of the substitution model and making it possible to write confusing exception-based code. This is the source of the folklore advice that exceptions should be used only for error handling, not for control flow.
· Exceptions are not type-safe. The type of failingFn, Int => Int tells us nothing about the fact that exceptions may occur, and the compiler will certainly not force callers of failingFn to make a decision about how to handle those exceptions. If we forget to check for an exception in failingFn, this won’t be detected until runtime.
Checked exceptions
Java’s checked exceptions at least force a decision about whether to handle or reraise an error, but they result in significant boilerplate for callers. More importantly, they don’t work for higher-order functions, which can’t possibly be aware of the specific exceptions that could be raised by their arguments. For example, consider the map function we defined for List:
def map[A,B](l: List[A])(f: A => B): List[B]
This function is clearly useful, highly generic, and at odds with the use of checked exceptions—we can’t have a version of map for every single checked exception that could possibly be thrown by f. Even if we wanted to do this, how would map even know what exceptions were possible? This is why generic code, even in Java, so often resorts to using RuntimeException or some common checked Exception type.
We’d like an alternative to exceptions without these drawbacks, but we don’t want to lose out on the primary benefit of exceptions: they allow us to consolidate and centralize error-handling logic, rather than being forced to distribute this logic throughout our codebase. The technique we use is based on an old idea: instead of throwing an exception, we return a value indicating that an exceptional condition has occurred. This idea might be familiar to anyone who has used return codes in C to handle exceptions. But instead of using error codes, we introduce a new generic type for these “possibly defined values” and use higher-order functions to encapsulate common patterns of handling and propagating errors. Unlike C-style error codes, the error-handling strategy we use is completely type-safe, and we get full assistance from the type-checker in forcing us to deal with errors, with a minimum of syntactic noise. We’ll see how all of this works shortly.
4.2. Possible alternatives to exceptions
Let’s now consider a realistic situation where we might use an exception and look at different approaches we could use instead. Here’s an implementation of a function that computes the mean of a list, which is undefined if the list is empty:

The mean function is an example of what’s called a partial function: it’s not defined for some inputs. A function is typically partial because it makes some assumptions about its inputs that aren’t implied by the input types.[1] You may be used to throwing exceptions in this case, but we have a few other options. Let’s look at these for our mean example.
1 A function may also be partial if it doesn’t terminate for some inputs. We won’t discuss this form of partiality here, since it’s not a recoverable error so there’s no question of how best to handle it. See the chapter notes for more about partiality.
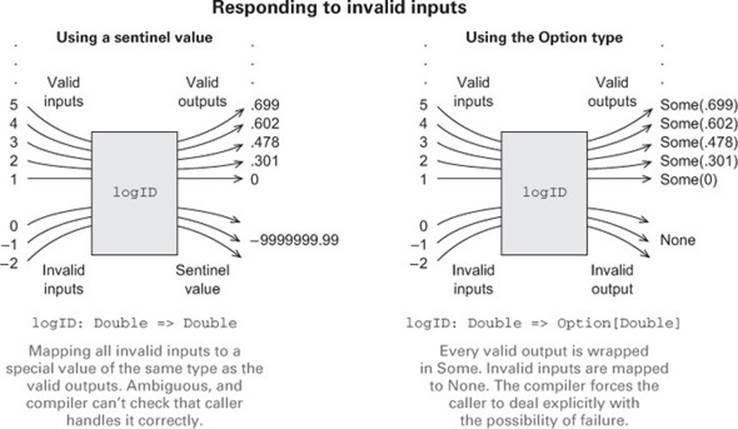
The first possibility is to return some sort of bogus value of type Double. We could simply return xs.sum / xs.length in all cases, and have it result in 0.0/0.0 when the input is empty, which is Double.NaN; or we could return some other sentinel value. In other situations, we might return null instead of a value of the needed type. This general class of approaches is how error handling is often done in languages without exceptions, and we reject this solution for a few reasons:
· It allows errors to silently propagate—the caller can forget to check this condition and won’t be alerted by the compiler, which might result in subsequent code not working properly. Often the error won’t be detected until much later in the code.
· Besides being error-prone, it results in a fair amount of boilerplate code at call sites, with explicit if statements to check whether the caller has received a “real” result. This boilerplate is magnified if you happen to be calling several functions, each of which uses error codes that must be checked and aggregated in some way.
· It’s not applicable to polymorphic code. For some output types, we might not even have a sentinel value of that type even if we wanted to! Consider a function like max, which finds the maximum value in a sequence according to a custom comparison function: def max[A](xs: Seq[A])(greater: (A,A) => Boolean): A. If the input is empty, we can’t invent a value of type A. Nor can null be used here, since null is only valid for non-primitive types, and A may in fact be a primitive like Double or Int.
· It demands a special policy or calling convention of callers—proper use of the mean function would require that callers do something other than call mean and make use of the result. Giving functions special policies like this makes it difficult to pass them to higher-order functions, which must treat all arguments uniformly.
The second possibility is to force the caller to supply an argument that tells us what to do in case we don’t know how to handle the input:
def mean_1(xs: IndexedSeq[Double], onEmpty: Double): Double =
if (xs.isEmpty) onEmpty
else xs.sum / xs.length
This makes mean into a total function, but it has drawbacks—it requires that immediate callers have direct knowledge of how to handle the undefined case and limits them to returning a Double. What if mean is called as part of a larger computation and we’d like to abort that computation ifmean is undefined? Or perhaps we’d like to take some completely different branch in the larger computation in this case? Simply passing an onEmpty parameter doesn’t give us this freedom.
We need a way to defer the decision of how to handle undefined cases so that they can be dealt with at the most appropriate level.
4.3. The Option data type
The solution is to represent explicitly in the return type that a function may not always have an answer. We can think of this as deferring to the caller for the error-handling strategy. We introduce a new type, Option. As we mentioned earlier, this type also exists in the Scala standard library, but we’re re-creating it here for pedagogical purposes:
sealed trait Option[+A]
case class Some[+A](get: A) extends Option[A]
case object None extends Option[Nothing]
Option has two cases: it can be defined, in which case it will be a Some, or it can be undefined, in which case it will be None.
We can use Option for our definition of mean like so:
def mean(xs: Seq[Double]): Option[Double] =
if (xs.isEmpty) None
else Some(xs.sum / xs.length)
The return type now reflects the possibility that the result may not always be defined. We still always return a result of the declared type (now Option[Double]) from our function, so mean is now a total function. It takes each value of the input type to exactly one value of the output type.
4.3.1. Usage patterns for Option
Partial functions abound in programming, and Option (and the Either data type that we’ll discuss shortly) is typically how this partiality is dealt with in FP. You’ll see Option used throughout the Scala standard library, for instance:
· Map lookup for a given key (http://mng.bz/ha64) returns Option.
· headOption and lastOption defined for lists and other iterables (http://mng.bz/Pz86) return an Option containing the first or last elements of a sequence if it’s nonempty.
These aren’t the only examples—we’ll see Option come up in many different situations. What makes Option convenient is that we can factor out common patterns of error handling via higher-order functions, freeing us from writing the usual boilerplate that comes with exception-handling code. In this section, we’ll cover some of the basic functions for working with Option. Our goal is not for you to attain fluency with all these functions, but just to get you familiar enough that you can revisit this chapter and make progress on your own when you have to write some functional code to deal with errors.
Basic Functions on Option
Option can be thought of like a List that can contain at most one element, and many of the List functions we saw earlier have analogous functions on Option. Let’s look at some of these functions.
We’ll do something slightly different than in chapter 3 where we put all our List functions in the List companion object. Here we’ll place our functions, when possible, inside the body of the Option trait, so they can be called with the syntax obj.fn(arg1) or obj fn arg1 instead offn(obj, arg1). This is a stylistic choice with no real significance, and we’ll use both styles throughout this book.[2]
2 In general, we’ll use this object-oriented style of syntax where possible for functions that have a single, clear operand (like List.map), and the standalone function style otherwise.
This choice raises one additional complication with regard to variance that we’ll discuss in a moment. Let’s take a look.
Listing 4.2. The Option data type

There is some new syntax here. The default: => B type annotation in getOrElse (and the similar annotation in orElse) indicates that the argument is of type B, but won’t be evaluated until it’s needed by the function. Don’t worry about this for now—we’ll talk much more about this concept of non-strictness in the next chapter. Also, the B >: A type parameter on the getOrElse and orElse functions indicates that B must be equal to or a supertype of A. It’s needed to convince Scala that it’s still safe to declare Option[+A] as covariant in A. See the chapter notes for more detail—it’s unfortunately somewhat complicated, but a necessary complication in Scala. Fortunately, fully understanding subtyping and variance isn’t essential for our purposes here.
Exercise 4.1
![]()
Implement all of the preceding functions on Option. As you implement each function, try to think about what it means and in what situations you’d use it. We’ll explore when to use each of these functions next. Here are a few hints for solving this exercise:
· It’s fine to use pattern matching, though you should be able to implement all the functions besides map and getOrElse without resorting to pattern matching.
· For map and flatMap, the type signature should be enough to determine the implementation.
· getOrElse returns the result inside the Some case of the Option, or if the Option is None, returns the given default value.
· orElse returns the first Option if it’s defined; otherwise, it returns the second Option.
Usage Scenarios for the Basic Option Functions
Although we can explicitly pattern match on an Option, we’ll almost always use the above higher-order functions. Here, we’ll try to give some guidance for when to use each one. Fluency with these functions will come with practice, but the objective here is to get some basic familiarity. Next time you try writing some functional code that uses Option, see if you can recognize the patterns these functions encapsulate before you resort to pattern matching.
Let’s start with map. The map function can be used to transform the result inside an Option, if it exists. We can think of it as proceeding with a computation on the assumption that an error hasn’t occurred; it’s also a way of deferring the error handling to later code:
case class Employee(name: String, department: String)
def lookupByName(name: String): Option[Employee] = ...
val joeDepartment: Option[String] =lookupByName("Joe").map(_.department)
Here, lookupByName("Joe") returns an Option[Employee], which we transform using map to pull out the Option[String] representing the department. Note that we don’t need to explicitly check the result of lookupByName("Joe"); we simply continue the computation as if no error occurred, inside the argument to map. If employeesByName.get("Joe") returns None, this will abort the rest of the computation and map will not call the _.department function at all.

flatMap is similar, except that the function we provide to transform the result can itself fail.
Exercise 4.2
![]()
Implement the variance function in terms of flatMap. If the mean of a sequence is m, the variance is the mean of math.pow(x - m, 2) for each element x in the sequence. See the definition of variance on Wikipedia (http://mng.bz/0Qsr).
def variance(xs: Seq[Double]): Option[Double]
As the implementation of variance demonstrates, with flatMap we can construct a computation with multiple stages, any of which may fail, and the computation will abort as soon as the first failure is encountered, since None.flatMap(f) will immediately return None, without runningf.
We can use filter to convert successes into failures if the successful values don’t match the given predicate. A common pattern is to transform an Option via calls to map, flatMap, and/or filter, and then use getOrElse to do error handling at the end:
val dept: String =lookupByName("Joe").map(_.dept).filter(_ != "Accounting").getOrElse("Default Dept")
getOrElse is used here to convert from an Option[String] to a String, by providing a default department in case the key "Joe" didn’t exist in the Map or if Joe’s department was "Accounting".
orElse is similar to getOrElse, except that we return another Option if the first is undefined. This is often useful when we need to chain together possibly failing computations, trying the second if the first hasn’t succeeded.
A common idiom is to do o.getOrElse(throw new Exception("FAIL")) to convert the None case of an Option back to an exception. The general rule of thumb is that we use exceptions only if no reasonable program would ever catch the exception; if for some callers the exception might be a recoverable error, we use Option (or Either, discussed later) to give them flexibility.
As you can see, returning errors as ordinary values can be convenient and the use of higher-order functions lets us achieve the same sort of consolidation of error-handling logic we would get from using exceptions. Note that we don’t have to check for None at each stage of the computation—we can apply several transformations and then check for and handle None when we’re ready. But we also get additional safety, since Option[A] is a different type than A, and the compiler won’t let us forget to explicitly defer or handle the possibility of None.
4.3.2. Option composition, lifting, and wrapping exception-oriented APIs
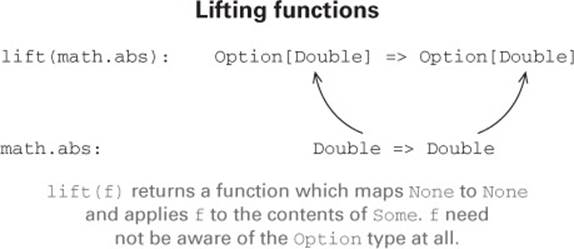
It may be easy to jump to the conclusion that once we start using Option, it infects our entire code base. One can imagine how any callers of methods that take or return Option will have to be modified to handle either Some or None. But this doesn’t happen, and the reason is that we can liftordinary functions to become functions that operate on Option.
For example, the map function lets us operate on values of type Option[A] using a function of type A => B, returning Option[B]. Another way of looking at this is that map turns a function f of type A => B into a function of type Option[A] => Option[B]. Let’s make this explicit:
def lift[A,B](f: A => B): Option[A] => Option[B] = _ map f
This tells us that any function that we already have lying around can be transformed (via lift) to operate within the context of a single Option value. Let’s look at an example:
val absO: Option[Double] => Option[Double] = lift(math.abs)
The math object contains various standalone mathematical functions including abs, sqrt, exp, and so on. We didn’t need to rewrite the math.abs function to work with optional values; we just lifted it into the Option context after the fact. We can do this for any function. Let’s look at another example. Suppose we’re implementing the logic for a car insurance company’s website, which contains a page where users can submit a form to request an instant online quote. We’d like to parse the information from this form and ultimately call our rate function:
/**
* Top secret formula for computing an annual car
* insurance premium from two key factors.
*/
def insuranceRateQuote(age: Int, numberOfSpeedingTickets: Int): Double
We want to be able to call this function, but if the user is submitting their age and number of speeding tickets in a web form, these fields will arrive as simple strings that we have to (try to) parse into integers. This parsing may fail; given a string, s, we can attempt to parse it into an Int usings.toInt, which throws a NumberFormat-Exception if the string isn’t a valid integer:
scala> "112".toInt
res0: Int = 112
scala> "hello".toInt
java.lang.NumberFormatException: For input string: "hello"
at java.lang.NumberFormatException.forInputString(...)
...
Let’s convert the exception-based API of toInt to Option and see if we can implement a function parseInsuranceRateQuote, which takes the age and number of speeding tickets as strings, and attempts calling the insuranceRateQuote function if parsing both values is successful.
Listing 4.3. Using Option
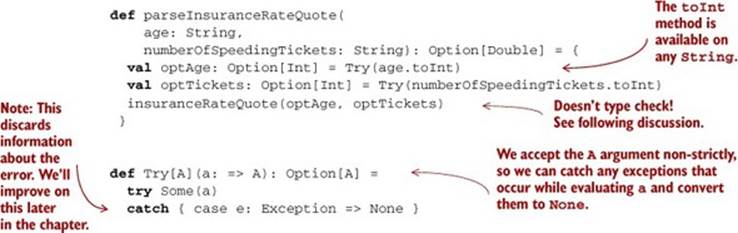
The Try function is a general-purpose function we can use to convert from an exception-based API to an Option-oriented API. This uses a non-strict or lazy argument, as indicated by the => A as the type of a. We’ll discuss laziness much more in the next chapter.
But there’s a problem—after we parse optAge and optTickets into Option[Int], how do we call insuranceRateQuote, which currently takes two Int values? Do we have to rewrite insuranceRateQuote to take Option[Int] values instead? No, and changinginsuranceRateQuote would be entangling concerns, forcing it to be aware that a prior computation may have failed, not to mention that we may not have the ability to modify insuranceRateQuote—perhaps it’s defined in a separate module that we don’t have access to. Instead, we’d like to lift insuranceRateQuote to operate in the context of two optional values. We could do this using explicit pattern matching in the body of parseInsuranceRateQuote, but that’s going to be tedious.
Exercise 4.3
![]()
Write a generic function map2 that combines two Option values using a binary function. If either Option value is None, then the return value is too. Here is its signature:
def map2[A,B,C](a: Option[A], b: Option[B])(f: (A, B) => C): Option[C]
With map2, we can now implement parseInsuranceRateQuote:

The map2 function means that we never need to modify any existing functions of two arguments to make them “Option-aware.” We can lift them to operate in the context of Option after the fact. Can you already see how you might define map3, map4, and map5? Let’s look at a few other similar cases.
Exercise 4.4
![]()
Write a function sequence that combines a list of Options into one Option containing a list of all the Some values in the original list. If the original list contains None even once, the result of the function should be None; otherwise the result should be Some with a list of all the values. Here is its signature:[3]
3 This is a clear instance where it’s not appropriate to define the function in the OO style. This shouldn’t be a method on List (which shouldn’t need to know anything about Option), and it can’t be a method on Option, so it goes in the Option companion object.
def sequence[A](a: List[Option[A]]): Option[List[A]]
Sometimes we’ll want to map over a list using a function that might fail, returning None if applying it to any element of the list returns None. For example, what if we have a whole list of String values that we wish to parse to Option[Int]? In that case, we can simply sequence the results of the map:
def parseInts(a: List[String]): Option[List[Int]] =
sequence(a map (i => Try(i.toInt)))
Unfortunately, this is inefficient, since it traverses the list twice, first to convert each String to an Option[Int], and a second pass to combine these Option[Int] values into an Option[List[Int]]. Wanting to sequence the results of a map this way is a common enough occurrence to warrant a new generic function, traverse, with the following signature:
def traverse[A, B](a: List[A])(f: A => Option[B]): Option[List[B]]
Exercise 4.5
![]()
Implement this function. It’s straightforward to do using map and sequence, but try for a more efficient implementation that only looks at the list once. In fact, implement sequence in terms of traverse.
For-comprehensions
Since lifting functions is so common in Scala, Scala provides a syntactic construct called the for-comprehension that it expands automatically to a series of flatMap and map calls. Let’s look at how map2 could be implemented with for-comprehensions.
Here’s our original version:
def map2[A,B,C](a: Option[A], b: Option[B])(f: (A, B) => C):
Option[C] =
a flatMap (aa =>
b map (bb =>
f(aa, bb)))
And here’s the exact same code written as a for-comprehension:
def map2[A,B,C](a: Option[A], b: Option[B])(f: (A, B) => C):
Option[C] =
for {
aa <- a
bb <- b
} yield f(aa, bb)
A for-comprehension consists of a sequence of bindings, like aa <- a, followed by a yield after the closing brace, where the yield may make use of any of the values on the left side of any previous <- binding. The compiler desugars the bindings to flatMap calls, with the final binding and yield being converted to a call to map.
You should feel free to use for-comprehensions in place of explicit calls to flatMap and map.
Between map, lift, sequence, traverse, map2, map3, and so on, you should never have to modify any existing functions to work with optional values.
4.4. The Either data type
The big idea in this chapter is that we can represent failures and exceptions with ordinary values, and write functions that abstract out common patterns of error handling and recovery. Option isn’t the only data type we could use for this purpose, and although it gets used frequently, it’s rather simplistic. One thing you may have noticed with Option is that it doesn’t tell us anything about what went wrong in the case of an exceptional condition. All it can do is give us None, indicating that there’s no value to be had. But sometimes we want to know more. For example, we might want a String that gives more information, or if an exception was raised, we might want to know what that error actually was.
We can craft a data type that encodes whatever information we want about failures. Sometimes just knowing whether a failure occurred is sufficient, in which case we can use Option; other times we want more information. In this section, we’ll walk through a simple extension to Option, the Either data type, which lets us track a reason for the failure. Let’s look at its definition:
sealed trait Either[+E, +A]
case class Left[+E](value: E) extends Either[E, Nothing]
case class Right[+A](value: A) extends Either[Nothing, A]
Either has only two cases, just like Option. The essential difference is that both cases carry a value. The Either data type represents, in a very general way, values that can be one of two things. We can say that it’s a disjoint union of two types. When we use it to indicate success or failure, by convention the Right constructor is reserved for the success case (a pun on “right,” meaning correct), and Left is used for failure. We’ve given the left type parameter the suggestive name E (for error).[4]
4 Either is also often used more generally to encode one of two possibilities in cases where it isn’t worth defining a fresh data type. We’ll see some examples of this throughout the book.
Option and Either in the standard library
As we mentioned earlier in this chapter, both Option and Either exist in the Scala standard library (Option API is at http://mng.bz/fiJ5; Either API is at http://mng.bz/106L), and most of the functions we’ve defined here in this chapter exist for the standard library versions.
You’re encouraged to read through the API for Option and Either to understand the differences. There are a few missing functions, though, notably sequence, traverse, and map2. And Either doesn’t define a right-biased flatMap directly like we do here. The standard libraryEither is slightly (but only slightly) more complicated. Read the API for details.
Let’s look at the mean example again, this time returning a String in case of failure:
def mean(xs: IndexedSeq[Double]): Either[String, Double] =
if (xs.isEmpty)
Left("mean of empty list!")
else
Right(xs.sum / xs.length)
Sometimes we might want to include more information about the error, for example a stack trace showing the location of the error in the source code. In such cases we can simply return the exception in the Left side of an Either:
def safeDiv(x: Int, y: Int): Either[Exception, Int] =
try Right(x / y)
catch { case e: Exception => Left(e) }
As we did with Option, we can write a function, Try, which factors out this common pattern of converting thrown exceptions to values:
def Try[A](a: => A): Either[Exception, A] =
try Right(a)
catch { case e: Exception => Left(e) }
Exercise 4.6
![]()
Implement versions of map, flatMap, orElse, and map2 on Either that operate on the Right value.

Note that with these definitions, Either can now be used in for-comprehensions. For instance:
def parseInsuranceRateQuote(
age: String,
numberOfSpeedingTickets: String): Either[Exception,Double] =
for {
a <- Try { age.toInt }
tickets <- Try { numberOfSpeedingTickes.toInt }
} yield insuranceRateQuote(a, tickets)
Now we get information about the actual exception that occurred, rather than just getting back None in the event of a failure.
Exercise 4.7
![]()
Implement sequence and traverse for Either. These should return the first error that’s encountered, if there is one.
def sequence[E, A](es: List[Either[E, A]]): Either[E, List[A]]
def traverse[E, A, B](as: List[A])(
f: A => Either[E, B]): Either[E, List[B]]
As a final example, here’s an application of map2, where the function mkPerson validates both the given name and the given age before constructing a valid Person.
Listing 4.4. Using Either to validate data
case class Person(name: Name, age: Age)
sealed class Name(val value: String)
sealed class Age(val value: Int)
def mkName(name: String): Either[String, Name] =
if (name == "" || name == null) Left("Name is empty.")
else Right(new Name(name))
def mkAge(age: Int): Either[String, Age] =
if (age < 0) Left("Age is out of range.")
else Right(new Age(age))
def mkPerson(name: String, age: Int): Either[String, Person] =
mkName(name).map2(mkAge(age))(Person(_, _))
Exercise 4.8
![]()
In this implementation, map2 is only able to report one error, even if both the name and the age are invalid. What would you need to change in order to report both errors? Would you change map2 or the signature of mkPerson? Or could you create a new data type that captures this requirement better than Either does, with some additional structure? How would orElse, traverse, and sequence behave differently for that data type?
4.5. Summary
In this chapter, we noted some of the problems with using exceptions and introduced the basic principles of purely functional error handling. Although we focused on the algebraic data types Option and Either, the bigger idea is that we can represent exceptions as ordinary values and use higher-order functions to encapsulate common patterns of handling and propagating errors. This general idea, of representing effects as values, is something we’ll see again and again throughout this book in various guises.
We don’t expect you to be fluent with all the higher-order functions we wrote in this chapter, but you should now have enough familiarity to get started writing your own functional code complete with error handling. With these new tools in hand, exceptions should be reserved only for truly unrecoverable conditions.
Lastly, in this chapter we touched briefly on the notion of a non-strict function (recall the functions orElse, getOrElse, and Try). In the next chapter, we’ll look more closely at why non-strictness is important and how it can buy us greater modularity and efficiency in our functional programs.